Forensic discrimination between traditional and compressive imaging by blurring kernel investigation

Abstract

Image forensics encompasses a set of scientific tests to investigation of a suspected event via intrinsic clues of imaging pipeline. Traditional image sensing at the Nyquist-Shannon rate as well as the new modality of compressive imaging below the rate are two main types of sensing in photography and imaging applications. Hence, for forensic investigators, it would importantly necessitate the ability to discriminate among images captured by them. However, due to the complex nonlinear nature of imaging processes, investigating imagers’ traces is a difficult task. To this intent, we first systematically model the imaging pipelines as an encoder-decoder pair. For exploring distinguishable traces, we mathematically simplify and linearize the pair for compressive imaging and two main forms of traditional image sensing with or without compression. Our theoretical analyses on the approximate linear models reveal blurring kernels of different imagers have discriminability. To validate it in real-world scenarios, we considered the whole imaging process as an inverse problem and estimated the blurring kernel based on a deconvolution approach, where the discriminability is also justified by information visualization. Then, we designed a pipeline classification system, where a deep convolutional neural network is trained by the estimated blurring kernels to be able to classify the three imaging systems. Our results in compressive imaging identification show an accuracy improvement about 3.7 % in comparison to the best result among compared methods. Implementation codes are available for research and development.

1 Introduction

Image forensics encompasses a set of scientific tests to investigation of a suspected event/crime via left image clues. The science enables governments, the police, and courts to discover the origin of events/crimes [18, 29, 39, 49]. To do the task, forensic experts require to know imaging pipelines which lead to the acquisition of digital images, from scene sensing to storage/transmission. This realizes by understanding of sorts of imaging and their differences. Two general types of image sensing exist: (1) traditional image acquisition, and (2) Compressive Sensing (CS)-based imaging. Conventional imagers such as surveillance cameras and those on portable devices first acquire an image at the Nyquist-Shannon rate, and then, if required for storage or transmission purposes, discard redundant data by compression like the widely used JPEG-family compression. However, the technology of Compressive Sensing (CS) which operats below the Nyquist-Shannon rate, has recently led a new generation of image acquisition modality, called compressive imaging [43]. This, as a type of computational imaging, provides advantages in comparison to conventional devices such as considerable reduction in hardware components, power consumption optimization, and fast image acquisition time. In a compressive imaging device, the sampling and compression processes are done simultaneously in one step [50]. In other words, the compression can be directly performed during sensing. Random sampling-based imagers such as single-pixel camera [16], imaging beyond the visible spectrum like hyperspectral and infrared cameras [10], dynamic [21] and intelligent CS-based sensing systems [50], radar imaging [2], wireless CS networks [56], constrained medical imaging systems such as CS-equipped magnetic resonance imaging [57] and lens-less imagers [46, 54], and scientific imaging devices [41] are paradigms of imaging based on the CS technology.

1.1 Literature review

In the conventional imaging, forensic analyses developed in the literature are categorized into two general categories, including: 1) approaches that classify the source of a questionable image by assigning the image to a device make and model [33, 55], and 2) methods that detect or localize forged regions in digital images [3, 4, 51]. In both categories, discovering intrinsic signatures left from recorded images plays a key role for forensic investigators. The forensic footprints themselves can be extracted by three general techniques [53]. We call them as: (a) feature engineering-based methods, in which forensic examiners extract handcrafted features for classification [3, 52]; (b) deep learning-based methods which try to extract forensic features directly from data in an automatic manner [4, 6]; and, (c) forensics-informed methods which represent hybridized variants of methods of (a) and (b). This paper falls into the category of forensics-informed methods, where we combine forensic clues with deep learning for incorporating the knowledge of forensic examiner in machine learning processes.

Although the above-mentioned valuable studies have been carried out in the context of traditional image forensics, a lack of theoretical and applied researches is seen for a deep understanding of parts and functions of the compressive imaging systems from the forensic perspective. This issue causes another important problem about the forensic cognition of differences between the kinds of imaging. For example, consider the case in which the task of a forensic examiner is identifying whether the source of a query image is from a traditional or a compressive imaging manner. Solving this problem necessitates extracting signatures that can discriminate well among the diverse systems.

Let us state that an image with an uncompressed file format such as Bitmap (BMP) be under an investigation. The image may come from a CS imaging or not. If the digital photo has been acquired from a conventional imager, it may have been already compressed via a source coder such as the well-known JPEG2000 (JP2) compression standard or acquired in an uncompressed file format, i.e., raw imaging. Hence, in the considered scenario, three main types of imaging systems are introduced to be identified, including compressive imaging, conventional sensing plus compression, and conventional raw imaging. It is notable that both JP2 and most of compressive sensing algorithms employ Discrete Wavelet Transform (DWT) [45, 47]. This points out the fact that the confusion between these types of imaging systems is more probable. Therefore, the main complexity is on JPEG2000 standard among other image compression techniques. In [11, 12], Chu et al. found empirical probability mass functions of wavelet coefficients for different imaging systems follow Laplace-like distributions with different parameters of location and diversity. Based on the observation, they employed a 2-step thresholding-based decision making process to separate traditional sensing from compressive one. Its first step contains a distribution detector based on maximum likelihood estimator to discriminate uncompressed images from JP2 and compressively sensed images. The second distribution-based detector gains Expectation Maximization (EM) algorithm to classify the remainder, namely traditionally sensed JP2 images from compressively sensed ones.

Table 1 Simplified encoder-decoder models of compressive and conventional imagers

1.2 Our approach and contributions

Due to the complex and nonlinear nature of imaging processes, investigating imagers’ traces is a difficult task. To address this issue, we first systematically model an imaging pipeline as an encoder-decoder pair to bring more insight into analytical investigations. To be able to explore distinguishable traces, we mathematically simplify and linearize the compressive imaging as well as the two main forms of traditional image sensing. Our theoretical analyses on the approximate linear models revealed imaging blurring kernels make discriminability, where we followed them for further analysis. Here, the discriminability means the degree to which an intelligent machine can separate an imaging source from another. To validate the discriminability of the proposed footprints in real-world nonlinear scenarios, we considered the whole imaging process as an inverse problem and estimated the blurring kernel numerically based on a deconvolution approach [30], where the discriminability is also justified by information visualization. Then, we schematized a deep learning based pipeline to automatically classify blurring kernels from diverse imaging sources. To this end, we trained a Convolutional Neural Network (CNN) by the estimated blurring kernels from an image set including images of the three imaging systems and evaluated the effectiveness of blurring kernel signatures. Main advantages of the proposed method over the approaches in categories of (a) and (b) are higher performance, due to incorporating the knowledge of forensic analyzer, and simpler deep-network architecture, because of learning from blurring kernel images which are very small in size and sparse in comparison to the images (See Table 1.). The novelties of this paper are:

• modeling compressive and conventional imagers and approximating them by linear models for simplifying forensic investigations,

• revealing blurring kernel clues left by different imaging systems as discriminative features and proving their dicsriminability both theoretically and statistically,

• proposing a deep learning framework for the application of imaging source identification based on the engineered blurring kernel features.

The rest of this paper is organized as follows. In Section 2, we derive three general models for the imaging systems. Section 3 proposes a CNN classifier for identifying the source of imaging based on learning from blurring kernels. Section 4 designs a series of experiments to show the effectiveness of the proposed approach in different situations. Finally, we conclude the paper in Section 5.

2 Modeling and linearization

2.1 Encoder-decoder modeling of compressive imaging

Different setups may be considered for designing application-specific compressive imagers, which share similar behaviors [16, 50]. For instance, in single-pixel camera [16], the scene image $\textbf{X} \in \mathbb {R}^{h\times w}$ is first concentrated by a primary lens on a light modulator such as Digital Micro-mirror Device (DMD) consisting of a configurable array of mirrors, LCD, and coded modulation. The dimensions h and w represent the height and the width of the image $\textbf{X}$, respectively. For each measurement cycle from a total of m measurements, a fraction of the analogy image projected onto DMD is selected by a predefined random pattern, modeled as the column vector $\textbf{a}_i\in \mathbb {R}^{n}$, in which $n=h\times w$. Then, the randomly sampled image is collected on a single photo-diode sensor by another secondary lens. The sensor signal corresponding to the modulated light is converted to a single discrete measurement $y_i \in \mathbb {R}, \forall i=1, 2, \cdots , m$. The cycle is repeated m times, which result in the measurement vector $\textbf{y}\triangleq \textbf{Ax}+\textbf{n}$, where $\textbf{y}\in \mathbb {R}^m$, $\textbf{A}\in \mathbb {R}^{m\times n}$ represents a wide sensing matrix arranged by $\textbf{A}=[\mathbf {{a}}_1^{\text{ T }}, \mathbf {{a}}_2^{\text{ T }}, \cdots , \mathbf {{a}}_m^{\text{ T }}]^{\text {T}}$, and $\textbf{n}\in \mathbb {R}^m$ models the additive noise of measurements. There is usually $m\ll n$. The sampling rate or compressive ratio is defined as:

$$\begin{aligned} R_s \triangleq \frac{m}{n}. \end{aligned}$$

(1)

The vector $\textbf{x}$ represents a vectorized version of the input compressible image $\textbf{X}$. The sensing matrix may be defined as $\textbf{A}\triangleq \textbf{MF}$, in which the matrices $\textbf{F}$ and $\textbf{M}$ denote the sparsifying transform and sampler, respectively. Therefore, rewriting the measurement vector $\textbf{y}$ in terms of the sparse-signal vector $\textbf{s}$ yields:

$$\begin{aligned} \textbf{y}= \underbrace{\textbf{A}}_{\mathbf {\triangleq MF}}\textbf{x}+\textbf{n}=\textbf{M}\underbrace{\textbf{Fx}}_{\triangleq \textbf{s}}+\textbf{n}=\textbf{Ms}+\textbf{n}. \end{aligned}$$

(2)

In practice, the light modulator requires calibration one or more times during the image acquisition process. A decoder algorithm gets both the measurement vector $\textbf{y}$ and the sensing matrix $\textbf{A}$, and then reconstructs the image scene. Single-pixel camera recovers the sparse signal $\widehat{\textbf{s}}$ using the ${\ell _1}$-norm convex minimization algorithm, also called Basis Pursuit (BP) in the literature [15]. This optimizer estimates $\widehat{\textbf{s}}$ in a search space as:

$$\begin{aligned} \begin{array}{ccc} \widehat{\textbf{s}}={\mathop {\min }_{\varvec{\text {s}}} {\left\| \varvec{\text {s}}\right\| }_{{\ell }_1}\ }&\text {s.t.}&{\left\| \varvec{\text {y}}-\varvec{\text {Ms}}\right\| }^2_{{\ell }_2}\le \epsilon , \end{array} \end{aligned}$$

(3)

where ${\left\| \varvec{\text {n}}\right\| }^2_{{\ell }_2}={\left\| \varvec{\text {y}}-\varvec{\text {Ms}}\right\| }^2_{{\ell }_2}$ denotes the energy of measurements noise. It is set to be less than or equal to the small value $\epsilon$ in sparse recovery algorithms. The symbol ${\parallel \cdot \parallel }_{\ell _p}$ represents the ${\ell _p}$-norm. Finally, the original vectorized signal is recovered by:

$$\begin{aligned} \widehat{\textbf{x}}=\textbf{F}^{-1}\widehat{\textbf{s}}. \end{aligned}$$

(4)

Generally, the process of imaging and representation of a digital image in the CS technique can be modeled by two basic blocks, including: the encoder $\mathcal {G}$ and the decoder $\mathcal {G}^{-1}$. Figure 1 shows the processes of encoding and decoding in a compressive imaging system. The encoding process is usually performed inside a compressive imager. The decoding process may be accomplished by using computers or servers with powerful hardware resources. The need to powerful hardware is due to the computational complexity of nonlinear decoding algorithms. Because compressive sensing performs a many-to-one transform in the encoding phase, the decoder is not exactly the inverse system of the encoder, i.e., the function $\mathcal {G}$ is not invertible and $\mathcal {G}^{-1}\{\mathcal {G}(\textbf{X})\}\ne \textbf{X}$. Therefore, we define $\widehat{\textbf{X}}\triangleq \mathcal {G}^{-1}\{\mathcal {G}(\textbf{X})\}$ and probe the information loss as intrinsic artifacts for compressive imaging forensics.

Fig. 1

Modeling a compressive imaging system by an encoder-decoder pair for imaging a 2-D scene, which includes the linear and nonlinear mathematical operators

In the encoding phase shown in Fig. 1, the operators $\mathcal {R}$, $\mathcal {A}$, $\mathcal {Q}$, and $\mathcal {C}$ represent the parallel raster scanner, sensing operator, quantizer, and coder, respectively. In the decoding phase, the blocks $\mathcal {R}^{-1}$, $\mathcal {F}^{-1}$, $\mathcal {M}^{-1}$, $\mathcal {Q}^{-1}$, and $\mathcal {C}^{-1}$ denote the inverse parallel raster scanner, inverse of the sparsifying transform ($\mathcal {F}$), reconstructor, dequantizer, and decoder, respectively. The task of the block $\mathcal {R}$ is to scan parallel-wise in the vertical direction of signal samples. This block converts a matrix to a vector, i.e., $\textbf{x}=\mathcal {R}\{\textbf{X}\}$, and its inverse system, $\mathcal {R}^{-1}$, is exactly available, i.e., $\widehat{\textbf{X}}=\mathcal {R}^{-1}\{\widehat{\textbf{x}}\}$. This also forensically means the scan operation is loss-less and does not has any traces. The operator $\mathcal {F}$ maps the signal onto a transform domain in which the signal is sparse. For instance, the transformations of Fourier, discrete cosine transform, wavelet, and Haar have such a property. The inverse of these transformations are exactly at hand without information loss. The sampling operator $\mathcal {A}$ can be modeled by the matrix $\textbf{A}$. To do this, two general CS approaches exist. One is using random Gaussian matrices, where each measurement may be consisted of a weighted linear combination of all signal samples [14]. Another is random sampling techniques [8], in which each measurement consists of a combination of some random samples of the signal. The latter mechanism, also used in single-pixel camera, exhibits simpler structure and yet higher performance in comparison to random Gaussian matrices for a wide range of applications [1, 17, 50, 58]. In the block $\mathcal {A}$, the information loss exists due to the many-to-one conversion. This means the operator $\mathcal {M}^{-1}$ recovers the signal by an approximate nonlinear method. The reconstruction of the signal is performed by convex optimization or iterative procedures [50], such as the algorithms of BP [15], IBA [59], IMAT [36], IMATI [58], ISTA [24], IHT [5], ADMM [7], BCS [27], and ISP [44]. The quantizer $\mathcal {Q}$ is a lossy system and leaves quantization errors in practice. The coder $\mathcal {C}$ is generally a loss-less operation such as Huffman or arithmetic codes and the related inverse system is completely available. Here, we assume the communication channel or storage space is ideal, i.e., error-, noise-, and distortion-less. The recovered image from a scene in compressive imaging can be formulated as:

$$\begin{aligned} \widehat{\varvec{\text {X}}}= \mathcal {R}^{-1}\left\{ {\mathcal {F}}^{-1}\left[ {\mathcal {M}}^{-1}\left( {\mathcal {Q}}^{-1}\left( {\mathcal {C}}^{-1}\left( \mathcal {C}\left( \mathcal {Q}\left( \mathcal {A}\left( \mathcal {R}\left( \varvec{\text {X}}\right) \right) \right) \right) \right) \right) \right) \right] \right\} . \end{aligned}$$

(5)

The above equation describes both the graphically shown steps of scene encoding and decoding in Fig. 1.

2.2 Simplification of compressive and conventional imagers

2.2.1 Linearized model of compressive imaging

As seen in (5), the model of a compressive imaging system is complex and nonlinear. This hardens its forensic investigations. For simplicity, we concentrate our focus on the measurement block $\mathcal {M}$ and ignore other negligible sources of errors such as the quantization noise. This consideration is due to the fact that the processes of quantization and binary coding shown in Fig. 1 may be arbitrary for a compressive imager. For instance, in single-pixel camera, the measurement vector $\textbf{y}$ is directly used in the decoding phase to restore an image from its unquantized measurements. However, the measurement process is always present, and because of combining data (i.e., the dimensionality reduction), introduces more significant traces than the quantizer. As mentioned earlier, in the decoding phase, the operator $\mathcal {M}^{-1}$ for signal reconstruction uses convex optimization methods such as the ${\ell _1}$-norm [15] or nonlinear iterative algorithms [5, 7, 24, 27, 36, 44, 50, 58, 59]. Applying such an operation may leave some artifacts such as blurring and high frequency oscillations. We will linearize the CS decoder to reveal artifacts as forensic footprints for compressive imaging identification purposes. The simplified model of compressive imaging is considered as:

$$\begin{aligned} \widehat{\varvec{\text {X}}}={\mathcal {R}}^{-1}\left\{ {\mathcal {F}}^{-1}\left[ {\mathcal {M}}^{-1}\left( \mathcal {A}\left( \mathcal {R}\left( \varvec{\text {X}}\right) \right) \right) \right] \right\} . \end{aligned}$$

(6)

For simplicity, we rewrite (6) in the following vector form:

$$\begin{aligned} \widehat{\varvec{\text {x}}}={\mathcal {F}}^{-1}\left\{ {\mathcal {M}}^{-1}\left[ \mathcal {A}\left( \varvec{\text {x}}\right) \right] \right\} . \end{aligned}$$

(7)

The details of all simplified imaging models including the above compressive sensing is summarized in Table 1. The input signal $\textbf{x}$ is sampled by using the measurement operator $\mathcal {M}$.

Example 1

(Random sampling as a case of CS) In [8], Candès et al. have used random sampling as a special case of CS for Fourier matrices. Here, for simplicity of the theoretical studies, we utilize this efficient mechanism in sampler. Consider a random sampling mask represented by the vector $\textbf{m}={\left[ m_1, m_2, \cdots , m_7\right] }^{\text {T}}={\left[ \begin{array}{ccccccc} 0&1&0&1&0&0&1 \end{array} \right] }^{\text {T}}$. In this model, each row of the measurement matrix $\textbf{M}$ consists of only a single 1 and all of the other entries are 0, so that:

$$\begin{aligned} {\textbf{M}}=\left( \begin{array}{ccccccc} {0} &{} {m_2} &{} {0} &{} {0} &{} {0} &{} {0} &{} {0} \\ {0} &{} {0} &{} {0} &{} {m_4} &{} {0} &{} {0} &{} {0} \\ {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {m_7} \\ \end{array} \right) . \end{aligned}$$

(8)

Lemma 1

(Blurring kernel for compressive imager) Consider the compressive sensing model in Table 1, where the recovered signal $\widehat{\varvec{\text {x}}}_C$ is determined by:

$$\begin{aligned} \widehat{\varvec{\text {x}}}_C={\mathcal {G}}^{-1}_C{\mathcal {G}}_C\left( \varvec{\text {x}}\right) . \end{aligned}$$

(9)

The encoder of compressive sensing, $\mathcal {G}_C$, is modeled as a linear under-determined system of equations. However, its decoder, $\mathcal {G}_C^{-1}$, is a nonlinear system, because the signal is generally recovered by nonlinear iterative algorithms. Figure 2 models the decoder. To be able to analyze the system behavior, we model the decoding function by an approximate linear system around the operating point. Appendix A provides details of the derivation of the linear model of compressive imaging decoder. In such a situation, the reconstructed signal $\widehat{x}_C(n)$ can be modeled by the convolution of the signal x(n) with the unknown blurring kernel $h_C(n)$, i.e., $\widehat{x}_C(n)=h_C(n)*x(n)$. Based on Toeplitz and circulant matrices [23], the convolution operation can be rewritten in an algebraic vector-matrix form as:

$$\begin{aligned} \widehat{\varvec{\text {x}}}_C\approx {\varvec{\text {H}}}_C\varvec{\text {x}}, \end{aligned}$$

(10)

where the matrix $\varvec{\text {H}}_C$ represents the blurring kernel of compressive imaging system. If the matrix ${\widehat{\textbf{M}}}^{-1}$ is the linearized approximate model of the system ${\mathcal {M}}^{-1}$, then:

$$\begin{aligned} \varvec{\text {H}}_C\approx {\left( \varvec{\widehat{\text {M}}\text {F}}\right) }^{-1}\left( \varvec{\text {MF}}\right) . \end{aligned}$$

(11)

By defining the matrix $\widehat{\textbf{A}}\triangleq {\widehat{\textbf{M}}}\textbf{F}$, we have:

$$\begin{aligned} \varvec{\text {H}}_C\approx {{\widehat{\textbf{A}}}}^{-1}\textbf{A}. \end{aligned}$$

(12)

Fig. 2

Closed-loop modeling of general iterative sparse recovery approaches

2.2.2 Linearized model of conventional imaging without compression

In cameras which deliver raw images, pixels are directly measured from CCD or CMOS sensors without any post-processing or compression on the sensed pixels. This type of imaging is usually utilized for professional digital photography. To formulate the problem in this case, we extend the simplified CS model shown in Table 1 to this type of conventional imaging. In the CS representation, the matrix $\textbf{M}$ may be considered as a diagonal matrix, where only a given percent of its main diagonal elements with randomly distributed locations, are 1 and in other entries are 0. The ratio of the number of main diagonal elements with the value 1 to the length of signal gives the sampling rate as $R_s = {\frac{{\parallel \text {diag}(\textbf{M}) \parallel }_{\ell _0}}{n}}\times 100$ in percent. The function $\text {diag}(\textbf{M})$ gets diagonal entries of the matrix $\textbf{M}$. By this interpretation, a conventional sensing model can be interpreted as a complete measurement of the vector containing the signal $\textbf{x}$. Table 1 shows the imaging system with uncompressed file format (hereafter RAW for simplicity). In this scheme, the measurement matrix is equal to the identity matrix, i.e., $\mathcal {I}\text {=}\varvec{\text {I}}$. In the decoding phase, just the main signal is usable.

Example 2

(Sampling matrix for RAW imaging) As mentioned above, the measurement matrix (8) can be rewritten in an equivalent form as:

$$\begin{aligned} \textbf{M}=\text {diag}(\textbf{m}). \end{aligned}$$

(13)

The function $\text {diag}(\textbf{m})$ creates the square diagonal matrix $\textbf{M}$ with the elements of vector $\textbf{m}$ on its main diagonal. In this case, the sampling rate is $R_s =42.86\%$. However, for conventional sensing, the matrix shown in (13) converts to an identity matrix, namely $\textbf{M}={\textbf{I}}_{7\times 7}$ with $R_s =100\%$.

Lemma 2

(Blurring kernel for RAW imager) Consider the traditional imaging model in Table 1 with raw image format. The recovered signal $\widehat{\varvec{\text {x}}}_U$ is determined by:

$$\begin{aligned} \widehat{\varvec{\text {x}}}_U={\mathcal {G}}^{-1}_U{\mathcal {G}}_U\left( \varvec{\text {x}}\right) , \end{aligned}$$

(14)

which the operators $\mathcal {G}_U$ and $\mathcal {G}_U^{-1}$ denote conventional encoder and decoder, respectively. Based on the vector-matrix representation, the raw imaging model can be described as:

$$\begin{aligned} \widehat{\varvec{\text {x}}}_U={\varvec{\text {H}}}_U\varvec{\text {x}}, \end{aligned}$$

(15)

where the matrix $\varvec{\text {H}}_U=\textbf{I}^{-1}\textbf{I}$ represents the blurring kernel of the raw imaging system. This results in:

$$\begin{aligned} \varvec{\text {H}}_U=\varvec{\text {I}}, \end{aligned}$$

(16)

which also means the identity matrix $\textbf{I}$ is the blurring kernel of raw imaging. Based on this model, the original signal is perfectly reconstructible in the decoder. Therefore, there exists ${\widehat{\varvec{\text {x}}}}_U=\varvec{\text {x}}$.

2.2.3 Linearized model of conventional imaging with compression

Most of ordinary cameras such as those embedded in today smart cell phones, at first, grab an image and then compress its content. Similar to uncompressed raw imaging, the total number of pixels are first measured. Then, after some optional post-processing operations, the 2-D signal is coded using a built-in source coder such as JP2 in order to reduce the bit rate. In Table 1, we have planned this kind of imaging, where the total compression operation has modeled by the operator $\mathcal {T}$. In JP2 compression standard, the main encoding steps include the transform to wavelet domain, quantization, and binary coding, which are performed sequentially (See Fig. 3 for details.). The compression ratio in the quantizer controls the required bit rate, defined as:

$$\begin{aligned} R_c\triangleq \frac{\text {The input image size}}{\text {The output compressed size}}. \end{aligned}$$

(17)

This parameter is a real number more than or equal to 1. In the decoder $\mathcal {T}^{-1}$, the reverse corresponding operations are applied, i.e., the binary decoding, dequantization, and inverse wavelet transform, respectively. Based on this model, the only intrinsic fingerprint of JP2 is the nonlinear quantizer system in the encoder and other operations are linear and losslessly decodable. For simplicity of analytical studies, the quantizer may be approximated by a linear model such as the linearized model of $\varSigma \text {-}\varDelta$ modulator [35, 42] for describing noise shaping phenomenon.

Lemma 3

(Blurring kernel for imaging with compression) Consider the traditional imaging with compression shown in Table 1. The recovered signal $\widehat{\varvec{\text {x}}}_J$ is determined by:

$$\begin{aligned} \widehat{\varvec{\text {x}}}_J={\mathcal {G}}^{-1}_J{\mathcal {G}}_J\left( \varvec{\text {x}}\right) , \end{aligned}$$

(18)

in which the operators $\mathcal {G}_J$ and $\mathcal {G}_J^{-1}$ denote the encoder and the decoder of conventional imager with JP2 compression, respectively. To find an approximate blurring kernel, we linearinze the model of JP2 compressor in Fig. 3. A derivation of the linearization of JP2 quantizer is provided in Appendix B. In this case, the reconstructed signal in the form of vector-matrix representation can be formulated as:

$$\begin{aligned} \widehat{\varvec{\text {x}}}_J\approx {\varvec{\text {H}}}_J\varvec{\text {x}}. \end{aligned}$$

(19)

The matrix $\varvec{\text {H}}_J\approx {\left( \textbf{TI}\right) }^{-1}\left( {\widehat{\textbf{T}}\textbf{I}}\right)$ represents the blurring kernel of conventional imaging with compression, in which the matrices $\widehat{\textbf{T}}$ and ${\textbf{T}}^{-1}$ denote the linearized approximate model of the compressor $\mathcal {T}$ and the linear decompressor $\mathcal {T}^{-1}$, respectively. The final blurring matrix is simplified as:

$$\begin{aligned} \varvec{\text {H}}_J\approx {\textbf{T}}^{-1}\widehat{\textbf{T}}. \end{aligned}$$

(20)

Fig. 3

Basic building blocks of JPEG2000 compressor

3 Imaging identification

In Section 2, we provided a rough estimate of the blurring kernel status for different imaging systems. Due to the differences among blurring matrices, they can potentially be exploited as features for the identification of imaging history. Here, we consider the whole imaging process as an inverse problem and calculate the blurring kernel matrix more accurately from each individual input image of a provided dataset based on a blind deconvolution approach. By leveraging Lemmas 1, 2, and 3, we justify the discriminability of matrices for different imagers theoretically; and, at the same time, we verify the discriminabilijty of the estimated kernels from real data statistically. At the end, we provide a learning and evaluation framework for the task of imaging source identification based on our proposed blurring kernel features. Figure 4 shows the architecture of our proposed imaging classification scheme, where its parts are introduced below.

Fig. 4

A pipeline for the forensic identification of traditional and compressive imaging based on our proposed blurring kernel signatures, including the two phases of learning and testing

3.1 Dataset preparation

Designing any classifier requires an appropriate dataset of training and test. To prepare our experimental data, we employed standard databases of raw images, which are widely used in image processing and forensics tasks [51]. We used the images set of Never-compressed Color Image Database (NCID) [32], including 5150 raw images with the dimensions $256\times 256$ and BMP file format. To manage hardware resources, we provided our experimental images set as follows. We first divided NCID images into $w\times h=128\times 128$ non-overlapping blocks. Then, we randomly selected a subset of them, including $N_r=655$ raw image patches. This yields the initial data set $\mathcal {D}_I=\{\textbf{x}^i\}_{i=1}^{N_r}$.

We performed experiments under different settings of imaging systems. The sampling rate in compressive sensing technology is usually set at the rates less than $50\%$ of the signal length [12]. To this intent, we drew the experimental sampling rates from the set $\mathcal {S}=\{25\%$, $40\%$, $50\%$, $67\%\}$ to generate different compressively sensed images based on the encoder/decoder designed in single-pixel camera [16]. This means that we used Gaussian measurements and BP algorithm for CS sampling and recovery, respectively. According to the above sampling rates, the total number of CS images is $N_r\cdot |\mathcal {S}|=2620$, where CS dataset is defined as $\mathcal {D}_C\triangleq \{\widehat{\textbf{x}}_C^i\}_{i=1}^{N_r\cdot |\mathcal {S}|}$. The symbol $|\cdot |$ denotes the cardinality of a set.

To create JP2 dataset, we adjusted the parameter of compression ratio, $R_c$, in MATLAB JPEG2000 coder similar to the mechanism utilized in [12]. In this case, for a fair comparison, we set the compression ratio of JPEG2000 coder in a manner that Peak Signal to Noise Ratio (PSNR) of conventional imager with compression is equal to PSNR of the compressive imaging system. Assume the elements of the set $\{C, J, U\}$ refer the compressive imager, conventional imaging with JP2 compression, and conventional imaging system with uncompressed file format, respectively. The expectation in the regime satisfies $\mathbb {E}\{\text {PSNR}|J\}\approx \mathbb {E}\{\text {PSNR}|C\}, \forall R_s \in \mathcal {S}$. For each $R_s$, there exists:

$$\begin{aligned} \mathbb {E}\lbrace \text {PSNR}|k\rbrace \triangleq \frac{10}{N_{r}}\sum _{i=1}^{N_{r}}{\log _{10}(\frac{M^{2}}{\frac{1}{n}\Vert \textbf{x}^{i}-\hat{\textbf{x}}_k^i\Vert _{\ell _{2}}^{2}})}, \forall k\in \lbrace C, J\rbrace . \end{aligned}$$

(21)

The parameter M is the maximum value of a pixel, which is 255 for an 8-bit unsigned integer image. In our experiments, the resultant set of compression ratio corresponding to the set $\mathcal {S}$ is equal to $\mathcal {P}=\{107.7899, 72, 54, 33.8\}$. This process results in $N_r\cdot |\mathcal {P}|=2620$ JP2 images of different compression ratios, where JP2 dataset is defined as $\mathcal {D}_J\triangleq \{\widehat{\textbf{x}}_J^i\}_{i=1}^{N_r\cdot |\mathcal {P}|}$. The wavelet basis employed for creating both CS and JP2 images was biorthogonal 4.4 with 4 levels of decomposition.

To prepare a balanced uncompressed images set $\mathcal {D}_U$, in addition to the database $\mathcal {D}_I$, we randomly chose other 1965 images from the $128\times 128$ patches without replacement, placed in the set $\mathcal {D}_O$. Then, we collected all of them into the balanced database $\mathcal {D}_U\triangleq \{\textbf{x}^i\}_{i=1}^{|\mathcal {D}_I|+|\mathcal {D}_O|}$, including $|\mathcal {D}_I|+|\mathcal {D}_O|=2620$ images. In this case, the number of data for each class in the set $\{C, J, U\}$ is the same. The reason behind this is that learning from balanced classes generally leads to an appropriate performance [26].

Our final database consists of the union of all the above datasets as:

$$\begin{aligned} \mathcal {D}\triangleq \bigcup _{i\in \{C, J, U\}}{\mathcal {D}_i}, \end{aligned}$$

(22)

in which the total number of images is $|\mathcal {D}|=7860$. We exploited the hold-out cross validation mechanism [20]. So, the first $75\%$ of data of each sub-class selected as the learning set and the remainder for testing, where their sizes are respectively equal to $\mathcal {D}_L=\frac{\lfloor 0.75N_r\rceil \cdot |\mathcal {D}|}{N_r}=5892$ and $\mathcal {D}_T=1968$ images. The symbol $\lfloor \cdot \rceil$ denotes the nearest integer function. Our data separation strategy guarantees to avoid any information leakage of images with the same scene/content from the learning phase to the test phase. For providing more training data, we have also used McGill CCID dataset [38]. We selected the central $128\times 128$ region from each of the 1096 TIFF images available in it [51].

For examining further the generalization capability, in addition to the 1968 test images, we provided two different test sets including 48 images chosen from Microsoft Research Cambridge Object Recognition Image Database and well-known image processing test-set images such as Baboon, Cameraman, Lena, etc. We utilized 27 randomly selected, cropped, and resized images from Microsoft database. Also, 21 images were chosen from well-known test images of the size $128\times 128$ [50].

3.2 Blurring kernel estimation

We model an imaging system as an inverse problem to be able to numerically estimate the blurring kernel matrix $\textbf{H}_i\in {\mathbb {R}}^{a\times b}, \forall i\in \{C, J, U\}$ by deconvolution. We are given an image from an imaging system, the problem is to reconstruct the blurring kernel of the original scene. Deconvolution is known as a paradigm of inverse problems [40]. Various direct and indirect deconvolution methods are available in order to estimate a degradation kernel and a deblurred version of an image such as Wiener filter and Richardson-Lucy algorithm [31, 48]. One of the best algorithms is the modified maximum-a-posterior-based deconvolution algorithm proposed in [30], which has used here. By using EM optimization, this algorithm iterates alternatively between two steps: one for solving a latent sharp image, and another for finding a blurring kernel. In order to blindly deconvolve the blurring kernel, it should be taken into consideration that the kernel dimensions are generally much less than the image dimensions [3]. Also, the shape of the degradation kernel is usually considered as a square with the length a. Table 1 illustrates the estimated blurring kernels of the length $a=9$ pertaining to Baboon image with the size $128\times 128$ for the three different imaging systems. In this example, the simulated compressive imager is based on Gaussian measurements and BP recovery algorithm with the sampling rate $R_s\approx 34\%$. The difference among blurring kernels can be clearly seen with the naked eye.

Theorem 1

(Blurring kernels discriminability of imagers) Let different imaging systems be modeled by $\widehat{\varvec{\text {x}}}_i\approx {\varvec{\text {H}}}_i\varvec{\text {x}}, \forall i\in \{C, J, U\}$, in which the vectors $\varvec{\text {x}}$ and $\widehat{\varvec{\text {x}}}_i$, and the matrix $\textbf{H}_i$ denote the latent original sharp signal, the output signal of the $i^{\text {th}}$ imaging system, and the blurring kernel of the $i^{\text {th}}$ imager, respectively. The elements of the set $\{C, J, U\}$ represent compressive imager, conventional imager with JPEG2000 compression, and conventional imaging system with uncompressed file format, respectively. Then, the blurring kernels of compressive $\textbf{H}_C$, conventional with uncompressed format $\textbf{H}_U$, and conventional with compression $\textbf{H}_J$ imaging systems are discriminable.

Proof

Distinct Lemmas 1, 2, and 3 demonstrate that the blurring kernels of compressive imager, conventional imager with uncompressed format, and conventional imager with compression are determined by inconsistent matrices $\textbf{H}_C\approx {{\widehat{\textbf{A}}}}^{-1}\textbf{A}$, $\textbf{H}_U=\varvec{\text {I}}$, and $\varvec{\text {H}}_J\approx {\textbf{T}}^{-1}\widehat{\textbf{T}}$, respectively, where the matrix $\textbf{I}$ is an identity matrix and the approximate kernels $\textbf{H}_C$ and $\textbf{H}_J$ are derived from affine models with different slope and $y\text {-intercept}$ parameters. Accordingly, the blurring kernels of various imaging models are discriminable, i.e., $\textbf{H}_i\ne \textbf{H}_j, \forall i,j\in \{C, J, U\}, i\ne j$, except for the following two worst cases:

• Case I: If the compressive ratio $R_s \rightarrow 100\%$, then CS imaging tends to conventional sensing. To demonstrate this, substituting $\textbf{M}=\textbf{I}$ in (11) gives $\textbf{H}_C={\left( \varvec{\text {IF}}\right) }^{-1}\left( \varvec{\text {IF}}\right) \Rightarrow \textbf{H}_C={\varvec{\text {F}}}^{\text {-1}}\underbrace{{\varvec{\text {I}}}^{\text {-1}}\varvec{\text {I}}}_{\varvec{\text {=}}\varvec{\text {I}}}\varvec{\text {F}}$, where results in $\textbf{H}_C=\textbf{F}^{-1}\textbf{F}$, and ultimately $\textbf{H}_C=\textbf{I}$. This situation means the lack of discriminability between CS imager and RAW imaging as the compressive ratio approaches the maximum rate $100\%$.

• Case II: If the compression ratio $R_c \rightarrow 1$, then $\widehat{\textbf{T}}=\textbf{T}=\textbf{I}$, which yields $\textbf{H}_J=\textbf{I}$. This means that as the compression ratio approaches the minimum rate 1, the conventional imaging with compression tends to RAW imaging. This leads to the lack of discriminability between conventional imaging systems with compression and without compression.

Also, to statistically validate the discriminability of the proposed signatures on real data as supportive evidence of our proof, we visualized the situation of estimated blurring kernels in a two-dimensional cluster representation by using the information visualization tool presented in [52]. This visualizer is a bi-level dimensionality reduction technique. At the first level, the kernel features are sparsely coded via the technology of compressive sensing and group least absolute shrinkage and selection operator algorithm. Using the unsupervised non-parametric t-SNE dimensionality reduction algorithm [34], sparse vectors are mapped onto a 2-D space with the components $v_1$ and $v_2$ at the second level of the visualizer. For visualization, we randomly selected with replacement $50\%$ of the dataset $\mathcal {D}$ for training and remainder for evaluation. In the visualizer, we adjusted the parameters of the number of measurements as $d=10$ and the regularizer as $\lambda =0.5$. Figure 5 illustrates the 2-D visualized results at two random runs. It is noticeable that due to the stochastic nature of the visualization algorithm [52], clustering results at various random runs are naturally different. The visualization results also justify the blurring kernels discriminability of imagers. Specifically, visualized information reveals that:

• point clouds pertaining to the cluster JP2 are separated well,

• special groups of CS and RAW samples have overlap, and

• distinct islands convey species information belonging to individual classes. These species may be generated by different ratios of coders and other latent variables of imaging systems (In experiments, we have analyzed the behavior of these sub-classes in Section 4.2.2.).

$\square$

Fig. 5

2-D visualization of the discriminability of blurring kernel features for various imaging systems at two different random runs (a) and (b)

3.3 Convolutional neural network for classification of imaging systems

CNN is one of the well-known models in deep machine learning, which is originally used for detection and identification of objects in images and videos [22]. Unlike feature engineering methods such as SVM which features are manually extracted by domain-specific experts, CNN determines characteristics in an automatic manner directly from image pixels. The structure of a CNN consists of two main building blocks. The first block contains feature detection layers and the second block includes classification layers. In the feature detection block, useful features are extracted by filtering, thresholding, and nonlinear down-sampling. These operations are applied by using a successive set of processing steps on the input image pixels including convolution, rectified linear unit (ReLU), and pooling, respectively. Convolution parameters can be obtained through training. In the classification stage, a vectorized version of the features obtained from the first block are fed to a Fully Connected (FC) network such as multi layer perceptron in order to train weights and biases of the network from learning data. CNN employs softmax activation function to predict output probabilities of classes.

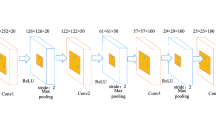
Different from the conventional usage of deep CNNs, here we train a network in a hybridized manner aware from the discriminability of blurring kernels. The scheme leads to a forensics-informed CNN for the application of source identification of the imaging systems. To do this, we convert the estimated 2-D blurring kernels $\textbf{H}$ to corresponding gray-level images $\widetilde{\textbf{H}}$ via a pre-processing step, and then feed them to a CNN as seen in Fig. 4. In the pre-processing of CNN learning/testing, we first normalize kernel values in the range [0, 1]. Then, the normalized values are converted into 8-bit unsigned integers in the range [0, 255]. We examined different topologies for learning CNN and finally selected the structure having maximum training accuracy. Based on our experiments on different architectures, a CNN network with a small number of convolutional and fully-connected layers is sufficient to learn the small, informative gray-level blurring kernel features. The employed optimal architecture consists of an $a\times b=9\times 9$ input blurring kernel image (Section 4.1 explains how we selected this optimal size.), a convolutional layer including 20 filters of the dimensions $5\times 5$, a ReLU layer, a non-overlapping max pooling layer with the pool size $2\times 2$, a fully-connected layer with 3 neurons, and an output layer with softmax activation function which generates the probabilities of classes $C_1$ to $C_3$. In the 3-class classification problem, we have defined the classes $C_1$, $C_2$, and $C_3$ as the representatives of CS, JP2, and RAW, respectively. The optimization procedure used for training was stochastic gradient descent algorithm with momentum. The settings of the maximum number of epochs and the initial learning rate equal to 30 and 0.0003, respectively.

Fig. 6

The performance under variations of blurring kernel dimensions for those methods that use our proposed blurring kernel traces as forensic features

4 Experiments

In this section, we design a series of numerical experiments to show the effectiveness of the proposed footprints as well support our theoretical findings. We have compared the proposed forensics-informed CNN approach to techniques of k-Nearest Neighbor (k-NN) [13], Multi-Layer Perceptron (MLP) neural network [25], SVM [9, 25], conventional CNN [22], and the method in [12]. We have performed two different experiments: 1) using only the BP algorithm [15], and 2) investigating the generalization capability under various unseen CS algorithms including BCS [27], IMAT [36], IMATI [58], and ISP [44]. It is important to note that the IMAT and IMATI algorithms utilize random sampling in sensing, and BCS and ISP approaches employ Gaussian measurements of all samples of signal.

4.1 Evaluation on different dimensions of blurring kernel

The dimensions of estimated blurring kernel are the parameters that may affect a restoration process. Here, the goal is to evaluate the accuracy (See (25).) of our proposed pipeline identification system vs the blurring kernel length a, ranging from 3 to 13. Among the compared approaches, the classifiers based on k-NN, MLP, and SVM are trained by our blurring kernel features for a fair comparison. Hence, we also sought their optimal sizes. Figure 6 depicts the accuracy vs blurring kernel dimensions. A growth-decline pattern is seen among methods. There is almost a congruency of the best accuracy on the size $9\times 9$. This size notifies that features information is enough for an appropriate classification without needing to redundancies due to increasing dimensions. Therefore, for next experiments of the paper, we set $a^{*}=9$ for all the methods.

4.2 Results and comparison

4.2.1 Implementation information of compared approaches

Simulations have done in MATLAB and run on an Intel Core i7 2.2GHz machine. In the k-NN classifier, we used the number of nearest neighbors $k=3$. The architecture of MLP includes: 81 input features, 2 hidden layers with 70 and 3 neurons respectively at the first and second layers, 3 neurons in the output layer with softmax activation function. The maximum number of epochs and the initial learning rate are the same with our method.

For the SVM, we utilized an one vs one division strategy with linear kernel. Its pre-processing step includes normalization of features in the range [0, 1]. To do this, we first considered an individual Gaussian distribution for each feature, in such a way that $\mathcal {N}({\mu }_{\lowercase {i}}, \sigma _{\lowercase {i}}), \forall i \in [1, a\times b]$. Then, we obtained the sample mean and standard deviation parameters for each feature from the training data. At the end, the normalization for a training/testing sample is performed as:

$$\begin{aligned} \widetilde{\mathbf{h}}=(\mathbf{h}-\boldsymbol{\mu})\quad \boldsymbol{\sigma}, \end{aligned}$$

(23)

where the vectors ${\textbf{h}}$ and ${\widetilde{{\textbf{h}}}}$ represent vectorized versions of matrices $\textbf{H}$ and $\widetilde{\textbf{H}}$, respectively. So, we have ${\varvec{\mu }}=[{\mu }_{1}, {\mu }_{2}, \cdots , {\mu }_{\lowercase {a\times b}}]^{\text {T}}$ and ${\varvec{\sigma }}=[{\sigma }_{1}, {\sigma }_{2}, \cdots , {\sigma }_{\lowercase {a\times b}}]^{\text {T}}$. The symbol denotes the entry-by-entry division. For implementing the SVM classifier, we used LIBSVM toolbox [9].

For the conventional CNN, the images of learning dataset are directly utilized to automatically extract features. In its training phase, we used an optimal structure including an input gray-level image set of the size $w\times h=128\times 128$, 30 filters of the dimensions $3\times 3$, the pool size $2\times 2$ without overlapping, and a fully-connected network with 3 outputs. The maximum number of epochs and the initial learning rate were 30 and 0.0001, respectively.

We reproduced the method [12] and approximated the thresholding parameters $\tau _1$ and $\tau _2$ of the first and second detectors from the learning set $\mathcal {D}_L$. In a grid search, we varied the threshold $\tau _1$ from 0.001 to 0.002 and the threshold $\tau _2$ from 0.002 to 0.003, and found the optimal $\tau _1^{*}=0.0015$ and $\tau _2^{*}=0.002$ values, so that the accuracy constraint on the learning data is maximized. In this method, we also utilized 5 levels of wavelet decomposition which lead to the best performance and set the number of iterations in EM algorithm equal to 100.

4.2.2 Performance under various compressive and compression ratios

It is important to obtain the performance of classification for sub-classes of each sensing system. The compressive ratio of compressive imaging in (1) and the compression ratio of JPEG2000 encoder in (17) are main parameters for controlling the required bandwidth. Settings of these ratios directly affect the quality of images in their decoding phase. Hence, the estimated kernels vary based on the amount of compressive/compression ratios. Figure 7(a) and (b) compare the accuracy of different methods for detecting CS and JP2 classes under various compressive and compression ratios, respectively.

As seen from Fig. 7(a), by increasing the compressive ratio, the accuracy for detecting the class CS decreases. It is due to the fact that the higher compressive ratio results in the lower compressive sensing artifacts. This increases the probability of error for misclassification of the class CS as the class RAW and vice versa, that justifies Case I from Theorem 1 (See also Table 2 for more details.). Inversely, the performance of detecting the class JP2 decreases by reducing the compression ratio, as seen in Fig. 7(b). The lower compression ratio leads to the lower compression artifacts, which increases the error probability of misclassification between the JP2 and RAW classes. This also justifies Case II from Theorem 1. The values in parentheses in the legend of Fig. 7(a) and (b) show the average accuracy on all corresponding ratios. The proposed approach has the first accuracy rank among different competing methods. The method in [12] exhibits almost the same accuracy for various ratios. However, its performance is unbalanced among the three classes and lower than other methods, especially for detecting the class CS depicted in Fig. 7(a). The overall performance for detecting the class JP2 is better than the class CS, as justified by the discriminability visualization in Section 3.2.

Fig. 7

(a) The performance comparison of identifying compressive sensing under various compressive ratios, and (b) the performance comparison of detecting JPEG2000 under various compression ratios. The values in parentheses in the legend of figures show averaging on their own x-axis values

Table 2 Confusion table for imaging identification of different approaches in $\%$

4.2.3 Confusion matrix of imaging identification

Confusion matrix is a standard means of quantifying performance of a classifier in detail [19]. In this paper, the confusion matrix $\textbf{C}$ for an imaging classifier is defined as:

$$\begin{aligned} \begin{aligned}&\begin{array}{ccc} \text {CS}&\text {JP2}&\text {RAW} \end{array}\\ \textbf{C}&= \begin{array}{c} \text {CS}\\ \text {JP2}\\ \text {RAW} \end{array} \left[ \begin{array}{ccc} \text {P(CS|CS)} &{} \text {P(CS|JP2)} &{} \text {P(CS|RAW)} \\ \text {P(JP2|CS)} &{} \text {P(JP2|JP2)} &{} \text {P(JP2|RAW)} \\ \text {P(RAW|CS)} &{} \text {P(RAW|JP2)} &{} \text {P(RAW|RAW)}\\ \end{array} \right] . \end{aligned} \end{aligned}$$

(24)

The conditional probabilities in the main diagonal elements of $\textbf{C}$ represent the correct classification and the remainder off-diagonal entries show the misclassification probabilities. For simplicity of comparison, we have collected confusion matrices of the compared approaches in Table 2. Overall accuracy in terms of percent is calculated by:

$$\begin{aligned} \text {Accuracy} = \frac{100}{3} [\text {P(CS|CS)}+\text {P(JP2|JP2)}+\text {P(RAW|RAW)}]. \end{aligned}$$

(25)

From Table 2, the accuracy is 80.28, 77.13, 73.68, 75.51, 82.01, and 55.64 for our purposed, k-NN, MLP, SVM, conventional deep CNN, and Chu et al. [12] approaches, respectively. This means that the methods of conventional CNN and our approach achieve the first and second ranks in terms of the overall accuracy, respectively. The first position of the conventional CNN is because of the performance difference in detecting the class $C_3$. However, the bold values in Table 2 reveal merits of our approach. Except for the class RAW, our method is ranked number one for detecting the classes CS and JP2 among competing approaches. The confusion matrices also show, for all compared methods, the misclassification errors between the classes CS and RAW are more than the other errors. The correct classification of the class JP2 is also more than the other imaging systems, because the blurring kernels of JPEG2000 images are more discriminative. Therefore, the best accuracy is obtained for predicting the class JP2 and the worst one for the class RAW. Specifically for the class RAW, comparing our detection result to that of conventional CNN shows that the automatically-extracted features by means of the convolution plus pooling represent better discriminability than the blurring kernels estimated by the deconvolver. However, in terms of the input image size, the speed of our scheme is more than the competing CNN with less memory requirement.

4.3 Generalization under unseen CS methods and datasets

This experiment examines the generalization capability of the pipeline identification system under different unseen compressive sensing approaches as well as unseen data. To this intent, we first trained our identification method on all 7860 data extracted from NCID database. It is noticeable that the CS recovery algorithm used for generating images of the compressive imaging class is BP algorithm. Then, for generalization test, we applied unseen CS algorithms of BCS, IMAT, IMATI, ISP, and BP (as a baseline) on unseen databases from the Microsoft and well-known test-set images. For a fair comparison, the sampling rate of all recovery algorithms set about 32% for Microsoft Object Recognition Database and 34% for well-known images test-set.

Figure 8 depicts the results of correct identification of the class CS, i.e., the probability $\text {P}(C_1|C_1)$ in %, for different CS algorithms on the databases of Microsoft and well-known test-set images. The reported performance metrics are average values for 10 training-testing runs. As shown in the chart, the identification system has promisingly predicted blurring kernels labels for both the unseen CS approaches and the unseen data. The best performance is belonging to the baseline BP, due to training on NCID kernels of the same recovery algorithm. The worst identification result is for IMATI method, where its interpolation mechanism during reconstructing iterations causes imaging artifacts to alleviate somewhat. Except for the method BP, the performance on Microsoft dataset is more than well-known images test-set in other sparse recovery algorithms.

However, it seems that learning blurring kernels of various recovery algorithms in the training phase can potentially improve the performance of compressive imaging identification. For instance, in the worst performance for IMATI, we curiously trained our approach with blurring kernels containing this type of CS to monitor how our model acts. For this purpose, at first, our network was trained with the datasets of NCID and CCID. Then, we evaluated its performance on the datasets of Microsoft and well-known images. Detailed confusion matrix in % is presented as:

$$\begin{aligned} \begin{aligned}&\begin{array}{ccc} \text {CS}&\text {JP2}&\text {RAW} \end{array}\\ \textbf{C}&= \begin{array}{c} \text {CS} \\ \text {JP2} \\ \text {RAW} \end{array} \left[ \begin{array}{ccc} 86.04 &{} 0 &{} 1.67 \\ 0 &{} 93.13 &{} 25 \\ 13.96 &{} 6.87 &{} 73.33 \\ \end{array} \right] . \end{aligned} \end{aligned}$$

(26)

The result $\text {P}(C_1|C_1)=86.04$ % shows a considerable 22.86 % improvement in IMATI CS identification than that one obtained in Fig. 8 with 63.18 %. Also, for the best result on the baseline BP, the confusion matrix would be:

$$\begin{aligned} \begin{aligned}&\begin{array}{ccc} \text {CS}&\text {JP2}&\text {RAW} \end{array}\\ \textbf{C}&= \begin{array}{c} \text {CS}\\ \text {JP2} \\ \text {RAW} \end{array} \left[ \begin{array}{ccc} 91.46 &{} 0 &{} 3.33 \\ 0 &{} 94.38 &{} 26.67 \\ 8.54 &{}5.62 &{} 70 \\ \end{array} \right] , \end{aligned} \end{aligned}$$

(27)

which shows 2.41 % improvement in BP CS identification.

Fig. 8

Correct identification of compressive imaging in % for different sparse recovery algorithms and two test-set databases

4.4 Effect of quantization noise on CS identification

In compressive imaging, CS measurements may be quantized by means of a quantizer. Such quantized measurements introduce quantization noise in CS encoding phase. So, the aim of this experiment is to investigate the effect of the quantization noise on the performance of compressive imaging identification under various compressive ratios and compare the obtained results with those of unquantized measurements. In case of quantized measurements, the entries of the measurement vector $\textbf{y}$ are rounded to the nearest integer values. For evaluation, we employed a set of unseen data chosen from the well-known test-set images. Figure 9 reports the performance of the pipeline compressive imaging identification system vs compressive ratio for both scenarios of unquantized and quantized CS measurements. The performance metrics are average values for 10 training-testing runs. The results demonstrate a perfect CS identification at the compressive rate $20\%$ for both unquantizedly and quantizedly measured data. This also means that for low compressive ratios, the quantization noise has no any effect on the performance. Although the identification performance in case of noisy quantized measurements is less than unquantized ones for the mid and high compressive rates, the results of unquantized measurements reveal that the dominant fall in performance is mainly related to the measurement process in CS encoding but not quantization.

Fig. 9

The performance of compressive imaging identification vs compressive ratio for both unquantized and quantized CS measurements

5 Conclusion

This paper modeled both compressive and traditional image sensing systems as an encoder-decoder pair. To analyze behavior of the complex imaging systems for forensic investigation purposes, simplification and linearization of the imagers were provided. Thanks to insights into the modeling of different imagers, we found blurring kernels of imaging systems make a discrimination capability for identifying the source imaging device that has been captured a suspect image. Therefore, we considered the process of image acquisition as a blind deconvolution problem and estimated the blurring kernel numerically. Theoretical and statistical tests were performed for analyzing the discriminability of blurring kernels of different imaging systems. We also fed our revealed traces to a pipeline deep learning-based system for the application of imaging source identification. We reached a promising correct classification of compressive imaging about $84\%$ on 1968 test samples. To manage hardware resources in simulations, we trained the network with a relatively small-scale training set including 5892 images for showing the concept of our method. As shown in experiments, the performance of our forensics-informed deep network can improve by increasing training data.

As future studies, being aware of noise characteristics or sharpness properties of edges can provide complementary footprints for imaging source identification purposes. Our modeling also facilitates developmental approaches for forensic investigations in connection with the next-generation, state-of-the-art compressive imaging systems. For instance, the forensic identification among a set of compressive sensing-based imaging systems can reveal the history of image acquisition such as make and model of the source compressive imaging device that has been generated a questionable image as well as settings under which the image has been captured.

Appendices

Appendix A: Derivation of the compressive decoder linear model

Consider the decoder of a compressive imaging system as:

$$\begin{aligned} \widehat{\textbf{x}}= \mathcal {G}^{-1}(\textbf{y})=\textbf{F}^{-1}\mathcal {M}^{-1}(\textbf{y}), \end{aligned}$$

(28)

where the vector $\textbf{y}\triangleq \textbf{Ax}$ contains measurements. Iterative algorithms are known as a general class of approximate sparse decoding approaches to solve (28). They can be modeled by successive linear filtering and point-wise thresholding [28], such as the algorithms of ISTA, IHT, IMAT, and ADMM. In Fig. 2, we have modeled an iterative compressive imaging decoder as a closed-loop system, in which the recovered signal $\textbf{x}$ at the $(k+1)^\text {th}$ iteration with the initial guess $\textbf{x}^{(0)}$ is formulated as:

$$\begin{aligned} \textbf{x}^{(k+1)}= f(\textbf{W}{\textbf{x}^{(k)}}), \end{aligned}$$

(29)

Fig. 10

The function of soft-thresholding and its approximation

which the matrix $\textbf{W}$ represents an algorithm-dependent linear filter, the nonlinear operator $f(\cdot )$ is a thresholding function, and $\widehat{\textbf{x}}\triangleq \textbf{x}^{(N)}$ after the last iteration N. One of the popular thresholding functions utilized in sparse recovery is soft-thresholding as:

$$\begin{aligned} y= f(x)=\left\{ \begin{array}{cc} \text {sgn}(x)(| \textbf{x} | - \varDelta ), &{} | \textbf{x} | \ge \varDelta \\ 0, &{} | \textbf{x} | < \varDelta \end{array} \right. , \end{aligned}$$

(30)

where the parameter $\varDelta$ is a threshold value. Based on Taylor series expansion [37], a linear approximation of soft-thresholding function around the known point $x_0$ can be represented by:

$$\begin{aligned} y=f(x)\approx f(x_0) + f'(x_0)(x-x_0), \end{aligned}$$

(31)

for which the derivative of the function f(x) can be rewritten by the unit step function u(x) terms as:

$$\begin{aligned} f'(x) = u(-x-\varDelta ) + u(x-\varDelta ). \end{aligned}$$

(32)

This function is one for $|x|\ge \varDelta$ and zero for $|x|<\varDelta$. Therefore, there exist $y\approx x-\varDelta$ and $y\approx x+\varDelta$ for $x\ge \varDelta$ and $x\le \varDelta$, respectively. Figure 10 simulates both soft-thresholding function and its linear approximation for $\varDelta =1$ and $\varDelta x\triangleq x-x_0=0.2$, which shows small errors. Without loss of generality for the linear approximation of an arbitrary thresholding function, (28) can be rewritten as $\widehat{\textbf{x}} \approx \textbf{F}^{-1}{\widehat{\textbf{M}}}^{-1}\textbf{y}$, in which the matrix $\widehat{\textbf{M}}^{-1}$ represents the linearized approximate model of the system $\mathcal {M}^{-1}$. By defining the matrix $\widehat{\textbf{A}}\triangleq {\widehat{\textbf{M}}}\textbf{F}$, we have $\widehat{\textbf{x}} \approx \widehat{\textbf{A}}^{-1}\textbf{Ax}$. $\square$

Appendix B: Derivation of the linearization of JPEG2000 quantizer

As shown in Fig. 3, the basic operations of JPEG2000 compressor are the forward DWT, quantization, and arithmetic coding. Since the binary decoder $\mathcal {C}^{-1}$ is exactly the inverse system of $\mathcal {C}$, the forensic model of JPEG2000 compressor can be formulated by:

$$\begin{aligned} \textbf{y}=\mathcal {T}(\textbf{x})=f(\textbf{Wx}). \end{aligned}$$

(33)

Here, the vectors $\textbf{x}$ and $\textbf{y}$, and the matrix $\textbf{W}$ denote the input signal, quantized coefficients, and the wavelet transform, respectively. The nonlinear quantization function $f(\cdot )$ for a given wavelet coefficient in JPEG2000 standard is formulated as:

$$\begin{aligned} y=f(x)= \text {sgn}(x)\lfloor \frac{|x|}{\varDelta _b}\rfloor , \end{aligned}$$

(34)

where the function $\varDelta _b$ determines the quantization step size. For small values of $\varDelta _b$, the function in (34) approaches the line $y\approx \frac{1}{\varDelta _b}x$. Hence, the quantizer can be linearized by the first-order approximation $y=f(x)\approx f(x_0) + f'(x_0)(x-x_0)$. The derivative of the function f(x) is as:

$$\begin{aligned} f'(x)= 2\delta (x)\lfloor \frac{|x|}{\varDelta _b}\rfloor + \text {sgn}(x) \frac{d}{dx} \lfloor \frac{|x|}{\varDelta _b}\rfloor , \end{aligned}$$

(35)

which the function $\delta (x)$ denotes the unit impulse function. Using the change of variable $\lambda \triangleq \frac{|x|}{\varDelta _b}$, the derivative $\frac{d}{dx} \lfloor \lambda \rfloor$ is equal to:

$$\begin{aligned} \frac{d}{d\lambda } \frac{d\lambda }{dx} \lfloor \lambda \rfloor = \frac{x}{\varDelta _b |x|}\{\cdots + \delta (\lambda +1) + \delta (\lambda ) + \delta (\lambda -1) + \cdots \}, \end{aligned}$$

(36)

where for $\lambda \in \mathbb {R}^{+}$ yields:

$$\begin{aligned} \frac{d}{dx} \lfloor \frac{|x|}{\varDelta _b} \rfloor =\frac{1}{\varDelta _b}\{\cdots - \delta (x+2\varDelta _b) - \delta (x+\varDelta _b) + \delta (x-\varDelta _b) + \delta (x-2\varDelta _b) + \cdots \}. \end{aligned}$$

(37)

By inserting (37) into (35) and utilizing the sampling property of the impulse function as $g(x)\delta (x-x_0)=g(x_0)\delta (x-x_0)$, we have ultimately:

$$\begin{aligned} f'(x)= \frac{1}{\varDelta _b}\{\sum ^{\infty }_{n=-\infty }[\delta (x-n\varDelta _b)] - \delta (x)\}. \end{aligned}$$

(38)

The function $f'(x)$ is only non-zero for $x=n\varDelta _b$, $\forall n=\pm 1, \pm 2, \cdots$. Therefore, for both $n<0$ and $n>0$, we have $y\approx \frac{1}{\varDelta _b}x$, which make sense. Figure 11 depicts JPEG2000 quantizer and its linear approximation for $\varDelta _b=1$ and $\varDelta x\triangleq x-x_0=0.2$. The differences are only seen for the discontinues points. For the above linearized model, (33) is approximated by $\textbf{y}\approx \widehat{\textbf{T}}\textbf{x}$, where the matrix $\widehat{\textbf{T}}$ corresponds to the linearized model of the compressor $\mathcal {T}$. JPEG2000 decompressor $\mathcal {T}^{-1}$, as the inverse of the system presented in Fig. 3, can be described by $\widehat{\textbf{x}}\approx \textbf{W}^{-1}{\varvec{\delta }}\odot \textbf{y} \triangleq \textbf{T}^{-1}\widehat{\textbf{T}}\textbf{x}$, in which the matrices $\textbf{W}^{-1}$ and $\textbf{T}^{-1}$, the vector ${\varvec{\delta }}$, and the symbol $\odot$ represent the inverse DWT, decompression matrix, quantization step entries, and point-wise multiplication, respectively. $\square$

Fig. 11

The function of JPEG2000 quantizer and its approximation