1 Introduction

Robe’s problem which is still a new kind of restricted three body problem incorporates the effect of buoyancy force, was formulated by Robe (1977). He regards the first primary m 1 as a rigid spherical shell filled with a homogeneous incompressible fluid of density ρ 1, the second primary as a point mass m 2 located outside the shell, and the third body which is the infinitesimal mass m 3 with density ρ 3 moves inside the shell under the influence of the gravitational attraction of the primaries and the buoyancy force of the fluid ρ 1. He considered two cases. In the first case, m 2 describes a circular orbit around the shell and in the second case, its orbit is elliptic but the shell is empty, or the densities ρ 1 and ρ 3 are equal. He established the center of the first primary as an equilibrium point and discussed its linear stability.

In estimating buoyancy force, Robe (1977) assumed that the pressure field of the fluid ρ 1 has spherical symmetry around the center of the shell and he considered only one out of the three components of the pressure field, which is that due to the own gravitational field of the fluid ρ 1. The other two components are arising from the centrifugal force and attraction of m 2. Plastino and Plastino (1995) took into account all these components of pressure field. But in their study, they assumed the hydrostatic equilibrium figure of the first primary as Roche’s ellipsoid. They found that when the density parameter D is zero, every point inside the fluid is an equilibrium point; otherwise, the ellipsoid’s center is the only equilibrium point. They also examined the linear stability of equilibrium points. Hallan and Mangang (2007) studied Robe’s circular restricted three body problem, assuming the hydrostatic equilibrium figure of the first primary as an oblate spheroid instead of a Roche’s ellipsoid. They obtained conditions for the existence of an infinite number of equilibrium points and their linear stability.

In nature, some celestial bodies are not perfect spheres. They are either oblate principal or triaxial principal. The Earth, Jupiter, Saturn and Ragulus are oblate, because two of the three moments of inertia are equal, while the Moon, Pluto and Charon are triaxial because all the three moment of inertia are distinct. The lack of sphericity of the heavenly bodies causes large perturbations from a two-body orbit. The motions of artificial Earth Satellites are example of this. This motivates several studies (Subbarao and Sharma 1975; Elipe and Ferrer 1985; Sharma et al. 2001; Singh 2009; Singh and Begha 2011) to include oblateness and triaxiality in the restricted three-body problem. So far, to the present authors’ knowledge, no work on the Robe’s Problem has been done by taking a primary as a triaxial body.

In this paper, we examine the Robe’s problem by taking into consideration all the three components of pressure field when the second primary moves in a circular orbit around the first primary. We assume the hydrostatic equilibrium figure of the first primary as an oblate spheroid and the second primary as a triaxial rigid body. We propose to find all the equilibrium points in the plane of motion and then discuss their stability. This paper is organized as follows: in Sect. 2, the pertinent equations of motion are presented; Sect. 3 locates the equilibrium points, while their stability is discussed in Sect. 4; finally, Sect. 5 concludes the results of this paper.

2 Equations of Motion

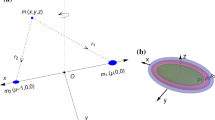
Let the first primary m 1 be a fluid of density ρ 1 in the shape of an oblate spheroid as assumed by Hallan and Mangang (2007); the second primary m 2 be a triaxial rigid body as Sharma et al. (2001) which describes a circular orbit around m 1. The infinitesimal mass m 3, whose density is ρ 3 ≠ ρ 1, moves inside the first primary (see Fig. 1). We consider a uniformly rotating coordinate system oxyz with the origin at the center of the mass m 1, ox points towards m 2 and oxy being the orbital plane of m 2 coinciding with the equatorial plane of m 1. Then, the equations of motion of the infinitesimal body of density ρ 3 in this coordinate system, as in Hallan and Mangang (2007) and Sharma et al. (2001), is given as:

$$ \begin{gathered} \ddot{x} - 2n\dot{y} = U_{x} \hfill \\ \ddot{y} + 2n\dot{x} = U_{y} \hfill \\ \ddot{z} = U_{z} \hfill \\ \end{gathered} $$
(1)

where

$$ U = V + \frac{{n^{2} \left\{ {\left( {x - \frac{{m_{2} }}{{m_{1} + m_{2} }}R} \right)^{2} + y^{2} } \right\}}}{2} $$
$$ V = B + B^{\prime } - \frac{{\rho_{1} }}{{\rho_{3} }}\left[ {B + B^{\prime } + \frac{{n^{2} \left\{ {\left( {x - \frac{{m_{2} }}{{m_{1} + m_{2} }}R} \right)^{2} + y^{2} } \right\}}}{2}} \right] $$
$$ B = \pi G\rho_{1} \left[ {I - A_{1} x_{{}}^{2} - A_{1} y_{{}}^{2} - A_{2} z_{{}}^{2} } \right] $$
$$ B^{\prime } = \frac{{Gm_{2} }}{{\left[ {\left( {R - x} \right)^{2} + y^{2} + z^{2} } \right]^{1/2} }} + \frac{{Gm_{2} \left( {2\sigma_{1} - \sigma_{2} } \right)}}{{2\left[ {\left( {R - x} \right)^{2} + y^{2} + z^{2} } \right]^{3/2} }} - \frac{{3Gm_{2} \left( {\sigma_{1} - \sigma_{2} } \right)y_{{}}^{2} }}{{2\left[ {\left( {R - x} \right)^{2} + y^{2} + z^{2} } \right]^{5/2} }} - \frac{{3Gm_{2} \sigma_{1} z_{{}}^{2} }}{{2\left[ {\left( {R - x} \right)^{2} + y^{2} + z^{2} } \right]^{5/2} }} $$
$$ I = 2a_{1}^{2} A_{1} + a_{2}^{2} A_{2} , $$
$$ A_{1} = a_{1}^{2} a_{2} \int\limits_{0}^{\infty } {\frac{du}{{\Updelta \left( {a_{1}^{2} + u} \right)}},} \quad A_{2} = a_{1}^{2} a_{2} \int\limits_{0}^{\infty } {\frac{du}{{\Updelta \left( {a_{2}^{2} + u} \right)}}} ,\quad \Updelta^{2} = \left( {a_{1}^{2} + u} \right)^{2} \left( {a_{2}^{2} + u} \right) $$
$$ n^{2} = \frac{{G\left( {m_{1} + m_{2} } \right)}}{{R^{3} }}\left[ {1 + \frac{3}{2}\alpha + \frac{3}{2}\left( {2\sigma_{1} - \sigma_{2} } \right)} \right] $$
$$ \alpha = \frac{{a_{1}^{2} - a_{2}^{2} }}{{5R^{2} }}, \, \sigma_{1} = \frac{{a^{2} - c^{2} }}{{5R^{2} }}, \, \sigma_{2} = \frac{{b^{2} - c^{2} }}{{5R^{2} }}, \, \alpha \ll 1,_{{}} \sigma_{i} \ll 1,\left( {i = 1,2} \right): $$

Here U x , U y and U z are the partial derivatives of U with respect to x, y and z respectively; V is the potential that explains the combined action of the forces upon the infinitesimal mass; B denotes the potential due to the fluid mass of the first primary in the shape of an oblate spheroid, B′ stands for the potential due to the second triaxial primary; R is the distance between the primaries and G is the gravitational constant. n is the mean motion. a 1, a 2 are the equatorial and polar radii of the first primary and α its oblateness coefficient, while a, b, c are semi axes of the second primary used in defining its triaxiality with the help of parameters σ 1, σ 2 in the tridimensional form. I is the polar moment of inertia of the oblate primary with index symbol A i (i = 1, 2). The last term in V arises from the buoyancy force per unit mass, as in Plastino and Plastino (1995), given as

Fig. 1
figure 1

The Robe’s CRTBP with an oblate first primary and a triaxial second primary. F1, F2 = Gravitational forces, FB = Buoyancy force. m 1 (oblate primary), m 2 (triaxial primary)

Full size image
$$ E = - \frac{{\rho_{1} }}{{\rho_{3} }}\Updelta \left[ {B + B^{\prime } + \frac{{n^{2} \left\{ {\left( {x - \frac{{m_{2} }}{{m_{1} + m_{2} }}R} \right)^{2} + y^{2} } \right\}}}{2}} \right] $$

Now, we choose the unit of mass such that the sum of the masses of the primaries is taken as unity, thus we take \( m_{2} = \mu ,\quad 0 < \mu = \frac{{m_{2} }}{{m_{1} + m_{2} }} < 1 \). For the unit of length, we take the distance between the primaries as unity i.e. R = 1 and the unit of time is also selected such that G = 1. With these units, the potential used in Eq. (1) becomes

$$ \begin{aligned} U = \,& D\left[ {\pi \rho_{1} \left( {I - A_{1} x^{2} - A_{1} y^{2} - A_{2} z^{2} } \right) + \frac{\mu }{{\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{1/2} }}} \right. + \frac{{\mu \left( {2\sigma_{1} - \sigma_{2} } \right)}}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{3/2} }} \\ & - \frac{{3\mu \left( {\sigma_{1} - \sigma_{2} } \right)y^{2} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} - \frac{{3\mu \sigma_{1} z^{2} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} + \left. {\frac{{n^{2} \left\{ {\left( {x - \mu } \right)^{2} + y^{2} } \right\}}}{2}} \right] \\ \end{aligned} $$
(2)
$$ \, n^{2} = 1 + \frac{3}{2}\alpha + \frac{3}{2}\left( {2\sigma_{1} - \sigma_{2} } \right), \, \alpha \ll 1,\sigma_{i} \ll 1,\left( {i = 1,2} \right) $$
(3)

3 Location of Equilibrium Points

The equilibrium points are those points at which the velocity and acceleration of the infinitesimal mass are zero. Therefore, these points are the solutions of the equations \( U_{x} = 0, \, U_{y} = 0, \, U_{z} = 0. \) That is,

$$ \begin{aligned} U_{x} = & D\left[ { - 2\pi \rho_{1} A_{1} x + \frac{{\mu \left( {1 - x} \right)}}{{\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{3/2} }} + \frac{{3\mu \left( {2\sigma_{1} - \sigma_{2} } \right)\left( {1 - x} \right)}}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} - \frac{{15\mu \left( {\sigma_{1} - \sigma_{2} } \right)\left( {1 - x} \right)y^{2} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{7/2} }} - \frac{{15\mu \sigma_{1} \left( {1 - x} \right)z^{2} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{7/2} }} + n^{2} \left( {x - \mu } \right)} \right] = 0, \\ U_{y} = & D\left[ { - 2\pi \rho_{1} A_{1} y - \frac{\mu y}{{\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{3/2} }} - \frac{{3\mu \left( {2\sigma_{1} - \sigma_{2} } \right)y}}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} - \frac{{3\mu \left( {\sigma_{1} - \sigma_{2} } \right)y}}{{\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} + \frac{{15\mu \left( {\sigma_{1} - \sigma_{2} } \right)y^{3} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{7/2} }} + \frac{{15\mu \sigma_{1} yz^{2} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{7/2} }} + n^{2} y} \right] = 0, \\ U_{z} = & D\left[ { - 2\pi \rho_{1} A_{2} z - \frac{\mu z}{{\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{3/2} }} - \frac{{3\mu \left( {2\sigma_{1} - \sigma_{2} } \right)z}}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} + \frac{{15\mu \left( {\sigma_{1} - \sigma_{2} } \right)y^{2} z}}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{7/2} }} - \frac{{3\mu \sigma_{1} z}}{{\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{5/2} }} + \frac{{15\mu \sigma_{1} z^{3} }}{{2\left\{ {\left( {1 - x} \right)^{2} + y^{2} + z^{2} } \right\}^{7/2} }}} \right] = 0. \\ \end{aligned} $$
(4)

In order to study the existence of equilibrium points lying in the orbital plane of motion, we consider the case where z = 0 and so the x, y coordinates of the equilibrium points are the solutions of the following systems of equations treated under case I and case II below:

4 Case I: Axial Equilibrium Points

The axial points are the solutions of the system (4) with y = z = 0. Thus, these points lie on the x-axis.and their x coordinates are the roots of the equation

$$ - 2\pi \rho_{1} A_{1} x + \frac{{\mu \left( {1 - x} \right)}}{{\left| {1 - x} \right|^{3} }} + \frac{{3\mu \left( {2\sigma_{1} - \sigma_{2} } \right)\left( {1 - x} \right)}}{{2\left| {\left( {1 - x} \right)} \right|^{5} }} + \left[ {1 + \frac{3}{2}\alpha + \frac{3}{2}\left( {2\sigma_{1} - \sigma_{2} } \right)} \right]\left( {x - \mu } \right) = 0 $$
(5)

We first find the roots by neglecting the oblateness and triaxiality terms, that is α = σ 1 = σ 2 = 0 so that, n 2 = 1, then we apply perturbation method to find the expected equilibrium points.

When α = σ 1 = σ 2 = 0, Eq. (5) becomes

$$ - 2\pi \rho_{1} A_{1} x + \frac{{\mu \left( {1 - x} \right)}}{{\left| {1 - x} \right|^{3} }} + x - \mu = 0 $$
(6)

Equation (6) is satisfied for x = 0. So the centre of the first primary, which is the origin, is an equilibrium point for all values of the parameters \( \mu ,A_{1} ,A_{2} ,\rho_{1} {\text{ and }}D \) whenever α = σ 1 = σ 2 = 0. Other roots of Eq. (6) satisfying the condition 0 < |x| < 1 can be obtained, when it is written as

$$ \left( {1 - 2\pi \rho_{1} A_{1} } \right)x^{2} + \left( {4\pi \rho_{1} A_{1} - 2 - \mu } \right)x + \left( {1 + 2\mu - 2\pi \rho_{1} A_{1} } \right) = 0 $$
(7)

The roots of Eq. (7) are

$$ x_{1} = 1 + \frac{{\mu + \sqrt {\mu^{2} + 8\pi \rho_{1} A_{1} \mu - 4\mu } }}{{2\left( {1 - 2\pi \rho_{1} A_{1} } \right)}}, \, _{{}} x_{2} = 1 + \frac{{\mu - \sqrt {\mu^{2} + 8\pi \rho_{1} A_{1} \mu - 4\mu } }}{{2\left( {1 - 2\pi \rho_{1} A_{1} } \right)}} $$
(8)

and are real if μ + 8πρ 1 A 1 − 4 ≥ 0.

An analysis of the roots (8) shows that the point (x 1, 0, 0) is an equilibrium point and it lies within the fluid when \( 1 - 2\pi \rho_{1} A_{1} < - \frac{3}{4}\mu \) and \( \left| {x_{1} } \right| < a_{1} \).

Therefore, for α = σ 1 = σ 2 = 0; x 1 = 0 is always a root of Eq. (5) and x = x 1 is also a root provided \( 1 - 2\pi \rho_{1} A_{1} < - \frac{3\mu }{4} \) and \( \left| {x_{1} } \right| < a_{1} \).

In order to find the roots of Eq. (5) when α ≠ 0, σ 1 ≠ 0, σ 2 ≠ 0; we let them be

$$ \begin{gathered} x = 0 + \beta_{1} ,\left| {\beta_{1} } \right| \ll 1 \hfill \\ x = x_{1} + \beta_{2} ,\left| {\beta_{2} } \right| \ll 1 \hfill \\ \end{gathered} $$

Putting these values of x in Eq. (5) and neglecting second and higher powers of α, β 1, β 2, σ 1, σ 2, we obtain

$$ \begin{gathered} \beta_{1} = - \frac{3}{2}\left[ {\frac{\mu \alpha }{{2\pi \rho_{1} A_{1} - \left( {1 + 2\mu } \right)}}} \right] \hfill \\ \beta_{2} = - \frac{3}{2}\left[ {\frac{{\left( {\alpha + 2\sigma_{1} - \sigma_{2} } \right)\left( {x_{1} - \mu } \right)\left( {1 - x_{1} } \right) + \mu \left( {2\sigma_{1} - \sigma_{2} } \right)\left( {1 - x_{1} } \right)^{ - 3} }}{{\left( {1 - 3x_{1} } \right)\left( {1 - 2\pi \rho_{1} A_{1} } \right) + 2\mu }}} \right] \hfill \\ \end{gathered} $$
(9)

Hence, when the oblateness of m 1 and triaxiality of m 2 are considered, the point (β 1, 0, 0) is always an equilibrium point and when \( 1 - 2\pi \rho_{1} A_{1} < - \frac{3\mu }{4} \) and \( \left| {x_{1} } \right| < a_{1} \), the point \( \left( {x_{1} + \beta_{2} ,0,0} \right) \) is another equilibrium point. These points constitute the axial equilibrium points. It is observed that the point (β 1, 0, 0) is the same as that of Hallan and Mangang (2007), and is only affected by oblateness of the first primary; whereas the point (x 1 + β 2, 0, 0) differs from therein and is affected by both oblateness and triaxiality of the primaries.

5 Case II: Elliptical Equilibrium Points

The elliptical equilibrium points are the solutions of the system of Eq. (4) with x ≠ 0, y ≠ 0, z = 0. Thus, these points lie in the xy- plane and their x and y coordinates are the solutions of the following equations

$$ \begin{gathered} - 2\pi \rho_{1} A_{1} x + \frac{{\mu \left( {1 - x} \right)}}{{\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{3/2} }} + \frac{{3\mu \left( {2\sigma_{1} - \sigma_{2} } \right)\left( {1 - x} \right)}}{{2\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{5/2} }} - \frac{{15\mu \left( {\sigma_{1} - \sigma_{2} } \right)\left( {1 - x} \right)y^{2} }}{{2\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{7/2} }} + n^{2} \left( {x - \mu } \right) = 0 \hfill \\ - 2\pi \rho_{1} A_{1} - \frac{\mu }{{\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{3/2} }} - \frac{{3\mu \left( {2\sigma_{1} - \sigma_{2} } \right)}}{{2\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{5/2} }} - \frac{{3\mu \left( {\sigma_{1} - \sigma_{2} } \right)}}{{\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{5/2} }} + \frac{{15\mu \left( {\sigma_{1} - \sigma_{2} } \right)y^{2} }}{{2\left[ {\left( {1 - x} \right)^{2} + y^{2} } \right]^{7/2} }} + n^{2} = 0 \hfill \\ \end{gathered} $$
(10)

Let

$$ r^{2} = \left( {1 - x} \right)^{2} + y^{2} $$
(11)

Then from the system (10), we obtain

$$ 2\pi \rho_{1} A_{1} = \frac{{ - 3\mu \left( {\sigma_{1} - \sigma_{2} } \right)\left( {1 - x} \right)}}{{r^{5} }} + n^{2} \left( {1 - \mu } \right) $$
(12)

and

$$ \frac{1}{{r^{3} }} + \frac{{3\left( {2\sigma_{1} - \sigma_{2} } \right)}}{{2r^{5} }} + \frac{{3\left( {\sigma_{1} - \sigma_{2} } \right)x}}{{r^{5} }} - \frac{{15\left( {\sigma_{1} - \sigma_{2} } \right)y^{2} }}{{2r^{7} }} - n^{2} = 0 $$
(13)

In the absence of oblateness and triaxiality terms, that is, α 1 = σ 1 = σ 2 = 0, we have r = 1. Now, in the presence of these oblateness and triaxiality terms, r will change slightly by ɛ, say, such that

$$ r = 1 + \varepsilon ,\quad \varepsilon \ll 1 $$
(14)

Substituting Eq. (14) into (13) and neglecting second and higher powers of ɛ, α, σ 1, σ 2 as well as the products of σ 1 and σ 2 too, we obtain an expression for ɛ:

$$ \varepsilon = - \frac{1}{2}\alpha + \left( {\sigma_{1} - \sigma_{2} } \right)x - \frac{{5\left( {\sigma_{1} - \sigma_{2} } \right)y^{2} }}{2} $$
(15)

By the use of Eqs. (14) and (15), Eq. (11) yields

$$ x^{2} - 2\left( {1 + \sigma_{1} - \sigma_{2} } \right)x + \left( {1 + 5\sigma_{1} - 5\sigma_{2} } \right)y^{2} + \alpha = 0 $$
(16)

This is an equation for a conic section, an ellipse to be precise. The center of the ellipse is located at (1 + σ 1 − σ 2, 0); if we take σ 1 > σ 2, the foci are at \( \left( {1 + \sigma_{1} - \sigma_{2} \pm \sqrt {5\left( {\sigma_{1} - \sigma_{2} } \right)} ,0} \right) \) and if σ 1 < σ 2, the foci are imaginary and they are neglected; thus the semi major axis is \( 1 - \frac{1}{2}\alpha + \sigma_{1} - \sigma_{2} \)and the semi minor axis is \( 1 - \frac{1}{2}\alpha - \frac{3}{2}\left( {\sigma_{1} - \sigma_{2} } \right) \). The eccentricity is obtained as \( \sqrt {5\left( {\sigma_{1} - \sigma_{2} } \right)} \). With the help of the eccentric angle θ, the general coordinates of a point on the ellipse can be written as

$$ \begin{aligned} x = & 1 + \sigma_{1} - \sigma_{2} + \left[ {1 - \frac{1}{2}\alpha + \sigma_{1} - \sigma_{2} } \right]\cos \theta \\ y = & \left[ {1 - \frac{1}{2}\alpha - \frac{3}{2}\left( {\sigma_{1} - \sigma_{2} } \right)} \right]\sin \theta \\ \end{aligned} $$
(17)

And so the value of r in Eq. (14) on neglecting the product of α and \( \sigma_{i} \left( {i = 1,2} \right) \) becomes

$$ r = 1 - \frac{1}{2}\alpha - \frac{1}{2}\left( {\sigma_{1} - \sigma_{2} } \right)\left( {3 - 2\cos \theta - 5\cos^{2} \theta } \right) $$
(18)

Thus the points on the ellipse (16) lying within the first primary are equilibrium points and we call them elliptical points. These points are affected by both oblateness and triaxiality of the primaries, and have no analogies in Hallan and Mangang (2007).

6 Stability of Equilibrium Points

In order to study the motion near any of the equilibrium points (x o , y o , z o ), we write

$$ \begin{aligned} x = & x_{o} + \xi \\ y = & y_{o} + \eta \\ z = & z_{o} + \zeta \\ \end{aligned} $$

where \( \xi ,\eta ,\zeta \) are small displacements in (x o , y o , z o ). Putting these values in Eq. (1), we obtain the variational equations of motion as

$$ \begin{aligned} \ddot{\xi } - 2n\dot{\eta } =\,& U^{o}_{xx} \xi + U^{o}_{xy} \eta + U^{o}_{xz} \zeta \\ \ddot{\eta } + 2n\dot{\xi } =\, & U^{o}_{yx} \xi + U^{o}_{yy} \eta + U^{o}_{yz} \zeta \\ \ddot{\zeta } =\, & U^{o}_{zx} \xi + U^{o}_{zy} \eta + U^{o}_{zz} \zeta \\ \end{aligned} $$
(19)

Here, only linear terms in \( \xi ,\eta {\text{ and }}\zeta \) have been taken. The second partial derivative of U are denoted by subscripts. The superscript o indicates that the derivatives are to be evaluated at the equilibrium point (x o , y o , z o ).

6.1 Stability of Axial Points

At axial equilibrium point (β 1, 0, 0), the values of the second order partial derivatives are

$$ \begin{aligned} U_{xy}^{o} = & 0,\quad U_{xz}^{o} = 0,\quad U_{yz}^{o} = 0, \\ U_{xx}^{o} = & D\mu \left[ {\frac{{2n^{2} \left( {1 - \beta_{1} } \right)^{5} - 3\left( {2\sigma_{1} - \sigma_{2} } \right)\left( {1 - 5\beta_{1} } \right) - 2\left( {1 - 3\beta_{1} } \right)\left( {1 - \beta_{1} } \right)^{2} }}{{2\beta_{1} \left( {1 - \beta_{1} } \right)^{5} }}} \right], \\ U_{yy}^{o} = & D\mu \left[ {\frac{{2n^{2} \left( {1 - \beta_{1} } \right)^{5} - 2\left( {1 - \beta_{1} } \right)^{2} - 3\left( {2\sigma_{1} - \sigma_{2} } \right)}}{{2\beta_{1} \left( {1 - \beta_{1} } \right)^{5} }}} \right], \\ U_{zz}^{o} = & - D\left[ {2\pi \rho_{1} A_{2} + \frac{{2\mu \left( {1 - \beta_{1} } \right)^{2} + 3\mu \left( {4\sigma_{1} - \sigma_{2} } \right)}}{{2\left( {1 - \beta_{1} } \right)^{5} }}} \right]. \\ \end{aligned} $$

Substituting these values in the system (19) in order to obtain

$$ \begin{aligned} \ddot{\xi } - 2n\dot{\eta } = & U_{xx}^{o} \xi \\ \ddot{\eta } + 2n\dot{\xi } = & U_{yy}^{o} \eta \\ \end{aligned} $$
(20)
$$ \ddot{\zeta } = - D\left[ {2\pi \rho_{1} A_{2} + \frac{{2\mu \left( {1 - \beta_{1} } \right)^{2} + 3\mu \left( {4\sigma_{1} - \sigma_{2} } \right)}}{{2\left( {1 - \beta_{1} } \right)^{5} }}} \right]\zeta $$
(21)

Equation (21) is independent of the system of Eq. (20), and its solution being periodic is bounded and therefore the motion of the infinitesimal mass along the z-axis is stable. The system (20) has solutions of the form

$$ \begin{aligned} \xi = & c_{1} \, \exp (\lambda t) \\ \eta = & c_{2} \, \exp (\lambda t) \\ \end{aligned}$$

where c 1 and c 2 are constants provided λ is a root of the characteristic equation

$$ \lambda^{4} - (U_{xx}^{o} + U_{yy}^{o} - 4n^{2} )\lambda^{2} + U_{xx}^{o} U_{yy}^{o} = 0 $$

This equation is quadratic in λ 2, and its roots are

$$ \begin{gathered} \lambda_{1}^{2} = \frac{1}{2}\left[ {U_{xx}^{o} + U_{yy}^{o} - 4n^{2} + \sqrt {(U_{xx}^{o} + U_{yy}^{o} - 4n^{2} )^{2} - 4U_{xx}^{o} U_{yy}^{o} } } \right] \hfill \\ \lambda_{2}^{2} = \frac{1}{2}\left[ {U_{xx}^{o} + U_{yy}^{o} - 4n^{2} - \sqrt {(U_{xx}^{o} + U_{yy}^{o} - 4n^{2} )^{2} - 4U_{xx}^{o} U_{yy}^{o} } } \right] \hfill \\ \end{gathered} $$

The equilibrium point is stable if the following conditions are satisfied

$$ \lambda_{1}^{2} + \lambda_{2}^{2} = U_{xx}^{o} + U_{yy}^{o} - 4n^{2} < 0 , $$
(22)
$$ \lambda_{1}^{2} \lambda_{2}^{2} = U_{xx}^{o} U_{yy}^{o} > 0 . $$
(23)

By neglecting second and higher powers of α, β1, σ1 and σ2, we can write

$$ \begin{aligned} U_{xx}^{o} = & 3D\mu \left( {\frac{\alpha }{{2\beta_{1} }}} \right), \\ U_{yy}^{o} = & 3D\mu \left( {\frac{\alpha }{{2\beta_{1} }} - 1} \right). \\ \end{aligned} $$

Here, we find that

$$ \begin{aligned} & \left( a \right){\text{ if }}\beta_{1} < 0,{\text{ then }}U_{xx}^{o} {\text{ < 0 and }}U_{yy}^{o} < 0; \\ & \left( b \right){\text{ if }}0 < \beta_{1} < \frac{1}{2}\alpha , {\text{ then }}U_{xx}^{o} {\text{ > 0 and }}U_{yy}^{o} > 0; \\ & \left( c \right){\text{ if }}0 < \frac{1}{2}\alpha < \beta_{1} , {\text{ then }}U_{xx}^{o} {\text{ > 0 and }}U_{yy}^{o} < 0. \\ \end{aligned} $$

Hence, if β 1 < 0, the equilibrium point is stable since the conditions required are satisfied. For \( 0 < \beta_{1} < \frac{1}{2}\alpha \), the condition (23) is satisfied; but if in addition (22) is satisfied, and then the equilibrium point is stable. Under the inequality \( 0 < \frac{1}{2}\alpha < \beta_{1} \), the condition (23) is not satisfied, so the equilibrium point is unstable. To the first order, the triaxiality of the second primary has thus no significant effect on the stability of the equilibrium point (β 1, 0, 0).

Similarly, for the stability of the axial equilibrium point (x 1 + β 2, 0, 0), the linearized variational equations are given as

$$ \begin{aligned} \ddot{\xi } - 2n\dot{\eta } = \,& U_{xx}^{\prime } \xi \\ \ddot{\eta } + 2n\dot{\xi } = \,& U_{yy}^{\prime } \eta \\ \end{aligned} $$
(24)
$$ \ddot{\zeta } = - D\left[ {2\pi \rho_{1} A_{2} + \frac{{2\mu \left( {1 - x^{\prime } } \right)^{2} + 3\mu \left( {4\sigma_{1} - \sigma_{2} } \right)}}{{2\left( {1 - x^{\prime } } \right)^{5} }}} \right]\zeta $$
(25)

where

$$ \begin{aligned} U_{xx}^{\prime } =\, & D\mu \left[ {\frac{{2n^{2} \left( {1 - x^{\prime } } \right)^{5} - 3\left( {2\sigma_{1} - \sigma_{2} } \right)\left( {1 - 5x^{\prime } } \right) - 2\left( {1 - 3x^{\prime } } \right)\left( {1 - x^{\prime } } \right)^{2} }}{{2x^{\prime } \left( {1 - x^{\prime } } \right)^{5} }}} \right], \\ U_{yy}^{\prime } =\, & D\mu \left[ {\frac{{2n^{2} \left( {1 - x^{\prime } } \right)^{5} - 2\left( {1 - x^{\prime } } \right)^{2} - 3\left( {2\sigma_{1} - \sigma_{2} } \right) - 6\left( {\sigma_{1} - \sigma_{2} } \right)x^{\prime } }}{{2x^{\prime } \left( {1 - x^{\prime } } \right)^{5} }}} \right], \\ x^{\prime } = \,& x_{1} + \beta_{2} \\ \end{aligned} $$

Equation (25) is independent of the system (24) and its solution being periodic is bounded. Thus, the motion along the z-axis is stable. The characteristic equation for the system (24) is given as

$$ \lambda^{4} - (U_{xx}^{\prime } + U_{yy}^{\prime } - 4n^{2} )\lambda^{2} + U_{xx}^{\prime } U_{yy}^{\prime } = 0 $$
(26)

Suppose \( \lambda_{1}^{\prime } \) and \( \lambda_{2}^{\prime } \) are its roots, then the axial equilibrium point is stable if the following conditions are satisfied:

$$ \lambda_{1}^{\prime 2} + \lambda_{2}^{\prime 2} = U_{xx}^{\prime } + U_{yy}^{\prime } - 4n^{2} < 0 $$
(27)
$$ \lambda_{1}^{\prime 2} \lambda_{2}^{\prime 2} = U_{xx}^{\prime } U_{yy}^{\prime } > 0 $$
(28)

Whenever, x 1 < 0, we have x ′ < 0 and since \( \left| {\beta_{2} } \right| \ll 1 \), we have \( U_{xx}^{\prime } < 0 \) and \( U_{yy}^{\prime } < 0 \), thus both conditions (27) and (28) are satisfied and so the equilibrium point is stable. Also, when x 1 > 0, the equilibrium point is stable provided the conditions (27) and (28) are satisfied.

Thus, we find that both oblateness and triaxiality of the primaries have significant effect on the stability of the equilibrium point (x 1 + β 2, 0, 0).

6.2 Stability of the Elliptical Points

At any elliptical point (x, y), the values of the second partial derivatives are

$$ \begin{aligned} U_{xz}^{o} = & 0, \, U_{yz}^{o} = 0, \\ U_{xx}^{o} = & 3D\mu \left[ {\left( {\sigma_{1} - \sigma_{2} } \right)\left( {1 + 2\cos \theta } \right) + } \right.\left. {\left\{ {1 + \frac{3\alpha }{2} - 3\sigma_{1} + \frac{{11\sigma_{2} }}{2} - 5\left( {\sigma_{1} - \sigma_{2} } \right)\left( {\cos \theta - \cos^{2} \theta } \right)} \right\}\cos^{2} \theta } \right] = U_{xx}^{*} ({\text{say}}), \\ U_{yy}^{o} = & 3D\mu \left[ {1 + \frac{3\alpha }{2} + 13\sigma_{1} - \frac{{21\sigma_{2} }}{2} - 5\left( {\sigma_{1} - \sigma_{2} } \right)\left( {\cos \theta + \sin^{2} \theta } \right)} \right]\sin^{2} \theta = U_{yy}^{*} ({\text{say}}), \\ U^{o}_{xy} = & 3D\mu \left[ {\left( {\sigma_{1} - \sigma_{2} } \right) + \left\{ {1 + \frac{3\alpha }{2} - \frac{{\sigma_{1} }}{2} + 3\sigma_{2} - 5\left( {\sigma_{1} - \sigma_{2} } \right)\left( {\cos \theta - \cos^{2} \theta } \right)} \right\}\cos \theta } \right]\sin \theta \, = U_{xy}^{*} ({\text{say}}), \, \\ U_{zz}^{o} = & - D\left[ {2\pi \rho_{1} A_{2} + 3\mu \sigma_{2} - 3\mu \left( {\sigma_{1} - \sigma_{2} } \right)\cos \theta + \mu n^{2} } \right] \\ \end{aligned} $$

So that the variational equations can be written as

$$ \begin{aligned} \ddot{\xi } - 2n\dot{\eta } = & U^{*}_{xx} \xi + U^{*}_{xy} \eta \\ \ddot{\eta } + 2n\dot{\xi } = & U^{*}_{xy} \xi + U^{*}_{yy} \eta \\ \end{aligned} $$
(29)
$$ \ddot{\zeta } = - D\left[ {2\pi \rho_{1} A_{2} + 3\mu \sigma_{2} - 3\mu \left( {\sigma_{1} - \sigma_{2} } \right)\cos \theta + \mu n^{2} } \right]\zeta $$
(30)

Equation (30) is independent of the system (29). Its solution is purely imaginary and so, the motion of the infinitesimal mass along the z axis is stable. The characteristic equation of motion of the system (29) can be written as

$$ \lambda^{4} - (U^{*}_{xx} + U^{*}_{yy} - 4n^{2} )\lambda^{2} + U^{*}_{xx} U^{*}_{yy} - (U^{*}_{xx} )^{2} = 0 $$

This equation is quadratic in λ 2 and so let λ 2 = Λ, then

$$ \Uplambda^{2} + h_{1} \Uplambda + h_{2} = 0 $$
(31)

where

$$ \begin{aligned} h_{1} = & 4n^{2} - \left( {U_{xx}^{*} + U_{yy}^{*} } \right) \\ h_{2} = & U_{xx}^{*} U_{yy}^{*} - \left( {U^{*}_{xy} } \right)^{2} \\ \end{aligned} $$

If Λ 1, Λ 2 be the two roots of Eq. (31), then elliptical points are stable if

$$ \begin{aligned} \Uplambda_{1} + \Uplambda_{2} = & - h_{1} \\ = & 3D\mu \left[ {1 + \frac{3}{2}\alpha + 9\sigma_{1} - \frac{13}{2}\sigma_{2} - 3\left( {\sigma_{1} - \sigma_{2} } \right)\left( {\cos \theta + 2\cos^{2} \theta } \right)} \right] - 4\left[ {1 + \frac{3}{2}\alpha + \frac{3}{2}\left( {2\sigma_{1} - \sigma_{2} } \right)} \right] < 0 \\ \end{aligned} $$
(32)

and

$$ \Uplambda_{1} \Uplambda_{2} = h_{2} = 9D^{2} \mu^{2} \left( {\sigma_{1} - \sigma_{2} } \right)\left[ {1 + 5\cos^{2} \theta - 6\cos^{4} \theta } \right] > 0 $$
(33)

Now, condition (32) holds for all values of D, σ 1 > σ 2, −1 ≤ cos θ ≤ 1, while condition (33) holds for D < 0, D > 0, σ 1 > σ 2, −1 < cos θ < 1. Therefore, the elliptical points are stable for, \( D > 0 \), σ 1 > σ 2 and −1 < cos θ < 1.

7 Conclusion

By considering the buoyancy force on the infinitesimal mass due to the fluid of the first primary, the hydrostatic equilibrium figure of the fluid of the first primary as an oblate spheroid and the shape of the second primary as a triaxial rigid body, we have seen the existence and stability of an axial equilibrium point (β 1, 0, 0) as in Hallan and Mangang (2007). When \( 1 - 2\pi \rho_{1} A_{1} < - \frac{3\mu }{4} \) and \( \left| {x_{1} } \right| < a_{1} \), there is another axial point (x ′, 0, 0) where x ′ = x 1 + β 2. If x 1 < 0, it is stable and if x 1 > 0, it is stable whenever both conditions (27) and (28) are satisfied. There also exist equilibrium points on the ellipse (16) lying within the first primary. These points, called the elliptical points, are stable if D > 0, σ 1 > σ 2 and −1 < cos θ < 1. The existence and stability of another axial point and elliptical points are affected by parameters involved due to buoyancy force, oblateness and triaxiality. The elliptical points have no analogies in the Robe’s problems studied under various aspects. It is also noticed that in the case when the second primary is spherical (σ 1 = σ 2 = 0), the elliptical points reduce to the circular points and are unstable. The model of this study can be applied to the study the oscillations of the Earth’s core caused by the attraction of the Moon because they are respectively oblate and triaxial.