Periodic Motions and their Stability in a N = ν + 1-body Regular Polygonal Configuration

Abstract

We present a systematic investigation of the parametric evolution of both retrograde and direct families of periodic motions as well as their stability in the inner region of the peripheral primaries of the planar N-body regular polygonal configuration (ring model). In particular, we study the change of the bifurcation points as well as the change of the size and dynamical structure of the rings of stability for different values of the parameters ν = N−1 (number of peripheral primaries) and β (mass ratio). We find some types of bifurcations of families of periodic motions, namely period doubling pitchfork bifurcations, as well as bifurcations of symmetric and non-symmetric periodic orbits of the same period. For a given value of N − 1, the intervals Δx and ΔC of the rings of stability (where the periodic orbits are stable) of both retrograde and direct families increase with β increasing, while for a given value of β, the interval ΔC decreases with increasing N − 1. In general, it seems that the dynamical properties of the system depend on the ratio (N − 1)/β. The size of each ring of stability tends to zero as the ratio (N − 1)/β → ∞, that is, if N − 1→∞ or β → 0, the size of each ring of stability tends to zero (Δx → 0 and ΔC → 0) and, in general, the retrograde and direct families tend to disappear. This study gives us interesting information about the evolution of these two families and the changes of the bifurcation patterns since, for example, in some cases the stability index A oscillates between −1 ≤ Α ≤ + 1. Each time the family becomes critically stable a new dynamical structure appears. The ratios of the Jacobian constant C between the successive critical points, C _i /C _i+1, tend to 1. All the above depend on the parameters N − 1, β and show changes in the topology of the phase space and in the dynamical properties of the system.

1 Introduction

The study of the basic qualitative properties of a multi-body problem is of considerable interest but has many difficulties. Many efforts have been made on this subject (Hadjidemetriou 1977, 1979; Palmore 1982; Meyer 1999; etc.). Reviews of this problem have been given by Hagihara (1970) and by Contopoulos (2002). The first who used models based on some geometrical properties of the real-physical systems were Euler in 1767 and Lagrange in 1773. They studied two particular cases of the planar three-body problem of equal masses: The collinear and the equilateral cases, respectively. In 1852 Maxwell extended these configurations in order to study the stability of the rings of Saturn. He considered, as a first approximation, a discrete particle ring of ν equal masses placed initially on the vertices of a regular polygon uniformly rotating around the central mass and introduced the planar N = ν + 1 body configuration. Several authors studied such models and found valuable qualitative and quantitative information (Willerding 1986; Ollongren 1988; Salo and Yoder 1988; Goudas 1991; Scheeres 1992; Scheeres and Vinh 1993; Moeckel 1995; Markellos et al. 1997; Roy and Steeves 1998; Mioc and Stavinschi 1998; Kalvouridis 1999a, b; Arribas and Elipe 2004; Pinotsis et al. 2002, Pinotsis 2005; Elipe et al. 2007; Arribas et al. 2007; 2008; Gousidou-Koutita and Kalvouridis 2009; Croustalloudi and Kalvouridis 2010, etc.).

Using this model of a coplanar N-body ring configuration (Scheeres 1992; Kalvouridis 1999a, b), which is supposed to be a “relative equilibrium configuration”, one can obtain interesting information about a test particle motion in different physical systems. This model consists of ν = N − 1 spherical and homogenous peripheral bodies of equal masses forming a regular polygon that rotates with constant angular velocity ω around a central spherical and homogenous primary. The mass of the central body M _C is equal to β times the mass m = m _i (i = 1, 2, …, ν) of a peripheral (β = M _C /m _i ). Thus, the N-bodies are considered as mass points. The test particle is considered as a massless body of motion, which does not influence the motion of the primaries of the system, that is, we have a restricted problem. The polygonal relative equilibrium configuration exists if and only if the masses on the vertices are equal (Perko and Walter 1985; Elmabsout 1988). We note that, in fact this configuration can be taken as an approximate ring if the number of the peripheral primaries is very large, ν > 10000.

The N-body ring model is a flexible dynamical system since the values of the parameters N − 1 and β can change. Thus, several systems of interest in the field of Celestial mechanics and stellar dynamics can be approached, using the N-body ring model. Such systems include the motions of a satellite in the asteroid belt and the motions of small bodies around planets or stars with rings. Also, some problems of two or more interacting galaxies as well as the planetary nebulae can be modeled (approximated) by the N-body ring problem.

Bang and Elmabsout (2003, 2004) gave the equations of a zero mass particle attracted by the above configuration, and the study of the existence and the stability of the relative equilibrium of this particle. Psarros and Kalvouridis (2005) studied the impact of the mass parameter β on the evolution of the characteristic curves and on the symmetric simple or multiple periodic orbits when N – 1 = 16, while in another paper (Hadjifotinou et al. 2006) these conclusions are extended to the families of three-dimensional periodic orbits for N – 1 = 7. Also, Kalvouridis (2008) presents many families of periodic motions in a variety of configurations (N – 1 = 8, 10, 12, 16, 32), while Mavraganis and Kalvouridis (2007) studied the regularization of the equations of motion.

In a previous work (Pinotsis 2005) we found four main families of periodic motions of test particle for different values of N − 1 and β in the planar Ν-body relative equilibrium configuration: Two families of periodic orbits around the central body, one retrograde in the fixed as well as in the rotating system and another one sidereally direct which is also synodically direct. Also two families around all the peripherals, one sidereally and synodically retrograde and another one direct in the fixed system and retrograde in the synodic system. We found that families of periodic orbits which surround one or more peripherals are generated from the four main families. For all these families, we gave their classification with respect to the relevant coordinate systems and primaries. We investigated their evolution as the Jacobian C changes as well as the type of their bifurcations, in the case of N – 1 = 7 and β = 2. The orbits of these families are stable and unstable. The stable orbits form rings of stability and we proposed a further study for different values of the parameters ν and β.

Although there exist many studies of the types of bifurcations and dynamical structure of the families of periodic orbits in the restricted three-body as well as in the general three body problem, there are only limited studies to this direction in the N-body ring problem. Therefore, these dynamical properties are worth of a further study for different values of the parameters N − 1 and β as we proposed in Pinotsis 2005. The aim of this work is to study the parametric evolution of both retrograde and direct families of periodic motions as well as their stability in the inner region of the peripheral primaries. In particular, we study the evolution of the different types of bifurcations as well as the change of the size and dynamical structure of their rings of stability, for different values of the parameters β (β = 0.01, 0.1, 2, 10, 100) and N − 1 (N – 1 = 4, 7, 24). The rings of stability are the intervals Δx, ΔC where the periodic orbits are stable. These rings are inside the peripheral primaries and encircle the central primary. In order to compare our results for different values of the parameters N − 1 and β, we consider the radius of the polygon, α, (i.e. the distance between the center of the polygon and the vertices) to be constant and discuss a general way to derive the equations of motion, using Cartesian tensors. This work shows, also, changes in the topology of phase space and gives interesting information for these dynamical systems.

Several authors studied the stability of the N-body relative equilibrium configurations, proved that the stability of such configurations depends on the parameters β and N − 1 and provided some bounds for these parameters in order the configuration to be stable (Tisserand 1889; Pendse 1935; Willerding 1986; Salo and Yoder 1988; Scheeres and Vinh 1991; Elmabsout (1994, 1996); Roberts 2000; Vanderbei and Koleman 2007; Vanderbei 2008; Arribas et al. 2008, etc.). Considering point-masses, in general, they have proved that for N – 1 ≤ 6 the relative equilibrium configuration is unstable, while for N – 1 ≥ 7 some of them gave some bounds for the parameter β in order the configuration to be stable. For example, Elmabsout (1994) studied the linear stability of these relative equilibrium configurations and found that these configurations can be linearly stable for ν ≥ 7, if β is greater than some function depending on ν and α. From this study we conclude for the linear stability of these configurations: (1) If 3 ≤ ν ≤ 6 then the configuration is linearly unstable for all values of β. (2) If 7 ≤ ν but not large (for very large values of ν, where the polygon approaches a ring, it can be linearly stable if $\beta > \frac{2}{5}\nu^{3}$) the configuration can be linearly stable if $\beta > \bar{\beta }_{o} (\nu )$ for an even ν, and if $\beta > \bar{\beta }_{1} (\nu )$ for an odd ν. Also, in Elmabsout (1996) it is proved that these configurations are not stable for the terms of the second order.

It has been also shown (Salo and Yoder 1988) that for ν ≤ 6 the configuration is locally unstable for equally spaced peripherals, for 2 ≤ ν ≤ 8 there exists another stable configuration (not equally spaced peripherals), for 7 ≤ ν and equally spaced peripherals the configuration is locally stable while for 9 ≤ ν the only possible stable configuration consists of equally spaced peripherals. Furthermore, Arribas et al. (2008) studied the linear stability of ring systems with generalized central forces and determined the region (μ, ε) (mass factor and radiation coefficient correspondingly) in which the system is stable for several values of N − 1. For N − 1 ≤ 6 (unstable cases) the system may become stable for negative values of ε.

Although the configuration is linearly unstable in some cases it makes sense, from theoretical interest as well as from an astronomical point of view, to study the motions of a test particle for the following reasons:

• The N = ν + 1 body configuration, where the ν = 3,4,5,… bodies have the same mass, m, and are located at the ν vertices of a regular polygon while the body having mass M _C is located at the center of the polygon, is only a theoretical model and not a realistic dynamical system. So, the investigation of the stability of such configurations as well as of the periodic motions of the test particle is a purely theoretical study. Our study aims to deliver an overview of the changes of the bifurcation patterns and the dynamical structure of such configurations when ν and β change.

Also, the test particle does not influence the motion of the primaries of the system (Szebehely 1967).

• The deformation (collapsing) time of the configuration is not known and may be considered very large. For example, the deformation time, in many dynamical systems in Astronomy, is of the order of Hubble time or of the evolution time of the star, as is the case in our planetary system.

• This work focuses on some extreme values of the parameters ν and β in order to get an insight of how the turning points in x and C and the bifurcation points as well as the size and dynamical structure of the rings of stability change with ν and β. If we omitted certain extreme values of the parameters ν and β (restricting thereby our study to stable configurations only) we could not obtain general conclusions and curves which will be useful in the future.

• The present study shows that the size of the rings of stability is larger in the retrograde case than in the direct case. Also, the direct family has more complex dynamical structure than the retrograde one and produces a large degree of chaos. These are very interesting for astronomical applications. Furthermore, the above work includes useful information which enriches our knowledge of various dynamical systems. These results can be compared with future work on e.g. the parametric evolution of families of non-symmetric periodic orbits, the study of the full N = ν + 1-rigid bodies ring configuration, the problem of different masses of the N = ν + 1-body ring configuration, etc.

2 Equations of Motion

In previous papers (Pinotsis et al. 2002, Pinotsis 2005) we used the equations of motion for a test particle in a N-body relative equilibrium configuration (ring model) appearing in Kalvouridis (1999a). In those equations the distance between two successive peripherals was considered constant. Thus, as the number of the peripherals increases the distance of each peripheral from the central body increases. The ring model is more realistic if we consider the radius of the polygon, α, to be constant. For example, we can approximate a continuous ring of matter where the gaps between the peripherals represent the variations of the ring’s density. These gaps are reduced in size as the number of the peripherals increases. Furthermore, we can compare the results for different values of ν and β as well as the corresponding relations are simpler. So, the equations of motion of a test particle are derived from scratch.

The equations of motion can be derived in three different ways (only the case of Cartesian tensors is presented here). We chose to derive the equations of motion of a test particle (Eqs. 12 or 14) by using Cartesian tensors. The present use of Cartesian tensors is an alternative approach which simplifies the calculations, especially in the case of higher dimensional problems. Let us suppose a rectangular fixed (sidereal) cartesian coordinate system OX₁X₂X₃ and a rectangular rotating (synodic) coordinate system Ox₁x₂x₃, with a common origin O. The central body is located at O, which is the common mass center of the relative equilibrium configuration (ring configuration). The transition from the coordinates of a test particle in the sidereal system to coordinates in a synodic system is a linear orthogonal transformation (first-order Cartesian tensor) and is given, in general, by (Goldstein 1980; Pinotsis 2002)

$$ {\rm {{\rm x}}}_{i} = \alpha_{ij}{\rm {\rm X}}_{j} ,\quad i, \,j = 1,2,3$$

(1)

or in matrix form x = ΑΧ where

$$ \alpha_{ij} = {\bf A} = \left( {\begin{array}{*{20}c}{\alpha_{11} } & {\alpha_{12} } & {\alpha_{13} } \\{\alpha_{21} } & {\alpha_{22} } & {\alpha_{23} } \\{\alpha_{31} } & {\alpha_{32} } & {\alpha_{33} } \\\end{array} } \right) $$

(2)

is the matrix of transformation or rotation matrix. Its elements are the direction cosines. The orthogonality conditions are |Α| = ±1 or

$$ \sum\limits_{k = 1}^{3} {\alpha_{ik} \alpha_{jk} } = \delta_{ij} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\;i = j} \\ 0 & {{\text{if}}\;i \ne j} \\ \end{array} } \right.,\quad i,\,j = 1,2,3 $$

(3)

where δ _ij is the Kronecker delta. The time in the fixed and synodic systems is the same, namely t _f  = t _r  = t. We take the time derivatives of the Eq. (1). Then,

$$ \ddot{x}_{i} = \alpha_{ij} \ddot{X}_{j} + 2\dot{\alpha }_{ij}\dot{X}_{j} + \ddot{\alpha }_{ij} X_{j}, \quad i,\,j = 1,2,3 $$

(4)

If we are restricted to two dimensional coordinate system we have i, j = 1, 2, x₁ → x, x₂ → y and X₁ → X, X₂ → Y, namely X, x are the abscissa and Y, y the ordinate of the particle motion in the sidereal OXY and the synodic Oxy systems, respectively (Fig. 1a). The rotating x-axis is the axis joining the central primary with one peripheral called peripheral 1. Also,

$$ \alpha_{ij} = {\rm \bf A} = \left( {\begin{array}{*{20}c}{\alpha_{11} }& {\alpha_{12} } \\ {\alpha_{21} }& {\alpha_{22} }\\\end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta}& {\sin \theta } \\ { - \sin \theta }&{\cos \theta }\\ \end{array} } \right) $$

(5)

where $\theta = \omega t\, (\dot{\omega } = 0)$ is the rotation angle which specifies the rotation. Then, Eqs. (1), (4) and (5) yield

$$ \begin{gathered} \left( {\begin{array}{*{20}c} {\rm{x}} \\\rm{y}\\\end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta} & {\sin \theta } \\ { - \sin \theta } & {\cos \theta } \\\end{array} } \right)\left( {\begin{array}{*{20}c} {\rm{X}} \\ {\rm{Y}} \\\end{array} } \right) \hfill \\ \left( {\begin{array}{*{20}c}{\dot{\rm{x}}} \\ {\dot{\rm{y}}} \\ \end{array} } \right) = \left({\begin{array}{*{20}c} {\cos \theta } & {\sin \theta } \\ { - \sin\theta } & {\cos \theta } \\ \end{array} } \right)\left({\begin{array}{*{20}c} {\dot{\rm{X}}} \\ {\dot{\rm{Y}}} \\\end{array} } \right) + \dot{\theta }\left( {\begin{array}{*{20}c}{ - \sin \theta } & {\cos \theta } \\ { - \cos \theta } & { - \sin\theta }\\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\rm{X}} \\ {\rm{Y}} \\\end{array} } \right) \hfill \\ \end{gathered} $$

(6)

and finally

$$ \left( {\begin{array}{*{20}c} {\ddot{\rm{x}}} \\{\ddot{\rm{y}}}\\\end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta} & {\sin \theta } \\ { - \sin \theta } & {\cos \theta }\\\end{array} } \right)\left( {\begin{array}{*{20}c} {\ddot{\rm{X}}} \\{\ddot{\rm{Y}}} \\ \end{array} } \right) + 2\dot{\theta }\left({\begin{array}{*{20}c} { - \sin \theta } & {\cos \theta } \\ {- \cos \theta } & { - \sin \theta } \\ \end{array} }\right)\left( {\begin{array}{*{20}c} {\dot{\rm{X}}} \\{\dot{\rm{Y}}} \\\end{array} } \right) + \dot{\theta }^{2} \left({\begin{array}{*{20}c} { - \cos \theta } & { - \sin \theta }\\ {\sin \theta } & { - \cos \theta }\\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\rm{X}} \\ {\rm{Y}} \\\end{array} } \right) $$

(7)

with ($\ddot{\theta } = \dot{\omega } = 0$).

Fig. 1

a The fixed (X, Y), and the rotating (x, y), coordinate systems. b The geometry of regular polygon and the relation of the angles

The transformation (1) is reversible and so we can write

$$ \text{\bf X} = {\text{\bf A}}^{ - 1} \text{\bf x} $$

(8)

if the Jacobian |Α| ≠ 0 and Α·Α ⁻¹ = Ι (Α ⁻¹ = Α ^Τ and Α ^Τ = Α ⁻¹).

Thus, Eq. (8) gives

$$ \left( {\begin{array}{*{20}c} {\text{X}} \\ {\text{Y}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } \\ {\sin \theta } & {\cos \theta } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\text{x}} \\ {\text{y}} \\ \end{array} } \right) $$

(9)

The gravitational forces applied to the test particle, P, by the central body and all the peripherals in the rotating Cartesian coordinate system are:

$$\begin{gathered} \text{F}_{\text{x}} = G\left[ {M_{C}{\frac{\text{x}}{{(\text{x}^{2} + {\text{y}}^{2})^{{{\raise0.7ex\hbox{3} \!\mathord{\left/ {\vphantom {32}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{2}}}}}}} + \sum\limits_{i = 1}^{\nu } {m_{i} } {\frac{{(\text{x -x}_{i} )}}{{[(\text{x - x}_{i} )^{2} + (\text{y - y}_{i} )^{2}]^{{\frac{3}{2}}} }}}} \right] \hfill \\ \text{F}_{\text{y}} =G\left[ {M_{C} {\frac{\text{y}}{{(\text{x}^{2} + \text{y}^{2})^{{{\raise0.7ex\hbox{3} \!\mathord{\left/ {\vphantom {32}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{2}}}}}}} + \sum\limits_{i = 1}^{\nu } {} m_{i} {\frac{(\text{{y -y}}_{{i}} )}{{[(\text{x - x}_{i} )^{2} + (\text{y - y}_{i} )^{2}]^{{\frac{3}{2}}} }}}} \right] \hfill \\ \end{gathered} $$

(10)

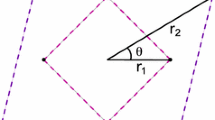
where $\text{r}_{c} = \sqrt {\text{x}^{2} + \text{y}^{2} },\text{r}_{i} = \sqrt {\left( {\text{x - x}_{i} } \right)^{2} +\left( {\text{y - y}_{i} } \right)^{2} } \quad (i = 1,2, \ldots\nu )$ are the distances of the test particle from the central body and each peripheral respectively and $\text{x}_{i} = \alpha \cos \varepsilon_{i} ,\,\text{y}_{i} = \alpha \sin \varepsilon_{i}$ (Fig. 1b)

If we take into consideration Eq. (6), the first and second derivatives of Eq. (9), as well as Eq. (10), then, in a rotating cartesian coordinate system, Eq. (7) becomes:

$$ \begin{gathered} \ddot{\text{x}} - 2\dot{\theta }\dot{\text{y}}- \dot{\theta }^{2} \text{x} = - G\left[ {M_{C}{\frac{\text{x}}{{(\text{x}^{2} + \text{y}^{2})^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {32}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}}}} + \sum\limits_{i = 1}^{\nu } {m_{i} } {\frac{{(\text{x -x}_{i} )}}{{[(\text{x - x}_{i} )^{2} + (\text{y - y}_{i} )^{2}]^{{\frac{3}{2}}} }}}} \right] \hfill \\ \ddot{\text{y}} +2\dot{\theta }\dot{\text{x}} - \dot{\theta }^{2} \text{y} = -G\left[ {M_{C} {\frac{\text{y}}{{(\text{x}^{2} + \text{y}^{2})^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {32}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}}}} + \sum\limits_{i = 1}^{\nu } {m_{i} } {\frac{{(\text{y -y}_{i} )}}{{[(\text{x - x}_{i} )^{2} + (\text{y - y}_{i} )^{2}]^{{\frac{3}{2}}} }}}} \right] \hfill \\ \end{gathered} $$

(11)

The above differential equations of motion are set in dimensionless form using the dimensionless variables x = x/α, y = y/α, r _C  = r_C/α, r _i  = r_i/α, β = M _C /m _i and τ = ωt, where α is the distance of each peripheral from the central body (as unit length), ω the angular velocity of the synodic frame and m _i is the mass of a peripheral. The following equations are obtained.

$$ \begin{gathered} \ddot{x} - 2\dot{y} - x = - {\frac{{Gm_{i} }}{{\alpha^{3} \omega^{2} }}}\left[ {\beta {\frac{x}{{r_{c}^{3} }}} + \sum\limits_{i = 1}^{\nu } {{\frac{{(x - x_{i} )}}{{r_{i}^{3} }}}} } \right], \hfill \\ \ddot{y} + 2\dot{x} - y = - {\frac{{Gm_{i} }}{{\alpha^{3} \omega^{2} }}}\left[ {\beta {\frac{y}{{r_{c}^{3} }}} + \sum\limits_{i = 1}^{\nu } {{\frac{{(y - y_{i} )}}{{r_{i}^{3} }}}} } \right] \hfill \\ \end{gathered} $$

(12)

The geometry of the regular polygon yields the following relations for the angles (Fig. 1b)

$$ \varepsilon_{i} = {\frac{2\pi }{\nu }}\left( {i - 1} \right)\quad \text{and}\quad \varphi_{i} = {\frac{{\pi - \varepsilon_{i} }}{2}},\quad i = 2, \ldots \nu $$

The distance between the peripheral (1), P ₁, lying on the x-axis of the synodic frame and the ith peripheral, P _i , is (Fig. 1b) $d = {\frac{{\alpha \sin \varepsilon_{i} }}{{\sin \varphi_{i} }}} = 2\alpha \, \sin {\frac{{\varepsilon_{i} }}{2}}$

Due to the planar circular motion of each peripheral the balance of the gravitational and centrifugal forces requires that

$$ {\frac{{\alpha^{3} \omega^{2} }}{{Gm_{i} }}} = \beta + \sum\limits_{i = 2}^{\nu } {{\frac{1}{{4\sin {\frac{{\varepsilon_{i} }}{2}}}}}} = {\rm K} $$

(13)

which is a generalization of Kepler’s third law. This relation is imposed by the relative equilibrium condition.

Finally, the dimensionless equations of motion have the form

$$ \ddot{x} - 2\dot{y} = - {\frac{\partial U}{\partial x}} \, ,\quad \, \ddot{y} + 2\dot{x} = - {\frac{\partial U}{\partial y}} $$

(14)

where U is the potential function. This potential function is time independent and is given by

$$ U = - \frac{1}{2}(x^{2} + y^{2} ) - \frac{1}{K}\left[ {{\frac{\beta }{{r_{c} }}} + \sum\limits_{i = 1}^{\nu } {{\frac{1}{{r_{i} }}}} } \right] $$

(15)

The Hamiltonian of the test particle in the sidereal system is time dependent, while in the rotating system the second members of the equations of motion Eqs. (14), (15) are time independent, so the system is of two degrees of freedom.

Thus, for N constant, this dynamical system is characterized by the parameter β, as in the case of the restricted three-body problem. In general, due to the symmetry of the problem, this dynamical system depends on the two parameters β and ν = N − 1 (Eqs. 12, 15). The Jacobian integral of Eq. (14) is given by the following relation

$$ C = {\frac{{\left( {\dot{x}^{2} + \dot{y}^{2} } \right)}}{2}} + U $$

(16)

where C is the so-called Jacobian constant. Equations (14) and (16) are similar to the respective ones of the restricted 3-body problem (Szebehely 1967). The above Jacobian constant is different from that of the previous paper (Pinotsis 2005).

3 Results and Discussion

We considered families of simple symmetric periodic orbits (main families) with respect to the rotating x-axis (the axis joining the central primary with one peripheral called peripheral 1), in the physical plane (x, y), starting perpendicularly to this axis with dy/dτ < 0 or dy/dτ > 0 for the retrograde and direct orbits correspondingly. The value of $\dot{y}$ can be calculated from the Jacobi integral. These periodic orbits, with initial conditions ($x_{o} ,\;y_{o} = 0,\;\dot{x}_{o} = 0,\;C\;{\text{or}}\;\dot{y}_{o}$), cross again also the x-axis perpendicularly inside all the peripherals and surround the central primary.

Also, we study non-symmetric periodic solutions with respect to the x-axis, with initial conditions ($x_{o} ,y_{0} = 0,\dot{x}_{o} ,\;C\;{\text{or}}\;\dot{y}_{o}$). By varying the Jacobi constant C, the values of x, $\dot{x}$ and $\dot{y}$ also vary continuously. In order to calculate a non-symmetric periodic orbit, initial conditions (x _o, y _o = 0, $\dot{x}_{0}$, $\dot{y}_{0}$) are given and a Newton method is then applied. Each orbit intersects again the y = 0 axis with $\dot{y}$ in the same direction as $\dot{y}_{0}$ and at the point x, $\dot{y}$, $\dot{x}$. If we consider x, $\dot{x}$ as functions f _i (i = 1, 2) of initial values of x ₀, $\dot{x}_{0}$ then (Pinotsis 2010),

$$ x = f_{1} (x_{0} ,\dot{x}_{0} ),\quad \dot{x} = f_{2} (x_{0} ,\dot{x}_{0} ) $$

(17)

In order to find a periodic orbit we give a small change of the initial conditions, Δx ₀, Δ$\dot{x}_{0}$ which implies a change of the final point Δx, Δ$\dot{x}$. In order for the orbit to be periodic we must have,

$$ \begin{gathered} x_{0} + \Updelta x_{0} = f_{1} (x_{0} + \Updelta x_{0} ,\dot{x}_{0} + \Updelta \dot{x}_{0} ) \hfill \\ \dot{x}_{0} + \Updelta \dot{x}_{0} = f_{2} (x_{0} + \Updelta x_{0} ,\dot{x}_{0} + \Updelta \dot{x}_{0} ) \hfill \\ \end{gathered} $$

(18)

Neglecting terms of order higher than one in Taylor’s expansion, in matrix form Eqs. (18) can be written

$$ \left( {\begin{array}{*{20}c} {x_{0} } \\ {\dot{x}_{0} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\Updelta x_{0} } \\ {\Updelta \dot{x}_{0} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} x \\ {\dot{x}} \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {a_{1} } & {a_{2} } \\ {a_{3} } & {a_{4} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\Updelta x_{0} } \\ {\Updelta \dot{x}_{0} } \\ \end{array} } \right) $$

(19)

or

$$ \left( {\begin{array}{*{20}c} {a_{1} - 1} & {a_{2} } \\ {a_{3} } & {a_{4} - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\Updelta x_{0} } \\ {\Updelta \dot{x}_{0} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {x_{0} - x} \\ {\dot{x}_{0} - \dot{x}} \\ \end{array} } \right) $$

(20)

where ${\frac{{\partial f_{1} }}{{\partial x_{0} }}} = a_{1} ,\;{\frac{{\partial f_{1} }}{{\partial \dot{x}_{0} }}} = a_{2} ,\;{\frac{{\partial f_{2} }}{{\partial x_{0} }}} = a_{3} ,\;{\frac{{\partial f_{2} }}{{\partial \dot{x}_{0} }}} = a_{4}$

The quantities a ₁, a ₂, a ₃, a ₄ can be found by calculating two orbits near the original one with deviations (Δx ₀, 0) and (0, $\Updelta \dot{x}_{0}$). Since we neglected higher order terms in Taylor’s expansion the solution of the system (20) does not give exactly the periodic orbit. Adding the increments Δx ₀, $\Updelta \dot{x}_{0}$, given by Eq. (20), to x ₀, $\dot{x}_{0}$ we obtain better initial conditions for the next iteration. This iterative process has to be repeated a number of times in order to give a periodic orbit with the required accuracy.

For the numerical integration of equations of motion (12) or (14) and the evaluation of the stability of periodic orbits, in double precision, we used the same methods as in the previous work (Pinotsis 2005). We used two programs for the computation of the symmetric and non-symmetric periodic orbits. In general, for each family we find the initial value of x, x _o , as a function of C. Thus the curve x _o  = x _o (C), which we call characteristic curve of a family of periodic orbits, is a curve giving the initial conditions (x _o , C) of the periodic orbits, so it gives the evolution of the family (Szebehely 1967; Contopoulos 2002).

The stability of periodic orbits is studied by evaluation of Hénon (1965) stability indices (coefficients) a, b, c, d, which are functions of the initial values $x_{0} , \dot{x}_{0}$ and the Jacobian C. The periodic orbits are stable if

$$ \left| {\rm A} \right| = \left| {a + d} \right|/2 < 1, $$

while for a symmetric periodic orbit we have a = d, hence |Α| = |a| < 1. The accuracy in the calculation of these coefficients is checked using their Jacobian determinant, which should be ad − bc = 1. We calculate the values of Α as a function of C. The stability index curve is the function A = A(C) (Hénon 1965). This curve gives the evolution of the stability of the family. Depending on the values of the stability coefficients we have for each characteristic curve six types of critical points (Hénon 1965).

In the case where A = +1 and c = 0, we have a critical point of type 1, 2 or 3. In the case of type 1 the main family—the characteristic curve of the main family—has an extreme in C, maximum or a minimum, at a point (x _o , C) (turning points in C) and is called a saddle-node bifurcation or a tangent bifurcation (Contopoulos 2002). There exist two branches, one stable and the other unstable. Also, in the critical point of type 2 we have intersection of a family of symmetric simple periodic orbits, while in the case of type 3 we have a bifurcation of a new family of symmetric simple periodic orbits of the same period which presents an extreme in C. In the case where A = +1 and b = 0 the main family produces by bifurcation a new family of simple non-symmetric periodic orbits of the same period (critical point of type 4). The bifurcating family is outside the plane (x _o , C), with initial conditions ($x_{o} ,\dot{x}_{o} ,C$). Whenever the stability curve reaches the value A = −1 a new family of symmetric double periodic orbits bifurcates. If c = 0 or b = 0 we have a critical orbit of type 5 or 6 correspondingly. In the critical point of type 5 the corresponding critical periodic orbit has a perpendicular (initial conditions (x _o , C)) and an oblique (initial conditions ($- x_{o} ,\dot{x}_{o} ,C$)) intersection with the x-axis and in the case of type 6 the critical orbit has an oblique (initial conditions ($x_{o} ,\dot{x}_{o} ,C$)) and a perpendicular (initial conditions (−x _o , C)) intersection with the x-axis (Hénon 1965). Because of the symmetry of the periodic motion we calculated only the first half of the orbit (Pinotsis 1987, 2005).

We considered the main families of simple symmetric periodic orbits, both retrograde and direct that surround the central body. We can say that the beginning of these families corresponds to Poincaré (1899) orbits of the first kind because these families are generated from infinitesimal (circular) orbits around the central primary (Pinotsis 2005).

We studied the evolution of these two main families as the parameters N − 1 and β change. In particular, we investigated the evolution of these families in x _o with respect to the Jacobian constant C, x _o = x _o(C) and in the cases of N − 1 = 4, 7, 24 and for the values of β = 0.01, 0.1, 2, 10, 100 for each case of N − 1. We focused on bifurcation points and types of their bifurcations as well as the size and dynamical structure of the rings of stability. We did not study orbits passing between the peripherals because they are generated from the four main families mentioned in the introduction (Pinotsis 2005). Also, these families are, in general, strongly unstable, while their number increases as the value of the parameter ν = N−1 increases (Pinotsis 2005).

The stability index curve Α = Α(C) is some times between −1 and 1 (and tends to 1 for large absolute value of C as x _o → 0) for an interval of C, which characterizes each case. We have successive bifurcations of different types from the same main family and interesting bifurcation patterns. We have found certain types of bifurcations, namely period doubling pitchfork bifurcations of families of periodic motions as well as families of symmetric and non-symmetric periodic orbits of the same period. The stable bifurcating families undergo further period doubling bifurcations. Due to lack of space we include only 16 plots of the functions x _o  = x _o (C) and A = A(C).

3.1 Retrograde family I _R (Sidereally and synodically retrograde orbits)

3.1.1 (a) Case N – 1 = 4 and β = 0.01, 0.1, 2, 10 and 100

The characteristic curves and the respective stability index diagrams of the family of retrograde periodic orbits, only for β = 0.01 and 100, are presented in Figs. 2a, b, 3a, b, respectively. From all such curves, that do not appear here, it is obvious that, in general, the orbits of this type evolve in a similar way for all values of β. Near the central body, for absolute C increasing and C → −∞, the orbits tend to shrink to the center (the absolute value of their initial condition x _oin → 0) while the stability index Α → 1 and so the orbits tend to be “critically” stable (Pinotsis 2005). We stopped the numerical calculations at the point (C _in, x _oin) characteristic for each value of β (Table 1 in Electronic supplementary material, ESM). When the absolute C decreases, the orbits go far from the central body (the absolute value of x _o becomes larger and larger). Furthermore, as the absolute C decreases the stability index also decreases until the value Α = −1 (b = c = 0) at a point (x _o, C), characteristic for each value of β (Table 1 in ESM). Thus, these points are bifurcation points 1 → 2 of type 5 and 6 simultaneously and we have there bifurcations of two new families of double symmetric periodic orbits, R _b , R _c , with two branches each in the form of a pitchfork. These families are symmetric to one another with respect to the origin and so they have similar stability curves and similar sequences of critical points. This is due to the symmetry of the problem. At each bifurcation point the stability curve is tangent to the straight line Α = −1. At this critical point the corresponding critical periodic orbit belongs to three different families: the main family of simple symmetric periodic orbits and the two families R _c , R _b of double symmetric periodic orbits, which contain periodic orbits symmetric to one another with respect to the origin. We found that for β = 100 the negative value of C becomes C = 0 and then C takes positive values (Figs. 2b, 3b).

Fig. 2

The characteristic curves of the family of retrograde periodic orbits, for the four cases a, b (N – 1 = 4, for β = 0.01, 100) and c, d (N – 1 = 24, for β = 0.01, 100), which have a turning point. The dotted (dashed) lines show that the characteristic curves approach very close to the central body

Fig. 3

The stability curves of the family of retrograde periodic orbits, for the four cases a, b (N – 1 = 4 for β = 0.01 and 100) and c, d (N – 1 = 24 for β = 0.01 and 100). Dotted lines show that the family is unstable and goes to larger and larger instability

After this critical point, as absolute C decreases, for β = 0.01–10, or the positive C increases, for β = 100, further, the stability index increases and the family becomes critically stable, with Α = 1 (c = 0, b ≠ 0), at a final critical point-turning point in C, (x _ofn, C _fn) characteristic for each value of β (Table 1 in ESM). The characteristic curve of the family has there a minimum absolute (negative) C, for β = 0.01–10, or a maximum (positive) C, for β = 100 (Fig. 2a, b). Following the family beyond this turning point the periodic orbits approach the peripherals, the absolute value of x _o increases, as the absolute C increases, for β = 0.01–10, or decreases for β = 100 while the family becomes more and more unstable until a collision with a primary occurs and then a new family of symmetric periodic orbits passing between the peripherals is generated. We stopped the numerical calculations at the points at which their stability parameter is very large (of order 10⁴–10⁶).

3.1.2 (b) Cases N – 1 = 7 and 24, for β = 0.01, 0.1, 2, 10 and 100

We found the characteristic curves and the respective stability diagrams of the family of retrograde periodic orbits, for N − 1 = 7 and 24 and β = 0.01, 0.1, 2, 10, 100. Figures 2c, d, 3c, d show the characteristic curves and the corresponding stability diagrams of the family only for β = 0.01 and 100 and N – 1 = 24. From all such diagrams (that do not show here) we conclude that in these two cases the family evolve, as C changes, in a similar way as in the previous case N – 1 = 4 and β = 0.01, 0.1, 2, 10, 100 (Tables 2, 3 in ESM). So we do not give a detailed description of the evolution of these orbits. We note that for β = 100 and N – 1 = 24 the characteristic curve does not extend to the positive values of C and so the family does not exist for positive C, as in the two cases N – 1 = 4 and 7.

In the two cases (N – 1 = 7, 24), we continued the evolution of the family after the final critical-turning-point in C (x _ofin, C_fin) for each value of β. As the absolute value of C increases or decreases for the case N − 1 = 7 and β = 100 the family, for each value of β, becomes more and more unstable and after a while, a collision with a primary appears and finally a new family of symmetric periodic orbits among the peripherals is generated. For the case N – 1 = 24 and β = 0.01, the family, after its turning point in C, presents a maximum absolute x _o-turning point in x _o-as the absolute value of C increases and then the initial conditions of the periodic orbits move towards the central primary (Fig. 2c, d; Tables 2, 3 in ESM). We stopped the numerical calculations at the points where the stability parameter is very large (of order 10⁵–10⁶).

As in the previous case (a), we stopped the numerical calculations at about the same distance from the central body and very close to it, x _oin, at which the Jacobi constant is C _in. In all cases (N – 1 = 4, 7 and 24) we found that for each value of β there exists a stable ring in the inner region of the peripherals between (x _oin < 0, x _ofin) and (−∞ < C _in, C _fin). The stable rings have a bifurcation point 1 → 2, one turning point in C and two stable segments.

We compared the results of the above (a) and (b) cases. Although these results seem to be similar for almost all the values of β and N − 1, there are differences between them. Specifically, for each N − 1, we see that the initial conditions of periodic orbits of the bifurcation point 1 → 2 as well as those of the final critical point-turning point in C (x _ofin, C _fn) shift towards the peripheral primaries more and more as the parameter β increases (Tables 1, 2, 3 in ESM). Also, for each N − 1, very close to the central primary, in approximately the same distance from it, x _oin, the Jacobian C _in takes larger and larger absolute values with increasing β. So, for each N − 1, the size of the ring of stability in x _o and C, that is the intervals Δx = |x _oin − x _ofn| and ΔC = |C_in − C_fn|, between the initial conditions (x _oin, C _in) and those of the final critical point-turning point in C (x _ofn, C _fn), becomes larger and larger as the parameter β increases (Figs. 4, 5). On the contrary, the size of the ring of stability shrinks more and more when the parameter β decreases and it tends to zero as β → 0.

Fig. 4

The interval Δx of the ring of stability as function of the cases N − 1 = 4, 7 and 24, for the values of β = 0.01, 0.1, 2, 10 and 100 in the retrograde family

Fig. 5

The interval ΔC of the ring of stability as function of the cases N − 1 = 4, 7 and 24, for the values of β = 0.01, 0.1, 2, 10 and 100 in the retrograde family

From Tables 1, 2 and 3 in ESM and Figs. 4 and 5 we see that: In general, for all values of the parameters β and N − 1 the rings of stability have similar bifurcation patterns and thus similar dynamical structure. There are two rings, one stable and another unstable. For each value of β the initial conditions of the turning point in C as well as those of the bifurcation points 1 → 2 of the family of periodic orbits shift towards the central body as the parameter N − 1 increases. Also, very close to the central body and at about same distance from it the absolute value of C decreases by increasing the parameter N − 1. Therefore, the size of each ring of stability, (Δx, ΔC), decreases more and more as the parameter N − 1 increases. Figures 6 and 7 show diagrams of the intervals ΔC and Δx, respectively as function of the ratio (N − 1)/β. From these diagrams we also see that as (N − 1)/β → ∞, that is, if (N − 1) → ∞ or β → 0 the size of the rings of stability tends to zero (Δx → 0 and ΔC → 0) and, in general, the retrograde family tends to disappear.

Fig. 6

ΔC as function of the ratio (N − 1)/β in the retrograde family

Fig. 7

Δx as function of the ratio (N − 1)/β in the retrograde family

3.2 Direct family I _D (Sidereally and synodically direct orbits)

In this case the results give us rich information for the dynamical behaviour of this family with respect to the change of the parameters β and N − 1. Actually, this family presents new dynamical properties compared to the retrograde cases.

We followed the evolution of the main family of direct symmetric periodic orbits with respect to C and for the cases N – 1 = 4, 7 and 24 and β = 0.01, 0.1, 2, 10, 100. In general, we found that, near the central body the characteristic curves have similar behavior in these cases, that is, as the absolute C decreases the orbits go far from the central primary, while they move towards it more and more and x _oin → 0 as the absolute C increases and C → −∞. In this case the orbits tend to be “critically” stable (Α → 1) (Pinotsis 2005) (here we do not show all the figures, see for example Figs. 8, 9). We stopped the numerical calculations at the point (C _in, x _oin) characteristic for each N − 1 and β (Tables 4, 5, 6 in ESM). Furthermore, as the absolute value of the Jacobian constant decreases, the change of the stability index presents some differences between these cases. Namely:

Fig. 8

The characteristic curves of the family of direct periodic orbits, for the four cases a, b (N – 1 = 4 for β = 0.01 and 100) and c, d (N – 1 = 24 for β = 0.01 and 100), which have a final critical-turning-point in C. In the case b three turning points in x _o appear (two maxima and one minimum that can not be seen here). The dotted (dashed) lines show that the characteristic curves approach very close to the central body

Fig. 9

The stability curves of the family of direct periodic orbits for the four cases a, b (N – 1 = 4 for β = 0.01 and 100) and c, d (N – 1 = 24 for β = 0.01 and 100). In the b case, nine critical points and three stable and three unstable rings are formed, while in the d case, seven critical points and seven stable segments appear, that can not be seen here. The dotted lines show that the family is unstable and goes to larger and larger instability

3.2.1 (a) Case N – 1 = 4 and β = 0.01, 0.1, 2, 10 and 100

For the case β = 0.01, the stability parameter decreases and after it reaches a minimum value (Α = 0.8394258) it starts to increase and becomes equal to A = 1 (b = c = 0) at the point (x _o, C) (Table 4 in ESM, Fig. 9a). In this transition point the stability curve is tangent to the straight line Α = 1. Thus, there is a bifurcation with two new families of symmetric and non-symmetric periodic orbits of the same period. As we continue to decrease the absolute C, the stability index decreases again and becomes Α = −1 (b = c = 0) at the point (x _o, C). Thus, this critical point is a bifurcation point 1 → 2 and produces two new families of double symmetric periodic orbits with two branches in the form of the pitchfork. These families are symmetric to one another with respect to the origin and the stability curve is tangent to the straight line Α = −1. Further calculations show that the coefficient Α increases again until the turning point (x _ofn, C _fn), at which the family has a minimum absolute C and loses its stability, with Α = 1 (c = 0, $b \ne 0$) (Table 4 in ESM, Figs. 8a, 9a). After this point, the absolute C increases while the orbits approach the peripherals-the absolute x _o increases-and the family continues to be unstable more and more until a collision with a primary occurs and then a new family passing between the peripherals is generated. We stopped the calculations at a point, at which the stability index is of order 10⁶. Thus, the family has two rings, one stable and another unstable. The ring of stability contains three critical points, with two bifurcation points and therefore it has three stable segments.

Regarding the value β = 0.1, as the absolute value of C decreases the stability index decreases until the value (Α = 0.81842542) and then starts to increase and it reaches the value Α = 1 (b = c = 0) as in the previous case. At this bifurcation point (x _o, C), (Table 4 in ESM) we have a bifurcation of two new families of symmetric and non-symmetric periodic orbits of the same period. The stability curve is tangent to the straight line Α = 1. Following the evolution of the family after this critical point the stability coefficient decreases and since it reaches a minimum negative value (Α = −0.010724) increases and takes again the value Α = 1 (b = c = 0) at the point (x _o, C). At this critical point two new families of symmetric and non-symmetric periodic orbits of the same period are generated. Further development of our calculations shows that as the characteristic curve extends to the peripheral primaries the stability parameter decreases continuously until the value A = −1 (b = c = 0) at the point (x _o, C). At this 1 → 2 transition point, at which the stability curve is tangent to the straight line A = −1, a bifurcation of two new families with double period emanates. With C decreasing further, the stability index begins to increase and at the point (x _o, C) we have again A = 1 (b = 0, $c \ne 0$). At this bifurcation point, which is of type 4, a new family of non-symmetric simple periodic orbits appears. After this point, as the characteristic curve goes towards the peripherals, the stability index increases more and more and takes very large values until the small body collides with a primary. We stopped the calculations at a point with A of order of 10⁶. Thus, the ring of stability has four bifurcation points and four stable segments.

We followed the evolution of the family for the cases β = 2 and 10 (Table 4 in ESM). A similar bifurcation pattern was found in these two cases. Near the central body, as the absolute C decreases, in the case β = 2, the stability index has a minimum (Α = 0.9705509). As the absolute C decreases further the stability index A increases and approaches very close 1 but does not become equal to 1. So, a bifurcation of a new family of symmetric or non-symmetric periodic orbits of the same period does not exist. Following the evolution of this family beyond the above point, the stability parameter decreases and reaches the critical value Α = −1 (b = c = 0). Also, regarding the case β = 10, as the absolute C decreases the stability index of the family does not present a minimum but it decreases continuously until the value A = −1 (b = c = 0). At this critical point of the two cases, two new families of double periodic orbits, symmetric to one another, are bifurcated. After this point, with the absolute value of C decreasing, the stability index increases and reaches the value A = 1 (b = 0, $c \ne 0$) and so the family (in the two cases) loses its stability. At this critical point of type 4 a new family of non-symmetric periodic orbits of the same period is generated. As C decreases further, beyond this point, the family in the two cases becomes more and more unstable. At the point (x _o, C) for the case β = 2 and (x _o, C) for the case β = 10 (Table 4 in ESM), the family has a maximum absolute x _o. The characteristics after this turning point extend towards the central primary with the absolute C decreasing while the stability index increases continuously and takes very large values. We stopped at the points at which the stability index is of order 10⁵–10⁶. In these two cases the ring of stability contains two bifurcation points and two stable segments.

Also, we found the characteristic curve of the family and its stability diagram for β = 100 (Table 4 in ESM, Figs. 8b, 9b). In this case, the main family of periodic orbits becomes successively stable and unstable and so successive bifurcating families from the main characteristic emanate, as the absolute C decreases. Namely, as in the previous case β = 10, the stability parameter decreases and takes the value Α = −1 (b = c = 0). With the absolute C decreasing, the stability index increases and becomes Α = 1 (b = 0, $c \ne 0$) and the family loses its stability. After this critical point the family presents a different dynamical behavior and a new bifurcation pattern. As the absolute Jacobian constant decreases further the family continues to be unstable, but at the point (x _o, C) it has a turning point in x _o. As the characteristic extends now towards the central primary the stability parameter reaches a maximum value (A = 14.0). As the absolute C decreases further the family has a second turning point in x _o at the point (x _o, C) and then the family becomes critically stable with A = 1 (c = 0, $b \ne 0$) at the point (x _o, C) (Table 4 in ESM). At this transition point, at which the family presents a second maximum —third turning point—in absolute x _o, a new family of simple symmetric periodic orbits is generated. So, the corresponding critical simple periodic orbit belongs to two different families. The new family is unstable in the neighborhood of the critical point. After this point, as the absolute C decreases further the characteristic extends again towards the central primary while the stability index of the main family decreases and after it comes very close to −1, it increases again until A = 1 (c = 0, $b \ne 0$) and the family becomes unstable. Here a new family of symmetric periodic orbits of the same period emanates. Continuing the main family to lower absolute values of C we found that the stability index reaches a maximum value (A = 3.638) then decreases and reaches the value A = 1 (b = 0, $c \ne 0$). Here a new family of non-symmetric periodic orbits emanates. Beyond this critical point the stability index oscillates between −1 ≤ Α ≤ 1. The stability curve is tangent to the straight lines Α = −1 and Α = 1 (Table 4 in ESM). At the last critical point A = 1 (c = 0, $b \ne 0$), the family has a turning point in C (minimum absolute C) and the characteristic extends towards the central body, while the stability parameter takes larger and larger values (Figs. 8b, 9b). We stopped the calculations at point at which the value of Α is of order 10⁶. Consequently:

In this case (β = 100) three stable and three unstable rings are formed. The first ring of stability has two bifurcation points and two stable segments. A ring of instability follows and then another stable ring, which contains a stable segment. After that, two rings follow: an unstable and another stable one, which contains four bifurcation points (and five critical points) and four stable segments. Finally, an unstable ring follows.

Also, there exist a large number of bifurcated stable and unstable families that produce a large degree of chaos. The successive stable and unstable intervals, ΔC, along the characteristic of the main family have bifurcation ratios ΔC _i /ΔC _i+1 which are not consistent with a universal ratio. This ratio depends on the particular case (in general on the particular dynamical system) considered. If we take the ratios of the Jacobian constant of the successive critical points, C _1,−1/C _−1,1 = 25.5247, C _−1,1/C _1,1 = 1.07578, C _1,1/C _1,1 = 1.06521, C _1,1/C _1,1 = 1.03791, C _1,1/C _1,1 = 1.0119, C _1,1/C _1,1 = 1.02484, C _1,1/C _1,−1 = 1.00126, C _−1,1/C _1,−1 = 1.00031, C _1,−1/C _−1,1 = 1.0001 it seems that they tend to 1.

We note that in the last two cases (β = 10, 100) the stability index does not present a minimum close to the central primary. There is a critical value of β, β_cr, after which this minimum becomes smaller and smaller as β changes and for a certain value of β it disappears. So, the stability parameter does not reach the value Α = 1 and a new bifurcating family of simple symmetric or non-symmetric periodic orbits does not exist, as opposed to the cases β = 0.01 and 0.1.

3.2.2 (b) Cases N − 1=7 and 24, for β = 0.01, 0.1, 2, 10 and 100

We followed the evolution of the main family and we found its stability curves for the two values of N – 1 = 7, 24 and for the five values of β (Tables 5, 6 in ESM). From all the characteristic curves and the respective stability index diagrams, that are not included (only the Figs. 8c, d, 9c, d, that give the characteristics and the stability curves for β = 0.01 and 100 and N – 1 = 24, respectively, are presented here) we found that the family, except some cases, has different dynamical behavior. Specifically:

The cases of N – 1 = 7 and β = 0.01, 0.1, 2 and N – 1 = 24 for β = 0.01, 2 and 10 present a similar dynamical structure with the previous case of N – 1 = 4 and β = 0.01. As absolute value of C decreases from large values near the central body the characteristic curve of each case extents to the peripherals while the stability parameter decreases until it reaches a minimum value characteristic for each N − 1 and β (for the case N – 1 = 7, Α = 0.705838 for β = 0.01, Α = 0.66677868 for β = 0.1, Α = 0.21295041 for β = 2; for the case N – 1 = 24, Α = 0.06798 for β = 0.01 and Α = 0.001231 for β = 2) it increases and at the point (x _o, C) (Tables 5, 6 in ESM) it becomes Α = 1 (b = c = 0). At this critical point we have a bifurcation with two new families of symmetric and non-symmetric simple periodic orbits. Continuing each characteristic curve after this critical point, at which the stability curve is tangent to the straight line Α = 1, the stability index decreases again, with decreasing absolute C, and becomes tangent to the straight line Α = −1 (b = c = 0) at the critical point (x _o, C). At this 1 → 2 bifurcation point two new families of double symmetric periodic orbits, symmetric to one another with respect to the origin, are generated. After this bifurcation point, as the absolute C decreases further the stability parameter increases and takes again the value Α = 1 (c = 0, $b \ne 0$) at the point (x _o, C) characteristic for each N − 1 and β and the family has a turning point in C (Tables 5, 6 in ESM). As the absolute value of C increases and the absolute x _o increases the family becomes more and more unstable until a collision with a primary appears and then a new family passing between the peripherals is generated. We stopped the numerical calculations at a point at which the stability coefficient takes very large values (10⁶). The ring of stability contains three critical points, with two bifurcation points and three stable segments.

However, there exists a difference for the case N − 1 = 24 and β = 10. That is, as the absolute C decreases from large absolute values very close to the central primary, the stability coefficient of the family decreases and reaches a minimum (Α = 0.80622) then it increases and goes very close to 1 but does not take the value Α = 1. After this point, as the absolute C decreases further the stability index decreases again and after it takes a minimum negative value (Α = −0.388934) it starts to increase and becomes Α = 1 (b = c = 0). After this point the family continues as in the above cases (Table 6 in ESM).

The next cases β = 10 and 100 for N − 1 = 7 as well as β = 0.1 and 100 for N – 1 = 24, present an interesting bifurcation pattern.

Regarding the case β = 0.1 and N – 1 = 24, as the absolute value of the Jacobian constant decreases from large values close to the central body, the stability index decreases until the value (Α = 0.138182) and then it increases and reaches A = 1 (c = 0, $b \ne 0$). This critical point is a turning point in C (Table 6 in ESM). After this point, the absolute Jacobian constant increases as the absolute x _o increases while the stability of the family becomes larger and larger until a collision with a primary occurs. The family does not present any bifurcation and the size of the ring of stability consists of one stable segment. So the family in this case is more stable than in the other cases. We stopped the calculations at the point where the stability index is very large (10⁶).

As regards the cases β = 10 and 100 for N – 1 = 7 and β = 100 for N – 1 = 24, we found a different bifurcation structure from the previous cases. The stability index oscillates between −1 ≤ Α ≤ 1 where the stability curve, each time, is tangent to the straight lines Α = −1 and Α = 1 (Tables 5, 6 in ESM). So, successive bifurcations from the main (same) family are generated. Each time the family becomes critically stable a new dynamical structure appears. In these cases the family has more bifurcation points and so more new stable and unstable families of periodic orbits are generated, that produce a large degree of chaos. Specifically:

For the cases β = 10 and 100 for N – 1 = 7, near the central body, the stability parameter decreases until Α = −1 (b = c = 0) as the absolute value of the constant C decreases from large absolute values. At this critical point two new families of double periodic orbits emanate from the main family (Table 5 in ESM). We note that in the case β = 10 the stability coefficient has a very small minimum and then increases and it reaches a value very close to 1 but after it decreases until the value A = −1. Following the evolution of each characteristic curve of the main family beyond the transition point 1 → 2, as C continues to decrease each characteristic curve extends to the peripherals, while the stability index increases until the value Α = 1 (b = c = 0). At this point two new families of simple symmetric and non-symmetric periodic orbits appear. This behaviour is repeated one time yet, as absolute C decreases, while the family approaches more and more the peripherals and at the point (x _o, C), characteristic for each β, the stability coefficient takes again the value Α = −1 (c = 0). At this transition point 1 → 2 a new family of double symmetric periodic orbits is bifurcated. As C decreases still further the family becomes more and more unstable and after that a collision of the particle motion with one of the primaries occurs. We stopped the numerical calculations at the points where Α is of order 10⁶.

Also, for the case N – 1 = 24 and β = 100, the characteristic curves and the respective stability diagrams of the family are presented in Figs. 8d and 9d. With decreasing the absolute C from large values (close to the central body) the characteristic curve goes away from the central primary, while the stability coefficient decreases and becomes Α = −1 (b = c = 0) at the 1 → 2 bifurcation point (x _o, C) (Table 6 in ESM). As the absolute C decreases further the index Α increases and takes the value Α = 1(b = c = 0). Furthermore, the stability coefficient decreases and since it reaches a minimum value (Α = 0.947128) it increases and becomes again equal to Α = 1 (b = c = 0). After this bifurcation point the stability parameter decreases again and it reaches the value Α = −1 (b = c = 0). Then, it increases again and becomes Α = 1 (b = c = 0). As the absolute C decreases further the stability index takes one more time the value Α = −1 (b = c = 0) and it finally becomes Α = 1 ($b \ne 0$, c = 0) at the turning point in C (Table 6 in ESM). After this critical point, as the absolute C increases the characteristic curve extends to large absolute values of x _o while the family becomes more and more unstable. We stopped the numerical calculations at the point at which the stability index is Α = 1.4 × 10⁶. Consequently:

In these three last cases we have two rings, a stable and another unstable. In the two cases β = 10 and 100 for N – 1 = 7 the ring of stability has five bifurcation points and five stable segments, while seven critical points with six bifurcation points and seven stable segments exist in the stable ring of the case N – 1 = 24 and β = 100 (Tables 5, 6 in ESM). For each one of these three cases the stable intervals ΔC between the successive critical points along the main family have ratios, ΔC _i /ΔC _i+1, which are not universal because they depend on the particular case (in general depend on the dynamical system) considered. The ratios of the Jacobian constant between the successive critical points, are: For N − 1 = 7 and β = 10, C _1,−1/C _−1,1 = 14.4718, C _−1,1/C _1,−1 = 1.01473, C _1,−1/C _−1,1 = 1.00117, C _−1,1/C _1,−1 = 1.00068, C _−1,1/C _1,−1 = 1.00017; for β = 100, C _1,−1/C _−1,1 = 24.2573, C _−1,1/C _1,−1 = 1.08537, C _1,−1/C _−1,1 = 1.019266, C _−1,1/C _1,−1 = 1.00449, C _−1,1/C _1,−1 = 1.001104. Also, for N − 1 = 24 and β = 100, C _1,−1/C _−1,1 = 20.879121, C _−1,1/C _1,1 = 1.070588, C _1,1/C _1,−1 = 1.061836, C _1,−1/C _−1,1 = 0.948027, C _−1,1/C _1,−1 = 1.00008, C _−1,1/C _1,−1 = 1.00001, C _1,−1/C _−1,1 = 1.0000000. It is evident that in the three cases the ratios tend to 1.

The comparison of the results of above cases (a) and (b) shows that the majority of the critical points, for the cases β = 100 and N – 1 = 4, 24 and β = 10, 100 and N – 1 = 7, appears. It is remarkable that the most stable case of the family appears for N – 1 = 24 and β = 0.1 and the most unstable for β = 100, N – 1 = 4 and 24.

Also, from all the above cases (Tables 4, 5, 6 in ESM; Figs. 10, 11) we see that for each N − 1 the initial conditions of the periodic orbit of the final critical points and for the first ring of stability for the case N – 1 = 4 and β = 100 (at which the family loses its stability and becomes unstable), (x _ofin, C _fin), as well as those of the other critical points (A = −1 or A = 1) approach more and more the peripheral primaries as the parameter β increases. Thus, for each β, there exists stable rings in the inner region of the peripherals between (x _oin < 0, x _ofin) and (−∞ < C _in, C _fin) characteristic for each β. Also, very close to the central primary the numerical calculations show that at about the same distant from it, x _oin, the absolute value of C, C _in, increases with increasing β. So, the size of the ring of stability in x _o and C, Δx = |x _oin − x _ofn| and ΔC = |C _in − C _fn|, becomes larger and larger as the parameter β increases. As β → 0 the size of the ring of stability tends to zero (Δx → 0, ΔC → 0).

Fig. 10

The size of the ring of stability in Δx as function of the cases N − 1 = 4, 7 and 24, for the values of β = 0.01,0.1,2,10 and 100 in the direct family

Fig. 11

The size of the ring of stability in ΔC as function of the cases N – 1 = 4, 7 and 24, for the values of β = 0.01, 0.1, 2, 10 and 100 in the direct family

From Tables 4, 5, 6 in ESM and Fig. 11 we observe that for each value of β, when N − 1 increases the interval ΔC decreases. Also, Fig. 12, which gives the diagram of ΔC as function of the ratio (N − 1)/β shows that as (N − 1)/β → ∞, i.e. if (N − 1) → ∞ or β → 0 then ΔC → 0. From the same tables and the Fig. 10 we see that for β = 0.01 and 0.1, with N − 1 increasing the interval Δx decreases. For the cases β = 2 and 10, as N − 1 increases Δx increases from N – 1 = 4 to 7 and decreases for N – 1 = 24. Finally, for β = 100, when N − 1 increases Δx also increases for the values N − 1 = 4, to 24. These differences are due to the number of the bifurcation points. However, from Fig. 13, Δx = Δx((N − 1)/β), it is evident that we have a similar behavior as in Fig. 12. Namely, as (N − 1)/β → ∞, i.e. if (N − 1) → ∞ or β → 0 the size of the ring of stability tends to zero, Δx → 0 and ΔC → 0, and the direct family tends to disappear.

Fig. 12

ΔC as function of the ratio (N − 1)/β in the direct family

Fig. 13

Δx as function of the ratio (N − 1)/β in the direct family

4 Concluding Remarks

We studied in a systematic way the change of the dynamical properties of both retrograde and direct main families of symmetric simple periodic motions around a central body. Namely, we investigated the evolution of these two families and their stability (Hénon 1965) as the Jacobian constant C changes, as well as the change of the types of bifurcation points and the size and dynamical structure of the rings of stability, using the values of the parameters N – 1 = 4, 7, 24 and β = 0.01, 0.1, 2, 10, 100 for each value of N − 1. This study showed changes in the dynamical structure and therefore in the topology of the phase space of this dynamical system.

The N − body relative equilibrium configuration (ring model) is more realistic if we consider the radius of the polygon (ring) to be constant. For example, using this model we can approximate a continuous ring of matter where the gaps between the peripherals represent the variations of the ring of density. These gaps are reduced in size as the number of the peripherals increases. Also, we can compare the results for different values of parameters N − 1 and β. For this reason we derived the equations of motion, using Cartesian tensors.

Also, the N-body relative equilibrium configuration is a flexible dynamical system where the values of the parameters N − 1 and β can change. Thus, several systems of interest in the field of celestial mechanics and stellar dynamics can be approximated, using the N-body ring model. Such systems include the motions of a satellite in the asteroid belt and the motions of small bodies around planets or stars with rings. Also, some problems of two or more interacting galaxies as well as the planetary nebulae can be modeled by the N-body ring model.

As the absolute value of the Jacobian C increases and C → −∞ the initial condition, x _oin, of the periodic orbits approaches the central body and shrinks to the center, x _oin → 0, while the stability index tends to A → 1 (Pinotsis 2005). On the other hand, as the absolute C decreases the initial condition x _o of the circular-shaped orbits approaches the peripherals.

Also, for any value of β and N − 1, the stability curves of two families have bifurcation points 1 → 2 (A = −1) (Hénon 1965). There are new bifurcating families of symmetric double periodic orbits with two branches in the form of a pitchfork. There also exist other critical points (with Α = 1) of types 1, 2, 3 or 4 (Hénon 1965). In particular, there exist either turning points in C or bifurcations of new families of symmetric or non-symmetric simple periodic orbits of the same period. In this manner we find both stable and unstable periodic orbits having different evolution as the Jacobi constant changes and forming stable and unstable regions.

For each value of the parameters N − 1 and β, for both retrograde and direct families, there exist stable rings in the inner region of the peripherals between the intervals (x _oin < 0, x _ofin) and (−∞ < C _in, C _fin). The stable rings contain bifurcation points and a number of stable segments, characteristic for each value of the parameters.

4.1 (I) Retrograde Family

As it is shown in Tables 1, 2, 3 in ESM and Figs. 2, 3, 4 and 5, the main retrograde family has a similar bifurcation pattern and dynamical structure for all the values of the parameters N − 1 and β. Namely, there exist two rings: one stable and another unstable. The stable ring has one bifurcation point 1 → 2 and one turning point in C (x _fn, C _fn), characteristic for each value of β and N − 1. Thus, each ring of stability contains two stable segments. The two new families of double periodic orbits that are generated in the above critical point are symmetric to one another with respect to the origin and have similar stability curves. Also, some differences between the various cases appear. In the case N − 1 = 24 and β = 0.01, the family, after its turning point in C, has a turning point in x _o and then it moves towards the central primary.

For a given value of N − 1, the initial conditions of the periodic orbits of the final critical points-turning points in C, (x _fn, C _fn), as well as those of the bifurcation point 1 → 2 shift towards the peripherals more and more as the parameter β increases. The size of the ring of stability in x _o and C, Δx and ΔC, increases as β increases and leads to an extension of the ring towards the peripherals, while with β decreasing the size of the ring of stability also decreases (Tables 1, 2, 3 in ESM; Figs. 4 and 5). So, for β → 0 the size of the ring of stability tends to Δx → 0 and ΔC → 0.

For given β the initial conditions of the turning point of periodic orbits as well as those of the bifurcation points 1 → 2 shift towards the central body as the parameter N − 1 increases. Also, the intervals Δx and ΔC decrease with increasing N − 1 (Figs. 4, 5). For any value of the parameter β, the size of the ring of stability in Δx and ΔC decreases more and more as the parameter N − 1 increases. Also, Figs. 6 and 7 show that if (N − 1)/β → ∞, i.e. (N − 1) → ∞ or β → 0, then Δx → 0 and ΔC → 0 and the size of the ring of stability tends to zero and, in general, the retrograde family tends to disappear. In general, it seems that the dynamical properties of the system depend on the ratio (N − 1)/β.

4.2 (II) Direct Family

From the Figs. 8, 9, 10, 11, 12, 13, 14, 15 and Tables 4, 5 and 6 in ESM it is evident that the cases N – 1 = 4 for β = 0.01, N − 1 = 7 for β = 0.01, 0.1 and 2, and N – 1 = 24 for β = 0.01, 2 and 10, present similar bifurcation pattern and so a similar dynamical behavior. Also, the cases β = 2 and 10 for N – 1 = 4 have similar bifurcation pattern and dynamical structure. In these two last cases, the family, after its final bifurcation point, presents a turning point in x _o and then it shifts towards the central body. There are no bifurcation points for N – 1 = 24 and β = 0.1, while in the cases N – 1 = 4 and 24, for β = 100, there exist the most bifurcation points (eight and six, respectively). Thus, for N – 1 = 24, the most stable family for β = 0.1 and the most unstable one for β = 100 and N – 1 = 4 and β = 100 appear.

Fig. 14

C_fin (of the final critical point) as function of the cases N – 1 = 4, 7 and 24, for the values of β = 0.01, 0.1, 2, 10 and 100 in the retrograde family

Fig. 15

C_fin (of the final critical point) as function of the cases N – 1 = 4, 7 and 24, for the values of β = 0.01, 0.1, 2, 10 and 100 in the direct family

In N – 1 = 4 (β = 100) case we observe that three stable and three unstable rings are formed. The first ring of stability has two bifurcation points and two stable segments. Then, οne ring of instability follows the above stable ring, at which three turning points in x _o appear, and the family finally moves towards the central primary. After this ring, another stable one, which contains a stable segment, appears. After that, two rings follow: an unstable and another stable, which contains four bifurcation points (and five critical points) and four stable segments. Finally, an unstable ring follows.

In the cases N – 1 = 24 and β = 100 as well as N – 1 = 7 and β = 10, 100, the family has a similar bifurcation pattern and new dynamical structures appear. The stability coefficient oscillates between −1 ≤ A ≤ 1 at which, each time, the stability curve is tangent to the straight lines Α = −1 and Α = 1. So, successive bifurcations from the main family are generated. However, in the N − 1 = 24 (β = 100) case two rings appear: one stable and another unstable. The ring of stability has seven critical points with six bifurcation points and contains seven stable segments. Also, for each one of the two cases, β = 10 and 100 for N – 1 = 7, we have two rings, one stable and another unstable. The ring of stability has five bifurcation points and five stable segments. In all these cases, each time the family becomes critically stable a new dynamical structure appears. There exist a large number of bifurcated stable and unstable families that produces a large degree of chaos.

In these four cases (N – 1 = 4 and β = 100, N − 1 = 7, β = 10 and 100 and N – 1 = 24, β = 100), the ratios of the intervals ΔC between the successive critical points along each main family, ΔC _i /ΔC _i+1, are not universal numbers. This ratio depends on the particular case (in general on the particular dynamical system) considered. Also, the ratios of the Jacobian C between these successive critical points, C _i /C _i+1, tend to 1.

From Figs. 10 and 11 we observe that for a given value of N − 1 the size of the ring of stability in Δx and ΔC decreases as β decreases. Thus, for β → 0, the size of the ring of stability tends to Δx → 0 and ΔC → 0.

For a given value of β, the interval ΔC decreases with increasing N − 1 (Fig. 11). Also, Figs. 12 and 13 show that as (N − 1)/β → ∞, i.e. if (N − 1) → ∞ or β → 0 then the size of the ring of stability tends to zero, Δx → 0 and ΔC → 0 and the direct family tends to disappear. It seems that the dynamical behaviour of the system depends on the ratio (N − 1)/β.

There is a similar behaviour of x _fin and Δx (Fig. 10): Specifically, as N − 1 increases there are two groups: for β = 0,01 and β = 0,1 there is a slight decrease of x _ofin and Δx from N – 1 = 4 to N − 1=24, while for β ≥ 2 it seems that they increase from N – 1 = 4 to N – 1 = 7 and then there is a decrease of them, except for β = 100 where there is a slight increase of x _ofin and Δx from N − 1=7 to N – 1 = 24.

Also, from Figs. 14 and 15 it is evident that for the retrograde and direct families there is a critical value of β: For the retrograde family, as N − 1 increases, for β < 2 there is an increase of the absolute C _fin, while for β > 2 the absolute C _fin decreases. For β = 2 the absolute C _fin decreases from N – 1 = 4 to N – 1 = 7 and increases from N – 1 = 7 to N – 1 = 24. For the direct family, we have almost similar behaviour except for the case β = 2 where C _fin increases from N – 1 = 4 to N – 1 = 24.

Thus, there are critical values of β and N − 1 at which the topology of the phase space changes. In general, the bifurcation pattern and so the dynamical structure, as well as the number of the equilibrium solutions and their initial conditions will depend on the parameters β and N − 1.

In general, the size of the rings of stability is larger in the retrograde case than in the direct case because of the orientation of the Coriolis force. Also, the direct family has more complex dynamical structure than the retrograde one and produces a large degree of chaos. These are very interesting for astronomical applications. In fact, the families of planetary type orbits present important astronomical and astrophysical interest. In general, the entire retrograde family appears to be more stable than the direct one.

The above work includes useful information which enriches our knowledge of various dynamical systems. These results can be compared with future work on e.g. the parametric evolution of families of non-symmetric periodic orbits, the study of the full N = ν + 1-rigid bodies ring configuration, the problem of different masses of the N = ν + 1-body ring configuration, etc.