Abstract
With the rise of wearable devices, which integrate myriad of health-care and fitness procedures into daily life, a reliable method for measuring various bio-signals in a daily setup is more desired than ever. Many of these physiological parameters, such as Heart rate (HR) and Respiratory Rate (RR), are extracted indirectly and using other signals such as Photoplethysmograph (PPG). Part of the reason is that in some cases, such as RR measurements, the devices which directly measure them are cumbersome to wear and thus, rather impractical. On the other hand, signals, such as PPG from which the RR can be extracted, are not very clean. This poses a challenge on reliable extraction of these metrics. The most important problem is that they are corrupted by motion artifacts. In this paper, we review the state of the art algorithms which are used to detect and filter motion artifacts in PPG signals and compare them in terms of their performance. The insight provided by this paper can help the scientists and engineers to obtain a better understanding of the field and be able to use the most suitable technique for their work, or come up with innovative solutions based on existing ones.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The face of health-care systems across the globe is changing thanks to Wearable Health-care Systems (WHS) and Internet of Things (IoT), and their benefits such as cost effectiveness and the extended information they provide [1,2,3,4,5,6]. Their applications ranges from daily well-being purposes to emotion recognition [7, 8], Early Warning Score (EWS) [4, 9, 10], and detection of epileptic seizures [11]. Moreover, typical medical devices in the health-care domain that are present in a hospital are expensive and need trained practitioners to operate them. In contrast, wearable devices can be operated by general public, cost little, and can be deployed to perform their job inside and outside hospitals [4, 6]. This can reduce hospitalization and play an important role for the aging population. [4, 6, 10, 12].
However, one of the main challenges that WHSs face is that of accuracy and noise [4, 10, 13]. This is an important factor since many of these devices have limited number of sensors and many of the extracted information are indirectly obtained through those sensors. Thus, their inaccuracy can propagate through the system and lead to false diagnoses. One of these fundamental and widely-used sensors is the Photoplethysmograph (PPG) because it is easy to use, cheap and can help in extracting many health-care parameters of interest. PPG measures the blood pulse wave from which the heart rate, its variations and even the respiratory rate can be extracted. Through physiological mechanisms respiration modulates the blood volume pulse in three different ways: Amplitude Modulation (AM), Baseline Wanderer (BW) and Frequency Modulation (FM) [14]. From these features respiratory rate can be extracted.
The largest problem with the proper extraction of these health parameters is that the PPG signals are often measured during various kinds of movement and therefore are corrupted with motion noise. This noise can appear in the form of unruly signals of large amplitudes in the PPG signals. It is also reflected in the frequency domain and overlaps with the frequency range of breath or heart rate [15]. Luckily, another fundamental sensor which is often integrated in wearable devices is an accelerometer which helps in detection and removal of this noise. With the accelerometer (or similar reference signals) it is possible to measure movement and link it to the part of the respiratory signal which is corrupted with motion artifacts [16, 17]. With a reference signal (such as the acceleration) it is easier to remove the motion noise. This is particularly important when the noise lays in the same frequency band as the signal of interest [16]. Therefore, traditional filtering methods may not work well since they cannot distinguish between the sought after signal and the movement noise.
Nevertheless, there are some possibilities to alleviate this issue (contamination of the signal due to motion artifacts) even if no acceleration signal is available. Mainly, thanks to the fact that if there is no noise, some statistical values are almost the same over time. Thus, it is possible to calculate values such as skewness and kurtosis [18], set them as thresholds and compare them to the upcoming periods and consequently mark parts of the PPG signal as corrupt. The disadvantage of these methods is that it only marks the faulty parts and cuts them out entirely. To overcome this problem it is possible to generate a syntethic reference signal out of the corrupted PPG signal [19] with the use of Empirical Mode Decomposition (EMD).
In this paper, we review the state of the art regarding all aforementioned methods as well as their advantages and disadvantages. This should provide designers with a good insight into design challenges and possible solutions in their specific applications. The rest of the paper is structured as follows: The methods for detection or reduction of motion artifacts which do not use acceleration data are presented in Section 2. Methods using synthetic reference signals are reviewed in Section 3 and those which measure the acceleration signal using a dedicated sensor are presented in Section 4. Afterwards the result of all different methods are summarized and compared in the Section 5. Finally, Section 6 concludes the paper.
2 No acceleration data
If there is no accelerometer or other reference signals available, the motion artifacts can mainly be marked and cut out - but not filtered out. In this section, we review three different methods for this purpose.
2.1 A statistical approach
The simplest approach does not use any extra sensors for acceleration or try to reproduce it. As proposed in [18], they use only statistical parameters of the PPG signal to detect and cut out signal parts contaminated with Movement Artifacts (MAs). As seen in Fig. 1, the first step of the algorithm is to filter the corrupted signal using a band-pass filter with the passing band of 0.5 to 6Hz, which is the main frequency band of interest for heart rate.
Flowchart of MA removal algorithm with no acceleration data [18]
Afterwards it is segmented based on the signal period and from the segmented signal the standard deviation, skewness, and kurtosis is calculated using Eqs. 1, 2, and 3, respectively, where \(\bar {x}\) is the mean value. If there is no movement during the recording, the statistical values such as kurtosis, skewness, and standard deviation for each cycle are almost equal. These values are then calculated and set as thresholds for the comparison algorithm.
If there are movement, the amplitude of the PPG signal changes greatly and consequently the statistical parameters rise above the formerly set thresholds and the signal is marked as corrupt. The corrupted signal is then cut out of the original signal and only the clean signal is left.
The method was tested with 10 healthy subjects who had to perform four different tasks: (i) no movement, (ii) finger movement, (iii) wrist movement, and (iv) elbow movement. They recorded the PPG signal with a TI’s AFE4400-SPO2EVM sensor, which is a chest strap. According to a set threshold, a part of the signal is marked as corrupted with movement and cut out as seen in Fig. 2. They compare their results with an Independent Component Analysis (ICA)-Least Mean Square (LMS) algorithm. The corrupted PPG signal had a mean Standard Deviation (STD) error of 7.16 ± 0.36 Beat Per Minute (BPM) for elbow movement, 6.12 ± 0.65 BPM for wrist movement and 11.02 ± 0.56 BPM for finger movement. The ICA-LMS method had an error of 6.39 ± 1.46 BPM for elbow movement, 6.41 ± 1.38 for wrist movements and 10.6 ± 1.67 for finger movement. Therefore, the statistical method had a mean error of 6.58 ± 1.32 BPM for elbow movement, 6.22 ± 0.8 for wrist movement and 10.77 ± 1.09 for finger movement. Overall, for all three motions, the proposed algorithm had a mean error of 7.85 BPM, compared to the original 8.1 BPM of the corrupted signal.
a Original PPG signal, b PPG after pre-processing, c detected movement, d cut-out algorithm applied [18]
2.2 Variable frequency complex demodulation
Here we describe another method which does not use a reference signal but an algorithm based on Variable Frequency Complex Demodulation (VFCDM) [20]. This detection method looks at dominant peak amplitudes and dominant frequency components. Each 30 seconds of the PPG signal was first band-pass filtered to 0.5Hz - 10Hz using a 6th order zero-phase Butterworth filter, detrended, and then normalized by the maximum. On this signal a peak detection method is used to mark all the peaks of the PPG signal. If there is a gap between the finger and the camera (their PPG sensor) this induces motion artifacts. Such motion artifacts are marked in the 30 second windows of the PPG signal with the pre-processing filtering and peak detection. Afterwards, to detect artifacts the VFCDM method is used to differentiate spectral characteristics of the noise from the clean PPG signal. The first step involves obtaining the initial time-frequency spectrum using fixed frequency complex demodulation. For the next step, the complex demodulation is calculated by using the center frequencies of the previously obtained time-frequency spectrum. In a clean signal, the dominant frequency for the heart rate is nearly continuously present and between 0.5 - 3.5 Hz but in a corrupted signal the dominant frequency can shift due to the noise and thus, lead to a wrong Heart rate (HR) detection. Out of these differences a threshold system was developed to mark signals as moderately corrupted and corrupted. After the signal is marked as corrupted it can be deleted as in the method before.
For this work 200 subjects took part of the experiments to test the algorithm and 521 recordings were made, each one minute long. The used signal was recorded using an iPhone camera and the PPG signal was extracted based on the average of 50x50 pixels of the green band. Out of these signals three features were extracted: root mean square of successive differences, Shannon entropy and sample entropy. These features are then used in a linear Support Vector Machine (SVM) classifier to detect irregular heart rhythms. The SVM was trained with 82 clean signals and tested with 898 segments (30 seconds each). Without the noise detection algorithm out of 449 recordings 156 were misclassified and with the noise detection only 29 were false positives.
2.3 Discrete wavelet transform
In the Discrete Wavelet Transform (DWT) method, it is tried to identify the heart rate out of the PPG signal [21] without any reference signal, even if it is corrupted with motion artifacts. This is a method that uses a few measurements of noise to generate an estimate of unknown states. First, as seen in Fig. 3, the data is pre-processed. In this step, the DC components are separated from the AC component and with a wavelet transformation the PPG signal is first decomposed and afterwards the components in the bandwidth of 0.39 - 12.5 Hz are reconstructed.
The Flowchart of the DWT algorithm with one path for training and the other to test it [21]
In the next step, the following features are extracted: standard deviation of peak-to-peak amplitudes as in Eq. 1, standard deviation of peak-to-peak intervals, the kurtosis as calculated in Eq. 3, and Mean Absolute Deviation (MAD) of peak-to-peak amplitudes as in
where An is the peak-to-peak amplitude and N is the number of peak-to-peak intervals in the signal.
An SVM is then used to classify the data sets after training and a 10-fold cross-validation. To remove motion artifacts Kalman filter is used. The filter observes a series of corrupted signals to generate an estimate of the unknown state. First the controlled process x, is calculated by
and a measurement, z, is described by
where wk and vk are random variables that represent the process and measurement noise. The matrix A is the state transition matrix and the matrix B is the optional input model for the control uk. Matrix H relates to the measurement zk, as shown in Eq. 6.
To test their algorithm, eleven subjects took part in the measurements and they had to perform two different motions; (i) keep their hand still for one minute, and (ii) wave their hand. This was done to identify and remove motion artifacts from two PPG sensors that were attached to the left and right index finger. During their analysis, they found out, that for their tests a window length of seven seconds had the best results. With their method, they could reduce the absolute bias from 13.97 BPM to 6.87 BPM.
3 Synthetic reference data
3.1 EMD technique
Another possible solution without an accelerometer signal is to generate a reference signal from the corrupted PPG signal using Complex Empirical Mode Decomposition (CEMD) technique [19]. To generate the reference noise signal the following steps have to be done. First, all the local minima and maxima of the originals signal (x(t) = d(t) = S(n) + N(n)) need to be found. The next step is to envelope all the maxima (umax) and all the minima (umin). After all the envelope signals are generated, the mean value, m(t), is calculated:
The value of the mean is then subtracted from the original signal: h(t) = x(t) − m(t). The new signal h(t) is decomposed into Intrinsic Mode Function (IMF) by sifting process until h(t) meets the IMF conditions. The next step is to identify the quasi-residue function r(t) = x(t) − c. This loop has to be repeated until r(t) has only one extrema. Afterwards, the spectrum of each IMF based on the predefined frequency range has to be computed. The last step to generate the reference noise signal is identifying the desired signal portion range and eliminating IMF corresponding to the desired frequency components of the PPG.
For the “adaptive step-size LMS algorithm” block, seen in Fig. 4, an estimate of the gradient to search the minimum error on the surface is used. The error of each step is reduced by updating the step size parameter. To implement the adaptive filter the following steps as seen in Eq. 8 to Eq. 12 are used.
where u(n) is the generated reference signal, y(n) the filter output, w(n) the filter coefficients, e(n) the error, d(n) the PPG signal (which would be the desired output if there is no noise), μ the step size, γH the gradient vector and ρ controls the step size parameter.
Adaptive filter using CEMD technique to generate the reference signal out of the PPG signal [19]
Figure 5 is an example of the results of the algorithm designed in [19]. The test subjects had to perform three different movements with their finger: (i) horizontal motion, (ii) vertical motion, and (iii) bending. For the measurement of the PPG signal a clip-on type PPG sensor with an Ni-DAQ Pad-6015 data acquisition system was used. To compare the original corrupted signal with the signal without noise, the peak to peak values of the PPG signal are compared. For corrupted PPG signal with horizontal motion the mean error is 0.426 ± 0.087 BPM, with vertical movement 0.514 ± 0.107, and for bending motion 0.459 ± 0.067. In comparison, the proposed algorithm had an error of 0.379 ± 0.036 BPM for horizontal movement, 0.435 ± 0.059 for vertical movement, and 0.363 ± 0.131 for bending motion. Overall, the mean error of the proposed algorithm is 0.392 BPM compared to 0.466 BPM of the (originally) corrupted signals.
a Original signal, b generated movement signal, c original signal minus the movement noise [19]
3.2 Dual PPG sensor
A similar approach that uses synthesized reference signal was shown in [22]. A second PPG sensor is used to generate the movement signal. The second PPG sensor is positioned a few millimetersFootnote 1 away from the skin, as seen in Fig. 6a, so it only measures when the subject is in motion. In Fig. 6b one can see typical outputs of both sensors, first few seconds without motion and afterwards with motion.
a Application of the two PPG sensors on the skin, where the second sensor is a few millimeter away. b The typical output of a two PPG setup [22]
This algorithm starts by band-pass filtering both of the recorded signals between 0.8 to 5 Hz with a Hanning window of 128 points and a sampling rate of 10 samples per second. Afterwards, an adaptive filter, as seen in Fig. 7, is applied. The u(n) input on Fig. 7 measures the movement and the d(n) is the PPG signal from the sensor which is fully in touch with skin. The adaptive filter tries to bring the difference between u(n) and d(n) down to zero. To do that a Normalized Least Mean Square (NLMS) and Recursive Least Square (RLS) algorithm are applied and two parameters, namely the number of taps, K, and the forgetting factor, λ, are optimized. The output is sliced into windows and fast Fourier transformed.
Adaptive filtering using a second PPG sensor, located a few millimeters afar from the skin of the subject [22]
In [22], only 10 data sets were used to test the algorithm. For their experiments the subjects had to walk, jump, and run. Two PPG sensors, as seen in Fig. 6, that were used were Hamamatsu S9706. They put them on the hip to measure the PPG signal and the movement as well. Since they had only 10 data sets a cross-validation was performed to alleviate this problem. They first selected the n-th data set for validation and use the rest as a training set. Afterwards, the parameters were chosen for the training set and on the chosen validation set the error, En, was calculated. These two steps were repeated for all data sets and at the end the average error was calculated. To find the optimal parameter values, the authors swept the K values from 5 to 50, and β from 0.01 to 0.9. With the optimal parameters, the algorithm can reduce root mean square error by 62% for the walking, 83% for the running, and 79% for the jumping. That is, a Root Mean Square Error (RMSE) of 6.5 BPM after reduction and 28.26 BPM RMSE before reduction.
4 Measured acceleration data
4.1 LMS filtering
One of the methods based on acceleration sensors to remove motion artifacts is presented by [16]. The flow diagram of the proposed algorithm is shown in Fig. 8. First, the raw PPG signal is band-pass filtered with a 4th order Butterworth Infinite Impulse Response (IIR) filter in the range of 0.3–5 Hz. For the motion data filtering block a Singular Value Decomposition (SVD) is used which generates a motion artifact reference for the adaptive filter. In the third block of the algorithm, the in-band removal takes place. There, they use a modified LMS adaptive filter, where the coefficients, h(n), are updated based on the least mean error, e(n). An identical filter is placed in the reference signal path to adjust the weights. This adjustment is called X-LMS. In Eqs. 13–16 the X-LMS calculations are shown,
Flow diagram of the algorithm that uses SVD and LMS adaptive filter to remove motion artifacts [16]
where u(n), d(n) and e(n) are input, desired output and error, respectively. w(n) are the weights of the estimated filter and μ the step size. \(c_{i}^{*}\) represents the coefficients of estimated filter for compensation, and \(u_{C^{*}}(n)\) is the reference signal as one can see in Fig. 9. In the last part, the peak tracking takes place with some adaptive threshold levels. This is done with the Slope Sum Method (SSM), where they use a window size of 2-3 seconds to detect onset and offset of each peak.
The flowchart of the LMS adaptive filter [16]
For the experiments in [16], 12 different subjects took part and they had to do different exercises such as running up to 12-15km/h. A dual channel PPG alongside a three-axis accelerometer sensor was used to record the data from the wrist with a sampling rate of 125Hz. With the X-LMS method they had an error of 1.37 BPM.
4.2 RLS filtering
A similar approach is proposed by [17]. Instead of X-LMS they use a DC Remover and an RLS adaptive filter. The first step of the algorithm, as shown in Fig. 10, is the DC removal. This IIR filter removes the offset of the PPG signal and thus the RLS adaptive filter has a faster convergence speed compared to an LMS algorithm. The output of the DC remover is the AC component of the PPG signal. The following, Eqs. 17–19, describe the DC remover.
Flow chart of a motion artifact removal algorithm that uses a 3-axis accelerometer to remove the movement artifacts [17]
In these equations, w(t) is the value of the operation process which records the DC drift, and a controls the filter cut-off frequency. When a becomes closer to 1, the slope of the filter response becomes sharper and only the frequencies that disturb the signal are damped, however, when it is 1, the filter effect will be lost. After the signal is removed of its DC values the RLS adaptive filter comes into play.
In Fig. 11, one can see that s(t) is the primary input, xt is the reference input of the accelerometer sensor, s1(t) is the noise-free PPG signal and n(t) is the motion noise. Equation 20 shows the formula for calculating the estimated motion noise, where \({\omega _{K}^{T}}\) represents the coefficients of the filter, Θ is the matrix of these coefficients, ϕ is the matrix of the accelerometer data, \(\hat {n}(t)\) is the estimated motion noise, and t is the sampling time.
Flow chart of the algorithm which uses an X-LMS adaptive filter [17]
To test their algorithm, in [17], the authors used two different databases. The first one is Multi-parameter Intelligent Monitoring for Intensive Care (MIMIC) and a second set of signals that were measured from 10 subjects, where subjects did small movements such as scratching themselves or shaking slightly. In Fig. 12, we can see the spectrum of a PPG signal after the algorithm removed the motion noise. From the database of the 10 subjects the results of the Bland Altman plot provides a range limit of -4.29 to 4.26 for the difference of the heart rate and the ground truth, with a STD of 3.91 BPM.
a Cleaned PPG signal, b raw PPG signal [18]
4.3 Hankel matrix filtering
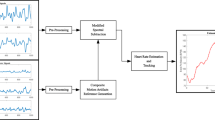
The authors of [23] try to overpass previous techniques with Motion Artifact Removal (MAR) and Adaptive Tracking (AT). In [23] they use datasets from subjects who were running. The flow chart of the proposed algorithm can be seen in Fig. 13.
Flow chart of a system that uses the Hankel matrix to remove motion artefacts [23]
In the first step, the pre-processing, the signals are windowed, filtered and a Hankel data matrix is constructed. The model for the acceleration data is shown in Eq. 21, where X, Y, Z are the three axes of the accelerometer signal and N, and L represent the observations of the three axes accelerometer. H can be decomposed by the SVD and its eigenvalues are calculated by
The same is done with the PPG signal (g) whose model is shown in Eq. 22, in which e is the heart rate and m is the movement artifact.
The corresponding Hankel data matrix of Eq. 22 can be decomposed using SVD. The result of the decomposed process are two orthonormal subsets. When compared with the artifact component, it shows that the artifact and the heart rate signal belong to two orthonormal sub-spaces.
The next step is to find the spectral peaks of the vectors. This is easily done using the calculation in Eq. 22 since the cardiac frequency is the dominant frequency in the matrix. To minimize the error, when motion comes into play, a rough estimation of the joint probability density function of the heart rate versus the motion artifact frequency is performed. This probability function is used to separate the fundamental harmonics of the heart rate from the motion artifact.
To validate the algorithm, the authors of [23] tested it on 25 test subjects where the subjects wore a wrist type PPG sensors and performed different kind of exercises.Footnote 2 In Figure 14, one can see that even for different starting points (red lines) all lines come to the ground truth (black line, an Electrocardiography (ECG) derived signal). The green line is the estimation of the proposed algorithm. They tested their algorithm on subjects that were running and overall had an average absolute error of 2.26 BPM.
The proposed algorithm with different starting points (shown in red lines) and ground truth (the black line) [23]
5 Results and discussion
In this section, we review and discuss the results of the previously presented algorithms. The results are presented following the same section division as before. In Table 1 we have inserted an overview of the reviewed algorithms and their results. This table provides information on which algorithm is only for detection and which also removes the motion artifact through filtering. The column Acc. shows which algorithm uses an accelerometer signal and which one does not. A pointer on the used method, number of subjects, and a summary of the results are the other information seen in the table. This information can help design engineers to choose the most suitable method for their application, given its constraints and requirements.
For example, if no accelerometer sensor is available and the mere detection of the motion artifacts suffices, a statistical threshold algorithm [18] can be used. This algorithm only uses statistical calculations like kurtosis or standard deviation. If these values exceed their respective thresholds, this means there were motion artifacts in the signal and it can be marked as such. The marked signal can be then cut out or if they are used for any health measurement, the result could be marked as potentially inaccurate. The Peak to Peak Error (PPE) for this method is 7.85 BPM compared to the corrupted PPG signal with 8.1 BPM PPE. Another way to detect motion artifacts without any accelerometer sensor is to look at the frequency components with VFCDM as seen in Section 2.2. This only needs some values without movement to set some ground truth and compare these values to every value to come. If the signal is corrupted it looks different in the frequency domain, just as in the time domain. With this approach out of 449 recordings only 29 were false positive, in other words, 6.45% miclassification in total.
However, we bear in mind that it is still possible to go beyond mere detection without an accelerometer too. For example, despite signal corruption, using Kalman filter and DWT, it is possible to decompose the signal and reconstruct the good parts [21]. Thus, the motion artifacts can be removed and one can extract the heart rate or Respiratory Rate (RR). The PPE of this method is 6.87 BPM comapred to 13.97 BPM without any filtering. It is also possible to generate a reference signal out of a corrupted PPG signal with EMD [19]. After the reference signal is generated, an adaptive filter can be used to remove motion artifacts. With this method the PPE can be reduced to 0.392BPM from 0.466 BPM. In case a second PPG sensor is available, it can be used to generate a movement signal [22]. The second PPG is applied a few millimeters away from the skin, such that if the subject moves, the distance from the sensor to skin is reduced or increased and therefore the signal changes. Using the difference of the two PPG signals a movement signal and the weights of an adaptive filter can be extracted. The RMSE can be reduced to 6.5 BPM compared to 28.26 BPM before filtering.
With an accelerometer data it is easier to differentiate between contaminated and motion-artifact-free signal and remove it. In one approach, out of the accelerometer data a reference signal is generated with an SVD to adjust the weights of an adaptive filter [16]. This approach has the lowest error of all proposed algorithms with only 1.37 BPM. Compared to the LMS algorithm of [16] a faster algorithm is the RLS [17]. It starts by removing the DC component of the signal and applies an RLS adaptive filter to the signal. Although it gains in speed, it loses in precision. This approach predicts the heart rate with a confidence of 95% in the interval of [-4.29–4.26] BPM of the ground-truth value and has a standard deviation of 3.81 BPM. The most complex algorithm uses MAR and AT [23]. Out of the filtered signals (PPG and accelerometer) the Hankel matrix has to be calculated. Out of this matrix, the noise part has to be calculated and subtracted from the original signal. It does not have the lowest error value (their error rate is 2.26 BPM), however, they claim that they have the most robust approach of all (which we could not evaluate independently since they do not provide metrics such as STD).
6 Conclusion
In this paper, we reviewed eight different algorithms that either detect motion artifacts or filter them based on a synthesized or measured reference signal. We presented their core idea and features, and summarized their characteristics and results to provide a large picture of the literature and existing methods. We hope that this study can be used by engineers to make a better choice in design regarding what algorithm to use in which situations. Although we did our best to provide a comparison between different methods, we keep in mind that to have a fair and proper comparison, one needs to implement all the algorithms and test them on the same dataset under the same conditions and restrictions. We consider this outside the scope of this paper and as an interesting potential future work.
Notes
We could not find what is the exact number for this gap.
We could not find exactly what kind of exercises were used.
References
Dohr A et al (2010) The internet of things for ambient assisted living. In: Proceedings of the international conference information technology: new generations
Atzori L et al (2010) The internet of things: a survey. Computer networks 54(15):2787–2805
Miorandi MD (2012) Internet of things: vision, applications and research challenges. Ad Hoc Networks 10 (7):1497–1516
Anzanpour A et al (2017) Self-awareness in remote health monitoring systems using wearable electronics. In: Proceedings of design and test europe conference (DATE), Lausanne, Switzerland
Parego P, Rahmani AM, Taherinejad N (eds.) (2017) Wireless communication and mobile healthcare. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering. Springer International Publishing
Yin H, Akmandor AO, Mosenia A, Jha NK (2018) Smart healthcare. Foundations and Trends®. In: Electronic design automation, vol 2(14), pp 401–466
TaheriNejad N, Pollreisz D (2016) Assessment of physiological signals during happiness, sadness, pain or anger. In: 6th MobiHealth
Pollreisz D, TaheriNejad N (2017) A simple algorithm for emotion recognition, using physiological signals of a smart watch. In: 2017 39th annual international conference of the ieee engineering in medicine and biology society (EMBC), pp 2353–2356
Götzinger M et al (2016) Enhancing the early warning score system using data confidence. In: International conference on wireless mobile communication and healthcare. Springer, pp 91–99
Götzinger M, Azanpour A, Azimi I, Taherinejad N, Rahmani AM (2017) Enhancing the self-aware early warning score system through fuzzified data reliability assessment. In: International conference on wireless mobile communication and healthcare. Springer
Forooghifar F, Aminifar A, Alonso DA (2018) Self-aware wearable systems in epileptic seizure detection, pp 7
Nia AM et al (2015) Energy-efficient long-term continuous personal health monitoring. IEEE Transactions on Multi-Scale Computing Systems 1(2):85–98
TaheriNejad N (2019) Wearable medical devices: challenges and self-aware solutions. In: IEEE life sciences newsletter, pp 5–6
Charlton P et al (2018) Breathing rate estimation from the electrocardiogram and photoplethysmogram: a review. IEEE Reviews in Biomedical Engineering PP(99):1–1
Liu J, Chen J, Jiang H, Jia W, Lin Q, Wang Z (2018) Activity recognition in wearable ECG monitoring aided by accelerometer data. In: 2018 IEEE international symposium on circuits and systems (ISCAS), pp 1–4
Tanweer KT, Hasan SR, Kamboh AM (2017) Motion artifact reduction from PPG signals during intense exercise using filtered x-LMS. In: 2017 IEEE international symposium on circuits and systems (ISCAS), pp 1–4
Wu CC, Chen IW, Fang WC (2017) An implementation of motion artifacts elimination for PPG signal processing based on recursive least squares adaptive filter. In: 2017 IEEE biomedical circuits and systems conference (BioCAS), pp 1–4
Hanyu S, Xiaohui C (2017) Motion artifact detection and reduction in PPG signals based on statistics analysis. In: 2017 29th Chinese control and decision conference (CCDC), pp 3114– 3119
Raghuram M, Sivani K, Reddy KA (2016) Use of complex EMD generated noise reference for adaptive reduction of motion artifacts from PPG signals. In: 2016 international conference on electrical, electronics, and optimization techniques (ICEEOT), pp 1816–1820
Bashar SK, Han D, Soni A, McManus DD, Chon KH (2018) Developing a novel noise artifact detection algorithm for smartphone PPG signals: preliminary results. In: 2018 IEEE EMBS international conference on biomedical health informatics (BHI). IEEE, pp 79–82
Lin WJ, Ma HP (2016) A physiological information extraction method based on wearable PPG sensors with motion artifact removal. In: 2016 IEEE international conference on communications (ICC), pp 1–6
Hara S et al (2017) Parameter optimization of motion artifact canceling PPG-based heart rate sensor by means of cross validation. In: 2017 11th international symposium on medical information and communication technology (ISMICT), pp 73– 76
Bacá A et al (2015) CARMA: a robust motion artifact reduction algorithm for heart rate monitoring from PPG signals. In: 2015 23rd European signal processing conference (EUSIPCO), pp 2646–2650
Funding
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pollreisz, D., TaheriNejad, N. Detection and Removal of Motion Artifacts in PPG Signals. Mobile Netw Appl 27, 728–738 (2022). https://doi.org/10.1007/s11036-019-01323-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11036-019-01323-6