Skip to main content
SpringerLink
Log in

Free Vibrations and Buckling of Laterlally Functionally Graded Material Columns

  • Published:
Mechanics of Composite Materials Aims and scope

A Correction to this article was published on 31 October 2023

This article has been updated

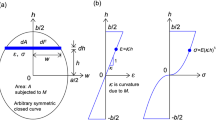
The paper aims to develop a unified modeling to analyze the free vibrations and buckling of laterally functionally graded material columns. The columns of rectangular cross-section, in which the mass density and Young’s modulus vary along the depth as a power-law function, were considered. The differential equation governing a mode shape of a deformed column was derived with the relevant boundary conditions, including the effect of rotatory inertia. The computation results for the natural frequencies and buckling load were compared well with those available in the open scientific literature. The effects of geometrical and material properties on natural frequencies and buckling loads with the mode shapes are highlighted.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Change history

References

  1. T. Horibe and K. Mori, “Large deflections of tapered cantilever beams made of axially functionally graded materials,” Mech. Eng. J., 5, No. 1, 1-10 (2015).

    Google Scholar 

  2. W. R. Chen and H. Chang, “Vibration analysis of functionally graded Timoshenko beams,” Int. J. Struct. Stab. Dy., 18, No. 1, 1850007 (2018).

  3. J. K. Lee and B. K. Lee, “Coupled flexural-torsional free vibration of an axially functionally graded circular curved beam,” Mech. Compos. Mater., 57, No. 6, 833-846 (2022).

    Article  Google Scholar 

  4. J. M. Gere and S. P. Timoshenko, Mechanics of Materials, PWS Publishing Company, Boston (1997).

    Google Scholar 

  5. K. W. Lee, “Bending analysis of nonlinear material members with a generalized elliptical cross-section,” Text. Res. J., 75, No. 10, 710-714 (2005).

    Article  CAS  Google Scholar 

  6. J. K. Lee and B. K. Lee, “Generalized second moment of areas of regular polygons for Ludwick type material and its application to cantilever column buckling,” Int. J. Struct. Stab. Dy., 19, No. 2, 1950010 (2019).

  7. A. E. Alshorbagy, M. A. Eltaher, and F. F. Mahmoud, “Free vibration characteristics of a functionally graded beam by finite element method,” App. Math. Mod., 35, 412-425 (2011).

    Article  Google Scholar 

  8. N. Celebi and N. Tutuncu, “Free vibration analysis of functionally graded beams using an exact plane elasticity approach,” J. Mech. Eng. Sci., 228, No. 14, 2488-2494 (2014).

    Article  Google Scholar 

  9. Y. Liu Y and D. W. Shu, “Free vibration analysis of exponential functionally graded beams with a single delamination,” Compos., Part B, 59, 166-172 (2014).

  10. Z. Shi, X. Yao, F. Pang, and Q. Wang, “An exact solution for the free-vibration analysis of functionally graded carbonnanotube- reinforced composite beams with arbitrary boundary conditions,” Sci. Rep., 7, No.1, 12909 (2017).

  11. L. Hadji and F. Bernard, “Bending and free vibration analysis of functionally graded beams on elastic foundations with analytical validation,” Adv. Materials Res., 9, No. 1, 63-98 (2020).

    Google Scholar 

  12. H. H. S. Al Said-Alwan and A. Mehmet, “Analytical solution of free vibration of FG beam utilizing different types of beam theories: A comparative study,” Comput. Concrete, 26, No. 3, 285-292 (2020).

  13. V. Kumar, S. J. Singh, V. H. Saran, and S. P. Harsha, “Exact solution for free vibration analysis of linearly varying thickness FGM plate using Galerkin–Vlasov’s method,” J. Mater., 235, No. 4, 880-897 (2021).

    Google Scholar 

  14. T. G. Nguyen, “Free Vibration exploration of rotating FGM porosity beams under axial load considering the initial geometrical imperfection,” Math. Probl. Eng., 2021, 1-16 (2021).

    Google Scholar 

  15. S. C. Han, G. R. Romboy, and K. D. Kim, “Mechanical vibration and buckling analysis of FGM plates and shells using a four-node quasi-conforming shell element,” Int. J. Struct. Stab. Dy., 8, No. 2, 203-229 (2008).

    Article  Google Scholar 

  16. F. Q. Zhao, Z. M. Wang, and R. P. Zhang, “Post-buckling analysis of FGM beam subjected to non-conservative forces and in-plane thermal loading,” Appl. Mech. Mater., 152/154, 474-479 (2012).

    Google Scholar 

  17. M. Raki, R. Alipour, and A. Kamanbedast, “Thermal buckling of thin rectangular FGM plate,” World Appl. Sci. J., 16, No. 1, 52-62 (2012).

    Google Scholar 

  18. F. Farhatnia, M. A. Bagheri, and A. Ghobadi, “Buckling analysis of FGM thick beam under different boundary conditions using GDQM,” Adv. Mat. Res., 433-440, 4920-4924 (2012).

    Google Scholar 

  19. T. H. Trinh, D. K. Nguyen, B. S. Gan, and A. Alexandrov, “Post-buckling responses of elastoplastic FGM beams on nonlinear elastic foundation,” Struc. Eng. Mech., 58, No. 3, 515-532 (2016).

    Article  Google Scholar 

  20. E. Y. Ali and Y. S. Bayleyegn, “Analytical and numerical buckling analysis of rectangular functionally-graded plates under uniaxial compression,” In: Proc. the Structural Stability Research Council Annual Stability Conference, St. Louis, MO, USA, (2019).

  21. L. Czechowski and Z. Kolakowski, “The study of buckling and post-buckling of a step-variable FGM box,” Materials, 12, No. 6, 918 (2019).

    Google Scholar 

  22. H. N. Nguyen, T. C. Tan, D. T. Luat, V. D. Phan, D. V. Thom, and P. V. Minh, “Research on the buckling behavior of functionally graded plates with stiffeners based on the third-order shear deformation theory,” Materials, 12, No. 8, 1262 (2019).

    Google Scholar 

  23. M. Zaczynska, and F. Kazmierczyk, “Multi-mode buckling analysis of FGM channel section beams,” Materials, 13, No. 11, 2567 (2020).

    Google Scholar 

  24. M. Fabiani, “Exact solutions of linear buckling for a class of FGM columns with varying cross-section,” Int. J. Struct. Stab. Dy., 21, No. 6, 2150079 (2021).

  25. A. K. Eqal, “Static buckling behavior of FGM Timoshenko beam theory resting on Winkler elastic foundation,” J. Mech. Eng. Research and Developments JERDFO, 44, No. 4, 168-177 (2021).

    Google Scholar 

  26. A. S. Sayyad, P. V. Avhad, and L. Hadiji, “On the static deformation and frequency analysis of functionally graded porous circular beams,” Forces Mech, 7, 10093 (2022).

    Article  Google Scholar 

  27. L. Hadji, M Avcar, and N. Zouatnia, “Natural frequency analysis of imperfect FG sandwich plates resting on Winkler-Pasternak foundation,” Mater. Today: Proc., 53, Part 1, 153-160 (2022).

  28. Y. Kumar, A. Gupta, and A. Tounsi, “Size-dependent vibration response of porous graded nanostructure with FEM and nonlocal continuum model,” Adv. Nano Res., 11, No. 1, 1-17 (2021).

    Google Scholar 

  29. S. I. Tahir, A. Chikh, A. Tounsi, M. A. Al-Oster, S. U. Al-Dulaijan, and M. M. Al-Zahrani, “Wave propagation analysis of a ceramic-metal functionally graded sandwich plate with different porosity distributions in a hygro-thermal environment,” Compos. Struct., 269, 114030 (2021).

    Article  Google Scholar 

  30. M. Royal, B. Shubhankar, and H. Lazleg, “Limit elastic speed analysis of rotating porous annulus functionally graded disks,” Steel Compos. Struct., 42, Issue 3, 375-338 (2022).

    Google Scholar 

  31. Y. A. Kang and X. F. Li, “Bending of functionally graded cantilever beam with power-law non-linearity subjected to an end force,” Int. J. Nonlin. Mech., 44, 696-703 (2009).

    Article  Google Scholar 

  32. M. Sitar, F. Kosel, and M. Brojan, “Large deflections of nonlinearly elastic functionally graded composite beam,” Arch. Civ. Mech. Eng., 14, No. 4, 700-709 (2014).

    Article  Google Scholar 

  33. F. Althoey and E. Ali, “Simplified stress analysis of functionally graded beams and influence of material function on deflection,” Appl. Sci., 11, 11747 (2021).

    Article  CAS  Google Scholar 

  34. M. Paz, Structural Dynamics, Van Nostrand Reinhold Company, New York (1980).

    Google Scholar 

  35. A. K. Chopra, Dynamics of structures, Upper Saddle River, NJ, USA, Prentice-Hall, Inc. (2001).

    Google Scholar 

  36. R. L. Burden, D. J. Faires, and A. M. Burden, Numerical Analysis, Cengage Learning, Boston (2016).

    Google Scholar 

Download references

Acknowledgement

This paper was supported by Wonkwang University in 2022. The first author, Professor G. S. Kim, would like to express his gratitude for this financial support.

Declaration of conflict of interest. The authors declare that they have no conflict of interest.

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, 460 Iksan-daero, Iksan-si, 54538, Jellabuk-do, Korea

    Gweon Sik Kim & Byoung Koo Lee

  2. Department of Civil Engineering, University of Seoul, 163 Seoulsiripdae-ro, Seoul, 02504, Dongdaemun-gu, Korea

    Joon Kyu Lee

  3. Bumhan Construction Corp. Ltd., 5 Hongsan-ro, Wansan-gu, Jeonju-si, 54966, Jellabuk-do, Korea

    Dai Soon Ahn

Authors
  1. Gweon Sik Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Joon Kyu Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dai Soon Ahn
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Byoung Koo Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Byoung Koo Lee.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, G.S., Lee, J.K., Ahn, D.S. et al. Free Vibrations and Buckling of Laterlally Functionally Graded Material Columns. Mech Compos Mater 59, 807–824 (2023). https://doi.org/10.1007/s11029-023-10133-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-023-10133-7

Keywords

Search

Navigation