Skip to main content
SpringerLink
Log in

Micromechanical Models for Analyzing Bending of Porous/Perfect FG Plates in a Hygro-Thermomechanical Environment by a Quasi-3D Theory

  • Published:
Mechanics of Composite Materials Aims and scope

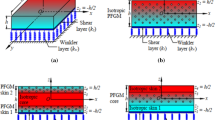
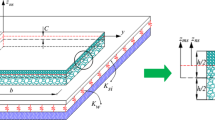
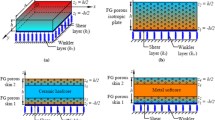
An analytical formulation based on a quasi-3D shear deformation theory is proposed to examine the bending response of functionally porous/perfect plates supported on a Kerr/Pasternak/Winkler elastic foundation in hygro-thermo-mechanical conditions. Two kinds of plates, perfect and porous, were studied. For the perfect plates, Mori–Tanaka, LRVE, Voigt, and Reuss models were employed to calculate their mechanical properties changing across the thickness. For the porous plates, different porosity patterns were considered to estimate their mechanical properties. After establishing the governing equations, the Navier solution for simply supported plates was used to calculate their displacements and stresses. The results obtained were compared with data published in the literature, and a good agreement was revealed. Some numerical results were used to investigate the effects of the porosity function, porosity percentage, micromechanical models, and the elastic foundation on the displacements and stresses of a simply supported porous/perfect plate under hygro-thermo-mechanical loadings. The results obtained reveal that these variables have a great influence on the response of the plate in hygro-thermo-mechanical environments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.

Similar content being viewed by others

References

  1. S. Dastjerdi and Y. Tadi Beni, “A novel approach for nonlinear bending response of macro and nanoplates with irregular variable thickness under non uniform loading in thermal environment,” Mech. Bas. Des. Struct. Mech., 47, No. 4, 453-478 (2019).

  2. A. Selmi, “Exact solution for nonlinear vibration of clamped-clamped functionally graded buckled beam,” Smart Structures and Systems, 26, No. 3, 361-371 (2020). https://doi.org/10.12989/SSS.2020.26.3.361

  3. A. Garg, M.-O. Belarbi, H. D. Chalak, and A. Chakrabarti, “A review of the analysis of sandwich FGM structures,” Compos. Struct., 258, 113427 (2021). https://doi.org/10.1016/j.compstruct.2020.113427

  4. A. Garg, H. D. Chalak, A. M. Zenkour, M. O. Belarbi, and M. S. A. Houari, “A review of available theories and methodologies for the analysis of nano isotropic, nano functionally graded, and cnt reinforced nanocomposite structures,” Archives of Computational Methods in Eng., 29, 2237-2270(2022). https://doi.org/10.1007/s11831-021-09652-0

    Article  Google Scholar 

  5. A. Garg and H. D. Chalak, “A review on analysis of laminated composite and sandwich structures under hygrothermal conditions,” Thin-Walled Struct., 142, 205-226 (2019). https://doi.org/10.1016/j.tws.2019.05.005.

    Article  Google Scholar 

  6. R. Vaghefi, M. R. Hematiyan, and A. Nayebi, “Three-dimensional thermo-elasto plastic analysis of thick functionally graded plates using the meshless local Petrov–Galerkin method,” Eng. Analysis with Boundary Elements, 71, 34-49 (2016).

    Article  Google Scholar 

  7. J. Guoyong, S. Zhu, S. Shuangxia, Y. Tiangui, and G. Siyang, “Three-dimensional exact solution for the free vibration of arbitrarily thick functionally graded rectangular plates with general boundary conditions,” Compos. Struct, 108, 565-77 (2014)

    Article  Google Scholar 

  8. K. Asemi and M. Shariyat, “Highly accurate nonlinear three-dimensional finite element elasticity approach for biaxial bucking of rectangular anisotropic FGM plates with general orthotropy directions,” Compos. Struct, 106, 235-49 (2013).

    Article  Google Scholar 

  9. H. T. Thai and S. E. Kim, “A simple quasi-3D sinusoidal shear deformation theory for functionally graded plates,” Compos. Struct., 99, 172-180 (2013).

    Article  Google Scholar 

  10. H. Zhang, J. Q. Jiang, and Z. C. Zhang, “Three-dimensional elasticity solutions for bending of generally supported thick functionally graded plates,” Appl. Math. and Mech., 35, 1467-1478 (2014).

    Article  Google Scholar 

  11. M. Jabbari, E. Shahryari, H. Haghighat, and M. R. Eslami, “An analytical solution for steady state three dimensional thermoelasticity of functionally graded circular plates due to axisymmetric loads,” Eur. J. Mech. A/ Solids, 47, 124-142 (2014).

    Article  Google Scholar 

  12. A. F. Radwan, “Quasi-3D integral model for thermomechanical buckling and vibration of FG porous nanoplates embedded in an elastic medium,” Int. J. Mech. Sci., 157-158, 320-335 (2019).

    Article  Google Scholar 

  13. S. A. Al Khateeb and A. M. Zenkour, “A refined four-unknown plate theory for advanced plates resting on elastic foundations in hygrothermal environment,” Compos. Struct., 111, 240-8 (2014).

  14. H. Sung-Cheon, P. Weon-Tae, and J. Woo-Young, “3D graphical dynamic responses of FGM plates on Pasternak elastic foundation based on quasi-3D shear and normal deformation theory,” Composites Part B: Engineering, 95, 324-334 (2016).

    Article  Google Scholar 

  15. F. Ebrahimi, A. Jafari, and M. R. Barati, “Vibration analysis of magneto-electro-elastic heterogeneous porous material plates resting on elastic foundations,” Thin-Walled Struct., 119, 33-46 (2017).

    Article  Google Scholar 

  16. H. Hachemi, A. Kaci, M. S. A. Houari, M. Bourada, A. Tounsi, and S. R. Mahmoud, “A new simple three-unknown shear deformation theory for bending analysis of FG plates resting on elastic foundations,” Steel and Compos. Struct., 25, No. 6, 717-726 (2017).

    Google Scholar 

  17. D. Shahsavari, M. Shahsavari, L. Li, and B. Karami, “A novel quasi-3D hyperbolic theory for free vibration of FG plates with porosities resting on Winkler/Pasternak/Kerr foundation,” Aerospace Sci. and Technol., 72, 134-149 (2018).

    Article  Google Scholar 

  18. S. J. Singh and S. P. Harsha, “Nonlinear dynamic analysis of sandwich S-FGM plate resting on pasternak foundation under thermal environment,” Eur. J. Mech. - A/Solids, 76, 155-179 (2019).

    Article  Google Scholar 

  19. M. G. Shantaram and S. S. Atteshamuddin, “Analysis of functionally graded plates resting on elastic foundation and subjected to nonlinear hygro-thermo-mechanical loading,” JMST Advances, 1, No. 4, 233-248 (2019).

    Article  Google Scholar 

  20. A. Garg, M.-O. Belarbi, H. D. Chalak, and A. M. Zenkour, ”Hygro-thermo-mechanical based bending analysis of symmetric and unsymmetric power-law, exponential and sigmoidal FG sandwich beams,” Mech. Adv. Mater. and Struct. (2021). https://doi.org/10.1080/15376494.2021.1931993

    Article  Google Scholar 

  21. A. Garg, H. D. Chalak, M.-O. Belarbi, A. Chakrabarti, and M. S. A. Houari, “Finite element-based free vibration analysis of power-law, exponential and sigmoidal functionally graded sandwich beams,” J. Inst. Eng. India Ser. C., 102, 1167-1201(2021). https://doi.org/10.1007/s40032-021-00740-5

    Article  Google Scholar 

  22. A. Garg, H. D. Chalak, and A. Chakrabarti, “Bending analysis of functionally graded sandwich plates using HOZT including transverse displacement effects,” Mech. Based Design of Struct. and Machines, 50, No. 10, 3563-3577 (2020). https://doi.org/10.1080/15397734.2020.1814157

    Article  Google Scholar 

  23. A. Garg, H. D. Chalak, and A. Chakrabarti, “Comparative study on the bending of sandwich FGM beams made up of different material variation laws using refined layerwise theory,” Mech. Mater., 151, 103634 (2020). https://doi.org/10.1016/j.mechmat.2020.103634

  24. A. Garg and H. D. Chalak, “Analysis of non-skew and skew laminated composite and sandwich plates under hygro thermomechanical conditions including transverse stress variations,” Journal of Sandwich Struct. & Mater., 23, No. 8, 3471-3494(2021). doi:https://doi.org/10.1177/1099636220932782

    Article  Google Scholar 

  25. P. V. Vinh and L. Q. Huy, “Finite element analysis of functionally graded sandwich plates with porosity via a new hyperbolic shear deformation theory,” Defense Technology, (2021). DOI: https://doi.org/10.1016/j.dt.2021.03.006

    Article  Google Scholar 

  26. P. M. Ramteke, S. K. Panda, and N. Sharma, “Effect of grading pattern and porosity on the eigen characteristics of porous functionally graded structure,” Steel and Compos. Struct., 33, No. 6, 865-875 (2019). DOI: https://doi.org/10.12989/scs.2019.33.6.865

    Article  Google Scholar 

  27. L. Hadji and M. Avcar, “Free Vibration Analysis of FG Porous Sandwich Plates under Various Boundary Conditions,” J. Appl. Comput. Mech, 7, No. 2, 505-519 (2021). https://doi.org/10.22055/jacm.2020.35328.2628

  28. M.-C. Trinh and S.-E. Kim, “A three variable refined shear deformation theory for porous functionally graded doubly curved shell analysis,” Aerospace Sci. and Technol., 94, 105356 (2019). https://doi.org/10.1016/j.ast.2019.105356

  29. B. Srikarun, W. Songsuwan, and N. Wattanasakulpong, “Linear and nonlinear static bending of sandwich beams with functionally graded porous core under different distributed loads,” Compos. Struct., 276, 114538 (2021). https://doi.org/10.1016/j.compstruct.2021.114538

  30. S. R. Mahmoud, E. Ghandourah, A. Algarni, M. Balubaid, A. Tounsi, and F. Bourada, “On thermo‑mechanical bending response of porous functionally graded sandwich plates via a simple integral plate model,” Archives of Civil and Mech. Eng., 22, 186 (2022). https://doi.org/10.1007/s43452-022-00506-5

    Article  Google Scholar 

  31. M. Yaylaci, M. Abnoz, E. U. Yaylaci, H. Ölmez, D. M. Sekban, and A. Birinci, “Evaluation of the contact problem of functionally graded layer resting on rigid foundation pressed via rigid punch by analytical and numerical (FEM and MLP) methods,” Archive of Appl. Mech., 92, 1953-1971 (2022). https://doi.org/10.1007/s00419-022-02159-5

    Article  Google Scholar 

  32. E. Öner, B. Şengül, E. U. Yaylaci, G. Adıyaman, M. Yaylaci, and A. Birinci, “On the plane receding contact between two functionally graded layers using computational, finite element and artificial neural network methods,” J. Appl. Math. and Mech., In Press, (2022). https://doi.org/10.1002/zamm.202100287

  33. M. Yaylaci, E. Adıyaman, E. Öner, and A. Birinci, “Investigation of continuous and discontinuous contact cases in the contact mechanics of graded materials using analytical method and FEM,” Computers and Concrete, 27, No. 3, 199-210 (2021). DOI: http://dx.doi.org/https://doi.org/10.12989/cac.2021.27.3.199

  34. M. Yaylaci, A. Eyüboğlu, G. Adıyaman, E. Uzun Yaylacı, E. Öner, and A. Birinci, “Assessment of different solution methods for receding contact problems in functionally graded layered mediums,” Mech. Mater., 154, 103730 (2021). https://doi.org/10.1016/j.mechmat.2020.103730

  35. M. Yaylaci, M. Yayli, U. E. Yaylacı, H. Ölmez, and A. Birinci, “Analyzing the contact problem of a functionally graded layer resting on an elastic half plane with theory of elasticity, finite element method and multilayer perceptron,” Structural Eng. and Mech., 78, No. 5, 585-597 (2021). DOI: https://doi.org/10.12989/sem.2021.78.5.585

    Article  Google Scholar 

  36. M. Yaylaci, E. Adıyaman, E. Öner, and A. Birinci, “Examination of analytical and finite element solutions regarding contact of a functionally graded layer,” Structural Eng. and Mech.. 76, No. 3, 325-336 (2020). http://dx.doi.org/https://doi.org/10.12989/sem.2020.76.3.325

  37. Y. Jaesang and K. Addis, “Modeling functionally graded materials containing multiple heterogeneities,” Acta Mech, 225, 1931-1943 (2014).

    Article  Google Scholar 

  38. Jr. L. Mishnaevsky, Computational Mesomechanics of Composites, John Wiley & Sons, England (2007).

  39. J. Ju and T. M. Chen, “Micromechanics and effective moduli of elastic composites containing randomly dispersed ellipsoidal inhomogeneities,” Acta Mech., 103, 103-121 (1994).

    Article  Google Scholar 

  40. A. H. Akbarzadeh, A. Abedini, and Z. T. Chen, “Effect of micromechanical models on structural responses of functionally graded plates,” Comp. Struct., 119, 598-609 (2015).

    Article  Google Scholar 

  41. Y. Benveniste, “A new approach to the application of Mori–Tanaka’s theory in composite materials,” Mech. Mat., 6, No. 2, 147-57 (1987). doi:https://doi.org/10.1016/0167-6636(87)90005-6

    Article  Google Scholar 

  42. N. Wattanasakulpong and A. Chaikittiratana, “Flexural vibration of imperfect functionally graded beams on Timoshenko beam theory,” Chebyshev Collocation Method Meccanica, 50, 1331-1342 (2015). https://doi.org/10.1007/s11012-014-0094-8

    Article  Google Scholar 

  43. A. Gupta and M. Talha, “Influence of porosity on the flexural and vibration response of gradient plate using nonpolynomial higher-order shear and normal deformation theory,” Int. J. Mech. Mater. Des., 14, No. 2, 277-296 (2018). https://doi.org/10.1007/s10999-017-9369-2

    Article  CAS  Google Scholar 

  44. L. J. Gibson and M. Ashby, “The mechanics of three-dimensional cellular materials,” Proce. R. Soc, London A, Math. Phys. Eng. Sci, 382, No. 1782, 43-59 (1982). https://doi.org/10.1098/rspa.1982.0088

  45. R. Bachir Bouiadjra, A. Mahmoudi, S. Benyoucef, A. Tounsi, and F. Bernard, “Analytical investigation of bending response of FGM plate using a new quasi 3D shear deformation theory: Effect of the micromechanical models,” Struct. Eng. Mech, 66, No. 3, 317-328 (2018). DOI: https://doi.org/10.12989/sem.2018.66.3.317

  46. A. S. Sayyad and Y. M. Ghugal, “Effects of nonlinear hygrothermomechanical loading on bending of FGM rectangular plates resting on two-parameter elastic foundation using four-unknown plate theory,” J. Therm. Stress. 42, No. 2, 213-232 (2019). https://doi.org/10.1080/01495739.2018.1469962

    Article  Google Scholar 

  47. I. M. Mudhaffar, A. Tounsi, A. Chikh, M. A. Al-Osta, M. M. Al-Zahrani, and S. U. Al-Dulaijan, “Hygro-thermo-mechanical bending behavior of advanced functionally graded ceramic metal plate resting on a viscoelastic foundation,” Structures, 33, 2177-2189 (2021). https://doi.org/10.1016/j.istruc.2021.05.090

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, University of Ferhat Abbas, Sétif 1, Algeria

    M. Mekerbi

  2. Material and Hydrology Laboratory, University of Sidi Bel Abbes, Faculty of Technology, Civil Engineering Department, Sidi Bel Abbes, Algeria

    M. Mekerbi, R. Bachir Bouiadjra, S. Benyoucef & A. Tounsi

  3. Department of Civil Engineering, University Mustapha Stambouli of Mascara, Mascara, Algeria

    R. Bachir Bouiadjra

  4. Department of Mathematics, Al-Aflaj College of Science and Humanities, Prince Sattam bin Abdulaziz University, 710-11912, Al-Aflaj, Saudi Arabia

    M. M. Selim

  5. YFL (Yonsei Frontier Lab), Yonsei University, Seoul, Korea

    A. Tounsi

  6. Department of Civil and Environmental Engineering, King Fahd University of Petroleum & Minerals, 31261, Dhahran, Eastern Province, Saudi Arabia

    A. Tounsi

  7. Interdisciplinary Research Center for Construction and Building Materials, KFUPM, Dhahran, Saudi Arabia

    A. Tounsi

  8. Department of Mathematics, Govt. College University Faisalabad, Faisalabad, 38000, Pakistan

    M. Hussain

Authors
  1. M. Mekerbi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Bachir Bouiadjra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Benyoucef
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. M. Selim
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. A. Tounsi
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. M. Hussain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Benyoucef.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mekerbi, M., Bachir Bouiadjra, R., Benyoucef, S. et al. Micromechanical Models for Analyzing Bending of Porous/Perfect FG Plates in a Hygro-Thermomechanical Environment by a Quasi-3D Theory. Mech Compos Mater 59, 693–712 (2023). https://doi.org/10.1007/s11029-023-10125-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-023-10125-7

Keywords

Search

Navigation