Skip to main content
SpringerLink
Log in

Buckling Analysis of Functionally Graded Sandwich Plates Resting on an Elastic Foundation and Subjected to a Nonuniform Loading

  • Published:
Mechanics of Composite Materials Aims and scope

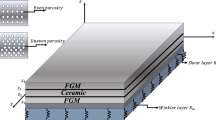
A buckling analysis of functionally graded plates of a complex form resting on an elastic foundation and subjected to an in-plane nonuniform loading is performed by the R-functions method for the first time. The mathematical formulation of the problem is presented within the framework of the classical laminate plate theory. The plates considered consist of three layers. The middle layer (core) is ceramic or metal, a face layers are fabricated of functionally graded materials (FGMs). The power-law distribution of volume fraction of constituents is used to compute the effective material properties of FGM layers. The approach proposed and the software developed consider the heterogeneous subcritical state of the plates. First, the problem of in-plane elasticity problem is solved, and then the stability problem is considered. To solve both the problems, the Ritz method combined with the R-functions theory is used. The method proposed and the software developed are verified by comparing the buckling loads of square plates subjected to a nonuniform loading. The critical loads for sandwich FG plates of a complex geometry in a nonuniform edge compression are calculated. The effects of boundary conditions, the scheme of layer arrangement, and the type of FGM on the critical load are studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. F. Z. Kettaf, M. S. A. Houari, M. Benguediab, and A. Tounsi, “Thermal buckling of functionally graded sandwich plates using a new hyperbolic shear displacement model,” Steel Compos. Struct., 15, 399-423 (2013).

    Article  Google Scholar 

  2. V. H. Nguyen, T. K. Nguyen, H. T. Thai, and T. P. Vo, “A new inverse trigonometric shear deformation theory for isotropic and functionally graded sandwich plates,” Compos., Part B, 66, 233-246 (2014).

    Article  Google Scholar 

  3. S. S. Akavci, “Mechanical behavior of functionally graded sandwich plates on elastic foundation,” Compos., Part B, 96, 136-152 (2016).

    Article  Google Scholar 

  4. A. M. A. Neves, A. J. M. Ferreira, E. Carrera, M. Cinefra, R. M. N. Jorge, C. M. Mota Soares, and A. L. Araújo, “Influence of zig-zag and warping effects on buckling of functionally graded sandwich plates according to sinusoidal shear deformation theories,” Mech. Adv. Mat. Struct., 24, 360-376 (2017).

  5. F. Z. Taibi, S. Benyoucef, A. Tounsi, R. Bachir Bouiadjra, E. A. Adda Bedia, and S. Mahmoud, “A simple shear deformation theory for thermo-mechanical behavior of functionally graded sandwich plates on elastic foundations,” J. Sandwich Struct. and Mater., 17, No. 2, 99-129 (2015).

  6. H. V. Tung, “Thermal and thermomechanical postbuckling of FGM sandwich plates resting on elastic foundations with tangential edge constraints and temperature dependent properties,” Compos. Struct., 131, 1028-1039 (2015).

    Article  Google Scholar 

  7. V. Birman and G. A. Kardomateas, “Review of current trends in research and applications of sandwich structures,” Compos., Part B, 142, 221-240 (2018).

    Article  CAS  Google Scholar 

  8. L. V. Kurpa and T. V. Shmatko, “Application of the R-functions method for vibration and buckling analysis of functionally graded plates and shallow shells with complex planform,” Literature review from 2014 to 2020, Zbornik Radova 19 (27), Dynamics of hybrid systems of complex structures, Matematiˇcki institut SANU, 237-261 (2022).

  9. K. R. Hedrih and J. Simonpvić, “Structural analogies for hybrid discrete-continuum systems of deformable bodies coupled with non-linear layers, Review paper,” The Eur. Physical J. Special Topics, 230, 18-20 (2021).

    Article  Google Scholar 

  10. H. Yaghoobi and P. Yaghoobi, “Buckling analysis of sandwich plates with FGM face sheets resting on elastic foundation with various boundary conditions: an analytical approach,” Meccanica, 48, 2019-2035 (2013).

    Article  Google Scholar 

  11. H. T. Thai and S. E. Kim, “Closed-form solution for buckling analysis of thick functionally graded plates on elastic foundation,” Int. J. Mech. Sci., 75, 34-44 (2013).

    Article  Google Scholar 

  12. Y. Kiani, E. Bagherizadeh, and M. R. Eslami, “Thermal and mechanical buckling of sandwich plates with FGM face sheets resting on the Pasternak elastic foundation,” Proceedings of the Institution of Mechanical Engineers, Part C. J. Mech. Eng. Sci., 226, 32-41 (2011).

  13. P. Malekzadeh, M. R. Golbahar Haghighi, and B. Alibeygi, “A Buckling analysis of functionally graded arbitrary straight-sided quadrilateral plates on elastic foundations,” Meccanica, 47, No. 2, 321-333 (2012).

  14. K. K. Devarakonda and C. W. Bert, “Buckling of rectangular plate with nonlinearly distributed compressive loading on two opposite sides: Comparative analysis and results,” Mech. Adv. Mater. and Struct., 11, Nos. 4-5, 433-444 (2004).

    Article  Google Scholar 

  15. H. Hu, A. Badir, and A. Abatan. “Buckling behavior of a graphite/epoxy composite plate under parabolic variation of axial loads,” Int. J. Mech. Sci., 45, Nos. 6-7, 1135-47 (2003).

    Article  Google Scholar 

  16. P. Jana and K. Bhaskar, “Stability analysis of simply-supported rectangular plates under nonuniform uniaxial compression using rigorous and approximate plane stress solutions,” Thin-Walled Structures, 44, No. 5, 507-16 (2006).

    Article  Google Scholar 

  17. R. Lal and R. Saini. “Buckling and vibration of non-homogeneous rectangular plates subjected to linearly varying inplane force,” Shock and Vibration, 20, No. 5, 879-94 (2013).

    Article  Google Scholar 

  18. J. Awrejcewicz, L. Kurpa, and O. Mazur, “Dynamical instability of laminated plates with external cutout,” Int. J. of Nonlinear Mech., 81, 103-114 (2016).

    Article  Google Scholar 

  19. L. V. Kurpa and T. V. Shmatko, “Investigation of free vibrations and stability of functionally graded three-layer plates by using the R-functions theory and variational methods,” J. Math. Sci. 249, No. 3, 496-520 (2020).

    Article  Google Scholar 

  20. L. Kurpa, V. Tkachenko, and A. Linnik, “Buckling of laminated plates subjected to nonuniform distributed in-plane force,” Mechanics Based Design of Structures and Machines 49, No. 8, 1145-1156 (2021).

    Article  Google Scholar 

  21. L. Kurpa, T. Shmatko, and J. Awrejcewicz, “Parametric vibrations of functionally graded sandwich plates with complex forms,” in: Lacarbonara W., Balachandran B., Ma J., Tenreiro Machado J., Stepan G. (eds) New Trends in Nonlinear Dynamics, 3, 66-77 (2020).

  22. L.V. Kurpa and T. V. Shmatko, “Buckling and free vibration analysis of functionally graded sandwich plates and shallow shells by the Ritz method and the R-functions theory,” J. Mech. Eng. Sci., 235, No. 20, 135-147 (2020).

    Google Scholar 

  23. J. N. Reddy, “Analysis of functionally graded plates,” J. Num. Meth. Eng., 47, 663-684 (2000).

    Article  Google Scholar 

  24. H. S. Shen, Functionally Graded Materials of Plates and Shells, CRC Press, Florida (2009).

    Google Scholar 

  25. M. Sobhy, “Buckling and free vibration of exponentially graded sandwich plates resting on elastic foundations under various boundary conditions,” Compos. Struct., 99, 76-87 (2013).

    Article  Google Scholar 

  26. A. M. Zenkour, “A comprehensive analysis of functionally graded sandwich plates: Part 2- buckling and free vibration,” J. Solid Struct., 42, Nos. 18-19, 5243-5258 (2005).

    Article  Google Scholar 

  27. V. L. Rvachev, The R-functions Theory and Its Applications [in Russian], Naukova Dumka Kiev (1982).

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, National Technical University “Kharkiv Polytechnic Institute,”, Kharkiv, Ukraine

    L. Kurpa & A. Linnik

  2. Department of Higher Mathematics, National Technical University “Kharkiv Polytechnic Institute,”, Kharkiv, Ukraine

    T. Shmatko

Authors
  1. L. Kurpa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Shmatko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Linnik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. Kurpa.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kurpa, L., Shmatko, T. & Linnik, A. Buckling Analysis of Functionally Graded Sandwich Plates Resting on an Elastic Foundation and Subjected to a Nonuniform Loading. Mech Compos Mater 59, 645–658 (2023). https://doi.org/10.1007/s11029-023-10122-w

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-023-10122-w

Keywords

Search

Navigation