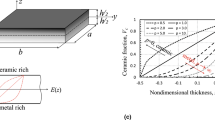
We propose a numerical-analytic method aimed at the investigation of free vibrations and stability of functionally graded sandwich-type plates and based on the refined Timoshenko-type theory of the first order. We considered various schemes of arrangement of the layers: (1) the filler is a functionally graded material and the top and bottom layers are made of isotropic materials and (2) vice versa, the filler is made of an isotropic material, whereas the top and bottom layers are made of functionally graded materials. The proposed method is based on the R-functions theory and the Ritz variational method. This method and the developed software take into account the presence of an inhomogeneous subcritical state of the plate. Analytic relations are obtained for the evaluation of the elastic constants and density of the material under the assumption that Poisson’s ratios are identical, for the components of functionally graded materials. The numerical results obtained for the eigenfrequencies and the critical load are compared with the available data and their good agreement is demonstrated. To illustrate the possibilities of the proposed approach, we perform the numerical analyses of plates of complex geometric shapes loaded in the middle plane. The influence of various geometric and mechanical parameters on the dynamic behavior of the plate, critical load, and the zones of dynamic instability is investigated.
Similar content being viewed by others
References
V. V. Bolotin, The Dynamic Stability of Elastic Systems, Holden-Day, San Francisco (1964).
L. V. Kurpa, O. S. Mazur, and V. V. Tkachenko, “Parametric vibration of multilayer plates of complex shape,” Mat. Met. Fiz.- Mekh. Polya, 56, No. 2, 136–150 (2013); English translation: J. Math. Sci., 203, No. 2, 165–184 (2014). https://doi.org/10.1007/s10958-014-2098-2.
L. V. Kurpa, O. S. Mazur, and T. V. Shmatko, Application of the R-Functions Theory to the Solution of Nonlinear Problems of the Dynamics of Multilayer Plates [in Russian], V Dele, Kharkov (2016).
V. L. Rvachev, Theory of R-Functions and Some of Its Applications [in Russian], Naukova Dumka, Kiev (1982).
A. Argento and R. A. Scott, “Dynamic instability of layered anisotropic circular cylindrical shells. Part II: Numerical results,” J. Sound Vibrat., 162, No. 2, 323–332 (1993). https://doi.org/10.1006/jsvi.1993.1121.
J. Awrejcewicz, L. Kurpa, and O. Mazur, “Dynamical instability of laminated plates with external cutout,” Int. J. Nonlin. Mech., 81, 103–114 (2016). https://doi.org/10.1016/j.ijnonlinmec.2016.01.002.
S. Dash, A. V. Asha, and S. K. Sahu, “Stability of laminated composite curved panels with cutout using finite-element method,” in: Proc. of the 3rd Internat. Conf. on Theoretical, Applied Computational & Experimental Mechanics (ICTACEM-2004), Indian Institute of Technology, Kharagpur (2004). http://hdl.handle.net/2080/316.
M. Koizumi, “The concept of FGM,” Ceramic Trans., 34, 3–10 (1993).
Y. Kumar, “The Rayleigh–Ritz method for linear dynamic, static and buckling behavior of beams, shells and plates: A literature review,” J. Vibrat. Control, 24, No. 7, 1205–1227 (2017). https://doi.org/10.1177/1077546317694724.
L. Kurpa, O. Mazur, and V. Tkachenko, “Dynamical stability and parametrical vibrations of the laminated plates with complex shape,” Lat. Amer. J. Solids Struct., 10, No. 1, 175–188 (2013).
Q. Li, V. P. Iu, and K. P. Kou, “Three-dimensional vibration analysis of functionally graded material sandwich plates,” J. Sound Vibrat., 311, Nos. 1-2, 498–515 (2008). https://doi.org/10.1016/j.jsv.2007.09.018.
H. Matsunaga, “Free vibration and stability of functionally graded shallow shells according to a 2D higher-order deformation theory,” Compos. Struct., 84, No. 2, 132–146 (2008). https://doi.org/10.1016/j.compstruct.2007.07.006.
N. E. Meiche, A. Tounsi, N. Ziane, I. Mechab, and E. A. Adda Bedia, “A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate,” Int. J. Mech. Sci., 53, No. 4, 237–247 (2011). https://doi.org/10.1016/j.ijmecsci.2011.01.004.
M. P. Nemeth, Buckling and Postbuckling Behavior of Laminated Composite Plates with a Cutout, NASA Technical Paper 3587 (1996).
A. M. A. Neves, A. J. M. Ferreira, E. Carrera, M. Cinefra, R. M. N. Jorge, and C. M. M. Soares, “Buckling analysis of sandwich plates with functionally graded skins using a new quasi-3D hyperbolic sine shear deformation theory and collocation with radial basis functions,” Z. Angew. Math. Mech., 92, No. 9, 749–766 (2012). https://doi.org/10.1002/zamm.201100186.
T. Y. Ng, K. Y. Lam, and J. N. Reddy, “Dynamic stability of cross-ply laminated composite cylindrical shells,” Int. J. Mech. Sci., 40, No. 8, 805–823 (1998). https://doi.org/10.1016/S0020-7403(97)00143-4.
S. K. Sahu and P. K. Datta, “Research advances in the dynamic stability behavior of plates and shells: 1987–2005, Part 1: Conservative systems,” Appl. Mech. Rev., 60, No. 2, 65–75 (2007). https://doi.org/10.1115/1.2515580.
H. S. Shen, Functionally Graded Materials of Plates and Shells, CRC Press, Boca Raton, Fl (2009).
G. J. Simitses, “Instability of dynamically loaded structures,” Appl. Mech. Rev., 40, No. 10, 1403–1408 (1987). https://doi.org/10.1115/1.3149542.
M. K. Singha and R. Daripa, “Nonlinear vibration and dynamic stability analysis of composite plates,” J. Sound Vibrat., 328, Nos. 4-5, 541–554 (2009). https://doi.org/10.1016/j.jsv.2009.08.020.
K. Swaminathan, D. T. Naveenkumar, A. M. Zenkour, and E. Carrera, “Stress, vibration and buckling analyses of FGM plates—A state-of-the-art review,” Compos. Struct., 120, 10–31 (2015). https://doi.org/10.1016/j.compstruct.2014.09.070.
H.-T. Thai and S.-E. Kim, “A review of theories for the modeling and analysis of functionally graded plates and shells,” J. Compos. Struct., 128, 70–86 (2015). https://doi.org/10.1016/j.compstruct.2015.03.010.
A. M. Zencour, “A comprehensive analysis of functionally graded sandwich plates: Part 2, Buckling and free vibration,” Int. J. Solids Struct., 42, Nos. 18–19, 5243–5258 (2005). https://doi.org/10.1016/j.ijsolstr.2005.02.016.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 61, No. 1, pp. 155–172, January–March, 2018.
Rights and permissions
About this article
Cite this article
Kurpa, L.V., Shmatko, T.V. Investigation of Free Vibrations and Stability of Functionally Graded Three-Layer Plates by Using the R-Functions Theory and Variational Methods. J Math Sci 249, 496–520 (2020). https://doi.org/10.1007/s10958-020-04955-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-020-04955-2