Skip to main content
SpringerLink
Log in

Mechanical Stability of Eccentrically Stiffened Auxetic Truncated Conical Sandwich Shells Surrounded by Elastic Foundations

  • Published:
Mechanics of Composite Materials Aims and scope

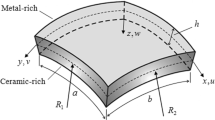
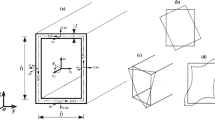
The static stability of auxetic truncated conical sandwich shells reinforced by stiffeners surrounded by elastic foundations is investigated. The shells are made from two isotropic outer layers and an auxetic core layer with a negative Poisson ratio. Based on the classical shell theory, combined with the displacement and Bubnov–Galerkin methods, the governing equations of the shells are derived and solved. The critical buckling load of the shells as a function of their geometrical parameters, the honeycomb structure, stiffeners, and types of elastic foundations are examined in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. A. H. Sofiyev and Z. Karaca, “The vibration and buckling of laminated non-homogeneous orthotropic conical shells subjected to external pressure,” Eur. J. Mech. A-Solid., 28, 317-328 (2018).

    Article  Google Scholar 

  2. A. H. Sofiyev, N. Kuruoglu, and M. Turkmen, “Buckling of FGM hybrid truncated conical shells subjected to hydrostatic pressure,” Thin-Walled Struct., 47, 61-72 (2009).

    Article  Google Scholar 

  3. A. H. Sofiyev, “The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler–Pasternak foundations,” Int. J. Pres. Ves. Pip., 87, 753-761 (2010).

    Article  Google Scholar 

  4. A. H. Sofiyev, “Influence of the initial imperfection on the non-linear buckling response of FGM truncated conical shells,” Int. J. Mech. Sci., 53, 753-761 (2011).

    Article  Google Scholar 

  5. A. M. Najafov and A. H. Sofiyev, “The non-linear dynamics of FGM truncated conical shells surrounded by an elastic medium,” Int. J. Mech. Sci., 66, 33-44 (2013).

    Article  Google Scholar 

  6. A. H. Sofiyev and E. Osmancelebioglu, “The free vibration of sandwich truncated conical shells containing functionally graded layers within the shear deformation theory,” Compos. Part B Eng., 120, 197-211 (2017).

    Article  Google Scholar 

  7. A. H. Sofiyev, F. Tornabene, R. Dimitri, and N. Kuruoglu, “Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading,” Nanomaterials., 10, No. 3, 1-19 (2020).

    Article  CAS  Google Scholar 

  8. D. V. Dung, L. K. Hoa, and N. T. Nga, “On the stability of functionally graded truncated conical shells reinforced by functionally graded stiffeners and surrounded by an elastic medium,” Compos. Struct., 108, 77-90 (2014).

    Article  Google Scholar 

  9. D. V. Dung and D. Q. Chan, “Analytical investigation on mechanical buckling of FGM truncated conical shells reinforced by orthogonal stiffeners based on FSDT,” Compos. Struct., 159, 827-841 (2017).

    Article  Google Scholar 

  10. N. D. Duc and P. H. Cong, “Nonlinear thermal stability of eccentrically stiffened functionally graded truncated conical shells surrounded on elastic foundations,” Eur. J. Mech. A-Solid., 50, 120-131 (2015).

    Article  Google Scholar 

  11. N. D. Duc, P. H. Cong, N. D. Tuan, P. Tran, and N. V. Thanh, “Thermal and mechanical stability of functionally graded carbon nanotubes (FG CNT)-reinforced composite truncated conical shells surrounded by the elastic foundations,” Thin-Walled Struct., 115, 300-310 (2017).

    Article  Google Scholar 

  12. N. D. Duc, K. Seung-Eock, and D. Q. Chan, “Thermal buckling analysis of FGM sandwich truncated conical shells reinforced by FGM stiffeners resting on elastic foundations using FSDT,” Therm. Stress., 41, No. 3, 331-365 (2018).

    Article  Google Scholar 

  13. D. Q. Chan, P. D. Nguyen, V. D. Quang, V. T. T. Anh, and N. D. Duc, “Nonlinear buckling and post-buckling of functionally graded carbon nanotubes reinforced composite truncated conical shells subjected to axial load,” Steel. Comp. Struct., 31, No. 3, 243-259 (2019).

    Google Scholar 

  14. D. Q. Chan, V. D. Long, and N. D. Duc, “Nonlinear buckling and post-buckling of FGM shear deformable truncated conical shells reinforced by FGM stiffeners,” Mech. Compos. Mater., 54, No. 6, 754-764 (2019).

    Article  Google Scholar 

  15. S. O. Dzhankhotov, V. A. Kireev, and N. T. Kulagin, “Experimental and theoretical study of the supporting power of longitudinally compressed slightly conical shells made of composite materials ,” Mech. Compos. Mater., 16, No. 6, 698-705 (1981).

    Article  Google Scholar 

  16. I. Yu. Babich, A. V. Boriseiko, and N. P. Semenyuk, “Stability of conical shells of metal composites beyond the elastic limit,” Mech. Compos. Mater., 37, No. 1, 1-66 (2001).

    Article  Google Scholar 

  17. S. M. F. Moghaddam and H. Ahmadi, “Active vibration control of truncated conical shell under harmonic excitation using piezoelectric actuator,” Thin-Walled Struct., 151, 106642 (2020).

    Article  Google Scholar 

  18. H. Aris and H. Ahmadi, “Nonlinear vibration analysis of FGM truncated conical shells subjected to harmonic excitation in thermal environment,” Mech. Res. Commun., 104, 103499 (2020).

    Article  Google Scholar 

  19. Y. Kiani, “Torsional vibration of functionally graded carbon nanotube reinforced conical shells,” Sci. Eng. Compos. Mater., 25, No. 1, 41-52 (2018).

    Article  CAS  Google Scholar 

  20. J. E. Jam and Y. Kiani, “Buckling of pressurized functionally graded carbon nanotube reinforced conical shells,” Compos. Struct., 125, 586-595 (2018).

    Article  Google Scholar 

  21. M. Mirzaei and Y. Kian, “Thermal buckling of temperature dependent FG-CNT reinforced composite conical shells,” Aerosp. Sci. Technol., 47, 42-53 (2015).

    Article  Google Scholar 

  22. N. D. Duc and P. H. Cong, “Nonlinear dynamic response and vibration of sandwich composite plates with negative Poisson’s ratio in auxetic honeycombs,” J. Sandw. Struct. Mater., 20, 692-717 (2018).

    Article  CAS  Google Scholar 

  23. P. H. Cong, N. D. Khanh, N. D. Khoa, and N. D. Duc, “New approach to investigate nonlinear dynamic response of sandwich auxetic double curves shallow shells using TSDT,” Compos. Struct., 185, 455-465 (2018).

    Article  Google Scholar 

  24. P. H. Cong, P. T. Long, N. V. Nhat, and N. D. Duc, “Geometrically nonlinear dynamic response of eccentrically stiffened circular cylindrical shells with negative poisson’s ratio in auxetic honeycombs core layer,” Int. J. Mech. Sci., 152, 443-453 (2019).

    Article  Google Scholar 

  25. N. D. Duc, S. E. Kim, P. H. Cong, N. T. Anh, and N. D. Khoa, “Dynamic response and vibration of composite double curved shallow shells with negative Poisson’s ratio in auxetic honeycombs core layer on elastic foundations subjected to blast and damping loads,” Int. J. Mech. Sci., 133, 504-512 (2017).

    Article  Google Scholar 

  26. N. D. Duc, S. E. Kim, N. D. Tuan, P. Tran, and N. D. Khoa, “New approach to study nonlinear dynamic response and vibration of sandwich composite cylindrical panels with auxetic honeycomb core layer,” Aerosp. Sci. Technol., 70, 396-404 (2017).

    Article  Google Scholar 

  27. T. Q. Quan, V. M. Anh, V. Mahesh, and N. D. Duc, “Vibration and nonlinear dynamic response of imperfect sandwich piezoelectric auxetic plate,” Mech. Adv. Mater. Struct., DOI: https://doi.org/10.1080/15376494.2020.1752864 (2020)

  28. M. H. Hajmohammad, R. Kolahchi, M. S. Zarei, and A. H. Nouri, “Dynamic response of auxetic honeycomb plates integrated with agglomerated CNT-reinforced face sheets subjected to blast load based on visco-sinusoidal theory,” Int. J. Mech. Sci., 153-154, 391-401 (2019).

  29. M. H. Hajmohammad, A. H. Nouri, M. S. Zarei, and R. Kolahchi, “A new numerical approach and visco-refined zigzag theory for blast analysis of auxetic honeycomb plates integrated by multiphase nanocomposite facesheets in hygrothermal environment,” Eng. Comput., 35, 1141-1157 (2019).

    Article  Google Scholar 

  30. J. Liu, Y. S. Cheng, and R. F. Li, “A semi-analytical method for bending, buckling, and free vibration analyses of sandwich panels with square-honeycomb cores,” Int. J. Struct. Stab. Dyn., 10, 127-151 (2010).

    Article  Google Scholar 

  31. K. Di and X. B. Mao, “Free flexural vibration of honeycomb sandwich plate with negative Poisson’s ratio simple supported on opposite edges,” Acta Mater. Compos. Sin., 33, 910-920 (2016).

    Google Scholar 

  32. J. Zhang, X. Zhu, X. Yang, and W. Zhang, “Transient nonlinear responses of an auxetic honeycomb sandwich plate under impact loads,” Int. J. Impact. Eng., 134, 103383 (2019).

    Article  Google Scholar 

  33. X. Jin, Z. Wang, J. Ning, G. Xiao, E. Liu, and X. Shu, “Dynamic response of sandwich structures with graded auxetic honeycomb cores under blast loading,” Compos. Part B Eng., 106, 206-217 (2016).

    Article  Google Scholar 

  34. C. Qi, A. Remennikov, L. Z. Pei, S. Yang, Z. H. Yu, and T. D. Ngo, “Impact and close-in blast response of auxetic honeycomb-cored sandwich panels: Experimental tests and numerical simulations,” Compos. Struct., 180, 161-178 (2017).

    Article  Google Scholar 

  35. G. Imbalzano, S. Linforth, N. D. Tuan, P. V. S. Lee, and T. Phuong, “Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs,” Compos. Struct., 183, 242-261 (2018).

    Article  Google Scholar 

  36. D. Banić, M. Bacciocchi, F. Tornabene, and A. J. M. Ferreira, “Influence of Winkler-Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes,” Appl. Sci., 7, No. 12, 1228 (2017).

    Article  CAS  Google Scholar 

  37. F. H. Roudbeneh, G. Liaghat, H. Sabouri, and H. Hadavinia, “Experimental investigation of impact loading on honeycomb sandwich panels filled with foam,” Int. J. Crashworthines., 24, No. 2, 199-210 (2018).

    Article  Google Scholar 

  38. F. H. Roudbeneh, G. Liaghat, H. Sabouri, and H. Hadavinia, “Experimental investigation of quasistatic penetration tests on honeycomb sandwich panels filled with polymer foam,” Mech. Adv. Mater. Struct., 27, No. 21, 1803-1815 (2018).

    Article  CAS  Google Scholar 

  39. T. C. Lim, “Vibration of thick auxetic plates,” Mech. Res., Commun., 61, 60-66 (2014).

    Article  Google Scholar 

  40. F. Tornabene, “General higher order layer-wise theory for free vibrations of doubly-curved laminated composite shells and panels,” Mech. Adv. Mater. Struct., 23, No. 9, 1046-1067 (2016).

    Article  CAS  Google Scholar 

  41. S. V. Shil’ko, E. M. Petrokovets, and Yu. M. Pleskachevskii, “An analysis of contact deformation of auxetic composites,” Mech. Compos. Mater., 42, No. 5, 477-484 (2006).

    Article  Google Scholar 

  42. C. Li, H. S. Shen, and H. Wang, “Nonlinear dynamic response of sandwich plates with functionally graded auxetic 3D lattice core,” Nonlinear. Dyn., 100, 3235-3252 (2020).

    Article  Google Scholar 

  43. C. Li, H. S. Shen, H. Wang, and Z. Yu, “Large amplitude vibration of sandwich plates with functionally graded auxetic 3D lattice core,” Int. J. Mech. Sci., 174, 105472 (2020).

    Article  Google Scholar 

  44. C. Li, H. S. Shen, and H. Wang, “Full-scale finite element modeling and nonlinear bending analysis of sandwich plates with functionally graded auxetic 3D lattice core,” J. Sandw. Struct. Mater., DOI: https://doi.org/10.1177/1099636220924657 (2020)

  45. C. Li, H. S. Shen, and H. Wang, “Postbuckling behavior of sandwich plates with functionally graded auxetic 3D lattice core,” Compos. Struct., 237, 111894 (2020).

    Article  Google Scholar 

  46. H. Eipakchi and F. M. Nasrekani, “Analytical Solution for Buckling Analysis of Composite Cylinders with Honeycomb Core Layer,” AIAA Journal, DOI: https://doi.org/10.2514/1.J060422 (2021)

  47. H. Eipakchi and F. M. Nasrekani “Axisymmetric analysis of auxetic composite cylindrical shells with honeycomb core layer and variable thickness subjected to combined axial and non-uniform radial pressures, Mech. Adv. Mater. Struct., DOI: https://doi.org/10.1080/15376494.2020.1841346 (2020)

  48. H. Eipakchi and F. M. Nasrekani, “Vibrational behavior of composite cylindrical shells with auxetic honeycombs core layer subjected to a moving pressure,” Compos. Struct., 254, 112847 (2020).

    Article  Google Scholar 

  49. D. Q. Tian and Y. Z. Chun, “Wave propagation in sandwich panel with auxetic core,” J. Solid. Mech., 2, 393-402 (2010).

    Google Scholar 

  50. A. B. Brush, Buckling of Bars, Plates, and Shells, McGraw-Hill, New York (1975).

    Book  Google Scholar 

  51. R. Naj, M. S. Boroujerdy, and M. R. Eslami, “Thermal and mechanical instability of functionally graded truncated conical shells,” Thin-Walled Struct., 46, 65-78 (2008).

    Article  Google Scholar 

  52. P. Seide, “Buckling of circular cones under axial compression,” J. Appl. Mech., 28, No. 2, 315-326 (1961).

    Article  Google Scholar 

Download references

Acknowledgement

This research was funded by the Grant number CN.21.06 of VNU Hanoi — University of Engineering and Technology. The authors are grateful for this support. Pham Dinh Nguyen was funded by Vingroup Joint Stock Company and supported by the Domestic Master/ PhD Scholarship Programme of Vingroup Innovation Foundation (VINIF), Vingroup Big Data Institute (VINBIGDATA), code VINIF.2020.TS.17.

Author information

Authors and Affiliations

  1. Department of Engineering and Technology of Constructions and Transportation, VNU – Hanoi – University of Engineering and Technology (UET), 144 – Xuan Thuy – Cau Giay, Hanoi, Vietnam

    Nguyen Dinh Duc, Duong Tuan Manh, Nguyen Dinh Khoa & Pham Dinh Nguyen

  2. NTT Institute of High Technology, Nguyen Tat Thanh University, Ho Chi Minh City, Vietnam

    Nguyen Dinh Duc

Authors
  1. Nguyen Dinh Duc
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Duong Tuan Manh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nguyen Dinh Khoa
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Pham Dinh Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nguyen Dinh Duc.

Additional information

Translated from Mekhanika Kompozitnykh Materialov, Vol. 58, No. 3, pp. 521-544, May-June, 2022. Russian DOI: https://doi.org/10.22364/mkm.58.3.04.

Appendix

Appendix

$$ {\displaystyle \begin{array}{c}{A}_{66}={Q}_{44}^T\left(\int_{\frac{h_2}{2}}^{\frac{h_2}{2}+{h}_1} dz+\int_{\frac{h_2}{2}{h}_3}^{\frac{h_2}{2}} dz\right)+{Q}_{44}^C\int_{-\frac{h_2}{2}}^{-\frac{h_2}{2}} dz,{B}_{66}={Q}_{44}^T\left(\int_{\frac{h_2}{2}}^{\frac{h_2}{2}+{h}_1} zdz+\int_{\frac{h_2}{2}{h}_3}^{\frac{h_2}{2}} zdz\right)+{Q}_{44}^C\int_{-\frac{h_2}{2}}^{-\frac{h_2}{2}} zdz,\\ {}{D}_{11}={Q}_{11}^T\left(\int_{\frac{h_2}{2}}^{\frac{h_2}{2}+{h}_1}{z}^2 dz+\int_{\frac{h_2}{2}{h}_3}^{\frac{h_2}{2}}{z}^2 dz\right)+\int_{-\frac{h_2}{2}}^{\frac{h_2}{2}}{z}^2 dz,{D}_{12}={Q}_{12}^T\left(\int_{\frac{h_2}{2}}^{\frac{h_2}{2}+{h}_1}{z}^2 dz+\int_{\frac{h_2}{2}{h}_3}^{\frac{h_2}{2}}{z}^2 dz\right)+{Q}_{12}^C\int_{-\frac{h_2}{2}}^{\frac{h_2}{2}}{z}^2 dz,\\ {}{D}_{22}={Q}_{22}^T\left(\int_{\frac{h_2}{2}}^{\frac{h_2}{2}+{h}_1}{z}^2 dz+\int_{-\frac{h_2}{2}{h}_3}^{-\frac{h_2}{2}}{z}^2 dz\right)+{Q}_{22}^C\int_{\frac{h_2}{2}}^{\frac{h_2}{2}}{z}^2 dz+{E}^S\frac{d_{\theta }}{s_{\theta }}\int_{\frac{h_2}{2}+{h}_1}^{\frac{h_2}{2}+{h}_1+h}{z}^2 dz,\\ {}{D}_{66}={Q}_{44}^T\left(\int_{\frac{h_2}{2}}^{\frac{h_2}{2}+{h}_1}{z}^2 dz+\int_{-\frac{h_2}{2}{h}_3}^{-\frac{h_2}{2}}{z}^2 dz\right)+{Q}_{44}^C\int_{-\frac{h_2}{2}}^{-\frac{h_2}{2}}{z}^2 dz.\\ {}{c}_{11}\left({u}_1\right)={A}_{11}\frac{\partial }{\partial x}\left({u}_1\right)-{A}_{22}\frac{\partial }{x}\left({u}_1\right)+x{A}_{11}\frac{\partial^2}{\partial {x}^2}\left({u}_1\right)+{A}_{66}\frac{1}{x\sin^2}\frac{\partial^2}{\partial {\theta}^2}\left({u}_1\right),\\ {}{C}_{12}\left({v}_1\right)=\left({A}_{66}+{A}_{12}\right)\frac{1}{\sin \alpha}\frac{\partial^2}{\partial x\partial \theta}\left({v}_1\right)-\left({A}_{66}+{A}_{22}\right)\frac{1}{x\sin \alpha}\frac{\partial }{\partial \theta}\left({v}_1\right),\\ {}{C}_{13}\left({w}_1\right)=\left({B}_{22}\frac{1}{x}+{A}_{12}\cot \alpha \right)\frac{\partial }{\partial x}\left({w}_1\right)-{A}_{22}\frac{1}{x}\cot \alpha \left({w}_1\right)-{B}_{11}x\frac{\partial^3}{\partial {x}^3}\left({w}_1\right)\\ {}+\left({B}_{12}+2{B}_{66}+{B}_{22}\right)\frac{1}{x^2{\sin}^2\alpha}\frac{\partial^2}{\partial {\theta}^2}\left({w}_1\right)-\left({B}_{12}+2{B}_{66}\right)\frac{1}{x\sin^2\alpha}\frac{\partial^3}{\partial x\partial {\theta}^2}\left({w}_1\right)-{B}_{11}\frac{\partial^2}{\partial {x}^2}\left({w}_1\right),\\ {}{C}_{21}\left({u}_1\right)=\left({A}_{66}+{A}_{12}\right)\frac{1}{\sin \alpha}\frac{\partial^2}{\partial x\partial \theta}\left({u}_1\right)+\left({A}_{66}+{A}_{22}\right)\frac{1}{x\sin \alpha}\frac{\partial }{\partial \theta}\left({u}_1\right),\\ {}{C}_{22}\left({v}_1\right)=\frac{A_{22}}{x\sin \alpha}\frac{\partial^2}{\partial {\theta}^2}\left({v}_1\right)+x{A}_{66}\frac{\partial^2}{\partial {x}^2}\left({v}_1\right)+{A}_{66}\frac{\partial }{\partial x}\left({v}_1\right)-{A}_{66}\frac{1}{x}\left({v}_1\right),\\ {}{C}_{23}\left({w}_1\right)={A}_{22}\frac{\cot \alpha }{x\sin \alpha}\frac{\partial }{\partial \theta}\left({w}_1\right)-\left({B}_{12}+2{B}_{66}\right)\frac{1}{\sin \alpha}\frac{\partial^3}{\partial {x}^2\partial \theta}\left({w}_1\right)\\ {}-{B}_{22}\frac{1}{x^2{\sin}^3\alpha}\frac{\partial^3}{\partial {\theta}^3}\left({w}_1\right)-{B}_{22}\frac{1}{x\sin \alpha}\frac{\partial^2}{\partial x\partial \theta}\left({w}_1\right).\\ {}{C}_{31}\left({u}_1\right)=\left(\frac{B_{22}}{x^2}-\frac{A_{22}}{x}\cot \alpha \right)\left({u}_1\right)-\left(\frac{B_{22}}{x}+{A}_{12}\cot \alpha \right)\frac{\partial }{\partial x}\left({u}_1\right)+2{B}_{11}\frac{\partial^2}{\partial {x}^2}\left({u}_1\right)\\ {}+\frac{1}{x^2{\sin}^2\alpha }{B}_{22}\frac{\partial^2}{\partial {\theta}^2}\left({u}_1\right)+\frac{1}{x\sin^2\alpha}\left(2{B}_{66}+{B}_{12}\right)\frac{\partial^3}{\partial x\partial {\theta}^2}\left({u}_1\right)+x{B}_{11}\frac{\partial^3}{\partial {x}^3}\left({u}_1\right),\\ {}{C}_{32}\left({v}_1\right)=\frac{1}{x\sin \alpha}\left(\frac{B_{22}}{x}-{A}_{22}\cot \alpha \right)\frac{\partial }{\partial \theta}\left({v}_1\right)-{B}_{22}\frac{1}{x\sin \alpha}\frac{\partial^2}{\partial x\partial \theta}\left({v}_1\right)\\ {}+{B}_{22}\frac{1}{x^2{\sin}^3\alpha}\frac{\partial^3}{\partial {\theta}^3}\left({v}_1\right)+\frac{1}{\sin \alpha}\left(2{B}_{66}+{B}_{12}\right)\frac{\partial^3}{\partial {x}^2\partial \theta}\left({v}_1\right),\\ {}{C}_{33}\left({w}_1\right)=\left({B}_{22}\frac{\cot \alpha }{x^2}-{A}_{22}\frac{\cot^2\alpha }{x}-x{K}_1\right)\left({w}_1\right)+\left({K}_2-{D}_{22}\frac{1}{x^2}\right)\frac{\partial \left({w}_1\right)}{\partial x}\\ {}+\left(x{K}_2+{D}_{22}\frac{1}{x}+2{B}_{12}\cot \alpha \right)\frac{\partial^2\left({w}_1\right)}{\partial {x}^2}\\ {}+\left(2{B}_{22}\frac{\cot \alpha }{x^2{\sin}^2\alpha }-\left({D}_{12}+{D}_{22}+2{D}_{66}\right)\frac{2}{x^3{\sin}^2\alpha }+\frac{K_2}{x\sin^2\alpha}\right)\frac{\partial \left({w}_1\right)}{\partial {\theta}^2}\\ {}-2{D}_{11}\frac{\partial^3\left({w}_1\right)}{\partial {x}^3}+\left({D}_{12}+2{D}_{66}\right)\frac{2}{x^2{\sin}^2\alpha}\frac{\partial^3\left({w}_1\right)}{\partial x\partial {\theta}^2}-x{D}_{11}\frac{\partial^3\left({w}_1\right)}{\partial {x}^4}-{D}_{22}\frac{1}{x^3{\sin}^4\alpha}\frac{\partial^4\left({w}_1\right)}{\partial {\theta}^4}\\ {}-D\left({D}_{12}+2{D}_{66}\right)\frac{2}{x\sin^2\alpha}\frac{\partial^4\left({w}_1\right)}{\partial {x}^2\partial {\theta}^2},{C}_{34}\left({w}_1\right)=-\frac{1}{\pi \sin \left(2\alpha \right)}\frac{\partial^2\left({w}_1\right)}{\partial {x}^2}.\\ {}{d}_{11}=\frac{A_{11}\pi \sin \left(\alpha \right)L\left(L+2{x}_0\right)}{4}\left[{A}_{22}\sin \left(\alpha \right)+\frac{A_{66}{n}^2}{4\sin \left(\alpha \right)}\right]\left[\frac{\pi L\left(L+2{x}_0\right)}{4}\right]\\ {}-\frac{A_{11}{m}^2{\pi}^3}{8{L}^2}\sin \left(\alpha \right)\left[{\left(L+{x}_0\right)}^4-{x_0}^4+\frac{3{L}^3\left(L+2{x}_0\right)}{m^2{\pi}^2}\right],\\ {}{d}_{12}=-\frac{\left({A}_{66}+{A}_{12}\right) mn{\pi}^2}{12L}\left[{\left(L+{x}_0\right)}^3-{x_0}^3+\frac{3{L}^3}{2{m}^2{\pi}^2}\right]-\frac{\left({A}_{66}+{A}_{22}\right)n{L}^2}{8m},\\ {}{d}_{13}=\left[{B}_{22} m\pi \sin \left(\alpha \right)+\frac{\left({B}_{12}+2{B}_{66}\right)m{n}^2\pi }{4\sin \left(\alpha \right)}\right]\frac{\pi \left(L+2{x}_0\right)}{4}\\ {}+\frac{A_{12}m{\pi}^2\cos \left(\alpha \right)}{6L}\left[{\left(L+{x}_0\right)}^3-{x_0}^3+\frac{3{L}^3}{2{m}^2{\pi}^2}\right]+\frac{A_{22}\cos \left(\alpha \right){L}^2}{4m}\\ {}-\frac{B_{11}m{\pi}^2\sin \left(\alpha \right)\left(L+2{x}_0\right)}{4},\\ {}{d}_{21}=-\frac{\left({A}_{66}+{A}_{12}\right) mn{\pi}^2}{12L}\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]-\frac{\left({A}_{66}+{A}_{22}\right)n{L}^2}{8m},\\ {}{d}_{22}=-\frac{A_{22}{n}^2 L\pi \left(L+2{x}_0\right)}{16\sin \left(\alpha \right)}-\frac{A_{22}\sin \left(\alpha \right) L\pi \left(L+2{x}_0\right)}{2}\\ {}-\frac{A_{66}{m}^2{\pi}^3\sin \left(\alpha \right)}{8{L}^2}\left[{\left(L+{x}_0\right)}^4-{x_0}^4\right]+\frac{3\pi {A}_{22}\sin \left(\alpha \right)L\left(L+2{x}_0\right)}{8},\\ {}\begin{array}{c}{d}_{23}=\frac{A_{22}\cot \left(\alpha \right) n L\pi \left(L+2{x}_0\right)}{8}+\frac{B_{22}{n}^3 L\pi}{16\sin^2\left(\alpha \right)}\\ {}+\frac{\left({B}_{12}+2{B}_{66}\right){m}^2{\pi}^3n}{12{L}^2}\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]+\frac{B_{22} n\pi L}{8},\\ {}{d}_{31}={B}_{22}\left[\frac{n^2}{4\sin \left(\alpha \right)}-\sin \left(\alpha \right)\right]\frac{L^2}{4m}+\frac{A_{22}\cos \left(\alpha \right){L}^2\left(L+2{x}_0\right)}{4m}\\ {}+\left[\frac{B_{22}m{\pi}^2\sin \left(\alpha \right)}{6L}+\frac{\left({B}_{12}+2{B}_{66}\right)m{\pi}^2{n}^2}{24\sin \left(\alpha \right)L}\right]\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]\\ {}+\frac{A_{12}\cos \left(\alpha \right)m{\pi}^2}{8L}\left[{\left(L+{x}_0\right)}^4-{x_0}^4-\frac{3{L}^3\left(L+2{x}_0\right)}{m^2{\pi}^2}\right]\\ {}+\frac{B_{11}m{\pi}^2\sin \left(\alpha \right)}{2L}\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]\\ {}+\frac{B_{11}{m}^3{\pi}^4\sin \left(\alpha \right)}{L^3}\left[\frac{{\left(L+{x}_0\right)}^5-{x_0}^5}{10}+\frac{3{L}^3}{4{m}^4{\pi}^4}+{L}^2\frac{{x_0}^3-{\left(L+{x}_0\right)}^3}{2{m}^2{\pi}^2}\right],\\ {}{d}_{32}={B}_{22}n\left[\frac{n^2}{8\sin^2\left(\alpha \right)}-1\right]\frac{L\pi \left(L+2{x}_0\right)}{4}+\frac{A_{22}\cot \left(\alpha \right) n\pi}{12}\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]\\ {}+\frac{\left({B}_{12}+2{B}_{66}\right){m}^2{\pi}^3n}{16{L}^2}\left[{\left(L+{x}_0\right)}^4-{x_0}^4-\frac{3{L}^3\left(L+{x}_0\right)}{m^2{\pi}^2}\right],\\ {}{d}_{33}={B}_{22}\cos \left(\alpha \right)\left[1-\frac{n^2}{2\sin^2\left(\alpha \right)}\right]\left[\frac{L\pi \left(L+2{x}_0\right)}{4}\right]\\ {}-\left[\frac{A_{22}{\cot}^2\left(\alpha \right)\sin \left(\alpha \right)\pi }{6}+\frac{D_{22}{m}^2{\pi}^3\sin \left(\alpha \right)}{6{L}^2}+\frac{\left({D}_{12}+2{D}_{66}\right){m}^2{n}^2{\pi}^3}{12{L}^2\sin \left(\alpha \right)}\right]\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]\\ {}+\left[{D}_{22}\sin \left(\alpha \right)+\frac{\left({D}_{12}+2{D}_{66}\right){n}^2}{2\sin \left(\alpha \right)}\right]\frac{\pi L}{4}\\ {}-\frac{B_{12}{m}^2{\pi}^3\cos \left(\alpha \right)}{4{L}^2}\left[{\left(L+{x}_0\right)}^4-{x_0}^4-\frac{3{L}^3\left(L+2{x}_0\right)}{m^2{\pi}^2}\right]\\ {}+\frac{L\pi {n}^2}{4\sin \left(\alpha \right)}\left[\left({D}_{12}+{D}_{22}+2{D}_{66}\right)-\frac{D_{22}{n}^2}{8\sin^2\left(\alpha \right)}\right]\\ {}-\frac{D_{11}{m}^2{\pi}^3\sin \left(\alpha \right)}{2{L}^2}\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right]\\ {}-\frac{D_{11}{m}^4{\pi}^5\sin \left(\alpha \right)}{L^4}\left[\frac{{\left(L+{x}_0\right)}^5-{x_0}^5}{10}+\frac{3{L}^5}{4{m}^4{\pi}^4}+\frac{{x_0}^3-{\left(L+{x}_0\right)}^3}{2{m}^2{\pi}^2}{L}^2\right],\\ {}{d}_{34}=\frac{m^2{\pi}^2}{16{L}^2\cos \left(\alpha \right)}\left[{\left(L+{x}_0\right)}^4-{x_0}^4-\frac{3{L}^3\left(L+2{x}_0\right)}{m^2{\pi}^2}\right],\\ {}{d}_{35}=-\sin \left(\alpha \right)\pi \left[\frac{{\left(L+{x}_0\right)}^5-{x_0}^5}{10}+\frac{3{L}^5}{4{m}^4{\pi}^4}+\frac{{x_0}^3-{\left(L+{x}_0\right)}^3}{2{m}^2{\pi}^2}{L}^3\right],\\ {}{d}_{36}=-\frac{\pi \sin \left(\alpha \right)}{4}\left[\left(L+{x_0}^3\right)-{x_0}^3\frac{3{L}^3}{2{m}^2{\pi}^2}\right]\\ {}\begin{array}{c}-\frac{m^2{\pi}^3\sin \left(\alpha \right)}{L^2}\left[\frac{{\left(L+{x}_0\right)}^5-{x_0}^5}{10}+\frac{3{L}^5}{4{m}^4{\pi}^4}+{L}^2\frac{{x_0}^3-{\left(L+{x}_0\right)}^3}{2{m}^2{\pi}^2}\right]\\ {}-\frac{n^2\pi }{24\sin \left(\alpha \right)}\left[{\left(L+{x}_0\right)}^3-{x_0}^3-\frac{3{L}^3}{2{m}^2{\pi}^2}\right].\end{array}\end{array}\end{array}} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Duc, N.D., Manh, D.T., Khoa, N.D. et al. Mechanical Stability of Eccentrically Stiffened Auxetic Truncated Conical Sandwich Shells Surrounded by Elastic Foundations. Mech Compos Mater 58, 365–382 (2022). https://doi.org/10.1007/s11029-022-10035-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-022-10035-0

Keywords

Search

Navigation