Abstract
Using the FUND model, an impact assessment is conducted over the 21st century for rises in sea level of up to 2-m/century and a range of socio-economic scenarios downscaled to the national level, including the four SRES (IPCC Special Report on Emissions Scenarios) storylines. Unlike a traditional impact assessment, this analysis considers impacts after balancing the costs of retreat with the costs of protection, including the effects of coastal squeeze. While the costs of sea-level rise increase with greater rise due to growing damage and protection costs, the model suggests that an optimum response in a benefit-cost sense remains widespread protection of developed coastal areas, as identified in earlier analyses. The socio-economic scenarios are also important in terms of influencing these costs. In terms of the four components of costs considered in FUND, protection dominates, with substantial costs from wetland loss under some scenarios. The regional distribution of costs shows that a few regions experience most of the costs, especially East Asia, North America, Europe and South Asia. Importantly, this analysis suggests that protection is much more likely and rational than is widely assumed, even with a large rise in sea level. This is underpinned by the strong economic growth in all the SRES scenarios: without this growth, the benefits of protection are significantly reduced. It should also be noted that some important limitations to the analysis are discussed, which collectively suggest that protection may not be as widespread as suggested in the FUND results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sea-level rise due to human-induced climate change has caused concern for coastal areas since the issue emerged more than 20 years ago. Rapid sea-level rise (>1-m/century) raises most concern as it is commonly felt that this would overwhelm the capacity of coastal societies to respond and lead to large losses and a widespread forced coastal retreat (e.g., Overpeck et al. 2006). The IPCC Fourth Assessment Report (IPCC 2007) suggests that a rise of >1-m/century is unlikely during the 21st Century, although no formal upper bound including contributions from the large ice sheets is provided. Others argue that this remains an important issue for scientific analysis based on simple models (Rahmstorf 2007), observations (Rahmstorf et al. 2007) and palaeo-analogues (Rohling et al. 2008). Less appreciated is the so-called ‘commitment to sea-level rise’ whereby even if the climate is stabilized immediately, sea levels continue to rise for many centuries due to the long timescales of the oceans and the large ice sheets (Nicholls and Lowe 2006; Nicholls et al. 2006).
To date few studies have considered large rises in sea-level—the few analyses tend to focus on exposure (i.e. potential impacts) only (Nicholls et al. 2006). This paper also includes a coastal protection response. It builds on the earlier global analysis of Nicholls et al. (2008) and provides evidence on the consequences of large rises in sea level over the 21st Century using the coastal module of an integrated assessment model (FUND: The Climate Framework for Uncertainty, Negotiation and Distribution) for scenarios of sea-level rise in the range of 0.5–2 meters by 2100 (which are consistent with the range proposed by Arnell et al. (2005) and the UKCP09 (UK Climate Projections) sea-level rise scenarios (Lowe et al. 2009)). The model calculates the welfare loss due to rising sea levels for a number of socio-economic scenarios, assumes some basic adaptation of humans to sea-level rise (a simple choice between protect and retreat) and aggregates damage costs for a number of damage types. The model operates at the national scale. Subnational variations are profound and important, but beyond the scope of the current paper.
The objective of this study is to estimate economic damages caused by substantial sea-level rise and to clarify to what extent societies can protect themselves from rising sea-levels.
2 Model
The Coastal Module of FUND 2.8n is used to calculate damagesFootnote 1 caused by various scenarios of sea-level rise over the next century (see Fig. 1). This section will give a brief outline of the model components relevant to the calculation of sea-level rise damages. More details of the FUND coastal module can be found in Tol (2007) and Nicholls et al. (2008).
The model is driven by exogenous scenarios of population and GDP (gross domestic product) growth on a per country scale. Five distinct socio-economic scenarios are evaluated for this study: the four well-known SRES scenarios A1, A2, B1 and B2 downscaled from the original source (Nakicenovic and Swart 2000) and a control scenario of constant population and GDP at 1995 levelsFootnote 2 over the 21st century (termed C1995).
Sea-level rise is specified as a global, exogenous scenario. Three distinct scenarios are examined: a rise of 0.5-m, 1.0-m and 2.0-m above today’s (2005) sea levels in the year 2100 (i.e. over 95 years). For the sake of simplicity, sea-level rise is treated as a linear interpolation between 2005 and 2100.
Rising sea levels are assumed to have four damage cost components: (1) the value of dryland lost, (2) the value of wetland lost, (3) the cost of protection (with dikes) against rising sea levels and (4) the costs of displaced people that are forced to leave their original place of settlement due to dryland loss (Fig. 1). FUND determines the optimum amount of protection (in benefit-cost terms) based on the socio-economic situation, the expected damage of sea-level rise if no protection existed, and the necessary protection costs. Unprotected dryland is assumed to be lost, while wetland loss is also influenced by the amount of protection: more protection leads to greater wetland loss via coastal squeeze. Wetland loss due to coastal squeeze is counted as a cost of protection. The number of people displaced is a linear function of dryland loss.
The area of dryland loss is assumed to be a linear function of sea-level rise and protection level up to 2-m of sea-level rise. The protection level is defined as the share of the coast protected. Anthoff et al. (2006) and Nicholls et al. (2008) suggest that the average slope of the coast increases above 1-m elevation (relative to high water). Hence, the linear assumption tends to overestimate the assets threatened by sea-level rise above 1-m, and hence will overestimate the length of protected coast. Further investigation of this issue is recommended. The value of lost dryland is assumed to be linear in income density ($/km2).
Wetland value is assumed to be logistic in per capita income, with a correction for wetland scarcity, and a cap:
where V t,i is wetland value at time t in country i; y is per capita income; L is the wetland lost to date; L max is a parameter, given the maximum amount of wetland that can be lost to sea-level rise; α is a parameter such that the average value for the OECD is $5 million per square kilometre; and σ = 0.05 is a parameter. Conceptually, the value of wetlands at first rises rapidly with income, but it increases much more slowly if incomes and wetland values are very high. Without such leveling off, wetland values become unrealistically high and coastal cities would be abandoned to make way for wetlands. Wetlands become more valuable as they get scarcer, but this effect has to be capped as well since coastal wetlands completely disappear in some countries for some scenarios.
The number of people forced to migrate from a country due to sea-level rise is a function of the average population density in the country and the area of dryland lost. The cost of people displaced is three times average per capita income (Tol 1995).
Following the method of Nicholls et al. (2008), average annual protection costs are assumed to be a bilinear function of the rate of sea-level rise as well as the proportion of the coast that is protected. This is a first step to overcoming the linear assumptions of the FUND model, necessary to avoid numerical optimization (Fankhauser 1994). The costs increase by an order of magnitude (based on expert knowledge (Olsthoorn et al. 2008)) if sea-level rise is faster than 1 cm per year (i.e., protection costs are much higher for the 1-m and 2-m rise scenarios than the 0.5-m scenarios). The level of protection is based on a cost-benefit analysis that compares the costs of protection (the actual construction of the protection and the value of the wetland lost due to the protection) with the benefits, i.e. the avoided dryland loss.
The level of protection is based on a cost-benefit analysis. The level of protection is modeled as the share of the coastline which is protected. The cost-benefit equation is
where L is the fraction of the coastline to be protected. PC is the net present value of the protection cost if the whole coast is protected, WL is the net present value of wetland lost if the whole coast would be protected and DL is the net present value of dryland lost if no protection would take place.
PC is calculated assuming annual protection costs are constant, which is justified for the following three reasons: Firstly, the coastal protection decision makers anticipate a linear sea-level rise. Secondly, coastal protection entails large infrastructural works, which which have a life of decades. Thirdly, the considered costs are direct investments only, and technologies for coastal protection are mature. Throughout the analysis, a pure rate of time preference, ρ, of 1% per year is used. The actual discount rate thus lies 1% above the growth rate of per capita income of the economy, g. The net present costs of protection PC are
where PCa is the average annual costs of protection, which is constant.
WL is the net present value of the wetlands lost due to full coastal protection. Land values are assumed to rise at the same pace as per capita income growth. The amount of wetland lost per year is assumed to be constant. The net present costs of wetland loss WL follow from
where WL t,i denotes the value of wetland loss in the year and country the decision is made (see above). W t,i is the use value of the wetlands that would be lost due to full protection in country i at time t.
DL denotes the net present value of the dryland lost if no protection takes place. Land values are assumed to rise at the same pace as per capita income growth. The amount of dryland lost per year is assumed to be constant. The net present costs of dryland loss DL are
where DL t,i is the value of dryland loss in the year and country the decision is made (see above). D t,i is the use value of the dryland that would be lost if no protection would take place in country i at time t.
For a more complete discussion of sea-level rise in the context of climate change, see Nicholls and Tol (2006) and Nicholls et al. (2008).
The damage costs presented in this paper are the net present value of total damage costs for the period 2005-2100. We use a standard Ramsey discount rate to compute the net present value:
where r t,i is the discount rate in country i at time t, ρ is the pure rate of time preference, η is the consumption elasticity of marginal utility (always set to 1 in this paper) and g t,i is the per capita growth rate of consumption in country i at time t.
3 Results
Results from the model runs are analyzed along the following dimensions: (1) global damage costs by scenario; (2) the damage cost components; (3) regional impacts; (4) sensitivity analysis with respect to protection and (5) sensitivity analysis with respect to discounting.
3.1 Global damage costs by socio-economic and sea-level rise scenarios
While the choice of socio-economic scenario has an influence on the global damage costs from sea-level rise for the time period analysed for this study, the damage costs vary more over the choice of sea-level rise scenario (Fig. 2).
The damage costs for a 1 m rise are between 4.8 and 5.2 times as high as the damage costs for the 0.5 m sea-level rise, depending on the scenario (except for the 1995 control scenario, where the increase in costs is only 4 times). The increase in costs from 1 m to 2 m is only 2.0 times the damage cost of the 1 m sea-level rise scenario. The assumed bilinear protection costs between the scenario with 0.5 m rise and 1 m rise explains these different increases in damage costs with respect to sea-level rise. While the increase in damage costs from the 1 m to 2 m sea-level rise scenario is almost a factor of two in each of the socio-economic scenarios, the difference between 0.5 m and 1 m sea-level rise does depend somewhat on the socio-economic scenario. In all cases (except the 1995 control scenario) the increase of the total damage is lower than the assumed tenfold increase in protection costs. The overall difference between the SRES scenarios is small.
While the damages from sea-level rise are substantial, they are small compared to the total economy, provided that coastal protection is built. This remains true for the largest 2-m rise scenario. Note that the global total of Fig. 2 hides considerable differences between countries. This issue is discussed in more detail below.
In order to understand the reasons for the differences between the scenarios, a closer look at the four damage cost components is needed.
3.2 Disaggregating damage costs by socio-economic and sea-level rise scenarios
Figure 3 shows the damage cost components as calculated by FUND and their share of the total damage cost for the 0.5 m sea-level rise scenario under the assumption that dikes are built, i.e. that people attempt to protect against rising sea levels following current practise against coastal flooding in much of the world (e.g., East Asia and Europe). Note that the results change dramatically if it is assumed that people do not protect; this scenario is analysed in a later section.
Ignoring the control scenario for a moment, three conclusions can be drawn. First, damage costs from dryland loss and migration are a fraction of the costs of protection in every scenario (dryland costs being about one fifth and migration being one tenth of protection costs). Protection costs on the other hand are the most important component for every scenario. This underlines the significance of protection (and adaptation in general). Second, protection costs are less affected by the choice of socio-economic scenario than dryland loss and migration costs. The biggest difference between scenarios for dryland loss and migration costs is a factor of 1.8, for protection costs it is 1.5. Damage costs from wetland loss are even less sensitive to the choice of scenario, with a maximum difference of factor 1.3. Wetland costs are the second most significant damage component in all scenarios. Third, for every cost component except wetland loss, the highest cost scenario is A2, followed by B2, B1 and A1 (the lowest). For wetland costs, the order is reversed, because wetland cost differences between scenarios are mainly driven by the differences in valuation between socio-economic scenarios: higher per capita income place a higher value on wetland loss and therefore produce higher wetland costs. With the other damage costs, higher per capita income mainly leads to more protection, which explains why the effect of higher per capita income is positive in those cases.
Figure 4 presents the disaggregation into damage components for the 1 m sea-level rise scenario. Wetland costs are the only ones that react roughly linearly to the doubling of sea-level rise, they are around two times as high as for the 0.5 m sea-level rise in all scenarios. Protection costs increase between 4.2 to 6.6 times compared to the lower sea-level rise scenario, while dryland loss and migration costs increase by an order of magnitude (factors between 10.7 and 11.4) compared to the lower sea-level rise scenario. Due to the increase in adaptation costs (i.e. the bilinear nature of protection costs), adaptation is significantly more costly in the 1 m sea-level rise scenario and the cost-benefit analysis finds that the optimal length of coast to protect is lower than in the 0.5 m scenario (e.g. it is about 40% lower averaged over time for the A1 scenario, 46% lower for A2, 42% lower for B1 and 45% lower for B2), which leads to a situation where total damage is more evenly divided between the four damage cost components.
While the step from 0.5 m to 1 m sea-level rise changed the distribution of costs between the four components significantly, the step to the 2 m scenario has no such surprises. As can be seen in Fig. 5, all costs roughly double compared to the 1 m scenario. This is not surprising, since the model does not have a change in cost assumptions build into this step.
3.3 Regional distribution of damage costs
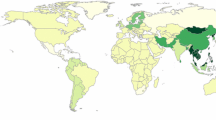
Sea-level rise damages are not evenly distributed over the world. Figure 6 compares the two scenarios that show the largest difference in total damage cost due to sea-level rise across all regions. While the distribution of damage costs is not the same for the two scenarios, the same regions bear the majority of damage costs in both scenarios. This should not be a surprise as relative exposure to sea-level rise is the main variable that drives relative damages and for example, East Asia and South Asia have large, densely-populated coastal lowlands irrespective of the scenario considered.
The three regions that are widely thought to be the most vulnerable to sea-level rise, i.e. the Pacific, Indian Ocean and Caribbean islands bear only a tiny share of the total global damage. At the same time these damage costs for the small island states are enormous in relation to the size of their economy (Nicholls and Tol 2006). Together with deltaic areas, they will find it most difficult to raise the finances necessary to implement protection.
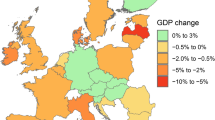
Figure 7 shows damage costs as percent of GDP for the ten countries with the highest relative impact in 2100 for the A1 scenario with a 1 m sea-level rise. The economies of these ten countries are relatively small. Consequently damages to those countries do not constitute any significant part of the global total or even regional total impact from sea-level rise.
3.4 Sensitivity analysis—protection
The level of protection, that is the length of coastline that is protected using dikes, is normally determined endogenously by a cost-benefit analysis in FUND. For the first time with a FUND analysis, another set of runs where no protection against sea-level rise is allowed were also conducted. Comparing these two sets of runs with and without protection is insightful for three reasons. First, it shows the huge benefits of protection to sea-level rise in terms of the damages avoided. Second, there might be countries that do not have the means to protect their coastline up to the optimal level that would follow from the cost-benefit analysis. This is especially relevant for large rises in sea level as considered in this analysis (Nicholls et al. 2008). Third, sea-level rise impacts are often presented without considering coastal protection (e.g., Dasgupta et al. 2009). This allows for a comparison between such studies and FUND.
Figure 8 clearly shows the importance of protection, in particular for the 0.5 m sea-level rise scenario. Total damages are between 3.4 and 3.7 times higher when no protection is build for that scenario, depending on the socio-economic scenario. For 1 m and 2 m sea-level rise the damages in the no-protection scenario are only around 1.4 times as high compared to a protection scenario. Since protection costs are assumed to be ten times higher than in the 0.5 m case, this is hardly surprising, as higher protection costs will lead to a lower protection level and therefore to a smaller change if that protection cannot be build. A look at the control Scenario C1995 is particularly interesting, as population and economic indicators are held constant at 1995 levels, while sea-level rise is assumed to occur. Especially in the two scenarios with the higher protection costs (1 m and 2 m), the importance of the significant economic development assumed in all the SRES scenarios can be seen. In both cases, there is little coastal protection in today’s socio-economic situation. The lesson to be learned from this is twofold: (1) protection can significantly lower total damages, but (2) only when economic growth enables this sometimes costly investment in protection to occur. Hence protection and economic growth are coupled, which has often been ignored in earlier analyses where socio-economic conditions are held constant as sea-level rises.
Some of the results for no protection scenarios are peculiar at first sight. For example, the Maldives are estimated to be completely inundated in 2085 for the 1-m rise scenario, which raises the value of its dryland for the time step 2080-4 to very large values. After 2085, the value is zero. This cannot be regarded as a satisfactory valuation from an economic point of view: Such non-marginal damages are outside of the realm of economic valuation. The Maldives disappear much earlier (2050) for the 2 m sea-level rise scenarios without protection, so that the costs of the 2 m scenario fall below that of the 1 m between 2050 and 2085.
Figure 9 displays the benefit gained from protection for specific countries. It shows that protection is a lot more important for some countries than for others, which reflects differences in the efficacy of coastal protection. In densely populated and rich countries, dike building has a high return in that a small expense prevents substantial damage. If people are dispersed and poor, the pay-off to coastal protection is much smaller.
Finally, we investigate how sensitive our cost estimates are to the assumptions made about the increase in costs when a threshold of sea-level rise is breached. The cost of building protection against sea-level rise is assumed to increase by an order of magnitude if sea-levels would rise by more than 1 cm per year for our central results. Figure 10 presents results of a sensitivity analysis that alters the assumed cost increase for a case of rapid sea-level rise. We keep the same threshold level of 1 cm per year, but change the parameter for the cost increase from the central value of 10 (cost increase of an order of magnitude) to a factor of 5 and a factor of 20. For sea-level rise slower than 1 cm per year this does not change predicted costs, as one would expect. For sea-level rise faster than 1 cm per year we find that overall damages increase when protection costs are higher and decrease when they are lower. The increase in overall damages is much more modest than the assumed increase in protection cost: For a protection cost increase of factor 20 instead of factor 10 we find an overall damage increase of 16%, while for a protection cost increase of factor 5 instead of factor 10 overall damage decreases by 22%. This is because protection levels change too, going up (down) if costs go down (up). This suggests that while different assumptions about protection costs matter for overall damage estimates, the general pattern of the results do not alter dramatically and are fairly robust to precise assumptions about protection costs.
3.5 Sensitivity analysis–discounting
Cost-benefit analysis of long term problems have proven to be highly sensitive to the discount rate used to compute net present value estimates. Debates about the appropriate discount rate to be used in climate change economics have been controversial and long standing. Figure 11 presents a sensitivity analysis of our results with respect to the discount rate. In particular, we altered the pure rate of time preference from its central value of 1% to compute estimates that use a pure rate of time preference of 0.1% and 3%, a range that spans commonly used discount rates in the literature on climate change. We find that the choice of discount rate is highly significant for the aggregate monetary estimate of impacts. With a low pure rate of time preference of 0.1% aggregate impact estimates are more than double the estimates that are computed with a high pure rate of time preference of 3%.
Note that we only altered the discount rate used to compute the net present value of the four damage components considered by FUND. We did not alter the discount rate used to compute the optimal protection level. The debate about discounting in climate change economics centers on the question how society should value future impacts from climate change and we investigate the sensitivity of our results to this question by altering the discount rate used to compute the net present value of the four damage components. The discount rate used to compute optimal protection levels on the other hand is not subject to these normative questions, it simply reflect how economic agents will respond to rising sea levels.
4 Discussion/conclusions
This analysis with FUND suggests that if sea-level rise was up to 2-m per century, while the costs of sea-level rise increase due to greater damage and protection costs, an optimum response in a benefit-cost sense remains widespread protection of developed coastal areas, as identified in earlier analyses (Nicholls and Tol 2006; Nicholls et al. 2008). This analysis also demonstrates that the benefits of protection increase significantly with time due to the economic growth assumed in the SRES socio-economic scenarios. The different assumptions about population and gross domestic product within the socio-economic scenarios are also important drivers of the value of the exposed assets. This influences the protection versus retreat decision explicit with FUND and hence the costs of sea-level rise (cf. Nicholls 2004).
In terms of the four components of costs considered in FUND, protection dominates, with substantial costs from wetland loss under some scenarios. The regional distribution of costs shows that a few regions experience most of the costs, especially South Asia, South America, North America, Europe, East Asia and Central America. Under a scenario of no protection, the costs of sea-level rise increase greatly due to the increase in land loss and population displacement: this scenario shows the significant benefits of the protection response in reducing the overall costs of sea-level rise.
While the FUND analysis suggests widespread protection, earlier analysis shows that the actual adaptation response to sea-level rise is more complex than the benefit-cost approach used in FUND (Tol and Fankhauser 1998; Nicholls and Tol 2006). Building on these views, there are several factors to consider. Firstly, the aggregated scale of analysis in FUND may overestimate the extent of protection as shown by more detailed multi-scale analyses of parts of the UK and Germany (Turner et al. 1995; Sterr 2008). It is also worth noting that retreat is now being considered more seriously, especially in parts of Europe (Eurosion 2004; DEFRA 2004, 2006; Rupp-Armstrong and Nicholls 2007), driven by multiple goals including maintaining coastal wetlands due to the EU Habitats Directive. However, this is unlikely to change the qualitative conclusion that protection can be justified in more developed locations, even given a large rise in sea level. Secondly, the SRES socio-economic scenarios are quite optimistic about future economic growth: lower growth may lead to lower damages in monetary terms, but it will also reduce the capacity to protect as shown in these analyses. Strong economic growth underpins the investment necessary to protect. Thirdly, the benefit-cost approach implies perfect knowledge and a proactive approach to the protection, while historical experience shows most protection has been a reaction to actual or near disaster. Therefore, high rates of sea-level rise may lead to more frequent coastal disasters, even if the ultimate response is better protection. Fourthly, even though it is economically rational to protect, there are questions of who pays and who benefits, and in some cases such as islands and deltas the diversion of investment from other uses could overwhelm the capacity of these societies to protect (cf. Fankhauser and Tol 2005). As the benefit-cost ratio improves with time, it appears that near-term decisions on protection may have important consequences for the long-term direction of the adaptation response to sea-level rise. Fifthly, building on the fourth point, FUND assumes that the pattern of coastal development persists and attracts future development. However, major disasters such as the landfall of hurricanes could trigger coastal abandonmentFootnote 3, and hence have a profound influence on society’s future choices concerning coastal protection as the pattern of coastal occupancy might change radically. A cycle of decline in some coastal areas is not inconceivable, especially in future worlds where capital is highly mobile and collective action is weaker. As the issue of sea-level rise is so widely known, disinvestment from coastal areas may even be triggered without disasters: for example, small islands may be highly vulnerable if investors are cautious (cf. Barnett and Adger 2003; Gibbons and Nicholls 2006).
For these above reasons, protection may not be as widespread as suggested in this analysis, especially for the largest scenario of 2 m/century. However, the FUND analysis shows that protection is more likely and rational than is widely assumed, even with a large rise in sea level. The common assumption of a widespread retreat from the shore is not inevitable and coastal societies will have more choice in their response to this issue than is often assumed.
While the no protection scenarios have damages that transcend the marginal valuation framework of economics and therefore have to be examined with care, it is also clear from this analysis that—under the assumption that protection is built—such non-marginal losses of land do not occur and calculation of damage costs is possible.
Notes
In this paper, all the costs of sea-level rise are considered damages, including protection costs.
1995 is the base year in FUND.
The population of New Orleans peaked before Hurricane Betsy in 1965 and never fully recovered (Grossi and Muir-Wood 2006). Hurricane Katrina in 2005 may mark another long-term decline in the city’s population.
References
Anthoff D, Nicholls RJ, Tol RSJ, Vafeidis AT (2006) Global and regional exposure to large rises in sea-level: a sensitivity analysis. Tyndall Working Paper 96. Tyndall Centre for Climate Change Research. http://www.tyndall.ac.uk/sites/default/files/wp96_0.pdf. Cited 3 March 2010
Arnell NW, Tompkins E, Adger NW, Delaney K (2005) Vulnerability to abrupt climate change in Europe. Tyndall Centre Technical Report 34. Tyndall Centre for Climate Change Research. http://www.tyndall.ac.uk/sites/default/files/tr34.pdf. Cited 2 March 2010
Barnett J, Adger NW (2003) Climate dangers and atoll nations. Clim Change 61(3):321–337. doi:10.1023/B:CLIM.0000004559.08755.88
Dasgupta S, Laplante B, Meisner C et al (2009) The impact of sea level rise on developing countries: a comparative analysis. Clim Change 93(3):379–388. doi:10.1007/s10584-008-9499-5
DEFRA (2004) Making space for water: developing a new Government Strategy for flood and coastal erosion risk management in England. A consultation exercise. Department of Environment, Food and Rural Affairs, London, UK
DEFRA (2006) Shoreline management plan guidance—volume 1: aims and requirements—volume 2: procedures. Department of Environment, Food and Rural Affairs, London, UK
EUROSION (2004) Living with coastal erosion in Europe: sediment and space for sustainability: major findings and policy recommendations of the EUROSION project. Directorate General Environment, European Commission. http://www.eurosion.org/reports-online/part1.pdf. Cited 3 March 2010
Fankhauser S (1994) Protection vs. retreat—the economic costs of sea level rise. Environ Plann A 27(2):299–319. doi:10.1068/a270299
Fankhauser S, Tol RSJ (2005) On climate change and economic growth. Resour Energy Econ 27(1):1–17. doi:10.1016/j.reseneeco.2004.03.003
Gibbons SJA, Nicholls RJ (2006) Island abandonment and sea-level rise: an historical analog from the Chesapeake Bay, USA. Glob Environ Change 16(1):40–47. doi:10.1016/j.gloenvcha.2005.10.002
Grossi P, Muir-Wood R (2006) Flood risk in New Orleans: implications for future management and insurability. Risk management solutions, London, UK. http://www.rms.com/Publications/NO_FloodRisk.pdf. Cited 3 March 2010
IPCC (2007) Climate change 2007. In: Solomon S, Qin D, Manning M et al (eds) The physical science basis. Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Lowe JA, Howard T, Pardaens A et al (2009) UK climate projections science report: marine and coastal projections. Met Office Hadley Centre, Exeter
Nakicenovic N, Swart R (2000) Emissions scenarios. Special report of the Intergovernmental panel on climate change. Cambridge University Press, Cambridge
Nicholls RJ (2004) Coastal flooding and wetland loss in the 21st century: changes under the SRES climate and socio-economic scenarios. Glob Environ Change 14(1):69–86. doi:10.1016/j.gloenvcha.2003.10.007
Nicholls RJ, Lowe JA (2006) Climate stabilisation and impacts of sea-level rise. In: Schellnhuber HJ, Cramer W, Nakicenovic N et al (eds) Avoiding dangerous climate change. Cambridge University Press, Cambridge
Nicholls RJ, Tol RSJ (2006) Impacts and responses to sea-level rise: a global analysis of the SRES scenarios over the twenty-first century. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 364(1841):1073–1095. doi:10.1098/rsta.2006.1754
Nicholls RJ, Tol RSJ, Vafeidis A (2008) Global estimates of the impact of a collapse of the West Antarctic ice sheet: an application of FUND. Clim Change 91(1):171–191. doi:10.1007/s10584-008-9424-y
Nicholls RJ, Hanson SE, Lowe JA et al (2006) Metrics for assessing the economic benefits of climate change policies: sea level rise. Organisation for Economic Co-operation and Development, Paris
Olsthoorn X, van der Werff P, Bouwer L, Huitema D (2008) Neo-Atlantis: The Netherlands under a 5-m sea level rise. Clim Change 91(1):103–122. doi:10.1007/s10584-008-9423-z
Overpeck JT, Otto-Bliesner BL, Miller GH et al (2006) Paleoclimatic evidence for future ice-sheet instability and rapid sea-level rise. Science 311(5768):1747–1750. doi:10.1126/science.1115159
Rahmstorf S (2007) A semi-empirical approach to projecting future sea-level rise. Science 315(5810):368–370. doi:10.1126/science.1135456
Rahmstorf S, Cazenave A, Church JA et al (2007) Recent climate observations compared to projections. Science 316:709. doi:10.1126/science.1136843
Rohling EJ, Grant K, Hemleben C et al (2008) High rates of sea-level rise during the last interglacial period. Nature Geosci 1(1):38–42. doi:10.1038/ngeo.2007.28
Rupp-Armstrong S, Nicholls N (2007) Coastal and estuarine retreat: a comparison of the application of managed realignment in England and Germany. J Coastal Res 23(6):1418–1430. doi:10.2112/04-0426.1
Sterr H (2008) Assessment of vulnerability and adaptation to sea-level rise for the coastal zone of Germany. J Coastal Res 24(2):380–393. doi:10.2112/07a-0011.1
Tol RSJ (1995) The damage costs of climate change toward more comprehensive calculations. Environ Resour Econ 5(4):353–374. doi:10.1007/BF00691574
Tol RSJ (2007) The double trade-off between adaptation and mitigation for sea level rise: an application of FUND. Mitig Adapt Strat Glob Change 12(5):741–753. doi:10.1007/s11027-007-9097-2
Tol RSJ, Fankhauser S (1998) On the representation of impact in integrated assessment models of climate change. Environ Model Assess 3(1–2):63–74. doi:10.1023/A:1019050503531
Turner RK, Adger N, Doktor P (1995) Assessing the economic costs of sea level rise. Environ Plann A 27(11):1777–1796. doi:10.1068/a271777
Acknowledgements
This research was funded by HM Treasury, London for the Stern Review on Climate Change (Project Officer: Dr. Nicola Patmore).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Anthoff, D., Nicholls, R.J. & Tol, R.S.J. The economic impact of substantial sea-level rise. Mitig Adapt Strateg Glob Change 15, 321–335 (2010). https://doi.org/10.1007/s11027-010-9220-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11027-010-9220-7