Skip to main content
SpringerLink
Log in

Approximate Methods of Solving Amplitude-Phase Problems for Continuous Signals

  • RADIO MEASUREMENTS
  • Published:
Measurement Techniques Aims and scope

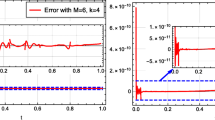
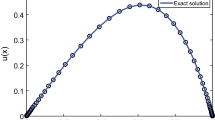
Amplitude and phase problems in physical research are examined. The construction of methods and algorithms for solving amplitude and phase problems is analyzed without drawing on additional information about the signal and its spectrum. Mathematical models of amplitude and phase problems are proposed for the case of one- and two-dimensional continuous signals and approximate methods are found for solving them. The models are based on using nonlinear singular and bisingular integral equations. The amplitude and phase problems are modeled by corresponding nonlinear singular and bisingular integral equations defined on the numerical axis (in the one-dimensional case) and on the plane (in the two-dimensional case). The constructed nonlinear singular and bisingular integral equations are solved using spline-collocation methods and the method of mechanical quadratures. The systems of nonlinear algebraic equations yielded by these methods are solved by a continuous method for solving nonlinear operator equations. A model example demonstrates the effectiveness of the proposed method for solving the phase problem in the two-dimensional case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

References

  1. V. V. Solodovnikov, "Introduction to the statistical dynamics of automatic control systems," GITTL, Moscow, Leningrad (1952).

    Google Scholar 

  2. K. A. Pupkov and N. D. Egupov, Methods of Classical and Modern Theory of Automatic Control: Textbook, Vol. 1, Mathematical Models, Dynamic Characteristics and Analysis of Automatic Control Systems, Bauman MGTU, Moscow (2004)

  3. K. A. Pupkov and N. D. Egupov, Methods of Classical and Modern Theory of Automatic Control: Textbook, Vol. 3, Synthesis of Regulators of Automatic Control Systems, Bauman MGTU, Moscow (2004).

  4. A. A. Potapov, Yu. V. Gulyaev, S. A. Nikitov, et al., Latest Image Processing Techniques, Fizmatlit, Moscow (2008).

    Google Scholar 

  5. A. Colombo, D. E. Galli, L. De Caro, et al., Sci. Rep., 7, 42236 (2017), https://doi.org/10.1038/srep42236.

    Article  ADS  Google Scholar 

  6. R. D. Arnal and R. P. Millane, 2016 Int. Conf. on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, Nov. 21–22, 2016, pp. 1–5, https://doi.org/10.1109/IVCNZ.2016.7804432.

  7. C. Heldt and A. Bockmayr, "Geometric constraints for the phase problem in x-ray crystallography," WCB10. Workshop on Constraint Based Methods for Bioinformatics, May 15, 2012, Vol. 4, pp. 20–26, 10.29007/p2pj.

  8. E. Wolf, Phys. Lett. A, 374, No. 3, 491–495 (2010), https://doi.org/10.1016/j.physleta.2009.10.074.

    Article  ADS  Google Scholar 

  9. E. Wolf, Adv. Imag. Electr. Phys., 165, 283–325 (2011), https://doi.org/10.1016/B978-0-12-385861-0.00007-5.

    Article  Google Scholar 

  10. M. R. Teague, J. Opt. Soc. Am., 73, 1434–1441 (1983), https://doi.org/10.1364/JOSA.73.001434.

    Article  Google Scholar 

  11. E. Kolenovic, J. Opt. Soc. Am., 22, 899–906 (1983), https://doi.org/10.1364/JOSAA.22.000899.

    Article  Google Scholar 

  12. A. Lewis, D. R. Honigstein, J. Weinroth, and M. Werman, ACS Nano, 6, 220–226 (2012), https://doi.org/10.1021/nn203427z.

    Article  Google Scholar 

  13. D. V. Sheludko, A. J. McCulloch, M. Jasperse, et al., Opt. Express, 18, 1586–1599 (2010), https://doi.org/10.1364/OE.18.001586.

    Article  ADS  Google Scholar 

  14. S. S. Nalegaev, N. V. Petrov, and V. G. Bespalov, "Special features of iteration methods for phase problem in optics," Nauch.-Tekhn. Vestn. Inf. Tekhnol., Mekh., Opt., No. 6 (82), 30–35 (2012).

  15. I. V. Boikov, "A continuous method for solving continuous operator equations," Diff. Uravn., 48, No. 9, 1308-1314 (2012).

    Google Scholar 

  16. Yu. L. Daletskii and M. G. Krein, Stability of Solutions of Differential Equations in Banach Space, Nauka, Moscow (1970).

    Google Scholar 

  17. I. V. Boikov, Approximate Methods for Calculating Singular and Hypersingular Integrals. Part 1. Singular Integrals, PSU, Penza (2005).

  18. F. D. Gakhov and Yu. I. Chersky, Convolution Type Equations, Nauka, Moscow (1978).

    Google Scholar 

  19. I. V. Boikov, Approximate Solution of Singular Integral Equations, PSU, Penza, (2004).

    MATH  Google Scholar 

  20. I. Boikov, Y. Zelina, and D. Vasyunin, 2020 Moscow Workshop on Electronic and Networking Technologies (MWENT): Proc. Int. Conf., Moscow, Russia, March 11–13, 2020, IEEE (2020), pp. 1–5, https://doi.org/10.1109/MWENT47943.2020.9067415.

  21. F. D. Gakhov, Boundary Value Problems, Nauka, Moscow (1977).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Penza State University, Penza, Russia

    I. V. Boikov & Ya. V. Zelina

Authors
  1. I. V. Boikov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ya. V. Zelina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. V. Boikov.

Additional information

Translated from Izmeritel'naya Tekhnika, No. 5, pp. 37–46, May, 2021.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Boikov, I.V., Zelina, Y.V. Approximate Methods of Solving Amplitude-Phase Problems for Continuous Signals. Meas Tech 64, 386–397 (2021). https://doi.org/10.1007/s11018-021-01944-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11018-021-01944-y

Keywords

Search

Navigation