Analytical and numerical optimization of broaching tool tooth distribution

Abstract

This paper presents a detailed mathematical analysis of the effect of tooth distribution on the stability of broaching operations. Analytic and numeric techniques are employed to analyse a simplified one-degree-of-freedom mechanical model of variable pitch broaching, to assess its stability, and to find the optimal tooth distances maximizing robustness against harmful self-excited chatter vibrations. A novel modelling approach, considering a theoretical infinitely long broaching tool, draws parallels with variable pitch milling, and analytic formulas for tuning milling cutters are extended to broaching tools. For a further increase of robustness, and to take feasibility constraints into account, a goal function based on the semi-discretization and spectral collocation techniques is implemented in a direct numeric optimisation framework. A new, detailed derivation of the corresponding parameter gradients is presented to enable the use of gradient descent techniques. Since broaching is inherently a time-limited process, optimal parameters found in this manner are then validated via time domain simulations to show the desirable transient behaviours achievable by this ideal tuning of the tool geometry.

1 Introduction

Broaching is often employed by demanding sectors such as the automotive, energy, and aeronautics industries for the high-precision manufacture of intricate features on high-value parts [1]. During such cutting operations, due to the high quality and precision requirements, even small faults in the machining process can lead to scrapped parts. Consequently, harmful self-excited vibrations characteristic of multi-step subtractive manufacturing operations, also known as chatter [2], pose a significant monetary risk. This is due to the already high added value of the machined parts, and the high potential costs associated with replacing broaching tools, whose teeth are susceptible to chipping and breaking due to their highly rigid material composition [3].

It has been shown empirically, that broaching is prone to the same harmful chatter vibrations as milling and turning [4]. Compared to the other two, however, the dynamic behaviour and stability analysis of this manufacturing process is scarcely researched. This is, on one hand, due to the difficulty of modelling and finding an appropriate stability definition for the otherwise limited ‘length’ process. On the other hand, the special groove geometry and its evolution on the workpiece is usually under private protection. Consequently, tool and part manufacturers are reluctant to disclose the design specifications of their broaching tools and strategies. Practically no literature is available on the stability analysis of broaching, and apart from a few studies, which present simple dynamic simulation results [5, 6], most mechanistic studies concerning the mechanical modelling of the process completely exclude the dynamic behaviour of the machine tool assembly.

Broaching is most often modelled as a static or quasi-static process, where only the geometrical aspects of chip formulation are taken into account. Complex spline curves may be used to provide accurate predictions of the cutting forces [7,8,9] and optimize cutting edge geometries based on spent cutting energy [10,11,12]. Finite element simulations are also often employed for the prediction of the cutting forces and analysis of thermo-mechanical effects [13,14,15], as well as for modelling the evolution of the workpiece surface and its integrity [16, 17].

When it comes to empirical analysis, and conducting cutting tests, the two most important aspects of the broaching process are tool wear monitoring [18, 19], and workpiece surface integrity analysis [20,21,22,23]. The former is critical due to the high cutting forces and consequent increased mechanical and thermal loads on the cutting edges, while the latter is important due to the high tolerance requirements broaching operations have to meet. Cutting tests are also useful for identifying the effect of process parameters[24] and certain process steps such as heat treatment [25], as well as conducting parameter optimizations [26].

To create a comprehensive dynamical model of the broaching process, on top of the dynamic characterisation of the machine tool assembly, the inclusion of thermo-mechanical effects and monitoring of continuous cutting edge deformations [27] is also necessary. Furthermore, when formulating a dynamic cutting force model, one must also account for non-smooth effects such as missed cuts [28, 29] and cutting edge fly-over [30, 31]. The dynamic characterisation of the cutting forces is further complicated by the complex cutting edge geometries characteristic of finishing operations [32, 33]. These can have a complex effect on the regenerative delay [34] distribution between consecutive cutting edge segments. In a full-scale mechanical model of the broaching process, the compilation of solutions is highly difficult, and the formulation of any kind of edge geometry optimisation is an almost infeasible task.

Accordingly, to avoid the mentioned issues, this paper presents a simplified one-degree-of-freedom (DoF) dynamical model of the broaching process. This heavily simplified model allows the in-depth stability analysis of operations with straight edge broaching tools. Furthermore, with the help of this model, the effect of axial tooth distribution on the robustness against chatter vibrations can also be captured. This study aims to demonstrate how pitch variation in broaching tools may lead to better stability properties and higher safely achievable material removal rates. For now, due to the exceptionally high design and production costs associated with creating variable pitch broaching tools, only an analytical and numerical design approach is presented, which is an important first step towards the industrial realisation of such tools.

Most broaching operations are done in a relatively low number of individual cuts, especially when compared to e.g. milling. This leads to a time-limited process where the governing dynamics is primarily dominated by transient behaviours. Because of this short timespan of broaching operations, determining asymptotic properties can become meaningless, and it becomes difficult to formulate an adequate stability measure.

Nevertheless, based on time domain simulation results it proved to be worthwhile to investigate a theoretical infinitely long broaching operation, which is carried out with an infinitely long tool. The optimal parameters found through the asymptotic analysis of its periodic orbits positively influenced the governing transient dynamics of the real, time-limited cutting operation. In the sense of stability, this theoretical infinitely long broaching process is almost identical to milling. The same time periodic regenerative forcing is present, with only minor differences in the calculation of cutting edge engagement. Consequently, during the optimization of variable pitch broaching analytic and numeric techniques already available for variable pitch milling could be employed [35,36,37,38]. In fact, the first proposed (graphical) methodology for variable pitch milling optimisation was actually developed on the basis that infinite tool broaching is a good approximation of simple conventional milling [39].

Employing the theoretical infinite broaching model, this paper proposes a multi-step axial tooth distribution optimisation process. First, an analytic approach is presented, which is based on zeroth-order approximation (ZOA) of the periodic forcing terms [40] and the D-subdivision method. Here, the tuning formulas proposed by [36] for variable pitch milling cutters are extended to infinitely long broaching tools. Even this simple analytical technique lead to noticeable improvements in both the asymptotic stability of the infinite problem, and the transient response of its time-limited version.

As a second stage of this optimization process, the semi-discretization method [41] and spectral collocation [42] have been employed to numerically study the stability of periodic orbits in infinite variable pitch broaching. This allowed direct optimisation of the tooth distribution through the minimization of the numerically approximated Floquet-multipliers. For this optimisation task, since the spectral radius of the discretized monodromy matrix is a difficult to minimize and highly non-smooth function, the Hybrid Algorithm for Non-smooth Optimization (HANSO) [43] MATLAB package has been employed.

This direct numeric optimization provided exceptionally great results in periodic orbit stability, however, it often led to physically infeasible solutions with negative chip thicknesses and cutting forces, as the investigated simplified mechanical model did not take contact loss events into account. A periodic orbit is generally undesirable if it contains fly-over segments, no matter how stable it is. Repeated cutting edge exit and entry events will lead to increased tool wear [44, 45] and subpar surface quality [17, 46]. Consequently, based on periodic orbits found through spectral collocation techniques, an additional constraint has been included in the optimization routine, to prevent finding optimal solutions containing fly-over segments. In this manner, infinite broaching tools with two-teeth-long repeating patterns have been optimized, and their finite-length versions have been tested through time domain simulations.

Finally, pseudo-stability maps have been generated based on transient simulation results using cutting edge contact loss events as the indicator for loss of stability. These maps validated the initial preposition that optimizing broaching tool tooth distributions based on asymptotic techniques is an effective way of improving robustness and productivity even in transient, time-limited broaching operations.

The remainder of this paper is structured as follows. Section 2. presents the one DoF mechanical model of variable pitch broaching, the ZOA of the periodic forcing terms, and the analytic stability analysis of infinite broaching operations. In Sect. 3. the employed semi-discretization method and spectral collocation techniques are explained in detail. Including the solution of periodic orbits, the formulation of the monodromy matrix, the calculation of the dominant chatter frequency, and finally the derivation of the spectral radius along with its gradient with respect to the tooth distances. Section 4 presents the simulation routines used for the investigation of transient behaviours in the time-limited broaching problem. Section 5 applies the established analytic and numeric techniques to two-teeth-long repeating patterns, and presents the optimization results in the form of stability and stabilizability maps. Finally, concluding remarks are given in Sect. 6.

2 Analytical optimisation of infinite broaching

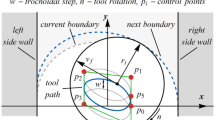
The dynamic study and stability analysis of broaching was carried out using the highly simplified one DoF mechanical model illustrated in Fig. 1a. To simplify matters, a roughing operation is modelled, manufacturing a straight rectangular slot of length L with uniform width w. This means that the width of all of the cutting edges, and the width of the chip formed by these edges, is also always w. Here, considering the exceptional hardness of tool materials and the very rigid tool fixture assemblies characteristic of broaching machines, this simple broaching tool is considered to be infinitely rigid. The machine tool assembly is left compliant only in a single direction perpendicular to the cutting speed. This is the direction relevant for chip regeneration, and these are the vibrations generally responsible for possible losses of stability. Broaching machines are generally more compliant in the chip width direction, however, due to the symmetry of the edges of this simple broaching tool, large amplitude vibrations in that direction are highly unlikely. Further complications may arise due to the axial vibrations of the tool. Compliance in this cutting speed direction is also not taken into account, due to the generally high stiffness of broaching machines in this direction, and to avoid having to deal with state-dependent delays. Overall, since the broaching tool is considered to be infinitely rigid, there are no displacements or rotations between subsequent cutting edges, and the whole tool moves in unison described by a single translational coordinate x(t).

An accurate description of the system dynamics is crucial for conducting a reliable stability analysis of the operation. As in some milling and turning literature [47, 48], to concentrate on the underlying process-induced principles, the dynamics of the machine tool assembly was characterised by only its first, most dominant mode. Reflected modal mass, stiffness, and damping m, k, and c can identified through experimental modal analysis [49]. The most straightforward approach is to conduct impact hammer tests on the machine tool assembly, and fit natural frequencies, modal damping, and mode shapes to the measurement results, e.g. using the poly-reference method [50]. In an industrial setting, the methodology presented in the paper can be easily extended to the multi DOF case, or a similar characterisation of system dynamics may be achieved with parameter fitting free methods, e. g. considering an impulse dynamic subspace (IDS) representation [51].

Fig. 1

a One DoF mechanical model of variable pitch broaching. b Periodic forcing in infinite variable pitch broaching with a two-teeth repeating pattern

Considering the geometry of the broaching tool, only tooth distributions containing repeating patterns were considered, as only these can be optimized through the asymptotic behaviour of periodic solutions. In this case, there is a set of tooth distances $\{d_i\}$ $i=1,\ldots n$ which are repeated along the length of the tool in an orderly manner, to create a forcing periodic in time and tool length in

$$\begin{aligned} T = \frac{D}{v_{\textrm{cut}}}, \,\, \textrm{and} \,\, D = \sum _{i=1}^{n}d_i. \end{aligned}$$

(1)

Figure 1b presents a typical time series of steady state cutting forces for a variable pitch broaching operation carried out with a tool containing a two teeth long repeating pattern. As illustrated by panel (a), this operation is done in a repeating pattern of cuts made by two different types of cutting edges. These are type 1, where the prescribed chip thickness is $h_1$ and the distance from the previous tooth is $d_1$ and type 2 where these same values are $h_2$ and $d_2$.

To find the cutting force in the only relevant x direction, a linear model was employed

$$\begin{aligned} F_{\textrm{cut}}(t) = K_{\textrm{c}}w \sum _{i=1}^{n} g_i(t)h_i(t). \end{aligned}$$

(2)

Here $g_i(t)$ is the number of teeth in contact at time t from the given type, and $K_{\textrm{c}}$ is an empirical force coefficient. This so called cutting coefficient $K_{\textrm{c}}$ may be acquired from orthogonal cutting data available on the given tool-workpiece material pair, or by direct parameter fitting based on cutting tests conducted with broaching tools of simple rectangular geometries.

Considering the regenerative effect characteristic of metal cutting, the depth of cuts are available as

$$\begin{aligned} h_i(t) = h_{0,i} + x(t-\tau _i) - x(t). \end{aligned}$$

(3)

Here for each different type of tooth in the pattern, the corresponding regenerative time delay is $\tau _i = \frac{d_i}{v_{\textrm{cut}}}$. Since a linear inclination is expected in the height of the cutting edges, the prescribed feed rate $h_{0,i}$ is proportional to the tooth distance $\left( \frac{h_{0,i}}{d_i} = \textrm{const}\right)$. This is a reasonable assumption to make, considering that on most broaching tools the geometric feed is manufactured via a linear path grinding operation [12].

To calculate individual tooth type engagements $g_i(t)$, tool exit and entry events must be identified first. If the first tooth enters the workpiece at $t_{1,\textrm{in}}=t_0$, it will exit the material when it reaches the other end of the workpiece at $t_{1,\textrm{out}}=t_0+\frac{L}{v_{\textrm{cut}}}$. The rest of the edges will follow along shifted in time by their corresponding time delays, as

$$\begin{aligned} t_{i,\textrm{in}}=t_0+\sum _{k=2}^{i}\tau _k, \,\, t_{i,\textrm{out}}=t_{i,\textrm{in}}+\frac{L}{v_{\textrm{cut}}}, \,\, i=1,\ldots n. \end{aligned}$$

(4)

Finally, if an infinitely long broaching operation is considered, due to the periodicity of the tooth distances and (1), at $t = t_0 + T$ an edge of the first type will enter the workpiece once again completing the periodic cycle of exit and entry events. Consequently, the individual tooth type engagements only depend on the modulo of the time with respect to the period T. Using the hat notation as $\hat{t}= \textrm{mod}(t,T)$, this means that

$$\begin{aligned} g_i(t) = \left\{ \begin{matrix} \lceil \Lambda _{\textrm{D}}\rceil &{} | &{} \hat{t}_{i,\textrm{in}}<\hat{t}<\hat{t}_{i,\textrm{out}},\\ \lceil \Lambda _{\textrm{D}}\rceil &{} | &{} \hat{t}<\hat{t}_{i,\textrm{out}}<\hat{t}_{i,\textrm{in}},\\ \lceil \Lambda _{\textrm{D}}\rceil &{} | &{} \hat{t}_{i,\textrm{out}}<\hat{t}_{i,\textrm{in}}<\hat{t},\\ \lfloor \Lambda _{\textrm{D}}\rfloor &{} | &{} \textrm{otherwise}, \end{matrix}\right. \end{aligned}$$

(5)

where $\Lambda _{\textrm{D}} = \frac{L}{D}$ is the average number of teeth periods in operation. Here, due to the inclusion of the modulo operation, three different conditions are needed to identify all possible cases, where the maximum number of teeth $\lceil \Lambda _{\textrm{D}}\rceil$ are active from a given tooth type. The first row marks the simplest case where the modulated version of the entry event is before the modulated exit event. The second and third lines are relevant, if this order is reversed. In this case an extra tooth is in contact before the exit and after the entry event, at the beginning and end of the period.

Taking machine tool dynamics into account the governing equation of motion of the broaching model seen in Fig. 1a will become

$$\begin{aligned} m\,\ddot{x}(t) + c\,\dot{x}(t) + k\,x(t) = F_{\textrm{cut}}(t), \end{aligned}$$

(6)

which can be brought to a nondimensionalized form using the dominant natural angular frequency $\omega _{\textrm{n}} = \sqrt{\frac{k}{m}}$ inverse as a time scaling unit, and the sum of the prescribed depth of cuts $H = \sum _{i=1}^{n}h_{0,i}$ as a displacement scaling unit. Converting to $\tilde{t} = \omega _{\textrm{n}}t$, $\tilde{x} = \frac{1}{H}x$ and leaving the tildes leads to

$$\begin{aligned} \ddot{x}(t) + 2\zeta \dot{x}(t) + x(t) = f(t), \end{aligned}$$

(7)

where $\zeta = \frac{c}{2\omega _{\textrm{n}}m}$ is the damping ratio, and the dimensionless cutting force is available as

$$\begin{aligned} f(t) = \tilde{w}\sum _{i=1}^{n}g_i(t)\tilde{h}_i(t). \end{aligned}$$

(8)

Here the dimensionless chip width is $\tilde{w} = \frac{K_{\textrm{c}}w}{\omega _{\textrm{n}}^2m}$, and the dimensionless chip thickness is

$$\begin{aligned} \tilde{h}_i(t) = \Delta _i + x(t-\tilde{\tau }_i) - x(t), \end{aligned}$$

(9)

where $\Delta _i = \frac{d_i}{D}$ is the ratio between the distance from the previous cutting edge and the length of the repeating pattern. To calculate the dimensionless time delays $\tilde{\tau }_i$, it is worthwhile to define a dimensionless cutting speed based on the length of the repeating pattern $\frac{n}{D}$ as $\tilde{v} = \frac{n}{D\omega _{\textrm{n}}}v_{\textrm{cut}}$, using which $\tilde{\tau }_i = \frac{n\Delta _i}{\tilde{v}}$, or if expressed in the original parameters $\tilde{\tau }_i = \omega _{\textrm{n}}\frac{d_{i}}{v_{\textrm{cut}}} = \omega _{\textrm{n}}\tau _i$. This definition of $\tilde{v}$ is beneficial as it makes operation pairs with topologically identical patterns such as $\Delta _1 = 1, \, n=1$ and $\Delta _{1,2} = 0.5, n=2$ identical, when the cutting speed is the same.

When evaluating the number of active teeth from a given type in its dimensionless form $\tilde{g}_i(t)$, the formula derived in (5) is still applicable with the modulo operation now done with respect to $\tilde{T} = \omega _{\textrm{n}}T$ if the exit and entry events from (4) are converted to their corresponding dimensionless forms as

$$\begin{aligned} t_{i,\textrm{in}}=\frac{n}{\tilde{v}}\sum _{k=2}^{i}\Delta _i, \,\, t_{i,\textrm{out}}=t_{i,\textrm{in}}+\frac{n\Lambda _{\textrm{D}}}{\tilde{v}}, \,\, i=1,\ldots n, \end{aligned}$$

(10)

where for the sake of simplicity $t_0$ was set to zero, meaning the broaching operation begins at $t=0$ with the entry of a “type 1” tooth.

Finally, for an easier numeric investigation (7) can be converted to a first order form introducing the state vector $\textbf{x}(t) = [x(t), \,\, \dot{x}(t)]^\intercal$, and the dimensionless time can be rescaled once again to arrive on a system periodic in $\tilde{T}=1$ using the dimensionless period length $\omega _{\textrm{n}}T = \frac{n}{\tilde{v}}$, leading to the form

$$\begin{aligned} \dot{\textbf{x}}(t) = \begin{bmatrix} \dot{x}_1(t)\\ \dot{x}_2(t) \end{bmatrix} = \frac{n}{\tilde{v}}\begin{bmatrix} x_2(t)\\ \tilde{f}(t)-x_1(t)-2\zeta x_2(t) \end{bmatrix}, \end{aligned}$$

(11)

where

$$\begin{aligned} \tilde{f}(t) = \tilde{w}\sum _{i=1}^{n} \gamma _i(t)\left( \Delta _i + x_1(t-\Delta _i) - x_1(t)\right) . \end{aligned}$$

(12)

This means that the time delays of the system are now simply $\Delta _i$, and during the calculation of immersion via (5) exploiting that $\gamma _i(t) = \tilde{g}_i\left( \frac{n}{\tilde{v}}t\right)$ the cutting edge entry and exit times in (4) also simplify down to

$$\begin{aligned} t_{i,\textrm{in}}=\sum _{k=2}^{i}\Delta _i, \,\, t_{i,\textrm{out}}=t_{i,\textrm{in}}+\Lambda _{\textrm{D}}, \,\, i=1,\ldots n. \end{aligned}$$

(13)

Furthermore instead of the modulo operation in (5), it is enough to take the fractional part of the rescaled dimensionless time, as the period length is now always 1.

In summary, the dimensionless version of variable pitch broaching defined by (11-13) depends only on $n+4$ parameters: $\Delta _i, \, i=1,\ldots n$, $\tilde{v}$, $\Lambda _\textrm{D}$, $\zeta$, and $\tilde{w}$, from which only $n+3$ are independent as $\sum _{i=1}^n\Delta _i = 1$ must always be fulfilled. Furthermore, in engineering practice, the tool geometry optimisation process can be focused solely on finding the optimal $\Delta _i$ and $\Lambda _{\textrm{D}}$ on different levels of the dimensionless cutting speed $\tilde{v}$, as $\tilde{w}$ is usually given by the bore geometry and the workpiece material, while $\zeta$ is a measured dynamic characteristic of the broaching machine.

Here it is worth mentioning, that since a linear force characteristic has been considered in (2), the final form of the dimensionless cutting force found in (12) is independent of the prescribed feed of the cutting edges $h_{0,i}$. Naturally, in industrial practice these uncut chip thickness values can have a significant effect on the stability of the broaching operation. Since in general, finishing tools have lower prescribed feed rates than roughing ones do, this parameter may also vary between manufacturing steps of the same bore. Considering a non-linear cutting force model, e.g. the exponential characteristics introduced by Enres & Loo in [52], this effect can be better accounted for. However, the tooth distribution optimisation techniques proposed by this paper all rely on linear stability analysis of the governing equation of motion. Thus, even if a more general cutting force model was to be considered, it would have to be linearised to the form found in (2), with the only difference, that $K_{\textrm{c}}$ would be a function of $h_{0,i}$. By considering a feed dependent cutting coefficient, the results presented in this paper are straightforward to adapt to applications where feed related non-linearities also have a significant effect on the stability of the operation.

Taking a closer look at (12) it is clear that the periodic nature of the cutting forces comes only from the tooth immersion functions, where $\gamma _{i}(t) = \gamma _{i}(t+1)$ due to the employed modulo operation by the rescaled period length. This function is very similar to the periodic directional factor often defined in dynamic models of milling operations [36, 40], and can be approximated in a similar manner using a zeroth order Fourier series, where the first and only kept term is

$$\begin{aligned} \begin{aligned} G_{0,i}& : =\int _{0}^{1}\gamma _i(t)\textrm{d}t = \lceil \Lambda _{\textrm{D}} \rceil \left( \Lambda _{\textrm{D}} - \lfloor \Lambda _{\textrm{D}} \rfloor \right) \\ &\quad +\lfloor \Lambda _{\textrm{D}} \rfloor \left( 1-\Lambda _{\textrm{D}} + \lfloor \Lambda _{\textrm{D}} \rfloor \right) \equiv \Lambda _{\textrm{D}}, \end{aligned} \end{aligned}$$

(14)

since $\gamma _i(t) = \lceil \Lambda _{\textrm{D}} \rceil$ for $\textrm{mod}(\Lambda _{\textrm{D}},1)$ long per period and is equal to $\lfloor \Lambda _{\textrm{D}} \rfloor$ the rest of the time. This is a very simple and non-surprising result, as $\Lambda _{\textrm{D}}$ was defined as the average number of teeth periods in contact, which can be directly interpreted for the individual tooth types of the repeating patterns as well.

Using this zeroth order approximation in (12), the cutting force becomes autonomous, and the linear delay differential equation seen in (11) will have a steady state equilibrium solution at $\bar{\textbf{x}} = \left[ \tilde{w}\Lambda _{\textrm{D}}, \, \, 0\right] ^\intercal$, since $\sum _{i=1}^{n}\Delta _i=1$. A relatively good approximation for the stability of the periodic orbits of infinitely long broaching operations can be given by examining the stability of this equilibrium similarly to a steady state solution of a turning process [53].

To evaluate the stability of such equilibria (11) has to be linearised about $\bar{\textbf{x}}$, which introducing $u(t) = x(t) - \tilde{w}\Lambda _{\textrm{D}}$ and converted back to second order form leads to

$$\begin{aligned} \begin{aligned} \ddot{u}(t) + \frac{2\zeta n}{\tilde{v}}\dot{u}(t) +&\frac{n^2+n^3\tilde{w}\Lambda _{\textrm{D}}}{\tilde{v}^2}u(t) \\ &= \frac{n^2\tilde{w}\Lambda _{\textrm{D}}}{\tilde{v}^2}\sum _{i=1}^{n}u(t-\Delta _i). \end{aligned} \end{aligned}$$

(15)

From here the well established D-subdivision method [34] can be employed to identify so-called zero crossing curves on the dimensionless chip width - cutting speed ($\tilde{w}$ - $\tilde{v}$) stability maps, by substituting in a critical trial solution $u_{\textrm{c}}(t) = A\textrm{e}^{\textrm{i}n\,\omega _{\textrm{c}}t}$ into (15), leading to the characteristic quasi-polynomial

$$\begin{aligned} \begin{aligned} P(\omega _{\textrm{c}}):=&-\tilde{v}^2 \omega _{\textrm{c}}^2+2\tilde{v}\zeta \textrm{i}\,\omega _{\textrm{c}} + 1+n\tilde{w}\Lambda _{\textrm{D}} \\&- \tilde{w}\Lambda _{\textrm{D}} \sum _{i=1}^{n}\textrm{e}^{-\textrm{i}n\omega _{\textrm{c}}\Delta _i} = 0. \end{aligned} \end{aligned}$$

(16)

Here for the critical Hopf (chatter) frequency $n\,\omega _{\textrm{c}}$ was used to account for the length of the periods, and make topologically identical patterns created through repetition equivalent stability wise. This polynomial can be separated into real and imaginary parts and solved together to find critical $\tilde{w}(\omega _{\textrm{c}})$ - $\tilde{v}(\omega _{\textrm{c}})$ parameter pairs as functions of the chatter frequency $\omega _{\textrm{c}}$, corresponding to Hopf-bifurcations on the stability boundaries.

$$\begin{aligned}&\mathrm {Re:}\,\, -\tilde{v}^2\omega _{\textrm{c}}^2 + 1 +n\tilde{w}\Lambda _{\textrm{D}} = \tilde{w}\Lambda _{\textrm{D}} \sum _{i=1}^{n}\cos n \omega _{\textrm{c}}\Delta _i,\end{aligned}$$

(17a)

$$\begin{aligned}&\mathrm {Im:}\,\, 2\tilde{v}\zeta \omega _{\textrm{c}} = -\tilde{w}\Lambda _{\textrm{D}} \sum _{i=1}^{n}\sin n \omega _{\textrm{c}}\Delta _i. \end{aligned}$$

(17b)

In case of uniform pitch broaching operations $n=1$ and $\Delta _1 = 1$, which simplifies (17) considerably, allowing explicit expression of the stability boundaries as

$$\begin{aligned}&\tilde{w}(\lambda _{\textrm{c}}) = \frac{1}{ \Lambda _{\textrm{D}}}\frac{(\lambda _{\textrm{c}}-1)^2+4\zeta ^2\lambda _{\textrm{c}}^2}{2(\lambda _{\textrm{c}}^2-1)},\end{aligned}$$

(18a)

$$\begin{aligned}&\tilde{v}(\lambda _{\textrm{c}}) = \frac{1}{2}\frac{\lambda _{\textrm{c}}}{\arctan \left( \frac{1-\lambda _{\textrm{c}}^2}{2\zeta \lambda _{\textrm{c}}}\right) + k\pi }, \,\, k \in \mathbb {Z}, \end{aligned}$$

(18b)

which are almost identical to the analytic stability lobes of turning operations [53] with $\lambda _{\textrm{c}} = \omega _{\textrm{c}}\tilde{v}$. From here the global minimum of the stability lobes, often referred to as the critical chip width can also be derived as

$$\begin{aligned} \tilde{w}_{\textrm{lim}} = \frac{1}{\Lambda _{\textrm{D}}}2\zeta (1+\zeta ). \end{aligned}$$

(19)

A general explicit expression of the stability lobes is also available for infinite repeating pattern variable pitch broaching in the form

$$\begin{aligned}&\tilde{v}(\omega _{\textrm{c}}) = \frac{2\zeta \omega _{\textrm{c}}\frac{C-n}{S} + \sqrt{\left( 2\zeta \omega _{\textrm{c}}\frac{C-n}{S}\right) ^2+2n\omega _{\textrm{c}}^2}}{2\omega _\textrm{c}^2},\end{aligned}$$

(20a)

$$\begin{aligned}&\tilde{w}(\omega _{\textrm{c}},\tilde{v}) = \frac{-2\zeta \omega _{\textrm{c}}}{\Lambda _{\textrm{D}}S}\tilde{v}, \end{aligned}$$

(20b)

where $S = \sum _{i=1}^{n}\sin n \omega _{\textrm{c}}\Delta _i$, $C = \sum _{i=1}^{n}\cos n \omega _{\textrm{c}}\Delta _i$, and the distribution of the pitch distances $\Delta _i$ is completely arbitrary. Solving this equation is a bit more complicated than (18). However, for relatively low pattern lengths n it is still computationally inexpensive to evaluate $\tilde{w}(\omega _{\textrm{c}})$ and $\tilde{v}(\omega _{\textrm{c}})$ numerically, by making a sweep on the possible range of chatter frequencies.

Taking a close look at (20) reveals that decreasing $\Lambda _{\textrm{D}}$ by extending the length of the repeating patterns D or increasing the damping coefficient $\zeta$ leads to an increase of robustness. Furthermore, decreasing the absolute value of S also leads to larger safely machinable slot widths $\tilde{w}$. When it comes to broaching machining tasks, $\Lambda _{\textrm{D}}$, $\zeta$, and $\tilde{v}$ are usually given fix parameters. By employing pitch modulation, only S may be affected. To do so, there is a wide range of strategies available for selecting $\Delta _i$. Direct numeric methods may be employed to select completely arbitrary distributions, while analytic formulas may be used to find more systematic layouts.

Since the stability lobes of infinite broaching(20) depend on $\Delta _i$ just like the stability lobes of milling depend on the pitch modulation of the used cutters, analytic formulas developed for variable pitch milling[36] may be adapted to broaching operations. There, the two most common analytic approaches are to use either repeating or linearly varying patterns. Since n in case of broaching has no physical meaning, contrary to milling where it would denote the number of cutting edges on the milling tool, it is meaningless to consider repeating patterns separately. When it comes to linearly varying patterns, where $\Delta _i = \Delta _0 + i\delta$, an optimal inclination $\delta$ may be found by setting S to zero on a given chatter frequency $\omega _{\textrm{c}}$.

For infinitely long variable pitch broaching tools, through trigonometric expansion, it can be shown that

$$\begin{aligned} \delta = \frac{\pi +2k\pi }{n\omega _{\textrm{c}}}, \,\, \Delta _0 = 1-\frac{n(n+1)}{2}\delta , \end{aligned}$$

(21)

guarantees that $S=0$ for a known fixed $\omega _{\textrm{c}}$. This theoretically allows chatter-free manufacture of infinitely large slot widths. Naturally, in engineering practice, the chatter frequency is not fixed and such infinitely robust cases are not possible. Furthermore, according to (20) considering finite chatter frequencies $S = 0$ would result in a physically meaningless case, where the corresponding cutting speed is infinitely large. Modifying the tooth distribution of the broaching tool will always lead to deviations in the primary chatter frequency, which means that finding the analytic optimal tooth distribution requires an iterative selection process [38]. In (21) for physical feasibility $k \in \mathbb {Z}$ is picked so that $0<\delta <\frac{2}{n(n+1)}$. If such a selection is not possible this technique is not applicable.

Nevertheless, optimizing repeating patterns by approximating the chatter frequency for a given cutting speed assuming uniform tooth distribution (18) and deriving the optimal tooth distances according to (21), works remarkably well. Even this first guess leads to a significant increase in robustness, and the derived simple analytic formulas considerably speed up the iterative selection process. This is mainly due to the fact that deviations in the chatter frequency induced by modification of the tooth distribution are usually quite minor. Most of the time, the chatter frequency is closely connected to the natural frequency of a problematic mode of the machine tool assembly, which is unaffected by the geometry of the used broaching tool.

The rest of this paper is devoted to improving this simple analytic optimisation technique by employing numerical techniques and accounting for further feasibility constraints.

3 Numerical optimisation of infinite broaching

The combination of the ZOA and D-subdivision methods allows fast, computationally inexpensive, semi-analytic optimisation of tooth distributions in theoretical infinitely long broaching operations. It does so by neglecting the time dependency of the problem, taking an average of the cutting edge engagement functions $\gamma _i(t)$. Furthermore, (21) also does not take chatter frequency deviations or any physical feasibility constraints into account. Consequently, the resulting $\Delta _i$ distributions may be sub-optimal or may correspond to physically meaningless periodic solutions. To incorporate true time dependency, and feasibility constraints in the optimisation process, direct numeric techniques must be employed for evaluating periodic orbit stability and finding cutting edge contact loss events. These numeric methods can also serve as experimental tests to validate the fast, semi-analytic stability predictions, by considering time dependency but neglecting non-linear effects, such as fly-over segments.

The governing equation of motion (11) is a linear time-dependent delay differential equation (DDE), which by linearising around a periodic solution and omitting the constant terms can be brought to the conventional form

$$\begin{aligned} \dot{\textbf{x}}(t) = \textbf{A}(t)\textbf{x}(t)+\sum _{i=1}^{n}\textbf{B}_i(t)\textbf{x}(t-\Delta _i), \end{aligned}$$

(22)

where the coefficient matrices

$$\begin{aligned} \begin{aligned} \textbf{A}(t) =&\frac{n}{\tilde{v}}\begin{bmatrix} 0 &{} 1 \\ -1 - \tilde{w}\sum _{i=1}^{n}\gamma _{i}(t) &{} -2\zeta \end{bmatrix}, \,\, \\ \textbf{B}_i(t) =&\frac{n}{\tilde{v}}\begin{bmatrix} 0 &{} 0 \\ \tilde{w}\gamma _{i}(t) &{} 0 \end{bmatrix}, \end{aligned} \end{aligned}$$

(23)

are independent of the state $\textbf{x}$. Consequently, the semi-discretization method [41] is directly applicable for evaluating stability, even without solving the corresponding boundary value problem (BVP) of the periodic orbits. Furthermore, if $\gamma _{i}(t)$ is approximated in a smooth manner using a free parameter $\kappa>>1$ as

$$\begin{aligned} \begin{aligned} \gamma _{i}(t) \approx&\frac{1}{2}\tanh \left( \kappa (\hat{t}-\hat{t}_{i,\textrm{in}})\right) -\frac{1}{2}\tanh \left( \kappa (\hat{t}-\hat{t}_{i,\textrm{out}})\right) \\ &\quad +\left\{ \begin{matrix} \lfloor \Lambda _{\textrm{D}} \rfloor &{} | &{} \hat{t}_{i,\textrm{in}}<\hat{t}_{i,\textrm{out}}\\ \lceil \Lambda _{\textrm{D}} \rceil &{} | &{} \hat{t}_{i,\textrm{in}}>\hat{t}_{i,\textrm{out}} \end{matrix}\right. , \end{aligned} \end{aligned}$$

(24)

the derivatives of the coefficient matrices in (23) with respect to the system parameters are all available analytically. This allows the calculation of not only the spectral radius of the Floquet multipliers but also its gradient with respect to any of the parameters. In the possession of this gradient, the HANSO MATLAB package [43] can find optimal parameters for infinite broaching operations, which maximise robustness against chatter vibrations, and lead to favourable transient behaviours in the time-limited version of the problem.

Even though the stability of the broaching operation can be evaluated without finding the periodic solutions of (11), it is worthwhile to solve the corresponding BVP to check that the

$$\begin{aligned} \tilde{h}_i(t) = \Delta _i + x_1(t-\Delta _i)-x_1(t) > 0 \end{aligned}$$

(25)

condition is not violated. If $\tilde{h}_i(t)$ becomes negative that would lead to a contact loss event, followed by a fly-over segment, where (11) no longer applies. To simulate trajectories, where cutting edges are allowed to exit the material, equation (3) defined for the evaluation of the dynamic chip thickness would have to be updated. First of all $h_i(t)$ should be reset to zero whenever it becomes negative. Furthermore, accounting for fly-over segments requires actively tracking which previous tooth left the mark the current edge is actually cutting into. This means $h_i(t)$ should be calculated by finding the minimum of all the distances compared to all marks left on the workpiece by all the previous cutting edges. As demonstrated in [54], this updated formula for evaluating $h_i(t)$ can be expressed in a compact, but highly non-smooth form. Employing this definition of the dynamic chip thickness leads to complicated non-smooth changes in the regenerative time delay, and makes identification and stability analysis of periodic solutions highly tedious.

This study only concerns itself with the detection and prevention of contact loss events and does not go into detail about what happens after. When it comes to broaching operations, where the surface integrity and accuracy requirements are exceptionally high, cutting edge fly-over is generally unacceptable. The individual marks of cutting edges and the vibratory periods of the tool are often noticeable on the final workpiece surface, even without the emergence of chatter [17]. Such drastic cases where a cutting edge exits the workpiece are highly unlikely to lead to an acceptable surface finish. Consequently, during the optimisation process, an additional constraint was introduced which heavily penalised the objective function if (25) was violated.

This was achieved by formulating a discretized multi-point BVP of the periodic orbits based on spectral collocation techniques [42]. To do so, the orbits have been divided up into smooth solution segments at the tooth entry and exit events defined by (13). This way a system of non-linear algebraic equations was formulated, which could be solved via Newton iteration, as the corresponding Jacobian matrix was available analytically. Furthermore, through this discretized BVP the gradient of (25) with respect to any system parameter could also be found. This allowed a more effective implementation of this penalty function in the optimisation algorithms of HANSO.

In summary, the semi-discretization and spectral collocation techniques allow both the evaluation of periodic orbit stability and the identification of contact loss events. Combinations of these techniques have been used to formulate different objective functions for the direct numeric optimization of variable pitch broaching tools. The rest of this section is devoted to the formulation of these goal functions and their implementation in the HANSO optimization framework.

3.1 Stability analysis of periodic orbits

To evaluate the stability of periodic orbits in infinitely long broaching operations the semi-discretization method [41] has been employed. Using this technique and considering a small time-step $\Delta t$, (22) can be reformulated as a discrete map

$$\begin{aligned} \textbf{z}_{j+1} = \textbf{S}_j \textbf{z}_j, \end{aligned}$$

(26)

where $\textbf{z}_{j} = [ \textbf{x}(j\Delta t)^\intercal ,\,\, \textbf{x}((j-1)\Delta t)^\intercal , \, \ldots ,\, \textbf{x}((j-N)\Delta t)^\intercal ]^\intercal$ is the extended state vector that contains a discretized version of the solution tail $\textbf{x}(t-\theta ), \, \theta \in [0,\,\, \max \{\Delta _i\}]$, and $\textbf{S}_j$ is the so-called step-matrix, which is a discretized version of the solution operator corresponding to (22). The detailed derivation of these $\textbf{S}_j$ matrices is presented in A.

The matrices $\textbf{S}_j$ all represent a small $\Delta t$ long forward step in time. To cover the full length of a periodic orbit, which is guaranteed to be 1, these have to be evaluated $M = \lceil 1/\Delta t \rceil$ times. Then the monodromy matrix can be found as the product

$$\begin{aligned} \varvec{\Phi } = \textbf{S}_{M-1} \textbf{S}_{M-2}\ldots \textbf{S}_{0}. \end{aligned}$$

(27)

Spectral analysis of $\varvec{\Phi }$ allows the derivation of Floquet multipliers and its spectral radius

$$\begin{aligned} \rho (\varvec{\Phi }) = |\mu _{\textrm{max}}|= \max \left\{ |\textrm{eig}(\varvec{\Phi })|\right\} , \end{aligned}$$

(28)

determines the stability of the periodic orbits.

Furthermore, as demonstrated in [55] for a mathematically equivalent milling model, the eigenvector of $\varvec{\Phi }$ corresponding to $\mu _{\textrm{max}}$ allows numeric evaluation of the real dominant chatter frequency. Converting the part of the eigenvector corresponding to the tool velocity $x_2(t)$ back to a time signal of length 1 makes Fourier analysis possible. The highest peak in energy content of the eigenvectors (considered in ‘velocity’) denotes the dominant modulation $k_{\textrm{max}}$ of the base frequency carried by the complex angle of the multiplier corresponding to the spectral radius (28)

$$\begin{aligned} \omega _{\textrm{chatter}} = |2\pi k_{\textrm{max}}+\angle \,\mu _{\textrm{max}}|. \end{aligned}$$

(29)

The lower the spectral radius of the monodromy matrix, the more robust the operation is against harmful chatter vibrations. The goal of the direct numeric optimisation should thus be the minimisation of (28). Due to the “max” operation found in this equation, this leads to a difficult to handle, highly non-smooth optimisation goal function. Luckily, the HANSO package is capable of effectively minimizing such objective functions on a given set of system parameters. However, this is only possible if the corresponding gradients are also provided.

These gradients can be highly non-smooth as well and do not have to exist everywhere, e.g. at critical points, where $\mu _{\textrm{max}}$ has a multiplicity larger than 1. Such non-differentiable cases, however, should only arise with zero probability, or when taking a derivative from a nearby point does not significantly affect the optimisation algorithm. Thus the only non-smooth effect in the goal function (28) should be the “max” operation. In the case of the present broaching problem, this can be fulfilled with appropriate smoothing of (22) through (24). This way the matrices $\textbf{A}(t)$ and $\textbf{B}(t)$ on top of $\zeta$ and $\tilde{w}$ become smoothly differentiable with respect to $\Lambda _{\textrm{D}}$ and the tooth distribution $\Delta _i$ as well. As demonstrated in detail in “Appendix 1” this allows the analytic derivation of all parameter gradients necessary for the direct numeric optimisation of $\mu _{\textrm{max}}$.

3.2 Contact loss events in periodic orbits

Minimizing the spectral radius (28) guarantees the highest possible robustness against loss of stability and chatter vibrations. However, it might not result in an optimal set of system parameters, as physically unfeasible periodic solutions containing contact loss events and fly-over segments may arise. This makes the stability calculations themselves meaningless, as the domain of the governing equation of motion (11) is left. To avoid these events the goal function of the optimization algorithm must be extended with a penalty function

$$\begin{aligned} \begin{aligned}&\epsilon = \left\{ \begin{matrix} \sigma - \tilde{h}_{\textrm{crit}} &{} | &{} \tilde{h}_{\textrm{crit}} < 0,\\ 0 &{} | &{} \textrm{otherwise}, \end{matrix} \right. \\&\tilde{h}_{\textrm{crit}} = \min _i\{\min _t(\tilde{h}_i(t))\}, \, t \in \left[ 0, \, 1\right] . \end{aligned} \end{aligned}$$

(30)

This formula is based on the contact loss condition introduced in (25), and is evaluated by determining the minimum of the geometrical chip thickness signal $h_{i}(t)$ for each tooth type and taking a minimum of those. Here $\sigma$ is a user defined parameter, which if contact loss events are completely unacceptable should be larger than the critical value of the Floquet multipliers at the stability boundary ($\sigma >1$). For most calculations presented in this paper $\sigma = 10$ was used.

Finally, the input of the HANSO optimisation algorithm, the extended goal function, will become

$$\begin{aligned} Q = \rho (\varvec{\Phi }) + \epsilon . \end{aligned}$$

(31)

Here, calculating $\rho (\varvec{\Phi })$ and its parameter gradient, can be done as presented in Sect. 3.1 and “Appendix 1”. However, evaluating $\epsilon$ and its parameter gradient will require finding the periodic solutions of (11) and determining $\tilde{h}_{\textrm{g,min}}$ as well as its corresponding gradient.

To find these periodic orbits of the governing time-dependent linear DDE, spectral collocation techniques have been employed [42]. First, the orbits were divided into smooth segments at the cutting edge entry and exit events defined in (13), then discretized versions of the orbits were formulated using a piecewise Legrende-Gauss-Lobatto(LGL) mesh [56]. Employing the spectral differentiation matrix for LGL meshes shown in [56], the governing infinite dimensional multi-point boundary value problem of the periodic orbits was reformulated as a system of nonlinear algebraic equations (NAEs). The derivation of this system of NAEs, as well as its Jacobian is detailed in “Appendix 2”.

Since its Jacobian was available analytically, this system of NAEs could be solved efficiently via Newton iteration. Based on the discrete periodic orbits obtained in this manner it was straightforward to evaluate the penalty part $\epsilon$ of the optimization goal function (31). To make this approach compatible with the HANSO optimisation framework, the corresponding parameter Jacobian of $\epsilon$ also had to be evaluated. Its detailed derivation is presented in “Appendix 2”.

With the appropriate linearisation of the governing NAE system, the spectral collocation approach also allows the direct formulation of the corresponding monodromy matrix. As demonstrated in “Appendix 2” the gradient of its spectral radius can also be obtained, even without the need to introduce smoothing in the governing equation of motion. Nevertheless, this approach is not used for stability analysis in this paper. This is due to the fact, that for orbits with high deviations between the lengths of their smooth segments, the accuracy of the stability predictions obtained in this manner was less reliable compared to the semi-discretization technique introduced in the previous section.

4 Transient simulation of time-limited broaching

The analytic and numeric techniques introduced in the previous two sections are great tools for optimizing the tooth distribution on a theoretical infinitely long broaching tool. In actual industrial practice, however, most broaching tools are relatively short containing only 20-40 individual cutting edges. Broaching machines require only a couple of seconds to finish their machining tasks. Such operations can hardly be characterised by the asymptotic periodic behaviours investigated in this paper so far. Consequently, the found optimal tooth distributions must be validated through transient simulations, to demonstrate their effect on the time-limited behaviour of real life broaching operations. Transient simulations can serve as numeric experiments, to validate the found optimal tooth geometries, taking the true time dependency of the operations into account. This step is invaluable before experimental cutting tests may begin, due to the exceptionally high costs of manufacturing broaching tools with different axial tooth distributions.

These transient simulations could also be used for the direct numeric optimisation of the tool geometry through a virtual black-box optimisation scheme. Unfortunately, this approach is extremely expensive computationally, and it is really not straightforward how to define a proper goal function based on the properties of the transient simulation results. Consequently, in this paper, a more theoretical approach was taken, where the extensive literature and the numerous mathematical insights available on periodic linear DDEs such as (22) could be exploited. The transient simulations were only employed for the purpose of validation.

The validation process of the optimisation methods presented in this paper is illustrated in Fig. 2. First asymptotically stable parameter combinations were found for the infinite-length-tool version of the problem, either through the previously discussed D-subdivision or semi-discretization methods. Then the corresponding periodic solutions were approximated via spectral collocation to locate contact loss events and fly-over segments. If the orbits did not contain such non-smooth effects, or these could be avoided through constrained numeric optimization, then transient simulations were employed to validate the found parameter sets on the time-limited version of the problem. Only then were parameter combinations deemed desirable.

Fig. 2

Flowchart on the validation process of optimisation results

Building a simulation framework for DDEs with fixed point time delays is quite straightforward, and there are also several pre-built solver packages available. The transient simulation results presented in this paper were all produced by the dde23 built-in solver of MATLAB, which could directly integrate the governing equation of motion of broaching in its first order form (11). The difficult part was evaluating the simulation results and distinguishing between desirable and undesirable transient dynamic behaviours based on the outputs of this solver. For the lack of a better indicator, contact loss events as defined in (25) were used to separate the solutions into these two categories.

To find such contact loss events the built-in event detection routines of dde23 and MATLAB have been employed. If a zero crossing was detected in (25), the solver was automatically stopped, as continuing the integration further would have led to physically meaningless solutions, as (11) is incapable of modelling the fly-over of the cutting edges. Such solutions were also automatically flagged as undesirable, and if no such event was reached in the timespan initially given to the DDE solver, the solution was marked as acceptable.

Only one major issue remains, the initialisation of the simulations, and the definition of the history function on the $t \in \left[ -\Delta _{\max }, \, 0 \right]$ interval. For the calculations presented in this paper, two different approaches have been implemented. One utilized the periodic orbits found through the collocation method discussed in “Appendix 2”, employing the corresponding Lagrange interpolation scheme, while the other used a constant 0 history function. For these two types of initialisation approaches, different cutting force models had to be defined. In the first case, the operation was started from the “periodic” steady state, where the plateau of the cutting forces has already been reached, and (5) was applicable for evaluating the immersion of the cutting edges from $t=0$. In the second case, the initial build-up of the cutting forces was also included in the time span of the simulation, and consequently for $t<\Lambda _{\textrm{D}}$ (5) was not applicable. Considering that the first tooth that entered the workpiece at $t=0$ was of the first type, rather

$$\begin{aligned} \gamma _{i}(t) = \left\lceil t - \sum _{l=2}^{i}\Delta _l \right\rceil \end{aligned}$$

(32)

had to be employed to evaluate the cutting forces on this initial segment.

It must be noted here, that true transient simulation of the process dynamics would also require the consideration of all non-linear and non-smooth effects arising from the possible fly-over of the cutting edges. At the detected contact loss events the simulation runs could be continued by setting the cutting force to zero, and keeping track of the active mark present on the workpiece surface [31, 54]. Then the cutting force could be reintroduced, once the given cutting edge re-entered the workpiece material, and the positive chip load condition prescribed in (25) is satisfied once again. The creation of such a comprehensive simulation framework was outside the scope of this present study, however, such a simulation algorithm is currently under development.

Using these simulation routines, the stability maps derived for infinite operations through the previously discussed analytic and numeric means could be validated on the time-limited version of the problem. For these numeric tests, the example parameter set shown in Table 1 and its corresponding dimensionless form from Table 2 has been used. Here the slot width w and the cutting speed $v_{\textrm{cut}}$, as well as their dimensionless counterparts $\tilde{w}$ and $\tilde{v}$ are not listed, as they were allowed to vary during the production of stability maps.

Table 1 Example parameter set of an infinite uniform pitch broaching operation

Table 2 Dimensionless parameter set of the example infinite uniform pitch broaching operation from Table 1, considering $n=2$

The formulation of these $\tilde{v}$ - $\tilde{w}$ maps is a great way to visualize how robust a broaching operation is against undesirable chatter vibrations. Unfortunately, these are a lot less straightforward to interpret than e.g. stability maps derived for milling operations, since in most broaching applications, both the geometry of the bore and the speed of cutting $v_{\textrm{cut}}$ are prescribed values that the operators of the machine tools are not allowed to modify. Nevertheless, comparing the prescribed dimensionless slot width $\tilde{w}$ to the maximal safely operable critical $\tilde{w}_{\textrm{crit}}(\tilde{v})$ value, allows the definition of a safety factor. The higher the value of $\frac{\tilde{w}_{\textrm{crit}}}{\tilde{w}}$ is, the more safe the broaching operation is against self excited vibrations. If this value goes below 1, it is highly unlikely, that the machining process will lead to an acceptable surface finish.

From the point of view of broaching tool and broaching machine manufacturers, the critical $\tilde{w}_{\textrm{crit}}(\tilde{v})$ value can also have other important implications. First of all, since the dimensionless slot width is defined as the ratio of the cutting stiffness $K_{\textrm{c}}w$ and the reflected stiffness of the machine $\omega _{\textrm{n}}^2m$, it can indicate how stiff the machine tool assembly must be for safe operation during the expected range of machining tasks. Furthermore, in case of more complicated bore geometries the equivalent slot width w is an accumulated value, which accounts for all active parts of the cutting edge. It can be found by integrating the dot product of the local edge normal vector and the vibration direction along the full arc of the cutting edge. To some extent, this equivalent w value may be tuned by the manufacturer of the tool. For example in the case of fir-tree geometries, the manufacture of different grooves may happen in the same or in separate machining steps.

Figure 3 presents two $\tilde{v}$ - $\tilde{w}$ stability maps. One with uniform pitch in panel (a) and another identical one, considering a two teeth repeating pattern in panel (b). These maps demonstrate that the stability predictions of the D-subdivision and semi-discretization techniques are in relatively good agreement with the simulation results. However, since these techniques are based on the asymptotic stability of periodic orbits, they provide more conservative results compared to the time-limited simulations. There the found transients might simply not have been long enough for harmful large amplitude vibrations to develop.

Fig. 3

Comparison of stability assessment techniques in the case of uniform (a) and variable pitch (b) broaching, considering the parameter set shown in Table 2

To illustrate the evaluation process of the transient simulation results, further details on two example operations each marked by an “x” in panels (a) and (b) are presented in Fig. 4. Here panels (I.a-c) illustrate the transient behaviour of an unstable uniform pitch broaching operation, while panels (II.a-c) show results obtained for a stable, variable pitch, but otherwise identical broaching machining task. Here, panels (I.a) and (II.a) show the periodic solutions found via spectral collocation, while panels (I.b) and (II.b) present transient simulation results started from these periodic orbits. Finally, in panels (I.c) and (II.c) results of transient simulations, which also included the build-up phase of the cutting forces, are presented. Here it is worth noting that chatter vibrations take longer to develop if the simulation is started from a found periodic orbit. This is indicated clearly by the difference of the produced stability maps in Fig. 3, and comparison of panels (I.b) and (II.b) with (I.c) and (II.c) from Fig. 4.

Fig. 4

Comparison of operations marked by “x” in Fig. 3. In panels (I.a-c) the periodic orbit and transient simulation results corresponding to an unstable uniform pitch ($\Delta _{1,2} = 0.5$) operation are shown, while panels (II.a-c) present a stable variable pitch ($\Delta _1 = 0.5882$, $\Delta _2 = 0.4118$) broaching operation. In both cases $\tilde{v}= 0.2$ and $\tilde{w} = 0.07$, while the rest of the operation parameters are taken from Table 2

Figure 3b demonstrates, how changing the tooth distribution might completely reshape the stability map of the operation, and how previously unstable parameter domains might turn stable due to the modification of the axial tooth distribution. The results shown in Fig. 4 also clearly validate the potential of pitch variation in increasing the stability and robustness of even the time-limited version of the problem. On panels (I.b-c) the undesirability of the transients is clear from the increasing amplitude of both the tool displacements x and the cutting forces F. A further indicator for this loss of stability is the peak found close to the natural frequency of the system ($\omega _{\textrm{n}}=1$) in the simulated vibratory spectrum. This is a clear indicator of a Hopf-bifurcation that causes the emergence of chatter vibrations. Furthermore, the simulation run shown in panel (I.c) even had to be terminated prematurely due to a simultaneous zero crossing of the $h_1$ and $h_2$ chip thickness signals, indicating the appearance of a contact loss event. In panels (II.b-c) no such undesirable increasing tendencies can be found. Thus this variable pitch operation can be deemed desirable.

As demonstrated by the stability maps in Fig. 3, the desirability of broaching operations can also be assessed via stability analysis of their infinite versions through the previously presented analytic and numeric techniques. In the uniform pitch case (I) based on (18) the chatter frequency corresponding to $\zeta =0.05$ and $\tilde{v}=0.2$ is $\omega _{\textrm{c}} = 1.032$, from which substituting in $\Lambda _{\textrm{D}} = 1.6$, the stability limit is at $\tilde{w}_{\textrm{crit}}(\tilde{v}) = 0.036$. Since the used dimensionless chip width $\tilde{w}=0.07$ is larger than $\tilde{w}_{\textrm{crit}}(\tilde{v})$ the transient behaviour of the time-limited operation is expected to be undesirable. A similar conclusion can be drawn by employing the semi-discretization method, which with dimension $M=80$ and interpolation order $p=1$, based on equations (28) and (29) along with $\omega _{\textrm{c}} = 1.055$ outputs $\rho (\varvec{\Phi }) = 1.129342$ which is greater than 1. Based on Fig. 4(I.b), even the chatter frequency predictions are in relatively good agreement with the simulation results, as the vibratory peak found here is at $\omega = 1.046$. By using (20) instead of (18) these techniques are also applicable to the variable pitch broaching problem presented in panels (II.a-c), where $\Delta _{1}= 0.5882$ and $\Delta _{2} = 0.4118$. The stability predictions now result $\tilde{w}_{\textrm{crit}}(\tilde{v}) = 0.07152>\tilde{w}$, $\rho (\varvec{\Phi }) = 0.98165<1$ and $\omega _{\textrm{c}}=1.067$, which all suggest a desirable transient behaviour in the time-limited case.

As a result of the nondimensionalisation process discussed in Sect. 2, one unit of dimensionless time is equivalent to the time it takes to cover one tooth period, meaning $t_{\textrm{u}} = \frac{D}{v_{\textrm{cut}}} = \frac{n}{\tilde{v}\omega _\textrm{n}}$. In case of the transient simulation results presented in panels (I.b-c) and (II.b-c) of Fig. 4, considering the dimensionless cutting speed $\tilde{v} = 0.2$, the tooth number $n=2$, and the natural frequency $\omega _{\textrm{n}} = 25$ rad/s taken from Table 1, this time unit is $t_{\textrm{u}} = 0.4$ s. Consequently, on panel (I.b) noticeable chatter takes approximately 8–10, while on panel (I.c) roughly 3-4 s to develop. This rate of growth can be correlated to the magnitude of the Floquet multipliers of the corresponding theoretical periodic orbits, however, it is also clear that the speed at which chatter emerges is heavily influenced by the level of external perturbations. Since actual broaching operations are usually shorter than 10 s, given low enough perturbations, even unstable broaching operations may yield acceptable results. Consequently, it is exceptionally important to validate optimisation results via transient simulations.

The cutting force diagram of a general broaching operation, unlike the ones presented in Fig. 4, apart from the initial build-up phase and the plateau of steady material removal also includes a descending phase, where the end of the broaching tool is exiting the material of the workpiece. Nevertheless, this final phase was not included in the transient simulation algorithms, as with the decrease of the number of teeth in contact, the machining operation becomes less and less likely to lose its stability or suffer a contact loss event. If a given parameter combination is undesirable, its effect will be already noticeable at the plateau phase, and there was consequently no need to model the end of the broaching operation.

Apart from the missing descending phase of the cutting forces, the transient signals shown in panels (I.c) and (II.c) of Fig. 4 closely resemble actual force signals reported in broaching experiments [8, 11]. The fact that the simulated chatter frequency is close to the natural frequency of the machine tool assembly is also in agreement with the findings reported in [4]. There the emergence of chatter vibrations was associated to impulse-like excitations induced by repeating tool exit and entry events. However, as our findings suggest, the regenerative effect, and self excited vibrations might have also played a role in the generation of the reported chatter marks.

In the next section the above described transient simulations will be employed to formulate acceptability maps, which will be able to validate the applicability of the numeric and analytic optimisation techniques on real time-limited broaching operations. In these maps, similarly to the ones presented in Fig. 3, the quality of a given parameter set will be assessed based on the ratio of the prescribed simulation timespan $t_{\mathrm {pre.}}$ (e.g. the length of 20 periods) and the time it took to reach the first contact loss event $t_{\textrm{stop}}$. If no such event is reached the transient behaviour is automatically deemed desirable, otherwise the lower this value, the better the given transient solution.

5 Optimisation of two teeth repeating patterns

The discussed analytical and numerical optimisation schemes from sections 2 and 3 are all straightforward to generalize to repeating tooth patterns of arbitrary length n. In the case of the analytical framework, (21) will always allow the selection of the corresponding optimal linearly increasing tooth distance set. Considering the numeric approach, since the semi-discretization and spectral collocation methods detailed in this paper can both handle multiple different point delays, any number of tooth distances or system parameters may be optimised simultaneously if the necessary parameter Jacobians are provided. In this paper, however, only the two-teeth repeating pattern optimisation problem will be investigated in detail. This is on one hand for the sake of simplicity, to allow simple and effective illustration of the optimisation results achievable by the proposed methods. On the other hand, it is because tool manufacturers are unlikely to adapt pitch-variation types with $n>2$, due to their generally conservative approach to tool design, as well as the manufacturing difficulties that the production of such geometries would entail. Furthermore, it has also been shown that in the case of variable-pitch milling tools, increasing the length of the repeating patterns above two only yields marginal improvements in the robustness of the operation [57].

The problem of an infinite broaching operation with a tool containing two-teeth repeating patterns can be fully characterised by only six dimensionless parameters: the chip thickness $\tilde{w}$, the cutting speed $\tilde{v}$, the workpiece length $\Lambda _{\textrm{D}}$, the damping ratio $\zeta$, and finally the tooth distances $\Delta _{1}$ and $\Delta _{2}$. However, these last two parameters are not independent from one another, since $\sum _{i=1}^{n}\Delta _{i} = 1$ must always hold. Consequently, a new dimensionless parameter, the pitch ratio $\alpha = \frac{\Delta _{2}}{\Delta _{1}} \in \left[ 0,\, 1 \right]$, was introduced to replace the tooth distances as

$$\begin{aligned} \Delta _{1} = \frac{1}{1+\alpha }, \,\, \Delta _{2} = \frac{\alpha }{1+\alpha }. \end{aligned}$$

(33)

Here $\alpha = 1$ corresponds to the case of uniform pitch broaching, and the lower its value goes, the higher the disparity between the time delays and prescribed chip thicknesses of the two tooth types becomes.

Since the main concern of this paper was the optimisation of the axial tooth distribution of broaching tools, only the effect of this $\alpha$ parameter was investigated in detail. It was done over a wide range of possible $\tilde{w}$ and $\tilde{v}$ combinations. In the presented calculations and results the $\Lambda _{\textrm{D}}$ and $\zeta$ parameters were always kept constant, as these could be considered as given fixed parameters of the machining task, which cannot be modified by the manufacturer or the operator of the broaching tools.

To evaluate the acceptability of individual $\tilde{w}$, $\tilde{v}$ and $\alpha$ parameter combinations, the algorithms listed in Table 3 have been used. The first and computationally most efficient one was to derive the stability lobes of the operation using the D-subdivision method and compare the actual chip width to the critical value shown in (). A more robust but computationally more demanding way was to evaluate the stability of the periodic orbits through the monodromy matrix (27) found via the semi-discretization method. The analysis of the periodic orbits may be aided by acquiring discretized periodic solutions via spectral collocation. This method was used to check the contact loss condition (25), and was also combined with the semi-discretization approach to create a joined acceptability condition. Finally, forward-time transient simulations have also been employed to separate desirable parameter combinations from undesirable ones. As discussed in detail in Sect. 4, two versions of this method have been implemented. A more conservative one, which included the build-up phase of the cutting forces as well, and a more inclusive one, which initialized the simulation runs using the previously found discrete periodic orbits. Here in both cases $t_{\mathrm {pre.}}$ was an arbitrarily prescribed length of time, while $t_{\textrm{stop}}$ was the final time of the either concluded or prematurely stopped simulation runs.

Table 3 Algorithms used for the evaluation of desirability for individual parameter sets of the broaching operation

Using all of these methods combined for the creation of stability and stabilasability maps was beneficial for the illustration of the proposed optimisation process. This way each discussed tuning approach could be validated with its own and with other differently motivated acceptability indicators. For example, the analytic approach relies solely on the D-subdivision method, while the more elaborate direct numeric optimisation scheme employs both the semi-discretization and spectral collocation techniques. Naturally, these are both only valid for the infinite version of the problem and had to be validated via transient simulations, to show their effectiveness in the time-limited case. The two simulation approaches were motivated by the differences between the time-limited and infinite models of the operation. Starting the simulations from a periodic orbit resembles the infinite case, while including the build-up phase better captures the real transient nature of the process.

5.1 Analytic optimisation

First, the analytic optimisation scheme detailed at the end of Sect. 2 was applied to the two-teeth repeating pattern broaching problem. This first required finding the chatter frequency of uniform pitch broaching corresponding to the current $\tilde{v}$ - $\tilde{w}$ combination by executing a numeric sweep of (18). After this, the analytic optimal pitch ratio could be found through (21) as

$$\begin{aligned} \alpha = \frac{1-\delta }{1+\delta }, \,\, \textrm{where} \,\, \delta = \tilde{v} \frac{\pi +2k\pi }{2\lambda _{\textrm{c}}}. \end{aligned}$$

(34)

Based on numeric stability analysis via the semi-discretization method and running transient simulations, even this simple analytic optimisation technique yielded significant improvements in the stability of the broaching operations. This robustness increasing effect of the pitch variation could already be demonstrated by comparing the stability maps shown in Fig. 3a, b. However, one can go even further by formulating stabilisability maps by selecting an optimal pitch ratio $\alpha _{\textrm{opt}}$ for every dimensionless cutting speed $\tilde{v}$, based on (18), (21), and (34).

The effect of this adaptive pitch ratio selection on the two teeth repeating pattern broaching problem is demonstrated by the analytic stabilisability map shown in Fig. 5. Here the dotted black line is the analytic uniform pitch stability boundary. The solid white line, which corresponds to points where the spectral radius (28) of the monodromy matrix (27) of the periodic orbits is exactly 1, is the stabilisability limit found via the semi-discretization method. The dashed white line is the contact loss boundary found using spectral collocation, while the solid red and grey lines are the acceptability maps acquired via transient simulations. Comparing the found acceptability limits to the original stability lobes of infinite uniform pitch broaching, the increase in robustness becomes clear.

Fig. 5

The effect of analytic pitch ratio optimization on the two teeth repeating pattern broaching problem ($\zeta = 0.05$, $\Lambda _\textrm{D} = 1.6$). Panel (I) presents a periodic orbit and its Floquet-multipliers corresponding to a found optimal parameter set. It is stable, but infeasible due to a contact loss event. Panel (II) illustrates a found optimum point, which is feasible but unstable. On the legend, the notation “$\infty$ tool” refers to theoretical infinitely long operations, while “$<\infty$ tool” marks the time-limited version of the problem

It is important to note that this analytic tuning strategy does not necessarily result physically feasible stable periodic solutions. Within the orbits, the contact loss condition (25) might be violated, especially in the case of low $\alpha _{\textrm{opt}}$ values. Such a problematic periodic orbit is presented in Fig. 5(I). Here, from the chip thickness signal of the type two teeth $h_2$, it is obvious that on a certain interval, the cutting force produced by the second tooth types $F_2(t) = \gamma _2(t) \tilde{w}h_2(t)$ will take on physically meaningless negative values. Based on just the Floquet-multipliers, this periodic orbit would be stable, however, due to presence of cutting edge fly-over this solution is physically infeasible. The orbit marked with (II) has no such fly-over segments, but based on its spectra, it is clearly unstable. Outside the contact loss boundaries, marked with a dashed white line in Fig. 5, at some point within the periodic orbits, the domain of the linearised equation motion (15) is left. In these regions, the presented analytic techniques are not applicable and a more sophisticated optimization scheme must be employed, which also penalises contact loss events in its goal function, according to (30).

Finally, to show that the analytic tuning strategy is also beneficially effecting the transient behaviours of the real time-limited broaching problem, the stabilisability map has been validated via transient simulations. The desirable parameter combinations ($\tilde{v}$, $\tilde{w}$, $\alpha _{\textrm{opt}}$), where no contact loss event was encountered during the timespan necessary for 20 tooth pattern periods to pass through, are found below the solid red and grey lines shown in Fig. 5. The red line, which marks the simulation results, where periodic orbits were used as initial history functions, is in good agreement with the combined stability and contact loss boundary identified based on the periodic orbits of the infinite version of the problem. The grey line, which was acquired via transient simulations that included the build-up phase of the cutting forces as well, marks a slightly more conservative stabilisability boundary, but otherwise follows a fairly similar topology. This reduction of the stabilisable region is due to contact loss events encountered during the build-up phase of the cutting forces or a faster emergence of chatter due to larger initial perturbations from the steady state periodic solution.

5.2 Direct numeric optimisation

To further improve upon the analytic optimisation results, and to include tool machinability ($\alpha >\alpha _{\min }$) and contact loss ($F_{i,\min }>0$) constraints, the numeric optimisation techniques detailed in Sect. 3 have also been employed on the two teeth repeating pattern broaching problem. This first required the evaluation of a few derivatives with respect to the newly introduced pitch ratio. The detailed derivation of these is presented in “Appendix 3”.

With the help of these derivatives, the gradient of the goal function formulated for maximizing the robustness of the broaching operation (31) can be evaluated. To finalize the input of the HANSO algorithm a further condition has also been added to this function, which sets its output to the user-defined penalty value $\sigma$ if the current $\alpha$ parameter was outside its physically feasible range $\left[ \alpha _{\min }, \, 1 \right]$. If there was a need for applying this penalty, the gradient with respect to $\alpha$ was simply set to $\pm 1$ depending on which boundary of the allowed range was crossed.

Using this finalized goal function in the HANSO algorithm, through the semi-discretization method and transient simulations, new and improved stabilisability maps have been generated for the two teeth repeating pattern broaching problem. These are presented in Fig. 6. Here the meaning of the colors is mostly the same as in Fig. 5. The dotted black line is the analytic uniform pitch stability boundary, the dashed black line is the acceptability map with analytic optimal tuning, the solid and dashed white lines are the found stabilisability and contact loss boundaries, and finally the solid black and grey lines are the acceptability maps acquired via transient simulations. The solid red line is there to demonstrate how the analytic stabilisability boundary may be improved through direct numeric optimisation.

First, to demonstrate the robustness increasing capabilities of direct numeric tuning, a low $\alpha _{\min }=0.2$ was selected to find the stabilisability maps presented in panels (a) and (b) of Fig. 6. Examining the solid white line in panel (a) corresponding to the stability boundary found via semi-discretization, it is clear that numeric optimisation can significantly improve upon the previously examined analytic tuning process. However, as seen here from the contact loss boundaries (dashed white line) and transient simulation results (solid black and grey lines) most of the found periodic orbits are infeasible due to contact loss events. Nevertheless, if the violation of the contact loss condition is penalised during the numeric optimisation, as it was done in the case of panel (b), this is no longer an issue. This time the stability and contact loss boundaries are almost the same, and the acceptability map produced via transient simulations is uniformly better than the one achieved via analytic tuning.

Fig. 6

The effect of direct numeric pitch ratio optimization on the two teeth repeating pattern broaching problem ($\zeta = 0.05$, $\Lambda _\textrm{D} = 1.6$). In a, b $\alpha _{\min } = 0.2$, while in c, d $\alpha _{\min } = 0.7$. a, c Present stabilisability maps, where the goal function did not include a penalty for contact loss events, while b, d present fully constrained optimisation results. On the legend, the notation “$\infty$ tool” refers to theoretical infinitely long operations, while “$<\infty$ tool” marks the time-limited version of the problem

Variable pitch broaching tools with highly different tooth distances are not only hard to manufacture but also create large amplitude oscillations in the arising cutting forces. Consequently, to achieve more practical results it is worthwhile to limit the pitch ratio of the tools to relatively high values. To show that the numeric optimisation scheme is still capable of improving the robustness of broaching operations, despite the presence of this manufacturability constraint, the stabilisability maps presented in panels (c) and (d) of Fig. 6 had been formulated considering $\alpha _{\min }=0.7$. On these maps, it is clearly visible that apart from high cutting speed regions, where the analytic tuning would result in $\alpha _{\textrm{opt}}<0.5$, optimisation with this more conservative constraint works just as well, if not better. Consequently, it has been demonstrated that even with small modifications of the tooth distances, the robustness of broaching processes can be significantly improved, if the right tuning is applied considering the operational cutting speed range of the tools.

Here it must be mentioned that the presented direct numeric optimisation scheme has a few key limitations. Minimizing such a highly non-smooth goal function as the spectral radius of a monodromy matrix is highly complicated and uncertain, especially if the contact loss penalty is also taken into account. Therefore, it is not guaranteed at all that the optimisation algorithm stops at a global minimum, thus in most cases, only local minima are found. This shortcoming can be partially compensated by initialising the optimisation algorithm with multiple starting values and taking the best found local minima, however, even this does not guarantee that a lower, not yet reached local minimum does not exist somewhere else in the allowed parameter domain. This explains, why the more conservative optimisation runs, with $\alpha _{\min }=0.7$ instead of $\alpha _{\min }=0.2$, shown in Fig. 6c, d, produced more favourable results in certain cutting speed ranges. To keep computational costs at a reasonable level, in both cases five equally spaced starting points were selected from the allowed $\left[ \alpha _{\min },\, 1 \right]$ range, and at some particular $\tilde{v}$-$\tilde{w}$ combinations the more conservatively selected starting points proved to be more advantageous for minimizing the optimisation goal function. Naturally, if in both cases, the same initial $\alpha$ values had been used, the stabilisability maps with $\alpha _{\min }=0.2$ would be uniformly better.

5.3 Validation of direct numeric tuning through transient simulations

Concerning the acceptability maps acquired via transient simulations, the solid black lines in Fig. 7, which were initialised with the found periodic orbits, are in good agreement with the asymptotic stability predictions and the contact loss boundaries. The other set of acceptability maps marked with grey lines, which considered the build-up phase of the cutting forces as well, presents a similar but more conservative picture. Within the white lines, which correspond to the asymptotic stability boundary, this reduction of the safe parameter regions can be attributed to contact loss events encountered during the initial build-up phase. If the operation can stabilize itself later on, in industrial practice such events are of relatively low significance, as they will not alter the final surface of the workpiece. Thus, here the black lines give a more accurate picture on the desirability of the transient solutions. On the outside of this same asymptotic stability boundary, this is no longer the case. Here, where the vibrations of the system are growing exponentially, the safe regions indicated by the grey lines are much more reliable, as the larger perturbations encountered using this second simulation type represent the real world cutting conditions more accurately.

To better understand the capabilities of the presented direct numeric optimisation technique and the results shown in Fig. 6, it is worth looking deeper into the individual periodic orbits and transient simulation results whose stability properties are presented on these stabilisability maps. Figure 7 presents a set of potential optimisation steps, which might be taken during the investigation of a high speed broaching operation with dimensionless cutting speed $\tilde{v} = 0.3$ and slot width $\tilde{w} = 0.21$, marked with an “x” in panels (a–d) of Fig. 6.

Fig. 7

Stability properties of two teeth repeating pattern broaching operations with $\Lambda _{\textrm{D}} = 1.6$, $\zeta =0.05$, $\tilde{v}=0.3$, and $\tilde{w} = 0.21$ considering different pitch ratios. Panels on the left present the engagement functions of the cutting edges $\gamma _i(t)$, the cutting forces $F_i$, as well as the displacement x and velocity $\dot{x}$ signals of the periodic orbits. In the middle column, the force and displacement signals of corresponding transient simulations are shown with the spectra of the simulated vibrations. Finally, on the right, the Floquet-multipliers of the periodic orbits are plotted to illustrate their stability

Panel (a) of Fig. 7 presents the initial highly unstable uniform pitch ($\alpha =1$) case to be improved upon by modifying the pitch ratio of the broaching tool. Here, taking a closer look at the engagement functions of the cutting edges $\gamma _i(t)$ reveals that apart from $T = 1$, the operation is also periodic in $T=0.5$, and the two teeth types follow the exact same paths. This is not surprising at all as the uniform pitch tool could be characterised by a one teeth repeating pattern as well, with $\Delta _1=1$ and $n=1$. Furthermore, since $\alpha = 1$ and $n=2$ means that $\Delta _1 = \Delta _2 = 0.5$ the period of the oscillations will be equal to the single time delay present in the system. This leads to a periodic orbit, where even though the tool oscillates, the cutting forces will remain constant between tool exit and entry events as $x(t)-x(t-\Delta _i) = 0$ is guaranteed by the periodicity of $\gamma _{i}(t)$. Despite this convenient characteristic of the steady state cutting force, it is clear from the Floquet-multpiliers of the periodic orbit and the transient simulation results, that this $\tilde{v}$ - $\tilde{w}$ parameter combination is not safely operable without employing some form of pitch variation.

Figure 7 panel (b) presents the pitch ratio and the corresponding periodic orbit at the point “x” in Fig. 6a, which was found via numeric optimization of Floquet-multipliers, completely disregarding contact loss events. Compared to the rest of the panels, this periodic orbit has the lowest spectral radius and therefore should be the most robust against chatter vibrations. However, it is clear from its steady state chip thickness and cutting force distributions that a fly-over segment is present in the paths of the type 2 teeth, where $F_2$ also goes below zero. Consequently, as illustrated by the transient simulation results, operating this tool will quickly lead to contact loss events, which will result in an undesirable cutting process.

If contact loss events are penalised during the numeric optimisation process, as in the case of Fig. 6b, a slightly less robust but physically feasible periodic orbit can be found, which is presented in Fig. 7c. This orbit has no fly-over segments, and as demonstrated by the simulation results, using this optimised tool enables chatter-free cutting. It is worth noting that the pitch ratio $\alpha =0.42$ found in this manner is close to the analytic optimal value $\alpha _{\textrm{opt}}(\tilde{v} = 0.2)$ = 0.4667, using which would also lead to a desirable stable cutting operation.

The only remaining issues are the manufacturability and design constraints of the proposed broaching tools. Even though they can theoretically solve the machining task, the found optimal tools have highly inhomogeneous tooth distances and chip thicknesses, and the actual manufacture of such tools might become problematic. Furthermore, creating enough space for the chip formulated during cutting might also cause issues on such low pitch ratio values. However, if a pith ratio limit e.g. $\alpha _{\min } = 0.7$ is also taken into account during the numeric optimisation process, as in the case of Fig. 6c, d, no stable periodic solution can be found. As demonstrated by Fig. 7d the most robust orbit that fulfils the design constraints is right on the parameter boundary and is still highly unstable.

Overall, it has been demonstrated by the simulated acceptability maps, that replacing conventional broaching tools with variable pitch ones, can be a valid solution for solving chatter related problems, even if only the simplest two-teeth repeating patterns are considered. Employing more general, more complicated, tooth distributions, such as longer repeating or nonperiodic patterns opens up even more optimisation possibilities, and can help further improve the robustness of the cutting process. Naturally one must be wary of the technique’s technical limitations, but based on the analytic and numeric optimisation results presented in this paper, the variation of broaching tool tooth distances shows a great deal of promise.

6 Conclusions

The potential positive effects of axial tooth distribution optimization have been demonstrated on a simplified one DoF mechanical model of broaching. Formulating a theoretical model, where an infinitely long tool consisting of repeating tooth patterns is used, asymptotic stability assessment techniques became available for the otherwise time-limited problem of broaching.

• The ZOA and D-subdivision methods have been employed to find approximate stability lobes of the operation in a fast and computationally effective manner.

• The mechanical model of theoretically infinite broaching was shown to be equivalent to variable pitch milling models available in the literature. This made it possible to adapt tuning methods developed for the pitch modulation of milling cutters to the optimization of broaching tool axial tooth distributions.

• Numeric, linear stability analysis of the periodic solutions in this infinite machining operation, through the semi-discretization method, allowed a more robust assessment of stability, considering the true time dependency of cutting edge engagement.

• Direct numeric solution of the multi-point boundary value problem corresponding to these periodic orbits, through spectral collocation, enabled the identification of contact loss events, and cutting edge fly-over.

Considering the infinite broaching problem, semi-analytic and direct numeric techniques have been developed for the optimisation of repeating tooth patterns. To demonstrate their effectiveness, the proposed algorithms were employed on two teeth repeating patterns. Generalisation of these methods to more complicated patterns is a straightforward task once the optimisation parameters and corresponding parameter Jacobians are provided.

• Analytic tuning formulae developed for milling cutters proved to be remarkably effective in increasing robustness against chatter vibrations. However, at times, the found tooth distances lead to physically unfeasible periodic orbits containing fly-over segments.

• The spectral collocation and semi-discretization methods were successfully adapted to the gradient descent based HANSO optimisation framework. This required the derivation of the corresponding parameter gradients, which is a novel contribution of this paper.

• Through direct numeric optimisation of the Floquet-multipliers it was possible to improve upon the semi-analytic optimization results. Formulating a constrained optimisation problem also made it possible to avoid unfeasible periodic solutions with fly-over segments.

• Both analytic and numeric optimisation results produced a significant increase in the critical slot width, below which the operation is universally stabiliseable. This shows that the approach works well on low cutting speeds charachteristic of some broaching operations as well.

Due to the exceptionally high costs associated with trying these designs out in an industrial experimental setting, numeric validation of these found optimal geometries is essential. To do so a simple linear transient simulation framework was built.

• As a form of numerical experiments, transient simulations were used to validate the semi-analytic and numeric asymptotic stability predictions on the time-limited version of the problem.

• The simulated transient behaviours, demonstrated that the employed asymptotic techniques produce favourable results even for the more realistic, time-limited version of the problem.

• Based on the validated stabilisability maps, pitch variation was shown to be an effective approach for increasing the robustness of the cutting process against harmful self-excited chatter vibrations.

In summary, through optimal selection of the tooth distances, the material removal rate, workpiece surface quality, and lifespan of the tools can all be potentially improved. Naturally, the presented analytical and numerical results still lack empirical validation. Nevertheless, based on their promising potential, further work and funding should be devoted to the production of variable pitch broaching tools, as well as their experimental testing.

Appendices

Appendix 1: Parameter gradients for the semi-discretization method

One of the major findings of this paper is the derivation of parameter gradients for the semi-discretization and spectral collocation numerical techniques. These gradients are indispensable to allow the integration of these methods in gradient descent based optimization routines.

The primary numerical approach for the linear stability analysis of the equation of motion of variable pitch broaching (22) was the semi-discretization method. As demonstrated in (27), this allows the discrete formulation of the monodromy matrix of periodic solutions as a product of so-called step matrices $\textbf{S}_j$. Following the derivations found in chapter 3 of [41], these can be found as

$$\begin{aligned} & {S}_j = \left[\begin{array}{ccccccccc} {P}_j &{} {0} &{} \dots &{} {0} &{} {0} \\ {I} &{} {0} &{} \dots &{} {0} &{} {0} \\ {0} &{} {I} &{} \dots &{} {0} &{} {0} \\ \vdots &{} &{}\ddots &{} &{} \vdots \\ {0} &{} {0} &{} \dots &{} {I} &{} {0} \end{array}\right] \\ {}&\quad + \sum _{i=1}^{n}\left[\begin{array}{ccccccccccccccc} {0} &{} {0} &{} \dots &{} {0} &{} {R}_{j,i,0} &{} \dots &{} {R}_{j,i,p}&{} {0} &{} \dots &{} {0} \\ {0} &{} {0} &{} \dots &{} {0} &{} {0} &{} \dots &{} {0}&{} {0} &{} \dots &{} {0} \\ {0} &{} {0} &{} \dots &{} {0} &{} {0} &{} \dots &{} {0}&{} {0} &{} \dots &{} {0} \\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots &{} &{} \vdots &{} \vdots &{} &{} \vdots \\ {0} &{} {0} &{} \dots &{} {0} &{} {0} &{} \dots &{} {0}&{} {0} &{} \dots &{} {0} \end{array}\right], \end{aligned}$$

(35)

where $\textbf{I}$ and $\textbf{0}$ are $2\times 2$ identity and zero matrices, and using the notations $\textbf{A}_j = \textbf{A}(j\Delta t)$ and $\textbf{B}_{j,i} = \textbf{B}_i(j\Delta t)$,

$$\begin{aligned} \begin{aligned}&\textbf{P}_j = \textrm{e}^{\Delta t \textbf{A}_j}, \,\, \textbf{R}_{j,i,k} = l_{i,k}\textbf{Q}_{j,i}, \\ {}&\textbf{Q}_{j,i} = (\textbf{P}_j-\textbf{I})\textbf{A}_j^{-1}\textbf{B}_{j,i}. \end{aligned} \end{aligned}$$

(36)

Here, the dimension of the system is 2N, where $N = \lceil \max \{\Delta _i\}/\Delta t \rceil + \lceil p/2 \rceil$ is the number of discretization points on the solution tail, and p is the order of the Lagrange interpolation used for evaluating the matrices $\textbf{R}_{j,i,k}$. In (36) $l_{i,k}$ are Lagrange interpolation coefficients and k goes from 0 to p. Finally, when formulating the step-matrix, the positions of $\textbf{R}_{j,i,k}$ in (35) can be found through the index

$$\begin{aligned} N_{j,i,k} = \left\lfloor \frac{\Delta _i}{\Delta t} \right\rfloor + \left\{ \begin{matrix} -p/2+k &{} | &{} \textrm{mod}(p,2) = 0\\ -(p-1)/2+k &{} | &{} \textrm{mod}(p,2) = 1 \end{matrix}\right. , \end{aligned}$$

(37)

meaning the first column of $\textbf{R}_{j,i,k}$ will be placed in the $2N_{j,i,k}^{\textrm{th}}$ column of $\textbf{S}_j$.

The monodromy matrix found by substituting (35) in (27) allows the derivation of the critical Floquet multiplier $\mu _{\textrm{max}}$ and the assessment of periodic orbit stability. An optimal highest robustness against chatter vibrations can be achieved through the direct numeric minimisation of $\mu _{\textrm{max}}$ in a given system parameter $\beta$. This however requires the parameter gradient $\frac{\partial (\rho (\varvec{\Phi }))}{\partial \beta }$.

In case of the investigated broaching model, after applying the smoothing introduced in (24), both $\textbf{A}_j$ and $\frac{\partial \textbf{A}_j}{\partial \beta }$, as well as $\textbf{B}_{j,i}$, $\frac{\partial \textbf{B}_{j,i}}{\partial \beta }$ are available analytically. This means (28) is differentiable with respect to the arbitrary system parameter $\beta$. The first step for obtaining this gradient is the differentiation of this equation, which leads to

$$\begin{aligned} \frac{\partial (\rho (\varvec{\Phi }))}{\partial \beta } = \frac{\bar{\mu }_{\textrm{max}}}{|\mu _{\textrm{max}}|} \frac{1}{{\textbf{w}_{\textrm{max}}^{\textrm{H}}\textbf{v}_{\textrm{max}}}} \textbf{w}_{\textrm{max}}^{\textrm{H}}\frac{\partial \varvec{\Phi }}{\partial \beta } \textbf{v}_{\textrm{max}}, \end{aligned}$$

(38)

where $\textbf{v}_{\textrm{max}}$ and $\textbf{w}_{\textrm{max}}$ are the left and right eigenvectors corresponding to $\mu _{\textrm{max}}$. Here the only unknown is the derivative of the monodromy matrix with respect to $\beta$, which should be evaluated through (27) using the product rule

$$\begin{aligned} \frac{\partial \varvec{\Phi }}{\partial \beta } = \sum _{j=0}^{M-1} \left( \prod _{l=M-1}^{j+1} \textbf{S}_l \right) \frac{\partial \textbf{S}_j}{\partial \beta }\left( \prod _{l=j-1}^{0} \textbf{S}_l \right) . \end{aligned}$$

(39)

Finally the derivative of the step-matrix should be evaluated term by term by differentiating to (35) and (36). Naturally, this derivative will be zero for all elements of $\textbf{S}_j$ apart from $\textbf{P}_j$ and $\textbf{R}_{j,i,k}$. Finding the derivative of the matrix exponential term $\textbf{P}_j$ with respect to $\beta$ is far from straightforward and can only be effectively executed through the diagonalization of $\textbf{A}_j$ following the formulas found in [58]. Consequently, it was evaluated as

$$\begin{aligned} \frac{\partial \textbf{P}_j}{\partial \beta } = \textbf{V}_{j} \textbf{G}_{j}\textbf{V}_{j}^{-1} \end{aligned}$$

(40)

where $\textbf{V}_{j}$ contains the right eigenvectors of $\textbf{A}_j$, and $\textbf{G}_{j}$ is calculated with the help of $\textbf{H}_{j} = \textbf{V}_{j}^{-1} \frac{\partial \textbf{A}_j}{\partial \beta } \textbf{V}_{j}$ element by element as

$$\begin{aligned} g_{j}^{(k,l)} = \left\{ \begin{array}{ccc} \frac{\textrm{e}^{\lambda _k \Delta t} - \textrm{e}^{\lambda _l \Delta t}}{\lambda _k - \lambda _l} h_{j}^{(k,l)}&{} | &{} k \ne l\\ \Delta t \textrm{e}^{\lambda _k \Delta t} h_{j}^{(k,l)} &{} | &{} k = l \end{array}\right. , \end{aligned}$$

(41)

where $\lambda _k$ are the eigenvalues of $\textbf{A}_j$, and $g_{j}^{(k,l)}$ and $h_{j}^{(k,l)}$ refer to elements found in the $k^{\textrm{th}}$ row of the $l^{\textrm{th}}$ column of the $\textbf{G}_{j}$ and $\textbf{H}_{j}$ matrices respectively.

Similarly to $\frac{\partial \textbf{P}_j}{\partial \beta }$ the derivative of $\textbf{R}_{j,i,k}$ with respect to $\beta$ can be found by differentiating (36) leading to the form

$$\begin{aligned} \frac{\partial \textbf{R}_{j,i,k}}{\partial \beta } = l_{i,k} \frac{\partial \textbf{Q}_{j,i}}{\partial \beta } + \frac{\partial l_{i,k}}{\partial \beta } \textbf{Q}_{j,i}, \end{aligned}$$

(42)

where based on simple matrix calculus identities

$$\begin{aligned} \begin{aligned}&\frac{\partial \textbf{Q}_{j,i}}{\partial \beta } = \frac{\partial \textbf{P}_j}{\partial \beta }\textbf{A}_j^{-1}\textbf{B}_{j,i} \\ &\quad +(\textbf{P}_j-\textbf{I})\left( -\textbf{A}_j^{-1}\frac{\partial \textbf{A}_j}{\partial \beta }\textbf{A}_j^{-1}\textbf{B}_{j,i} + \textbf{A}_j^{-1}\frac{\partial \textbf{B}_{j,i}}{\partial \beta }\right) , \end{aligned} \end{aligned}$$

(43)

and by employing the chain rule

$$\begin{aligned} \frac{\partial l_{i,k}}{\partial \beta } = - \frac{\partial l_{i,k}}{\partial t}\frac{\partial \Delta _{i}}{\partial \beta }. \end{aligned}$$

(44)

Here the time derivatives of the Lagrange interpolation coefficients are also available analytically. It is important to note that for those $\beta$ parameters where $\frac{\partial \Delta _{i}}{\partial \beta } \ne 0$, meaning the parameter has a direct influence on the time delay and thus the Lagrange interpolation coefficients $l_{i,k}$, it is necessary to use at least first-order interpolation ($p\ge 1$) to properly capture this parameters influence on the stability of the periodic orbits.

Appendix 2: Parameter gradients for the spectral collocation method

During the direct numeric optimization of variable pitch broaching tools, periodic orbits which contained contact loss segments were identified and penalised with the help of a spectral collocation framework. Here a discrete solution of the corresponding multi-point boundary value has been obtained on a piecewise Legrende-Gauss-Lobatto(LGL) mesh [56].

Let $\textbf{u} = \left[ \dots \textbf{u}_j^\intercal \dots \right] ^\intercal , \, j=1,\dots N$ denote this discrete version of a periodic orbit, where $\textbf{u}_j = \left[ \textbf{x}_{j,1}^\intercal , \, \textbf{x}_{j,2}^\intercal \right] ^\intercal$ contains the state variables of the system at the LGL mesh points of the $j^\textrm{th}$ segment $t_{j,k}, \, k=1,\dots M$ as column vectors $\textbf{x}_{j,l} = \left[ \dots x_l(t_{j,k}) \dots \right] ^\intercal , \, l=1,2$. Here N is the number of smooth segments and M is the order of the used polynomial base, which was always the same for all segments. Unfortunately, there is no explicit formula for finding the LGL mesh points $t_{j,k}$, however, by shifting and rescaling each segment to the $\left[ 0, \, 1 \right]$ interval via

$$\begin{aligned} \tilde{t}_{k} = \frac{1}{T_j}\left( t_{j,k}-\sum _{l=1}^{j-1}T_l\right) , \end{aligned}$$

(45)

a uniform $\tilde{t}_k \in \left[ 0, \, 1 \right] ,\, k=1,\dots M$ mesh can be used for all segments, which only has to be found numerically once. Here $T_j = t_{j,M}-t_{j,1}$ refers to the length of the $j^\textrm{th}$ smooth segment. Rescaling the mesh according to (45) also allows the use of a uniform spectral differentiation matrix $\tilde{\textbf{D}}$ defined on $\tilde{t}_k$, which is available analytically as shown in [56]. From $\tilde{\textbf{D}}$ the individual differentiation matrices for each segment corresponding to the original $t_{j,k}$ mesh can be found as $\textbf{D}_j = \frac{1}{T_j}\tilde{\textbf{D}}$.

Considering the discrete state vector of a periodic orbit $\textbf{u}$, a discretized multi-point boundary value problem (MP-BVP) can be formulated for finding approximate periodic solutions to the governing equation of motion (11). This leads to the system of algebraic equations

$$\begin{aligned} \textbf{F}(\textbf{u}) = \textbf{J}_{\textrm{u}}\textbf{u} - \varvec{\phi }, \end{aligned}$$

(46)

with

$$\begin{aligned} \textbf{J}_{\textrm{u}} = \sum _{j=1}^{N}\textbf{E}_{j,N}\otimes \left( \textbf{I}_2\otimes \hat{\textbf{D}}_{j}\right) + \hat{\textbf{I}}_{N}\otimes \left( \textbf{I}_2\otimes \textbf{E}_{(M,1),M}\right) , \end{aligned}$$

(47)

where $\textbf{E}_{j,N}$ denotes an $N \times N$ matrix that is all zeros apart from the $j^{\textrm{th}}$ diagonal element which is set to 1, $\textbf{E}_{(M,1),M}$ is a similar almost zero matrix with the single non-zero element placed in its $M^\textrm{th}$ row and $1^{\textrm{st}}$ column, $\textbf{I}_2$ is a $2 \times 2$ identity matrix, and $\otimes$ refers to the Kronecker product. The modification of the spectral differentiation matrix from $\textbf{D}_j$ to $\hat{\textbf{D}}_j$ by replacing its last row with zeros is necessary to make room for the interface conditions between the solution segments, which are meant to enforce the continuity and periodicity within the orbits.

The governing equation of motion (11) is included in the MP-BVP (47) through the vector $\varvec{\phi } = \left[ \ldots \varvec{\phi }_j^{\intercal} \ldots \right]^{\intercal} , \, j=1,\ldots N$ which contains the evaluations of its right hand side at the LGL mesh points in the same column vector form as $\textbf{u}$, meaning $\varvec{\phi }_j = \left[ \textbf{f}_{j,1}^\intercal , \, \textbf{f}_{j,2}^\intercal \right] ^\intercal$ and $\textbf{f}_{j,l} = \left[ f_{j,1,l}, \dots , f_{j,M-1,l}, \, x_l(t_{j,M}) \right] ^\intercal , \, l=1,2$. Here $f_{j,k,l} = \dot{x}_{l}(t_{j,k})$, and the last element of $\textbf{f}_{j,l}$ is replaced by $x_l(t_{j,M})$ to ensure that the following continuity and periodicity conditions

$$\begin{aligned} x_l(t_{j,M}) = \left\{ \begin{matrix} x_l(t_{j+1,1})&{} | &{} j<N\\ x_l(t_{1,1})&{} | &{} j=N \end{matrix}\right. \end{aligned}$$

(48)

between the solution segments are met. Finally, the other side of these interface conditions is introduced to (47) in the form of the $\hat{\textbf{I}}_{N}\otimes \left( \textbf{I}_2\otimes \textbf{E}_{(M,1),M}\right) \textbf{u}$ product, where

$$\begin{aligned} \hat{\textbf{I}}_N = \begin{bmatrix} 0 &{} 1 &{} 0 &{} \dots &{} 0&{} \\ 0 &{} 0 &{} 1 &{} \dots &{} 0&{} \\ \vdots &{} \vdots &{} &{} \ddots &{} \vdots &{} \\ 0 &{} 0 &{} 0 &{} \dots &{} 1&{} \\ 1 &{} 0 &{} 0 &{} \dots &{} 0&{} \end{bmatrix} \in \mathbb {R}^{N\times N}. \end{aligned}$$

(49)

In summary, (47) guarantees through spectral differentiation that the governing DDE is fulfilled at all inner LGL mesh points, and with the inclusion of (48) that the found solutions are periodic and their segments connect continuously.

Since in the case of broaching, the governing equation of motion (11) is a DDE, evaluating $f_{j,k,l}$ and consequently $\varvec{\phi }$ requires finding the delayed terms $x_l(t_{j,k}-\Delta _{i})$. Fortunately, calculating these based on $\textbf{u}$ is fairly straightforward if the periodicity of the solutions and the interpolation scheme provided by the Legendre polynomial base are both exploited. First considering periodic solutions $t_{j,k}-\Delta _{i}$ must be mapped back to the $\left[ 0, \, 1 \right]$ interval by adding an integer multiple of the period length ($\sum _{j=1}^{N}T_j = 1$) to it in the following manner

$$\begin{aligned} \theta _{j,k,i} = t_{j,k}-\Delta _{i} + H(\Delta _i-t_{j,k})\left\lceil \Delta _{i}-t_{j,k}\right\rceil , \end{aligned}$$

(50)

where H denotes the Heaviside step function. Then an approximation of the state variables at $\theta _{j,k,i}$ can be found using Lagrange interpolation on the LGL mesh of the $m^\textrm{th}$ solution segment $t_{m,k}$ as

$$\begin{aligned} x_l(t_{j,k}-\Delta _{i}) = x_l(\theta _{j,k,i}) \approx \textbf{l}_{j,k,i}\textbf{x}_{m,l}, \end{aligned}$$

(51)

where $\textbf{l}_{j,k,i}$ is the row vector of interpolation coefficients obtained for the point $\theta _{j,k,i}$, and m is the smallest index for which $\theta _{j,k,i} \ge \sum _{l=1}^{m-1}T_l$ is fulfilled.

Using (51) to approximate the delayed terms, the elements of $\varvec{\phi }$ can be easily evaluated through (11). Furthermore, since the Jacobians of the governing equation of motion with respect to $\textbf{x}(t)$ and $\textbf{x}(t-\Delta _i)$ are available as the $\textbf{A}(t)$ and $\textbf{B}_i(t)$ matrices from (23), even it’s Jacobian with respect to $\textbf{u}$ is available analytically in the form

$$\begin{aligned} \begin{aligned} \textbf{J}_{\phi } &=\sum _{j=1}^{N} \textbf{E}_{j,N} \otimes \left( \sum _{k=1}^{M-1} \textbf{A}(t_{j,k})\otimes \textbf{E}_{k,M} \right) \\ &\quad +\sum _{j=1}^{N}\sum _{k=1}^{M-1}\sum _{i=1}^{n} \textbf{E}_{(j,m),N} \otimes \left( \textbf{B}_i(t_{j,k})\otimes \textbf{L}_{j,k,i}\right) \\&\quad + \textbf{I}_N \otimes \left( \textbf{I}_2 \otimes \textbf{E}_{M,M}\right) . \end{aligned} \end{aligned}$$

(52)

Here the m index always refers to the solution segment which includes $\theta _{j,k,i}$, and $\textbf{L}_{j,k,i}$ is formulated by replacing the $k^\textrm{th}$ row of an $M \times M$ zero matrix with the row vector of the corresponding Lagrange interpolation coefficients $\textbf{l}_{j,k,i}$.

With the help of (52) the governing discretized MP-BVP of the periodic orbits of theoretical infinite broaching operations (47) can be solved effortlessly via Newton iteration since the Jacobian of the system is available analytically as $\textbf{J}_{\textrm{F}} = \textbf{J}_{\textrm{u}} - \textbf{J}_{\phi } \in \mathbb {R}^{2NM\times 2NM}$.

This Jacobian matrix can also be used for evaluating the stability of the periodic orbits, by separating $\textbf{J}_{F}$ into two parts $\textbf{J}_{\textrm{F},t^+}$ and $\textbf{J}_{\textrm{F},t^-}$ and exploiting the implicit function theorem to formulate the monodromy matrix as

$$\begin{aligned} \varvec{\Phi } = -\textbf{J}_{\textrm{F},\textrm{t}^+}^{-1}\textbf{J}_{\textrm{F},\textrm{t}^-}, \end{aligned}$$

(53)

where using the notations $\Delta _{\max } = \max \{ \Delta _i\}$ and $H_{j,k,i} = H(\theta _{j,k,i}-1+\Delta _{\max })$

$$\begin{aligned} \begin{aligned} \textbf{J}_{\textrm{F},\textrm{t}^-}&= -\sum _{j=1}^{N}\sum _{k=1}^{M-1}\sum _{i=1}^{n} H_{j,k,i} \textbf{E}_{(k,m),N}\otimes \\ {}&\left( \textbf{B}_i(t_{j,k})\otimes \textbf{L}_{j,k,i}\right) -\textbf{E}_{N,N} \otimes \left( \textbf{I}_2 \otimes \textbf{E}_{M,M}\right) , \end{aligned} \end{aligned}$$

(54)

and $\textbf{J}_{\textrm{F},\textrm{t}^+} = \textbf{J}_{\textrm{F}} - \textbf{J}_{\textrm{F},\textrm{t}^-}$. Here the Heaviside step function was employed to check if $\theta _{j,k,i}>1-\Delta _{\max }$, which means that the corresponding $\textbf{x}(t_{j,k}-\Delta _i)$ point is found on the initial solution tail $\textbf{x}(t), \, t\in \left[ -\Delta _{\max },\, 0\right]$. These formulae are only applicable if the length of the period is larger than the maximum of the delays ($1>\max \{\Delta _i\}$), which is always fulfilled in the case of the broaching model investigated in this paper, however, in order to successfully analyse different DDEs, the expansion of the periodic orbits through repetition and concatenation might become necessary until this condition is met.

Similarly to the case of semi-discretization, the monodromy matrix found through this spectral collocation scheme could also be used in the goal function of the HANSO optimisation algorithm (31). The necessary gradients would also be available, since the derivative of the monodromy matrix with respect to an arbitrary parameter $\beta$ can be evaluated as

$$\begin{aligned} \frac{\partial \varvec{\Phi }}{\partial \beta } = \textbf{J}_{\textrm{F},\textrm{t}^+}^{-1}\frac{\partial \textbf{J}_{\textrm{F},\textrm{t}^+}}{\partial \beta }\textbf{J}_{\textrm{F},\textrm{t}^+}^{-1}\textbf{J}_{\textrm{F},\textrm{t}^-} - \textbf{J}_{\textrm{F},\textrm{t}^+}^{-1}\frac{\partial \textbf{J}_{\textrm{F},\textrm{t}^-}}{\partial \beta }. \end{aligned}$$

(55)

Here the derivatives of the Jacobian matrices can be evaluated through differentiating $\textbf{A}(t_{j,k})$ and $\textbf{B}_i(t_{j,k})$, and for parameters which directly affect the segment lengths, also $\textbf{D}_j$ and $\textbf{l}_{j,k,i}$ employing the chain rule similarly to (44). Since the effect of these parameters can be captured directly through their effect on $T_j$, there is also no need to introduce any smoothing in the governing equation of motion, making this approach favourable compared to the semi-discretization method.

Acquiring $\tilde{h}_{\textrm{crit}}$ and $\frac{\partial \tilde{h}_{\textrm{crit}}}{\partial \beta }$ from the penalty part of the goal function (30) requires solving the MP-BVP of periodic orbits (47). Based on the obtained discrete solution $\textbf{u}$ and the Lagrange interpolation scheme of the delayed terms (51), the chip thickness can be evaluated using (25) for each different tooth type on all points of the piecewise LGL mesh. Taking the minimum of all these values, while neglecting the solution segments where $\gamma _{i}(t_{j,k})=0$ leads to the form

$$\begin{aligned} \tilde{h}_{\textrm{crit}} = \min \{\tilde{h}_i(t_{j,k})\} = \Delta _{i_\textrm{c}} + x_1(\theta _{j_\textrm{c},k_\textrm{c},i_\textrm{c}})-x_1(t_{j_\textrm{c},k_\textrm{c}}). \end{aligned}$$

(56)

Here the $i_\textrm{c}$, $j_\textrm{c}$, and $k_\textrm{c}$ indices correspond to the type and location of the critical chip thickness in the discrete version of the periodic orbit. Taking a derivative of (56) with respect to $\beta$ leads to

$$\begin{aligned} \begin{aligned} \frac{\partial \tilde{h}_{\textrm{crit}}}{\partial \beta } &=\frac{\partial \Delta _{i_\textrm{c}}}{\partial \beta } + \frac{\partial \textbf{l}_{j_\textrm{c},k_\textrm{c},i_\textrm{c}}}{\partial \beta }\textbf{x}_{m_\textrm{c},1} \\ &\quad +\textbf{l}_{j_\textrm{c},k_\textrm{c},i_\textrm{c}}\frac{\partial \textbf{x}_{m_\textrm{c},1}}{\partial \beta }-\frac{\partial x_1(t_{j_\textrm{c},k_\textrm{c}})}{\partial \beta }, \end{aligned} \end{aligned}$$

(57)

where $m_{\textrm{c}}$ is the index of the solution segment containing $\theta _{j_\textrm{c},k_\textrm{c},i_\textrm{c}}$. Here the derivatives of all state variables $\frac{\partial x_l(t_{j,k})}{\partial \beta }$ can be found by employing the implicit function theorem as

$$\begin{aligned} \frac{\partial \mathbf {\textbf{u}}}{\partial \beta } = -\textbf{J}_{\textrm{F}}^{-1} \frac{\partial \textbf{F}(\textbf{u})}{\partial \beta }, \end{aligned}$$

(58)

and the derivatives of the Lagrange interpolation coefficients can be found similarly to (44) using the chain rule. Finally, based on (47)

$$\begin{aligned} \begin{aligned} \frac{\partial \textbf{F}(\textbf{u})}{\partial \beta } &=\left( -\sum _{j=1}^{N}\textbf{E}_{j,N}\otimes \left( \textbf{I}_2\otimes \frac{1}{T_j^2}\frac{\partial T_{j}}{\partial \beta }\hat{\textbf{D}}\right) \right) \textbf{u} \\ {}&\quad - \frac{\partial \varvec{\phi }}{\partial \beta }, \end{aligned} \end{aligned}$$

(59)

where $\hat{\textbf{D}}$ is the uniform spectral differentiation matrix provided by an LGL mesh defined on the $\left[ 0, \, 1 \right]$ interval, with its last row replaced by zeros. The derivatives of the elements of $\varvec{\phi }$ can be evaluated by differentiating the governing equation of motion (11).

Appendix 3: Derivatives with respect to the pitch ratio

Employing the semi-discretization and spectral collocation methods for the direct, gradient descent based, numeric optimization of two teeth repeating patterns required the evaluation of a few derivatives with respect to the newly introduced pitch ratio $\alpha$. First from the governing equation of motion (11)

$$\begin{aligned} \begin{aligned} \frac{\partial \dot{x}_1(t)}{\partial \alpha } &=0,\\ \frac{\partial \dot{x}_2(t)}{\partial \alpha } =&\frac{2\tilde{w}}{\tilde{v}}\sum _{i=1}^{2}\left( \gamma _{i}(t)\frac{\partial \Delta _{i}}{\partial \alpha }\left( 1-\dot{x}_1(t-\Delta _{i})\right) \right. \\&\quad + \left. \frac{\partial \gamma _{i}(t)}{\partial \alpha }\left( \Delta _i + x_1(t-\Delta _{i}) - x_1(t)\right) \right) , \end{aligned} \end{aligned}$$

(60)

then from its linearised version (22)

$$\begin{aligned} \begin{aligned}&\frac{\partial \textbf{A}(t)}{\partial \alpha } = -\frac{2\tilde{w}}{\tilde{v}}\begin{bmatrix} 0 &{} 0 \\ \frac{\partial \gamma _{1}(t)}{\partial \alpha } + \frac{\partial \gamma _{2}(t)}{\partial \alpha } &{} 0 \end{bmatrix}, \\ {}&\frac{\partial \textbf{B}_i(t)}{\partial \alpha } = \frac{2\tilde{w}}{\tilde{v}} \begin{bmatrix} 0 &{} 0 \\ \frac{\partial \gamma _{i}(t)}{\partial \alpha } &{} 0 \end{bmatrix}. \end{aligned} \end{aligned}$$

(61)

Here the derivative of the delayed terms is available as $\dot{x}_1(t-\Delta _{i}) = x_2(t-\Delta _{i})$, while according to (33)

$$\begin{aligned} \frac{\partial \Delta _{1}}{\partial \alpha } = -\frac{1}{(1+\alpha )^2} \,\, \textrm{and} \,\,\frac{\partial \Delta _{2}}{\partial \alpha } = \frac{1}{(1+\alpha )^2}. \end{aligned}$$

(62)

Based on (24) considering $\hat{t}_{1,\textrm{in}} = 0$, $\hat{t}_{1,\textrm{out}} = \textrm{mod}(\Lambda _\textrm{D},1)$, $\hat{t}_{2,\textrm{in}} = \Delta _{2}$, and $\hat{t}_{2,\textrm{out}} = \textrm{mod}(\Delta _{2}+\Lambda _\textrm{D},1)$

$$\begin{aligned} \begin{aligned} \frac{\partial \gamma _1(t)}{\partial \alpha } \approx&\,0, \\ \frac{\partial \gamma _2(t)}{\partial \alpha } \approx&\, \frac{\kappa }{2} \left( -\frac{1}{\cosh ^2\left( \kappa (t-\hat{t}_{2,\textrm{in}})\right) } \right. \\ {}&+ \left. \frac{1}{\cosh ^2\left( \kappa (t-\hat{t}_{2,\textrm{out}})\right) }\right) \frac{\partial \Delta _2}{\partial \alpha }. \end{aligned} \end{aligned}$$

(63)

If no smoothing has been applied, and $\gamma _{i}(t)$ is only defined in a piecewise manner, its gradient with respect to the pitch ratio is simply 0. This definition of the immersion functions was only used in the spectral collocation method employed to detect and avoid contact loss events, but there it has considerably simplified the problem, as the derivatives of the $\textbf{A}(t_{j,k})$ and $\textbf{B}_i(t_{j,k})$ matrices became 0. This was only possible, because contrary to the semi-discretization method, here the effect of the pitch ratio on the exit and entry events can be captured through the length of the smooth solutions segments $T_j$. Nevertheless, their derivatives will still be needed for evaluating (59) which depending on the order of events will either be 0 or $\pm \frac{\partial \Delta _{2}}{\partial \alpha }$. For example if $\hat{t}_{1,\textrm{in}}< \hat{t}_{1,\textrm{out}}< \hat{t}_{2,\textrm{in}} < \hat{t}_{2,\textrm{out}}$

$$\begin{aligned} \frac{\partial T_1}{\partial \alpha } = \frac{\partial T_3}{\partial \alpha } = 0, \,\, \frac{\partial T_2}{\partial \alpha } = -\frac{\partial T_4}{\partial \alpha } = \frac{\partial \Delta _{2}}{\partial \alpha }. \end{aligned}$$

(64)