The effect of propulsion system design on the response of the novel yoke–bell–clapper system with a proportional–integral controller

Abstract

This article focuses on the influence of the propulsion mechanism design on the transient and steady-state response of the yoke–bell–clapper system with a proportional–integral controller. The analysis is made using the mathematical model validated in our previous paper. Three different propulsion system designs are considered. Analyzed cases are compared and assessed, taking into account the launching time of the system, additional loads in the supports, and final steady-state response. The subject of the analysis contributes to the topic devoted to the dynamic interaction between the bells and their supporting structures that is recently widely considered by the scientific community.

1 Introduction

Loads transferred between the swinging bells and their supporting structures is a problem widely considered by the scientific community. Horizontal forces and dynamic loads due to impacts can be especially harmful to the supporting structures. For masonry towers—that often are supports for the bells—severe phenomena of resonance, excessive deflection of the building or the effect of tower rocking were reported and investigated by researchers recently and in the past [1,2,3,4,5,6,7]. Consequently, various methods to estimate the loads produced by swinging bells were developed over the years. In the mid-seventies of the last century, two English scientists Heyman and Therefal performed an experiment in order to determine the magnitude of inertia forces produced by swinging bells [8]. The experiment was complemented by mathematical modeling. Researchers calculated horizontal and vertical reaction forces in the bell’s supports using second order differential equation with one-degree-of-freedom (DoF) and small angle approximations. Laboratory results and analytical investigation gave similar results. A few years later, in 1978, a DIN 4178 [9] standard describing the design of bell towers was published in Germany. It was revised in 2005.In the standard, there are semi-empirical formulas for calculating forces produced by the swinging bells. Formulas are derived assuming the static equilibrium in the system that consists of the bell itself. The next significant documented attempts to tackle the problem are, for example, the work of Ivorra et. al [10] published in 2006. The author repeated the experiments performed by Heyman and Therefal for different types of bell mounting layouts. The research comprised mathematical modeling and experimental work. In the mathematical model, the authors used a compound pendulum (the mass of the clapper was neglected), and they derived analytically equations for reaction forces in the supports in horizontal and vertical directions. The study showed that the mounting layout and swinging amplitude significantly influence the dynamic loads produced by bells. Similarly, the loads are estimated in other related studies in the last several years [11,12,13].

All examples mentioned in the previous paragraph consider the steady-state of the bell’s swinging. It may be a perilous simplification when the structure’s health is considered. In some of the scientific papers devoted to the dynamics of the bell towers, the authors emphasize the influence of the transient time on the supporting structure dynamics. Ivorra et al. [14] investigated the tower with six bells mounted in various manners. The displacement of the top of the tower was extreme during the transient period of the bell swinging because of the dynamic interaction between the frequencies of the horizontal forces produced by the bells and the tower. It was concluded that the bell’s launching time should be reduced to limit the dynamic problem. In [15], Bru et al. indicated that during the transient period of the bell motion, the displacement of the supporting tower could exceed the safe values even if the bell and tower were designed according to standards [9] and the steady-state of the bell operation causes no harm to the structure.

When the bell steady-state response is analyzed, the yoke geometry and the excitation force magnitude (or swinging amplitude) determine the system dynamics [10, 16]. However, when the transient period is considered, the system’s excitation is crucial. The methods of bell excitation have changed over the centuries. The oldest method is the manual control of the bell by professional ringers using ropes. Following the revolution in science and technology, ringers were replaced by AC motors, chain transmissions, and sprockets. Currently, there is a tendency to use modern linear motors, since this kind of propulsion is much simpler, imitates better manual control, and makes the phase of free motion of the bell possible. The linear motors are usually controlled using a proportional–integral-derivative (PID) mathematical algorithm (usually limited to a proportional–integral (PI) algorithm) that is embedded in the programmable logic controller (PLC).

In our previous paper [16], we introduced and validated the mathematical model of the novel yoke–bell–clapper system with variable geometry. We used a four-degree-of-freedom model that comprises the bell, the clapper and the supports of the yoke. We assessed the influence of the yoke geometry and excitation force magnitude on the system response. Aspects important from an engineering point of view, namely the ringing scheme of the bell and associated forces in the supports, were analyzed. Still, in the paper, we assessed only the steady state of the system response. In the present work, we focus on the transient time of system response, but some attention is also paid to the steady-state. We use validated mathematical model to consider various positions of the motor with respect to the rotation axis, different yoke geometries, and a range of swinging amplitudes. We implement a PI algorithm that imitates real controllers used to propel bells in real-world applications. We assess different propulsion designs with regard to launching time, final ringing scheme, and additional loads in the supports. Launching time determines the length of the transient part of the system response when the dynamic interaction between the bell and the tower is increased. Additional loads in the supports are understood as impact forces due to initial high-energy collisions between the bell and the clapper or due to the nature of the piece-wise excitation of the bell. These forces can be especially severe to the bearings that support the bell and can increase the dynamic interaction between the bell and its supporting structure. The sample-based methods complement the analysis. Values of system parameters are randomly sampled from the analyzed set of parameter values. The algorithm is parallelized, therefore multiple simulations are run at the same time.

This paper is organized as follows. Section 2 explains our approach to simulate and assess different propulsions. In the Sect. 2.1 we describe the mathematical model and the idea behind the novel design. Then, in Sect. 2.2, we explain the PI algorithm that is used to control the excitation. Finally, in the Sect. 2.3 we describe different propulsion set-ups that are analyzed. Section 3 presents the influence of the propulsion system design on the final ringing scheme, overloads in the supports, and launching time. At the end of this section also, the steady-state response is presented. We summarise our results in the Sect. 4.

2 Methodology

2.1 Mathematical model

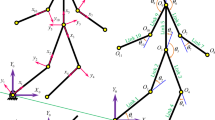
The mathematical model representing the yoke–bell–clapper system consists of a set of ordinary differential equations (ODEs) that describe its motion. The mathematical model is built based on the physical model that is schematically presented in Fig. 1. It is a four-degrees-of-freedom system accommodating the yoke with the bell, the clapper, and the yoke’s supports. The yoke consists of a rectangular frame and a moving beam that alters the system’s geometry. Four generalized coordinates describe the model. The angle between the bell’s axis and downward vertical is given by $\varphi _{1}$. Whereas the angle between the clapper’s axis and the downward vertical is given by $\varphi _{2}$. The horizontal compliance of the supports is given by $x_{s}$, while the vertical is by $y_{s}$. A System of four coupled second-order ODEs that describe the system’s motion is presented below. The meaning and values of the parameters appearing in the equations are given in the following paragraphs.

$$\begin{aligned}&(M+m)\ddot{x}_{s}+(ML\cos \varphi _{1}+ml_{c}\cos \varphi _{1})\ddot{\varphi }_{1}+(ml\cos \varphi _{2})\ddot{\varphi }_{2} \nonumber \\&=ML\dot{\varphi }_{1}^{2}\sin \varphi _{1}+ml_{c}\dot{\varphi }_{1}^{2}\sin \varphi _{1}+ml\dot{\varphi }_{2}^{2}\sin \varphi _{2}-k_{x}x_{s}-d_{x}\dot{x}_{s}, \end{aligned}$$

(1)

$$\begin{aligned}&\quad -(ml_{c}\sin \varphi _{1}+ML\sin \varphi _{1})\ddot{\varphi }_{1}-ml\sin \varphi _{2}\ddot{\varphi }_{2}+(M+m)\ddot{y}_{s} \nonumber \\&=ml_{c}\cos \varphi _{1}\dot{\varphi }_{1}^{2}+ml\cos \varphi _{2}\dot{\varphi }_{2}^{2}+ML\cos \varphi _{1} \dot{\varphi }_{1}^{2}\nonumber \\&\quad +g(m+M)-k_{y}y_{s}-d_{y}\dot{y}_{s}, \end{aligned}$$

(2)

$$\begin{aligned}&(ML\cos \varphi _{1}+ml_{c}\cos \varphi _{1})\ddot{x}_{s}+(B_{B}+ml_{c}^{2})\ddot{\varphi }_{1}\nonumber \\&\quad +mll_{c} \cos (\varphi _{1}-\varphi _{2})\ddot{\varphi }_{2}\nonumber \\&\quad -(ml_{c}\sin \varphi _{1}+ML\sin \varphi _{1})\ddot{y}_{s} =\nonumber \\&\quad -mll_{c}\sin (\varphi _{1}-\varphi _{2})\dot{\varphi }_{2}^{2}-(ML+ml_{c})g\sin \varphi _{1} -d_{b}\dot{\varphi }_{1}\nonumber \\&\quad -d_{c}(\dot{\varphi }_{1}-\dot{\varphi }_{2})\nonumber \\&\quad -d_{bf}\frac{2}{\pi }\arctan (10^{5}\dot{\varphi }_{1})-d_{cf}\frac{2}{\pi }\arctan (10^{5}(\dot{\varphi }_{1} -\dot{\varphi }_{2}))+M_{t}, \end{aligned}$$

(3)

$$\begin{aligned}&ml\cos \varphi _{2}\ddot{x}_{s}+mll_{c}\cos (\varphi _{1}-\varphi _{2})\ddot{\varphi }_{1}+B_{C}\ddot{\varphi }_{2}-ml\sin \varphi _{2}\ddot{y}_{s} \nonumber \\&=mll_{c}\dot{\varphi }_{1}^{2}\sin (\varphi _{1}-\varphi _{2})-mgl\sin \varphi _{2}-d_{c}(\dot{\varphi }_{2} -\dot{\varphi }_{1})\nonumber \\&\quad -d_{cf}\frac{2}{\pi }\arctan (10^{5}(\dot{\varphi }_{2}-\dot{\varphi }_{1})). \end{aligned}$$

(4)

Fig. 1

The physical model of the system along with its physical and geometrical quantities

The yoke and the bell are treated as one part with mass M and moment of inertia $B_{b}$. Mass M is obtained by simply adding masses of all elements of the yoke and bell. Considering the resultant moment of inertia $B_{b}$, it is calculated using the following relation:

$$\begin{aligned} B_{b}& = {} B_{bo}+M_{0}(d-d_{2})^{2}+B_{boo}+M_{1}(l_{mb}+d_{4}-d_{2})^{2}\nonumber \\{} & {} +B_{b01}+M_{2}(d_{2}-l_{mb}-d_{5})^{2}, \end{aligned}$$

(5)

where $B_{bo}$, $B_{b00}$, $B_{b01}$ are the moments of inertia of the rectangular frame, the bell, and the moving beam, respectively. Whereas $M_{0}$, $M_{1}$, $M_{2}$ are corresponding masses and d, $d_{4}$, $d_{5}$ corresponding dimensions describing position of each element gravity center. Variables $d_{2},l_{2},l$ are geometric parameters resulting from the design. The position of the movable beam is described by $l_{mb}$ dimension. Dimensions $S,l_{c},L$ are depended on $l_{mb}$ and received using the following formulas:

$$\begin{aligned} S& = {} \frac{M_{0}d+M_{1}(d_{4}+l_{mb})+M_{2}(l_{mb}+d_{5})}{M}, \end{aligned}$$

(6)

$$\begin{aligned} L& = {} S-d_{2}, \end{aligned}$$

(7)

$$\begin{aligned} l_{c}& = {} l_{2}+l_{mb}-d_{2}. \end{aligned}$$

(8)

Consecutively, these dimensions are the position of the yoke-bell system gravity center, its distance from the yoke axis of rotation ($O_{1}$), and the distance between the clapper’s pivot joint $O_{2}$ and $O_{1}$. The yoke is supported by the rolling bearings, the stiffness of the supports is described by $k_{x}$ and $k_{y}$ while the associated viscous damping by $d_{x}$ and $d_{y}$. Clapper parameters are constant, its moment of inertia with respect to its rotation axis is described by $B_{C}$, mass by m, and the distance between the clapper axis of rotation and its gravity center is marked with l.

As far as energy dissipation is considered, we take advantage of the Rayleigh dissipation function, which accounts for the viscous damping in the bell $(d_{b})$ and the clapper $(d_{c})$ joints. We also introduce the dry friction component of damping that is represented by Coulomb friction torque for the bell $(d_{bf})$ and the clapper $(d_{cf})$. The dry friction component is modeled according to the Coulomb model, and we approximate it using smooth $\textrm{arctan}$ function. Thanks to that, we obtain the continuous model of damping; consequently, we simplify the model that, due to discontinuities, piece-wise nature, and four degrees of freedom, requires significant computational effort. The combination of Rayleigh’s viscous damping and Coulomb’s dry friction gives a satisfactory approximation of the investigated real-world system. A good accordance between numerical and experimental results was shown in [16]. The excitation torque $M_{t}$ is described in Sect. 2.2.

The values of the parameters used in the mathematical model have been obtained and validated in our previous article [16], where we introduced the mathematical model. Values of parameters are the following: $M_{0}=36.87\;[\textrm{kg}]$, $M_{1}=96.72\;[\textrm{kg}]$, $M_{2}=13.97\;[\textrm{kg}]$ $B_{b0}=11.43\;\left[ \frac{\textrm{kg}}{\textrm{m}^{2}}\right]$, $B_{00}=4.27\;\left[ \frac{\textrm{kg}}{\textrm{m}^{2}}\right]$, $B_{b01}=0.838\;\left[ \frac{\textrm{kg}}{\textrm{m}^{2}}\right]$, $d=0.565\;[\textrm{m}]$, $d_{2}=0.500\;[\textrm{m}]$, $d_{4}=0.474\;[\textrm{m}]$, $d_{5}=0.035\;[\textrm{m}]$, $B_{C}=0.525\;\left[ \frac{\textrm{kg}}{\textrm{m}^{2}}\right]$, $m=5.49\;[\textrm{kg}]$, $l=0.274\;[\textrm{m}]$, $d_{b}=0.22\;[\textrm{Ns}]$, $d_{c}=0.10\;[\textrm{Ns}],$ $d_{bf}=0.10\;[\textrm{Nm}]$, $d_{cf}=0.15\;[\textrm{Nm}]$. Stiffness coefficients $k_{x}$ and $k_{y}$ were determined experimentally and are equal $k_{x}=813770\;\left[ \frac{\textrm{N}}{\textrm{m}}\right]$, $k_{y}=10939000\;\left[ \frac{\textrm{N}}{\textrm{m}}\right]$, while $d_{x}=260.30\;\left[ \frac{\textrm{Ns}}{\textrm{m}}\right]$ and $d_{y}=954.00\;\left[ \frac{\textrm{Ns}}{\textrm{m}}\right]$.

The mathematical model of the clapper-to-the-bell impact is well described and validated in another work of ours [17]. It is a discrete model based on the coefficient of restitution. The provided algebraic formulas allow us to calculate the collision effect based on the description of the pre-collision dynamical state of the system. The impact occurs when:

$$\begin{aligned} |\varphi _{1}-\varphi _{2}|=\alpha , \end{aligned}$$

(9)

where $\alpha$ is an angular parameter associated with bells mouth. When this condition is fulfilled, we stop the integration process. Then, we restart the simulation, updating the initial conditions of equations 1–4 by switching the bell’s and clapper’s angular velocities from the values before the impact on the ones after the impact. The angular velocities (after the impact) are obtained by taking into account the energy dissipation function and conservation of the system’s angular momentum that are expressed by the following formulas:

$$\begin{aligned}{} & {} \frac{1}{2}B_{c}(\dot{\varphi }_{2,AI}-\dot{\varphi }_{1,AI})^{2}=k\frac{1}{2}B_{c}(\dot{\varphi }_{2,BI}-\dot{\varphi }_{1,BI})^{2}, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} [B_{b}+ml_{c}^{2}+ml_{c}l\cos (\varphi _{2}-\varphi _{1})]\dot{\varphi }_{1,BI}\nonumber \\{} & {} \quad +[B_{c}+ml_{c}l\cos (\varphi _{2}-\varphi _{1})]\dot{\varphi }_{2,BI}\nonumber \\{} & {} = [B_{b}+ml_{c}^{2}+ml_{c}l\cos (\varphi _{2}-\varphi _{1})]\dot{\varphi }_{1,AI}\nonumber \\{} & {} \quad +[B_{c}+ml_{c}l\cos (\varphi _{2}-\varphi _{1})]\dot{\varphi }_{2,AI} \end{aligned}$$

(11)

where index AI stands for “after impact”, index BI for “before impact” and parameter k is the coefficient of energy restitution. For this particular yoke–bell–clapper system we assume $k=0.15\,[-]$. This value was estimated by performing curve fitting while comparing experimental and numerical results. In reality, the consecutive impacts between the bell and the clapper vary. It was first reported by Menghetti and Rossi [18], where authors analyzed the clapper acceleration before the impact. Proposed value of k refers to estimated average energy dissipated during each impact. However, the difference between particular impacts may be significant (see [18]). The set value of k gives a satisfactory accordance between the experimental and numerical results for this particular system [16].

2.2 System excitation

The analyzed yoke–bell–clapper system is propelled by a linear electric motor. The schematic view of the propulsion system is presented in Fig. 2. The “unrolled” stator is designated by red color, while the rotor is yellow. The stator is anchored to the bell-supporting structure. The rotor is in the form of a curved-shaped plain metal sheet connected to the yoke. The force generated by the linear motor pushes the rotor against the stator in the direction recognized as horizontal (along the X axis in Fig. 1). The rotor is placed at a distance from the yoke axis of rotation; hence, the torque around the yoke rotation axis is created and the bell is set in swinging motion.

It is a typical propulsion system found in modern bell control systems. In this paper, the excitation model is based on the motor and the control unit provided by Rduch company. Both are the components commonly used in industrial applications. Because it is a commercial product, the exact logic between the control unit is unknown, and we treat it as a black box. The input for the control unit is based on the desired swinging amplitude. The unit uses proportional–integral (PI) algorithm.

In our model, the logic behind the control algorithm is as follows. Firstly, as in the commercial design, the user has to define the desired bell oscillation amplitude $\varphi _{1}(max)$. Then, taking advantage of the mechanical energy conservation law, $\dot{\varphi }_{1}(max)$ is calculated and set as the set-point value $\dot{\varphi }_{SP}$. The difference between the value of $\dot{\varphi _{1}}$, when the bell goes through its stable equilibrium position, and the set-point $\dot{\varphi }_{SP}$ value is defined as control error e.

$$\begin{aligned} e=\dot{\varphi }_{SP}-\dot{\varphi _{1}} \end{aligned}$$

(12)

Control error is calculated in each half-period of motion. The control signal is designated by F, which is the force in Newtons generated by the propulsion system. The control signal F consists of two terms $S_{k}$ and $x_{k}$.

$$\begin{aligned} F& = {} x_{k}+S_{k} \end{aligned}$$

(13)

$$\begin{aligned} S_{k}& = {} S_{(k-1)}+k_{i}e \end{aligned}$$

(14)

$$\begin{aligned} x_{k}& = {} k_{p}e \end{aligned}$$

(15)

where, $k_{i}$ is an integral gain and, $k_{p}$ is a proportional gain. In case of the term $S_{(k)}$ the value form previous step $S_{(k-1)}$ is saved and used in the calculations. Parameters $k_{i}$ and $k_{p}$ are tuning parameters they are equal to $k_{i}=15\;[-]$ and $k_{p}=100\;[-]$. Set values of $k_{i}$ and $k_{p}$ provide that the propulsion dynamics in the numerical model and the real-world system are comparable (i.e. the number of periods of motion needed to reach the desired amplitude when the ball is hanging high, or significantly lowered). Figure 3 schematically presents the idea behind the control algorithm. One can observe the control signal F, the bell angular displacement $\varphi _{1}$ and the bell angular velocity $\dot{\varphi }_{1}$, each with its individual scale. The error value e and the control signal F are calculated according to Eqs. 12–15 when the bell goes through its stable equilibrium position, i.e. $\varphi _{1}=0$. Then, the bell reaches the tilting point and is about to turn back ($\dot{\varphi }_{1}=0$), the algorithm is using calculated force F that will be generated by the propulsion mechanism when the stator and rotor overlap again. The figure shows that the force is reduced as the swinging amplitude approaches the set-point value.

Fig. 2

3D model of the linear motor propelling the yoke–bell–clapper system

Fig. 3

Exemplary time trace of the system response explaining the idea behind the proportional–integral algorithm

The excitation generated by the motor is introduced to the model by the torque $M_{t}(\varphi _{1})$ described by the following piece-wise formula:

$$\begin{aligned} M_{t}(\varphi _{1})={\left\{ \begin{array}{ll} Frsgn(\dot{\varphi }_{1}), &{} for\;|\varphi _{1}|\le \varphi _{critical}\\ 0, &{} for\;|\varphi _{1}|>\varphi _{critical} \end{array}\right. }. \end{aligned}$$

(16)

where F is force generated by the motor (control signal), and r is the distance between the force application point and the yoke axis of rotation.

2.3 Propulsion system set-ups

Alternating the location of the stator in the vertical direction (y direction according to Fig. 1), one can change the maximum torque generated by the motor. In this paper, we investigate three different positions of the motor. Two different propulsion system set-ups are schematically presented in Fig. 4. What can be seen from the figure is that by increasing r we augment torque magnitude $M_{t}$, but the bell angular displacement $\varphi _{critical}$ for which the rotor and the stator overlap is reduced. Therefore, greater torque can be generated but at the cost of motor activation range.

Fig. 4

Schematic presentation of the difference between two distinct motor positions

The relationship between the parameters r and $\varphi _{critical}$ is linear and depends on the design of the propulsion elements. In the case of the considered system: $\varphi _{critical}(r)=-1.263r+1.107$, where r is expressed in meters and $\varphi _{critical}$ in radians. In the numerical model, the motor is activated when the centerline of the rotor plate overlaps with the stator. The three different positions of the linear motor are investigated. In the first case (case W) $r=0.255\;[\textrm{m}]$ and $\varphi _{critical}=0.785\;[rad]$. In the second case (case S), we lower the linear motor with respect to the yoke axis of rotation, $r=0.411\;[\textrm{m}]$ and $\varphi _{critical}=0.588\;[rad]$. In the third case (case N), $r=0.566\;[\textrm{m}]$ and $\varphi _{critical}=0.392\;rad$. In every case, we assess the launching time $t_{l}$ of the system, the maximum accelerations in the supports $\ddot{y}_{s}$ and $\ddot{x}_{s}$, and the final ringing scheme. The methodology behind calculating the launching time $t_{l}$ is as follows, first, we check if the 90% of the desired swinging amplitude is reached. Then, the moment when the first collision between the bell and the clapper occurs is marked as a launching time $t_{l}$.

In the analysis, we use a sample-based approach. This approach is especially efficient when we want to assess the influence of several parameters simultaneously and analyze higher dimensional systems where classical methods are difficult to apply [16, 19]. In each simulation, the value of $\varphi _{SP}$, which is defined as the desired swinging angle of the bell, is drawn from the range $\varphi _{SP}\in <\frac{\pi }{6},\frac{\pi }{2}>\,[\textrm{rad}]$, while the value of $l_{mb}$ that determines the yoke geometry is drawn from the range $l_{mb}\in <0.15,0.5>\;[\textrm{m}]$. The distribution of both drawn parameters is uniform. In each of the three cases, we perform 100, 000 number of numerical trials. Every time we start the simulation when the bell is in the hanging down position, hence simulations begin with the following initial conditions: $\varphi _{1}=0$, $\varphi _{2}=0$, $x_{s}=0$, $y_{s}=0$. These are the natural conditions for the bells to start operating.

3 Results

3.1 Final ringing scheme

Fig. 5

Two-parameter($l_{mb}$ and $\varphi _{SP}$) ringing schemes diagram showing variety of existing attractors. a Case N b Case S c Case W

The ringing schemes are classified according to the number of impacts between the bell and the clapper in one period of motion (1, 2, 3, or more impacts). They are also distinguished by types of impacts (If the bell and the clapper are performing in phase motion during the impact, we deal with a flying clapper, otherwise, we call it a falling clapper). Because this work focuses on the transient response, extensive information about different ringing schemes will not be given. A more detailed explanation can be found in [16]. In this system, what in practice is defined as the ringing scheme would be an attractor in the nomenclature of the non-linear dynamics. Figure 5 shows possible ringing schemes (attractors) for three different propulsion system designs. Each plot is a two-parameter map that shows the influence of $l_{mb}$ and $\varphi _{SP}$ on the system response. As a reminder, $\varphi _{SP}$ is the swinging amplitude of the bell, $l_{mb}$ is determining the yoke geometry..

In numerical simulations, depending on the case (N, S, and W), there are minor differences between reached attractors. They can be found in the left lower corner of the plot and in close vicinity to the transition region between the attractor marked with blue (2 impacts) and black (No impacts) color. These differences comprise up to a few percent of the plot and are considered irrelevant. Where the disparities are spotted, there are attractors whose contribution to the two-parameter map is minor, or the aperiodic motion is observed, these regions are prone to obstructions and parameter fluctuations. These variations are also present when extreme parameter values are considered, hence, the accuracy of the numerical model is diminished.

The same final ringing scheme is obtained regardless of the linear motor position. Systems exhibit various ringing schemes depending on the $l_{mb}$ and $\varphi _{SP}$ parameters.

3.2 Overloads

Panels (a)–(f) in Fig. 6 show maximum accelerations $\ddot{y}_{s}(max)$ and $\ddot{x}_{s}(max)$ during transient time depending on two parameters $l_{mb}$ and $\varphi _{SP}$. Each map on the horizontal axis has $l_{mb}$ parameter determining yoke geometry, while the vertical axis presents the bell swinging amplitude $\varphi _{SP}$. Color intensity indicates the values of the maximum accelerations $\ddot{y}_{s}(max)$ and $\ddot{x}_{s}(max)$.

Considering horizontal direction, one can observe that the plots differ qualitatively and quantitatively. For the case W (Fig. 6a) the $\ddot{x}_{s}(max)$ values are increasing gradually up to the value of $0.4\;\left[ \frac{\textrm{m}}{\textrm{s}^{2}}\right]$, the growth is only due to changing yoke geometry. The color intensity changes gradually. The swinging amplitude has nearly no effect on the $\ddot{x}_{s}$. For the case S (Fig. 6b), we observe step change in the produced acceleration value when the parameter describing yoke geometry $l_{mb}$ is equal to approximately $0.2\;[\textrm{m}]$. Above that value, $\ddot{x}_{s}(max)$ is increasing gradually, the linear motor is not able to push the rotor plate away from the stator in the first period of motion (Situation that is schematically presented in Fig. 4). Therefore, the motor has to switch the direction of acting force when the rotor and stator still overlap. The difference in time traces of the system response in terms of $\ddot{x}_{s}$ when the $l_{mb}$ is below and above $0.2\;[\textrm{m}]$ is schematically presented in Fig. 7. In Fig. 7, there are two plots. On both plots, the excitation force F, the bell angular displacement $\varphi _{1}$, the bell angular velocity $\dot{\varphi }_{1}$, and the horizontal accelerations in the supports $\ddot{x}_{s}$ are visible. Each variable has its individual scale. The plots show the launching of the system for two different parameter $l_{mb}$ values and comprehensibly illustrate the phenomena visible in Fig. 6b and c. In Fig. 7a we can see the phase of free motion of the bell in the first period of motion, i.e. the rotor plate and stator do not overlap and the bell performs motion without any excitation. In this case the phenomena of changing the direction of acting force is smooth because the motor propels the yoke when the rotor plate is moving towards the stator and bell angular displacement is below $\varphi _{critical}$. In other words, the yoke changes its direction during the free motion phase without any external excitation. A contrary situation is observed when the motor cannot push the rotor plate away from the stator in a single period of motion. If it occurs, the phenomena of changing the direction of the acting force is abrupt, which is manifested by increased accelerations in the supports. Consequently, the impact effect, this situation is visible in Fig. 7b. The time traces also show that increased accelerations $\ddot{x}_{s}$ are caused either by the control signal or by the impact. For the case N (Fig. 6c) we observe the same phenomena as in the case of S, however, the threshold when there is no free motion phase in the first period of motion is moved on the horizontal axis when $l_{mb}\approx 0.318\;[\textrm{m}]$. There is no step change in maximum acceleration $\ddot{x}_{s}(max)$ in the case W because the situation when the rotor plate is pushed away from the stator in the first period of motion never happens, regardless of the yoke geometry.

Considering vertical accelerations $\ddot{y}_{s}$, case W is presented in Fig. 6d. There are clearly visible step changes in produced accelerations. The steps are determined by the fact in which period (or half-period) of motion the phase of the bell’s free motion occurs. By increasing $l_{mb}$, the inertia of the combined bell and yoke is growing exponentially. Therefore, the linear motor needs more periods of bell motion to push the rotor plate beyond the stator and allow for the phase of free motion. The excitation is explicitly dependent on bell velocity, the later in the time domain the rotor is pushed away from the stator, the greater the velocity of the bell in the last period before the creation of the phase of free motion of the bell. Consequently, the bigger the acceleration $\ddot{y}_{s}$ when the force direction is changed. The situation is repeated also in the case S (Fig. 6e) and N (6f). We can observe two-step changes in case S and one-step changes in case N. In panels (d)–(f) corresponding to vertical accelerations, we observe more step changes than in panels (a)–(c) related to horizontal accelerations. Hence, the $\ddot{y}_{s}(max)$ is more sensitive to the changes of yoke geometry than $\ddot{x}_{s}(max)$. However, maximum accelerations in the vertical direction are almost 3 times smaller than in the horizontal direction.

In summary, the propulsion system’s position significantly influences the overloads produced during the transient time of the system response. The main influencing factor is whether the phase of the bell-free motion can be reached in the first period of motion. The bell-supporting structure and bearings will be subjected to additional loads if not.

3.3 Launching time

Panels (g)–(i) in Fig. 6 show how the launching time depends on the yoke geometry and swinging amplitude in each analyzed case. When $l_{mb}$ or $\varphi _{SP}$ parameters are increased, we observe a rise in launching time $t_{l}$. The step changes visible on the plots are created because 90% of the desired swinging amplitude is reached in different half-periods of bell motion. Therefore, we observe a discrete change in the launching time equal to approximately half of the period of the bell motion. One can also notice that there are more discrete regions for Case W than for Case S. The fewest discrete regions for Case N. Case W is, therefore, the most sensitive to parameter changes and Case N the least sensitive. Considering the influence of linear motor position on the launching time, we can observe that the difference between case N and case S is approximately $1\;[\textrm{s}]$, regardless of the system parameters, while the difference between case S and W is equal approximately $3.7\;[\textrm{s}]$. The dark blue region on the plots in the bottom right corner corresponds to the situation when there are no impacts between the bell and the clapper, hence, we assume that the launching procedure is never finished. This region size is comparable for all cases.

In summary, the position of the propulsion system can be optimized to reduce the system’s launching time and, consequently, the transient time. In analyzed cases, the possible gain is approximately $4\;[s]$.

Fig. 6

Influence of the parameters $l_{mb}$ and $\varphi _{SP}$ on the maximum accelerations in the supports during transient response (a–f) and launching time $t_{l}$ (g–i) for each analyzed case

Fig. 7

Time traces showing the angular displacement of the bell $\varphi _{1}$, angular velocity of the bell $\dot{\varphi }_{1}$, force generated by linear motor F and horizontal acceleration in the supports $\ddot{x}_{s}$ when: a $l_{mb}=0.18\;[\textrm{m}]$ and $\varphi _{SP}=1.01\;[\textrm{rad}]$. b $l_{mb}=0.23\;[\textrm{m}]$ and $\varphi _{SP}=1.02\;[\textrm{rad}]$. Case S

Fig. 8

Steady state response of the system. a Clapper’s oscillation amplitude b Maximum reaction force in the supports in the vertical direction c Maximum reaction force in the supports in the horizontal direction as function of the $l_{mb}$ and $\varphi _{SP}$ parameters

3.4 Steady-state response

Figure 8 presents maximum clapper’s oscillation amplitude $\varphi _{2}(max)$ and maximum accelerations $\ddot{y}_{s}(max)$, $\ddot{x}_{s}(max)$ depending on the $l_{mb}$ and $\varphi _{SP}$ parameters for case N. This figure refers to the steady-state response of the system, transient time is omitted.

Considering clapper oscillations (Fig. 8a) we can observe the lines that correspond to the transitions between different ringing schemes presented in Fig. 5. This is because the clapper motion determines the ringing schemes. The clapper angular displacement increases with the bell-swinging amplitude. The influence of the parameter $l_{mb}$ on the clapper angular displacement is minor compared to the parameter $\varphi _{SP}$. The asymmetric ringing schemes are pronounced in the figure. Figure 8b and c present maximum accelerations $\ddot{y}_{s}(max)$, $\ddot{x}_{s}(max)$ values. In both figures, there are also visible lines corresponding to transitions between different ringing schemes. In the case of the vertical direction, the magnitude of the maximum acceleration is determined mainly by the ringing scheme, i.e., the number and type of collisions between the bell and the clapper. Therefore, the greatest vertical accelerations are observed for a working regime with 4 impacts per one period of motion. On the other hand, Fig. 8c suggests that the maximum horizontal accelerations are observed when the swinging amplitude of the bell and the inertia of the system are the greatest (extreme values of $l_{mb}$ parameter). Moreover, the excitation force is acting only in the horizontal direction, influencing the $\ddot{x}_{s}$ values. Accelerations in the horizontal direction are still somehow determined by the ringing scheme, however, the inertia of the bell and excitation force are predominant. The maximum acceleration values in the horizontal direction are approximately 40% greater than in the vertical direction. Parameter $l_{mb}$ has minor influence on the $\ddot{y}_{s}(max)$, $\ddot{x}_{s}(max)$ in comparison to parameter $\varphi _{SP}$.

4 Conclusions

In the paper, we assess the influence of the propulsion design on the system response. We focus on the transient response. Some attention is paid to steady-state motion because we show that the same attractors are reached regardless of the investigated case. In the analysis, we use the validated mathematical model of the novel yoke–bell–clapper system with variable geometry. We investigate three exemplary configurations of propulsion. Using a sample-based approach for each configuration, and we perform 100,000 numerical trials for various yoke geometries and swinging amplitudes. After the analysis, the following conclusions were drawn:

• Lowering the propulsion system vertically with respect to the yoke axis of rotation decreases the launching time of the bell at the cost of increased horizontal accelerations in the supports during transient time.

• The vertical accelerations during the transient time are increased when the linear motor is closer to the yoke axis of rotation.

• Considering steady-state response, the accelerations in the supports in the vertical direction depends mainly on the number and type of impacts between the bell and the clapper, while accelerations in the horizontal direction are predominantly determined by the inertia of the bell.

• Regardless of the propulsion system set-up, the steady-state response of the system is considered the same (As shown in Fig. 5)

The last conclusion somehow diverts attention from proper propulsion system design. When the control for the bell is designed, attention is paid only to the appropriate ringing scheme. However, what was shown in this paper, in practice, one may obtain the desired ringing scheme in different ways with distinct propulsion system designs and consequently with different transient responses of the system. The presented results are of practical importance as they enable the tool to optimize the system’s transient response in terms of reducing the time needed to achieve proper ringing and minimizing unwanted overloads of yoke bearings and supporting structure. The presented outcomes are the first comparative analysis considering different propulsion designs for the yoke–bell–clapper system. The subject of the analysis contributes to the topic devoted to the dynamic interaction between the bells and their supporting structures that is recently widely considered by the scientific community.