1 Introduction

Natural phenomena involve the risk of undesired cable vibration on such cable structures as power transmission lines or cable-stayed bridges. The type of vibration depends on the phenomenon that causes the dynamic load. Wind may cause aeolian vibration when the periodic shedding of vortices results in high-frequency and low-amplitude vibration. Wind acting on a transmission line conductor with asymmetric cross section may lead to galloping that is characterized by high amplitude and low frequency. High-amplitude vibration may also develop after ice shedding from a conductor, although only the first few cycles involve risk of damage in this case, because the vibration decays due to structural damping. High-amplitude vibrations are associated with great dynamic forces, which may damage the elements of the structure in a relatively short time. High-frequency, low-amplitude vibrations are not so destructive in general, but their repeated occurrence may be harmful due to fatigue of the cable. These issues justify the effort made in order to develop methods to attenuate cable vibration in relevant engineering structures.

Viscous dampers and torsional dampers help reduce the amplitude of high-frequency vibrations in bridges and in transmission lines [1]. One of the first devices that was applied on power transmission lines to attenuate aeolian vibration is the Stockbridge damper. This device was designed to dissipate vibration energy by moving two end-masses with multiple resonant frequencies [2]. The magnetorheological damper is another conventional vibration control technique that was implemented on stay cables of bridges [3]. High-amplitude vibrations of transmission line conductors may be mitigated by forming bundles of several conductors with spacer dampers or by connecting phases with interphase spacers [4, 5]. The effects of spacer dampers on conductor vibration following sudden ice shedding were examined in [6]. Conductor vibration due to ice shedding propagation was simulated in [7], where authors also revealed the diminishing effects of interphase spacers on the vibration. The limitations of passive dampers motivated the research to develop semi-active and active control methods, as the semi-active control method in [8] or the voice coil motor-based active vibration absorber in [9].

The vibration system is controlled digitally by a computer when active control is applied. Samples are taken in discrete time intervals in such systems, and the corresponding control force acts after processing the measured data. Time delay due to sampling and processing tends to destabilize dynamical systems, and above a critical value of time delay, successful control becomes impossible [10,11,12,13]. The effects of time delay on vibration control of a suspended cable at a specific location was studied in the author’s recent research [14]. Results revealed that the limitation in the control due to time delay concerned the case of highest excitation frequencies that may consider wind effect, because successful control required very quick sampling in that case. When the control force is provided by a motor via mechanical driving, then backlash occurs at the driving of the motor. The control force is not transmitted in the domain of backlash each time when the motor changes the direction of rotation, as it is the case e.g. for gear pairs [15]. Backlash may lead to the fact that the equilibrium of the vibration system cannot be stable, but a periodic motion appears around this equilibrium. When a suspended cable is exposed to wind, then a periodic excitation acts on the corresponding vibration system, and a periodic motion develops around the equilibrium. The aim of the control in this case is to reduce the amplitude of that periodic motion. The influence of backlash in such vibration control was investigated in [16], where conclusions warned that successful control with backlash might require a driving system that can produce frequent changes in the direction of rotation.

Both of time delay and backlash influence the stability of vibration systems and result in limitation of the vibration control. Considering them together is a challenging problem in the modelling and in providing successful control as well. Apart from the combined limitations due to time delay and backlash, an irregular motion arises that was observed in delayed piecewise linear systems [17, 18]. The main goals in the present paper are (i) constructing a simplified mechanical model for the controlled vibration of a suspended cable considering time delay due to sampling and backlash at the driving; (ii) providing the conditions for control that successfully reduces vibration amplitude when periodic excitation acts in such systems; and (iii) characterize the resulting motions. Accordingly, this paper first explains the mechanical model. Then, a parameter set-up is chosen according to a validated procedure and that describes a specific position of a transmission line conductor with wind effect. This is followed by the stability analysis that provides the control parameters required for successful vibration attenuation, and their dependence on the sampling delay. Then, results that are obtained by the application of the model are discussed. They concern the conditions of successful control and the dynamics of resulting motions. Finally, conclusions are drawn from these results.

2 Mathematical model of controlled cable vibration

This section presents the details of the mathematical model that describes controlled cable vibration with time delay and backlash. Vibration control is achieved by the application of an electrical vibration absorber on the cable or conductor. Construction of the model and the related parameters are based on transmission line conductors, but the model can be adapted for other applications, e.g. for cables that support bridges. The model is simplified so that it consists of the conductor at the position where the vibration absorber is attached and the vibration absorber itself. The electrical vibration absorber implements active vibration control that determines the control force from sampled data and applies this force after a short time delay following the data measurement. In a possible design, the origin of control force is a DC motor and the force is transmitted via a teeth belt where backlash occurs.

2.1 Forced vibration of conductor with vibration absorber

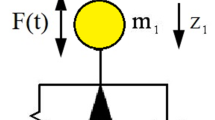
The mathematical model of the conductor with vibration absorber is a two-degree-of-freedom (2DOF) system that considers the vibration absorber and the conductor reduced to the position where the absorber is attached. Such simplified model for the conductor was proposed in [19] that studied the effects of ice shedding on a spacer damper fixed at mid-span in a conductor bundle. This model was further developed in [14] and [16] in order to become applicable to consider the conductor at any position. The present model is based on that of [14], which is improved in three aspects: (i) the location of the absorber is considered when the natural frequencies are prescribed for the calculation of the mass of reduced conductor and the spring stiffness of the absorber; (ii) the damping of the absorber is not neglected; (iii) backlash at the driving is taken into account. The 2DOF model applied in the present research is shown in Fig. 1. Vibration occurs mainly in the vertical direction that is indicated by z. The model involves mass, spring and damping that are denoted by m, k and c, respectively. Index 1 refers to the conductor, whereas index 2 refers to the vibration absorber. Force excitation F(t) is applied on mass m1, which may consider wind effect. The control force u(t) acts between masses m1 and m2.

Fig. 1
figure 1

2DOF model of conductor with vibration absorber

Full size image

The parameters of the vibration system m1, k1, c1, m2, k2 and c2 are determined from the geometrical and material properties of the conductor and absorber. The calculation of the spring stiffness of the conductor k1 is based on the statics of suspended cables [20]. The vertical displacement of the conductor wp can be determined at any position \(0 \leqslant x \leqslant L\), where L is the span length, when a vertical point load Pz is applied at a specified position \(0 \leqslant {x_p} \leqslant L\) as follows

$${w_p}\left( x \right)=\left\{ {\begin{array}{*{20}{c}} {\frac{{{P_z}L}}{{H+h}}\left[ {\left( {1 - \frac{{{x_p}}}{L}} \right)\frac{x}{L} - \frac{{\mu gLh}}{{2 H{P_z}}}\frac{x}{L}\left( {1 - \frac{x}{L}} \right)} \right]}&{0 \leqslant x \leqslant {x_p}} \\ {\frac{{{P_z}L}}{{H+h}}\left[ {\frac{{{x_p}}}{L}\left( {1 - \frac{x}{L}} \right) - \frac{{\mu gLh}}{{2 H{P_z}}}\frac{x}{L}\left( {1 - \frac{x}{L}} \right)} \right]}&{{x_p} \leqslant x \leqslant L} \end{array}} \right.$$
(1)

In Eq. (1), µ denotes the mass per unit length of the conductor, g is the gravitational acceleration, H is the initial horizontal tension in the conductor, and h is the additional horizontal tension due to the application of the force Pz. The additional horizontal tension can be obtained as the solution of a cubic equation that includes further parameters, the Young’s modulus E and the cross section A of the conductor, and the sag f. In the present model, the force Pz acts at the position of the absorber, and the vertical displacement wp should be known at the same position; therefore, x = xp should be substituted in Eq. (1). The relationship between the force Pz and the displacement wp is approximately linear for small displacements that characterizes the high-frequency, small-amplitude vibrations of transmission line conductors. The spring stiffness of the conductor k1 is obtained from the linear approximation of the force-displacement relationship when the vertical force is varied in the proximity of the weight of absorber

$${k_1}=\frac{{\Delta {P_z}}}{{\Delta {w_p}}}$$
(2)

The mass of the absorber m2 is based on its design. Once the spring stiffness of the conductor k1 is determined, and the mass of the absorber m2 is known, then the mass of the conductor m1 and the spring stiffness of the absorber k2 can be calculated together from the dynamics of suspended cables [21]. These parameters are obtained from the condition that the natural frequencies of the 2DOF system are equal to two of the natural frequencies at dominant vertical vibration modes of the conductor. One of them is the first vertical mode, and the second one is a mode that has local maximum close to the position where the absorber is installed.

The damping coefficient of conductor c1 is calculated from the formula

$${c_1}=2{m_1}{\omega _1}\zeta$$
(3)

where ω1 is the natural circular frequency of the single DOF system that describes the conductor at the position where the vibration absorber would be placed, and ζ is the damping ratio of the conductor that can be obtained experimentally [6]. The damping coefficient of the absorber c2 was neglected in [14], and that model provided a close approximation of the first peak in the vibration after force removal. The damping coefficient c2 is determined in the present model from comparing the decay of conductor vibration following load removal at the position where the absorber is fixed with that obtained under the same conditions by a finite element model that was developed and validated in [6]. Calculation of the damping coefficient c2 this way assures a close estimate of not only the first peak in the vibration, but the period and the logarithmic decrement as well.

The excitation force F(t) considers wind effect and is written in the form of a harmonic function

$$F\left( t \right)={F_m}\cos \left( {\omega t} \right)$$
(4)

where Fm and ω are amplitude and circular frequency, respectively, of the excitation. The amplitude is calculated from the lift force that acts in the vertical direction. The circular frequency is determined so that it characterizes aeolian vibration of transmission line conductors. The frequency of such vibration is in the range of 3-150 Hz [4, 5].

2.2 Vibration control with time delay

The vibration absorber is an auxiliary system that is attached to the primary system and that provides a force to balance the excitation force. If the natural frequency of the absorber, which is determined by its mass and its elastic properties, is tuned to the natural frequency of the primary system and the excitation frequency is also close to that frequency, then the absorber functions as a passive control. However, the application of active control may be efficient to reduce vibration amplitude even if the excitation frequency varies in a wide range. The PD control strategy practically means that the spring stiffness and the damping coefficient of the vibration absorber can be changed during the vibration according to measured displacement and velocity data. The preceding research [14, 16] applied PD control, although Reference [16] also discussed some issues concerning the integral term in a PID control.

The control system measures the displacement and velocity of the conductor at the position where the absorber is attached, then a control force is calculated from these data, and this force is applied on the conductor. Consequently, the response to the measured data is provided after time delay. Then, the control force can be written in the following form

$$u\left( t \right)=P{z_1}\left( {t - \tau } \right)+D{\dot {z}_1}\left( {t - \tau } \right)$$
(5)

where P and D are the proportional and differential gains, respectively, and τ is the time delay. The proportional gain P is determined so that considering spring stiffness k2 as well, the vibration absorber will be adequately tuned for the actual excitation frequency. Thus, if ω denotes the excitation circular frequency, then the proportional gain can be obtained as follows

$$P={k_2} - {m_2}{\omega ^2}$$
(6)

The vibration control works without the differential gain D, but its application makes the control more efficient in some cases by a faster reduction of the vibration amplitude.

2.3 Backlash at the driving

The PD control may be implemented using a DC motor and a set of mechanical driving units. Driving via gear wheel or teeth belt results in backlash that influences the control and the resulting motion. When the direction of rotation in the motor changes, the control force is not transmitted in the domain of backlash where the contact between the teeth ceases. Let the value of backlash be r0, and assume that the relative displacement Δz = z2 – z1 is directly proportional to the angle of rotation of the DC motor. Reference [16] applied two conditions to imply that the system is in the domain of backlash. Condition 2 is improved here in order to consider in what direction the motor was rotating when it entered into the domain of backlash:

  • Condition 1: The angular velocity of the driving wheel of the motor is zero, which may be expressed using the relative velocity as follows.

$${\dot {z}_2} - {\dot {z}_1}=0$$
(7)

It should be noted that this is an instantanuous equilibrium when the direction of rotation changes. Let Δzbl denote the relative displacement in this time instance.

  • Condition 2: The interval that describes the domain of backlash depends on the sign of relative velocity just before it became zero, and it can be expressed with the relative displacement Δzbl as follows.

    $$\Delta {z_{bl}} - {r_0} \leqslant \Delta z \leqslant \Delta {z_{bl}}\;\text{if the relative velocity was previously positive}$$
    (8a)
$$\Delta {z_{bl}} \leqslant \Delta z \leqslant \Delta {z_{bl}}+{r_0}\;\text{if the relative velocity was previously negative}$$
(8b)

The system is in the domain of backlash as long as the relevant condition (either (8a) or 8(b)) is satisfied.

When the system is outside the domain of backlash, then the computational process first verifies Condition 1. If it is not satisfied then the system is still not in the domain of backlash. If it is satisfied then Δzbl is calculated, Condition 2 is verified, and the system is in the domain of backlash as long as this latter condition is satisfied. In this case, Condition 1 is not verified, because Δzbl and the boundaries of the domain of backlash do not change even if the relative velocity changes its sign. If Condition 2 is not satisfied then the system is outside the domain of backlash, and Condition 1 has to be verified again.

2.4 Equations of motion

The governing equations of motion of the 2DOF model can be written as follows

$${\mathbf{\dot {z}}}\left( t \right)={\mathbf{Az}}\left( t \right)+{\mathbf{b}}u\left( t \right)+{\mathbf{c}}F\left( t \right)$$
(9)

where \({\mathbf{z}}={\left[ {\begin{array}{*{20}{c}} {{z_1}}&{{{\dot {z}}_1}}&{{z_2}}&{{{\dot {z}}_2}} \end{array}} \right]^T}\) is the vector including the coordinates z1 and z2 and their derivatives, or in other words, the displacements and the velocities of the masses modelling the conductor and the absorber. The coefficient matrix A and vectors b and c include the parameters of the vibration system

$${\mathbf{A}}=\left[ {\begin{array}{*{20}{c}} 0&1&0&0 \\ { - \frac{{{k_1}+{k_2}}}{{{m_1}}}}&{ - \frac{{{c_1}+{c_2}}}{{{m_1}}}}&{\frac{{{k_2}}}{{{m_1}}}}&{\frac{{{c_2}}}{{{m_1}}}} \\ 0&0&0&1 \\ {\frac{{{k_2}}}{{{m_2}}}}&{\frac{{{c_2}}}{{{m_2}}}}&{ - \frac{{{k_2}}}{{{m_2}}}}&{ - \frac{{{c_2}}}{{{m_2}}}} \end{array}} \right];\quad \quad {\mathbf{b}}=\left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{{{m_1}}}} \\ 0 \\ { - \frac{1}{{{m_2}}}} \end{array}} \right];\quad \quad {\mathbf{c}}=\left[ {\begin{array}{*{20}{c}} 0 \\ {\frac{1}{{{m_1}}}} \\ 0 \\ 0 \end{array}} \right]$$
(10)

The control force u(t) is given by Eq. (5), but it can be organized in the following form using the vector z and considering backlash

$$u\left( t \right)=\left\{ {\begin{array}{*{20}{c}} {{\mathbf{Dz}}\left( {t - \tau } \right)}&{{\text{outside}}\;{\text{backlash}}} \\ 0&{{\text{domain of}}\;{\text{backlash}}} \end{array}} \right.$$
(11)

where \({\mathbf{D}}=\left[ {\begin{array}{*{20}{c}} P&D&0&0 \end{array}} \right]\) includes the control parameters. The excitation force F(t) is provided by Eq. (4).

In digital control, samples are taken in discrete time intervals. The control is based on the sample-and-hold technique [22, 23], which means that the sampled value and the corresponding control force are assumed to be constants until the next sample is taken. Moreover, the model assumes that the sampling time and the processing delay, i.e. the time that passes between taking a sample and applying the corresponding control force, are equal to each other. Correspondingly, if samples are taken at time instants tj = jτ, j = 0,1,2,…, then the expression of control force that takes this process into account should be modified as follows

$$u\left( t \right)=\left\{ {\begin{array}{*{20}{c}} {{\mathbf{Dz}}\left( {\left( {j - 1} \right)\tau } \right)\quad t \in \left[ {j\tau ;\left( {j+1} \right)\tau } \right)}&{{\text{outside}}\;{\text{backlash}}} \\ {0\quad \quad \quad \quad \quad \quad \quad \quad }&{{\text{domain of}}\;{\text{backlash}}} \end{array}} \right.$$
(12)

If the initial state z0, u0, F0 is known, then the values of these parameters in the subsequent time instants may be obtained from the discrete-time model

$${{\mathbf{z}}_{j+1}}={{\mathbf{A}}_{\mathbf{d}}}{{\mathbf{z}}_j}+{{\mathbf{b}}_{\mathbf{d}}}{u_j}+{{\mathbf{c}}_{\mathbf{d}}}{F_j}$$
(13)

\({u_{j+1}}=\left\{ {\begin{array}{*{20}{c}} {{\mathbf{D}}{{\mathbf{z}}_j}}&{{\text{outside}}\;{\text{backlash}}} \\ 0&{{\text{domain of}}\;{\text{backlash}}} \end{array}} \right.\)

\({F_j}={F_m}\cos \left( {\omega {t_j}} \right)\)

Alternatively, system (13) can be organized in the following form

$${\mathbf{\tilde{z}}}_{{j + 1}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{S}}{\mathbf{\tilde{z}}}_{j} + {\mathbf{\tilde{c}}}F_{j} } & {{\text{outside}}\;{\text{backlash}}} \\ {{\mathbf{S}}^{*} {\mathbf{\tilde{z}}}_{j} + {\mathbf{\tilde{c}}}F_{j} } & {{\text{domain of}}\;{\text{backlash}}} \\ \end{array} } \right.$$
(14)

where \({{\mathbf{\tilde {z}}}_j}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{z}}_j}} \\ {{u_j}} \end{array}} \right]\), \({\mathbf{S}}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{A}}_{\mathbf{d}}}}&{{{\mathbf{b}}_{\mathbf{d}}}} \\ {\mathbf{D}}&0 \end{array}} \right]\), \({{\mathbf{S}}^ * }=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{A}}_{\mathbf{d}}}}&{{{\mathbf{b}}_{\mathbf{d}}}} \\ {\mathbf{0}}&0 \end{array}} \right]\) and \({\mathbf{\tilde {c}}}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{c}}_j}} \\ 0 \end{array}} \right]\)

Further details on deriving the discrete-time model can be found in [14, 22, 23].

3 Parameter set-up and model validation

The mechanical model of the small-scale laboratory set-up of a transmission line described in [6] is constructed as explained in Sect. 2. Dampers should not be located at a node for the expected frequencies of vibration, they are usually placed close to a suspension clamp. The vibration absorber in the present model is attached at one-tenth of the span length where there is no node for the first nine natural frequencies of the conductor. Force excitation is applied at the same position. Since the aeolian vibration is characterized by small amplitude in the range of conductor diameter and the conductor diameter was 3.2 mm in the experimental set-up of [6], the spring stiffness of the conductor k1 is determined from the linear approximation of the force-displacement relationship considering about 7–8 mm below and above the position of the conductor with absorber. The mass of absorber m2 is chosen to be 0.16 kg. The mass of reduced conductor m1 and spring stiffness of absorber k2 are determined from the condition that the natural frequencies of the 2DOF model are equal to the natural frequencies in the first and sixth vertical vibration modes of the conductor. Note that the same natural frequencies are applied to determine the coefficients of Rayleigh damping in the finite element model of [6], which is used for validation as described later in this section. The damping coefficient of conductor c1 is calculated from Eq. (3), and the damping coefficient of absorber c2 is determined as explained in Sect. 2.1. Model parameters were calculated using the commercial software Matlab, and they are listed in Table 1 together with the parameters of the laboratory set-up.

Table 1 Parameters of the conductor and its mechanical model with vibration absorber at one-tenth of the span
Full size table

The static behaviour of the model is validated first. Displacements due to the application of concentrated forces are calculated and compared to the displacements obtained under the same conditions by the finite element model of [6], which was validated by measurements on the same experimental set-up that is modelled here. The force in the modelled small-scale laboratory set-up during small-amplitude vibrations is in the range of 0.1 N. The displacement-force relationships obtained by the 2DOF model and by the finite element model coincide for such forces (see Fig. 2a). Note that the zero force and displacement in this figure mean the weight of absorber and the corresponding vertical position, respectively, and that the additional downward forces and corresponding displacements are positive. The discrepancy reaches 10% when the force exceeds 0.4 N above or below the weight of absorber, since the material behaviour of the conductor could be modelled by a nonlinear spring for higher forces and displacements.

Fig. 2
figure 2

Validation of static and dynamic behaviour of 2DOF model by comparison with finite-element model; a displacement-force relationship when force additional to the weight of absorber is applied; b initial peak in the vibration following the removal of the same load in the two models; c initial peak in the vibration following the removal of the load leading to the same displacement in the two models; d time histories of vibration following the removal of the load leading to displacement of 3.76 mm (0.2 N in the finite element model)

Full size image

The dynamic behavior of the model is validated by simulating the vibration following the removal of concentrated forces and comparing the initial peaks in such vibration to those obtained by the finite element model. Figure 2b shows that the discrepancy between the initial peaks obtained by the two models does not reach 10% as long as the removed force is smaller than 0.4 N. Figure 2c compares the initial peaks when the initial displacements are the same in the two models. It should be noted that the removed force is slightly different in the two models in this case due to the discrepancy of the force-displacement relationships as was discussed in the validation of the static behavior. The coincidence of the two curves is excellent in this case, the discrepancy is below 5% even when the removed force reaches 1 N. Time histories can be compared in Fig. 2d when the initial displacement is 3.76 mm, i.e. the removed force is about 0.2 N. Note that there is a small wave due to a higher-frequency component at the beginning of vibration obtained by the fnite element model. This wave causes a short delay in the appearance of the first peak, that the simplifed model cannot reproduce. Therefore, the initial time instance in the time history obtained by the finite-element model is shifted in Fig. 2d.

Consequently, the simplified, 2DOF model is reliable to simulate vibration at the position of absorber when small forces act what is the case during such small-amplitude vibration as the aeolian vibration.

4 Dynamics of controlled cable motion with time delay and backlash

In this section, first the stability of the controlled system will be examined with particular attention to the effects of time delay. Then, the dynamics of the system with force excitation and backlash at the driving will be investigated numerically in detail. The study is carried out using the commercial software Matlab.

4.1 Stability of the digitally controlled vibration system

Stability analysis of a system similar to that described in Sect. 2 was examined in [14], but the present model is improved as described in Sect. 2.1. The equilibrium z = 0 of system (9) without excitation and control (i.e. \(F\left( t \right) \equiv 0\) and \(u\left( t \right) \equiv 0\)) is asymptotically stable. However, vibration develops when excitation F(t) acts on the system due to wind effect, and the control is applied to reduce the amplitude of the forced vibration. If the control parameters P and D are not chosen properly, then the amplitude of vibration may increase, or the equilibrium may even become unstable. The stability domain of the system without considering time delay is obtained after the application of the Routh-Hurwitz criterion [24]. The z = 0 equilibrium of the controlled system is asymptotically stable if the real parts of all the characteristic roots are negative, which condition is satisfied if all the coefficients of the characteristic polynomial and the Hurwitz determinants are positive. Since the characteristic polynomial of the 2DOF system is a fourth-degree polynomial, the above statement means the following conditions

$${a_j}>0,\quad j=0, \ldots ,4;\quad \quad {H_2}>0;\quad \quad {H_3}>0$$
(15)

where aj, j = 0,…,4, are the coefficients of the characteristics polynomial and H2 and H3 are the 2 × 2 and 3 × 3 Hurwitz determinants, respectively.

Stability chart for system (9) with the parameter values that are listed in Table 1 is drawn in Fig. 3. The coefficient a4 is always positive, the coefficients a0 and a1 may become negative for extremely high values of P and D, respectively, what is out of practical interest. The curves corresponding to the remaining conditions are plotted in Fig. 3. If the time delay is not considered, then the stability domain (shaded in Fig. 3) is infinitely large, and its boundary is defined by the curve H3 = 0. It should be noted that this curve consists of another part for positive values of P and D, but that part is not shown, because the other three conditions shown in the figure are not satisfied there, so the equilibrium is unstable for those values of P and D.

Fig. 3
figure 3

Stability domain on the plane of control parameters P and D when time delay is neglected

Full size image

When time delay is considered, the stability of the z = 0 equilibrium of system (13) without excitation should be examined. This equilibrium is asymptotically stable if all of the characteristic roots are in modulus less than one. In this case, stability conditions may be provided by the Routh-Hurwitz criterion after the application of the Moebius-Zukovski transformation [24] that maps the interior of the unit circle into the left half of the complex plane. The conditions of the Routh-Hurwitz criterion are applied for the coefficients of the polynomial obtained after the Moebius-Zukovski transformation bj, j = 0,…,4, and for the Hurwitz matrices that are constructed by these coefficients Hb2 and Hb3. The stability domain is finite when time delay occurs in the system, and its size shrinks with increasing time delay. Figure 4a and b show stability domains obtained for time delays of 10 ms and 50 ms, respectively. The boundary of stability domains in these figures is determined by the curves b0 = 0 and Hb3 = 0.

Fig. 4
figure 4

Stability domain on the plane of control parameters P and D with time delay considered; a τ = 10 ms; b τ = 50 ms

Full size image

Control parameters are selected considering the results of stability analysis. The choice of the proportional gain P is explained in Sect. 2.2. Reference [14] proposed choosing the differential gain D close to the boundary of stability domain where the absolute value of the differential gain is highest, because it assured an oscillation with the smallest amplitude for a given value of the proportional gain. However, the present model takes the damping of the absorber into account; consequently, the size of the stability domain is significantly greater, and vibration with the smallest amplitude may be achieved if the differential gain in absolute value is significantly smaller than that at the boundary of stability domain. Furthermore, the line that represents b0 = 0 reduces the size of stability domain when time delay increases. Therefore, sampling delay should be considered when choosing differential gain. As an example, if the frequency of excitation is 10 Hz, then P = − 557 N/m according to Eq. (6), and the differential gain at the boundary is D = − 33.7 Ns/m as it can be seen in Fig. 3. However, if the sampling delay is 10 ms, then D = − 15.5 Ns/m at the boundary that is determined by b0 = 0 in this case (see Fig. 4a). If the sampling delay further increases then the absolute value of the differential gain should be even smaller. The equilibrium cannot be stabilized at all for the calculated value of the proportional gain if the sampling delay is 50 ms (Fig. 4b). Practically, it means that if the sampling delay is as high as 50 ms, then the control does not help reducing the vibration amplitude due to an excitation with frequency of 10 Hz. The highest value of the time delay when active control may contribute to reducing the amplitude depends on the excitation frequency. This relationship is depicted in Fig. 5, which means that high-frequency vibration may be reduced by active control only if the sampling delay is in the range of 1 ms or smaller. Sampling delay may be the greatest for an excitation frequency of 4.1 Hz (dotted line in Fig. 5), which is the natural frequency of the 1DOF system representing the conductor without absorber. Active control is not necessary in this case, because the vibration absorber acts as a passive control and reduces vibration amplitude significantly. Control parameters are close to zero; thus, even a high sampling delay will not affect vibration control. Vibration frequency during aeolian vibration is characterized by such frequency or higher, when the maximum sampling delay decreases with excitation frequency. In the example mentioned above, the vibration due to an excitation frequency of 10 Hz may be attenuated by active control if the sampling delay does not exceed about 30 ms.

Fig. 5
figure 5

Variation of maximum sampling delay with excitation frequency when vibration may be attenuated by active control

Full size image

The control force is not transmitted in the domain of backlash, which means that the equilibrium is stable, but the amplitude of forced vibration cannot be reduced. In practice, the system passes the domain of backlash each time when the direction of motion changes. If the backlash is very small then its effects may be negligible. In the other extreme case, when the value of backlash is very high, the system behaves as if control was not applied. In between, the backlash influences the resulting motion what will be discussed in Sect. 4.2.

4.2 Vibration control with sampling delay and backlash

This section is devoted to the description of motion arising in the system that is exposed to force excitation and controlled with both sampling delay and backlash at the driving considered. References [17, 18] found irregular motion in digitally controlled piecewise linear systems where the control was applied in order to stabilize an unstable equilibrium. The motion was characterized to be more complicated than quasiperiodic, but it was not classified as chaotic since it did not satisfy all the conditions of chaos. The motion obtained in the present study also involves control with time delay and backlash that is described by a piecewise linear system, but the control is applied to attenuate the vibration caused by force excitation. The system described by the parameters listed in Table 1 is considered with a specified excitation and with specified control parameters, and the effects of time delay and backlash are studied in details.

Assume that the amplitude and frequency of excitation is 0.5 N and 10 Hz, respectively; and the control parameters are chosen as P = − 557 N/m and D = − 13 Ns/m. Figure 6 shows a typical example for the time history of the displacement of mass m1 that represents the simplified model of the conductor when the sampling delay is 1 ms and the value of backlash is 0.5 mm. The first second of vibration is plotted in Fig. 6a, which represents the effects of control on reducing the initial peak in the vibration. The highest peak above the equilibrium position is about four times greater without control (blue curve) than with control (red curve). However, if time delay and backlash are considered, then this reduction is significantly smaller, the peak in the controlled vibration (green curve) is approximately 63% of that without control. This ratio decreases to almost 50% if the amplitudes of the steady-state vibrations are compared (blue and green curves in Fig. 6b). As it was mentioned in Sect. 4.1, if the value of backlash is very high, then the entire motion occurs in the domain of backlash, meaning that practically no control is applied. In this specific example, it would happen when the value of backlash reaches approximately 3 mm.

Fig. 6
figure 6

Time histories for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m, sampling delay τ = 1 ms, and backlash r0 = 0.5 mm; a first second after initiating the vibration; b steady-state motion (9 s after initiating the vibration)

Full size image

The effects of external perturbation are examined by applying a 3-mm-displacement disturbation at a time instance when the disturbance increases the displacement of the conductor with respect to its equilibrium position. The sampling delay is 1 ms, the value of backlash is 0.5 mm, and the disturbation is added at 0.95 s in Fig. 7a. The first peak in the vibration following the application of the perturbation is significantly greater than that without the perturbation, and then it takes about 15 cycles, i.e. about 1.5 s, to reach the vibration with the same amplitude as was obtained without the perturbation. The sampling delay and the value of backlash increased to 10 ms and 2 mm, respectively, and the disturbation is applied at 0.84 s in Fig. 7b. Time histories show that the first peak after the application of the perturbation did not increase to a greater extent than in the previous case, but it took longer time, i.e. more than 2 s, to reach the vibration with the same amplitude as was obtained without the perturbation.

Fig. 7
figure 7

Time histories for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m, with and without a 3-mm-displacement perturbation; a τ = 1 ms, and backlash r0 = 0.5 mm, perturbation is applied at t = 0.95 s; b τ  = 10 ms, and backlash r0 = 2 mm, perturbation is applied at t = 0.84 s

Full size image

Identifying the domain of backlash would be difficult from the time history or the phase diagram; therefore, the relative velocity \({\dot {z}_2} - {\dot {z}_1}\) during the steady-state motion for sampling time of 1 ms and backlash of 0.5 mm is drawn by the blue curves in Fig. 8. The motion enters the domain of backlash when this relative velocity reaches zero. The red curve is plotted only to visualize the domain of backlash, but the values on the curve have no physical meaning. It shows a value of zero in the domain of backlash, whereas the value is 0.1 outside the domain of backlash. An interval of 0.05 s is enlarged in Fig. 8b, which helps analyze the motion. The relative velocity was positive and changes its sign at 9.065 s. However, it remains negative for two time steps only (i.e. 0.002 s), because it increases. This may be explained by the effects of the spring between masses m1 and m2. After one more time step, i.e. at 9.068 s, the system leaves the domain of backlash via its upper boundary; therefore, the control force acts again. The relative velocity becomes negative in one time step (at 9.069 s) due to the application of the control force; therefore, the system enters to the domain of backlash and the control force is not transmitted again. Consequently, the relative velocity slightly increases again; however, now it does not reach zero, but it becomes decreasing after 9.073 s. The system reaches the other, i.e. the lower, boundary of the domain of backlash at 9.095 s, and then the control force acts again.

Fig. 8
figure 8

Time history of relative velocity \({\dot {z}_2} - {\dot {z}_1}\) (or v2 – v1) in the steady-state motion for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m, sampling delay 1 ms, and backlash r0 = 0.5 mm; blue curve: time history, red curve: 0 inside the domain of backlash and 0.1 outside the domain of backlash; a interval of 0.5 s; b interval of 0.05 s enlarged

Full size image

Phase diagrams showing the trajectories on the \({\dot {z}_1} - {z_1}\) plane in the steady-state motion are drawn in Fig. 9 for the example considered in this section. The sampling delay is 1 ms and the value of backlash is 0.5 mm in Fig. 9a that clearly shows the periodic solutions obtained. The limit cycle is significantly smaller with the application of control (cf. the blue and red curves), and the green curve is obtained in between, which represents the case of control with time delay and backlash considered. The value of backlash is increased to 2 mm in Fig. 9b. The size of limit cycle described by the green curve increases and more frequency components dominate in the motion. Irregularity is observed in the motion when the sampling time increased to 11 ms. The phase diagram of this motion is shown by the green curve in Fig. 9c.

Fig. 9
figure 9

Phase diagrams during steady-state motion for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m; a sampling delay τ = 1 ms, backlash r0 = 0.5 mm; b sampling delay τ = 1 ms, backlash r0 = 2 mm; c sampling delay τ = 11 ms, backlash r0 = 2 mm

Full size image

The behaviour of the motions described above looks periodic; however, the irregularity observed requires further investigation of the characteristics of the motions. Although chaos has no uniformly accepted definition, chaotic motions are characterized by an attractive set, sensitive dependence on initial conditions, topological transitivity, and at least one positive Lyapunov exponent [24,25,26,27]. The attractive set exists in case of the motions described above, and the other characteristics will be examined by applying the fast Fourier transform (FFT), studying the behaviour of trajectories, and calculating the Lyapunov exponents numerically. The Fourier spectra for the case considered in this section are shown in Fig. 10 when the value of backlash r0 = 2 mm, and for two different values of sampling delay. The prevailing frequency of vibration can clearly be seen in Fig. 10a where the sampling delay is 1 ms. This frequency is 10 Hz that corresponds to the excitation frequency. There are two further, but significantly smaller peaks on the Fourier spectrum at 2.2 and 30 Hz. When the sampling delay is 11 ms, then the highest peak still occurs at 10 Hz; however, many other small peaks appear in the Fourier spectrum. These observations suggest that the motions are periodic, but further investigation is recommended in the latter case.

Fig. 10
figure 10

Fourier spectra for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m; a sampling delay τ = 1 ms, backlash r0 = 2 mm; b sampling delay τ = 11 ms, backlash r0 = 2 mm

Full size image

The sensitive dependence on initial conditions may be revealed by the deviation between nearby trajectories. If the trajectories initially are close enough to each other, e.g. z10,b – z10,a = 10− 5 m, and other coordinates are zero initially in both solutions in the examples shown in Fig. 11, then nearby trajectories approach each other in most of the cases. This property is observed even in the example of this section with sampling time of 11 ms (see Fig. 11b) when the irregularity was noticed in the phase plane. However, when the sampling time is 1 ms, then nearby trajectories neither approach nor stretch each other (see Fig. 11a) even though the motion was characterized as periodic.

Fig. 11
figure 11

Deviation between nearby trajectories for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m; a sampling delay τ = 1 ms, backlash r0 = 2 mm; b sampling delay τ = 11 ms, backlash r0 = 2 mm

Full size image

Occurrence of a trajectory in any small domain inside the attractive set during the motion may refer to topological transitivity. A small part of the \({\dot {z}_1} - {z_1}\) phase plane drawn with a trajectory calculated for sampling time of 11 ms in Fig. 9c is enlarged in Fig. 12a. Comparison of Fig. 12a and b illustrates that the trajectory occurs in a significantly greater part of the domain considered when simulation time increases from 10 to 100 s. However, further increasing simulation time from 100 to 1000 s does not mean that trajectories would become denser in this domain (cf. Figure 12b and c). Consequently, these numerical results suggest that the condition of topological transitivity is not satisfied.

Fig. 12
figure 12

Trajectories in a small domain of the \({\dot {z}_1} - {z_1}\) phase plane for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m, sampling delay τ = 11 ms, and backlash r0 = 2 mm; simulation time a 10 s; b 100 s; c 1000 s

Full size image

The Lyapunov exponents are calculated numerically by applying the following algorithm [27]. First, choose an initial orthogonal basis \(\left\{ {{\mathbf{w}}_{1}^{0}, \ldots ,{\mathbf{w}}_{5}^{0}} \right\}\). Then, compute the vectors \(\left\{ {{\mathbf{v}}_{1}^{1}, \ldots ,{\mathbf{v}}_{5}^{1}} \right\}\) by multiplying the basis by the matrix S or S* defined in (14) at the initial condition. Use the Gram-Schmidt orthogonalization to obtain a new orthogonal basis \(\left\{ {{\mathbf{\bar {w}}}_{1}^{1}, \ldots ,{\mathbf{\bar {w}}}_{5}^{1}} \right\}\). Normalize these vectors in order to eliminate the problem of extremely large and small numbers to get the orthogonal basis of the next step \(\left\{ {{\mathbf{w}}_{1}^{1}, \ldots ,{\mathbf{w}}_{5}^{1}} \right\}\). Repeating these steps n times, the Lyapunov exponents may be estimated as follows

$${\lambda _i}=\frac{{\ln \left\| {{\mathbf{\bar {w}}}_{i}^{n}} \right\|+ \ldots +\ln \left\| {{\mathbf{\bar {w}}}_{i}^{1}} \right\|}}{n},\quad i=1, \ldots ,5$$
(16)

Lyapunov exponents are calculated in each time step for the two cases examined in Figs. 10 and 11, and the results are shown in Fig. 13. The Lyapunov exponents that are significantly smaller than zero are not shown in the diagram. The values obtained with at least 1% accuracy are listed in Table 2.

Table 2 Lyapunov exponents obtained for two cases: sampling delay τ = 1 ms, backlash r0 = 2 mm; and sampling delay τ = 11 ms, backlash r0 = 2 mm
Full size table
Fig. 13
figure 13

The largest Lyapunov exponents as calculated in the first 10 s for excitation F0 = 0.5 N, f = 10 Hz, control parameters P = − 557 N/m and D = − 13 Ns/m; a sampling delay τ = 1 ms, backlash r0 = 2 mm; (b sampling delay τ = 11 ms, backlash r0 = 2 mm

Full size image

Results clearly show that all the Lyapunov exponents are less than one. Thus, the Lyapunov exponents confirm the findings of the previous analysis. Although motions that seem irregular may arise in the system studied, but those motions are not chaotic.

5 Conclusion

Model for the active control of forced vibration of suspended cables has been developed in the present study. A formerly preposed model was improved by considering the damping of the vibration absorber that provided the control force, its location along the cable when the system parameters were determined, and backlash at the driving of the control system. Practical applications are transmission line conductors or cable-stayed bridges where the conductor or the cable vibrates due to wind effect. The model considers the conductor or the cable together with the absorber locally where the absorber is placed. The static and dynamic behavior of this simplified model without control was verified by comparing results to those of numerical simulations that had previously been validated by experimental observations. The application of control contributes to reducing vibration amplitude and the first peak of vibration as well. The limitation of the model is that it cannot be applied for high-amplitude vibrations since it was validated for vibrations with amplitudes that are comparable with the cable diameter. However, even low-amplitude vibration covers such practical problems as the aeolian vibration of transmission line conductors.

The stability analysis revealed that the stability domain on the plane of control parameters may significantly shrink with increasing time delay that occurs due to sampling in the digital control. When backlash is also present at the driving, then irregularity was observed in the motion depending on the value of backlash. However, the motion was characterized periodic according to the numerical study. Although nearby trajectories do not approach each other in some cases, but they do not stretch each other either. Orbits are not dense, and the condition of topological transitivity is not satisfied. Furthermore, all the Lyapunov exponents are less than zero. The irregular motion that was obtained in digitally controlled unstable systems with backlash and that was characterized more complicated that quasiperiodic, but not chaotic [18], was not observed in the present study. The similarity between the two studies is that the systems examined are piecewise linear due to backlash, and digital control with time delay is applied in both cases. However, the control is applied to stabilize unstable equilibrium in either case, whereas the aim is to attenuate forced vibration about a stable equilibrium in the other case. It may be concluded that digitally controlled forced vibration in piecewise linear systems results in periodic motions with the irregularities described in Sect. 4. From the practical point of view, unpredictable motion is not expected if control parameters, sampling time and backlash are properly chosen. However, sampling delay and backlash result in limitations in the control. Sampling delay should be small enough for successful control, i.e. in the range of 10 ms when the excitation frequency is around 10 Hz. The maximum sampling delay reduces below 1 ms when the excitation frequency exceeds 50 Hz. The presence of backlash may require quick changes (i.e. in the range of few ms) in the direction of rotation of the driving motor. Backlash does not have great influence on the motion when it is in the range of 0.1 mm or smaller; however, irregulaties in the motion occur if the value of backlash is in the range of 1 mm.