Digital control of cable vibration with time delay

Abstract

A simplified model for active control of vibration of a suspended cable is proposed. The model is constructed so that it considers the dynamic characteristics of the cable at the location where a vibration absorber is attached together with the absorber itself. The control is applicable for attenuating high-frequency, low-amplitude cable vibration due to periodic excitation that may model the wind effect. The methodology to choose control parameters is based on the dynamics of the vibration absorber and the stability analysis of the controlled system. The model takes into account the time delay that is always present in digital control due to sampling. Results reveal that the application of active control reduces vibration amplitude significantly provided that samples are taken in short time intervals. Increasing time delay reduces the effects of control and above a critical value, the vibration amplitude becomes even greater than without control. The importance of time delay grows with increasing excitation frequency, which means a limitation of the application of the control methodology developed. This limitation concerns the highest excitation frequencies.

1 Introduction

Cable structures are often exposed to natural phenomena that induce cable vibration. The main application areas where such problems occur are power transmission lines and cable-stayed bridges. The sources of cable vibration include wind, ice accretion, ice shedding, or impact of another body. The characteristics of the resulting vibration depends on the inducing mechanism. The regular shedding of vortices due to wind results in high-frequency, low-amplitude vibration, the so-called aeolian vibration. Another type of wind-induced vibration, the galloping, is a movement-induced excitation, which leads to high-amplitude, low-frequency vibration. Vibration with a great jump height of the cable may also be caused by shedding of heavy ice chunks from the suspended cable, although the vibration decays due to structural damping. The present paper focuses on high-frequency, low-amplitude vibration.

The aeolian vibration is characterized by frequency in the range of 3–150 Hz and by amplitude in the range of cable diameter [1, 2]. The forces developing during such vibration are relatively small; therefore, quick damage in the cable structure is not probable. However, frequent occurrence of this high-frequency vibration leads to reduced reliability and lifespan due to fatigue of the cable and other accessories of the structure. These problems justified the research effort made in the last few decades in order to develop damping devices and methods to mitigate high-frequency cable vibration. Damping devices have been applied for decades. One of the most commonly used device is the Stockbridge damper whose dynamics was studied in a number of publications [3,4,5]. Several types of dampers have been developed, and they attenuate the vibration to a non-damaging level, but their application has limitations. An overview on the vibration control of transmission lines is presented in [6], including the description of different types of dampers.

Overcoming the limitations of the passive dampers has become the motivation of further research to suppress cable vibration. Saadabad et al. [7] designed a semi-active control method to suppress forced vibrations induced by wind excitation. Wang et al. [8] proposed a voice coil motor-based active vibration absorber for single and multiple frequency vibration control. An active vibration control method was proposed in a recent research [9]. The authors developed the idea of an electrical vibration absorber that can be installed at any location of the cable and that is effective in a relatively wide frequency range. The effects of tuned-mass-dampers on reduction of forced vibration in power transmission lines are investigated and optimum design of such dampers is presented in [10]. Vibration of transmission line conductors may be induced by ice accretion as well; therefore, research efforts has also been made to develop such devices for icing monitoring as the vibration-sag-tension-based sensor [11].

When active control is applied, the time delay must also be taken into account. Consideration of time delay affects the dynamics of the controlled system. In general, increasing time delay tends to destabilize the dynamical system [12,13,14,15]. When a system is controlled digitally by a computer, then samples are taken in finite time intervals and the action of control system is applied after processing the measured data. Thus, sampling delay and processing delay are included in the system that can be described by a discrete-time model. Time delay influences the stability of such systems as well [16]. Samukham [17] proposed an approach to quickly generate stability charts for delay differential equations that govern dynamic processes involving time delay. In most of the studies, time delay is an undesired property of the dynamics, but it is also employed as a control design parameter. Olgac and Holm-Hansen [18] proposed an active vibration absorption technique that utilizes a controlled time delay in the feedback loop. This delayed resonator can remove oscillations for a wide range of frequencies with the proper selection of time delay and feedback gain. The authors also investigated how the delayed resonator could handle time dependent excitation frequency [19]. Active control via a time-delayed absorber was also studied experimentally in [20]. They carried out stability analysis, and examined the efficiency of the time-delayed absorber as well as the effects of the time delay and feedback gain on the performance of the absorber.

The aim of the present study is to build a simplified model for active vibration control with sampling delay of a suspended cable exposed to periodic excitation, and to investigate the effects of time delay in the digital control in detail. The periodic excitation considers the effects of wind under such circumstances that cause high-frequency, low-amplitude vibration. First, construction of the simplified model for cable exposed to wind is described, and a control strategy is applied in order to reduce vibration amplitude. Meng and Kollár [9] proposed two methodologies for the control of such vibration systems: the PID control methodology and the virtual spring stiffness control methodology. Depending on the choice of proportional and differential gains, the PID control may be successful without applying integral gain. The PD control obtained will be considered in the present paper including time delay due to sampling the data that are used to determine the control force. The discrete-time model is then developed, the stability of the system is examined, and the effects of sampling delay on the control is discussed. The vibration control is successful for a wide range of excitation frequencies; however, the sampling delay results in a limitation of the control applied, which is an important conclusion drawn from this research.

2 Mathematical model

The mathematical model of a suspended cable exposed to wind will be constructed in this section. A vibration absorber is attached to the cable, which applies active control so that it reduces the amplitude of cable vibration. The discrete-time model of the system is also developed that can describe the digital control of the system including the cable with absorber.

2.1 Simplified model of cable with vibration absorber exposed to wind

The simplified model of the cable is a vibration system that considers the cable at the position where the absorber is attached together with its elasticity and structural damping, which determines the vertical motion of the suspended cable. Simplified models of cables in a conductor bundle with spacer dampers were proposed in [21]. The mass of cable was represented by a mass in the vibration system, which was assumed in the middle of the span where the spacer damper was also attached to the cable. The elastic behaviour of the cable was based on the statics of suspended cables. That model was applicable in mid-span only, but it also took into account the elasticity of the cable in the transverse direction. The motion that is subject of the present study is principally vertical; therefore transverse motion is not simulated and corresponding parameters are not considered in the model. However, the present model considers the natural frequencies of the modelled system, what is crucial for successful control of the vibration, and the elastic properties are calculated so that the model becomes applicable at positions other than mid-span.

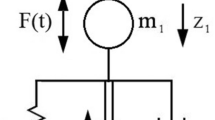
The simplified model of the cable with vibration absorber is the two degree-of-freedom (DOF) system depicted in Fig. 1. The coordinate system is chosen so that x, y and z refer to the longitudinal, transverse and vertical directions, respectively. The simplified model describes motion in the vertical direction that is indicated by z in Fig. 1. The parameters m, k and c denote mass, spring stiffness and damping coefficient, respectively. Index 1 refers to the cable where the excitation F(t) acts, which considers the effects of the wind. Index 2 refers to the vibration absorber that can apply a control force between the cable (m₁) and the absorber itself (m₂). The vibration absorber can be placed at different positions along the cable, and its actual position is considered in the calculation of the parameters of the simplified cable model.

Fig. 1

Simplified model of cable with vibration absorber

The spring stiffness k₁ is determined by the elastic properties of the cable, and it can be calculated based on the statics of suspended cables [22]. If a vertical force P_z is applied on the cable at a specified position x_p along the cable, then the vertical displacement caused by this force at a position x for $0 \le x \le x_{p}$ can be obtained as follows

$$ w_{p} \left( x \right) = \frac{{P_{z} L}}{H + h}\left[ {\left( {1 - \frac{{x_{p} }}{L}} \right)\frac{x}{L} - \frac{\mu gLh}{{2HP_{z} }}\frac{x}{L}\left( {1 - \frac{x}{L}} \right)} \right] $$

(1)

where μ is the mass per unit length of the cable, g is the gravitational acceleration, L is the span length, and H is the initial horizontal tension in the cable. The additional horizontal tension h due to the application of the concentrated force P_z is the solution of the following equation

$$ h^{3} + \left( {2 + \frac{{\lambda^{2} }}{24}} \right)Hh^{2} + \left( {1 + \frac{{\lambda^{2} }}{12}} \right)H^{2} h - \lambda^{2} \frac{{P_{z} H^{3} }}{2\mu gL}\left( {1 + \frac{{P_{z} }}{\mu gL}} \right)\left( {\frac{{x_{p} }}{L} - \frac{{x_{p}^{2} }}{{L^{2} }}} \right) = 0 $$

(2)

where the parameter λ is obtained from the expression

$$ \lambda^{2} = \left( {\frac{8f}{L}} \right)^{2} \frac{EA}{{H\left( {1 + 8\left( {f/L} \right)^{2} } \right)}}. $$

The parameters E and A denote the Young’s modulus and the cross section of the cable, respectively, and f stands for sag. In order to obtain the spring stiffness, the relationship of the force P_z and the displacement w_p at the position x_p should be determined, which may be obtained after substituting x = x_p in Eq. (1). The relationship of the force P_z and the displacement w_p may closely be approximated by a third-order polynomial in a wide range of displacements [21]. However, the amplitude of vibration under examination is in the range of cable diameter; and a linear relationship is acceptable for such small displacements

$$ P_{z} = k_{1} w_{p} $$

(3)

The spring stiffness k₁ is obtained as the tangent of the line fitted on the curve provided by this relationship for small values of displacements.

The damping coefficient c₁ can be determined from the geometrical and material properties of the cable [21, 23]. However, the presence of the vibration absorber changes the damping coefficient locally; therefore, it is determined from comparing the decay of vibration with that obtained under the same conditions by the finite element model that was developed in [24].

The mass m₂ is a constant based on the design of the vibration absorber. The damping c₂ of the vibration absorber is so small that it is neglected in the model. The remaining parameters, the mass m₁ and the spring stiffness k₂ are determined together from the condition that the natural frequencies of the 2DOF system are equal to the first two natural frequencies, in vertical vibration modes, of the cable with the vibration absorber. It should be noted that this calculation may provide complex numbers for the mass and spring stiffness. In this case, the higher natural frequency is increased until either it reaches the next natural frequency of the original vibration system or the value of the mass becomes real number. The in-plane motion of cable vibration consists of antisymmetric and symmetric in-plane modes [22, 25]. The natural frequencies in the nth antisymmetric in-plane mode are given by

$$ \omega_{n,a} = \frac{2n\pi }{L}\sqrt {\frac{H}{\mu }} $$

(4)

The natural frequencies in the nth symmetric in-plane mode are given by

$$ \omega_{n,s} = \beta_{n} \sqrt {\frac{H}{\mu }} $$

(5)

where β_n is the solution of the following transcendental equation

$$ \tan \left( {\frac{1}{2}\beta_{n} L} \right) = \frac{1}{2}\beta_{n} L - \frac{4}{{\lambda^{2} }}\left( {\frac{1}{2}\beta_{n} L} \right)^{3} . $$

These natural frequencies approximate closely those of the system where the vibration absorber is attached to the cable. More accurate calculation of natural frequencies is possible by such a numerical method as the finite element model developed in [23].

The force F(t) due to wind is considered by a harmonic excitation:

$$ F\left( t \right) = F_{0} \cos \left( {\omega t} \right) $$

(6)

where F₀ is the amplitude, and ω is the circular frequency of excitation. The components of the force due to wind that is perpendicular to the plane of the suspended cable are lift and drag, of which the fluctuating component that acts in the vertical direction is the lift force. The amplitude of this force may be calculated from the following formula

$$ F_{0} = \frac{1}{2}C_{L} \rho Av^{2} $$

(7)

where ρ is the air density, A is the cross-section that is exposed to wind, v is the wind speed, and C_L is the lift coefficient that may be obtained from experimental observations [26]. The circular frequency ω is obtained from the frequency that characterizes aeolian vibration.

2.2 Control methodology

The PD control methodology is applied in this study. Meng and Kollár [9] discusses some relevant details of the PID control methodology, including the advantage and disadvantage of the application of the integral term. The control force u(t) without the integral gain can be written as follows:

$$ u\left( t \right) = {\mathbf{Dz}}\left( {t - \tau } \right) = Pz_{1} \left( {t - \tau } \right) + D\dot{z}_{1} \left( {t - \tau } \right) $$

(8)

where

$$ {\mathbf{D}} = \left[ {\begin{array}{*{20}c} P & D & 0 & 0 \\ \end{array} } \right];\quad {\mathbf{z}} = \left[ {\begin{array}{*{20}c} {z_{1} } & {\dot{z}_{1} } & {z_{2} } & {\dot{z}_{2} } \\ \end{array} } \right]^{T} ; $$

P and D are the proportional and differential gains, respectively, and τ denotes time delay. The control parameters are determined from the excitation frequency. When the excitation frequency is equal to the natural frequency of the simplified 1DOF system modelling the cable, then the vibration amplitude of the mass in the primary system may significantly be reduced by the addition of an adequately tuned vibration absorber without applying active control. However, this vibration absorber does not work for different values of the excitation frequency. Therefore, the active control is applied and the proportional gain P is chosen so that together with the spring stiffness k₂, they provide the adequately tuned vibration absorber for the actual excitation frequency. The proportional gain that satisfies this condition is obtained by the following formula

$$ P = k_{2} - m_{2} \omega^{2} $$

(9)

The vibration control works without differential gain D when small absolute values of the proportional gain P should be applied. However, when the excitation frequency is significantly greater than the natural frequency of the primary system, then the attenuation of vibration requires great absolute value of the proportional gain P, and the differential gain D will become necessary for reducing vibration amplitude. The absolute value of the differential gain D increases with that of the proportional gain P, but it is relatively small compared to the proportional gain. The choice of the differential gain will be explained after deriving the stability domain in Sect. 4.

The governing equations of motion of the 2DOF model including control can be organized in the following form:

$$ {\dot{\mathbf{z}}}\left( t \right) = {\mathbf{Az}}\left( t \right) + {\mathbf{b}}u\left( t \right) + {\mathbf{c}}F\left( t \right) = {\mathbf{Az}}\left( t \right) + {\mathbf{Bz}}\left( {t - \tau } \right) + {\mathbf{f}}\left( t \right) $$

(10)

where B = bD; f = cF and

$$ \begin{aligned} & {\mathbf{A}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ { - \frac{{k_{1} + k_{2} }}{{m_{1} }}} & { - \frac{{c_{1} + c_{2} }}{{m_{1} }}} & {\frac{{k_{2} }}{{m_{1} }}} & {\frac{{c_{2} }}{{m_{1} }}} \\ 0 & 0 & 0 & 1 \\ {\frac{{k_{2} }}{{m_{2} }}} & {\frac{{c_{2} }}{{m_{2} }}} & { - \frac{{k_{2} }}{{m_{2} }}} & { - \frac{{c_{2} }}{{m_{2} }}} \\ \end{array} } \right]; \\ & {\mathbf{b}} = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{1}{{m_{1} }}} \\ 0 \\ { - \frac{1}{{m_{2} }}} \\ \end{array} } \right]\quad {\mathbf{c}} = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{1}{{m_{1} }}} \\ 0 \\ 0 \\ \end{array} } \right]. \\ \end{aligned} $$

The first term includes system parameters, the second term with time delay includes the control force, and the third term includes the excitation force. Since a digital computer carries out the control, it is more convenient to use a discrete-time model.

2.3 Discrete-time model

The digital control takes samples of the controlled parameters at discrete time instants or sampling time, and the corresponding control force acts after the processing delay. The control is based on the sample-and-hold technique [27]. The control force is held constant until the next sample is taken, and the time interval between taking samples and the processing delay are the same. Thus, if samples are taken at time instants jτ, j = 1, 2, …, then the control force is written in the form

$$ u\left( t \right) = Pz_{1} \left( {\left( {j - 1} \right)\tau } \right) + D\dot{z}_{1} \left( {\left( {j - 1} \right)\tau } \right)\quad t \in \left[ {j\tau ;\left( {j + 1} \right)\tau } \right) $$

(11)

It can be derived that the solution to system (10) at the first sampling takes the form

$$ {\mathbf{z}}\left( \tau \right) = {\text{e}}^{{{\mathbf{A}}\tau }} {\mathbf{z}}\left( 0 \right) + \int\limits_{0}^{\tau } {{\text{e}}^{{{\mathbf{A}}\left( {\tau - s} \right)}} {\text{d}}s} {\mathbf{b}}u\left( 0 \right) + \int\limits_{0}^{\tau } {{\text{e}}^{{{\mathbf{A}}\left( {\tau - s} \right)}} {\text{d}}s} {\mathbf{c}}F\left( 0 \right). $$

(12)

The initial state z(0), u(0), F(0) is assumed to be known. Then, the discrete-time model is described by the following equation

$$ {\mathbf{z}}_{n + 1} = {\mathbf{A}}_{{\mathbf{d}}} {\mathbf{z}}_{n} + {\mathbf{b}}_{{\mathbf{d}}} u_{n} + {\mathbf{c}}_{{\mathbf{d}}} F_{n} $$

(13)

where

$$ {\mathbf{A}}_{{\mathbf{d}}} = {\text{e}}^{{{\mathbf{A}}\tau }} ;\quad {\mathbf{b}}_{{\mathbf{d}}} = \int\limits_{0}^{\tau } {{\text{e}}^{{{\mathbf{A}}\left( {\tau - s} \right)}} {\text{d}}s} {\mathbf{b}};\quad {\mathbf{c}}_{{\mathbf{d}}} = \int\limits_{0}^{\tau } {{\text{e}}^{{{\mathbf{A}}\left( {\tau - s} \right)}} {\text{d}}s} {\mathbf{c}}. $$

Similarly to Eq. (10), the first term in Eq. (13) includes system parameters, the second term includes the control force, and the third term includes the excitation force. In the dicrete-time model, however, the state z, u, F changes only after each time interval with duration τ.

3 Validation of the static and dynamic behaviour of the model

The model is applied for a representative example that considers the parameters of a small-scale laboratory model of a transmission line described in [24] with a vibration absorber attached at one-tenth of the span length. Parameters of the conductor and the span are given in the first column of Table 1, whereas the parameters of the mechanical model calculated as described in Sect. 2 are listed in the second column of Table 1. Calculations throughout this study including stability analysis were carried out using Matlab.

Table 1 Parameters of the suspended cable and its mechanical model with vibration absorber

The static behaviour of the model is validated by calculating the displacements due to the application of concentrated forces, and comparing them to the displacements obtained under the same conditions by the finite element model of [24]. The force under the conditions describing a small-scale laboratory model of a transmission line is in the range of 0.1 N according to Eqs. (6)–(7), whereas it is at least an order of magnitude greater for full-scale lines. The force–displacement relationships are drawn in Fig. 2a. The simplified model approximates closely, i.e. with difference in the range of few percent, the relationship obtained by the finite element model when the force is in the range of 0.1 N. The discrepancy grows above 20% as the force increases above 1 N. This observation is a consequence of the nonlinear material behaviour of the cable. However, the parameter values in the simplified model depends on the structure examined, and a greater spring stiffness would be chosen to model a full-scale structure where significantly greater forces may act due to wind. It should be noted that if the force varies in a wide range, then a model with nonlinear spring should be applied, as is the case for such high-amplitude vibrations as galloping or vibration following ice shedding.

Fig. 2

Comparison of static and dynamic behaviour of the simplified model and the finite element model of [24]; a displacement due to concentrated force; b initial peak in the vibration following force removal

The dynamic behaviour of the model is validated via simulations of the free vibration following the removal of concentrated forces. The jump height after the force removal, i.e. the initial peak in the vibration, is determined and compared to the initial peak obtained under the same conditions by the finite element model of [24]. According to Fig. 2b, the simplified model overestimates the jump height by about 20%. This discrepancy means a relatively small error in the displacement for forces in the range of 0.1 N, but it becomes substantial for greater values of the forces.

Consequently, the simplified model may be applicable when the external force is relatively small. It means that the model can be adjusted for different size of suspended cables by changing parameter values as long as the force is small enough to cause only small-amplitude vibration. However, the nonlinear material behaviour of the cable should be considered, when modelling high-amplitude vibration with relatively greater forces.

4 Stability of the controlled system

4.1 Stabililty analysis of the controlled system without time delay

The static equilibrium of the cable is stable, but wind causes vibration that should be damped by the application of control. Mathematically, the z = 0 equilibrium of system (10) without excitation and control (which is a linear homogenous system of ordinary differential equations) is stable, but vibration develops due to a harmonic excitation leading to a nonhomogenous system of equations. When feedback control is added, system parameters are changed so that the decay of vibration may be faster; however, the wrong choice of control parameters may make the equilibrium of the system unstable. The stability domain of the system without considering time delay can be obtained by the application of the Routh-Hurwitz criterion [28]. The conditions when the Routh-Hurwitz criterion is satisfied guarantee local stability. The limitation of the linear stability analysis is based on the fact that great enough perturbation leads to nonlinear behaviour of the spring modelling cable elasticity. Thus, the linear model in this case will not be applicable as was discussed in Sect. 2.1, and consequently, the stability is not guaranteed for such great perturbations.

The z = 0 equilibrium of the homogenous system with control is stable if the real parts of all of the characteristic roots, i.e. the zeros of the characteristic polynomial

$$ p_{1} \left( \lambda \right) = \det \left( {\lambda {\mathbf{I}} - \left( {{\mathbf{A}} + {\mathbf{B}}} \right)} \right) $$

(14)

are negative, where I is the identity matrix. This polynomial is a fourth-degree polynomial for the present model, i.e. p₁(λ) can be written in the form

$$ p_{1} \left( \lambda \right) = a_{4} \lambda^{4} + a_{3} \lambda^{3} + a_{2} \lambda^{2} + a_{1} \lambda + a_{0} . $$

(15)

The Routh-Hurwitz criterion assures asymptotic stability if the coefficients of the polynomial a₀, …, a₄ and the 2 × 2 and 3 × 3 Hurwitz determinants, H₂ and H₃, respectively, are positive:

$$ \begin{aligned} & a_{j} > 0,\quad j = 0, \ldots ,4;\quad H_{2} = \left| {\begin{array}{*{20}c} {a_{1} } & {a_{0} } \\ {a_{3} } & {a_{2} } \\ \end{array} } \right| > 0\; {\text{and}}\;\\ & \quad H_{3} = \left| {\begin{array}{*{20}c} {a_{1} } & {a_{0} } & 0 \\ {a_{3} } & {a_{2} } & {a_{1} } \\ 0 & {a_{4} } & {a_{3} } \\ \end{array} } \right| > 0.\end{aligned} $$

(16)

Stability analysis is carried out for the example that is described by the parameters listed in Table 1, and stability domain is shown in the plane of control parameters. The coefficients a₀, a₁, a₄ of the characteristic polynomial are positive numbers independently on the control parameters. The coefficients a₂ and a₃ provide upper boundary for P and D, respectively. The corresponding lines are drawn by the dashed lines in Fig. 3. The conditions for the Hurwitz determinants are plotted by the dash dotted line and the continuous curve. The main part of the stability domain when all the four conditions are satisfied is found in the quarter where both of the control parameters are negative, but stability conditions are also satisfied for some small positive values of P and D. Note that the condition for the 3 × 3 Hurwitz determinant is represented by a quadratic curve that consists of another part for positive values of P and D, but that part is not shown in the figure, because the other three conditions, i.e. a₂ > 0, a₃ > 0 and H₂ > 0, are not satisfied, and thus, the system is unstable there.

Fig. 3

Stability domain on the plane of control parameters P and D for the system of cable with absorber neglecting time delay; the boundary is determined by the curve H₃ = 0

The proportional gain P is chosen by Eq. (9) as it was already explained in Sect. 2.2. In order to choose the differential gain D, the results of stability analysis and the behaviour of the particular solution are considered. For a given value of P, when D decreases inside the stability domain, i.e. when it increases in absolute value, the real part of the characteristic root with the greatest real part increases, then it becomes positive at the boundary of the stability domain. This is indicated by the vertical line in Fig. 3 with a circle where it reaches the boundary of the stability domain. The stability domain is obtained by studying the homogeneous system; however, the motion of the system with the excitation force is described by the sum of the homogenous and particular solutions. Since the excitation is assumed to be harmonic, the particular solution can be written in the form

$$ {\mathbf{z}}_{p} = {\mathbf{z}}_{1} \cos \left( {\omega t} \right) + {\mathbf{z}}_{2} \sin \left( {\omega t} \right). $$

(17)

After substitution into the equations of motion (10) with neclecting time delay and assuming that f = f₀cos(ωt), the constants z₁ and z₂ are calculated as follows

$$ {\mathbf{z}}_{2} = \left( {\omega {\mathbf{I}} + \frac{1}{\omega }\left( {{\mathbf{A}} + {\mathbf{B}}} \right)^{2} } \right)^{ - 1} \cdot {\mathbf{f}}_{0} \quad {\text{and}}\quad {\mathbf{z}}_{1} = - \frac{1}{\omega }\left( {{\mathbf{A}} + {\mathbf{B}}} \right) \cdot {\mathbf{z}}_{2} . $$

(18)

When D decreases for a fixed value of P, e.g. the pair of control parameters is varied along the vertical line toward the circle in Fig. 3, the amplitude of the particular solution decreases. In other words, D should be chosen close to the border of the stability domain in order to obtain an oscillation with as small as possible amplitude. Therefore, first the value of P is determined by Eq. (9), then the value of D is chosen near the boundary of the stability domain.

4.2 Stabililty analysis of the controlled system with time delay

In order to show the effects of time delay on the stability of the controlled system, stability analysis of system (13) without excitation is also carried out. Again, the z = 0 equilibrium of system (13) without excitation and control is stable, but vibration develops due to the excitation. When feedback control is added, the decay of vibration may be faster; however, the equilibrium of the system becomes unstable for the wrong choice of control parameters. The z = 0 equilibrium of the homogenous system with control is asymptotically stable if all of the characteristic roots are in modulus less than one, i.e. the zeros of the characteristic polynomial

$$ \tilde{p}_{2} \left( {\tilde{\nu }} \right) = \det \left( {\tilde{\nu }{\mathbf{I}} - \left( {{\mathbf{A}}_{d} + {\mathbf{b}}_{d} {\mathbf{D}}} \right)} \right) $$

(19)

lie inside the unit circle of the complex plane. Criteria for the asymptotic stability of the system considering time delay can be obtained from the Routh-Hurwitz criterion after applying the Moebius-Zukovski transformation

$$ \tilde{\nu } = \frac{\nu + 1}{\nu - 1}. $$

(20)

Thus, the polynomial $\tilde{p}_{2} \left( {\tilde{\nu }} \right)$ given by Eq. (19) has all its roots in the interior of the unit circle if and only if the polynomial

$$ p_{2} \left( \nu \right) = \left( {\nu - 1} \right)^{4} \tilde{p}_{2} \left( {\frac{\nu + 1}{\nu - 1}} \right) = b_{4} \nu^{4} + b_{3} \nu^{3} + b_{2} \nu^{2} + b_{1} \nu + b_{0} $$

(21)

satisfies the Routh-Hurwitz criterion. In other words, conditions (16) after replacing the coefficients a_j by b_j, j = 0, …, 4 gurantee stability.

Stability charts are drawn in Fig. 4 for two different values of time delay. The conditions b₃ > 0 and b₄ > 0 are satisfied in the entire domain shown in the figure; therefore they are not indicated. When time delay is present, the size of the stability domain becomes finite, and it decreases with increasing time delay. The stability domain is bounded by the curves b₀ = 0 and H₃ = 0. The entire stability domain is not shown in Fig. 4a, because it is significantly bigger than the visible part, and the same scale was chosen in Fig. 4a, b for the sake of better comparison. It should be noted that although the size of stability domain shrinks with increasing time delay, the case P = 0; D = 0 always remains stable, because the equilibrium of the system without excitation and control is stable. It will be shown in Sect. 5 that the amplitude of oscillation due to excitation cannot be decreased by the application of control if the time delay is not small enough.

Fig. 4

Stability domains on the plane of control parameters P and D for the system of cable with absorber considering time delay τ; the boundary is determined by the curves b₀ = 0 and H₃ = 0; a τ = 0.02 s; b τ = 0.04 s

5 Dynamics of the controlled system with time delay

Dynamics of the uncontrolled and controlled systems is compared in this section. This study reveals the effects of control on the vibration under consideration together with the effects of time delay due to sampling. The success of control and the sensitivity on the time delay depend on the excitation frequency; therefore, results are presented for varying values of this parameter.

The subject of this study is the mechanical model whose parameters are listed in Table 1. The amplitude of the excitation force is obtained from Eq. (7), and it is in the range of 0.1 N and 1 N in a 1-m-long section of a small-scale model and in a full-scale model, respectively, of a suspended conductor. The excitation frequency is varied up to 50 Hz. In the simulations where time histories are examined the initial conditions are determined so that they correspond to a displacement that is caused by a force of 0.2 N acting on mass m₁ without initial velocity.

Typical time histories of the motion of the mass m₁ modelling the cable where the vibration absorber is attached are plotted in Fig. 5. They are obtained in three cases for the same parameter values, for excitation amplitude of 0.2 N, and for excitation frequency of 20 Hz: (i) without active control; (i) with control, time delay neglected; (iii) with control, time delay of 10 ms is considered. The application of control reduces the initial peak during the vibration to less than one-fifth of its value without control, although this reduced value is more than double with time delay considered. The rate of reduction in the amplitude of vibration is significantly smaller, but it takes several seconds to reach the steady-state amplitude without control, whereas it is reached in a fraction of a second with control. The rate of reduction in the initial peak and in the vibration amplitude depends on the excitation frequency and on the time delay. This will be discussed in the following.

Fig. 5

Time histories of vibration of mass m₁ modelling the cable where the vibration absorber is attached

The vibration amplitude may be reduced close to zero even without the application of active control when the excitation frequency is equal to the natural frequency of the primary system including mass m₁ and spring k₁. This is the case of passive control with the application of a dynamic vibration absorber (see e.g. [29]), because the auxiliary system including mass m₂ and spring k₂ is attached. However, two high peaks occur when the excitation frequency is equal to the natural frequencies of the 2DOF system. The amplitudes at these peaks can be reduced by a factor of more than ten by the application of active control. When the excitation frequency increases, then the amplitude is reduced to a smaller extent. The effects of active control on steady-state amplitude becomes negligible after the excitation frequency exceeds 10 Hz and 20 Hz when the amplitude of excitation force is 0.1 N and 1 N, respectively. These tendencies can be observed in Fig. 6.

Fig. 6

Vibration amplitude of mass m₁ with and without active control; a amplitude of excitation force F₀ = 0.1 N; b amplitude of excitation force F₀ = 1 N

The active control also reduces significantly the initial peak in the vibration. This effect holds in almost the entire range of excitation frequencies considered, i.e. up to 50 Hz, except for excitation frequencies close to the natural frequencies of the 2DOF system. These results can be observed in Fig. 7.

Fig. 7

Initial peak in the vibration of mass m₁ with and without active control; a amplitude of excitation force F₀ = 0.1 N; b amplitude of excitation force F₀ = 1 N

Time delay due to sampling in the control means that the control required at a given state of the system is applied after the next sample is taken and the system is already in a different state. Obviously, if this delay is too long, then successful control is impossible. Figure 5 shows an example how the amplitude of vibration increases compared to the ideal case when the sampling time is zero. This example also reveals that if the time delay is short enough then the active control still successfully reduces the amplitude and the initial peak of the vibration compared to the case when control is not active. The critical value of time delay above which the control cannot be successful is plotted against the excitation frequency in Fig. 8. The critical time delay is greatest when the excitation frequency is equal to the natural frequency of the primary system, which is 3.7 Hz in the case studied (see the dotted vertical line in Fig. 8). As it was discussed earlier, active control is not necessary in this case, or in other words, the control parameters are chosen closely to zero. Thus, increasing sampling time does not influence the motion considerably, because passive control works and the active control force that is applied with delay is approximately zero. For smaller values of the excitation frequency, the critical time delay becames quite small, i.e. in the range of 1–10 ms. However, the 3.7 Hz frequency mentioned above is around the lower limit of frequencies that characterizes the vibration during such phenomena as aeolian vibration. On the other hand, when the excitation frequency increases, then the critical time delay decreases, but it does not drop below 10 ms for excitation frequencies smaller than 20 Hz. Then, after further increasing the excitation frequency, the critical time delay approaches 1 ms when the excitation frequency exceeds 50 Hz. This result reveals a limitation of the control applied, which concerns the case of high excitation frequency where very quick sampling is required for successful active control. It should be noted that for such high frequencies the amplitude of vibration is very small even without the application of active control; however, the reduction of the initial peak is significant. Therefore, a possible solution for such high-frequency excitations is the application of active control initially, and then turning off the active control.

Fig. 8

Variation of critical time delay with excitation frequency

6 Conclusions

A model is developed for the active control of vibration of suspended cables exposed to high-frequency, low-amplitude periodic excitation. The model simulates the dynamic behaviour of the cable with a vibration absorber at the location where the absorber is attached, and considers the effects of time delay due to taking samples during the control process. Model parameters are determined by the geometrical, material and dynamic properties of the system. The model is reliable provided that relatively small excitation forces are applied what characterizes such wind effects as the aeolian vibration.

The active control successfully reduces the initial peak of the vibration in the frequency range that characterizes aeolian vibration. It is also successful to reduce vibration amplitude from the lower limit of this frequency range up to about 10 Hz. This upper limit depends on further parameters as the amplitude of excitation force. Very quick sampling, i.e. sampling time in the range of 1 ms or lower, is required for successful active control for the highest excitation frequencies, i.e. above 50 Hz. This result reveals a limitation of the control developed, which concerns the case of high excitation frequencies. However, the vibration amplitude that is high enough to cause fatigue in the material of the suspended cable due to high-frequency vibration usually develops for the frequencies when the active control is successful even with relatively longer sampling time.