Rayleigh–Bénard convection of water-aluminum and water-AA7075 nanoliquids in a vertically vibrated very-shallow cylinder

Abstract

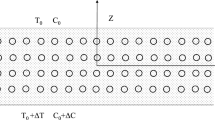
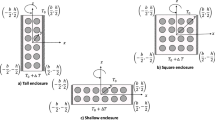
Stability and heat transfer efficiency of the Rayleigh–Bénard-convective system (RBCS) in a vertically vibrated very-shallow cylinder are investigated in the paper for two conventional nanoliquid media, i.e., water-aluminum and water-AA7075 nanoliquids. Using a normal mode solution involving zeroth- and first-order Bessel functions, linear stability analysis is performed. The influence of added aluminum and AA7075 nanoparticles, and sinusoidal waveform of vertical vibration on the onset in a RBCS is reported by obtaining analytical expressions for the marginal and the correction Rayleigh numbers. A minimum number of eigenfunctions is used to arrive at the modified, non-autonomous Lorenz model which is then projected into a Stuart–Landau equation using the method of multiscales. The solution of the Stuart–Landau equation is used to compute the time-averaged Nusselt number. The study reveals that the presence of nanoparticles in water is to destabilize the system and opposite is the influence of vertical vibration. For large frequency of periodic vibrations, its influence on the onset of convection is negligible. Further, the influence of nanoparticles in a baseliquid is to enhance heat transport and this can be used as a remedy for recovering the loss of heat due to a vertical vibration.

Appendix: Derivation of Eqs. (9) from (2)

Applying curl twice on the momentum equation (2) and considering the z component, we get

$$\begin{aligned} \rho _{nl_0} \dfrac{\partial }{\partial t}[\nabla \times (\nabla \times \mathbf {q})]_{{\hat{e}}_z} =&- [\nabla \times (\nabla \times \nabla p)]_{{\hat{e}}_z} + \mu _{nl} \nabla ^2 [\nabla \times (\nabla \times \mathbf {q})]_{{\hat{e}}_z} \nonumber \\&- \nabla \times (\nabla \times [\rho _{nl_0}-\rho _{nl_0}\beta _{nl}(T-T_0)]) g\cdot {\hat{e}}_z. \end{aligned}$$

(A1)

The definition of curl operation on $\mathbf {G}$ in cylindrical coordinate system is:

$$\begin{aligned} \nabla \times \mathbf {G} = \dfrac{1}{r} \left[ \begin{matrix} {\hat{e}}_r \;\;\; & r{\hat{e}}_{\theta } \;\;\; & {\hat{e}}_z \\ \\ \dfrac{\partial }{\partial r} & \dfrac{\partial }{\partial \theta } & \dfrac{\partial }{\partial z} \\ \\ G_r & rG_{\theta } & G_z \end{matrix} \right] , \end{aligned}$$

(A2)

where $\theta$ represents the azimuthal angle, $({\hat{e}}_r, {\hat{e}}_{\theta }, {\hat{e}}_z)$ are unit vectors corresponding to the coordinates $(r, \theta , z)$ respectively and $(G_r, G_{\theta }, G_z)$ are the $(r, \theta , z)$ components $\mathbf {G}$.

Using the above definition of curl into $\mathbf {q}$ (which is two-dimensional) gives us,

$$\begin{aligned} \nabla \times \mathbf {q} = \dfrac{1}{r} \left[ \begin{matrix} {\hat{e}}_r \;\;\; & r{\hat{e}}_{\theta } \;\;\; & {\hat{e}}_z \\ \\ \dfrac{\partial }{\partial r} & 0 & \dfrac{\partial }{\partial z} \\ \\ u & 0 & w \end{matrix} \right] =\left( \dfrac{\partial u}{\partial z}-\dfrac{\partial w}{\partial r}\right) {\hat{e}}_{\theta }. \end{aligned}$$

(A3)

Applying curl once again to Eq. (A3) and considering only the $z -$ component, we get

$$\begin{aligned}\left[\nabla \times (\nabla \times \mathbf {q})\right]_{{\hat{e}}_z} = -\left( \dfrac{\partial ^2 w}{\partial r^2}+\dfrac{1}{r} \dfrac{\partial w}{\partial r}\right) +\dfrac{\partial }{\partial z}\left( \dfrac{\partial u}{\partial r}+ \dfrac{1}{r}u\right) . \end{aligned}$$

(A4)

Using the continuity equation (8) in the above equation gives us

$$\begin{aligned}\left[\nabla \times (\nabla \times \mathbf {q})\right]_{{\hat{e}}_z} = -\nabla ^2 w, \end{aligned}$$

(A5)

where $\nabla ^2 = \dfrac{\partial ^2 }{\partial r^2}+\dfrac{1}{r}\dfrac{\partial }{\partial r}+\dfrac{\partial ^2}{\partial z^2}$.

Further,

$$\begin{aligned} \nabla ^2 [\nabla \times (\nabla \times \mathbf {q})]_{{\hat{e}}_z} = -\nabla ^4 w. \end{aligned}$$

(A6)

Furthermore, applying curl to the gradient of pressure gives us,

$$\begin{aligned} \nabla \times (\nabla p) = \dfrac{1}{r} \left[ \begin{matrix} {\hat{e}}_r \;\;\; & r{\hat{e}}_{\theta } \;\;\; & {\hat{e}}_z \\ \\ \dfrac{\partial }{\partial r} & 0 & \dfrac{\partial }{\partial z} \\ \\ \dfrac{\partial p}{\partial r} & 0 & \dfrac{\partial p}{\partial z} \end{matrix} \right] = 0, \end{aligned}$$

(A7)

The last term of Eq. (A1) is written as:

$$\begin{aligned}\left[\nabla \times (\nabla \times [\rho _{nl_0}-\rho _{nl_0}\beta _{nl}(T-T_0)]) g\cdot {\hat{e}}_z\right]_{{\hat{e}}_z}=-\rho _{nl_0}\beta _{nl} g [\nabla \times (\nabla \times T {\hat{e}}_z)]_{{\hat{e}}_z}. \end{aligned}$$

(A8)

Using curl once to $T {\hat{e}}_z$, we get

$$\begin{aligned} (\nabla \times T {\hat{e}}_z) = \dfrac{1}{r} \left[ \begin{matrix} {\hat{e}}_r \;\;\; & r{\hat{e}}_{\theta } \;\;\; & {\hat{e}}_z \\ \\ \dfrac{\partial }{\partial r} & 0 & \dfrac{\partial }{\partial z} \\ \\ 0 & 0 & T \end{matrix} \right] = -\dfrac{\partial T}{\partial r} {\hat{e}}_{\theta }. \end{aligned}$$

(A9)

Applying curl once again to the above equation and considering only z component, we get

$$\begin{aligned}\left[\nabla \times (\nabla \times T {\hat{e}}_z)\right]_{{\hat{e}}_z}= -\left( \dfrac{\partial ^2 T}{\partial r^2}+\dfrac{1}{r}\dfrac{\partial T}{\partial r}\right) . \end{aligned}$$

(A10)

Substituting Eqs. (A4)–(A7) and Eq. (A10) in Eq. (A1) and rearranging, we get the momentum equation of the form of Eq. (9).