Topology optimization using the discrete element method. Part 1: Methodology, validation, and geometric nonlinearity

Abstract

Structural Topology optimization is attracting increasing attention as a complement to additive manufacturing techniques. The optimization algorithms usually employ continuum-based Finite Element analyses, but some important materials and processes are better described by discrete models, for example granular materials, powder-based 3D printing, or structural collapse. To address these systems, we adapt the established framework of SIMP Topology optimization to address a system modelled with the Discrete Element Method. We consider a typical problem of stiffness maximization for which we define objective function and related sensitivity for the Discrete Element framework. The method is validated for simply supported beams discretized as interacting particles, whose predicted optimum solutions match those from a classical continuum-based algorithm. A parametric study then highlights the effects of mesh dependence and filtering. An advantage of the Discrete Element Method is that geometric nonlinearity is captured without additional complexity; this is illustrated when changing the beam supports from rollers to hinges, which indeed generates different optimum structures. The proposed Discrete Element Topology Optimization method enables future incorporation of nonlinear interactions, as well as discontinuous processes such as during fracture or collapse.

1 Introduction

In structural mechanics, Topology Optimization (TO) refers to a family of computational methods to find structural solutions that optimize a set of target performance indicators under a set of constraints [1, 2]. Common examples are to minimize compliance to certain loads using a prescribed amount of material, or vice versa minimize mass while obtaining a target compliance. TO is valuable in the design of more sustainable structures, where target performance may include minimal material waste or maximum robustness towards uncertainties, linked for example to malicious attacks or climate change. The scope of TO is being further extended by the fast-paced development of additive manufacturing, which is streamlining the production of complex structures that were too difficult and expensive to fabricate in the past [3].

The idea of optimising the use of structural material originates with the seminal work of Michell, who put forward the concept of fully stressed structures [4]. First formulations of TO were based on homogenization methods [5,6,7]. In the 1990s these were largely supplanted by the Solid Isotropic Material with Penalisation (SIMP) method, which proved more efficient especially for complex TO problems requiring discretization and numerical solution [5, 8]. In SIMP-based TO, the objective function to optimize (e.g. minimum compliance to certain loads) is a function of one design variable only: a density field assigning a value between 0 and 1 to each point in the design domain, or to each element in a discretized system. In the objective function, the value of the design variable is raised to a power p, which penalises intermediate values and pushes the optimal solution towards a 0-1, void-solid only configuration. SIMP-based TO problems can be solved using various methods; a particularly efficient and very popular one is the Optimality Criteria method. [8,9,10,11,12]. In recent years TO has expanded to applications in various areas, such as compliant mechanism design [13], natural convection problems [14], and fibre reinforced material design [15], also including new design objectives such as structural vibration [16] and damage tolerance [17,18,19]. New approaches have been developed too, notably based on the Level Set [20, 21] and on the Phase Field methods [22].

When solving a discretized TO problem, the objective function is computed multiple times, typically using the Finite Element Method (FEM)¹. For example, when maximizing structural stiffness, FEM analyses are repeatedly used to compute displacements. The FEM is extremely efficient for linear elastic analyses. Including geometric and mechanical nonlinearities is more demanding, but use of nonlinear FEM analyses is common too [25,26,27]. FEM analyses become more problematic as a structure approaches failure, and indeed applications of topology optimization to problems involving fracture are only very recent [28]. The reliance on FEM analyses has hindered application of TO methods to inherently discrete problems, such as fragmentation, structural collapse, and granular mechanics across length scales (atoms, nanoparticles, colloids, and macroscopic grains). These problems are typically analysed with discrete simulations [29, 30]. Therefore, arguably, a TO scheme that uses for example the Discrete Element Method (DEM) [31] would be desirable.

The DEM is a numerical approach describing the mechanical behavior of assemblies of discrete, interacting particles. The method was first formulated by Cundall [32] and used to describe granular media such as sands, soils, and powders [33]. The DEM can also be applied as an approximation of continua, in particular when describing processes that involve fracture [34, 35], fragmentation [36, 37], or structural collapse [38,39,40]. Rigid body motion, impacts, and geometric and mechanical nonlinearity [41] are naturally captured by explicitly integrating the equations of motion, or by finding static equilibrium configurations using energy minimization techniques. The incorporation of these features into a TO procedure would thus open up applications to a new and wide range of quasi-static and dynamic, discrete problems.

This paper couples DEM simulations with classical SIMP-based topology optimization, leading to a new Discrete Element Topology optimization (DETO) method. Sect. 2 provides a brief background on SIMP-based TO, solved using the Optimality Criteria method, and on the DEM. Sect. 3 presents the optimization problem for a 2D system of disks interacting via harmonic potentials, equivalent to linear elastic springs. A penalization scheme is proposed, whereby the interactions between neighboring particles are modulated by a particle-specific design variable $\chi$. This variable ranges between 0 and 1, akin to the density in continuum-based problems, but we do not call it “density” because its only role is to penalise mechanical interactions, not the inertial behavior of the particles. We then formulate the objective function, which here is the complementary energy of the system, whose minimization leads to maximum stiffness. We propose an approximate updating scheme for $\chi$, which is exact for linear elastic systems under small displacements, but not when geometric or material nonlinearities are significant. However, using a perturbation method, we show that the approximate scheme is satisfactory for the examples in this manuscript. This is detailed in Supplementary Information Section 1. A numerical implementation of the DETO method is provided. Sect. 4 validates the new method by comparing results on simple beams with established ones from the literature. Then a parametric study highlights the effects of mass fraction, filter length, and number of particles per unit volume, which is akin to mesh fineness in FEM. The parametric study highlights the impact of topological complexity on the optimized values of the objective function, confirms that the solutions from DETO are mesh-independent, and shows that the checkerboard problem that may arise in FEM-based optimization is absent in DETO. Finally, Sect. 4 shows that DETO naturally accounts for geometric nonlinearity, which has a marked effect on the optimal topologies. Part 2 of the present manuscript series [42], incorporates material nonlinearity in DETO, generalizing it to problems of ductility maximization under large deformations, and presenting results for several case studies that provide design-relevant insights. All these results indicate the viability of the proposed method, as well as its potential for further development and application to more complex, discrete structural problems.

2 Background on SIMP-TO and DEM

This section presents some basic concepts in SIMP-based Topology optimization and in the Discrete Element Method. The aim is to enable a better appreciation of the innovative aspects introduced later in Sect. 3. Readers who are already familiar with the techniques can proceed directly to Sect. 3.

2.1 Basics of SIMP-based topology optimization

SIMP-based TO is a well established technique that nowadays encompasses sophisticated algorithms and applications, and can include multiple design variables, constraints, and objectives [43, 44]. This section will not cover such richness. By contrast, we will present SIMP-based TO only for one simple but very influential example by Sigmund [45]. Thanks to its simplicity, this example became the entry point into TO for many researchers. We hope for a fraction of a similar success when presenting the same example in the context of our new Discrete Element TO method, later in Sect. 3.

A numerical TO problem starts from defining the boundary conditions, external loads, supports, and spatial domain within which to define the geometric detail of the structure. The domain is discretized into individual elements and, in the SIMP method, each element is associated with one continuously distributed design variable $\chi _e \in [0;1]$. The design variable represents the density of material at that point, between void ($\chi _e= 0$) and fully solid ($\chi _e= 1$). A uniform density field is usually chosen as a starting point and an objective function $c(\varvec{\chi })$ is defined, which specifies the performance indicator to be optimized. $\varvec{\chi }$ is the vector collecting the $\chi _e$ of all the individual elements.

A typical optimization problem is that of stiffness maximization, which can be achieved by minimizing the complementary energy of the system under imposed loads or displacements [2]. For a linear elastic material under small displacements, complementary energy and strain energy coincide, so a problem of stiffness maximization can also be written as:

$$\begin{aligned} \min _{\varvec{\chi }} \;&: \; c(\varvec{\chi }) = \sum _{e=1}^N \; \mathbf{u} _e^T \mathbf{k} _e \mathbf{u} _e \end{aligned}$$

(1)

$$\begin{aligned} \mathrm {subject\;to}&: \frac{V(\varvec{\chi })}{V_0} = f \end{aligned}$$

(2)

$$\begin{aligned}&: 0 \le \chi _{min} \le \chi _e \le 1 \end{aligned}$$

(3)

In Eq.1 the objective function is twice the total, linear-elastic strain energy of the system. $\mathbf{u} _e$ is the vector of nodal displacements at equilibrium under a set of imposed external loads. $\mathbf{u} _e$ depends on $\varvec{\chi }$, but the notation in Eq. 1 omits it for better readability. Eqs. 2 and 3 are constraints that the optimal solution must satisfy. The first constraint fixes the target volume of solid, as $V(\varvec{\chi }) = \sum _e \chi _e$; $V_0$ is V when the whole domain is solid with $\varvec{\chi }= 1$ everywhere; $f\in (0,1)$ is a constant. The second constraint sets the bounds for $\chi _e$ between a minimum value $\chi _{min}$ and the fully solid $\chi _e = 1$. In principle one could use $\chi _{min}=0$, but in this section we will show that a small but nonzero $\chi _{min}$, e.g. $10^{-3}$, is needed for two reasons: first, the element stiffness $\mathbf{k} _e$ will be related to $\chi _e$ in such a way that $\chi _e=0$ would entail $\mathbf{k} _e=0$, making the structural stiffness matrix singular and thus the FEM problem unsolvable; second, $\chi _e>0$ will be required for the type of filtering that will be presented and used in this manuscript.

In Eq. 1, $\mathbf{k} _e$ is the element stiffness matrix. The distinguishing feature of SIMP is that $\mathbf{k} _e$ depends on $\chi _e$ as a power law:

$$\begin{aligned} \mathbf{k} _e = \chi _e^{\,p}\, \mathbf{k} _0 \end{aligned}$$

(4)

where $\mathbf{k} _0$ is a constant, base stiffness matrix. This penalisation scheme plays a central role in the solution of the optimization problem; this will be discussed later in this section. The dependence of $\mathbf{k} _e$ on $\chi _e$, also omitted for clarity in Eq. 1, causes the aforementioned dependence of $\mathbf{u} _e$ on $\chi _e$. At a generic step in the optimization process, the structure features a certain $\varvec{\chi }$ vector and therefore each element has a corresponding $\mathbf{k} _e$; a Finite Element analysis provides the $\mathbf{u} _e$ corresponding to the imposed external loads for the current distribution of $\mathbf{k} _e$, and all this determines the current value of the objective function c.

The optimization problem in Eqs. 1–3 can be solved using various methods. The most popular one is the Optimality Criteria method, which provides the updating scheme, viz. the expressions and algorithms to update $\varvec{\chi }$ at the generic optimization step while respecting the imposed constraints (or tending towards a solution that respects them). Using the Optimality Criteria method and imposing the constraints at each optimization step, Sigmund obtained the following updating scheme [45]:

$$\begin{aligned} \chi ^{\mathrm {new}}_e=\chi ^{\mathrm {old}}_e \cdot \left( -\frac{d c}{d \chi _e}\lambda \right) ^\alpha \end{aligned}$$

(5)

$\frac{d c}{d \chi _e}$ is an entry of the gradient of c with respect to $\varvec{\chi }$, which is called sensitivity. $\alpha = \frac{1}{2}$ is a numerical damping coefficient to improve convergence. $\lambda$ is a parameter that changes at every step of the optimization and rescales the sensitivity so that $\varvec{\chi }^{\mathrm {new}}$ respects the constraint on total volume in Eq. 2. Additional care must be taken to also guarantee that $\varvec{\chi }^{\mathrm {new}}$ falls between $\chi _{min}$ and 1, as per constraint in Eq. 3. This can be achieved by capping the values of $\chi _e$ predicted by Eq. 5, but this would affect the first constraint. Therefore, an iterative algorithm is usually needed to find a value of $\lambda$ that respects both the imposed constraints; for example, the bi-sectioning algorithm implemented by Sigmund [45].

The analytical expression of the sensitivity can be obtained by combining the definition of c in Eq. 1 with the expression of the penalised $\mathbf{k} _e$ in Eq. 4 and applying the adjoint method [2]:

$$\begin{aligned} \frac{d c}{d \chi _e} = -p\chi _e^{\,p-1}\,\mathbf{u} _e^T\,\mathbf{k} _0\,\mathbf{u} _e \end{aligned}$$

(6)

The combined effect of Eqs. 5 and 6 is to push material away from under-utilised areas and move the design towards a solid-void only solution. The penalisation scheme, combined with the presented udating scheme, are only effective if $p>1$; however, a value of $p \geqslant 3$ is usually preferred for reasons linked to the fabrication of actual structures using only void or fully solid parts: see Ref. [46] for discussion on this point. Higher values of p enforce stricter solid-void only solutions and also improve the speed of convergence, but reduce the ability to escape local minima of $c(\varvec{\chi })$ and therefore increase the probability of finding sub-optimal solutions.

2.2 Basics of the discrete element method

The DEM describes a system of mechanically interacting particles. The particles can be subjected to external forces, and exchange interaction forces that depend on their relative positions $\mathbf{r}$ and sometimes orientations. Velocity-dependent dissipative forces are often included too, but here we will not consider them for simplicity, and because in this manuscript we will only address performance at static equilibrium.

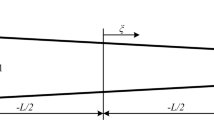
As a simple example of interaction, consider a harmonic potential representing pairs of particles connected by linear springs, as depicted in Fig. 1. The interaction potential energy $U_{ij}$ and the intensity of the repulsive interaction force $F_{ij}$ between the two particles i and j are:

$$U_{ij}= \frac{1}{2} k_{ij}\,\, (r_{ij}-r_0)^2$$

(7)

$$\begin{aligned}&F_{ij}=-\frac{dU_{ij}}{dr_{ij}} = -k_{ij}\,\, (r_{ij}-r_0) \end{aligned}$$

(8)

$k_{ij}$ is the stiffness of the connecting spring, $r_{ij}$ is the inter-particle distance, and $r_0$ is the equilibrium distance.

Fig. 1

Schematic of the interaction force between two particles emerging from a harmonic interaction potential

The displacements of the particles under external and interaction forces can be solved either dynamically, by explicitly integrating Newton’s second law of motion for all particles, or by minimizing the total interaction energy of the system $U_{tot}=\sum _{i,j} U_{ij}$; the latter approach leads to a final configuration at static equilibrium, similar to what one would obtain with a linear-elastic, static FEM solution. Various quantities can be computed during a dynamic solution or at final static equilibrium, including the total strain energy that defined c in the optimization problem in Eq. 1, and that in the example here coincides simply with $U_{tot}$.

3 Methodology

This section starts with introducing the new combination of Topology optimization with DEM-based solutions of structural behavior. A simple implementation of the new method in MATLAB to perform stiffness maximization in 2D problems with circular disks hexagonally packed in rectangular domains, is then presented. The code is available on GitHub [47].

3.1 Discrete element topology optimization

Here we introduce some fundamental changes to the SIMP-TO method in Sect. 2.1 to apply it to a system described using the DEM. The first change is straightforward: the design variable $\chi _e$, which previously was specified for each finite element, here becomes a per-particle quantity $\chi _i$. For the task of maximizing the stiffness of the system, we address the problem of minimizing the complementary energy of the system, $U^*$. In this manuscript we consider the harmonic interaction potential presented in Sect. 2.2, which corresponds to a linear elastic material; nonlinear materials will be addressed in Part 2 [42], Nevertheless, geometric nonlinearities at least are always possible in DEM simulations, therefore one cannot simply equate $U^*$ with the strain energy U of the system. The optimization problem therefore becomes:

$$\begin{aligned} \min _{\varvec{\chi }} \;&: \; c(\varvec{\chi }) = U^*(\varvec{\chi }) = \sum _{i=1}^{N}\mathbf{F} _i\mathbf{u} _i - U_{tot} \nonumber \\&\;\;\;\; = \sum _{i=1}^{N}\mathbf{F} _i\mathbf{u} _i - \frac{1}{2}\sum _{i=1}^N \sum _{j>i}^N\; k_{ij}\,\,(r_{ij}-r_0)^2 \end{aligned}$$

(9)

$$\begin{aligned} \mathrm {subject\;to}&: \frac{V(\varvec{\chi })}{V_0} = f \end{aligned}$$

(10)

$$\begin{aligned}&: 0 \le \chi _{min} \le \chi _i \le 1 \end{aligned}$$

(11)

The term $\sum _{i=1}^{N}\mathbf{F} _i\mathbf{u} _i$ is the external work, viz. the product of the external forces on each particle times their corresponding displacement at equilibrium. If displacements are small, the sum equals $2U_{tot}$ and the FEM-based problem in Eq. 1 is recovered, except that the strain energy now features a sum over all pairs of particles, instead of over individual elements. The interparticle distance $r_{ij}$ and the interaction stiffness $k_{ij}$ are now scalar quantities pertaining to pairs of particles, whereas the FEM framework featured a vector of nodal displacements and a stiffness matrix pertaining to individual elements. The constraints in Eqs. 10 and 11 are the same as for the FEM-based problem. Unlike FEM solvers, DEM algorithms are not compromised if $\chi _i=0$ causes some interactions to vanish (viz. if some $k_{ij}$ are zero). However, here we will still use $\chi _{min}>0$ because of the type of filtering that will be employed: see Eq. 20.

A key change in the DEM framework concerns the penalisation scheme. In the FEM-based approach, since each finite element contributes individually to c, the $\chi _e$ of each element penalises only the stiffness matrix of the element itself, as shown in Eq. 4. In the DEM context, however, $k_{ij}$ is associated with pairs of particles rather than individual ones. Therefore, we propose the following penalisation scheme:

$$\begin{aligned} k_{ij} = \chi _i^p\,\chi _j^p\,k_0 \end{aligned}$$

(12)

where $k_0$ is a constant base stiffness and $\chi _i$ and $\chi _j$ are the design variables of the two interacting particles. The penalisation exponent p plays an analogous role as discussed in Sect. 2.1. If one takes $p=1$ then $k_{ij}$ from Eq. 12 scales as the harmonic average of $\chi _i$ and $\chi _j$, which correctly ensures $k_{ij}=0$ when either $\chi _i=0$ or $\chi _j=0$. However, $p=2$ is used in this manuscript after numerical experiments have indicated that such value provides a good compromise between optimality of the solution, solid-void only result, and numerical performance. Sect. 1 in the Supplementary Information shows simulation results on how p impacts the optimization for the examples considered later in this manuscript.

The penalisation scheme in Eq. 12 imposes that the interaction stiffness $k_{ij}$ is a function of $\chi _i$ and $\chi _j$. Therefore, under a given set of external forces, also the interparticle distance $r_{ij}$ at equilibrium (or at a generic step during a simulated dynamic response) will depend on $\varvec{\chi }$. In Eq. 9 the dependence of $k_{ij}$ and $r_{ij}$ on $\varvec{\chi }$ have been omitted for clarity of notation. The idea of penalizing interactions was previously proposed in the truss optimization method [48], where a set of nodes is defined and the design variables are the cross sectional areas of each bar connecting any pair of nodes. The main difference in Eq. 12 is that penalisation is applied through per-particle $\chi$’s rather than directly to each interaction. This may better suit DE simulations, where often the interactions between particles at or near contact are determined, in reality, by per-particle quantities such as chemical composition or physical and mechanical properties, e.g. the indentation moduli of contacting particles in Hertz potentials [31] or the Young moduli of connected particles in cohesive nanoparticle models [49].

The solution of the optimization problem in Eqs. 9–11 can be obtained with the same updating scheme as in Eq.5. However, computing sensitivity $\frac{dc}{d\chi _i}$ now is more difficult than in Eq. 6, which benefited from simplifications that arise when the adjoint method is applied in the linear regime [2]. In the nonlinear regime, the adjoint method requires the tangent stiffness matrix of the system [2]; we prefer to avoid it because one of the strengths of DEM simulations is to not rely on stiffness matrices. The alternative is to compute directly the change in $U^*$ due to a small perturbation of $\chi _i$, which entails two terms. The first term is the change in $U_{tot}$ when particles stay fixed at their equilibrium position $\mathbf{r} _{eq}$: this is due to the change of interaction stiffness, viz. $\left. \frac{\partial U^*}{\partial k_{ij}}\frac{\partial k_ij}{\partial \chi _i}\right| _{\mathbf{r}=\mathbf{r}_{eq}}$. This is easy to compute, because it does not require any new equilibration of the system. The second term is the change in external work and $U_{tot}$ due to the small change in particle positions, away from $\mathbf{r}_{eq}$, when $\chi _i$ is perturbed. Computing this term is computationally expensive, as one must find a new equilibrium configuration for each perturbation of $\chi _i$. Sect. 1 in the Supplementary Information shows optimization results obtained using a perturbation method, which computes both the terms in the gradients. The same section also shows optimization results where the sensitivity is approximated by its first term only:

$$\begin{aligned} \frac{d c}{d \chi _i} \approx \left. \frac{\partial U^*}{\partial k_{ij}}\frac{\partial k_{ij}}{\partial \chi _i}\right| _{\mathbf{r}=\mathbf{r}_{eq}} = -\frac{1}{2}\sum _{j\ne i} p\chi _i^{p-1}\,\chi _j^p\,k_0\,(r_{ij}-r_0)^2 \end{aligned}$$

(13)

It turns out that, for case studies similar to those in this manuscript (Sect. 4), the approximation in Eq. 13 yields almost identical optimization results as simulations using the full gradient. Also, the values of $\frac{dc}{d\chi _i}$ obtained with the two methods are not very different, meaning that, for the examples in this manuscript, Eq. 13 captures indeed the main part of the gradient of $U^*$. Based on this, we decided to use the more efficient Eq. 13 for the simulations in the body of this manuscript. The applicability of Eq. 13 to other systems should be checked on a case-by-case basis, as the approximation may in principle generate local minima, solutions that differ from those in the original problem, and influence mesh effects too. Instead, the perturbation approach described in the Supplementary Information is general.

Equations 9 to 13 complete the formulation of DEM-based TO for the specific case of stiffness maximization using a harmonic pairwise interaction potential. A full generalisation of the method is beyond the scope of this manuscript, but one immediate and important extension concerns more complex interaction potentials. The harmonic potential considered here represents linear springs connecting the particles; this is analogous to a linear elastic constitutive law in the FEM. However, one can replace the potential in Eq. 7 with a more complex form such as:

$$\begin{aligned} U_{ij...} = k(\chi _i,\chi _j,...)g(\mathbf{r} _i,\mathbf{r} _j,...) \end{aligned}$$

(14)

where k is now a generic function of the design variables of the interacting particles, and g is a function of the position vectors r of the interacting particles. The ellipsis indicate that the interactions can involve more than pairs of particle, including three-body terms, four-body, etc. The objective function then simply becomes

$$\begin{aligned} c = U^* = \sum _{i=1}^{N}\mathbf{F} _i\mathbf{u} _i - \sum _{i,j} U_{ij} \end{aligned}$$

(15)

having omitted multi-body terms and ellipsis only for clarity of notation. When the approximation in Eq. 13 holds, the resulting sensitivity would then be:

$$\begin{aligned} \frac{d c}{d \chi _i} \approx \sum _{j,...\ne i} -\frac{\partial k}{\partial \chi _i} \,g(\mathbf{r} _i,\mathbf{r} _j,...) \end{aligned}$$

(16)

Mechanical nonlinearities embedded into $g(\mathbf{r} _i,\mathbf{r} _j,...)$ can be seamlessly considered in this DEM framework. For example, a potential that is widely used in nanoscale materials modeling is the Lennard-Jones potential, which is akin to a nonlinear spring with a softening regime after a peak force in tension. For the Lennard Jones potential, k can be expressed simply as in Eq. 12 and $g=4\left[ \left( \frac{\sigma }{r_{ij}} \right) ^{12} - \left( \frac{\sigma }{r_{ij}} \right) ^6 \right]$, where $\sigma$ is a constant. Writing Eqs. 15 and 16 for the Lennard-Jones potential would thus be straightforward. The details on how to incoporate material nonlinearity in DETO are given in the companion Part 2 manuscript [42].

The numerical efficiency of solving a TO problem is typically governed by the solver to compute the $\varvec{\chi }$-dependent c and sensitivities at each step of the optimization. For the energy minimization problem in this manuscript, efficiency is thus controlled by the FEM or DEM solvers that provide the configuration of the system under load: $\mathbf{u}$ for FEM, $\mathbf{r}$ for DEM. The efficiency of the DEM solver depends on the type of analysis that is performed. For the specific case of harmonic potentials and for sufficiently small external loads, the DEM analysis could also be expressed as a linear algebra inverse problem, as for the FEM in linear elasticity; in such a case, the performance of DEM and FEM would be similar. However, a strength of the DEM is the simplicity to consider geometric and mechanical nonlinearities, also including fracture and rigid motion, both in quasi-static and dynamic regimes. To address this complexity, DEM problems are typically solved using energy minimization or explicit integration, which are more time-consuming than linear-elastic Finite Element analyses. However, the numerical efficiency of the DEM is again comparable with that of the FEM when the latter includes geometric and material nonlinearities, or even fracture [50].

3.2 Numerical implementation of DETO

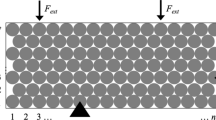
This section describes a simple implementation of the proposed DETO method, to solve the optimization problem in Eqs. 9–11 for a simple 2D system of monodisperse circular disks interacting via a harmonic potential. The initial configuration features $nelx \times nely$ disks² arranged in a close-packed hexagonal lattice that fills a rectangular domain of size $(D\cdot nelx)\times \left( \frac{\sqrt{3}}{2}D\cdot nely\right)$, where D is the disk diameter: see Fig. 2. Initially all disks have $\chi _i = f \in (0,1)$. The parameters nelx, nely, D, and f, are chosen and provided by the user. Various external forces and constraints can be applied to each particle: these will be specified in the next section for each of the examples studied there.

Fig. 2

Hexagonal close packing of DE disks with linear elastic interaction potentials between immediate neighbors

Each particle interacts only with its immediately adjacent neighbors in the hexagonal lattice. The harmonic potential is the same as in Eq. 7, with equilibrium distance $r_0 = D$, stiffness $k_{ij}$ penalised as per Eq. 12, and base constant stiffness $k_0$ chosen by the user. The harmonic bonds are modelled as unbreakable and the particles are not allowed to create new bonds with other particles that initially were not among their first neighbors. This restricts the scope of the DEM, which usually deals with particles that move widely across the system, creating new bonds or colliding with particles that initially might have been far away. In this manuscript, however, we will validate and test the new DETO method for the classical example of a simple beam under point load, for which we expect relatively small deformations. In such applications, the particles will indeed interact only with their initial first neighbors.

Fig. 3 shows the flow chart for the program. First the system geometry is generated from the inputs as explained above, adding also the required external forces and constraints (e.g. pinned or roller supports). The initial neighbor list is recorded and stays the same during the whole simulation, for the reason discussed above. This is much faster than a general case in which the neighbor list must be updated dynamically during the DEM simulation.

Fig. 3

Flow chart of the DETO algorithm implementation

The optimization loop begins by computing the interaction stiffness $k_{ij}$ for each pair of neighboring particles, following Eq. 12. The DEM minimization module computes the particle positions at static equilibrium using a damped dynamics algorithm by Sheppard et al. [51]. The DEM solution is considered as converged when the change in total strain energy between two successive steps is sufficiently small: $\frac{(U_{tot}^{current}-U_{tot}^{previous})}{U_{tot}^{previous}}\le etol$. The values of etol used in this manuscript will be in the $10^{-10} - 10^{-8}$ range. The energy minimization algorithm requires two parameters: a time step dt and a maximum particle displacement allowed at the generic step $d_{max}$. These should be fine tuned depending on the system that the user wants to analyse. The algorithm also uses the masses of the particles, here all set to the same value m.

After the DEM module converges, the DETO program computes the objective function c (i.e. the total interaction energy $U_{tot}$) and the sensitivity to update $\varvec{\chi }$ as per Eq. 13. The stress tensor for each particle is also computed; this is not strictly needed for the optimization process, but knowing the stress field inside the system will support the interpretation of the results. The per-particles stress tensor is based on the virial stress expression [52]:

$$\begin{aligned} \sigma _{ab,i} = \frac{1}{2V_i}\sum _{j\ne i}\left( r_{a,i} F_{ij,b,i} + r_{a,j} F_{ij,b,j} \right) \end{aligned}$$

(17)

$\sigma _{ab,i}$ is the ab (xx, xy, or yy) stress component at particle i, $r_{a,i}$ and $r_{a,j}$ are the a-component (x or y) of the positions of particles i and j, $F_{ij,b,i}$ and $F_{ij,b,j}$ are the b-component of the force on particle i due to the interaction with particle j and vice versa. $V_i$ is the averaging volume, here taken equal to the tributary volume of particle i, viz. $\frac{V_{tot}}{N}$, where $V_{tot}$ is the total volume of the rectangular domain (assuming unit thickness in the third dimension) and N is the number of particles in the system. In particular, in this manuscript we will compute and plot the hydrostatic and Von Mises deviatoric components of the per-particle stress tensors:

$$\begin{aligned} \sigma _{hyd}&= \frac{\sigma _{xx}+\sigma _{yy}}{3} \end{aligned}$$

(18)

$$\begin{aligned} \sigma _{dev}&= \sqrt{\sigma _{xx}^2 - \sigma _{xx}\sigma _{yy}+\sigma _{yy}^2 +3\sigma _{xy}^2} \end{aligned}$$

(19)

When the sensitivity is computed, the program can proceed with updating $\varvec{\chi }$. However, TO algorithms often add an intermediate step of filtering. The idea is that the updating scheme in Eq.5 does not use directly the sensitivity from Eqs. 6 or 13. Instead, it uses a new coarse-grained sensitivity $\widehat{\frac{\partial c}{\partial \varvec{\chi }}}$ that, for the generic element e or particle i, depends also on the sensitivities of neighboring elements or particles:

$$ \widehat{{\frac{{\partial c}}{{\partial \chi _{i} }}}} = \frac{{\sum\nolimits_{{k = 1}}^{{n_{f} }} {\frac{{\partial c}}{{\partial \chi _{k} }}} W_{k} \chi _{k} }}{{\chi _{i} \sum\nolimits_{{k = 1}}^{{n_{f} }} {W_{k} } }}{\text{ }} $$

(20)

In Eq. 20 we used the notation for the DEM-based algorithm, thus referring to particle i; however, the exact same expression also applies to FEM-based algorithms, just replacing subscript i with e. In the equation, the sums are over the $n_f$ particles (or elements) at a distance $r_{ik}<r_{min}$ from particle i, including particle i too³. The filtering length $r_{min}$ is chosen and provided by the user. $W_k = \max \left( 1 - \frac{r_{ik}}{r_{min}} \,,\,0\right)$ is a factor that linearly reduces the weight of neighboring particle k with its distance from the centre of particle i: its value is 1 for particle i and becomes zero for particles with $r_{ik}>r_{min}$. The presence of $\chi _i$ at the denominator in Eq. 20 is the reason why one should enforce $\chi _{min} > 0$. In this manuscript we will always set $\chi _{min} = 10^{-3}$, as is customary in the literature [45].

The reasons to include filtering are both practical and numerical. The practical reason is that $r_{min}$ imposes a minimum size of solid and void regions in the final structure; this provides some control over the complexity of the optimal structure, which may help with fabricability. The numerical reason is that optimization processes not including filtering often converge too rapidly to solid-void solutions getting effectively stuck into sub-optimum local minima. Some filtering (viz. a small $r_{min} \approx D$) usually removes these local minima and leads to a better solution, although one must be careful as a larger $r_{min}$ may also smoothen the global minimum and thus affect the optimality of the solution. These effects will be shown and discussed later in Sect. 4. When FEM analyses are used, another benefit of filtering is to remove the checkerboarding problem [53, 54]: when a fine FE mesh is used, individual neighboring elements in the optimal solution typically create an alternating pattern of void and solid. The problem arises from a locking effect in certain types of finite elements [53, 54]. We will see that DETO does not suffer from checkerboarding.

The last step in the optimization loop is to update $\varvec{\chi }$ following Eq. 5, but using the filtered sensitivities instead of the original ones. The optimization loop is repeated until $\chi _i^{new} - \chi _i^{old} \le 4\cdot 10^{-3}$ for every particle. In the final solution, some particles will feature $\chi _i = \chi _{min}$ and others, especially at solid-void interfaces, might be “gray”, viz. feature a $\chi _i$ that is intermediate between 0 and 1. The MATLAB implentation of DETO that accompanies this manscript includes an optional post-processsing module to reduce the solution to a solid-void only system, where all particles have either $\chi _i=0$ or 1, while respecting the constraint on the total solid volume fraction f. In the simulations for this manuscript, however, we did not perform any post-processing to present straight optimization results without further manipulations. All the outputs from the simulation are recorded in an XYZ configuration file following the evolution of the structural topology, and in a text file collecting values such as c and $V(\varvec{\chi })$ after each optimization step.

4 Results

This section starts by comparing results from DETO with others from established optimization methods. The comparison is done using a base system representing a simple beam under point load. We then present a parametric study where the base system is altered one feature at the time. The simulations reveal how the optimal solutions from DETO are impacted by the target solid volume fraction f, the filtering length $r_{min}$, and the number of particles per unit volume (akin to mesh resolution in the FEM). Finally, the supports of two simple beams are arranged in such a way to show how DETO captures the effect of geometric nonlinearity on the optimal solutions. All of the simulations snapshots in this section have been obtained using the open source software OVITO [55].

4.1 Validation

New topology optimization methods are typically tested on simple structures with known optimal geometries. Two such structures are the simply-supported and pin-supported beam systems shown in Fig. 4. The figure shows results from DETO side by side with optimal geometries from established methods. The input parameters for the DETO simulations are shown in Table 1. The intensity of the external force is 1 kN in both cases.

Fig. 4

Optimal structures for the beam problem under point load. a Simply supported system with b result from the FEM-based TO code in Ref. [45], with inputs: $nelx = 67$, $nely = 39$, $volfrac = 0.6$, $penal = 3$ and $rmin = 2$ (see Ref. [45] for details on the meaning of those inputs), and c result from DETO. d Pin-supported system with results from e Michell’s analysis in Ref. [4] and f DETO

Table 1 Input parameters for the DETO simulations on the base system in Fig.4

To improve the physical interpretation of the results, consider that $k_0 \sim \frac{EA}{r_0}$, where E is the Young modulus of the material, and A and $r_0 = D$ are the cross-sectional area and the length at rest of the cohesive bridge, viz. the spring connecting neighboring disks. Assuming that the width of the cohesive bridge is proportional to the disk diameter, $A \sim Dt_z$ [49], and rearranging the expression of $k_0$ we can estimate an equivalent Young modulus:

$$\begin{aligned} E = \frac{k_0r_0}{A} = \frac{k_0}{t_z} \end{aligned}$$

(21)

The values in Table 1 return $E=100$ GPa, thus one can consider the simulated structures as made of sintered metallic powder.

For the simply supported beam in Fig. 4a the optimal geometry from DETO is qualitatively similar to that from the FEM code in Ref.[45], when similar inputs are provided. For the pinned structure in Fig. 4d, the optimal layout predicted by DETO is analogous to the theoretical solution of fully stressed structures by Michell [4]. In this case the similarity is less striking because Michell’s solution features one-dimensional members with the additional constraint that all members must have equal cross section. Overall, Fig. 4 shows that the optimal solutions obtained using DETO are comparable to those coming from other more established methods in the literature.

Fig. 5 shows the evolution of the objective function c (viz. $U_{tot}$) and of the corresponding geometry during the optimization process. Significant changes in both c and geometry take place during the first 50 optimization steps. Between steps 50 and 500, the geometry has practically converged and c remains nearly constant.

Fig. 5

Simply supported beam case in Fig.4a: evolution of geometry and objective function c during the first 500 optimization steps

Figure 6 shows the distribution of hydrostatic and deviatoric stress in the optimized structure from Fig. 4a. The hydrostatic stress distribution is clearly bimodal, with the lower deck of the structure and the lateral diagonal elements carrying the tensile stresses, and with the upper arch and central diagonal struts being under compression. The distribution of deviatoric von Mises stress is instead centered around a value of 75 MPa quite uniformly distributed over the structure, with stress concentrations at midspan (top and bottom points) where the axial stresses due to the bending moment are highest, and near the supports, where the shear stress gets concentrated before transferring to the pointwise supports.

Fig. 6

Hydrostatic and Von Mises deviatoric stress distributions in the optimized structure from Fig. 4c

4.2 Parametric study: volume fraction

The base system in Fig. 4.c featured a final volume fraction of solid $f=0.6$, as per Table 1. Here the system is kept the same except f, for which 4 additional values are explored between 0.5 and 0.7. Fig. 7 shows the impact of f on the final 0-1 optimized structure. As expected, small f values force the system to create fewer elements and lead to less optimal solutions, with higher c compared to more topologically rich solutions at high f as can be seen in Fig. 8. However, these results are not sufficient to determine how much the lower c values at higher f come from topological complexity rather than just having used more material. The next section will add insight to this point.

Fig. 7

Effect of target solid volume fraction f on optimized solutions to the simply supported beam problem in Fig.4a

Fig. 8

Effect of volume fraction on objective function

4.3 Parametric study: filtering length

Figure 9 shows how the filtering length $r_{min}$ impacts the optimized geometries. The figure also shows a result for the unfiltered case.

Fig. 9

Effect of filtering length on optimized geometries. For generality, the values of $r_{min}$ are given in units of particle diameters D. The label off indicates the unfiltered case.

Predictably, the optimized topologies become simpler at higher $r_{min}$ values, which force the solid to concentrate into fewer, thicker structural elements. Reducing topological complexity by filtering, however, constrains the optimization problem; as a result, c is expected to increase as the solutions become less optimal at larger $r_{min}$ values. This is confirmed in Fig. 10, which shows c growing from 0.111 J to 0.117 J as $r_{min}$ is increased from 1.1D to 3D. This complements the discussion of Fig. 7 in the previous section, showing indeed that more optimal solutions can be obtained by increasing topological complexity while keeping f fixed.

As the optimal topologies get simpler with filtering, the structural geometries with $f=0.6$ for $r_{min}\ge 2D$ in Fig. 9 end up resembling those in Fig. 7 for smaller $f=0.5$. Comparing these two examples confirms the expected trend that similar geometries with smaller f lead to higher values of c : cf. $c = 0.132$ J for the structure with $f=0.5$ in Fig. 7 with $c=0.114$ J for the structure with $r_{min} = 2 D$ in Fig. 9.

Fig. 10

Effect of filter length on objective function

The top image in Fig. 9 shows a case without filtering. Expectedly, the resulting topology is most complex compared to the other cases with filtering on. However, less intuitively, the resulting c is higher than in most filtered cases: see Fig. 10. This confirms the effect that we already mentioned in Sect. 3, whereby lack of filtering causes fast convergence to a local minimum of c. Filtering tends to smoothen out and remove local minima, thus leading to more optimal solutions. The top structure in Fig. 9, obtained without filtering, shows a few very thin elements but no checkerboard effect, viz. an alternating pattern of individual particles with $\chi _i = 0$ and 1. This is because the locking problem leading to the checkerboard effect is specific to FEM-based analyses [53].

4.4 Parametric study: mesh resolution

In FE analyses, the size of the elements discretizing the continuum is in principle arbitrary. Therefore, when performing FEM-based TO one must monitor the impact of mesh resolution on the results, as in some cases the problem might display nonuniqueness and even nonexistence of the solution [54]. By contrast the DEM, in its basic formulation, does not feature a mesh at all, as particles represent physically distinct units. However, in practice, the particles in DE analyses are often coarse grained representations of richer underlying microstructures; for example one particle might summarise a collection of smaller grains. In other cases, like the simple beams in this manuscript, the particles actually discretize a continuum to explore its behavior under scenarios that the FEM might struggle with, e.g. collisions, fracture, fragmentation, or collapse. Therefore, also in the DEM there can be some arbitrariness in deciding the number and size of particles, which thus becomes analogous to deciding the mesh resolution in FE analyses.

To mimic the role of mesh resolution in FE analyses, here we consider a rectangular design domain with fixed dimensions and we use different numbers of particles nelx and nely initially filling the domain. When solving problems with greater nelx and nely than our base case, we reduced accordingly the particle diameters D to always fill the same domain. When changing particle sizes in DE analyses, one should be careful that the intensity of the interaction may depends on D, as opposed to FE analyses where the constitutive parameters describing the material are intrinsically mesh-independent, e.g. the Young modulus E. Specifically for our system, however, Eq. 21 shows that $k_0$ and E are simply linked by the thickness of the simulation domain in the z direction, $t_z$; since we keep the latter always constant and equal to 1 mm, we do not need to change $k_0$ when changing D. This is not always the case; for example, in a 3D simulation with spherical discrete elements, $k_0\sim ED$ and therefore $k_0$ would be proportional to D.

Figure 11 presents optimization results for structures with a range of mesh resolutions around our base case. In all cases, a filtering length $r_{min} = 1.5$ mm is applied, as in our base case. The resulting geometries are generally insensitive to the mesh resolution, except for small differences such as an additional horizontal element appearing at low resolution. Fig. 12 shows that the quality of the solution is very similar for all the structures in Fig. 11, viz. they all feature a similar value of c at the end of the optimization process. This result also proves that, for the 2D examples in this manuscript, it is indeed correct to consider $k_0$ as independent of D.

Fig. 11

Effect of mesh resolution on optimum geometries: filtering included with length $r_{min}=1.5$ mm in all cases

Fig. 12

Effect of mesh resolution on the evolution of c during the optimization process, for the systems whose final geometries are shown in Fig. 11

Mesh-independent filtering, with fixed $r_{min}$ irrespective of the mesh resolution, is known to enforce mesh independence also in mesh-sensitive FEM-based TO [53]. Results obtained without filtering are reported in Sect. 1 of the Supplementary Information section, where DEM results are also compared with results from FEM-based optimization. For the range of meshes analysed in this manuscript, the results in the Supplementary Information section do not indicate a significant impact of mesh fineness on resulting topologies nor values of the objective function; this applies to both the FEM and DEM results. By contrast, the results in the Supplementary Information section clearly show how FEM optimization leads to the checkerboard problem, which is never an issue for our DEM-based method.

4.5 Geometric nonlinearity

When structures are subjected to high loads and undergo large displacements, geometric nonlinearity should impact the optimal topologies [56]. In FEM-based TO, accounting for geometric nonlinearity requires additional complexity in the formulation of the problem [25, 27]. Furthermore, finite elements with low density can experience large distortions that may affect convergence [57]. By contrast, geometric nonlinearities are captured in DETO without any change to the theoretical framework, because interactions are always computed with reference to the system in its deformed configuration. This also removes the issues that may be caused by elements with vanishing $\chi _i$.

Fig. 13

Solutions of topology optimization problems highlighting the impact of geometric nonlinearity. a Simply-supported and e pinned systems, with supports and forces applied to the central axis of the beam; b, f solutions from linear elastic FEM-based TO using the code in Ref. [45], with inputs: $nelx = 67$, $nely = 39$, $volfrac = 0.6$, $penal = 3$ and $rmin = 2$ (see Ref. [45] for details on the meaning of those inputs); (c,g) solutions from the DEM-based TO method presented in this manuscript, which naturally accounts for geometric nonlinearity; (d,h) spatial distribution of hydrostatic stresses for the DETO solutions, identifying the elements working in tension (blue) and in compression (red)

Fig. 14

Distribution of bond strain in the optimized structures with pinned and roller supports.

Fig. 13 highlights the potential impact of geometric nonlinearity by considering two beam systems that are identical to our base case study in Fig. 4a,c, except that: (i) the supports are applied to the central axis instead of the bottom corners, and (ii) a larger point load of 10 kN is applied to the center of the beams instead of above or below them; this larger load has been chosen to induce larger displacements and thus better appreciate the effect of geometric nonlinearity (midspan deflection are now approximately 1.3% of the beam length and Fig. 14 shows that bond strains are as high as 1%). Under these new conditions, simulations assuming small displacements should return identical solutions for both the simply-supported and the pinned systems, because the length of the central axis remains unchanged after small displacements. Indeed the results from linear elastic FEM-based TO in Fig. 13b, f are identical. By contrast, considering large displacements should lead to different optimum geometries, because the length of the central axis would remain unchanged in the simply-supported case, where the rollers can move inward, but would increase in the pinned scenario due to the finite deflection. The impact of geometric nonlinearity is indeed captured by our DETO solutions in Fig. 13c,g, which feature very different geometries for the two systems.

The optimum solution for the simply-supported beam in Fig.13c is similar to the linear-elastic solution in Fig. 13b. The reason is that the inward motion of the rollers allows the structure to behave in pure bending also when geometric nonlinearities are included. The distribution of hydrostatic stresses in Fig. 13.d shows indeed a symmetric distribution of elements working in tension and in compression. The qualitative difference in Fig. 13g stems from the catenary action induced by the pinned supports. During the deflection, the central axis of the pinned system is stretched and this generates a tensile stress along the beam. During the optimization process, this additional tensile stress drives material away from the compressed regions and towards the parts under tension. As a result, Fig. 13h displays a thickening of the lower deck, which carries most of the catenary force, whereas the upper arch in compression becomes smaller and migrates towards the centre of the beam.

5 Conclusion

We have formulated SIMP-based TO for a problem of complementary energy minimization in a 2D system of circular disks, modelled and analysed using the Discrete Element Method. Key features of the new DETO method are:

• The expression of the cost function c, viz. the complementary energy of the system, features the total strain energy of the system $U_{tot}$ as a function of the harmonic interactions between pairs of neighboring particles;

• A new penalisation scheme for the intensity of the interactions, featuring the per-particle design variable $\chi _i \in [0,1]$ of both interacting particles in each pair;

• Derivation of sensitivity based on the new cost function and penalisation scheme. Through the text we adopt an approximate expression of sensitivity which is computationally efficient but may result in incorrect solutions. For the examples in the manuscript, the validity of the approximation has been checked using a numerical perturbation approach, presented in the Supplementary Information, which computes the full sensitivity;

• Possibility to compute local stresses using the virial expression;

• Automatic consideration of geometric nonlinearity.

The new method has been tested for the optimization of a simply supported and a pinned beams under point load. For these, DETO produced similar optimum geometries as from other more established methods in the literature: linear-elastic FEM-based TO and Michell analysis. A subsequent parametric study looked into the effects of solid volume fraction, filtering length, and mesh resolution, leading to the following observations:

• Structures with higher volume fractions of solid f reach better solutions, i.e. lower c, and feature more topological complexity;

• The impact of the filtering length $r_{min}$ on the results showed c can be reduced both by adding more material (i.e. increasing f) while keeping the topology fixed, and by increasing the topological complexity while keeping f fixed;

• Similar to FEM-based TO, filtering is effective in imposing a minimum element size in DETO; this can be used to satisfy practical constraints on fabrication. Additionally, filtering allows the system to escape local minima that would otherwise trap unfiltered systems in sub-optimum configuration;

A last application addressed the effect of geometric nonlinearity, by considering a simply-supported and pinned beam problems with supports and loads applied to the central axis. We showed how linear-elastic FEM-based analyses, not including geometric nonlinearity, predict the same optimum structure for both problems. By contrast, the solution from DETO was significantly different for the pinned system. Stress analyses clarified how the difference emerged from an additional field of tensile stress due to catenary action.

The method presented in this paper is a proof of concept for the application of TO to discrete systems. In this first work we have considered only the quasi-static behavior of a linear-elastic material. However, we have briefly shown how more complex materials could be investigated without changing the presented framework, just by using more complex interaction potentials that may also include multi-body and orientation-dependent terms. The inclusion of such mechanical nonlinearies in the method will be further developed in Part 2 of this manuscript [42]. Extending the method to dynamic analyses would also be straightforward, as well as including processes that would challenge continuum-based analyses, such as collisions, fracture, fragmentation, collapse, and rigid motion. Complications may arise depending on the objective function to be minimized, but this is an intrinsic feature of gradient-based solution methods rather than being determined by the DEM or FEM solver.

Further developments of DETO should now focus on discontinuous problems, for which gradient-based methods might not be the most convenient approach. An example might be the optimization of the blades of a planetary mixer operating on a granular material, whose mass and size distribution of the grains might be optimized too, with an overall aim of minimizing, for instance, the energy to perform a certain number or rotations. In this manuscript we did not address problems of such complexity and, as a matter of fact, the problem of stiffness maximization considered here does not require a discrete description at all. However, this problem gave us the opportunity to validate the new method, and our implementation of it, against results and numerical behaviors that are well understood. We also hope that, by choosing this simple problem, we have managed to highlight the most fundamental changes that are required when moving from FEM-based to DEM-based optimization, with particular emphasis on penalizing the interactions and on the beneficial implications of computing forces in the deformed configuration (e.g. avoiding singular stiffness matrices and seamless account of geometric nonlinearity).

All in all, the presented method is a first step to engage with scientific communities whose focus on discrete behaviors has traditionally impeded adoption of topology optimization. The communities that we envision could be positively impacted from this work include those of granular mechanics, structural design against progressive collapse, and nanoscale materials science, also including atomistic modeling and simulation.