1 Introduction

Small-scale devices [1,2,3,4], biological and bioinspired materials [5,6,7], advanced porous nanostructures [8, 9], self-healing matter [10], hierarchical and periodic structures [11, 12], new-generation of complex composites [13,14,15] require sophisticated methodologies and advanced models to predict their mechanical behavior. Usually, classical models of local continuum elasticity are not accurate enough to simulate the mechanical behavior of these nonconventional structural elements. Therefore, researching of new mechanical formulations able to predict complex behaviors represent an open problem of the structural mechanics. In this context, this manuscript deals with the simulation of two phenomena which occur in some mechanical behaviors providing a new approach to solve the bending problem of hereditary nonlocal beam.

Hereditariness is the property of such materials that posses mechanical memory of past effects. Usually, in these materials stress decay under constant strain as well as strain increments under constant stress showing a time-dependent material behavior. This phenomenon cannot be modeled by the classical theory of elasticity and regards several nonconventional materials. An approach to model this mechanical phenomena is based on the linear theory of viscoelasticity [16, 17]. Specifically, in the integral formulation of hereditariness the stress–strain relation is given as an integral Volterra-Boltzamann relation where the kernel is a time-dependent function which takes into account the memory of the material. Among the various model of linear viscoelasticity, hereditary model based on the fractional calculus is able to represent the real time-dependent behavior of a wide variety of materials, like polymers [18], biological tissues [19], clays [20], non-newtonian fluids [5], rubbers [21], bones [22], and so on [23, 24]. Moreover, these models are also recently used to model nonlinear time-dependent behavior [25,26,27]. For these capabilities viscoelastic models based upon fractional calculus will be used in this paper to obtain a versatile time-dependent stress–strain relation useful to model several advanced bending problems where hereditary effects cannot be neglected.

The other considered phenomenon in this paper is related to the nonlocal effects. Nonlocality regards various mechanical issues where the mechanical interactions cannot be considered as local. In fact, in nonlocal problem the stress (or the strain) at a point of the continuum is function of the stress (or strain) field of the entire domain [28, 29]. Size-effects at small scale [30], strain and stress localizations [31, 32], anomalous waves dispersions in complex materials with marked microstructures [33, 34], structures forced by long-range force field [35,36,37] are some examples where nonlocal phenomena cannot be neglected. Among the various nonlocal models, Eringen’s formulation is probably the most famous one [38, 39]. In such a model stress–strain relation is described by a convolution integral where the long-range interactions are weighted by the averaging kernel characterized by an internal-length parameter. Thus, the nonlocal stress is obtained by a Fredholm integral equation of the first kind between the averaging kernel and the local strain [40]. That approach was useful to describe screw dislocations and wave propagation in nonlocal unbounded domains. However, some mathematical issues and physical paradoxes occur when the model is applied in a bounded domain [41, 42]. Nevertheless, there are other various nonlocal approaches to overcome these difficulties, e.g., two-phase models [43, 44], strain-difference approaches [45, 46], strain and stress gradient theory [47,48,49,50,51,52,53], displacement-based nonlocal model [54,55,56,57], stress-driven integral formulation [58, 59]. Among these well-posed nonlocal formulations the stress-driven approach is used in this paper to perform the study of the nonlocal interactions in bending problem. Recent papers have proved that the stress-driven formulation is able to simulate nonlocal behavior providing exact solutions for several structural problems of applicative interests [60,61,62,63,64].

In summary, in this paper fractional hereditariness and integral stress-driven formulation of nonlocality are combined providing analytical solution of bending nonlocal viscoelastic problem. Closed-form solutions will allow us to obtain some interesting parametric results in order to show the influence of nonlocal and viscoelastic parameters in the mechanical response. This study can be useful to show the difference between the considered complex case and the classical local elastic bending response. The outcomes can be useful for design and optimization of structures at small-scale, bioinspired structural elements, porous viscoelastic devices, and so on. Therefore, the proposed formulation can be useful to capture different phenomena related to nonlocality and hereditariness, such as,

  • size effects in small-scale structures where molecular interactions and long-range force cannot be neglected,

  • time-dependent behavior of non-elastic materials like polymeric and nonconventional structural continua,

  • nonlocalities in non-continuous materials with microstructures like artificial and biological tissues,

  • mechanical behavior of multiphase materials in advanced smart composites.

The manuscript is organized as follows. Section 2 introduces integral formulation of viscoelasticity with special regard to the uniaxial stress–strain relation useful in bending problems. Section 3 is devoted to the fractional stress–strain relations. Specifically, three time-dependent models are described in detail showing the influence of the fractional order in the mechanical response of the viscoelastic material. Fractional stress–strain relation and stress-driven integral approach are used in conjunction in Sect. 4 providing a new formulation of bending behavior of a nonlocal hereditary beam. Such a section contains analytical solution of this time-dependent problem where hereditariness and nonlocality can be modeled varying two specific mechanical parameters. Numerical simulations and detailed parametric studies are reported in Sect. 5. Finally, Sect. 6 summarizes and highlights the main concluding remarks.

2 Viscoelastic stress–strain relation

This section introduces integral formulation of linear viscoelasticity used to model hereditariness in real materials. Uniaxial constitutive law for viscoelastic isotropic homogeneous material are introduced below and will be used to formulate the nonlocal beam problem. That constitutive relation is suitably derived from the tridimensional stress–strain relation.

2.1 Integral formulation of viscoelasticity

Let us assume that strain and stress are space- and time-dependent functions related by a convolution integral where the kernel takes into account memory effects of an homogeneous viscoelastic material [16, 17]. Specifically, this constitutive relation is given as

$$\begin{aligned}\sigma_{ij}(t)&=\int_{-\infty}^t\mathcal{G}_{ijkl}(t-\bar t)\,\mathrm{d}\varepsilon_{kl}(\bar t)\\&=\int_{-\infty}^t\mathcal{G}_{ijkl}(t-\bar t)\partial_{\bar t}\varepsilon_{kl}(\bar t)\mathrm{d}{\bar t} \end{aligned}$$
(1)

where \(i,j \in \{1,2,3\}\), \(\varepsilon _{kl}\) represents the viscoelastic strain tensor, \(\sigma _{ij}\) is the stress tensor and \({\mathcal {G}}_{ijklm}\) is the forth-order relaxation tensor which contains the time-dependent mechanical parameters of the viscoelastic material. The symmetry of the strain and stress tensors implies that

$$\begin{aligned} {\mathcal {G}}_{ijkl}(t)={\mathcal {G}}_{jikl}(t)={\mathcal {G}}_{ijlk}(t) \end{aligned}$$
(2)

If the material is isotropic the relaxation tensor can be represented by two independent function as follows

$$\begin{aligned} {\mathcal {G}}_{ijkl}=\frac{1}{3}\left[ {\mathcal {G}}_1(t)-{\mathcal {G}}_2(t)\right] \delta _{ij} \delta _{kl}+\frac{1}{2}{\mathcal {G}}_2(t)(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}) \end{aligned}$$
(3)

where \({\mathcal {G}}_1(t)\) and \({\mathcal {G}}_2(t)\) are independent relaxation functions and \(\delta _{ij}\) is the Kronecker symbol. The first relaxation function \({\mathcal {G}}_1(t)\) is defined to states of dilatation whereas \({\mathcal {G}}_2(t)\) is defined relative to states of shear. Specifically, by introducing the deviatoric components of the stress \(s_{ij}\) and the strain \(e_{ij}\), Eq. (1) reduces to

$$\begin{aligned} \sigma _{kk}(t)& = \int _{-\infty }^t{\mathcal {G}}_1(t-{\bar{t}})\,\partial _{{\bar{t}}}\varepsilon _{kk}({\bar{t}})\mathrm {d}{\bar{t}} \end{aligned}$$
(4a)
$$\begin{aligned} s_{ij}(t)& = \int _{-\infty }^t{\mathcal {G}}_2(t-{\bar{t}})\,\partial _{{\bar{t}}} e_{ij}({\bar{t}})\mathrm {d}{\bar{t}} \end{aligned}$$
(4b)

being

$$\begin{aligned} s_{ij}(t)& = \sigma _{ij}(t)-\frac{1}{3}\sigma _{kk}(t)\delta _{ij},\;\;\;\;\;s_{ii}(t)=0, \end{aligned}$$
(5a)
$$\begin{aligned} e_{ij}(t)& = \varepsilon _{ij}(t)-\frac{1}{3}\varepsilon _{kk}(t)\delta _{ij},\;\;\;\;\;e_{ii}(t)=0. \end{aligned}$$
(5b)

2.2 Uniaxial stress–strain relation for bending problem

Now, let us consider the state of the stress and the strain in a 3D continuum beam element referred to a coordinate cartesian axis (x, y, z), where z coincides with the centroidal axis of the beam while x and y are the principal intertia axes of the cross-section. Under the kinematic assumptions of the Bernoulli–Euler beam model the sole axial deformation \(\varepsilon _z(t)\) is sufficient to describe the entire displacement field and the problem is ruled only by the axial stress \(\sigma _z(t)\). Thus, from Eq. (4) the isotropic viscoelastic stress-strain relation of that structural element becomes

$$\begin{aligned} \sigma _z(t)=\frac{1-2\nu }{3}\int _{-\infty }^t{\mathcal {G}}_1(t-{\bar{t}})\partial _{{\bar{t}}}\varepsilon _z({\bar{t}})\mathrm {d}{\bar{t}}+\frac{2(1+\nu )}{3} \int _{-\infty }^t{\mathcal {G}}_2(t-{\bar{t}})\partial _{{\bar{t}}}\varepsilon _z({\bar{t}})\mathrm {d}{\bar{t}} \end{aligned}$$
(6)

where \(\nu \) is the Poisson’s ratio. Moreover, we assume that Poisson’s ratio is a constant during the time [17, 65], this assumption implies that

$$\begin{aligned} \frac{{\mathcal {G}}_1(t)}{{\mathcal {G}}_2(t)}=\frac{1+\nu }{1-2\nu } \end{aligned}$$
(7)

Thus, taking into account this relation between the two relaxation functions we can assume that

$$\begin{aligned} {\mathcal {G}}_1(t)=\frac{{\mathcal {E}}(t)}{1-2\nu },\;\;\;\;\; {\mathcal {G}}_2(t)=\frac{{\mathcal {E}}(t)}{1+\nu } \end{aligned}$$
(8)

and Eq. (6) yields

$$\begin{aligned}\varepsilon_z(t)&=\int_{-\infty}^t\mathcal{J}(t-\bar t)\partial_{\bar t}\sigma_z(\bar t)\mathrm{d}\bar t\\&=\sigma_z(0)\mathcal{J}(t)+\int_0^t\mathcal{E}(t-\bar t)\partial_{\bar t}\sigma_z(\bar t)\mathrm{d}\bar t \end{aligned}$$
(9)

where \({\mathcal {E}}(t)\) is the axial relaxation modulus. The inverse relation of Eq. (9) is

$$\begin{aligned} \varepsilon _z(t)=\int _{-\infty }^t {\mathcal {J}}(t-{\bar{t}})\;{\partial _{{\bar{t}}}\sigma _z({\bar{t}})}{}\mathrm {d}{\bar{t}}\\&=\sigma _z(0){\mathcal {J}}(t)+\int _{0}^t {\mathcal {J}}(t-{\bar{t}})\;{\partial _{{\bar{t}}}\sigma _z({\bar{t}})}{}\mathrm {d}{\bar{t}} \end{aligned}$$
(10)

where the integral kernel \({\mathcal {J}}(t)\) represents the creep compliance. The two integral kernels in Eqs. (9) and (10) represent the relaxation and the creep functions and take into account the memory of the material. In linear viscoelasticity they are related in the Laplace domain by the following relation

$$\begin{aligned} {\hat{{\mathcal {J}}}}(s)\hat{{\mathcal {E}}}(s)=s^{-2} \end{aligned}$$
(11)

where \({\hat{\cdot }}\) denotes the Laplace transform. Such integral transform is defined as

$$\begin{aligned} {\hat{f}}(s)={\mathcal {L}}\left\{ f(t),s\right\} :=\int _{-\infty }^\infty f(t)e^{-s t}\mathrm {d}t \end{aligned}$$
(12)

being s a complex number.

3 Uniaxial fractional-order viscoelasticity

Among the various time-dependent kernel function used in the viscoelastic stress–strain relation in Eqs. (9) and (10) the power-law type is considered to simulate hereditariness in the bending problem studied in this manuscript. This choice is motivated by experimental evidences reported in various works [18, 19, 21, 23]. These cited papers have proved that power-law functions are able to fit experimental data of relaxation tests modeling long-time memory effects in several hereditary materials. Moreover, with a proper selection of the power-law as kernel function in Eqs. (9) and (10) fractional operators can be appeared in the stress–strain relation [24, 66, 67]. This kind of formulation is called fractional-order viscoelasticity and allows us to model time-dependent mechanical behavior with a selection of a few number of parameters.

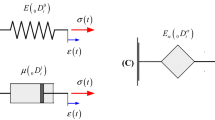
In this section three different kind of power-law law functions as time-dependent kernel are considered. These kernels provide the stress–strain relation of three fractional order models. That is, the spring-pot, the fractional Kelvin–Voigt and the fractional Maxwell model [68, 69].

3.1 One-term fractional model

Among the fractional order models, the simplest one is known as spring-pot (SP) model [70,71,72]. It is ruled by a one-term fractional differential equation characterized by a fractional order \(\beta :0\leqslant \beta \leqslant 1\) and a viscoelastic parameter \(\mathrm {E}_\beta \,\left[ \mathrm {Pa\, s}^\beta \right] \). Specifically, choosing as relaxation modulus a power-law decaying function of the type

$$\begin{aligned} {\mathcal {E}}_{\mathrm {sp}}(t)=\frac{\mathrm {E}_\beta t^{-\beta }}{\Gamma (1-\beta )},\;\;\;\;\;0\leqslant \beta \leqslant 1 \end{aligned}$$
(13)

placing it into the Eq. (9) and assuming that \(\varepsilon _z(0)=0\), the following relation holds true

$$\begin{aligned} \sigma _z(t)=\mathrm {E}_\beta \left( {}\mathrm {D}^\beta _{0^+}\varepsilon _z\right) (t) \end{aligned}$$
(14)

where \(\Gamma (\cdot )\) is the Euler’s gamma function, \(\left( {}\mathrm {D}^\beta _{0^+}\cdot \right) (t)\) represents the time-derivative of order \(\beta \) with lower bound \(t=0\). Eq. (14) represents the strain-driven constitutive law of the SP and involves fractional differential operator that generalizes the classical integer order derivative. Specifically, for \(t>0\) it is defined as

$$\left(\mathrm{D}^\beta_{0^+}\varepsilon _z\right)(t):=\left\{\begin{aligned}&\frac{1}{\Gamma(1-\beta)} \int_0^t {(t-\bar t)^{1-\beta}}\partial_{\bar t}\,\varepsilon_z(\bar t)\mathrm{d}\bar t &\mathrm{if} \; &0\leqslant\beta<1\\&\frac{\mathrm{d}}{\mathrm{d} t} \varepsilon _z(t) &\mathrm{if}\; &\beta=1 \end{aligned}\right.$$
(15)

Moreover, fractional stress-driven viscoelastic relation of the SP can be obtained by performing integration of Eq. () or considering integral formulation and selecting a proper creep function. Specifically, taking into account the relaxation function in Eq. (13) and the relation in Laplace domain in Eq. (11) the creep function is

$$\begin{aligned} {\mathcal {J}}_{\mathrm {sp}}(t)=\frac{t^{\beta }}{\mathrm {E}_\beta \Gamma (1+\beta )},\;\;\;\;\;0\leqslant \beta \leqslant 1 \end{aligned}$$
(16)

by placing Eq. (16) into Eq. (10) we obtain

$$\begin{aligned} \varepsilon _z(t)=\frac{1}{\mathrm {E}_\beta }\left( \mathrm {I}^\beta _{0^+}\sigma _z\right) (t) \end{aligned}$$
(17)

where \(\left( \mathrm {I}^\beta _{0^+}\cdot \right) (t)\) is the Riemann–Liouville fractional integral with order \(\beta \) and lower bound \(t=0\) defined as

$$\begin{aligned} \left( \mathrm {I}^\beta _{t^+}\sigma _z\right) (t):= \frac{1}{\Gamma (\beta )} \int _0^t {(t-{\bar{t}})^{\beta -1}}{\sigma _z ({\bar{t}})}\mathrm {d}{\bar{t}} \end{aligned}$$
(18)

Stress–strain relation of SP is ruled by the relation in Eqs. (14) and (17). The fractional-order constitutive laws are the generalization of the classical elastic and viscous model. Specifically, for the bounded limit of the order \(\beta \) the fractional-order relations describe Young elastic law and Newton–Petroff viscous law. That is,

$$\begin{aligned}&\mathrm{if}\; \beta=0\Rightarrow \mathrm{E}_\beta=\mathrm{E},\;\;{\textit{{Elastic}}}\;\;\left\{\begin{aligned}&\varepsilon^{e}_z(t)=\frac{1}{\mathrm{E}}\,\sigma^e(t)\\&\sigma^{e}_z(t)={\mathrm{E}}\,\varepsilon^e(t)\end{aligned}\right.\\&\mathrm{if}\; \beta=1\Rightarrow \mathrm{E}_\beta=\mu,\;\;{\textit{{Viscous}}}\;\left\{\begin{aligned}&\varepsilon^{v}_z(t)=\int_0^t {\frac{\sigma_z (\bar t)}{\mu}}\mathrm{d}\bar t\\&\sigma^{v}_z(t)={\mu}\,\dot\varepsilon^v(t)\end{aligned}\right.\end{aligned}$$
(19)

where \(\mathrm {E}\) is the Young modulus \([\mathrm {Pa}]\), and \(\mu \) is the viscosity \([\mathrm {Pa}\, \mathrm {s}]\).

3.2 Two-terms fractional models

SP model is able to simulate the stress–strain relation of several materials by means of two mechanical parameters. However, some viscoelastic materials exhibit mechanical behaviors that need more than two parameters, e.g., rubbery-transition phenomena is well described by fractional Kelvin–Voigt model [73], some damper materials used to mitigate vibrations for seismic protection applications require the use of fractional Maxwell model [74]. Both these other fractional-order models are characterized by three mechanical parameters, their stress–strain relations are reported below. SP model and the other two fractional models are considered in this paper to derive the nonlocal behavior of viscoelastic Bernoulli–Euler beam.

Fractional Kelvin–Voigt (FK) model is characterized by the following relaxation function \({\mathcal {E}}_{\mathrm {fk}}(t)\) and creep compliance \({\mathcal {J}}_{\mathrm {fk}}(t)\)

$$\begin{aligned} {\mathcal {E}}_{\mathrm {fk}}(t)& = \mathrm {E}+\frac{\mathrm {E}_\beta \, t^{-\beta }}{\Gamma (1-\beta )},\;\;\;\;\;0\leqslant \beta \leqslant 1 \end{aligned}$$
(20a)
$$\begin{aligned} {\mathcal {J}}_{\mathrm {fk}}(t)& = \frac{1}{\mathrm {E}}\left[ 1-{\mathbb {E}}_\beta \left( -\frac{\mathrm {E}}{\mathrm {E}_\beta }t^{\beta }\right) \right] ,\;\;\;\;\;0\leqslant \beta \leqslant 1 \end{aligned}$$
(20b)

where \(\mathrm {E}\) is a purely elastic modulus which represent the limit for \(t\rightarrow \infty \) of the relaxation function and \({\mathbb {E}}_\beta \left( \cdot \right) \) is one-parameter Mittag-Leffler function defined as

$$\begin{aligned} {\mathbb {E}}_\beta \left( t\right) =\sum _{k=0}^\infty \frac{t^k}{\Gamma \left( k\beta +1\right) } \end{aligned}$$
(21)

By using Eqs. (20) into the integral formulation in Eqs. (9) and (10) the following fractional-order stres-strain relations hold true

$$\begin{aligned} \sigma _z(t)& = \mathrm {E}\,\varepsilon _z(t)+\mathrm {E}_\beta \left( {}\mathrm {_CD}^\beta _{0^+}\varepsilon _z\right) (t) \end{aligned}$$
(22a)
$$\begin{aligned} \varepsilon _z(t)& = \frac{\sigma _z(t)}{\mathrm {E}}-\frac{1}{\mathrm {E}}\sum _{k=0}^\infty \left( -\frac{\mathrm {E}}{\mathrm {E}_\beta }\right) ^k\left( \mathrm {I}^{k\beta }_{0^+}\sigma _z\right) (t) \end{aligned}$$
(22b)

these costitutive laws represent the stress–strain relation of an elastic spring connected in parallel with a SP.

The fractional Maxwell (FM) model is characterized by the following relaxation function \({\mathcal {E}}_{\mathrm {fm}}(t)\) and creep compliance \({\mathcal {J}}_{\mathrm {fm}}(t)\)

$$\begin{aligned}&{\mathcal {E}}_{\mathrm {fm}}(t)=\mathrm {E}\,{\mathbb {E}}_\beta \left[ -\left( \frac{\mathrm {E}}{\mathrm {E}_\beta }t\right) ^{\beta }\right] ,\;\;\;\;\;0\leqslant \beta \leqslant 1 \end{aligned}$$
(23a)
$$\begin{aligned}&{\mathcal {J}}_{\mathrm {fm}}(t)=\frac{1}{\mathrm {E}}+\frac{t^\beta }{\mathrm {E}_\beta \Gamma (1+\beta )},\;\;\;\;\;0\leqslant \beta \leqslant 1 \end{aligned}$$
(23b)

by using these function as kernels in the integral formulation Eqs. (9) and (10) we obtain

$$\begin{aligned}&\sigma _z(t)=\mathrm {E}\,\varepsilon _z(t)+\sum _{k=1}^\infty (-1)^{1+k}\frac{\mathrm {E}^{\beta +1}}{\mathrm {E}^\beta _\beta }\left( {}\mathrm {I}^{k\beta }_{0^+}\varepsilon _z\right) (t) \end{aligned}$$
(24a)
$$\begin{aligned}&\left( \mathrm {_CD}^\beta _{0^+}\varepsilon _z\right) (t)=\frac{1}{\mathrm {E}}\left( \mathrm {_CD}^\beta _{0^+}\sigma _z\right) (t)+\frac{1}{\mathrm {E}_\beta }\sigma _z(t) \end{aligned}$$
(24b)

in this case the constitutive laws represent a viscoelastic model composed by an elastic spring connected in series with a SP.

In the next section these fractional viscoelastic models are used to describe the time-dependent bending behavior of a nonlocal Bernoulli–Euler beam. Nonlocal effects will be modeled by stress-driven approach. Following this approach the nonlocal viscoelastic strain field will be derived from the local one defined in Eq. (10) where creep function is the integral kernel of the costitutive law. The considered creep functions used in the next section are reported in Fig. 1. It shows the creep function of the SP, the FK and the FM, respectively evaluated from Eqs. (16), (20b) and (23b), for different values of the fractional order \(\beta \). It can be observed that SP creep function yields the elastic constant compliance for \(\beta =0\) and linear viscous one for \(\beta =1\). Moreover, classical Kelvin–Voigt model is a particular case of FK with \(\beta =1\) and classical Maxwell model can be obtained from FM by placing \(\beta =1\).

Fig. 1
figure 1

Creep functions of fractional viscoelastic models

Full size image

4 Viscoelastic nonlocal Bernoulli–Euler beam

Let us consider the viscoelastic beam element length L and cross section A. The volume of the beam is described with respect to a cartesian coordinate system \((x,\,y,\,z)\) oriented in such a way that z coincides with the centroidal longitudinal axis and the other two are the principal intertia axes of the cross-section, the domain of this structural element is \({\mathcal {B}}:0\leqslant z \leqslant L\).

The beam is loaded by time-dependent transversal load \(q_y(z,t)\) as it is shown in Fig. 2. The beam is characterized by viscoelastic behavior and nonlocal phenomena. To simulate the viscoelastic time dependent effects the fractional models introduced in the previous section are considered. While the nonlocal behavior is modeled by means of the stress-driven integral formulation [58]. This approach allows us to obtain the analytical solution of several problems avoiding the physical paradoxes of classical strain-driven Eringen’s formulation that appear in various nonlocal problems of bounded domains [75]. Specifically, for the considered bending problem, after the definition of the local viscoelastic curvature-moment relation \(\chi _z^{\mathrm {ve}}(z,t)\text {-}M_x(z,t)\) the nonlocal curvature \(\chi _z(z,t)\) is obtained as convolution integral relation between a kernel function \(\phi _\lambda (z)\) and the local moment.

Fig. 2
figure 2

Layout of the beam model

Full size image

4.1 Local viscoelastic bending problem

Considering kinematic Bernoulli–Euler hypothesis, being the element loaded only in y-direction all the strain field in the deformed configuration is described from the knowledge of the displacement v(z, t) of the longitudinal axis and rotation \(\varphi _x(z,t)\) of the cross-section. In this case, bending curvature is

$$\begin{aligned} \chi _x(z,t)=-{\partial ^2_zv(z,t)} \end{aligned}$$
(25)

which is related with axial strain \(\varepsilon _z(z,t)\) by the following relation

$$\begin{aligned} \varepsilon _z(z,t)=y\,\chi _x( z,t)=-y\,{\partial ^2_zv(z,t)} \end{aligned}$$
(26)

Stress \(\sigma _z(t)\) and bending moment \(M_x\) are related by the following relations

$$\begin{aligned} \sigma _z(t)=\frac{M_x(z,t)}{{\mathcal {I}}_x}y \end{aligned}$$
(27)

where \({\mathcal {I}}_x\) is the moment of inertia of the cross section respect to x-axis. That is,

$$\begin{aligned} {\mathcal {I}}_x=\int _Ay^2\mathrm {d}A \end{aligned}$$
(28)

Considering the beam domain \({\mathcal {B}}:0\leqslant z \leqslant L\), and by taking into account Eqs. (26) and (27), viscoelastic relation in Eq. (10) becomes

$$\begin{aligned} \chi _x^{\mathrm {ve}}(z,t)=\frac{1}{{\mathcal {I}}_x} \int _{-\infty }^t {\mathcal {J}}_j(t-{\bar{t}})\,{\partial _{\bar{t}} M_x({{z}},\bar{t})}\mathrm {d}{\bar{t}} \end{aligned}$$
(29)

where the considered kernels \({\mathcal {J}}_j(t)\) for \(j=\left\{ \mathrm {sp,\,fk,\,fm}\right\} \) are defined in Eqs. (16), (20b) and (23b).

4.2 Nonlocal stress-driven formulation

Nonlocal phenomena modeled by stress-driven approach is characterized of a constitutive law in which the nonlocal viscoelastic curvature \(\chi _x(z,t)\) is a function of the entire local viscoelastic curvature \(\chi _x^{\mathrm {ve}}(z,t)\) in Eq. (29). This relation is expressed by a convolution integral where the kernel is an attenuation space-function \(\phi _\lambda (z)\) which weighs the effects of the local curvature in each point of the domain \({\mathcal {B}}\). That is,

$$\begin{aligned} \chi _x(z,t)=\phi _\lambda (z)*\chi _x^{\mathrm {ve}}({z},t)=\int _0^L {\phi _\lambda (z-{\bar{z}})}\chi _x^{\mathrm {ve}}(\bar{z},t)\,\mathrm {d}{\bar{z}} \end{aligned}$$
(30)

the kernel is characterized by the nonlocal parameter \(\lambda \). The local viscoelastic curvature is defined in Eq. (29), therefore, Eq. (30) becomes

$$\begin{aligned} \chi _x(z,t)=\int _0^L \frac{\phi _\lambda (z-{\bar{z}})}{{\mathcal {I}}_x} \int _{-\infty }^t {\mathcal {J}}_j(t-{\bar{t}})\,{\partial _{\bar{t}} M_x({\bar{z}},{\bar{t}})}\mathrm {d}{\bar{t}} \, \mathrm {d}{\bar{z}} \end{aligned}$$
(31)

this equation represents the stress-driven nonlocal viscoelastic relation in terms of bending nonlocal curvature and moment. The convolution kernel must be selected among the symmetric positive functions with limit impulsivity propriety. It can be selected among exponential, Gaussian, power-law function, and so on. We consider as convolution kernel the following bi-exponential function

$$\begin{aligned} \phi _\lambda (z)=\frac{1}{2\,l_\lambda }\exp \left( -\frac{|z|}{l_\lambda }\right) \end{aligned}$$
(32)

where \(l_\lambda =\lambda L\) measure the long-range nonlocal interaction. With this selection of the kernel, the integral relation in Eq. (29) is equivalent to the following integro-differential relation

$$\begin{aligned} {\partial ^2_z\chi _x(z,t)}-\frac{\chi _x(z,t)}{l_\lambda ^2}=-\frac{1}{l_\lambda ^2 \,{\mathcal {I}}_x}\int _{-\infty }^t {\mathcal {J}}_j(t-{\bar{t}})\,{\partial _{\bar{t}} M_x(z,{\bar{t}})}\mathrm {d}{\bar{t}} \end{aligned}$$
(33)

under the following constitutive boundary condition

$$\begin{aligned} \left\{ \begin{aligned}&{\partial _z\chi _x(0,t)}=\frac{1}{l_\lambda }\chi _x(0,t)\\&{\partial _z\chi _x(L,t)}=-\frac{1}{l_\lambda }\chi _x(L,t) \end{aligned} \right. \end{aligned}$$
(34)

Taking into account Eq. (25) and the following equilibrium equation

$$\begin{aligned} {\partial ^2_z M_x(z,t)}=-{q_y(z,t)} \end{aligned}$$
(35)

Eq. (33) yields

$$\begin{aligned} {\partial _z^6v(z,t)}-\frac{1}{l_\lambda ^2}{\partial _{{\bar{t}}}^4v(z,t)}=-\frac{1}{l_\lambda ^2 \,{\mathcal {I}}_x}\int _{-\infty }^t {\mathcal {J}}_j(t-{\bar{t}})\,{\partial _{\bar{t}} q_y(z,{\bar{t}})}\mathrm {d}{\bar{t}} \end{aligned}$$
(36)

and the constitutive boundary conditions in Eq. (34) become

$$\begin{aligned} \left\{ \begin{aligned}&\partial _z^3v(0,t)=\frac{1}{l_\lambda }{\partial _z^2 v(0,t)}\\&{\partial _z^3v(L,t)}=-\frac{1}{l_\lambda }{\partial _z^2 v(L,t)} \end{aligned} \right. \end{aligned}$$
(37)

Bending moment \(M_x(z,t)\) and the shear force \(T_y(z,t)\) become

$$\begin{aligned} M_x(z,t)& = {\mathcal {I}}_x\int _{-\infty }^t {\mathcal {E}}_j(t-{\bar{t}})\,\partial _{\bar{t}} \Big [l_\lambda ^2\partial _z^4v(z,{\bar{t}})-\partial _z^2v(z,{\bar{t}})\Big ]\mathrm {d}{\bar{t}} \end{aligned}$$
(38a)
$$\begin{aligned} T_y(z,t)& = {\mathcal {I}}_x\int _{-\infty }^t {\mathcal {E}}_j(t-{\bar{t}})\,\partial _{\bar{t}} \Big [l_\lambda ^2\partial _z^5v(z,{\bar{t}})-\partial _z^3v(z,{\bar{t}})\Big ]\mathrm {d}{\bar{t}} \end{aligned}$$
(38b)

where the considered kernels \({\mathcal {E}}_j(t)\) for \(j=\left\{ \mathrm {sp,\,fk,\,fm}\right\} \) are defined in Eqs. (13), (20a) and (23a).

5 Sample applications and parametric study

Stress-driven nonlocal approach allows us to obtain some analytical solutions useful to investigate the influence of the nonlocal parameter and viscoelastic phenomena in the structural response. This section shows the analytical solutions and the parametric analysis of two sample cases. Specifically, the first sample application is a simply supported beam where the influence of the viscoelastic and nonlocal parameters is investigated. The second one is a cantilever micro beam used to model some small-scale devices.

In both case the system is quiescent at \(t=0\), therefore, the Eq. (36) yields

$$\begin{aligned} {\partial _z^6v(z,t)}-\frac{1}{l_\lambda ^2}{\partial _z^4v(z,t)}=-\frac{1}{l_\lambda ^2 \,{\mathcal {I}}_x}\int _{0}^t {\mathcal {J}}_j(t-{\bar{t}}){\partial _{{\bar{t}}} q_y({\bar{z}},{\bar{t}})}\mathrm {d}{\bar{t}} \end{aligned}$$
(39)

5.1 Simply supported beam forced by uniform distributed load

By assuming that beam is forced by an uniform distributed load along z and constant in time, thus \(q_y(z,t)=a\,U(t)\), where a is a constant value and U(t) is the unit step function defined as

$$\begin{aligned} U(t)=\left\{ \begin{array}{ll} 0&{}\quad \mathrm {if}\;t<0 \\ 1&{}\quad \mathrm {if}\;t\geqslant 0 \end{array} \right. \end{aligned}$$
(40)

the derivative of the unit step function is the Dirac delta function \(\delta (t)=\dot{U}(t)\), therefore Eq. (39) yields

$$\begin{aligned} {\partial _z^6v(z,t)}-\frac{1}{l_\lambda ^2}{\partial _z^4v(z,t)}=-\frac{a}{l_\lambda ^2 \,{\mathcal {I}}_x}\int _{0}^t {\mathcal {J}}_j(t-{\bar{t}})\delta ({\bar{t}})\mathrm {d}{\bar{t}} \end{aligned}$$
(41)

for the sampling property of the delta function Eq. (41) becomes

$$\begin{aligned} {\partial _z^6v(z,t)}-\frac{1}{l_\lambda ^2}\partial _z^4v(z,t)=-\frac{a\,{\mathcal {J}}_j(t)}{l_\lambda ^2 \,{\mathcal {I}}_x} \end{aligned}$$
(42)

and its solution is

$$\begin{aligned} v(z,t)& = \frac{a\,{\mathcal {J}}_j(t)}{24{\mathcal {I}}_x}z^4+ l_\lambda ^4 \left[ c_1(t) \mathrm {e}^{{z}/{l_\lambda }}+c_2(t) \mathrm {e}^{-{z}/{l_\lambda }}\right] \nonumber \\&\quad +c_3(t) z^3+c_4(t) z^2+c_5(t) z+c_6(t) \end{aligned}$$
(43)

the six coefficients \(c_k\) must be evaluated by imposing the costitutive boundary conditions in Eq. (37) and the following static and kinematic ones

$$\begin{aligned}v(0,t)=0,\,\partial _z^4v(0,t)-\frac{1}{l_\lambda ^2}\partial _z^2v(0,t)=0,\end{aligned}$$
(44)
$$\begin{aligned}v(L,t)=0,\,\partial _z^4v(L,t)-\frac{1}{l_\lambda ^2}\partial _z^2v(L,t)=0 \end{aligned}$$
(45)

The figures shown below are obtained considering the normalized displacement \({\tilde{v}}(\zeta ,t)\) defined as

$$\begin{aligned} {\tilde{v}}(\zeta ,t)=\frac{\mathrm {E}_\beta {\mathcal {I}}_x}{a} v(\zeta ,t) \end{aligned}$$
(46)

where \(\zeta =z/L\) is the normalized abscissa. For the FK and the FM model it is assumed that \(\mathrm {E}_\beta /\mathrm {E}=1\). The influence of nonlocal parameter \(\lambda \) and the effects of fractional order \(\beta \) for the three viscoelastic models SP, FK and FM on the structural response are discussed below.

5.1.1 Influence of nonlocal parameter

By assuming that \(\beta =1/2\) the nonlocal effects are highlighted in Fig. 3. It shows time-evolution of the normalized displacement along the normalized abscissa \(\zeta \) considering three different viscoelastic models.

Fig. 3
figure 3

Displacement for different values of \(\lambda \)

Full size image

The chosen viscoelastic model influences the time-evolution of the response, while the nonlocal parameter \(\lambda \) modifies the response along the space coordinate \(\zeta \). Specifically, in any time the response is stiffer when \(\lambda \) increases. The main difference between the nonlocal viscoelastic responses in Fig. 3 consists in a variation of the shape during the time. Thus, the nonlocal effects can be observed independently of the chosen viscoelastic model considering a generic time and different values of \(\lambda \). Therefore, without loss of generality, we consider below the effect of the nonlocal parameter in terms of normalized nonlocal rotation \({\tilde{\varphi }}_x(\zeta ,t)\) and normalized nonlocal curvature \({\tilde{\chi }}_x(\zeta ,t)\) in a generic \(t=1~\mathrm {s}\) when the chosen viscoelastic model is the spring-pot with \(\beta =1/2\).

For different values of \(\lambda \) the normalized nonlocal viscoelastic rotation of the cross-section \(\tilde{\varphi }_x(\zeta ,1)\) is shown in Fig. 4. Whereas, Fig. 5 shows the influence of the nonlocal parameter on the normalized viscoelastic curvature \({\tilde{\chi }}_x(\zeta ,1)\).

Fig. 4
figure 4

Normalized rotation for different values of \(\lambda \) for \(t=1\,\hbox {s}\)

Full size image
Fig. 5
figure 5

Normalized curvature for different values of \(\lambda \) for \(t=1\,\hbox {s}\)

Full size image

In accordance with Fig. 3 also these other two pictures show that when the nonlocal parameters grows up the beam become stiffer.

5.1.2 Viscoelastic effects

To study the viscoelastic phenomena in nonlocal viscoelastic beam we consider the influence of the fractional order \(\beta \) in the structural response in terms of normalized displacement, rotation and curvature. For this study, we fix the nonlocal parameter \(\lambda =0.10\).

Figure 6 shows the displacements at a fixed time \(t=2\) s for the considered viscoelastic model and different values of the fractional order \(\beta =\{1/4,\,1/2,\,3/4\}\).

Fig. 6
figure 6

Normalized displacement at \(t=2\,\hbox {s}\)

Full size image

Time evolution of the maximum normalized displacement \(\tilde{v}(1/2,t)\) is depicted in Fig. 7. It shows the difference in terms of the maximum displacement for different viscoelastic model and different viscoelastic parameter \(\beta \).

Fig. 7
figure 7

Maximum normalized displacement

Full size image

These pictures show that the time response is ruled by the chosen creep function \({\mathcal {J}}_j(t)\). The fractional order \(\beta \) influences the viscoelastic response, specifically, when it increases the viscous response grows up and the viscoelastic response, after a certain time, becomes less stiff. At the initial times the response is ruled by the viscous phase, therefore, an increment of \(\beta \) causes an apparent stiffening in the response.

5.2 Cantilever micro-beam inflected by end-point load

We consider now another application where the viscoelastic nonlocal beam is forced by an end-point time-dependent force. This load condition is typical of several small-scale applications, e.g., nano-actuator modeled by a nano-cantilever beam forced by an end-point load [50]. In this application we consider a microelectromechanical system (MEMS). Usually, MEMS are made of a piezoresistive nanocomposite where the matrix is an epoxy resin filled by nanofibers [76]. In this case a proper mechanical model is a viscoelastic cantilever nonlocal micro-beam. Where the viscoelastic properties are due to the polymeric matrix and the nonlocal phenomena are related to the size effects at the micro-scale. The viscoelastic stress–strain relation of the epoxy resin is modeled as the fractional-order law in Eq. (17) where the mechanical parameters are \(\beta =0.04\) and \(C_\beta =2660\,\mathrm {MPa\, s}^\beta \) [18]. The size-effect influences the mechanical response and to take into account this effect we consider the stress-driven approach described before and report the response in terms of displacement, rotation and curvature for different value of the nonlocal parameter \(\lambda \).

For this sample application the Eq. (36) yields

$$\begin{aligned} {\partial _z^6v(z,t)}-\frac{1}{l_\lambda ^2}{\partial _{{\bar{t}}}^4v(z,t)}=0 \end{aligned}$$
(47)

the constitutive boundary conditions are the same in Eq. (37) and the kinematic and the static ones are

$$\begin{aligned}v(0,t)=0,\partial _z^4v(L,t)-\frac{1}{l_\lambda ^2}\partial _z^2v(L,t)=0, \end{aligned}$$
(48)
$$\begin{aligned}\partial _zv(0,t)=0,\partial _z^5v(L,t)-\frac{1}{l_\lambda ^2}\partial _z^3v(L,t)=\frac{\left( \mathrm {I}^\beta _{t^+}F_y\right) (t)}{l_\lambda ^2 \,{\mathcal {I}}_x\,C_\beta } \end{aligned}$$
(49)

where \(F_y(t)\) is a time-dependent vertical force applied at \(z=L\).

For this numerical application we consider a cantilever micro-beam of length \(L=300\,\upmu \mathrm {m}\) and rectangular cross section \(A=30\times 25\,\upmu \mathrm {m}^2\) forced at the end-point by the following force

$$\begin{aligned} F_y(t)=a\, U(t) \end{aligned}$$
(50)

where \(a=1\,\mathrm {mN}\).

The response in terms of transversal displacement v(z, t) of the cantilever micro-beam made of epoxy resin for different values of the nonlocal parameter \(\lambda \) is shown in Fig. 8. Specifically, that picture contains the time-evolution of the transversal displacement of the longitudinal axis for \(\lambda =\{0.1,\,0.2,\,0.3,\,0.4\}\).

Fig. 8
figure 8

Displacement for different values of \(\lambda \)

Full size image

The time evolution of the maximum displacement v(L, t) is reported in Fig. 9a, while the displacement for a fixed time \(t=1\,\hbox {s}\) is shown in Fig. 9b.

Fig. 9
figure 9

Displacement at \(z=L\) and at a fixed time for different values of \(\lambda \)

Full size image

Whereas rotation and bending curvature of the cross section at \(t=1~\mathrm {s}\) are reported in Fig. 10.

Fig. 10
figure 10

Rotation and bending curvature for different values of \(\lambda \)

Full size image

All these figures show that the nonlocal parameter influences the viscoelastic response. Specifically, when \(\lambda \) increases the magnitude of displacement and rotation decrease. The nonlocal curvature shows a particular behavior where the maximum value decreases when \(\lambda \) increases and the distribution along the space domain changes in function of the nonlocal parameter. This behavior is a consequence of the increment of the long-range interactions when \(\lambda \) grows up.

6 Concluding remarks

Analytical solutions of bending problems of hereditary nonlocal Bernoulli–Euler beam have been presented in this paper. Two main nonconventional mechanical phenomena have been considered in this paper, that is, hereditariness and nonlocality. They have been simulated by means of fractional operators and stress-driven nonlocal formulation.

Time-dependent hereditary behavior, that is typical of viscoelastic materials, has been modeled considering three long-memory models. Specifically, spring-pot, fractional Kelvin–Voigt and fractional Maxwell models have been considered. All these models have a constitutive law based on the differential and integral operators with non-integer orders. They are versatile models that by means of a proper selection of a few number of parameters provide good results in the simulation of the real hereditary mechanical behavior.

Nonlocal phenomena have been simulated by means of the integral stress-driven formulation. This consists in a well-posed integral nonlocal formulation avoiding the paradoxical problems of Eringen’s strain-driven counterpart and providing some useful analytical solutions. Combining fractional hereditary constitutive law and stress-driven nonlocal model a new formulation of nonlocal hereditary relation has been derived. This formulation has been applied to solve bending problems of nonlocal hereditary Bernoulli–Euler beams. Specifically, some closed-form solutions have been obtained and a detailed parametric study has been presented.

Thanks to the proposed closed-form solutions, nonlocal effects and hereditary behaviour in the bending problem have been highlighted. This study has shown the influence of both nonlocal and hereditary parameters in the time-dependent bending response. Proposed formulation and presented outcomes can be useful for design and optimization of structures at small-scale, for the mechanical simulation of bioinspired structural elements, for describing the strain localization in porous viscoelastic devices, and for all those mechanical applications where the local elastic theory cannot be adopted.