Nonlinear vibration of a nonlocal functionally graded beam on fractional visco-Pasternak foundation

Abstract

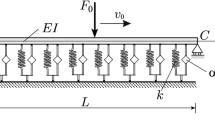
This paper investigates the nonlinear dynamic behavior of a nonlocal functionally graded Euler–Bernoulli beam resting on a fractional visco-Pasternak foundation and subjected to harmonic loads. The proposed model captures both, nonlocal parameter considering the elastic stress gradient field and a material length scale parameter considering the strain gradient stress field. Additionally, the von Karman strain–displacement relation is used to describe the nonlinear geometrical beam behavior. The power-law model is utilized to represent the material variations across the thickness direction of the functionally graded beam. The following steps are conducted in this research study. At first, the governing equation of motion is derived using Hamilton’s principle and then reduced to the nonlinear fractional-order differential equation through the single-mode Galerkin approximation. The methodology to determine steady-state amplitude–frequency responses via incremental harmonic balance method and continuation technique is presented. The obtained periodic solutions are verified against the perturbation multiple scales method for the weakly nonlinear case and numerical integration Newmark method in the case of strong nonlinearity. It has been shown that the application of the incremental harmonic balance method in the analysis of nonlocal strain gradient theory-based structures can lead to more reliable studies for strongly nonlinear systems. In the parametric study, it is shown that, on the one hand, parameters of the visco-Pasternak foundation and power-law index remarkable affect the amplitudes responses. On the contrary, the nonlocal and the length-scale parameters are having a small influence on the amplitude–frequency response. Finally, the effects of the fractional derivative order on the system’s damping are displayed at time response diagrams and subsequently discussed.

Appendices

Appendix 1

Elements of the Jacobi matrix ${\varvec{M}}=\varvec{M_1}+\varvec{M_2^{\alpha }}$, the corrective vector ${\varvec{R}}=\varvec{R_1}+\varvec{R_2^{\alpha }}$, and vector ${\varvec{V}}=\varvec{V_1}+\varvec{V_2^{\alpha }}$ are defined as:

$$\begin{aligned} \varvec{M_1}= & {} \frac{1}{2\pi }\int _{0}^{2\pi }\left[ \Omega ^2\varvec{C^T}\frac{d^2 {\varvec{C}}}{d{\overline{\tau }}^2} \right. \nonumber \\&\quad \left. + \omega _0^2 \varvec{C^T}{\varvec{C}} + 3\theta q_0^2\varvec{C^T}{\varvec{C}}\right] d{\overline{\tau }}, \end{aligned}$$

(67)

$$\begin{aligned} \varvec{M_2^{\alpha }}= & {} \frac{1}{T}\int _{0}^{T}\varvec{C^T}\left[ \gamma \Omega ^{\alpha } D_{{\overline{\tau }}}^\alpha ({\varvec{C}}) \right] d{\overline{\tau }}, \end{aligned}$$

(68)

$$\begin{aligned} \varvec{R_1}= & {} -\frac{1}{2\pi }\int _{0}^{2\pi } \left[ \left( \Omega ^2\varvec{C^T}\frac{d^2 {\varvec{C}}}{d{\overline{\tau }}^2} + \omega _0^2 \varvec{C^T}{\varvec{C}} \right. \right. \nonumber \\&\quad \left. + \theta q_0^2\varvec{C^T}{\varvec{C}}\right) d{\overline{\tau }}\varvec{A_0}\nonumber \\&\left. +f_0\varvec{C^T}+f_0\cos {{\overline{\tau }}}\varvec{C^T} \right] d{\overline{\tau }}, \end{aligned}$$

(69)

$$\begin{aligned} \varvec{R_2^{\alpha }}= & {} -\frac{1}{T}\int _{0}^{T}\varvec{C^T}\left[ \gamma \Omega ^{\alpha } D_{{\overline{\tau }}}^\alpha ({\varvec{C}}) \right] d{\overline{\tau }}\varvec{A_0}, \end{aligned}$$

(70)

$$\begin{aligned} \varvec{V_1}= & {} \frac{1}{2\pi }\int _{0}^{T}\left[ 2\Omega _0\varvec{C^T}\frac{d^2 {\varvec{C}}}{d{\overline{\tau }}^2}\right] d{\overline{\tau }}\varvec{A_0}, \end{aligned}$$

(71)

$$\begin{aligned} \varvec{V_2^{\alpha }}= & {} 0. \end{aligned}$$

(72)

Within each incremental step, only a set of linear equations Eq. (58) has to be solved to obtain the data for the next stage. By applying the procedure established at [47, 69] elements of the matrix $\varvec{M_2^{\alpha }}$, and vectors $\varvec{R_2^{\alpha }}$ and $\varvec{V_2^{\alpha }}$ can be expressed as

$$\begin{aligned} \varvec{M_2^{\alpha }}= & {} \begin{bmatrix} \varvec{\left[ M_{11}\right] ^{\alpha }} &{} \varvec{\left[ M_{12}\right] ^{\alpha }} \\ \varvec{\left[ M_{21}\right] ^{\alpha }} &{} \varvec{\left[ M_{22}\right] ^{\alpha }} \end{bmatrix}, \quad \varvec{R_2^{\alpha }}= \begin{bmatrix} R_{10}^{\alpha } \\ \varvec{R_{1}^{\alpha }} \\ \varvec{R_{2}^{\alpha }} \end{bmatrix}, \nonumber \\ \varvec{V_2^{\alpha }}= & {} \begin{bmatrix} V_{10}^{\alpha } \\ \varvec{V_{1}^{\alpha }} \\ \varvec{V_{2}^{\alpha }} \end{bmatrix}. \end{aligned}$$

(73)

Elements of matrix $\varvec{M_2^{\alpha }}$, and vectors $\varvec{R_2^{\alpha }}$ and $\varvec{V_2^{\alpha }}$ from Eq. (73) are:

$$\begin{aligned}&\begin{aligned} \left[ M_{11}\right] _{ij}^{\alpha }&=\delta _{ij}\gamma \Omega ^{\alpha }\frac{i^{\alpha }}{2}\cos \left( \frac{\alpha \pi }{2}\right) ,\\&\qquad \quad i=0,1,2,...,N, \quad j=0,1,2,...,N.\\ \left[ M_{12}\right] _{ij}^{\alpha }&=\delta _{ij}\gamma \Omega ^{\alpha }\frac{i^{\alpha }}{2}\sin \left( \frac{\alpha \pi }{2}\right) ,\\&\qquad \quad i=0,1,2,...,N, \quad j=1,2,...,N.\\ \left[ M_{21}\right] _{ij}^{\alpha }&=-\delta _{ij}\gamma \Omega ^{\alpha }\frac{i^{\alpha }}{2}\sin \left( \frac{\alpha \pi }{2}\right) ,\\&\qquad \quad i=1,2,...,N, \quad j=0,1,2,...,N.\\ \left[ M_{22}\right] _{ij}^{\alpha }&=\delta _{ij}\gamma \Omega ^{\alpha }\frac{i^{\alpha }}{2}\cos \left( \frac{\alpha \pi }{2}\right) ,\\&\qquad \quad i=1,2,...,N, \quad j=1,2,...,N. \end{aligned} \end{aligned}$$

(74)

$$\begin{aligned}&\begin{aligned} R_{10}^{\alpha }&=0,\\ R_{1i}^{\alpha }&=-\gamma \Omega ^{\alpha }\left[ a_i\frac{i^{\alpha }}{2}\cos \left( \frac{\alpha \pi }{2}\right) +b_i\frac{i^{\alpha }}{2}\sin \left( \frac{\alpha \pi }{2}\right) \right] , \\&\qquad \qquad \qquad \qquad \qquad \qquad i=1,2,...,N, \\ R_{2i}^{\alpha }&=-\gamma \Omega ^{\alpha }\left[ a_i\frac{i^{\alpha }}{2}\sin \left( \frac{\alpha \pi }{2}\right) +b_i\frac{i^{\alpha }}{2}\cos \left( \frac{\alpha \pi }{2}\right) \right] , \\&\qquad \qquad \qquad \qquad \qquad \qquad i=1,2,...,N, \\ \end{aligned} \end{aligned}$$

(75)

$$\begin{aligned}&\begin{aligned} V_{10}^{\alpha }&=0,\\ V_{1i}^{\alpha }&=\gamma \alpha \Omega ^{\alpha -1}\left[ a_i\frac{i^{\alpha }}{2}\cos \left( \frac{\alpha \pi }{2}\right) +b_i\frac{i^{\alpha }}{2}\sin \left( \frac{\alpha \pi }{2}\right) \right] ,\\&\qquad \qquad \qquad \qquad \qquad \qquad i=1,2,...,N, \\ V_{2i}^{\alpha }&=\gamma \alpha \Omega ^{\alpha -1}\left[ a_i\frac{i^{\alpha }}{2}\sin \left( \frac{\alpha \pi }{2}\right) +b_i\frac{i^{\alpha }}{2}\cos \left( \frac{\alpha \pi }{2}\right) \right] ,\\&\qquad \qquad \qquad \qquad \qquad \qquad i=1,2,...,N, \\ \end{aligned} \end{aligned}$$

(76)

where $\delta _{ij}$ is Kronecker delta.

Appendix 2

1.1 Multiple scales method

Multiple scales is the analytical perturbation method for constructing approximate solutions of nonlinear differential equations. This method is well established in the literature, but it is only valid for small nonlinearities and damping. Therefore, we will use it here only for validation purposes. Equation (46) is well known as the forced Duffing fractional-order differential equation, which can be expressed in terms of small scale parameter $\epsilon$ as in Eq. (77). Let assume for simplicity $f_0=0, f=f_1$.

$$\begin{aligned} \ddot{q}+ \epsilon {\overline{\gamma }}D_\tau ^\alpha q + \omega _0^2 q + \epsilon {\overline{\theta }} q^3=f\cos \Omega \tau . \end{aligned}$$

(77)

Here, we introduce new parameters as $\gamma =\epsilon {\overline{\gamma }}$ and $\theta =\epsilon {\overline{\theta }}$. The small bookkeeping parameter $\epsilon$ is put in front of the fractional and nonlinear terms to have weak damping and weak nonlinearity. Please note that the forcing term in Eq. (77) is of the order one (also known as hard forcing), which will help us to study secondary resonances in the system by using the perturbation analysis of the first order. Forcing of order $\epsilon$ would indicate a primary resonance that is the same as in the Duffing equation [52].

Using the multiple scales method, we will seek the solution of Eq. (77) in the following form:

$$\begin{aligned} q(T_0,T_1,\epsilon )= q_0(T_0,T_1)+\epsilon q_1(T_0,T_1)+\cdots . \end{aligned}$$

(78)

Here, $T_0=\tau$ is the fast time scale and $T_1=\epsilon \tau$ is the slow time scale. We will analyze the system for superharmonic resonance conditions. Firstly, let us define the time derivatives as

$$\begin{aligned} \frac{d}{d\tau }= & {} D_0+\epsilon D_1+O(\epsilon ^2), \end{aligned}$$

(79)

$$\begin{aligned} \frac{d^2}{d\tau ^2}= & {} D_0^2+2\epsilon D_0 D_1+O(\epsilon ^2), \end{aligned}$$

(80)

$$\begin{aligned} D^\alpha= & {} D^\alpha _{0+}-\epsilon \alpha D^{\alpha -1}_{0+}D_1+\cdots , \end{aligned}$$

(81)

where $D_n=\frac{\partial }{\partial T_n}, (n=0,1,2,\dots )$ and $D^{\alpha -n}_{n+}=\frac{\partial ^{\alpha -n}}{\partial T_{n+}^{\alpha -n}}, (n=0,1,2,\ldots )$ are classical and Riemann–Liouville’s fractional derivative for new time scales [58]. For the fractional derivative of the exponential function [58], restricted to the first- and second-order approximations, the following relationship will be used:

$$\begin{aligned} D^\alpha _{0+}\exp ^{i\omega \tau }=(i\omega )^\alpha \exp ^{i\omega \tau }, \end{aligned}$$

(82)

where i is the imaginary unit. Substituting Eqs. (78), (79), (80), (81) into Eq. (77) and then extracting coefficients of $\epsilon ^0$ and $\epsilon ^1$, we obtain the following equations

$$\begin{aligned}&\epsilon ^0: D_0^2q_0+\omega _0^2 q_0=f\cos \Omega \tau , \end{aligned}$$

(83)

$$\begin{aligned}&\epsilon ^1: D_0^2q_1+\omega _0^2 q_1=-2D_0D_1q_0- {\overline{\gamma }}D^\alpha _{0+}q_0\nonumber \\&- {\overline{\theta }}q_0^3. \end{aligned}$$

(84)

The solution of Eq. (83) is sought in the form

$$\begin{aligned} q_0= & {} A(T_1)e^{i\omega _0T_0} + \Lambda e^{i\Omega T_1} + {\overline{A}}(T_1)e^{-i\omega _0T_0} \nonumber \\&+ \Lambda e^{-i\Omega T_1}, \end{aligned}$$

(85)

where A is a complex function in terms of slow time scale, and $\Lambda$ is defined as:

$$\begin{aligned} \Lambda =\frac{f}{2(\omega _0^2-\Omega ^2)}. \end{aligned}$$

(86)

1.1.1 Superharmonic resonance $3\Omega \approx \omega _0$

Since we have only cubic nonlinearity in Eq. (77), we will consider the case when $3\Omega =\omega _0+\epsilon \sigma$, where $\sigma$ is the detuning parameter. By substituting $q_0$ from Eq. (85) into Eq. (84) and removing the secular terms that grow in time unbounded, i.e., the coefficients of $e^{i\omega _0 T_0}$, we obtain the corresponding solvability conditions as:

$$\begin{aligned}&-2i\omega _0 A' - {\overline{\gamma }}A(i\omega _0)^\alpha \nonumber \\&\quad - {\overline{\theta }}(3A^2{\overline{A}}+6A\Lambda ^2+\Lambda ^3e^{i\sigma T_1})=0, \end{aligned}$$

(87)

where $A'=D_1A$. Then, we use the polar form $A=\frac{1}{2}ae^{i\varphi }$, where the real-valued functions a and $\varphi$ are the amplitude and phase lag of time response, respectively. By substituting A in Eq. (87) and separation of real and imaginary parts, we obtain

$$\begin{aligned}&\omega _0 a \varphi '-\frac{1}{2}{\overline{\gamma }}a\omega _0^\alpha \cos \frac{\alpha \pi }{2}\nonumber \\&\quad - \frac{3}{8}{\overline{\theta }}a^3 -3{\overline{\theta }}a\Lambda ^2-{\overline{\theta }}\Lambda ^3\cos \zeta =0, \end{aligned}$$

(88)

$$\begin{aligned}&\omega _0 a' +\frac{1}{2}{\overline{\gamma }}a\omega _0^\alpha \sin \frac{\alpha \pi }{2}\nonumber \\&\quad +{\overline{\theta }}\Lambda ^3\sin \zeta =0, \end{aligned}$$

(89)

with $\zeta =\sigma T_1-\varphi$ denoting the new phase angle. Then, we utilize steady-state conditions $a'=0$, $\zeta '=0$ in Eq. (88) and Eq. (89), which leads to the relationship between the response amplitude and the detuning parameter in the following form

$$\begin{aligned} \frac{{\overline{\theta }}\Lambda ^3}{\omega _0 a}\cos \zeta= & {} \sigma -\frac{1}{2}{\overline{\gamma }}\omega _0^{\alpha -1} \cos \frac{\alpha \pi }{2} - \frac{3}{8}\frac{{\overline{\theta }}a^2}{\omega _0}\nonumber \\&-3\frac{{\overline{\theta }}\Lambda ^2}{\omega _0}, \end{aligned}$$

(90)

$$\begin{aligned} \frac{{\overline{\theta }}\Lambda ^3}{\omega _0 a}\sin \zeta= & {} -\frac{1}{2}{\overline{\gamma }}\omega _0^{\alpha -1} \sin \frac{\alpha \pi }{2}. \end{aligned}$$

(91)

After simple algebra transformations over Eq. (90) and Eq. (91), the following polynomial equation can be obtained

$$\begin{aligned} \sigma ^2-2\sigma K + M = 0, \end{aligned}$$

(92)

with K and M given as

$$\begin{aligned} K= & {} \frac{1}{2}{\overline{\gamma }}\omega _0^{\alpha -1} \cos \frac{\alpha \pi }{2}+\frac{3}{8}\frac{{\overline{\theta }}a^2}{\omega _0} -3\frac{{\overline{\theta }}\Lambda ^2}{\omega _0}, \end{aligned}$$

(93)

$$\begin{aligned} M= & {} K^2+\left( \frac{1}{2}{\overline{\gamma }}\omega _0^{\alpha -1}\sin \frac{\alpha \pi }{2} \right) ^2, \end{aligned}$$

(94)

from where the relationship for amplitude–frequency curves can be obtained as:

$$\begin{aligned} \sigma _{1,2}=K\pm \sqrt{K^2-M}. \end{aligned}$$

(95)

One can notice that all the parameters contribute to the appearance of the superharmonic resonance of order 1/3, i.e., we have interaction of terms of fractional-order, nonlinear, and external excitation.

Appendix 3

1.1 Newmark method

We use Grunwald–Letnikov representation of fractional derivative and apply the Newmark–Beta method for numerical integration. We use two different meshes, coarse mesh for time integration and fine mesh for fractional derivative approximation. Grunwald–Letnikov representation of a fractional derivative of a function $q({\overline{\tau }})$ at a point of time ${\overline{\tau }}$ is:

$$\begin{aligned} {} _{GL}D^{\alpha }_{0,{\overline{\tau }}} q({\overline{\tau }})=\lim _{h \rightarrow 0} h^{-\alpha } \sum _{k=0}^{n} GL_k q({\overline{\tau }}-kh) \end{aligned}$$

(96)

where

$$\begin{aligned} GL_k=(-1)^k \left( \begin{array}{c} \alpha \\ k \end{array} \right) \end{aligned}$$

(97)

Grunwald–Letnikov coefficients can also be represented in recursive form as:

$$\begin{aligned} GL_{k=0}=1, \qquad GL_k=\frac{k-\alpha -1}{k}GL_{k-1} \end{aligned}$$

(98)

$$\begin{aligned} \frac{\Delta {\overline{\tau }}}{h}=p=5\div 20 \end{aligned}$$

(99)

where $\Delta {\overline{\tau }}$ is time step for coarse mesh, and h is time step for fine mesh.

Representation of fractional derivative given by Eq.(96) in fine mesh is:

$$\begin{aligned} q_i^{(\alpha )}=h^{-\alpha } \left[ \begin{array}{cccc} GL_0&GL_1&\cdots&GL_{kjp} \end{array} \right] \left[ \begin{array}{c} q_i \\ q_{i-1} \\ \vdots \\ q_{i-p} \\ q_{i-p-1} \\ \vdots \\ q_{i-2p} \\ q_{i-2p-1} \\ \vdots \\ q_{kjp} \end{array} \right] \nonumber \\ \end{aligned}$$

(100)

where:

p is the number of past terms of length h in a time integration step of length $\Delta {\overline{\tau }}$,

j are previous time steps of length $\Delta {\overline{\tau }}$ that can be approximated accurately by a backward Taylor expansion using the displacement, velocity, and acceleration at a certain time step i,

k represents overall chunks of j time steps that must be taken into consideration to accurately approximate the fractional derivative at a given point.

Taylor backward expansion for the last jp time steps can be represented as in Eq. (101).

$$\begin{aligned} \begin{aligned} q_{i-1}&=q_i - h{\dot{q}}_i + \frac{h^2}{2}\ddot{q}_i + O(h^3)\\ q_{i-2}&=q_i - 2h{\dot{q}}_i +\frac{4h^2}{2}\ddot{q}_i + O(h^3)\\ q_{i-3}&=q_i - 3h{\dot{q}}_i +\frac{9h^2}{2}\ddot{q}_i + O(h^3)\\&\vdots \\ q_{i-jp}&=q_i -jph{\dot{q}}_i +\frac{j^2p^2h^2}{2}\ddot{q}_i + O(h^3)\\ \end{aligned} \end{aligned}$$

(101)

where $q_i$, ${\dot{q}}_i$ and $\ddot{q}_i$ are displacement, velocity, and acceleration, respectfully, at time step i.

Let us neglect higher-order terms. Equation (101) can be written in the matrix form Eq. (102).

$$\begin{aligned} \left[ \begin{array}{c} q_i \\ q_{i-1} \\ q_{i-2} \\ q_{i-3} \\ \vdots \\ q_{i-(jp-1)} \end{array} \right]= & {} \left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 1 &{} -h &{} \frac{h^2}{2} \\ 1 &{} -2h &{} \frac{4h^2}{2} \\ 1 &{} -3h &{} \frac{9h^2}{2} \\ \vdots &{}\vdots &{}\vdots \\ 1 &{} -(jp-1)h &{} \frac{(jp-1)^2h^2}{2} \\ \end{array} \right] \left[ \begin{array}{c} q_i \\ {\dot{q}}_i \\ \ddot{q}_i \end{array} \right] \nonumber \\= & {} \left[ H_0 \right] \left[ \begin{array}{c} q_i \\ {\dot{q}}_i \\ \ddot{q}_i \end{array} \right] \end{aligned}$$

(102)

By analogy, the displacements from the step $i-jp$ to the $i-(2jp-1)$ in matrix form in terms of displacements, velocity and acceleration of the $i-jp$ are given by Eq. (103). Here can jerk also be included, but we didn’t do this.

$$\begin{aligned} \left[ \begin{array}{c} q_{i-jp} \\ q_{i-jp-1} \\ q_{i-jp-2} \\ q_{i-jp-3} \\ \vdots \\ q_{i-(2jp-1)} \end{array} \right]= & {} \left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 1 &{} -h &{} \frac{h^2}{2} \\ 1 &{} -2h &{} \frac{4h^2}{2} \\ 1 &{} -3h &{} \frac{9h^2}{2} \\ \vdots &{}\vdots &{}\vdots \\ 1 &{} -(jp-1)h &{} \frac{(jp-1)^2h^2}{2} \\ \end{array} \right] \left[ \begin{array}{c} q_{i-j} \\ {\dot{q}}_{i-j} \\ \ddot{q}_{i-j} \end{array} \right] \nonumber \\= & {} \left[ H \right] \left[ \begin{array}{c} q_{i-j} \\ {\dot{q}}_{i-j} \\ \ddot{q}_{i-j} \end{array} \right] \end{aligned}$$

(103)

Since we omitted jerk, $\left[ H \right] =\left[ H_0 \right]$. Substituting Eq. (101), Eq. (102) and Eq. (103) in Eq. (100), we obtain the following expressions:

$$\begin{aligned}&\begin{aligned} q_i^{(\alpha )}=&h^{-\alpha } \left[ \begin{array}{cccc} GL_0&GL_1&\cdots&GL_{jp-1} \end{array} \right] \left[ H_0 \right] \left[ \begin{array}{c} q_i \\ {\dot{q}}_i \\ \ddot{q}_i \end{array} \right] \\&+ h^{-\alpha } \left[ \begin{array}{cccc} GL_{jp}&GL_{jp+1}&\cdots&GL_{2jp-1} \end{array} \right] \\&\qquad \left[ H \right] \left[ \begin{array}{c} q_{i-j} \\ {\dot{q}}_{i-j} \\ \ddot{q}_{i-j} \end{array} \right] + \cdots \\&+ h^{-\alpha } \left[ \begin{array}{ccc} GL_{(k-1)jp}&\cdots&GL_{kjp-1} \end{array} \right] \\&\qquad \left[ H \right] \left[ \begin{array}{c} q_{i-(k-1)j} \\ {\dot{q}}_{i-(k-1)j} \\ \ddot{q}_{i-(k-1)j} \end{array} \right] \end{aligned} \end{aligned}$$

(104)

$$\begin{aligned}&\begin{aligned} q_i^{(\alpha )}=&\left[ \begin{array}{ccc} D_{01}&D_{02}&D_{03} \end{array} \right] \left[ \begin{array}{c} q_i \\ {\dot{q}}_i \\ \ddot{q}_i \end{array} \right] \\&+ \left[ \begin{array}{ccc} D_{11}&D_{12}&D_{13} \end{array} \right] \left[ \begin{array}{c} q_{i-j} \\ {\dot{q}}_{i-j} \\ \ddot{q}_{i-j} \end{array} \right] \\&+ \cdots + \left[ \begin{array}{ccc} D_{(k-1)1}&D_{(k-1)2}&D_{(k-1)3} \end{array} \right] \\&\left[ \begin{array}{c} q_{i-(k-1)j} \\ {\dot{q}}_{i-(k-1)j} \\ \ddot{q}_{i-(k-1)j} \end{array} \right] \end{aligned} \end{aligned}$$

(105)

$$\begin{aligned}&\begin{aligned} \Delta q_i^{(\alpha )}=&\left[ \begin{array}{ccc} D_{01}&D_{02}&D_{03} \end{array} \right] \left[ \begin{array}{c} \Delta q_i \\ \Delta {\dot{q}}_i \\ \Delta \ddot{q}_i \end{array} \right] \\&+ \left[ \begin{array}{ccc} D_{11}&D_{12}&D_{13} \end{array} \right] \left[ \begin{array}{c} \Delta q_{i-j} \\ \Delta {\dot{q}}_{i-j} \\ \Delta \ddot{q}_{i-j} \end{array} \right] \\&+ \cdots + \left[ \begin{array}{ccc} D_{(k-1)1}&D_{(k-1)2}&D_{(k-1)3} \end{array} \right] \\&\quad \left[ \begin{array}{c} \Delta q_{i-(k-1)j} \\ \Delta {\dot{q}}_{i-(k-1)j} \\ \Delta \ddot{q}_{i-(k-1)j} \end{array} \right] \end{aligned} \end{aligned}$$

(106)

Lets consider equation of motion Eq.(48) in two consecutive time instants.

$$\begin{aligned}&\Omega ^2\Delta \ddot{q}_i + \omega _0^2\Delta q_i + \theta (\Delta q_i)^3 \nonumber \\&\qquad + \gamma \Omega ^{\alpha } \left( _{GL}D_{0,{\overline{\tau }}_i}^\alpha q_i - { _{GL}D_{0,{\overline{\tau }}_{i-1}}^\alpha } q_{i-1} \right) \nonumber \\&\quad =f_0 + \Delta f_i \end{aligned}$$

(107)

where

$$\begin{aligned} \Delta f_i=f_1\cos {\overline{\tau }}_i \end{aligned}$$

(108)

By substituting Eq.(106) in Eq.(107), we obtain

$$\begin{aligned}&\left( \Omega ^2+\gamma \Omega ^{\alpha }D_{03}\right) \Delta \ddot{q}_i + \gamma \Omega ^{\alpha }D_{02}\Delta {\dot{q}}_i \nonumber \\&\quad + \left( \omega _0^2 + \gamma \Omega ^{\alpha }D_{01}\right) \Delta q_i\nonumber \\&\quad + \theta (\Delta q_i)^3=f_0 + \Delta f_i - \Delta f_{correction} \end{aligned}$$

(109)

where

$$\begin{aligned} \begin{aligned} \Delta f_{correction}=\gamma \Omega ^{\alpha } \left[ \begin{array}{ccc} D_{11}&D_{12}&D_{13} \end{array} \right] \left[ \begin{array}{c} \Delta q_{i-j} \\ \Delta {\dot{q}}_{i-j} \\ \Delta \ddot{q}_{i-j} \end{array} \right] + \cdots + \\ \gamma \Omega ^{\alpha }\left[ \begin{array}{ccc} D_{(k-1)1}&D_{(k-1)2}&D_{(k-1)3} \end{array} \right] \left[ \begin{array}{c} \Delta q_{i-(k-1)j} \\ \Delta {\dot{q}}_{i-(k-1)j} \\ \Delta \ddot{q}_{i-(k-1)j} \end{array} \right] \end{aligned}\nonumber \\ \end{aligned}$$

(110)

Note that in case of $\Delta f_i=const$, Eq.(109) can be solved using the Runge–Kutta method (function ode45 in Matlab). If this is not the case, Eq.(109) can be solved using the Newmark–Beta method.

For validation of the IHB solution, the Newmark–Beta method for nonlinear systems is used and implemented according to the procedure presented in [7, 13].