Backbone curves, Neimark-Sacker boundaries and appearance of quasi-periodicity in nonlinear oscillators: application to 1:2 internal resonance and frequency combs in MEMS

Abstract

Quasi-periodic solutions can arise in assemblies of nonlinear oscillators as a consequence of Neimark-Sacker bifurcations. In this work, the appearance of Neimark-Sacker bifurcations is investigated analytically and numerically in the specific case of a system of two coupled oscillators featuring a 1:2 internal resonance. More specifically, the locus of Neimark-Sacker points is analytically derived and its evolution with respect to the system parameters is highlighted. The backbone curves, solution of the conservative system, are first investigated, showing in particular the existence of two families of periodic orbits, denoted as parabolic modes. The behaviour of these modes, when the detuning between the eigenfrequencies of the system is varied, is underlined. The non-vanishing limit value, at the origin of one solution family, allows explaining the appearance of isolated solutions for the damped-forced system. The results are then applied to a Micro-Electro-Mechanical System-like shallow arch structure, to show how the analytical expression of the Neimark-Sacker boundary curve can be used for rapid prediction of the appearance of quasiperiodic regime, and thus frequency combs, in Micro-Electro-Mechanical System dynamics.

1 Introduction

Nonlinear dynamical phenomena in mechanical systems are often connected with the description of complex features that have no counterpart in linear theory, like jump phenomena, hysteresis, quasiperiodicity and chaotic vibrations [18, 39, 54]. In recent years, a number of studies appeared in several fields of Physics and Mechanics, highlighting the occurrence of Frequency Comb (FC) in the observed dynamical responses, especially when the system is driven by a single harmonic component. In the frequency domain a FC is characterized by a collection of spectral lines of frequency $m\varOmega \pm n\omega _{\rm {NS}}$, where m and n are integers, $\varOmega$ is the driving frequency and $\omega _{\rm {NS}}$ is a new incommensurate frequency. In the time domain a FC is associated with a signal showing both amplitude and frequency modulation.

FCs have been largely investigated in optics where they have important applications in metrology, see e.g. [10, 29, 60, 63]. A strong link also exists with the so-called modulation instability studied in the physics of nonlinear waves [9, 64].

In recent years several occurrences of FCs have been documented in Micro Electro-Mechanical Systems (MEMS). These devices display a wide range of complex nonlinear phenomena, mainly due to their large quality factors Q, typically ranging from $10^3$ to $10^6$. Indeed MEMS are often monolithic structures encapsulated in near vacuum packages and their dissipation is drastically reduced with respect to macrostructures. Internal resonance (IR) plays an important role in triggering more complex motions and facilitate energy transfer between modes and also the onset of quasiperiodicity  [1, 2, 6, 22, 23, 44, 58, 59]. Indeed in most cases, FCs in MEMS are associated with IR phenomena. FCs have been experimentally observed in [7, 8] addressing a MEMS resonator with strong 1:3 IR between bending and torsional modes. Another example is provided in [31], where a resonator is proposed in which the dissipation can be dynamically eliminated, leading to the appearance of a tunable FC. In [45] the formation, evolution, and tuning of FCs in a piezoelectric MEMS resonator, based on nondegenerate parametric pumping, is presented. The tuning mechanisms of FCs are discussed with specific attention to the dependence of the center frequency and the frequency spacing between the spectral lines on the external input. In [22] a 1:2 IR between the first two symmetric vibrational modes of a MEMS arch resonator is investigated experimentally and theoretically. The MEMS structure is electro-thermally tuned and electro-statically driven. Here FCs are observed amid a variety of other complex behaviours. Other noteworthy studies on IR in MEMS arch resonators, with experimental data supported by theoretical models, can be found in [46, 47]. In the context of MEMS piezoresonators, similar phenomena have been demonstrated in [14,15,16]. In particular, if the system has two modes with eigenfrequencies $f_1$ and $f_2$ such that $f_2\approx f_1/2$, an excitation can activate parametric resonance and trigger a FC. However, it is worth mentioning that FCs in MEMS might be associated with different phenomena. An example is discussed in [19] where FCs arise as a consequence of intermittent contact between deformable beams in a MEMS structure.

The issue of predicting the onset of a FC is strongly linked to the stability analysis of the associated periodic response. Once it gets unstable, a Quasi-Periodic (QP) regime might arise thus creating a FC. Restraining ourselves to the case of nonlinear vibrations, this problem can be reformulated as finding the locus of bifurcation points in periodic responses originating quasi-periodicity. In most cases these can be classified as Neimark-Sacker (NS) bifurcations [41, 48], which represent the main focus of this work. It is however worth stressing that the onset of QP solutions and FCs have been also observed in [7, 8] as a consequence of a Saddle-Node-Invariant-Circle (SNIC) bifurcation [51]. Besides, the stability of QP solutions developing on a torus is a fundamental aspect for questioning the appearance of chaos related to the stability of the period-three solutions [3, 4, 21, 28, 42].

The appearance of NS bifurcations in systems with IR has already been reported for systems featuring 1:1 IR, see e.g. [56] for arches or [57] for circular cylindrical shells, as well as for systems with 1:2 IR [39, 40, 54] such as arches [55]. Other examples involve different physical phenomena like, for instance, the aero-elastic behaviour of a flexible elastic suspended cable with linear eigenfrequencies in an almost 1:2 ratio driven by the wind speed [30]. Finally, NS bifurcations can also originate in more complex 1:2:2 and 1:2:4 resonance scenarios as reported in [36].

One can also remark that the computation of the locus of specific bifurcation points, as parameters are varied, has recently stimulated intensive research also on numerical techniques. For instance, continuation methods can be suitably adapted with additional constraints to follow the evolution of a given bifurcation point in the parameter space [11, 61, 62].

This work focuses on the appearance of QP solutions in nonlinear oscillators featuring 1:2 internal resonance. In this context NS bifurcation points have been known for a long time, see e.g. [35, 37, 38, 40] and references therein. Consequently the viewpoint of the present contribution is to revisit a classical example in nonlinear oscillations, bring new results and use them in the perspective of better understanding and predicting the occurrence of frequency combs in MEMS dynamics. The main outcomes of the present study are to derive an analytical formula for the locus of NS boundaries, exhibit the two different families of periodic solutions connected to the two backbone curves of the system, named them as parabolic modes, and clearly highlight the links between the backbones, the frequency-response curves, the existence of isolated solutions and the locus of NS points. Since applications to MEMS-like structure are targeted, an arch structure is used in order to show how the findings can be used for fast prediction of the onset of FC in MEMS dynamical solutions.

The formulas derived analytically give simplified models that can be applied in systems that admit order reduction. In this work we consider systems in which it is possible to apply the center manifold theorem and more generally invariant and inertial manifold theory (see [24, 33, 34, 52]). In this framework, strong but reliable simplifications can be applied and even continuous systems may be reduced to a limited number of degrees of freedom.

Future investigations will address the cases of 1:1 and 1:3 IRs, framing all these systems within the same setting and offering a unified view on the appearance of quasiperiodicity and link to backbones in assemblies of nonlinear oscillators featuring IR.

The paper is organized as follows. Sect. 2 is devoted to the analysis of conservative systems with the multiple scales technique. Two families of parabolic modes are identified and associated with two different backbone curves. The behaviour of these families of solution, for system parameters variation, is investigated. Sect. 3 is concerned with the analysis of the forced-damped system. A connection with the limit values of the conservative solution is given, and the appearance of isolas is explained. The NS boundary curve is computed and its dependence upon parameters and shape variation is analysed in detail.

Finally, in Sect. 4, a MEMS-like arch structure is analysed and the analytical expression of NS boundary curves is utilized to predict the occurrence of QP solutions, which represents the primary goal of the paper. Reduced order models using implicit static condensation [13, 25, 50] are obtained starting from the Finite Element (FE) discretization. The dynamics of the system is studied numerically through harmonic balance and direct time integration techniques in order to validate and refine the analytical estimate.

2 Conservative system: backbone curves

Let us consider the normal form of a system of two coupled nonlinear oscillators featuring 1:2 IR:

$$\begin{aligned}&\ddot{q}_{1}+\omega _{1}^{2} q_{1}+2\mu _{1} {\dot{q}}_{1}+\alpha _{12} q_1 q_2=F \cos \left( \varOmega t\right) , \end{aligned}$$

(1a)

$$\begin{aligned}&\ddot{q}_{2}+\omega _{2}^{2} q_{2}+2\mu _{2} {\dot{q}}_{2}+\alpha _{11} q_1^2=0, \end{aligned}$$

(1b)

in which $q_i$, $(i=1,2)$ denote the displacement of each oscillator, $\omega _i$ the eigenfrequencies, $\alpha _{12},\alpha _{11}$ the nonlinear positive quadratic coupling coefficients, $\mu _i$, $(i=1,2)$ the linear damping coefficients and $\varOmega$ the angular frequency of the forcing term with intensity F. Since we are interested in the 1:2 IR, the eigenfrequencies are such that $\omega _2\approx 2\omega _1$. In a conservative context, where internal forces derive from a potential, we have $\alpha _{11}=\alpha _{12}/2$. However, since the results discussed in what follows can be used in more general contexts such as e.g. economy, chemistry or biology, in Appendix 1 we will relax this assumption and show examples of the behaviour for more general cases of quadratic coupling coefficients.

In this section, we address conservative dynamics and discard consequently the damping and forcing terms from the equations of motion. We apply the method of Multiple Scales (MS) to system (1) following [40]. Only the main results are recalled with emphasis on new findings. The detailed MS procedure is given in Appendix 2 for the sake of completeness.

2.1 Multiple scales solution

The method of MS expresses the solution as a composition of different time scales $T_j=\varepsilon ^j t$ for $j=0,1$, and decomposes the solution as $q_i(t)= q_{i0}(T_0,T_1)+\varepsilon q_{i1}(T_0,T_1)+ O(\varepsilon ^2)$ with $i=1,2$ and $\varepsilon$ a small bookkeeping parameter. We also assume that the nonlinear coefficients are small and can be expressed as $\alpha _{12}=\varepsilon {\bar{\alpha }}_{12}$ and $\alpha _{11}=\varepsilon {\bar{\alpha }}_{11}$. Starting from Eq. (1) and introducing the MS expansions, we sort non-linearities according to $\varepsilon$ and we ignore the forcing F and the damping terms $\mu _i$ (see details in Appendix 2). The closeness of the fulfilment of the 1:2 ratio between the eigenfrequencies is quantified by introducing an internal detuning parameter $\sigma _1$ such that

$$\begin{aligned} \omega _2=2\omega _1+\varepsilon \sigma _1. \end{aligned}$$

(2)

We introduce a polar form for $q_{10}(t)$

$$\begin{aligned}&q_{10}(t)=\frac{a_1(T_1)}{2}\exp (\mathbb {i}\theta _1(T_1)+\mathbb {i}\omega _1 T_0)+c.c. , \end{aligned}$$

(3a)

$$\begin{aligned}&q_{20}(t)=\frac{a_2(T_1)}{2}\exp (\mathbb {i}\theta _2(T_1)+\mathbb {i}\omega _2 T_0)+c.c., \end{aligned}$$

(3b)

where c.c. stands for complex conjugate; $a_1(T_1)$, $a_2(T_1)$ are unknown amplitudes; $\theta _1(T_1)$, $\theta _2(T_1)$ are unknown phases, varying at the slow time scale $T_1$ and $\mathbb {i}$ is the imaginary unit. Developing the solvability condition (see details given in Appendix 2), we arrive at the modulation equations for amplitudes and phases:

$$\begin{aligned}&a_1 '=\frac{{\bar{\alpha }}_{12} a_1 a_2 \sin \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _1}, \end{aligned}$$

(4a)

$$\begin{aligned}&a_1\theta _1'=\frac{{\bar{\alpha }}_{12} a_1 a_2 \cos \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _1} , \end{aligned}$$

(4b)

$$\begin{aligned}&a_2'=-\frac{{\bar{\alpha }}_{11} a_1^2 \sin \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _2}, \end{aligned}$$

(4c)

$$\begin{aligned}&a_2\theta _2'=\frac{{\bar{\alpha }}_{11} a_1^2 \cos \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _2}. \end{aligned}$$

(4d)

Inspecting Eq. (4), three different classes of possible solutions can be identified: 1) uncoupled solution with $a_1\ne 0$ and $a_2=0$, denoted A1-mode in what follows; 2) uncoupled solution with $a_2\ne 0$ and $a_1=0$, denoted A2-mode; 3) coupled solutions with both $a_2\ne 0$ and $a_1\ne 0$. The A1-mode is not admissible because of the invariant-breaking term $\alpha _{11} q_1^2$ in Eq. (1) considering the conservative condition. Indeed inserting $q_2=0$ in Eq. (1b) implies that also $q_1=0$. The A2-mode is admissible, since inserting $q_1=0$ Eq. (1b) reduces to a linear oscillator, while Eq. (1a) is trivially satisfied.

Considering now the coupled solutions with both $a_1$ and $a_2$ different from zero, we simplify Eq. (4), dividing by the non-zero amplitudes $a_1$ and $a_2$:

$$\begin{aligned}&a_1 '=\frac{{\bar{\alpha }}_{12} a_1 a_2 \sin \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _1}, \end{aligned}$$

(5a)

$$\begin{aligned}&\theta _1'=\frac{{\bar{\alpha }}_{12} a_2 \cos \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _1}, \end{aligned}$$

(5b)

$$\begin{aligned}&a_2'=-\frac{{\bar{\alpha }}_{11} a_1^2 \sin \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _2 }, \end{aligned}$$

(5c)

$$\begin{aligned}&\theta _2'=\frac{{\bar{\alpha }}_{11} a_1^2 \cos \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 a_2 \omega _2 }. \end{aligned}$$

(5d)

To analyse the permanent solutions corresponding to fixed points of Eq. (5), the system needs to be made autonomous. We observe that the phases appearing in the sine and cosine functions involve the same quantity $2 \theta _1-\theta _2-\sigma _1 T_1$. This means that the system can be made autonomous with only two amplitudes and one phase. However, if one adopts such a choice an indeterminate quantity will appear when reconstructing the whole solutions for $q_1$ and $q_2$, since both $\theta _1$ and $\theta _2$ will need to have an initial phase. To solve this issue, it has been preferred to make the system autonomous using two angular variables.

$$\begin{aligned}&\gamma _1=\theta _1, \end{aligned}$$

(6a)

$$\begin{aligned}&\gamma _{p}=2\theta _1-\sigma _1 T_1 - \theta _2. \end{aligned}$$

(6b)

The resulting autonomous system reads

$$\begin{aligned}&a_1 '=\frac{{\bar{\alpha }}_{12} a_1 a_2 \sin \left( \gamma _{p}\right) }{4 \omega _1}, \end{aligned}$$

(7a)

$$\begin{aligned}&\gamma _1'=\frac{{\bar{\alpha }}_{12} a_2 \cos \left( \gamma _{p}\right) }{4 \omega _1}, \end{aligned}$$

(7b)

$$\begin{aligned}&a_2'=-\frac{{\bar{\alpha }}_{11} a_1^2 \sin \left( \gamma _{p}\right) }{4 \omega _2 }, \end{aligned}$$

(7c)

$$\begin{aligned}&\gamma _{p}'=-\frac{{\bar{\alpha }}_{11} a_1^2 \cos \left( \gamma _{p}\right) }{4 a_2 \omega _2 }-\sigma _1+\frac{{\bar{\alpha }}_{12} a_2 \cos \left( \gamma _{p}\right) }{2 \omega _1}. \end{aligned}$$

(7d)

Obviously, Eq. (7b) is redundant since only $\gamma _{p}$ appears elsewhere in the system.

2.2 Coupled solutions: parabolic modes and backbone curves

The fixed point solutions of Eq. (7) exist only when $\sin (\gamma _{p})=0$ and consequently $\cos (\gamma _{p})=\pm 1=p$, where the notation $p=\pm 1$ is introduced for the rest of the paper. Consequently, the only possible coupled solutions correspond to limit cycles with $a_1$ and $a_2$ constants independent of time $T_1$.

The strong constraints imposed on the angular variables define two classes of solutions: one related to $p=1$ and one to $p=-1$. We will show in the following that each of these solutions is associated to a family of periodic orbits with a given amplitude-frequency relationship (or backbone curve). To better describe the typology of these two solutions, let us first reconstruct the first order amplitudes $q_{10}$ and $q_{20}$. Combining Eq. (3) with Eq. (6), the first order solutions are obtained as

$$\begin{aligned}&q_{10}(t)=a_1\cos (\gamma _1+\omega _1 t), \end{aligned}$$

(8a)

$$\begin{aligned}&q_{20}(t)= a_2\cos (2(\gamma _1+\omega _1 t)-\gamma _{p}). \end{aligned}$$

(8b)

When $p=+1$, then $\gamma _{p}=2 m\pi$ with m integer and the following relationship between the amplitudes holds:

$$\begin{aligned} 2\frac{q_{10}^2}{a_1^2}-1=\frac{q_{20}}{a_2}. \end{aligned}$$

(9)

Eq. (9) dictates that the amplitudes lie on a parabola with positive concavity in the configuration plane $(q_{10},q_{20})$. In the whole four-dimensional phase space (including both velocities), we hence obtain a family of periodic orbits developing on a manifold such that its projection on $(q_{10},q_{20})$ is a parabola. This solution is called parabolic mode, following also the designation given in [6, 17, 32] for the case of 1:1 resonance, where normal modes and elliptic modes are the two families of coupled solutions. More precisely, in the case $p=+1$, this solution is denoted as $p^{+}$-mode.

When $p=-1$ a second family of periodic orbit is obtained, where $\gamma _{p}=(2 m+1)\pi$, with m integer. The amplitudes now define a parabola with negative concavity in the configuration plane $(q_{10},q_{20})$:

$$\begin{aligned} -2\frac{q_{10}^2}{a_1^2}+1=\frac{q_{20}}{a_2}, \end{aligned}$$

(10)

denoted as $p^{-}$-mode . These two families of solutions are represented in Fig. 1. It should be noted that for the $p^{+}$-mode $q_1$ and $q_2$ have the same phase, while for the $p^{-}$-mode the phase difference is equal to $\pi$.

Fig. 1

Sketch of the parabolic modes corresponding to the coupled solutions in the configuration plane $(q_{10},q_{20})$. a) $p^+$-mode, b) $p^-$-mode

In order to express the frequency-amplitude relationship (backbone curves) for these two families of coupled solutions, we elaborate on the relationship between the amplitudes $a_1$ and $a_2$ given by the fixed point equation associated to Eq. (7d):

$$\begin{aligned} \varepsilon \left( \frac{{\bar{\alpha }}_{11} a_1^2 p}{4 a_2 \omega _2}+\frac{{\bar{\alpha }}_{12} a_2 p}{2 \omega _1}\right) +\omega _2-2\omega _1 = 0, \end{aligned}$$

(11)

where we have replaced the detuning variable $\sigma _1$ with its expression in terms of eigenfrequencies $\omega _{1,2}$ to have a more straightforward insight into the system. Denoting with ${\bar{q}}_i$ the maximum amplitude of $q_i(t)$ (${\bar{q}}_i=a_i, i=1,2$), we now replace the non-linear coefficients with the original $\alpha _{12}$ and $\alpha _{11}$, and we express ${\bar{q}}_1$ in terms of ${\bar{q}}_2$:

$$\begin{aligned} {\bar{q}}_1^2= \left( \frac{2 {\bar{q}}_2 \alpha _{12} }{ \omega _1} -\frac{4 (\omega _2-2\omega _1)}{ p} \right) \frac{{\bar{q}}_2\omega _2}{\alpha _{11}}. \end{aligned}$$

(12)

which holds for both parabolic modes, setting either $p=1$ or $p=-1$. To obtain the amplitude-frequency relationship we first solve the first-order equations at the slow time scale $T_1$, Eq. (7), and get the following expressions for the phase angles:

$$\begin{aligned}&\gamma _1=\frac{{\bar{\alpha }}_{12} a_2 p}{4 \omega _1}T_1+\phi _1, \end{aligned}$$

(13a)

$$\begin{aligned}&\gamma _{p}=-\frac{{\bar{\alpha }}_{11} a_1^2 p}{4 a_2 \omega _2}T_1-\frac{(\omega _2-2\omega _1)}{\varepsilon } T_1-\frac{{\bar{\alpha }}_{12} a_2 p}{2 \omega _1}T_1+\phi _{p}, \end{aligned}$$

(13b)

with $\phi _1$ and $\phi _{p}$ integration constants. Using Eq. (6), the original nonlinear coefficients $\alpha _{12}$ and $\alpha _{11}$ and using $T_1=\varepsilon t$ we have:

$$\begin{aligned}&\theta _1=\frac{\alpha _{12} a_2 p}{4 \omega _1} t+\phi _1, \end{aligned}$$

(14a)

$$\begin{aligned}&\theta _2= \frac{\alpha _{11} a_1^2 p}{4 a_2 \omega _2} t+2\phi _1-\phi _{p}, \end{aligned}$$

(14b)

Inserting these equations in Eq. (3) we get

$$\begin{aligned}&q_{10}(t)=a_1 \cos {( \frac{\alpha _{12} a_2 p}{4 \omega _1}t+\omega _1 t+\phi _1)}, \end{aligned}$$

(15a)

$$\begin{aligned}&q_{20}(t)=a_2 \cos {( a_1^2 \frac{p}{ 4}\frac{ \alpha _{11}}{ a_2\omega _2} t+\omega _2 t+2\phi _1-\phi _{p})}. \end{aligned}$$

(15b)

From Eq. (15), substituting ${\bar{q}}_{1,2}$ , one obtains the nonlinear oscillation frequencies $\omega _{\rm {NLi}}$ of each oscillator:

$$\begin{aligned}&\omega _{\rm {NL}1}=\omega _1 + \frac{\alpha _{12} {\bar{q}}_2 p}{4 \omega _1}, \end{aligned}$$

(16a)

$$\begin{aligned}&\omega _{\rm {NL}2}=\omega _2 + {\bar{q}}_1^2 \frac{p}{ 4}\frac{ \alpha _{11}}{ {\bar{q}}_2\omega _2}. \ \end{aligned}$$

(16b)

We remark in particular that the relationship $\omega _{\rm {NL}2}=2\omega _{\rm {NL}1}$ is always fulfilled, as can be shown inserting Eq. (12) into Eq. (16b).

For the sake of clarity, $\omega _{\rm {NL}1}$ will be simply denoted $\omega _{\rm {NL}}$ in what follows. Note that Eq. (16a), together with Eq. (12), identifies the solution manifold in the space $(\omega _{\rm {NL}}, {\bar{q}}_1, {\bar{q}}_2)$ where the backbone solutions are lying. The two families of solutions are discriminated by replacing p with $\pm 1$ in all expressions. Since the amplitudes ${\bar{q}}_1$, ${\bar{q}}_2$ are assumed to be positive, one arrives at the conclusion that: when $\omega _{\rm {NL}}<\omega _1$, only the $p^-$ mode exists, while when $\omega _{\rm {NL}}>\omega _1$, one only has the $p^+$-mode. This gives a first condition for the existence of the backbone curves.

An additional condition can be derived by inserting Eq. (16a) in the rhs of Eq. (12) that must be positive to guarantee the existence of a solution for ${\bar{q}}_1$:

$$\begin{aligned} \left( -2\omega _{\rm {NL}} +\omega _2 \right) \left( \omega _1-\omega _{\rm {NL}}\right) \left( \frac{16 \omega _1\omega _2 }{\alpha _{12} \alpha _{11} p^2}\right) >0. \end{aligned}$$

(17)

In Eq. (17), the third term is always positive due to the assumptions on $\alpha _{12}$. The first two factors of Eq. (17) impose that ${\bar{q}}_1$ exists only for values of $\omega _{\rm {NL}}$ outside the limit points $\omega _{\rm {NL}}=\omega _1$ and $\omega _{\rm {NL}}=\omega _2/2$.

Fig. 2

Schematic representation of the existence region for the coupled parabolic modes, in the plane $(\omega _{\rm {NL}}-\omega _1,\omega _2-2\omega _1)$. The abscissa represents the shifted nonlinear oscillation frequency while the ordinate is the detuning between the eigenfrequencies of the system

The existence regions of each parabolic modes are summarized in Fig. 2 in terms of the shift of the nonlinear oscillation frequency $\omega _{\rm {NL}}-\omega _1$ (on the x-axis) and of the detuning $\omega _2 - 2\omega _1$ (on the y-axis). For a given system, the detuning is fixed so that a single horizontal line gives the existence region. The blue region (respectively the red region) corresponds to the existence of $p^{-}$ (resp. $p^{+}$) mode. From Eq. (17), the lines $\omega _{\rm {NL}}=\omega _2/2$ (highlighted with a green color) and the y-axis $\omega _{\rm {NL}}=\omega _1$, delimit a region in which no coupled solutions exist. The green hatched region delimited by $\omega _{\rm {NL}}=\omega _2/2$ and $\omega _{\rm {NL}}=\omega _2/6 + 2\omega _1/3$ is commented in Sect. 2.3.

It is worth looking at the behaviour of the backbones at the limit point of their existence regions. At the first boundary $\omega _{\rm {NL}}= \omega _1$ we get:

$$\begin{aligned} \lim _{\omega _{\rm {NL}}\rightarrow \omega _1} {\bar{q}}_1=0, \quad \lim _{\omega _{\rm {NL}}\rightarrow \omega _1} {\bar{q}}_2 =0, \end{aligned}$$

(18)

meaning that close to $\omega _1$, the backbone curve amplitudes are going to zero as expected. The situation is different in the vicinity of $\omega _2/2$. Indeed at this second boundary $\omega _{\rm {NL}}=\omega _2/2$, one obtains:

$$\begin{aligned}&\lim _{\omega _{\rm {NL}}\rightarrow \omega _2/2} {\bar{q}}_1=0, \end{aligned}$$

(19a)

$$\begin{aligned}&\lim _{\omega _{\rm {NL}}\rightarrow \omega _2/2} {\bar{q}}_2 =\frac{2 \omega _1 (\omega _2-2\omega _1)}{\alpha _{12} p}. \end{aligned}$$

(19b)

In particular the limit value of ${\bar{q}}_2$ is non-zero at the limit point of the backbone when $\omega _{\rm {NL}} \longrightarrow \omega _2/2$, which could appear conflicting with the coupled solution assumptions. One should note that this is only true in the limit, and that the uncoupled A2-mode solution still exists for the system. Consequently the limit point of the backbone connects with this solution at this specific point. This particular situation induces a jump in the backbone solution (see the detuned condition in Fig. 3 commented in Sect. 2.4) and, as shown in Sect. 3.2, will also lead to the emergence of isolated solutions in the forced and damped system.

2.3 Stability of coupled solutions

The stability of coupled solutions is governed by the eigenvalues of the Jacobian matrix J of the conservative system (see Appendix 2 for details). The determinant $\text{ det }(\lambda I- J)$ of the characteristic polynomial, expressing the angular variables in terms of ${\bar{q}}_i,i=1,2$, writes:

$$\begin{aligned} \begin{aligned} \text{ det }(\lambda I- J)=&\frac{\lambda ^2}{16 {\bar{q}}_2^2 \omega _1 \omega _2^2} \left( 4 \alpha _{12} \alpha _{11} p^2 {\bar{q}}_1^2 {\bar{q}}_2^2 \omega _2 \right. \\&\left. +\omega _1 \left( \alpha ^{2}_{11} p^2 {\bar{q}}_1^4+16 \lambda ^2 {\bar{q}}_2^2 \omega _2^2\right) \right) . \end{aligned} \end{aligned}$$

(20)

The nonzero eigenvalues $\lambda$ are given by:

$$\begin{aligned} \lambda =\pm \sqrt{\left( 6 \omega _{\rm {NL}}-4 \omega _1-\omega _2\right) \left( \omega _2-2 \omega _{\rm {NL}}\right) }. \end{aligned}$$

(21)

and have negative real part if:

$$\begin{aligned} \omega _{\rm {NL}}<\frac{2\omega _1}{3}+\frac{\omega _2}{6} \quad \text {and} \quad \omega _{\rm {NL}}>\frac{\omega _2}{2}. \end{aligned}$$

(22)

The unstable region delimited by conditions in Eq. (22) is shown in Fig. 2 as the green hatched region. We observe that this region completely falls in a non-existence area of coupled solutions. Consequently, the conservative backbone curves are always stable.

Fig. 3

Backbone curves of the two families $p^{+}$ (red curves) and $p^{-}$-modes (blue curves), in the plane $(\omega _{\rm {NL}},a_1)$ (first row) and $(\omega _{\rm {NL}},a_2)$ (second row), and for three different possible cases. First column: $\omega _2/2<\omega _1$, second column: $\omega _2/2=\omega _1$, third column: $\omega _2/2>\omega _1$. In the figure, $\omega _1=1$, $\alpha _{12}=1\cdot 10^{-2}$, $\alpha _{11}=5\cdot 10^{-3}$

2.4 Backbone curves

In this section, we show how the backbone curves of the two different parabolic modes organize when the detuning parameter is varied. Note that some of the results presented here are close to those presented in [27], where a different point of view was adopted on the same system. Fig. 3 shows the three different possible cases: when the detuning is negative, when it is vanishing, and when it is positive. The figure plots the projection of the solutions in the planes $(\omega _{\rm {NL}}, {\bar{q}}_1)$ and $(\omega _{\rm {NL}}, {\bar{q}}_2)$. However, an optimal representation would be in the 3D space $(\omega _{\rm {NL}},{\bar{q}}_1, {\bar{q}}_2)$, as will be shown in Sect. 3 when the solutions will be fully reconstructed.

One can note that, consistently with Eq. (12)-(16), the backbones in the $(\omega _{\rm {NL}}, {\bar{q}}_2)$ plane are always straight lines, while their projection in the $(\omega _{\rm {NL}}, {\bar{q}}_1)$ plane are line segments only when the detuning vanishes, and otherwise have a parabolic shape. While increasing the detuning from negative to positive, one can observe the following features. When $\omega _2/2<\omega _1$, the backbone starting at $\omega _1$ is a $p^{+}$-mode, while the backbone starting at $\omega _2/2$ is a $p^{-}$-mode. According to Eq. (19b), the $p^-$-mode backbone starts from a nonzero value in $(\omega _{\rm {NL}}, {\bar{q}}_2)$ plane. In the case of perfect 2:1 resonance, $\omega _2/2=\omega _1$, the backbones of the two families start from the same point and from zero amplitude. Symmetrically, when $\omega _2/2>\omega _1$, the backbone emanating from $\omega _1$ is now a $p^{-}$-mode, meaning that in the process of the transition a switch of family occurs. Consequently, the family of periodic solutions emanating from $\omega _2/2$ is now a $p^{+}$-mode, and it starts at a non-zero value in the $(\omega _{\rm {NL}}, {\bar{q}}_2)$ plane.

3 Forced system and NS boundaries

This section investigates the Frequency Response Functions (FRF) of the oscillators described by Eq. (1), with a forcing term applied on the low-frequency oscillator and damping. While the appearance of quasi-periodic solutions has been already documented for this case e.g. in [40, 55], our aim here is to provide an exact expression of the NS boundary curve. Note also that quasiperiodic solutions are usually not addressed in the case where the forcing is applied on the high-frequency mode since the main concern is typically to investigate the loss of stability of the uncoupled solution [40, 53]. As for the conservative case, first-order perturbative solutions are derived with the MS method. Since this derivation is classical, most of the details are reported in Appendix 3, and emphasis is rather set on the derivation of the NS boundary curve, its dependence on parameters and the link between the FRF and the backbones.

3.1 Multiple Scales solution

First, the equations of motion in Eq. (1) are rewritten considering the MS expansion for time and oscillators degrees of freedoom using a bookkeeping parameter $\varepsilon$ (see Appendix 3). We also introduce the assumptions that the non-linearities, the forcing amplitude and the damping are small, and can be expressed as $\alpha _{12}=\varepsilon {\bar{\alpha }}_{12}$, $\alpha _{11}=\varepsilon {\bar{\alpha }}_{11}$, $\mu _1=\varepsilon {\bar{\mu }}_1$ and $F=\varepsilon {\bar{F}}$. The forcing angular frequency is in the vicinity of the first eigenfrequency $\omega _1$, and an external detuning parameter $\sigma _2$ is introduced to describe this nearness as:

$$\begin{aligned} \varOmega =\omega _1+\varepsilon \sigma _2. \end{aligned}$$

(23)

The first-order system governing the modulation of the amplitude is derived in a similar way as in the previous section. At the slow time scale $T_1$, the resulting system reads:

$$\begin{aligned} a_1 '=&\frac{{\bar{\alpha }}_{12} a_1 a_2 \sin \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _1} \nonumber \\&-\frac{{\bar{F}} \sin \left( \theta _1-\sigma _2 T_1\right) }{2 \omega _1}-{\bar{\mu }}_1 a_1, \end{aligned}$$

(24a)

$$\begin{aligned} a_1 \theta _1'=&\frac{{\bar{\alpha }}_{12} a_1 a_2 \cos \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _1}\nonumber \\&-\frac{{\bar{F}} \cos \left( \theta _1-\sigma _2 T_1\right) }{2 \omega _1} , \end{aligned}$$

(24b)

$$\begin{aligned} {a_2'=}&{-\frac{{\bar{\alpha }}_{11} a_1^2 \sin \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _2}-{\bar{\mu }}_2 a_2 }, \end{aligned}$$

(24c)

$$\begin{aligned} a_2 \theta _2'=&\frac{{\bar{\alpha }}_{11} a_1^2 \cos \left( 2 \theta _1-\theta _2-\sigma _1 T_1\right) }{4 \omega _2}. \end{aligned}$$

(24d)

When the forcing is applied on the low-frequency oscillator, only coupled solutions exist (see Appendix 3).

The system is made autonomous by introducing $\gamma _1$ and $\gamma _2$ such that:

$$\begin{aligned}&\gamma _1=\theta _1-T_1 \sigma _2, \end{aligned}$$

(25a)

$$\begin{aligned}&\gamma _2=2\theta _1-\sigma _1 T_1 - \theta _2, \end{aligned}$$

(25b)

and reads:

$$\begin{aligned}&a_1 '=\frac{a_1 \left( {\bar{\alpha }}_{12} a_2 \sin \left( \gamma _2\right) -4 {\bar{\mu }}_1 \omega _1\right) -2 {\bar{F}} \sin \left( \gamma _1\right) }{4 \omega _1}, \end{aligned}$$

(26a)

$$\begin{aligned}&\gamma _1'=\frac{{\bar{\alpha }}_{12} a_1 a_2 \cos \left( \gamma _2\right) -2 {\bar{F}} \cos \left( \gamma _1\right) }{4 a_1 \omega _1}-\sigma _2 , \end{aligned}$$

(26b)

$$\begin{aligned}&{a_2'=-\frac{{\bar{\alpha }}_{11} a_1^2 \sin \left( \gamma _2\right) }{4 \omega _2} - {\bar{\mu }}_2 a_2,} \end{aligned}$$

(26c)

$$\begin{aligned}&\gamma _2'=\frac{1}{2} \cos \left( \gamma _2\right) \left( \frac{{\bar{\alpha }}_{12} a_2}{\omega _1}-\frac{{\bar{\alpha }}_{11} a_1^2}{2 a_2\omega _2}\right) -\frac{{\bar{F}} \cos \left( \gamma _1\right) }{a_1 \omega _1}-\sigma _1. \end{aligned}$$

(26d)

It is worth highlighting that the definitions of Eqs. (25) and (6) and the structure of Eqs. (26) and (7) are similar and only differ for the additional terms associated to ${\bar{F}}$, ${\bar{\mu }}_i$ and $\sigma _2$.

The fixed points, associated to forced oscillations of constant amplitudes, can be expressed as function of the maximum amplitudes of $({\bar{q}}_1,{\bar{q}}_2)$ only. Internal and external detunings $\sigma _1$ and $\sigma _2$ can also be replaced by the frequency differences to have a more straightforward insight into the system. The amplitude equations, considering the original system parameters, reads:

$$\begin{aligned} {\bar{q}}_2^3&+\frac{8\omega _1\varGamma }{\alpha _{12}}((\varOmega -\omega _1) (\omega _2-2\varOmega )+\mu _1\mu _2){\bar{q}}_2^2 \nonumber \\&+\frac{16\omega _1^2}{\alpha ^2_{12} }((\varOmega -\omega _1)^2+\mu _1^2){\bar{q}}_2-\frac{\varGamma \alpha _{11} F^2}{\alpha ^2_{12}\omega _2}=0, \end{aligned}$$

(27a)

$$\begin{aligned} {\bar{q}}_1&=\sqrt{\frac{4\omega _2 {\bar{q}}_2}{\alpha _{11} \varGamma }}, \end{aligned}$$

(27b)

with $\varGamma =\sqrt{\frac{1}{\mu _2^2+\left( \omega _2-2\varOmega \right) ^2}}$. Eq. (27b) can be seen as the solution manifold in the space $(\varOmega ,{\bar{q}}_1,{\bar{q}}_2)$.

Eq. (27a) is a polynomial of the third-order in ${\bar{q}}_2$ and can give, depending on the parameters, from one to three solutions. The phases of fixed points are given by:

$$\begin{aligned}&{\cos (\gamma _1)=\frac{{\bar{q}}_1}{2 F} \left( \alpha _{12} \cos (\gamma _2) {\bar{q}}_2+4 \omega _1 \left( \omega _1-\varOmega \right) \right) ,} \end{aligned}$$

(28a)

$$\begin{aligned}&\sin (\gamma _1)=\frac{{\bar{q}}_1}{2 F} \left( \alpha _{12} \sin (\gamma _2) {\bar{q}}_2-4 \mu _1 \omega _1\right) , \end{aligned}$$

(28b)

$$\begin{aligned}&\cos (\gamma _2)=\frac{4 {\bar{q}}_2 \omega _2(2\varOmega -\omega _2)}{\alpha _{11} {\bar{q}}_1^2}, \end{aligned}$$

(28c)

$$\begin{aligned}&\sin (\gamma _2)=-\frac{4 \mu _2 {\bar{q}}_2 \omega _2}{\alpha _{11} {\bar{q}}_1^2}. \end{aligned}$$

(28d)

These equations are not strictly necessary to build FRFs, but are needed to reconstruct the amplitude variations in time. They can also be used to establish existence conditions for the solutions exploiting the bounds of the trigonometric functions.

Fig. 4

Typical frequency-response functions and orbit in configuration space $(q_{1},q_{2})$, for different cases of detuning. First line, positive detuning, $\omega _2/2>\omega _1$. Second line, no detuning, $\omega _2/2 = \omega _1$. Third line, negative detuning $\omega _2/2<\omega _1$. Stability is not reported. Selected values of the parameters: $\omega _1=1$, $\alpha _{12}=5\cdot 10^{-2}$, $\alpha _{11}=2.5\cdot 10^{-2}$, $\mu _1=\mu _2=2.5\cdot 10^{-3}$, $F=8\cdot 10^{-2}$

Fig. 4 shows the type of solutions obtained when varying the frequency detuning and the link with the backbone curve and the $p^{+}$ or $p^{-}$ modes. Note that in Fig. 4 emphasis is put on the shape of the solution, while stability is addressed in the following section.

In the first line, the case of a positive detuning between the eigenfrequencies is considered, $\omega _2/2>\omega _1$. In particular one can observe that close to $\varOmega = \omega _2/2$, the FRF has a local minimum for $a_1$ and a maximum for $a_2$. The resonant branches follow the backbones of the two families of periodic orbits $p^{+}$ and $p^{-}$. Fig. 4 c) depicts the solution in the configuration plane $(q_1,q_2)$ for the three points marked with coloured circles on the FRF. As expected, the blue point corresponds to $p^{-}$-mode and one recovers the shape of the parabola in $(q_1,q_2)$, with a slight dephasing corresponding to the addition of forcing and damping (exact parabola is retrieved for the backbone only). The same reasoning applies for the red point corresponding to $p^{+}$-mode. The black point is selected exactly at $\varOmega = \omega _1$ and is a $p^{-}$-mode also.

The second line of Fig. 4 considers the tuned case $\omega _2/2=\omega _1$. In Fig. 4 f), while $p^{+}$ and $p^{-}$ mode are still perfectly well retrieved, the black point at $\varOmega = \omega _1$ shows a combination of the two solutions resulting in a symmetrical shape in the $(q_1,q_2)$ plane. Finally, the third line shows the case of a negative detuning, and behaves symmetrically as compared to the case of positive detuning. Increasing the detuning from negative to positive values, we see how the solution emanating from the forced low-frequency $\omega _1$ switches from the $p^{-}$ to the $p^{+}$ mode, with the intermediate step being the symmetric shape shown in Fig. 4 f). This result is in line with those presented in [27] and complement their analysis by underlining the parabolic nature of the two families of periodic orbits, with different curvature.

3.2 Isolas

Interestingly, the first-order solution obtained by MS analysis contains isolated branches of solutions, as already remarked in [27]. In addition to their analysis, it is here underlined that the manifestation of these isolas is the consequence of the non-vanishing starting point on the ${\bar{q}}_2$ axis when the internal detuning is different from zero. This particular feature is illustrated in Fig. 5 for the case of a positive detuning, $\omega _2/2 > \omega _1$. As shown in the previous section, the limit value of the $p^{+}$-mode corresponds to a non-vanishing value of ${\bar{q}}_2$. Since the forced-damped solutions emanate from the backbone curves [5], this eventually creates the condition for the appearance of isolas.

Fig. 5

FRF and backbone curves close to the isolated solution branches, obtained for $\sigma _1=0.05$, $\alpha _{12}=5\cdot 10^{-2}$ and $\alpha _{11}=2.5\cdot 10^{-2}$. The black continuous lines are the FRF (forced and damped solutions). The red lines are the backbones corresponding to the $p^+$ mode. The black dashed line marks $\varOmega =\omega _2/2$. Damping values as $\mu _1 =\mu _2=1\cdot 10^{-3}$. Selected values of the forcing amplitude are $F=2.5\cdot 10^{-2},2.75\cdot 10^{-2},3\cdot 10^{-2}$

3.3 Stability analysis and Neimark-Sacker boundary

The stability analysis of the solutions is based on the eigenvalues $\lambda$ of the Jacobian matrix of Eq. (26), analysed in Appendix 3. The characteristic polynomial can be written as:

$$\begin{aligned} \lambda ^4+c_1 \lambda ^3+c_2 \lambda ^2+c_3\lambda +c_4=0, \end{aligned}$$

(29)

with all the coefficients detailed in Appendix 4. Since all expressions are available in closed form, one can explicitly compute the stability of the solutions and follow bifurcation points.

We focus on the definition of the Neimark-Sacker (NS) boundary curve. The NS bifurcation requires that a pair of eigenvalues are complex conjugate with zero real part. Using the compact definition of the characteristic polynomial of Eq. (29), this implies that the four eigenvalues are ${\mathbb {i}A,-\mathbb {i}A, B, C}$ where $A\in {\mathbb {R}}$ and $B,C \in {\mathbb {C}}$. Then Eq. (29) can be rewritten as [26]:

$$\begin{aligned} \begin{aligned}&\lambda ^4+c_1 \lambda ^3+c_2 \lambda ^2+c_3 \lambda +c_4\\& =(\lambda -\mathbb {i}A)(\lambda +\mathbb {i}A)(\lambda -B)(\lambda -C). \end{aligned} \end{aligned}$$

(30)

Equating the same power terms one obtains a system of four equations:

$$\begin{aligned}&c_1=-(C+B), \end{aligned}$$

(31a)

$$\begin{aligned}&c_2=A^2-BC, \end{aligned}$$

(31b)

$$\begin{aligned}&c_3=-A^2(C+B), \end{aligned}$$

(31c)

$$\begin{aligned}&c_4=A^2 BC. \end{aligned}$$

(31d)

Isolating $A^2$ as the ratio between Eq. (31a) and Eq. (31c), expressing the product BC using Eq. (31d) and inserting both terms in Eq. (31d), the condition for a NS bifurcation can be expressed in terms of the $c_i$’s only, reading:

$$\begin{aligned}&c_1c_2c_3=c_3^2-c_4c_1^2,\end{aligned}$$

(32a)

$$\begin{aligned}&\frac{c_3}{c_1}=A^2. \end{aligned}$$

(32b)

Inserting the detailed expressions of each coefficient in Eq. (32), the definition of the NS boundary curve is obtained as a polynomial in ${\bar{q}}_2$, and reads:

$$\begin{aligned} \begin{aligned} b_1 {\bar{q}}_2^4+b_2 {\bar{q}}_2^3+b_3 {\bar{q}}_2^2+b_4 {\bar{q}}_2+b_5=0. \end{aligned} \end{aligned}$$

(33)

where the expressions of $b_i$ are reported in Appendix 4. For fixed values of the system parameters $\mu _1$, $\mu _2$, $\alpha _{12}$, $\omega _2$, $\omega _1$ and spanning the values of $\varOmega$ one gets the boundary curve for the NS bifurcation as a function ${\bar{q}}_2(\varOmega )$.

3.4 FRFs, backbone curves and NS boundary

We now discuss the complete solutions including the FRF, their connection with the backbone curves and the location of the NS boundaries.

Fig. 6

FRF, backbone curves and NS boundary when $\omega _1=1$, $\omega _2=2\omega _1$, $\mu _1=\mu _2=1\cdot 10^{-3}$, $\alpha _{12}=5\cdot 10^{-2}$ and $\alpha _{11}=2.5\cdot 10^{-2}$. The black continuous lines are the FRF (forced and damped solutions). The red and the blue lines are the backbones corresponding to the $p^+$ and $p^-$ mode respectively. The black dashed line marks the $\varOmega =\omega _2/2$ frequency. The green dash-dotted line is the NS boundary. In 3D figure in the space $\varOmega -a_1-a_2$ the orange surface is the manifold on which all the possible forced and damped solution lies and is given by Eq. (27b). Selected values of the forcing amplitude are $F=2.5\cdot 10^{-2},5\cdot 10^{-2},7.5\cdot 10^{-2}$

We select a fixed set of parameters $\omega _1=1$, $\mu _1=\mu _2=1\cdot 10^{-3}$, $\alpha _{12}=5\cdot 10^{-2}$ and $\alpha _{11}=2.5\cdot 10^{-2}$. First, the case of a vanishing internal detuning, thus $\omega _2=2\omega _1$, is shown in Fig. 6 collecting the FRF, Eq.  (27), the NS boundary, Eq. (33); and the backbones given by Eqs. (16) and (12). Fig. 6 a) is a view in the 3D space $(\varOmega ,\, a_1, \,a_2)$. The solution manifold given by Eq. (27b) is represented as an orange surface and all solution branches as well as the NS boundary curve lie on this manifold. In this case the figure is fully symmetric with respect to $\varOmega =\omega _1=\omega _2/2$. Figure 6 b), c) show the projection of the 3D plot respectively on planes $(\varOmega ,\, {\bar{q}}_1)$ and $(\varOmega ,\, {\bar{q}}_2)$. The FRF develops according to the backbone curves of the $p^{+}$ and $p^{-}$ modes. When $\varOmega$ approaches $\omega _1$ the FRF have a local peak for ${\bar{q}}_2$, and correspondingly ${\bar{q}}_1$ approaches a nearly zero value. In this case, the NS boundary is symmetric and displays a unique minimum centred at $\varOmega =\omega _1$, as shown in the enlarged view Fig. 6 d) and e).

Fig. 7

FRF, backbone curves and NS boundary when $\sigma _1=5\cdot 10^{-2}$, $\mu _1=\mu _2=1\cdot 10^{-3}$, $\alpha _{12}=5\cdot 10^{-2}$ and $\alpha _{11}=2.5\cdot 10^{-2}$. The black continuous lines are the FRF (forced and damped solutions). The red and the blue lines are the backbones corresponding to the $p^+$ and $p^-$ mode respectively. The black dashed line marks the $\varOmega =\omega _2/2$ frequency. The green line is the NS boundary. In 3D figure in the space $\varOmega -{\bar{q}}_1-{\bar{q}}_2$ the orange surface is the manifold on which all the possible forced and damped solution lies and is given by Eq. (27b). Selected values of the forcing amplitude are $F=2.5\cdot 10^{-2},5\cdot 10^{-2},7.5\cdot 10^{-2}$

Fig. 8

FRF, backbone curves and NS boundary when $\sigma _1=-5\cdot 10^{-2}$, $\mu _1=\mu _2=1\cdot 10^{-3}$, $\alpha _{12}=5\cdot 10^{-2}$ and $\alpha _{11}=2.5\cdot 10^{-2}$. The black continuous lines are the FRF (forced and damped solutions). The red and the blue lines are the backbones corresponding to the $p^+$ and $p^-$ mode respectively. The black dashed line marks the $\varOmega =\omega _2/2$ frequency. The green line is the NS boundary. In 3D figure in the space $\varOmega -{\bar{q}}_1-{\bar{q}}_2$ the orange surface is the manifold on which all the possible forced and damped solution lies and is given by Eq. (27b). Selected values of the forcing amplitude are $F=2.5\cdot 10^{-4},5\cdot 10^{-4},1\cdot 10^{-3}$

Fig. 7 shows the case of a positive detuning, with $\omega _2=2\omega _1 + 5\cdot 10^{-2}$, all the other parameters being unchanged. In this case the symmetry is broken, as can be appreciated by inspecting the shape of the solution manifold in the 3D space, showing a minimum with respect to ${\bar{q}}_1$ at $\varOmega =\omega _2/2$. The solution branches arising in the vicinity of $\varOmega =\omega _1$ belong to the $p^{-}$ family, in line with previous remarks. The shape of NS boundary curve (see Fig. 7d) and e)), also shows important modifications, having two minima and one local maximum, particularly visible in the $(\varOmega , {\bar{q}}_1)$ projection. Interestingly, the projection on the $(\varOmega , {\bar{q}}_2)$ plane shown in Fig. 7c) underlines the closeness of the NS boundary to the non-zero point where the backbone of the $p^{+}$-mode emerges.

Finally, the case of a negative detuning with $\omega _2=2\omega _1 - 5\cdot 10^{-2}$ is addressed in Fig. 8. The solutions around $\omega _1$ now belong to $p^{+}$-mode. The NS boundary shows again the two minima and the local maximum, and its closeness to the emerging point of the $p^{-}$-mode is symmetrically observed.

These results underline that a further investigation of the minima and maxima of the NS boundary curve, together with its relationship with the backbones, would provide a better understanding of the dynamics. This is the aim of the following sections.

3.5 NS boundary behaviour and extrema

In this section the parametric dependence of the NS boundary curve with respect to detuning and damping is investigated with specific attention to special points corresponding to extrema of the boundary. Fig. 9 first displays the shape of the NS boundary curve when the detuning is varied from negative to positive values, in both planes $(\varOmega ,{\bar{q}}_1)$ and $(\varOmega ,{\bar{q}}_2)$. The plots have been obtained for $\omega _1=1$, $\mu _1=\mu _2=5\cdot 10^{-4}$, $\alpha _{12}=1 \cdot 10^{-2}$ and $\alpha _{11}=5\cdot 10^{-3}$ and different values of $\omega _2$. As already underlined, the boundary curve has a single minimum in the case of no detuning, obtained from Eq. (33) assuming $\omega _2=2\omega _1=2\varOmega$:

$$\begin{aligned}&{\bar{q}}_2=\frac{4 \left( \mu _1+\mu _2\right) \omega _1}{\alpha _{12}}, \end{aligned}$$

(34a)

$$\begin{aligned}&{\bar{q}}_1=4\sqrt{\frac{\left( \mu _1+\mu _2\right) \omega _1 \omega _2}{\alpha _{12}\alpha _{11} \varGamma }}. \end{aligned}$$

(34b)

For non-vanishing detuning two minima occur in the plane $(\varOmega ,{\bar{q}}_1)$, and they correspond to points where there is a change of curvature in $(\varOmega ,{\bar{q}}_2)$ projection. This result is of prime importance since the locations of the minima convey meaningful information about the minimum forcing and amplitude levels that are needed to reach a quasiperiodic solution.

Fig. 9

Behaviour of the NS boundary curve when the detuning $\sigma _1=\omega _2-2\omega _1$ is changed. The system parameter here considered are $\alpha _{12}=1\cdot 10^{-2}$, $\alpha _{11}=5\cdot 10^{-3}$, $\mu _1=\mu _2=5\cdot 10^{-3}$. The square markers correspond to the minima predicted by the analytical expression given in Appendix 5, namely $\varOmega =\omega _2/2$ and $\varOmega =(\omega _1+\omega _2)/3$

In Fig. 9, two points for each curve are marked with a black square, corresponding to $\varOmega =\omega _2/2$ and $\varOmega =(\omega _1+\omega _2)/3$. These are minima of the NS boundary curve predicted by asymptotic analysis as detailed in Appendix 5.

Fig. 10

Behaviour of the NS boundary curve, for $\omega _1=1$, $\omega _2=2.05$, $\alpha _{12}=1\cdot 10^{-2}$, $\alpha _{11}=5\cdot 10^{-3}$ and different values of $\mu _1=\mu _2$ as detailed in the legend. The blue and red continuous lines are the backbone of the $p^-$ and $p^+$ mode while the black dashed lines correspond to $\varOmega =\omega _2/2$ and $\varOmega =(\omega _1+\omega _2)/3$

These specific points are obtained in the limit of small damping and are thus only approximate values. This is further illustrated in Fig. 10, obtained for $\omega _1=1$, $\omega _2=2.05$, $\alpha _{12}=1\cdot 10^{-2}$, $\alpha _{11}=5\cdot 10^{-3}$ and different values of damping assuming $\mu _1=\mu _2$. The detuned frequency condition is considered because the loci of the minima change only in this case. The figure shows that the NS boundary tends to have sharper minima and values closer to the proposed approximation as damping tends to zero. On the other hand, the behaviour of the NS boundary curve at large values of amplitudes is asymptotically identical and not very sensitive to variations of the damping.

Fig. 11

Behaviour of the NS boundary curve, for $\omega _1=1$, $\omega _2=2.05$, $\alpha _{12}=5\cdot 10^{-2}$, $\alpha _{11}=2.5\cdot 10^{-2}$ and different ratio $\mu _1/\mu _2$ keeping $\mu _1=5\cdot 10^{-3}$ fixed. The blue and red continuous lines are the backbone of the $p^-$ and $p^+$ mode while the black dashed lines mark $\varOmega =\omega _2/2$ and $\varOmega =(\omega _1+\omega _2)/3$. The other lines corresponds to different damping levels as detailed in the legend

A different case is analysed in Fig. 11, obtained for $\omega _1=1$, $\omega _2=2.05$, $\alpha _{12}=5\cdot 10^{-2}$, $\alpha _{11}=2.5\cdot 10^{-2}$ and different values of the ratio $\mu _1/\mu _2$, while keeping $\mu _1=5\cdot 10^{-3}$ fixed. The figure shows that increasing the damping $\mu _2$ makes the NS boundary smoother. It moreover underlines that in this specific case the asymptotic behaviour of the curve at large amplitudes is also affected. It is worth stressing that, except for the largest value of $\mu _2$, all the curves in the $(\varOmega ,{\bar{q}}_2)$ plane stay close to the specific point where the $p^{+}$ backbone emerges, underlining again the particular role of this point in the dynamics.

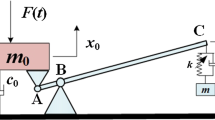
4 Test example: a clamped shallow double-arch MEMS structure

In this section we validate our previous findings by predicting the appearance of FCs in a MEMS clamped shallow arch. To highlight possible limits of the MS solution, we progressively add features in the model and comparisons and discussions are proposed for each step. First we check the MS solution reliability assuming that the structure behaviour is governed by Eq. (1) featuring only two quadratic nonlinear terms. The MS results, given by Eq. (27) are compared with the numerical solution of Eq. (1) when the detuning parameter vanishes, i.e. $\omega _2=2\omega _1$, and in the general case $\omega _2\ne 2\omega _1$, the latter condition being more realistic from a practical point of view since process imperfections typically prevent a perfect match between the two eigenfrequencies. Finally a comparison between a reduced-order model including all nonlinearities, the corresponding MS solution and a full Finite Element Simulation is proposed using a custom code [43].

4.1 Reduced order model

The arch geometry and dimensions are reported in Fig. 12.

Fig. 12

a 3D view of the FEM model used for the arch, b scheme of the geometry of the shallow arch considered. B=20 $\mu$m, H=5 $\mu$m, L=530 $\mu$m, rise=13.4 $\mu$m, s=10 $\mu$m

The device is made of polycrystalline silicon with density $\rho =2330$ kg/$\hbox {m}^3$. A linear elastic constitutive model (Saint-Venant Kirchhoff) is considered, with Young modulus $E=167000$ MPa and Poisson coefficient $\nu =0.22$ [49]. The double-arch has a large radius of curvature and it can be considered as shallow. The structure is inspired by the design proposed in [12], and it exploits two clamped arches connected at their center points in order to shift the anti-symmetric modes to higher frequencies. The first six eigenfrequencies of the structure, obtained from a Finite Element (FE) analysis using the mesh in Fig. 12 b, are reported in Tab. 1, and the corresponding mode shapes are shown in Fig. 13. In particular, one can observe that it is possible to achieve a 1:2 resonance between the first and the sixth eigenmodes, Fig. 13 a and f.

Fig. 13

First six eigenmodes of the arch. The contour of the displacement magnitude is shown in colour

A reduced-order model (ROM) is obtained from the full FE model using a static condensation approach [13, 25]. The ROM retains as master modes only the two eigenmodes involved in the 1:2 resonance. The approach uses static loadings proportional to the inertia of the master modes to create a stress manifold which is then fitted with a third order polynomial to obtain an explicit expression of the nonlinear restoring forces. The reduced-order dynamics, expressed with nondimensional time $\tau =\omega _1 t$ and mass-normalized values, reads:

$$\begin{aligned} q''_1&+\mu _1 q'_1+k^{(1)}_1 q_1+k^{(1)}_2 q_2+a_{11}^{(1)}q_1^2\nonumber \\&+a_{12}^{(1)}q_1q_2+a_{22}^{(1)}q_2^2+b_{111}^{(1)}q_1^3+b_{112}^{(1)}q_1^2q_2\nonumber \\&+b_{122}^{(1)}q_1q_2^2+b_{222}^{(1)}q_2^3=F\cos \varOmega \tau ,\nonumber \\ q''_2&+\mu _2 q'_2+k^{(2)}_1 q_1+k^{(2)}_2 q_2+a_{11}^{(2)}q_1^2\nonumber \\&+a_{12}^{(2)}q_1q_2+a_{22}^{(2)}q_2^2+b_{111}^{(2)}q_1^3+b_{112}^{(2)}q_1^2q_2 \nonumber \\&+b_{122}^{(2)}q_1q_2^2+b_{222}^{(2)}q_2^3=0, \end{aligned}$$

(35a)

where $q_1$ and $q_2$ are the generalized modal coordinates expressed in [$\mu$m] and $k_{i}^{(k)}, a_{ij}^{(k)}$ and $b_{ijs}^{(k)}$ are the linear, quadratic and cubic coefficients, respectively, for eigenmode k. The load multiplier considered in our benchmark is $F=0.0201$ $\mu$N$\mu$$\hbox {s}^2$/ng. The first and second order derivatives with respect to the nondimensional time are denoted with $'$ and $''$ respectively. Even if $\varOmega$ is now a nondimensional frequency, the same symbol of the previous sections has been used since we fixed $\omega _1=1$ in all the examples presented therein.

The damping factor is $\mu _i=\frac{\omega _i}{Q_i \omega _1}$ with $Q_{1}$ and $Q_2$ factors set to 500 and 1000 respectively, which is consistent with a mass proportional damping. The coefficients of the polynomial are reported in Tab. 2.

Arch displacements can be reconstructed with good accuracy from the linear modes and in particular the midspan deflection is

$$\begin{aligned} u(t)=0.11 q_1(t)+0.0707 q_2(t) \,\, [\mu \text {m}]. \end{aligned}$$

(36)

We notice that the selected damping values are slightly lower than the ones assumed in the previous examples concerning the MS solutions. This condition is typical of MEMS structures that are often packaged in near vacuum. The impact of these choices will be discussed in the following sections.

Table 1 First six eigenfrequencies of the arch. The third column reports the ratio with respect to the first eigenmode. The fourth column refers to their graphical representation in Fig. 13

Table 2 Coefficients describing the internal nonlinear elastic force in the ROM

4.2 Multiple scales model

In order to apply the MS formulas, the nonlinear terms of Eq. (35) that are not included in Eq. (1) are neglected. First we consider the perfectly tuned case by enforcing $\omega _2=2\omega _1$. We compare the FRF given by Eq. (27) and the solution computed via direct numerical continuation of periodic orbits applied to Eq. (1) using the continuation package MANLAB [20]. The numerical continuation solution is also assessed by comparison with a direct time-marching algorithm on system Eq. (1) in order to investigate the QP regime behaviour. For this case, a Runge-Kutta order 4 (RK4) integration scheme is used and QP solutions are plotted as Poincaré sections obtained by stroboscopy at the forcing frequency. Upward and downward sweeps of the forcing frequency are performed and for each frequency 5000 ($=10Q_1$) cycles are simulated to reach the steady state regime and collect time history data. The time step adopted is 1/500 of the forcing period $2\pi /\varOmega$.

Results are plotted in Fig. 14a). The MS and continuation (MANLAB) FRF are superimposed everywhere except close to the peaks. The numerical solution of Eq. (1) predicts a larger amplitude at the lower frequency peak and a smaller amplitude at the high frequency one. Indeed at the peaks the assumption of the MS solution that nonlinear terms are small starts being violated. On the contrary, the NS boundary intersections with the FRF predicted by the MS have a nearly perfect agreement with the bifurcation analysis performed by MANLAB (see the enlarged view in Fig. 14 b). This is reasonable since the NS boundary crosses the FRF at low amplitudes, where the MS approximation is fully respected.

Inspection of the time-marching solution reveals additional information. The match with the FRF obtained thanks to numerical continuation is almost exact in the periodic regions, the only difference being that the RK4 results present jumps in the solution (highlighted with arrows in the plot) since unstable solutions cannot be simulated. The time-marching solution allows appreciating amplitude modulation in the QP region. For a fixed frequency value a cloud of points is observed, as expected in a QP regime. The incommensurate frequency can be estimated from the Fourier Transform (FT) of the response and results are reported in Table 3 for both the upward and downward span.

The MS solution developed in this work cannot predict the behaviour of $\omega _{\rm {NS}}$ inside the QP region, but it can be used to estimate the values at its boundary, since here the purely imaginary eigenvalues define the oscillating frequency of $a_i$. The NS bifurcations occur at $\varOmega =0.99838$ and $\varOmega =1.00161$ respectively, corresponding to the eigenvalues $\lambda =\pm \mathbb {i}5.49 \cdot 10^{-3}$, that have the same value at both frequencies. The computed analytical value of $\lambda$ can be compared with the numerical results of Tab. 3. It is worth stressing that the agreement is good at the left of the NS in the upward sweep and at the right of the NS in the downward sweep, i.e. at the onset of the instability. The agreement then changes proceeding in the NS region since the numerical solution follows the QP solution branch on which the additional frequency of the torus is varying, a feature not provided by the MS analysis. Examples of the FT and time histories encountered in the frequency span are illustrated in Fig. 15 a and b referring to $\varOmega =0.99838$ and $\varOmega =0.98711$ respectively.

In Fig. 15 a, the QP regime has just settled down and one can observe a clear modulation of the envelope in the time domain, and a well shaped spectrum with clean spacings between all the frequency peaks, following the rule $n\varOmega \pm m\omega _{\rm {NS}}$ with n and m integers. Fig. 15 b has been obtained for $\varOmega =0.98711$ in the upward frequency sweep, thus the QP regime is further along the branch of QP solution. One can appreciate how the QP is modified along the solution branch, with a more complex envelope modulation, and a more important number of frequency peaks in the spectrum. One can also observe the enlargement of the frequency peaks, indicating that the QP solution will probably lose its stability in favour of a chaotic behaviour further in the solution branch. One can also note that the direct time integration results underline the facts that the NS bifurcation is supercritical with emergence of a stable torus at both side of the branching points, symmetric, with probably a small portion of unstable torus close to the branching points.

Fig. 14

Tuned condition $\omega _2=2\omega _1$. Comparison between the analytical solution from Eq. (27) (black line), continuation of periodic orbits of Eq. (1) (red lines) and the time-marching integration of Eq. (1) (circle markers). The analytical NS boundary is the green dash-dotted line. The red star markers define the bifurcation points identified by MANLAB

Table 3 Estimate of the incommensurate frequency $\omega _{\rm {NS}}$ for the upward and downward external frequency sweeps $\varOmega$ considered, in the perfectly tuned case $\omega _2=2\omega _1$. The RK4 estimates are extracted from the FT of the system (resolution $\approx 5\cdot 10^{-4}$). The value not specified in the RK4 values correspond to a chaotic regime were the FC spacing is not defined. Analytical values of $\omega _{\rm {NS}}$ provided by the MS method at the onset of the QP regime as reported in the last lines

Fig. 15

FT and time histories from the RK4 solution on $\varOmega =0.99838$ a) and $\varOmega =0.98711$ b)

Before moving to the detuned condition, phase space representation from time-marching solution are inspected.

The torus emerging from the NS bifurcation is represented in Fig. 16, obtained from direct RK4 integrations with $\varOmega =1$. A 3D representation in the space ($q_1,{\dot{q}}_1,q_2$) and in the planes $(q_1,{\dot{q}}_1)$ and $(q_1,q_2)$ are shown. For sake of clarity, only a short portion of the time history, corresponding to few quasi-periods, is considered. Fig. 16 a represents the phase space $(q_1,{\dot{q}}_1,q_2)$ while Fig. 16b) is a cross-section of the four dimensional torus considering the portion included in the green and the blue planes. The red dots mark the crossing region. Figure 16c) and d) are the 2D version of the phase space considering its two projections in the planes $q_1,{\dot{q}}_1$ and $q_1,q_2$.

Fig. 16

Torus obtained by direct integration with RK4 algorithm of Eq. (1) in the tuned case $\omega _2=2\omega _1$. Only a short portion of the time history is plotted for sake of clarity

The detuned case is now investigated with $\omega _2=1.989\omega _1$, and the same analysis is repeated. The FRF results are plotted in Fig. 17 and the $\omega _{\rm {NS}}$ values are collected in Tab. 4. By comparing the MS and the numerical continuation (MANLAB) solutions, the FRFs and the NS bifurcation crossing points share the same degree of accuracy of the previous case. Focusing on the incommensurate frequencies, the MS solution predicts $\omega _{\rm {NS}}=4.37\cdot 10^{-3}$ at $\varOmega =0.99372$ and $\omega _{\rm {NS}}=6.19\cdot 10^{-3}$ at $\varOmega =0.99679$. Fig. 17b) shows how the QP time-marching solution is completely embedded in the region estimated by MS. An outstanding match is found close to $\varOmega =0.99679$ while the values on $\varOmega =0.99372$ are lower than expected. The underlying reason is that at $\varOmega =0.99679$ a supercritical NS bifurcation appears, which is also confirmed by the identical values of $\omega _{\rm {NS}}$ found close to this point when sweeping the forcing frequency in the increasing or decreasing direction. On the other hand, a subcritical NS bifurcation takes place at $\varOmega =0.99679$, consequently the added frequency predicted by the MS method corresponds to unstable quasi-periodic solutions that are not found with direct time integration. Instead, the numerical solution jumps to the branch of stable QP solutions and then travels up to the other supecritical bifurcation point.

Fig. 17

Detuned condition $\omega _2=1.989\omega _1$. Comparison between the analytical solution from Eq. (27) (black line), continuation of periodic orbits of Eq. (1) (red lines) and the time-marching integration of Eq. (1) (circle markers). The analytical NS boundary is the green dash-dotted line. The red star markers define the bifurcation points identified by MANLAB

Table 4 Estimate of the incommensurate frequency $\omega _{\rm {NS}}$ for the upward and downward frequency sweeps $\varOmega$ considered, in the case $\omega _2= 1.989\omega _1$. The RK4 estimates are extracted from the FT of the system (resolution $\approx 5\cdot 10^{-4}$). Analytical values obtained from MS analysis at the bifurcation points reported in the last two lines

4.3 Reduced order model and full order simulation

Finally we consider a comparison between the MS solution and the ROM retaining all nonlinear terms. Results obtained with the ROM are further validated with analyses performed on the full FE model using two different techniques. First, an Harmonic Balance approach (HB) is used, from which a reference FRF is computed. However, this technique in our implementation cannot detect QP solutions. As a consequence, a costly direct time integration of the full FE model is also performed with a Newmark-$\beta$ scheme for specific values of $\varOmega$. The time-marching solution adopts a time step equal to 1/300 of the forced eigenmode period and 3000 cycles are simulated for each frequency. The full FEM model uses as external forcing a body force having the same shape of the first eigenmode, which is consistent with the ROM loading in Eq. (35). The comparison between the MS solution and the ROM is plotted in Fig. 18. As expected and mostly because of the presence of the cubic terms in the ROM, some quantitative differences appear between the two solutions. However no qualitative difference is reported since the simplified system studied in the MS development contains the most important resonant monomial terms that convey the important bifurcation information. Moreover in the low amplitude region and close to $\varOmega =1$ the MS solution is nearly exact. Also the prediction of the NS boundary intersections with the FRF shows a very good match with numerical results on the ROM. This is expected since the MS approach is reliable in a low amplitude region where the smallness assumptions still hold, and thus underlines that the analytical formula of the NS boundary curve can be used for rapid prediction of the occurrence of FC in such a case.

Fig. 18

Comparison between the analytical solution (black line) and the static condensation ROM (red line). The analytical NS boundary is the green dash-dotted line. The red star markers define the bifurcation points identified by MANLAB

Finally we compare the ROM solution with a Full FEM simulation considering the maximum absolute midspan displacement $\max |u|$. The results are plotted in Fig. 19 where the NS boundary curve from the MS solution is also included. We notice the excellent agreement between the FRF obtained using numerical continuation and HB for the full FEM model and for the ROM, respectively, validating the reduction technique adopted. As expected, the NS boundary from the MS predicts correctly the onset of the QP regime also in this case.

Fig. 19

Comparison between the static condensation ROM (red line), the HB FEM model (dashed blue line) and the time-marching FEM integration (circle markers). The analytical NS boundary is the green dash-dotted line. The red star markers define the bifurcation points identified by MANLAB. The circle markers highlighted with different colors correspond to the frequencies plotted in Fig. 20

Fig. 20 shows three representative quasi-periodic solutions obtained from direct time integration on the full FE model. Note that these solutions are obtained from a decreasing sweep so that the solutions follow the QP branch of solution by order of decreasing frequencies. The first line in Fig. 20 corresponds to $\varOmega$=0.9965, which is the onset of the QP regime, just after the NS bifurcation point. The amplitude modulation displays a simple pattern in Fig. 20 a) and the frequency spectrum shows the appearance of the extra peaks indicating the birth of the FC. At this point one can compare the $\omega _{\rm {NS}}$ value predicted by the MS at the boundary (see Table 4) and that from from direct numerical integration. The comb spacing in Fig. 20b reveals the value $\omega _{\rm {NS}}=5.93\cdot 10^{-3}$, very close to the values reported in Table 4 and thus underlining again the good predictive capacity of the simple analytical model. The second line in Fig. 20 corresponds to $\varOmega$=0.9956, a point further along the branch of QP solutions. One can observe that the amplitude modulation is more complex but still clearly periodic, resulting in a well defined frequency comb. In this case the new frequency $\omega _{\rm {NS}}$ cannot be determined from the MS analysis. Finally, the third line shows the results obtained for $\varOmega$=0.9939. In this case one can clearly observe that the envelope modulation has no clear periodicity at the reported time scales, underlining that the torus is on the way to lose its stability by creating longer and longer periods which will result in a chaotic solution. The frequency spectrum is more densely filled. A complete study of the chaotic nature of this solution could be performed by computing the Lyapunov spectrum or a more involved stability analysis of the torus solution. This point is however not the scope of the present study which is focused on the appearance of quasiperiodic solutions and their link to Frequency combs in MEMs dynamics.

Fig. 20

Time histories (left column) and corresponding Frequency spectrum (right column) obtained by direct time integration of the full FE model, following the branch of QP solution by order of decreasing frequencies. First line: $\varOmega$ = 0.9965, birth of the QP solution. Second and third lines: $\varOmega=0.9956$ and 0.9939

5 Conclusion and further developments

In this paper we have developed analytical results for 1:2 internally resonant coupled oscillators. Even though this analysis is classical in nonlinear vibration theory, new insights have been reported, in particular with regard to the identification of the two backbones and their corresponding parabolic mode shapes and the analytical derivation of the NS boundary curves. All these results have been also put under the frame of explaining the appearance of FC in MEMs dynamics, a subject that give rise to numerous investigations in the recent years, and all the results have been applied to a MEMS arch structure in order to underline the predictive capacity of the analytical NS boundary curve. This result can be helpful in a context of MEMs design for accurate and fast predictions since the QP solutions are sometimes intentionally searched for.

Starting from the normal form of the dynamical system we inspected the conservative solution providing a clear identification of the mode shapes and solution branches. By extending our study to the forced and damped condition we were able to retrieve a closed form solution for the NS boundary curve. We inspected in depth the behaviour of the bifurcation boundary by varying the system parameters and comparing it with the conservative and the non-conservative solutions. We proved the validity of our findings in the challenging simulation of a MEMS structure example. The analytical solution has been validated against several numerical methods including numerical continuation procedures (MANLAB), reduced order models solved with direct time integration or the Harmonic Balance Method and eventually also with full FEM approaches.

A good agreement between the analytical results and the numerical approach is always observed. In particular, the NS boundary provides a nearly perfect prediction of the quasi-periodic regime arising and a very good estimate of the incommensurate frequency. The formulas proposed prove useful for design applications on real devices and structures. The closed form solution allows exploring in depth the resonance phenomena with low computational effort. Further development are currently undertaken in order to reframe the cases of 1:1 and 1:3 internal resonance within the same analyses, underlining the existence of different families of periodic orbits , deriving accurate predictive solutions for the NS boundary curve, in order to shed new light and unify analyses of the emergence of QP solutions in nonlinear oscillators with applications to MEMs dynamics.

Appendices

Appendix

1. General nonlinear coefficients in Eq. 1

This section shows how the formulas proposed in the paper can be used into the general case of uncorrelated $\alpha _{12}$ and $\alpha _{11}$. We will mainly focus on the effect of a different sets of nonlinear coefficients on backbones and NS boundary. Considering the backbone curves, keeping the frequency detuning $\omega _2 -2\omega _1$ fixed and varying the non-linear coefficients $\alpha _{12}$ and $\alpha _{11}$ ratios, the results are shown in Figs. 21 and 22.

Fig. 21 assumes $\alpha _{12}=1\cdot 10^{-2}$ and it considers different values of the ratio $\alpha _{12}/\alpha _{11}$. Figure 21 a) and b) refer to a detuning value $\sigma _1=0$, while Fig. 21c) and d) refer to $\sigma _1=5\cdot 10^{-3}$. The backbones of the second oscillator response is invariant with respect to the ratio $\alpha _{12}/\alpha _{11}$. This is reasonable because only $\alpha _{12}$ appears in Eq. (16a). The ${\bar{q}}_1$ backbone tends to grow with the ratio $\alpha _{12}/\alpha _{11}$ preserving the same shape . The $\sigma _1$ value introduces a curvature in the ${\bar{q}}_1$ mode response and left unchanged the starting point of the ${\bar{q}}_2$ backbone.

Fig. 22 assumes $\alpha _{11}=1\cdot 10^{-2}$ and considers different values of the ratio $\alpha _{11}/\alpha _{12}$. Fig. 22 a) and b) refer to $\sigma _1=0$, while Fig. 22c) and d) to $\sigma _1=5\cdot 10^{-3}$. The backbone of both oscillators grow with the ratio $\alpha _{11}/\alpha _{12}$ preserving their shape. The $\sigma _1$ value introduces a curvature in the ${\bar{q}}_1$ mode response and shifts to higher amplitudes the starting point of the ${\bar{q}}_2$ backbone.

Fig. 21

Behaviour of the backbones when $\alpha _{12}/\alpha _{11}$ is changed keeping fixed $\alpha _{12}=1\cdot 10^{-2}$. In these plots the line color marks with blue the $p^-$ and with red the $p^+$ mode, the black dashed line marks $\varOmega =\omega _2/2$. Figure a) and b) represent the backbone ${\bar{q}}_1$ and ${\bar{q}}_2$ respectively when $\omega _2 -2\omega _1=0$. Figure c) and d) represent the backbone ${\bar{q}}_1$ and ${\bar{q}}_2$ respectively when $\omega _2 -2\omega _1=5\cdot 10^{-3}$

Fig. 22

Behaviour of the backbones when $\alpha _{11}/\alpha _{12}$ is changed keeping fixed $\alpha _{11}=1\cdot 10^{-2}$. In these plots the line color marks with blue the $p^-$ and with red the $p^+$ mode, the black dashed line marks $\varOmega =\omega _2/2$. Figure a) and b) represent the backbone ${\bar{q}}_1$ and ${\bar{q}}_2$ respectively when $\omega _2 -2\omega _1=0$. Figure c) and d) represent the backbone ${\bar{q}}_2$ and ${\bar{q}}_2$ respectively when $\omega _2 -2\omega _1=5\cdot 10^{-3}$

We now inspect the NS boundary behaviour. We consider the system parameters $\omega _1=1$, $\omega _2=2.005$, $\mu _1=\mu _2=1.5 \cdot 10^{-3}$ and we plot in Fig. 23 the NS boundaries corresponding to different ratio $\alpha _{12}/\alpha _{11}$, keeping $\alpha _{12}=5 \cdot 10^{-2}$. The plots show that in the ${\bar{q}}_1$ amplitude the NS boundary tends to enlarge with a lower ratio (higher $\alpha _{11}$) while it is identical in the ${\bar{q}}_2$ response. This is reasonable because only $\alpha _{12}$ appears in Eq. (33). Considering the same system, in Fig. 24 the NS boundaries for different ratio $\alpha _{11}/\alpha _{12}$, keeping $\alpha _{11}=5 \cdot 10^{-2}$ are plotted. The plots show that in both the amplitudes the NS boundary tends to enlarge with lower ratio (higher $\alpha _{12}$).

Fig. 23

The figures show the NS boundary behaviour corresponding to $\omega _1=1$, $\omega _2=2.005$, $\mu _1=\mu _2=1.5 \cdot 10^{-3}$ for different ratio $\alpha _{12}/\alpha _{11}$ keeping $\alpha _{12}=5 \cdot 10^{-2}$

Fig. 24

The figures show the NS boundary behaviour corresponding to $\omega _1=1$, $\omega _2=2.005$, $\mu _1=\mu _2=1.5 \cdot 10^{-3}$ for different ratio $\alpha _{11}/\alpha _{12}$ keeping $\alpha _{11}=5 \cdot 10^{-2}$

2. Conservative system

This section presents the details of the MS solution in Sect. 2.1 for the conservative case, i.e. with no forcing and damping. We insert the MS approximation $q_i(t)= q_{i0}(T_0,T_1)+\varepsilon q_{i1}(T_0,T_1)$ into Eq. (1) and split the resulting terms using $\varepsilon$ as sorting parameter. Consequently, we get a first order system:

$$\begin{aligned} \begin{aligned}&D_0^2 q_{10}+\omega _{1}^{2} q_{10}=0,\\&D_0^2 q_{20}+\omega _{2}^{2} q_{20}=0, \end{aligned} \end{aligned}$$

(37)

and a second order system:

$$\begin{aligned} \begin{aligned}&D_0^2 q_{11}+\omega _{1}^{2} q_{11}=-2 D_0 D_1 q_{10} +{\bar{\alpha }}_{12} q_{10} q_{20},\\&D_0^2 q_{12}+\omega _{2}^{2} q_{12}=-2 D_0 D_1 q_{20} +{\bar{\alpha }}_{11} q_{10}^2, \end{aligned} \end{aligned}$$

(38)

in which $D_i^k$ denotes the order k derivative with respect to the time scale $i=0,1$. Eq. (37) describes two linear uncoupled oscillators with motion given by:

$$\begin{aligned} q_{11}&= A_1 e^{\mathbb {i}\omega _1 T_0}+{\bar{A}}_1 e^{-\mathbb {i}\omega _1 T_0} \end{aligned}$$

(39a)

$$\begin{aligned} q_{21}&= A_2 e^{\mathbb {i}\omega _2 T_0}+{\bar{A}}_2 e^{-\mathbb {i}\omega _2 T_0} \end{aligned}$$

(39b)

Inserting the solution of Eq. (37) in Eq. (38) we get an expression with $A_i$ as unknowns. Nullifying secular terms we get the conditions:

$$\begin{aligned} {\bar{\alpha }}_{12} A_2 {\bar{A}}_{1} e^{\mathbb {i}T_1 \sigma _1}+2 \mathbb {i}\omega _1 A_1'&=0, \end{aligned}$$

(40a)

$$\begin{aligned} A_1^2 {\bar{\alpha }}_{11} +2\mathbb {i}\omega _2 A_2' e^{\mathbb {i}T_1 \sigma _1}&=0. \end{aligned}$$

(40b)

To solve Eq. (40) we need to expand $A_i$ in polar form as $A_i(T_1)=\frac{1}{2}a_i(T_1)\exp {(\mathbb {i}\theta _i(T_1))},\quad i=1,2$. Insert $A_i$ in Eq. (40) and imposing that the real and imaginary part vanish independently, we get Eq. (4).

As required by the stability analysis in Sect. 2.3 we finally compute the Jacobian matrix of system. (7), i.e.:

$$\begin{aligned} J= \left( \begin{array}{cccc} J_{11} &{} 0 &{} J_{13} &{} J_{14}\\ 0 &{} 0 &{} J_{23} &{} J_{24}\\ J_{31} &{} 0 &{} 0 &{} J_{34}\\ J_{41} &{} 0 &{} J_{43} &{} J_{44}\\ \end{array} \right) , \end{aligned}$$

(41)

with:

$$\begin{aligned} \begin{aligned}&J_{11}=\frac{{\bar{\alpha }}_{12} a_2 \sin \left( \gamma _p\right) }{4 \omega _1}, \quad J_{13}=\frac{{\bar{\alpha }}_{12} a_1 \sin \left( \gamma _p\right) }{4 \omega _1},\\&J_{14}=\frac{{\bar{\alpha }}_{12} a_1 a_2 \cos \left( \gamma _p\right) }{4 \omega _1}, \quad J_{23}=\frac{{\bar{\alpha }}_{12} \cos \left( \gamma _p\right) }{4 \omega _1},\\&J_{24}=-\frac{{\bar{\alpha }}_{12} a_2 \sin \left( \gamma _p\right) }{4 \omega _1}, \quad J_{31}=-\frac{{\bar{\alpha }}_{11} a_1 \sin \left( \gamma _p\right) }{2 \omega _2},\\&J_{34} = -\frac{{\bar{\alpha }}_{11} a_1^2 \cos \left( \gamma _p\right) }{4\omega _2}, \quad J_{41}= -\frac{{\bar{\alpha }}_{11} a_1 \cos \left( \gamma _p\right) }{2 a_2 \omega _2},\\&J_{43}=\frac{1}{2} \cos (\gamma _p ) \left( \frac{{\bar{\alpha }}_{12}}{\omega _1}+\frac{{\bar{\alpha }}_{11} a_1^2}{2 a_2^2 \omega _2}\right) \\&J_{44}= -\frac{\sin \left( \gamma _p\right) }{4 a_2} \left( \frac{2 {\bar{\alpha }}_{12} a_2^2}{\omega _1} -\frac{{\bar{\alpha }}_{11} a_1^2}{\omega _2}\right) . \end{aligned} \end{aligned}$$

3. Forced and damped system

Starting from Eq. (1) we sort the non-linearities using a book-keeping parameter $\varepsilon$. We assume a first order approximation, thus we rewrite Eq. (1) in the form:

$$\begin{aligned}&\ddot{q}_{1}+\omega _{1}^{2} q_{1}=\varepsilon [-2{\bar{\mu }}_{1} {\dot{q}}_{1}-{\bar{\alpha }}_{12} q_1 q_2+{\bar{F}} \cos \left( \varOmega t\right) ] , \end{aligned}$$

(42a)

$$\begin{aligned}&\ddot{q}_{2}+\omega _{2}^{2} q_{2}=\varepsilon [-2{\bar{\mu }}_{2} {\dot{q}}_{2}-{\bar{\alpha }}_{11} q_1^2]. \end{aligned}$$

(42b)

The external forcing angular frequency is related to the eigenfrequency through Eq. (23). Proceeding as for the conservative case (see from Eq. (38) to Eq. (40)), we get the solvability condition:

$$\begin{aligned} {\bar{\alpha }}_{12} A_2 {\bar{A}}_{1} e^{\mathbb {i} T_1 \sigma _1}+2 \mathbb {i} \omega _1 \left( A_1 {\bar{\mu }}_1+A_1'\right) -\frac{1}{2} {\bar{F}} e^{\mathbb {i} T_1 \sigma _2}&=0, \end{aligned}$$

(43a)

$$\begin{aligned} A_1^2 {\bar{\alpha }}_{11}+2 {\mathbb {i}} e^{\mathbb {i} T_1 \sigma _1} \omega _2 \left( A_2 {\bar{\mu }}_2+A_2'\right)&=0. \end{aligned}$$

(43b)

Inserting the polar form of $A_i,\; i=1,2$ (see Appendix 2) in Eq. (43) and imposing that the real and imaginary parts vanish, we get the system of four equations in Eq. (24).

Considering the A1-mode condition $a_1\ne 0$ and $a_2=0$, Eq. (1) admit a nonzero solution for $a_1$ only if $\alpha _{11}$ is zero, but this is a degenerate condition. Thus, the A1-mode is not allowed.

Considering the A2-mode condition $a_2\ne 0$ and $a_1=0$, Eq. (1) implies a zero forcing value, and consequently nonzero solutions exist only if the damping term also is zero. This is a degenerate condition since it is the one predicted by the conservative case, thus the A2-mode in damped and forced conditions is impossible.

The coupled solutions are obtained from Eq. (24), as detailed in Sect. 3, and are given by Eq.  (26).

In order to address the stability of the coupled solutions derived in Sect. 3, one needs the Jacobian matrix for Eq. (26), i.e.:

$$\begin{aligned} J= \left( \begin{array}{cccc} J_{11} &{} J_{12} &{} J_{13} &{} J_{14}\\ J_{21} &{} J_{22} &{} J_{23} &{} J_{24}\\ J_{31} &{} 0 &{} J_{33} &{} J_{34}\\ J_{41} &{} J_{42} &{} J_{43} &{} J_{44}\\ \end{array} \right) , \end{aligned}$$

(44)

with:

$$\begin{aligned} \begin{aligned}&J_{11}=\frac{{\bar{\alpha }}_{12} a_2 \sin \left( \gamma _2\right) -4 {\bar{\mu }}_1 \omega _1}{4 \omega _1},\\&J_{12}=-\frac{{\bar{F}} \cos \left( \gamma _1\right) }{2 \omega _1},\\&J_{13}=\frac{{\bar{\alpha }}_{12} a_1 \sin \left( \gamma _2\right) }{4 \omega _1}, J_{14}=\frac{{\bar{\alpha }}_{12} a_1 a_2 \cos \left( \gamma _2\right) }{4 \omega _1},\\&J_{21}=\frac{ {\bar{F}} \cos \left( \gamma _1\right) }{2 a_1^2 \omega _1},\\&J_{22}=\frac{{\bar{F}} \sin \left( \gamma _1\right) }{2 a_1 \omega _1}, \\&J_{23}= \frac{{\bar{\alpha }}_{12} \cos \left( \gamma _2\right) }{4 \omega _1}, \\&J_{24}=-\frac{{\bar{\alpha }}_{12} a_2 \sin \left( \gamma _2\right) }{4 \omega _1},\\&J_{31}= -\frac{{\bar{\alpha }}_{11} a_1 \sin \left( \gamma _2\right) }{2 \omega _2},\\&J_{33} = -{\bar{\mu }}_2, \\&J_{34} =-\frac{{\bar{\alpha }}_{11} a_1^2 \cos \left( \gamma _2\right) }{4 \omega _2},\\&J_{41}= \frac{{\bar{F}} \cos \left( \gamma _1\right) }{a_1^2 \omega _1}-\frac{{\bar{\alpha }}_{11} a_1 \cos \left( \gamma _2\right) }{2 a_2 \omega _2},\\&J_{42}= \frac{{\bar{F}} \sin \left( \gamma _1\right) }{a_1 \omega _1},\\&J_{43}=\frac{1}{4} \cos \left( \gamma _2\right) \left( \frac{2{\bar{\alpha }}_{12}}{\omega _1}+\frac{{\bar{\alpha }}_{11} a_1^2 }{a_2^2 \omega _2}\right) \\&J_{44}=-\frac{1}{2} \sin \left( \gamma _2\right) \left( \frac{{\bar{\alpha }}_{12} a_2}{\omega _1}-\frac{{\bar{\alpha }}_{11} a_1^2}{2a_2\omega _2}\right) . \end{aligned} \end{aligned}$$

4. Coefficients of polynomials Eq. (29) and Eq. (33)

$$\begin{aligned} c_1 =&2 \left( \mu _1+\mu _2\right) ,\nonumber \\ c_2 =&\frac{a_2 \alpha _{12}}{\omega _1} \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) ^2}-\frac{a_2^2 \alpha ^2_{12}}{16 \omega _1^2} \nonumber \\&+\mu _1^2+\mu _2^2+4 \mu _1 \mu _2-2 \omega _1 \varOmega -4 \omega _2 \varOmega \nonumber \\&+\omega _1^2+\omega _2^2+5 \varOmega ^2, \nonumber \\ c_3=&\frac{a_2 \alpha _{12}}{\omega _1} \left( \mu _1+\mu _2\right) \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) ^2}\nonumber \\&-\frac{a_2^2 \alpha ^2_{12} \mu _2}{8 \omega _1^2} +2 \mu _1 \left( \mu _2^2+\left( \omega _2-2 \varOmega \right) ^2\right) \nonumber \\&+2 \mu _2 \left( \varOmega -\omega _1\right) {}^2+2 \mu _2 \mu _1^2,\nonumber \\ c_4=&\frac{\sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) {}^2}}{16 \omega _1^2} \left( 3 a_2^2 \alpha ^2_{12} \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) {}^2}\right. \nonumber \\&\left. +16 a_2 \alpha _{12} \omega _1 \left( \mu _1 \mu _2-\left( \varOmega -\omega _1\right) \left( 2 \varOmega -\omega _2\right) \right) \right. \nonumber \\&\left. +16 \omega _1^2 \left( \mu _1^2+\left( \varOmega -\omega _1\right) {}^2\right) \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) ^2}\right) , \end{aligned}$$

(45)

$$\begin{aligned} b_1=&\frac{\alpha ^4_{12} \mu _1 \mu _2}{64 \omega _1^4}, \nonumber \\ b_2=&-\frac{\alpha ^3_{12} \left( \mu _1+\mu _2\right) ^2 \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) ^2}}{8 \omega _1^3}, \nonumber \\ b_3=&-\frac{\alpha ^2_{12} }{2 \omega _1^2}\mu _1 \mu _2 \cdot \nonumber \\&\left( \mu _1^2+\mu _2^2+2 \mu _1 \mu _2-2 \omega _1 \varOmega +4 \omega _2 \varOmega +\omega _1^2-\omega _2^2-3 \varOmega ^2\right) , \nonumber \\ b_4=&\frac{2 \alpha _{12}}{\omega _1} \left( \mu _1+\mu _2\right) ^2 \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) ^2} \cdot \nonumber \\&\left( \mu _1^2+2 \mu _2 \mu _1+\mu _2^2+\left( \omega _1+\omega _2-3 \varOmega \right) ^2\right) ,\nonumber \\ b_5=&4 \Bigg (\bigg (\mu _1 \big (\mu _2^2+\left( \omega _2-2 \varOmega \right) ^2\big ) +\mu _2 \left( \varOmega -\omega _1\right) ^2+\mu _2 \mu _1^2\bigg )\cdot \nonumber \\&\bigg (\mu _1 \left( 4 \mu _2^2+\left( \varOmega -\omega _1\right) ^2\right) +\mu _2 \left( \mu _2^2+\left( \omega _2-2 \varOmega \right) ^2\right) \nonumber \\&+\mu _1^3+4 \mu _2 \mu _1^2\bigg )-\left( \mu _1+\mu _2\right) {}^2 \left( \mu _1^2+\left( \varOmega -\omega _1\right) ^2\right) \nonumber \\&\left( \mu _2^2+\left( \omega _2-2 \varOmega \right) {}^2\right) \Bigg ). \end{aligned}$$

(46)

5. Asymptotic analysis of the extrema of the NS boundary curve

In order to search for the extrema of the NS boundary curve, we compute the derivative of Eq. (33), defining the NS boundary, with respect to the external forcing frequency $\varOmega$:

$$\begin{aligned} d_1(\varOmega ) {\bar{q}}_2^3+d_2(\varOmega ) {\bar{q}}_2^2+d_3(\varOmega ){\bar{q}}_2+d_4(\varOmega ) =0, \end{aligned}$$

(47)

where the explicit expressions for all the coefficients read:

$$\begin{aligned} \begin{aligned} d_1&=-\frac{\alpha ^3_{12} \left( \mu _1+\mu _2\right) ^2 \left( 2 \varOmega -\omega _2\right) }{4 \omega _1^3 \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) {}^2}},\\ d_2&=\frac{\alpha ^2_{12} \mu _1 \mu _2 \left( \omega _1-2 \omega _2+3 \varOmega \right) }{\omega _1^2},\\ d_3&=\frac{4 \alpha _{12}}{\omega _1 \sqrt{\mu _2^2+\left( \omega _2-2 \varOmega \right) {}^2}} \Bigg ( \left( \mu _1+\mu _2\right) ^2 \bigg ( \mu _1^2 \left( 2 \varOmega -\omega _2\right) \\&+2 \mu _2 \mu _1 \left( 2 \varOmega -\omega _2\right) +\mu _2^2 \left( -3 \omega _1-4 \omega _2+11 \varOmega \right) \\&+\left( 2 \varOmega -\omega _2\right) \Big (-21 \omega _2 \varOmega +\omega _1 \left( 5 \omega _2-12 \varOmega \right) \\&+\omega _1^2+4 \omega _2^2+27 \varOmega ^2\Big ) \bigg ) \Bigg ),\\ d_4&=16 \mu _1 \mu _2 \Bigg ( \mu _1^2 \left( -\omega _1-2 \omega _2+5 \varOmega \right) \\&+\mu _2^2 \left( -\omega _1-2 \omega _2+5 \varOmega \right) +2 \mu _1 \mu _2 \left( -\omega _1-2 \omega _2+5 \varOmega \right) \\&+9 \omega _1 \varOmega ^2-18 \omega _2 \varOmega ^2-\omega _1^2 \varOmega +11 \omega _2^2 \varOmega -8 \omega _1 \omega _2 \varOmega \\&-\omega _1^3-2 \omega _2^3+\omega _1 \omega _2^2+2 \omega _1^2 \omega _2+9 \varOmega ^3 \Bigg ). \end{aligned} \end{aligned}$$

(48)

Due to the complexity of the expressions, a numerical solution is mandatory in general. However, in specific cases one can get an analytical estimate for the extrema. First, we simplify Eq. (47) considering $\mu _1=\mu _2=\mu$ and by sorting it with respect to $\mu$ we get:

$$\begin{aligned} \frac{(g_1\mu ^4+g_2\mu ^2)}{\omega _1^3 \sqrt{\mu ^2+(2 \varOmega -\omega _2)^2}}+g_3\mu ^2=0, \end{aligned}$$

(49)

with

$$\begin{aligned} \begin{aligned} g_1&=272 \alpha _{12} {\bar{q}}_2 \omega _1^2 \varOmega -48 \alpha _{12} {\bar{q}}_2 \omega _1^3-112 \alpha _{12} {\bar{q}}_2 \omega _2 \omega _1^2 \\&-64 \omega _1^4 \sqrt{\mu ^2+\left( 2 \varOmega -\omega _2\right) ^2}+320 \omega _1^3 \varOmega \sqrt{\mu ^2+\left( 2 \varOmega -\omega _2\right) ^2}\\&-128 \omega _2 \omega _1^3 \sqrt{\mu ^2+\left( 2 \varOmega -\omega _2\right) ^2},\\ g_2&=864 \alpha _{12} {\bar{q}}_2 \omega _1^2 \varOmega ^3-384 \alpha _{12} {\bar{q}}_2 \omega _1^3 \varOmega ^2-1104 \alpha _{12} {\bar{q}}_2 \omega _2 \omega _1^2 \varOmega ^2\\&+32 \alpha _{12} {\bar{q}}_2 \omega _1^4 \varOmega +352 \alpha _{12} a_2 \omega _2 \omega _1^3 \varOmega \\&+464 \alpha _{12} {\bar{q}}_2 \omega _2^2 \omega _1^2 \varOmega -16 \alpha _{12} {\bar{q}}_2 \omega _2 \omega _1^4-80 \alpha _{12} {\bar{q}}_2 \omega _2^2 \omega _1^3\\&-64 \alpha _{12} {\bar{q}}_2 \omega _2^3 \omega _1^2+\alpha ^3_{12} {\bar{q}}_2^3 \omega _2-2 \alpha ^3_{12} {\bar{q}}_2^3 \varOmega ,\\ g_3&=3 \alpha ^2_{12} {\bar{q}}_2^2 \omega _1 \varOmega +\alpha ^2_{12} {\bar{q}}_2^2 \omega _1^2-2 \alpha ^2_{12} {\bar{q}}_2^2 \omega _2 \omega _1\\&+144 \omega _1^3 \varOmega ^3+144 \omega _1^4 \varOmega ^2-288 \omega _2 \omega _1^3 \varOmega ^2\\&-16 \omega _1^5 \varOmega -128 \omega _2 \omega _1^4 \varOmega +176 \omega _2^2 \omega _1^3 \varOmega \\&-16 \omega _1^6+32 \omega _2 \omega _1^5+16 \omega _2^2 \omega _1^4-32 \omega _2^3 \omega _1^3. \end{aligned} \end{aligned}$$

(50)

Inserting $\varOmega =\omega _2/2$ in Eq. (50) we remark that $g_2$, the leading term in $\mu$, vanishes. Thus $\varOmega =\omega _2/2$ is an asymptotical extrema for the problem and corresponds to a minimum.

We next consider the limit $\mu \rightarrow 0$. The leading order term is proportional to $\mu ^2$ and is given by:

$$\begin{aligned} \frac{g_2}{\omega _1^3 \sqrt{(2 \varOmega -\omega _2)^2}}+g_3=0. \end{aligned}$$

(51)

This expression is the asymptotic approximation of Eq. (47) and it can be be expressed in the same form as Eq. (47), with:

$$\begin{aligned} \begin{aligned}&d_1=-\frac{\alpha ^3_{12}}{\omega _1^3},\\&d_2= \frac{\alpha ^2_{12} \left( \omega _1-2 \omega _2+3 \varOmega \right) }{\omega _1^2}, \\&d_3=\frac{16 \alpha _{12}}{\omega _1}\left( -21 \omega _2 \varOmega +\omega _1 \left( 5 \omega _2-12 \varOmega \right) +\omega _1^2+4 \omega _2^2+27 \varOmega ^2\right) ,\\&d_4=-16 \Bigg (18 \omega _2 \varOmega ^2-\omega _1 \left( -8 \omega _2 \varOmega +\omega _2^2+9 \varOmega ^2\right) \\&-11 \omega _2^2 \varOmega +\omega _1^2 \left( \varOmega -2 \omega _2\right) +\omega _1^3+2 \omega _2^3-9 \varOmega ^3\Bigg ). \end{aligned} \end{aligned}$$

(52)

Eq. (51) can be directly solved with respect to $\varOmega$ if we consider that the NS boundary tends to approach zero when the damping tends to zero. With this assumption, only the lower order terms with respect to ${\bar{q}}_2$, i.e. $d_4$ and $d_3$, are relevant. This provides a linearised version of the NS minima problem and has the solution $\varOmega =(\omega _2+\omega _1)/3$ independent of its amplitude.