Dynamic and stability analysis of a cantilever beam system excited by a non-ideal induction motor

Abstract

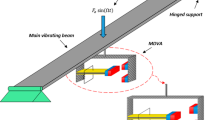
In this paper, Sommerfeld effect of a non-ideal induction motor in a simple cantilever beam system is studied. On basis of fully considering the interaction between the beam structure and the induction motor and its non-ideal characteristic, a continuous electromechanical coupling model of the typical non-ideal vibration system is developed and discretized by using the assumed mode method. Neglecting the fluctuation of the speed of the induction motor, the average speed at any power frequency is obtained and its stability is analyzed by using the perturbation method. The feasibility of the approach is validated by using some numerical simulations. The results indicate there appears the jump phenomenon, namely the Sommerfeld effect in the beam-motor system. The effects of the unbalance mass and power of induction motor on Sommerfeld effect are analyzed.

Appendix 1

According to Eq. (10), the derivatives of w can be obtained as

$$\dot{w} = \sum\limits_{j = 1}^{N} {\psi_{j} (x)\dot{\xi }_{j} (t)}$$

(29)

$$\ddot{w} = \sum\limits_{j = 1}^{N} {\psi_{j} (x)\ddot{\xi }_{j} (t)}$$

(30)

$$w^{(4)} = \sum\limits_{j = 1}^{N} {\psi_{j}^{(4)} (x)\xi_{j} (t)}$$

(31)

Substituting Eqs. (A.1) -(A.3) into the first equation of Eq. (9), we can obtain

$$\rho A\sum\limits_{j = 1}^{N} {\psi_{j} (x)\ddot{\xi }_{j} (t)} { + }EI\sum\limits_{j = 1}^{N} {\psi_{j}^{(4)} (x)\xi_{j} (t)} { + } \left (m\sum\limits_{j = 1}^{N} {\psi_{j} (x)\ddot{\xi }_{j} (t)} + mr\ddot{\varphi }\cos \varphi - mr\dot{\varphi }^{2} \sin \varphi \right)\delta (x - x_{{1}} ) = 0$$

(32)

Multiplying both sides of Eq. (A.4) by $\psi_{1} (x)$ and integrating them from 0 to L with respect to x, we can obtain

$$\begin{gathered} \int_{0}^{L} {\psi_{1} (x)\rho A\sum\limits_{j = 1}^{N} {\psi_{j} (x)\ddot{\xi }_{j} (t)} } {\text{d}}x + \int_{0}^{L} {\psi_{1} (x)EI\sum\limits_{j = 1}^{N} {\psi_{j}^{(4)} (x)\xi_{j} (t)} } {\text{d}}x \hfill \\ + \int_{0}^{L} {\psi_{1} (x)\left( {m\sum\limits_{j = 1}^{N} {\psi_{j} (x)\ddot{\xi }_{j} (t)} + mr\ddot{\varphi }\cos \varphi - mr\dot{\varphi }^{2} \sin \varphi } \right)\delta (x - x_{{1}} )} {\text{d}}x \hfill \\ { = }\rho A\left( {\int_{0}^{L} {\psi_{1} (x)\psi_{1} (x){\text{d}}x\ddot{\xi }_{1} (t)} + \int_{0}^{L} {\psi_{1} (x)\psi_{2} (x){\text{d}}x\ddot{\xi }_{2} (t)} + \cdots \int_{0}^{L} {\psi_{1} (x)\psi_{N} (x){\text{d}}x\ddot{\xi }_{N} (t)} } \right) \hfill \\ + EI\left( {\int_{0}^{L} {\psi_{1} (x)\psi_{1}^{(4)} (x){\text{d}}x\xi_{1} (t)} + \int_{0}^{L} {\psi_{1} (x)\psi_{2}^{(4)} (x){\text{d}}x\xi_{2} (t)} + \cdots + \int_{0}^{L} {\psi_{1} (x)\psi_{N}^{(4)} (x){\text{d}}x\xi_{N} (t)} } \right) \hfill \\ + \int_{0}^{L} {\left( {(m\sum\limits_{j = 1}^{N} {\psi_{1} (x)\psi_{j} (x)\ddot{\xi }_{j} (t)} + mr\psi_{1} (x)\ddot{\varphi }\cos \varphi - mr\psi_{1} (x)\dot{\varphi }^{2} \sin \varphi )\delta (x - x_{1} )} \right){\text{d}}x} \hfill \\ = 0 \hfill \\ \end{gathered}$$

(33)

According to the orthogonality of the mode shape functions, we can obtain

$$\int_{0}^{L} {\psi _{j} (x)\psi _{k} (x){\text{d}}x} = \left\{ {\begin{array}{*{20}c} {\int_{0}^{L} {\psi _{j}^{2} (x){\text{d}}x,} } & {j = k} \\ {0,} & {j \ne k} \\ \end{array} } \right.$$

(34)

$$\int_{0}^{L} {\psi _{j} (x)\psi _{k} (x){\text{d}}x} = \left\{ {\begin{array}{*{20}c} {\int_{0}^{L} {\psi _{j}^{2} (x){\text{d}}x,} } & {j = k} \\ {0,} & {j \ne k} \\ \end{array} } \right.$$

(35)

Substituting Eqs. (A.6)–(A.7) into Eq. (A.5) and considering the characteristics of the Dirac delta function, we can obtain the first equations of Eq. (11) as

$$\begin{gathered} \rho A\left[ {\int_{0}^{L} {\psi_{1}^{2} (x){\text{d}}x} } \right]\ddot{\xi }_{1} (t) + EI\left[ {\int_{0}^{L} {\psi_{1}^{(4)} (x)\psi_{1} (x){\text{d}}x} } \right]\xi_{1} (t) + m\sum\limits_{j = 1}^{N} {\left( {\psi_{1} (x_{1} )\psi_{j} (x_{1} )\ddot{\xi }_{j} (t)} \right)} \hfill \\ = mr\psi_{1} (x_{1} )(\dot{\varphi }^{2} \sin \varphi - \ddot{\varphi }\cos \varphi ) \hfill \\ \end{gathered}$$

(36)

Similarly, multiplying both sides of Eq. (A.4) by $\psi_{2} (x)$, $\psi_{3} (x)$, …, $\psi_{{\text{N}}} (x)$, respectively, and integrating them from 0 to L with respect to x, we can obtain

$$\begin{gathered} \rho A\left[ {\int_{0}^{L} {\psi_{{2}}^{2} (x){\text{d}}x} } \right]\ddot{\xi }_{{2}} (t) + EI\left[ {\int_{0}^{L} {\psi_{{2}}^{(4)} (x)\psi_{{2}} (x){\text{d}}x} } \right]\xi_{{2}} (t) + m\sum\limits_{j = 1}^{N} {\left( {\psi_{{2}} (x_{1} )\psi_{j} (x_{1} )\ddot{\xi }_{j} (t)} \right)} \hfill \\ = mr\psi_{{2}} (x_{1} )(\dot{\varphi }^{2} \sin \varphi - \ddot{\varphi }\cos \varphi ) \hfill \\ \vdots \hfill \\ \rho A\left[ {\int_{0}^{L} {\psi_{N}^{2} (x){\text{d}}x} } \right]\ddot{\xi }_{N} (t) + EI\left[ {\int_{0}^{L} {\psi_{N}^{(4)} (x)\psi_{N} (x){\text{d}}x} } \right]\xi_{N} (t) + m\sum\limits_{j = 1}^{N} {\left( {\psi_{N} (x_{1} )\psi_{j} (x_{1} )\ddot{\xi }_{j} (t)} \right)} \hfill \\ = mr\psi_{N} (x_{1} )(\dot{\varphi }^{2} \sin \varphi - \ddot{\varphi }\cos \varphi ) \hfill \\ \end{gathered}$$

(37)

Finally, Eq. (11) is deduced.