1 Introduction

Fiber reinforced composites (FRC) have found extensive use in advanced applications of many engineering fields thanks to their high stiffness/weight ratio and high structural performances, which are often the result of specific design and manufacturing strategies that aim to optimize the response of these composite structures to specific working conditions. This determined an increasing interest in the study of new possible design solutions aimed to enhance the performances of laminate shell structures under prescribed regimes through the appropriate choice of materials and the determination of the optimal fiber orientation for each FRC layer [21, 47]. Experiments have shown that the optimal fiber orientation can increase structural stiffness, failure loading and buckling stress over the traditional quasi-isotropic fiber distribution without increasing the weight [27, 43, 52, 54], resulting particularly attractive for applications where weight is critical [31, 34]. It is well known that the composite stiffness is significantly higher in the direction of fibers, and therefore different strategies, such as sizing, shape and topology optimization (TO), have been presented in the literature to optimize the fiber orientation in a way to gain higher mechanical performance. The optimization process is usually gradient-driven. The so-called strain-based method [25, 40, 41], the stress-based method [14, 17, 25] and the energy-based method [35] represent in particular three principal approaches, corresponding to three different orthotropic material TO strategies, proposed to solve the optimal orientation problems. All these procedures consider the effect of the material orientation on the internal strains and stresses, by exploring the condition that returns the stiffest structure possible, which represents the one whose material symmetry planes allow to minimize the total elastic energy and thus minimize mean compliance. Moreover, all methods assume the invariance of strain and stress fields inside each design cell. The optimality criterion of the strain- and stress-based methods is formulated in the stress and strain form, respectively. On the other hand, the energy-based method requires that the dependency of strain and stress fields on the material orientation needs to be explored by involving an energy factor in the inclusion model.

Different gradient-driven procedures are represented by material selection methods, such as the optimal material selection technique [46] adapted by [47] in the so-called discrete material optimization for the design of laminated composite structures, shape function with penalization (SFP) [12] and bi-value coding parameterization (BCP) [24]. An improved curvilinear parameterization method [51, 54] exploits the Level Set method to optimize fiber paths by enforcing the continuity of fiber angles at the element interfaces [10]. In [56] the authors proposed a non-deterministic robust topology optimization of ply orientation for multiple fiber-reinforced plastic materials under loading uncertainties.

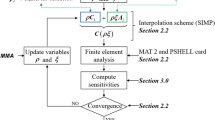
Other wide applications of TO strategies are based on the exploration of the optimal material distribution within a prescribed design domain, to maximize the stiffness of the structure by fixing the volume or the mass of the system [8, 19]. These methods employ particularly advantageous distribution methods, i.e. the homogenization approach [6] and the solid isotropic material with penalization method (SIMP) [5], in which the material properties are interpolated by using smooth functions of the material density, which serves as design variable.

The above discussed pioneering contributions have been recently extended to a wide range of design problems, including heat transfer [11, 49], acoustics [18], fluid flow [9], electromagnetics [13, 16], biomechanics [22, 28] and many other multi-physics applications [20, 30, 38, 50].

Different criteria have been developed to drive the optimization processes, extensively reviewed by Sigmund and Maute [45]. Some of them adopt continuous density design variables with gradient-based optimization algorithms [7, 57] or level set operating with boundaries instead of local densities [2, 53], while other evolutionary approaches instead provide the removal of the elements with lowest strain energy density [55]. The technique proposed by Stolpe [48] investigated, in topology optimization problems, the differences in selecting continuous and discrete variables.

By invoking the theory of homogenization for anisotropic materials, Esposito et al. [20] adapt the topology optimization to fiber-reinforced composites, by prescribing the materials of both matrix and reinforcement and also constraining within technological (process-induced) ranges the volume fraction of fibers, in this manner searching elastic solutions at minimal energy over all the possible families of curves that the continuous fibers can draw in any composite layer. Furthermore, Minutolo et al. [36] proposed to abandon the classical design and topology optimization approaches by introducing a “third way” for mechanically optimizing materials and structures, baptized as Galilei’s Optimization. Based on the concept of equalizing a proper stress measure at any point of the body and maximizing the global toughness of a given structure, the proposed strategy traded spatially homogeneous stress maps with spatially inhomogeneous resizing, with the toughening effect of killing stress peaks that are potentially onset of crack nucleation and fracture initiation.

In the present work, the optimal orientation of fibers in multilayer composite shells is pursued through design optimization method by assuming as objective function the strain energy of the structure and as design variables the orientation of the fibers in the plies.

Different examples of plane and curved shells, subjected to several load and boundary conditions, have been analyzed using custom-made routines developed in APDL (Ansys Parametric Design Language) in Ansys® Multiphysics environment (Ansys Inc., [1]. In particular, the case studies described in the following sections analyze the behavior of a rectangular panel subject to in-plane boundary conditions and torsional regime, and a square panel subject to out-of-plane loading, such as symmetric and asymmetric bending regime. In these examples, the quality of the optimization procedure has been evaluated through a specific indicator, i.e. the strain energy gain (SEG), which measures the perceptual variation of strain energy before and after the optimization. Besides, the response of three-dimensional structures is investigated. In particular, a layered cylindrical shell subjected to one point concentrated force is first studied. Lastly, the proposed procedure is applied to optimize the mechanical performances of carbon fiber reinforced polymer (CFRP) composite cylinders under high compression regimes, used as primary structural components for advanced applications in aerospace engineering. However, the generality of these results suggests their possible extension to many other applications in which the prevention of critical load conditions is crucial to ensure the functionality of the structure [23, 37, 39]. Here, design optimization leads to conceive a new possible optimal microstructural arrangement of the CFRP able to avoid critical stress conditions that are associated with the instability mechanisms observed in composites with standard fiber orientation.

The remainder of the paper is organized as follows. The following section presents a remark on the design optimization formulation, firstly describing the ruling equations in a general form and then detailing them for the optimal orientation in FR composites. Section 3 illustrates and discusses the results obtained from the application of the described design optimization procedure to plane and curved FRC panels subject to in-plane or out-of-plane loading conditions. Section 4 closes with a conclusion and outlook.

2 Optimal orientation in FR composites: remarks on problem formulation

The general problem of Design Optimization can be classically stated as:

$$ \begin{array}{*{20}l} {\text{minimize}} \hfill & {\Im \left( {\mathbf{t}} \right)} \hfill & {} \hfill & { ( {\text{objective function)}}} \hfill \\ {\text{subject to}} \hfill & {s_{j}^{L} \le s_{j} \left( {\mathbf{t}} \right) \le s_{j}^{U} } \hfill & {j = 1,..,m} \hfill & { ( {\text{state constraints)}}} \hfill \\ {} \hfill & {T_{i}^{L} \le t_{i} \le T_{i}^{U} } \hfill & {i = 1,..,n} \hfill & { ( {\text{design constraints)}}} \hfill \\ \end{array} $$
(1)

where \( \Im \left( {\mathbf{t}} \right) \) is the cost or objective function to be minimized. The \( n \) design variables \( t_{i} \) are the independent quantities, collected into the vector \( {\mathbf{t}} \), that varies to pursue the optimum design. The domain of the design variables is defined by the design constrains (1)3, while additional constraint equations can be stated as in (1)2 in terms of the state functions \( s_{j} \left( {\mathbf{t}} \right) \), which depend on the design variables. In the work by Esposito et al. [20], an analytical solution is provided for an orthotropic layer where the optimal orientation of the fibers has been determined by minimizing the mean compliance of the structure under either prescribed tractions or imposed displacements. By considering the total potential energy \( \varPhi \), the weak formulation of the linear elastostatic problem for a plane structure under the action of both body forces \( \varvec{f}\left( {\mathbf{x}} \right),\,{\mathbf{x}}\, \in \Omega \), surface tractions \( \varvec{t}\left( {\mathbf{x}} \right),\,\,{\mathbf{x}} \in \partial \Omega_{t} \) and prescribed displacements \( \varvec{u}^{0} \left( {\mathbf{x}} \right),\,{\mathbf{x}} \in \partial \Omega_{u} \), requires that

$$ \mathop {\hbox{min} }\limits_{\varvec{v}} \varPhi ,\quad \varPhi = \int\limits_{\Omega } {\frac{1}{2}C_{ijkl} } \frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{{\partial v_{k} }}{{\partial x_{l} }}d\Omega - \int\limits_{\Omega } {f_{i} v_{i} } d\Omega - \int\limits_{{\partial \Omega_{t} }} {t_{i} v_{i} d\varGamma } $$
(2)

where \( C_{ijkl} \) are the components of the 4th order stiffness tensor of the orthotropic material that here depends on the fiber orientation \( \theta \), while \( u_{i} \) and \( v_{i} \) are the displacement satisfying the first momentum balance and a kinematically admissible virtual displacement, respectively.

The stiffest structure guarantees the minimum amount of total internal elastic energy, or, equivalently, the minimum compliance. Therefore, the objective function to be minimized can be identified by the elastic energy:

$$ 2\varPi = \int\limits_{\Omega } {\sigma_{ij} \varepsilon_{ij} d\Omega } = \int\limits_{\Omega } {C_{ijkl} } \varepsilon_{ij} \varepsilon_{kl} d\Omega = \int\limits_{\Omega } {C_{ijkl} } \frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{{\partial u_{k} }}{{\partial x_{l} }}d\Omega $$
(3)

defined in terms of the Cauchy stresses \( \sigma_{ij} \) and of the strains \( \varepsilon_{ij} \) when the solution is found for any value of \( \theta \), here representing the design variable. The optimality condition is obtained by imposing stationarity of \( \varPi \left( \theta \right) \), that is:

$$ \frac{\partial \varPi }{\partial \theta } = \int\limits_{\Omega } {\left[ {\frac{{\partial C_{ijkl} }}{\partial \theta }\frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{{\partial u_{k} }}{{\partial x_{l} }} + 2C_{ijkl} \frac{\partial }{\partial \theta }\left(\frac{{\partial u_{i} }}{{\partial x_{j} }}\right)\frac{{\partial u_{k} }}{{\partial x_{l} }}} \right]d\Omega } = 0 $$
(4)

By virtue of the principle of virtual displacements, under the condition \( v_{k} = u_{k} \), the following relation through direct derivation with respect to \( \theta \):

$$ \int\limits_{\Omega } {\frac{{\partial C_{ijkl} }}{\partial \theta }\frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{{\partial u_{k} }}{{\partial x_{l} }}} d\Omega = - \int\limits_{\Omega } {C_{ijkl} \frac{\partial }{\partial \theta }\left(\frac{{\partial u_{i} }}{{\partial x_{j} }}\right)\frac{{\partial u_{k} }}{{\partial x_{l} }}d\Omega } , $$
(5)

can be finally obtained. Substituting Eq. (5) in Eq. (4) gives the optimality condition:

$$ \frac{\partial \varPi }{\partial \theta } = - \int\limits_{\Omega } {\frac{{\partial C_{ijkl} }}{\partial \theta }\frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{{\partial u_{k} }}{{\partial x_{l} }}} d\Omega = 0 $$
(6)

Finite element-based discretization of the domain \( \Omega \) in m elements implies that the optimality condition is rewritten as:

$$ \frac{\partial \varPi }{{\partial \theta_{e} }} = - \int\limits_{{\Omega^{e} }} {\frac{{\partial C_{ijkl} }}{{\partial \theta_{e} }}\frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{{\partial u_{k} }}{{\partial x_{l} }}} d\Omega^{e} = - \int\limits_{{\Omega^{e} }} {\frac{{\partial C_{ijkl} }}{{\partial \theta_{e} }}\varepsilon_{ij} \varepsilon_{kl} } d\Omega^{e} = 0 $$
(7)

where \( \Omega^{e} \) represents the measure of the \( e^{th} \) design cell. Assuming, for a sufficiently small element size, a uniform strain and stress fields within each homogeneous design cell, the optimality condition in terms of strains (prescribed displacements) reads as:

$$ \frac{{\partial \varPi_{\varepsilon } }}{{\partial \theta_{e} }} = - {\varvec{\upvarepsilon}}_{e}^{T} \frac{{\partial {\mathbf{C}}}}{{\partial \theta_{e} }}{\varvec{\upvarepsilon}}_{e} A_{e} = 0\quad e = 1,2, \ldots ,m $$
(8)

where \( {\varvec{\upvarepsilon}}_{e} \) represents the strain vector, \( {\mathbf{C}} \) is the rotated orthotropic stiffness matrix and \( A_{e} \) is the area of the \( e^{th} \) design cell, set as unity. Dually, the optimality condition in the stress form (prescribed tractions) is:

$$ \frac{{\partial \varPi_{\sigma } }}{{\partial \theta_{e} }} = - {\varvec{\upsigma}}_{e}^{T} \frac{{\partial {\mathbf{S}}}}{{\partial \theta_{e} }}{\varvec{\upsigma}}_{e} = 0\quad e = 1,2, \ldots ,m $$
(9)

where \( {\varvec{\upsigma}}_{e} \) is the stress vector and \( {\mathbf{S}} \) is the rotated orthotropic compliance matrix [32, 42].

For the design cell element, the orthotropic stress–strain equations, as well as the uncoupled constitutive equations for interlaminar shear stresses, can be written as [3, 4]:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{1} } \\ {\sigma_{2} } \\ {\sigma_{6} } \\ \end{array} } \right\}_{e} = \left[ {\begin{array}{*{20}c} {\frac{{E_{1} }}{{1 - \upsilon_{12} \upsilon_{21} }}} & {\frac{{\upsilon_{12} E_{2} }}{{1 - \upsilon_{12} \upsilon_{21} }}} & 0 \\ {\frac{{\upsilon_{12} E_{2} }}{{1 - \upsilon_{12} \upsilon_{21} }}} & {\frac{{E_{2} }}{{1 - \upsilon_{12} \upsilon_{21} }}} & 0 \\ 0 & 0 & {G_{12} } \\ \end{array} } \right]_{e} \left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ {\varepsilon_{6} } \\ \end{array} } \right\}_{e} \;{\text{and}}\;\left\{ {\begin{array}{*{20}c} {\sigma_{4} } \\ {\sigma_{5} } \\ \end{array} } \right\}_{e} = \left[ {\begin{array}{*{20}c} {G_{23} } & 0 \\ 0 & {G_{13} } \\ \end{array} } \right]_{e} \left\{ {\begin{array}{*{20}c} {\varepsilon_{4} } \\ {\varepsilon_{5} } \\ \end{array} } \right\}_{e} $$
(10)

where subscripts 1 and 2 denote the fiber and the orthogonal-to-the-fiber directions, respectively, \( \left( {E_{1} ,E_{2} } \right) \) are the orthotropic Young moduli, \( \left( {G_{12} ,G_{13} ,G_{23} } \right) \) are the shear moduli and \( \upsilon_{12} \) is the Poisson’s ratio in the plane referred to the subscripts. The inverse relationships is:

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ {\varepsilon_{6} } \\ \end{array} } \right\}_{e} = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{1} }}} & { - \frac{{\upsilon_{12} }}{{E_{1} }}} & 0 \\ { - \frac{{\upsilon_{12} }}{{E_{1} }}} & {\frac{1}{{E_{2} }}} & 0 \\ 0 & 0 & {\frac{1}{{G_{12} }}} \\ \end{array} } \right]_{e} \left\{ {\begin{array}{*{20}c} {\sigma_{1} } \\ {\sigma_{2} } \\ {\sigma_{6} } \\ \end{array} } \right\}_{e} \;{\text{and}}\;\left\{ {\begin{array}{*{20}c} {\varepsilon_{4} } \\ {\varepsilon_{5} } \\ \end{array} } \right\}_{e} = \left[ {\begin{array}{*{20}c} {\frac{1}{{G_{23} }}} & 0 \\ 0 & {\frac{1}{{G_{13} }}} \\ \end{array} } \right]_{e} \left\{ {\begin{array}{*{20}c} {\sigma_{4} } \\ {\sigma_{5} } \\ \end{array} } \right\}_{e} $$
(11)

By introducing the rotation matrix \( {\mathbf{T}} \):

$$ {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & {\sin^{2} \theta } & {2\cos \theta \sin \theta } \\ {\sin^{2} \theta } & {\cos^{2} \theta } & { - 2\cos \theta \sin \theta } \\ { - \cos \theta \sin \theta } & {\cos \theta \sin \theta } & {\cos^{2} \theta - \sin^{2} \theta } \\ \end{array} } \right] $$
(12)

the stress and strain vectors, as well as the compliance and stiffness matrices, can be transformed from the material coordinate system \( \left( {1,2,3} \right) \) of the fibers to the global coordinate system \( \left( {x,y,z} \right) \)—for which an over-lined notation is adopted in what follows—so that:

$$ \begin{aligned} \overline{{\mathbf{C}}} & = {\mathbf{T}}^{ - 1} {\mathbf{CT}}^{ - T} \\ \overline{{\mathbf{S}}} & = {\mathbf{T}}^{ - 1} {\mathbf{ST}}^{ - T} \\ \end{aligned} $$
(13)

Specifically, the elastic moduli \( \overline{E}_{ij} \) for the orthotropic design cell element are [29]:

$$ \begin{aligned} \overline{E}_{11} & = E_{11} \cos^{4} \theta + 2(E_{12} + 2E_{66} )\sin^{2} \theta \cos^{2} \theta + E_{22} \sin^{4} \theta \\ \overline{E}_{12} & = (E_{11} + E_{22} - 4E_{66} )\sin^{2} \theta \cos^{2} \theta + E_{12} (\sin^{4} \theta + \cos^{4} \theta ) \\ \overline{E}_{22} & = E_{11} \sin^{4} \theta + 2(E_{12} + 2E_{66} )\sin^{2} \theta \cos^{2} \theta + E_{22} \cos^{4} \theta \\ \overline{E}_{16} & = (E_{11} - E_{12} - 2E_{66} )\sin \theta \cos^{3} \theta + (E_{12} - E_{22} + 2E_{66} )\sin^{3} \theta \cos \theta \\ \overline{E}_{26} & = (E_{11} - E_{12} - 2E_{66} )\sin^{3} \theta \cos \theta + (E_{12} - E_{22} + 2E_{66} )\sin \theta \cos^{3} \theta \\ \overline{E}_{66} & = (E_{11} + E_{22} - 2E_{12} - 2E_{66} )\sin^{2} \theta \cos^{2} \theta + E_{66} (\sin^{4} \theta + \cos^{4} \theta ) \\ \bar{E}_{44} & = E_{44} \cos^{2} \theta + E_{55} \sin^{2} \theta \\ \bar{E}_{55} & = E_{44} \sin^{2} \theta + E_{55} \cos^{2} \theta \\ \bar{E}_{45} & = (E_{55} - E_{44} )\sin \theta \cos \theta \\ \end{aligned} $$
(14)

where:

$$ E_{11} = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{12} }},\,\,E_{12} = \frac{{\nu_{12} E_{1} }}{{1 - \nu_{12} \nu_{12} }},\,\,E_{22} = \frac{{E_{2} }}{{1 - \nu_{12} \nu_{12} }},\,\,E_{66} = G_{12} ,\,\,E_{44} = G_{23} ,\,\,E_{55} = G_{13} . $$
(15)

Similarly, the components \( \overline{S}_{ij} \) of the rotated compliance matrix can be obtained as:

$$ \begin{aligned} \overline{S}_{11} & = S_{11} \cos^{4} \theta + 2(S_{12} + S_{66} )\sin^{2} \theta \cos^{2} \theta + S_{22} \sin^{4} \theta \\ \overline{S}_{12} & = (S_{11} + S_{22} - S_{66} )\sin^{2} \theta \cos^{2} \theta + S_{12} (\sin^{4} \theta + \cos^{4} \theta ) \\ \overline{S}_{22} & = S_{11} \sin^{4} \theta + (2S_{12} + 2S_{66} )\sin^{2} \theta \cos^{2} \theta + S_{22} \cos^{4} \theta \\ \overline{S}_{16} & = (2S_{11} - 2S_{12} - S_{66} )\sin \theta \cos^{3} \theta - (2S_{22} - 2S_{12} - S_{66} )\sin^{3} \theta \cos \theta \\ \overline{S}_{26} & = (2S_{11} - 2S_{12} - S_{66} )\sin^{3} \theta \cos \theta - (2S_{22} - 2S_{12} - S_{66} )\sin \theta \cos^{3} \theta \\ \overline{S}_{66} & = 2(2S_{11} + 2S_{22} - 4S_{12} - S_{66} )\sin^{2} \theta \cos^{2} \theta + S_{66} (\sin^{4} \theta + \cos^{4} \theta ) \\ \bar{S}_{44} & = S_{44} \cos^{2} \theta + S_{55} \sin^{2} \theta \\ \bar{S}_{55} & = S_{44} \sin^{2} \theta + S_{55} \cos^{2} \theta \\ \bar{S}_{66} & = \left( {S_{55} - S_{44} } \right)\sin \theta \cos \theta \\ \end{aligned} $$
(16)

where:

$$ S_{11} = \frac{1}{{E_{1} }},\,\,S_{12} = \frac{{ - \nu_{12} }}{{E_{1} }},\,\,S_{22} = \frac{1}{{E_{2} }},\,\,S_{66} = \frac{1}{{G_{12} }},\,\,S_{44} = \frac{1}{{G_{23} }}\,\,{\text{and}}\,\,S_{55} = \frac{1}{{G_{13} }} $$
(17)

Algebraic manipulations allow rewriting the optimality conditions (8) and (9) respectively as:

$$ \begin{aligned} \frac{{\partial \varPi_{\varepsilon } }}{{\partial \theta_{e} }} & = \frac{1}{2}[(E_{11} - E_{22} )\varepsilon_{6} (\varepsilon_{1} + \varepsilon_{2} ) + 2( - E_{44} + E_{55} )\varepsilon_{5} \varepsilon_{4} ]\cos 2\theta_{e} \\ & \quad + \frac{1}{2}(E_{11} - 2E_{12} + E_{22} - 4E_{66} )\varepsilon_{6} (\varepsilon_{1} - \varepsilon_{2} )\cos 4\theta_{e} \\ & \quad - \frac{1}{2}[(E_{11} - E_{22} )(\varepsilon_{1} - \varepsilon_{2} )(\varepsilon_{1} + \varepsilon_{2} ) - (E_{44} - E_{55} )(\varepsilon_{6} - \varepsilon_{5} )(\varepsilon_{6} + \varepsilon_{5} )]\sin 2\theta_{e} \\ & \quad - \frac{1}{4}(E_{11} - 2E_{12} + E_{22} - 4E_{66} )(\varepsilon_{1} - \varepsilon_{6} - \varepsilon_{2} )(\varepsilon_{1} + \varepsilon_{6} - \varepsilon_{2} )\sin 4\theta_{e} \\ & = 0 \\ \end{aligned} $$
(18)

and:

$$ \begin{aligned} \frac{{\partial \varPi_{\sigma } }}{{\partial \theta_{e} }} & = [(S_{11} - S_{22} )\sigma_{6} (\sigma_{1} + \sigma_{2} ) + ( - S_{44} + S_{55} )\sigma_{5} \sigma_{4} ]\cos 2\theta_{e} \\ & \quad + (S_{11} - 2S_{12} + S_{22} - S_{66} )\sigma_{6} (\sigma_{1} - \sigma_{2} )\cos 4\theta_{e} \\ & \quad - \frac{1}{2}[(S_{11} - S_{22} )(\sigma_{1} - \sigma_{2} )(\sigma_{1} + \sigma_{2} ) - (S_{44} - S_{55} )(\sigma_{5} - \sigma_{4} )(\sigma_{5} + \sigma_{4} )]\sin 2\theta_{e} \\ & \quad - \frac{1}{4}(S_{11} - 2S_{12} + S_{22} - S_{66} )[ - 4\sigma_{6}^{2} + (\sigma_{1} - \sigma_{2} )^{2} ]\sin 4\theta_{e} \\ & = 0 \\ \end{aligned} $$
(19)

where both strain and stress components refer to values at the centroid of the design cell. Both Eqs. (18) and (19) are of the type:

$$ a\cos 2\theta_{e} + b\cos 4\theta_{e} + c\cos 2\theta_{e} + d\sin 4\theta_{e} = 0 $$
(20)

where the coefficients \( a,b,c \) and \( d \) are:

$$ \begin{aligned} a & = \frac{1}{2}[(E_{11} - E_{22} )\varepsilon_{6} (\varepsilon_{1} + \varepsilon_{2} ) + 2( - E_{44} + E_{55} )\varepsilon_{5} \varepsilon_{4} ] \\ b & = \frac{1}{2}(E_{11} - 2E_{12} + E_{22} - 4E_{66} )\varepsilon_{6} (\varepsilon_{1} - \varepsilon_{2} ) \\ c & = \frac{1}{2}[ - (E_{11} - E_{22} )(\varepsilon_{1} - \varepsilon_{2} )(\varepsilon_{1} + \varepsilon_{2} ) + (E_{44} - E_{55} )(\varepsilon_{5} - \varepsilon_{6} )(\varepsilon_{5} + \varepsilon_{6} )] \\ d & = - \frac{1}{4}(E_{11} - 2E_{12} + E_{22} - 4E_{66} )(\varepsilon_{1} - \varepsilon_{6} - \varepsilon_{2} )(\varepsilon_{1} + \varepsilon_{6} - \varepsilon_{2} ) \\ \end{aligned} $$
(21)

in the strain formulation and:

$$ \begin{aligned} a & = (S_{11} - S_{22} )\sigma_{6} (\sigma_{1} + \sigma_{2} ) + ( - S_{44} + S_{55} )\sigma_{5} \sigma_{4} \\ b & = (S_{11} - 2S_{12} + S_{22} - S_{66} )\sigma_{6} (\sigma_{1} - \sigma_{2} ) \\ c & = \frac{1}{2}[ - (S_{11} - S_{22} )(\sigma_{1} - \sigma_{2} )(\sigma_{1} + \sigma_{2} ) + (S_{44} - S_{55} )(\sigma_{5} - \sigma_{4} )(\sigma_{5} + \sigma_{4} )] \\ d & = - \frac{1}{4}(S_{11} - 2S_{12} + S_{22} - S_{66} )[ - 4\sigma_{6}^{2} + (\sigma_{1} - \sigma_{2} )^{2} ] \\ \end{aligned} $$
(22)

for prescribed tractions. It is worth noticing that the coefficients listed in Eqs. (21) and (22) depend both on stiffness and compliance moduli and on the stress and strain levels, including interlaminar shear stresses and strains. By setting \( x = 2\theta_{e} \) and by substituting \( t = tg\frac{x}{2} \), Eq. (20) can be finally expressed as:

$$ c_{1} t^{4} + c_{2} t^{3} + c_{3} t^{2} + c_{4} t + c_{5} = 0 $$
(23)

where \( c_{1} = b - a \), \( c_{2} = 2c - 4d \), \( c_{3} = - 6b \), \( c_{4} = 2c + 4d \) and \( c_{5} = a + b \). The fourth-order polynomial Eq. (23) admits analytical solutions \( t_{i} \) by virtue of the Ferrari–Cardano formula, so that the fiber angles in the design element cell are finally obtained as:

$$ \theta_{{e_{i} }} = \text{arctg} \left( {t_{i} } \right) $$
(24)

Among the real solutions, the optimal fiber orientation \( \theta_{OPT} \) provides the minimum value of the strain energy. To avoid undesired computational costs related to the implementation of numerical procedures based on theoretical variational approaches including constraints (for instance Lagrange multipliers and inequalities), the optimization algorithm is designed to control, step-by-step, that the von Mises stress does not overcome a prescribed yield value. Nevertheless, a selected criterion for redistributing the exceeding stresses at the subsequent step of the analysis, in case of critical stress occurrence, was a priori established. As a consequence, in case of over-load at a given optimization step, the algorithm was written to perform two parallel analyses. A first one is launched by starting from a trial configuration by assigning ply-by-ply sets of fibers orientation characterized by angles placed at intermediate positions between the ones obtained at the previous step (when no critical stresses occurred) and the ones corresponding to the step at which inadmissible stresses were somewhere found.

3 Results and discussion

3.1 Optimization of plane and curved shells

Design Optimization procedures have been applied to optimize the mechanical response of different composite structures. In order to catch the optimal composite stacking sequences, a FE design optimization algorithm has been developed with the aid of Ansys solver. The algorithm uses the subproblem approximation method (an advanced zero-order method) that can be efficiently applied to many engineering problems [33]. The algorithm considers the reinforcement orientations of laminae as design variables and the Strain Energy as objective function to be minimized. This section illustrates and discusses the results obtained from the application of the described design optimization procedure to plane and curved FRC panels subject to in-plane or out-of-plane loading conditions. More in detail, the addressed examples concern composite materials made of two symmetrically positioned components, each comprising four adjacent orthotropic layers containing fibers arranged to form angles of 0°, 90°, 45° and − 45°, respectively, to generate a symmetrical stacking sequence, from here on identified as \( \left( {0^\circ ,90^\circ ,45^\circ , - 45^\circ } \right)_{s} \). The material properties considered in the FEM simulations for the single layer are relative to the ThermoPlastic Composite APC-2/AS4. Therefore, with reference to a local (i.e. layer-specific) orthogonal coordinate system \( \left( {x_{1} ,x_{2} ,x_{3} } \right) \) having the \( x_{1} \)-axis aligned along the fibers direction, the nine elastic constants for each layer are the following:

$$ \begin{aligned} & \left( {E_{1} ,E_{2} ,E_{3} } \right) = \left( {138,10,10} \right)\;{\text{MPa}}, \\ & \left( {G_{12} ,G_{13} ,G_{23} } \right) = \left( {5.65,5.65,3.7} \right)\;{\text{MPa}} \\ & \left( {\upsilon_{12} ,\upsilon_{13} ,\upsilon_{23} } \right) = \left( {0.28,0.28,0.33} \right) \\ \end{aligned} $$

Based on the adopted stacking sequence, the overall behavior of the multi-ply deriving from the assembly of the eight single layers can be assumed as quasi-isotropic. For those composite systems, optimized distributions of the fibers orientations in each layer, leading to a strain energy minimization for prescribed geometries and boundary conditions, have been determined through a custom-made procedure developed by APDL (Ansys Parametric Design Language) and implemented in Ansys® Multiphysics environment (Ansys Inc., [1].

The effects of the optimization process are described in the following paragraphs, and compared with the original case of symmetrical sequence. In particular, to measure the advantage obtained by adopting an optimally configured structure in place of the original quasi-isotropic one, the strain energy gain (SEG) parameter, defined as the strain energy percentage difference for the structure before and after the optimization:

$$ SEG = \frac{{SE_{PRE - OPT} - SE_{OPT} }}{{SE_{OPT} }} $$
(25)

is calculated for each investigated example.

3.1.1 Rectangular panel under in-plane loading conditions

The first example concerns the optimization of a rectangular panel (length = 500 mm, height = 200 mm, thickness = 2.24 mm) laying in the classical cantilever-like configuration pictorially represented in Fig. 1b, with one of the shorter sides fully constrained and the opposite subject to a vertical load \( F = 1000\,{\text{N}} \). The FE model of the structure has been achieved by hexahedral multi-layer solid-shell element type, with eight nodes having three degrees of freedom for each node and linear shape functions. The starting, symmetrical, sequence of layers \( \left( {0^\circ ,90^\circ ,45^\circ , - 45^\circ } \right)_{s} \), generating a quasi-isotropic structure, and the optimized sequence \( \left( {46^\circ ,0^\circ ,0^\circ ,0^\circ } \right)_{s} \) are respectively illustrated in Fig. 1a, c for one half of the structure, the other being symmetrical. It is worth noticing that the proposed approach allows to choose any real value for the orientation angles of the reinforcing fibers, although the angle values resulting from the numerical procedure and reported in the next figures, are approximated to the closest integer. As a matter of fact, as not hardly predictable, the resulting optimal orientations of the fibers approximately follow the principal directions of stress and strain in the bending cantilever.

Fig. 1
figure 1

a The symmetrical stacking sequence generating the quasi-isotropic rectangular FRC panel; b Sketch of the geometry and boundary conditions considered for the rectangular FRC panel; c Fibers’ orientations for (one half of) the optimized configuration of the structure; Contour plots of the d–e vertical displacement and f–g Von Mises stress through the first layer of the panel in the quasi-isotropic and optimized case

Full size image

Figure 1d–g shows the vertical displacements and the von Mises stresses arising within the panel in both the original and the optimized configuration. In this regard, it is worth noting that, in the optimized case, the magnitude of the vertical displacement is significantly reduced with respect to the quasi-isotropic configuration and the von Mises stress results to be homogeneous almost everywhere, with the higher values localized around the force application point.

The advantage—in terms of strain energy reduction—deriving from the optimization process for the considered application is expressed by a SEG equal to 29.77%.

3.1.2 Square panel bending under normal force

The present paragraph focuses on the design optimization of the square panel (side length = 500 mm, thickness = 2.24 mm) shown in Fig. 2b. The panel is constrained on two of its edges and subjected to a force F = 10 N orthogonal to the panel’s plane. The analyses are performed by employing the same FE discretization adopted in the previous application.

Fig. 2
figure 2

a The symmetrical stacking sequence generating the quasi-isotropic square FRC panel; b Sketch of the geometry and boundary conditions considered for the square FRC panel; c Fibers’ orientations for (one half of) the optimized configuration of the structure; Contour plots of the d–e vertical displacement and f–g Von Mises stress through the first layer of the panel in the quasi-isotropic and optimized case

Full size image

The starting and optimized fibers orientations maps are shown in Fig. 2a, c, respectively. In particular, the latter shows that, resembling the previous outcomes, the optimal orientations of the fibers result to nearly coincide with the principal directions of stress and strain in the bending plate. In addition, the vertical displacements, reported in Fig. 2e, appear reduced in magnitude in the optimized condition with respect to the quasi-isotropic structure (Fig. 2d) and the von Mises stresses exhibit a distribution mainly oriented toward the external load (Fig. 2f, g). The advantage deriving from the optimization process for this case turns out to be higher than the previous one, with a resulting SEG of about 48.80%.

3.1.3 Square panel under pure bending regime

The optimal configuration of the same composite square structure considered above is here addressed for boundary conditions reproducing the pure bending regime illustrated in Fig. 3b. In this case, the four corners are fully constrained and all the edges of the structure are loaded via external bending moments \( M = 2.24\;{\text{Nmm}} \).

Fig. 3
figure 3

a The symmetrical stacking sequence generating the quasi-isotropic square FRC panel; b Sketch of the geometry and boundary conditions considered for the square FRC panel under pure bending; c Fibers’ orientations for (one half of) the optimized configuration of the structure; Contour plots of the d–e vertical displacement and f–g Von Mises stress through the first layer of the panel in the quasi-isotropic and optimized case

Full size image

The main outcomes of the optimization procedure related to this application are shown in Fig. 3, in comparison with the mechanical response provided by the non-optimized configuration.

It is worth underling that the present case is the one attaining the lowest advantage from the optimization process in terms of strain energy reduction, with an estimated SEG value to be approximately 12.25%.

3.1.4 Rectangular panel under torsion

The design optimization is here performed on a rectangular panel (length = 500 mm, height = 200 mm, thickness = 2.24 mm) fully constrained at the center of both its shorter edges and subject, through the imposition of linearly variable vertical forces, to a torsion moment M = 5 Nmm and vanishing resultant force. The described boundary conditions are sketched in Fig. 4b, while the fibers distributions for the original and optimized systems are shown, in the order, in Fig. 4a, c. It is possible to observe that, even in this case, optimal orientations for the fibers essentially coincide with the principal stress directions. Additionally, the results achieved in terms of out-of-plane displacements and von Mises stress maps in the case of isotropic composite (Fig. 4d, f) and optimized structure (Fig. 4e, g), still show a lower displacements magnitude and a smoother and widely spread distribution of von Mises stress in the optimized case. Under these conditions, the SEG results to be about 34.40%.

Fig. 4
figure 4

a The symmetrical stacking sequence generating the quasi-isotropic rectangular FRC panel; b Sketch of the geometry and boundary conditions considered for the rectangular FRC panel under torsion; c Fibers’ orientations for (one half of) the optimized configuration of the structure; Contour plots of the d–e vertical displacement and f–g Von Mises stress through the first layer of the panel in the quasi-isotropic and optimized case

Full size image

3.1.5 Cylindrical vault under prescribed point-force

The previously described design optimization examples deal with the optimization of the fibers’ distribution in multi-ply composite plates, aimed to minimize the strain energy of the system under prescribed loading conditions. In all the analyzed cases, the optimized structures show preferential alignment of the fibers very close to the principal stress and strain directions and, as highlighted by the lower displacements magnitude, they exhibit a stiffer response in comparison with the non-optimized, quasi-isotropic, composites.

An advanced application of the same strategy regards the characterization of optimal fibers maps in three-dimensional FRC shells discussed in the following.

By way of example, a parametric analysis of the cylindrical vault illustrated in Fig. 5, fully constrained at its edges and loaded by a vertical point-force F = 10 N at a prescribed position, has been performed through the implementation of a FE model employing a classical laminated shell element with four nodes and six degrees of freedom for each node. In this way, different results have been provided by the optimization algorithm depending on the span-to-rise ratio of the vault—namely by varying the rise (h) as a function of the span (d)—in terms of optimal angles’ sequences and corresponding SEG values, as reported in Table 1.

Fig. 5
figure 5

a Sketch of the geometry and boundary conditions considered for the studied FRC cylindrical vault under external point-load; b Schematization of the structure’s cross section for different rise-to-span (i.e. h-to-d) ratios and fixed (not symmetrical) point of application of the external force

Full size image
Table 1 Stacking sequence and strain energy gain resulting by the optimization procedure for a FRC cylindrical vault under external point-force
Full size table

The plots of the vertical displacements and the von Mises stresses induced by the application of the vertical point-load on both the quasi-isotropic and optimized structures, are reported in Fig. 6. Therein, it is worth highlighting that the same maximum value of stress is reached, with a different distribution, in the original and optimized configurations of the system. In particular, in the quasi-isotropic structure, high stress values are localized around the point of application of the force, resulting distributed with low magnitudes over wider areas in the corresponding optimized solutions.

Fig. 6
figure 6

Contour plots of the displacements (on the left column) and Von Mises stresses (on the right column) obtained for the original and optimized cylindrical vaults under external point-load, for different rise-to-span ratios (from top to bottom)

Full size image

Figure 6 clearly shows that the stiffness optimization process is generally accompanied by an improvement of the average stress level everywhere: in fact, when this improvement does not correspond to a reduction of the stress magnitude (as it happens for statically determinate problems, for example), the same stress level leads however to have a greater safety factors with respect to the not-optimized case, because the optimized materials is solicited along directions of maximum stiffness that are often associated to maximum strength as well.

3.2 Carbon fiber-reinforced polymer (CFRP) structures

Experimental studies on the mechanical performances of combustion chambers made up with CFRP multi-layer cylinders have been made, in order to highlight the effects that specific fiber orientations and the scaling of the mechanical properties of the cylindrical laminae had on the onset of damages and their propagation in both undamaged and repaired structures [26]. In particular, the two CFRP cylindrical structures with diameter and height are about 377 mm were manufactured by using a high strength carbon fiber epoxy pre-preg tape by building up a quasi-isotropic layup of 24 plies \( \left( {\left[ {0_{2} ; \pm 45;90_{2} } \right]_{2s} } \right) \) through the Filament Winding technology. The constitutive properties of each lamina (with thickness of about \( 0.195\;{\text{mm}} \)) are collected in Table 2. Two identical specimens were realized with the same procedure and, successively, one of them was damaged and repaired with a specific repair resin.

Table 2 Constitutive properties of the CFRP laminae
Full size table

The mechanical response of both undamaged and repaired cylinders have been tested under compressive load by means of a servoidraulic machine ITALSIGMA—with a capability of 3000 kN in compression and a maximum crosshead displacement equal to 75 mm—with the aim to evaluate the stiffness of cylinders, their elastic strength and the critical load at which failure occurs. The experimental setup is shown in detail in Fig. 7.

Fig. 7
figure 7

Experimental setup. a Placement of the strain gauges 1 V, 2 V, 3 V, 4 V—(four of them in axial direction, spaced of 45° each other along the cylindrical surface; and others in tangential direction, spaced out of 180° each other). b, c Location of the LVDT sensors A, B, C, D (on the external surface of the specimens) and N, O, B60 (fixed to the rigid plates). d Complete setup

Full size image

The compression tests reported in Fig. 8 mainly evidenced the occurrence of structural damages close to the potting zone, caused by the compressive over-load associated with delamination phenomena and followed by unstable buckling behavior due to the high stresses in the constrained zone. These localized damages under increasing load slowly propagated, until the entire structure collapsed. Additional non-axisymmetrical damages were also observed at the ends of not-repaired cylinders, suggesting that potting imperfections could cause an incorrect load transfer along the thickness of cylinder, by inducing a premature failure of the system because of localized bulging effects.

Fig. 8
figure 8

Highlights from compression tests on CFRP skirts showing the specific damaging mechanisms due to compression load

Full size image

In the light of such experimental evidence, an optimized design of the CFRP microstructure able to improve the composite mechanical strength would help to better resist to the high-pressure levels occurring in the combustion chamber during the flight, and an optimized stiffness allow to reduce the stresses responsible for local damages and bulging effects detected. Both these aspects are in fact diriment to prevent—or at least contain—the undesired failure mechanisms in CFRP above described, by preserving its structural integrity. To this aim, the proposed design optimization procedure has been applied to obtain the optimal fiber orientation in the composite laminae of the CFRP cylinder, in order to minimize the von Mises stress in the critical distal region and to preserve the composite longitudinal stiffness within prescribed limits (±10%). To reduce the computational efforts, the geometry of the cylinder has been meshed with 15,544 elements with bending and membrane regimes and 15,776 nodes with six degrees of freedom. The microstructural stacking sequence across the thickness has been modeled through multilayered shell features allowing large savings in terms of computational efforts. Anisotropic constitutive properties of the single lamina reproduced the manufactured ones by modelling an initially 24-ply structure with the symmetrical quasi-isotropic stacking sequence \( \left[ {\left( {0^\circ_{2} / - 45^\circ /45^\circ /90^\circ_{2} } \right)_{2} } \right]_{S} \) shown in Fig. 9. Herein, the applied boundary conditions are also illustrated, which consist in both an imposed axial displacements and vanishing rotations, in order to induce a compressive state inside the cylinder and reproduce the constraining effects of the potting, respectively.

Fig. 9
figure 9

FE model of the composite scaled cylinder, with the considered boundary conditions. The stacking sequence of composite laminae in pre-optimized structure is also illustrated

Full size image

A first FE analysis has been performed to evaluate the elastic stiffness of the undamaged pre-optimized composites. In order to replicate the experimental conditions an axial displacement \( \left( {\Delta U_{z} = - 0.85\;{\text{mm}}} \right) \) has been imposed at the cylinder bases, obtaining a maximum value of the reaction force \( F_{MAX}^{num} \simeq 920\;{\text{kN}} \), very close to the measured value achieved during compression tests (\( F_{\hbox{max} } = 913\;{\text{kN}} \), see Fig. 10). By considering both the initial height \( \left( {L_{0} } \right) \) and the initial cross-section \( \left( {A_{0} } \right) \) of the composite structure, it is then possible to estimate the homogenized Young modulus of the composite [15] as:

Fig. 10
figure 10

Comparison of experimental and FE results in terms of load–strain curves

Full size image
$$ E_{Z}^{num} = \frac{{\sigma_{z} }}{{\varepsilon_{z} }} = \frac{{F_{Z}^{num} \,L_{0} }}{{A_{0} \,\Delta U_{Z} }} \simeq 66,5\;{\text{GPa}} $$
(26)

A successive eigenvalue analysis allowed to estimate numerically the critical compressive loads at which the wall of composite cylinder undergoes buckling instability exhibiting specific deformation modes. In particular, by considering a symmetrical prescribed load in which the bases are moved in parallel, the first four buckling modes corresponding to load multipliers \( \lambda_{1} = 4.3221,\;\lambda_{2} = 4.3221,\;\lambda_{3} = 4.4684,\;\lambda_{4} = 4.4684 \) are reported in Fig. 11. Due to the higher values of the associated critical loads, these deformation modes did not occur during experiments, and a moderate asymmetry of the load at the top base of the CFRP cylinder was considered in order to simulate an undesired partial detachment of the potting phase around the composites. This imperfection was numerically implemented by prescribing the linear variation of the applied nodal displacement by means:

$$ \Delta U_{Z}^{ASYM} = \Delta U_{Z} + \left( {\frac{{R + \bar{x}_{i} }}{2R}} \right)\alpha \;\Delta U_{Z} $$
(27)

in which \( \bar{x}_{i} ,{\text{ R and }}\alpha \, \) are the position of the i-th node, the radius of the cylindrical structure and the slope assigned as imperfection, respectively. In this case, the value of the critical loads decrease to about \( F_{MAX}^{ASYM} \simeq 1050\;{\text{kN}} \) with multipliers \( \lambda_{1} = 1.9796,\;\lambda_{2} = 1.9797,\;\lambda_{3} = 2.1346,\;\lambda_{4} = 2.1347 \). The associated deformation modes, reported in Fig. 12, qualitatively reproduce the localized failure mechanisms experimentally observed, by confirming the hypothesis that imperfections of the potting phase could induce premature failure of the undamaged scaled skirt.

Fig. 11
figure 11

First four deformation modes and associated critical loads resulting from the eigenbuckling FE analysis under symmetric (top) and asymmetric (bottom) load conditions

Full size image
Fig. 12
figure 12

Results of the design optimization in the CFRP cylinder. a radial displacements; b circumferential stress; c von Mises stress and d longitudinal stress

Full size image

Starting from this these results, design optimization was performed on the quasi-isotropic structure with stacking sequence \( \left[ {\left( {0^\circ_{2} / - 45^\circ /45^\circ /90^\circ_{2} } \right)_{2} } \right]_{S} \) in order to find a new possible microstructure of the laminae able to prevent the undesired damaging phenomena experimentally observed and investigated by means of the above described in silico simulations. By requiring the minimization of von Mises stress in the potting region and by choosing a constant axial stiffness as design constraint, the implemented design optimization routine highlights the possibility to determinate an optimal fiber placement within the CFRP plies. In particular, the stacking sequence in the post-optimized situation showed angles equal to \( \left[ {\left( {90^\circ_{2} /88^\circ /33^\circ /0^\circ_{2} } \right)_{2} } \right]_{S} \). This particular arrangement, although it does not change the quasi-isotropic global behavior of the structure, reduce drastically the von Mises stress in the potting region, where buckling mechanisms occur, without compromising the axial response of the cylinder. Results in Fig. 12 highlight as the optimized composite structure exhibits improved stress conditions with a volume-averaged von Mises stress in the post-optimized case more of one order of magnitude lower than the one in the pre-optimized condition. Furthermore, lateral expansion appears to be moderated by approximately 50% (see Fig. 12a–c), whereas the specific fiber angles determined induce a sensible increase of the composite axial stiffness in the post-optimized case with respect to the initial disposition, also recalling the nonlinear scaling of composite moduli with the fiber directions. In addition, the reduced longitudinal stress peaks in the potting zones of the post-optimized CFRP suggest a minor risk of localized bulging phenomena (Fig. 12d).

4 Conclusions

In the present work, the application of a classical design optimization technique to fiber-reinforced composites was discussed. In particular, it was aimed to determine the optimal sequences of fibers orientations within plane and curved multilayered shells, to minimize the strain energy of the system under prescribed boundary conditions. The implementation of the optimization strategy and all the simulations were performed in Ansys® Multiphysics environment (Ansys Inc., Canonsburg, PA, USA) by developing a custom-made procedure based on the Ansys Parametric Design Language. The effectiveness of the optimization was evaluated in relation to the mechanical performances offered by quasi-isotropic composite structures consisting in sequences of layers with symmetrically oriented fibers. Specifically, a Strain Energy Gain parameter was defined as the measure of the advantage deriving from the employment of optimally arranged structures, thus obtaining more or less significant results depending on the specific geometry and loading conditions of the systems. As a matter of fact, in all the analyzed cases, the optimization process provided anisotropic fiber-reinforced composites exhibiting reduced displacements magnitude and, as a consequence, an overall stiffer response with respect to the quasi-isotropic configurations, the importance of this effect is being directly correlated to the SEG value. On the other hand, variations of the stress distributions—here evaluated in terms of von Mises stress [44]—were also obtained as a result of the optimization, with high stress levels in some cases spread over wider areas of the optimized structure compared to the non-optimized case, suggesting that a different strategy could be hereafter implemented if one needed to minimize the strain energy by simultaneously containing the stress levels.

Finally, the proposed design optimization strategy has allowed to find a new optimal fiber arrangement in CFRP multi-layer cylinders by ensuring minimum von Mises stress and by preserving the longitudinal response under compression, in a way to prevent buckling phenomena associated to the failure mechanisms experimentally observed in the structures with conventional quasi-isotropic stacking sequences.