Abstract
In this paper we carry out an in-depth experimental and numerical investigation of a vibro-impact rig with a two-sided constraint and an external excitation given by a rectangular waveform. The rig, presenting forward and backward drifts, consists of an inner vibrating shaft intermittently impacting with its holding frame. Our interests focus on the multistability and the bifurcation structure observed in the system under two different contacting surfaces. For this purpose, we propose a mathematical model describing the rig dynamics and perform a detailed bifurcation analysis via path-following methods for nonsmooth dynamical systems, using the continuation platform COCO. Our study shows that multistability is produced by the interplay between two fold bifurcations, which give rise to hysteresis in the system. The investigation also reveals the presence of period-doubling bifurcations of limit cycles, which in turn are responsible for the creation of period-2 solutions for which the rig reverses its direction of progression. Furthermore, our study considers a two-parameter bifurcation analysis focusing on directional control, using the period of external excitation and the duty cycle of the rectangular waveform as the main control parameters.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Vibrating systems exhibiting impacts and friction are very common in engineering applications, such as ground moling [1], percussive drilling [2], for which impacting behaviour is a part of the original design, or gearboxes [3], bearings, and rotor systems [4], which may be the result of component wear or asymmetry during system operation. The vibro-impact system to be studied in this paper, the so-called vibro-impact capsule [5], is a self-propelled mechanism under internal harmonic excitation, moving rectilinearly when overcoming environmental resistance. It has abundant coexisting attractors, including both chaotic and periodic solutions caused by the near-grazing dynamics of its internal impacts or low speed progression under nonlinear frictional environment [6]. Among these attractors, only few of them are useful from motion control or energy saving points of view. Hence, the study of controlling the capsule system involves addressing several key research issues, such as annihilation of multiple undesired attractors, basin hopping protection, attractor switching, and chaos control. These types of dynamical responses are typical in multistable vibro-impact systems, such as the one considered in the present paper, due to which a combination of theoretical and experimental approaches will be used for the investigation in this work.
Control of multistable systems has received considerable attention from the research community in the past few decades [7]. Multistability occurs when a system presents two or more coexisting attractors, and such a phenomenon can be found in many applications. According to the review [7], most of the studies in control of multistability are for optics, and there are very few works related to engineering multistability. From an engineering perspective, there are two major issues related to multistability. On the one hand, the performance of multistable systems can be easily altered with changing its control parameters. Examples of such systems range from drilling machinery [8] and milling processes [9] to gearboxes [3]. For these systems, maintaining some desired states can greatly improve their performance. On the other hand, some coexisting attractors may correspond to the states causing costly failure, e.g. rotor-stator impacts in an unbalanced rotor [10] or stick-slip oscillations in oil and gas drilling [11], due to which avoiding such states becomes crucial. Consequently, the issues described above will be driven to a large extent by the investigation presented in this work, with special focus on multistability phenomena in the considered capsule system and how this is affected by the control parameters, both from an experimental and numerical perspective.
Experimental studies for vibro-impact systems have been rather limited in the literature. Previous experimental studies have mainly focused on impact oscillators [12,13,14], in which typically has an oscillating mass making intermittent contact with a single obstacle, without considering further nonlinear effects, such as friction. In [15], anisotropic friction was adopted in the impact-free shell robot for planar locomotion. Duong et al. [16] developed a two-sided bidirectional drifting oscillator, but experimental results showed forward progression only. In [17], Nguyen et al. studied both theoretically and experimentally a vibro-impact moling rig for underground pipe installation, where both impacts and friction were considered. In the present work, we will introduce an experimental rig where all aspects mentioned above will be investigated, including two-sided impacting motion and complex progression patterns in both directions, forward and backward. By using this novel experimental rig, we will also investigate near-grazing dynamics and friction-induced oscillations under parameter-variations, and compare the experimental observations with some of the theoretical predictions obtained in this work.
The idea of vibro-impact self-propulsion for the capsule system was inspired by the high frequency vibro-impact drilling [8, 18], where a linear actuator impacts upon a drilling rod transferring the potential energy into the kinetic energy of the drill-bit [19]. Capsule’s research work was initiated by mathematically modelling a vibro-impact capsule with one-sided constraint [5] where a fundamental understanding of its dynamics was provided. Then the dynamics of the model was studied by using different friction models in [20], and revealed that the Coulomb friction model was fair for relatively large mass ratio of the system. Experimental verification of the model was carried out in [21] by using a proof-of-concept experimental rig which was 170 mm in length and 60 mm in width. It is worth noting that the experimental rig studied in this paper is 42 mm in length, 19.4 mm in diameter and with two-sided constraints, while the standard-sized capsule for gastrointestinal endoscopy is 26 mm in length and 11 mm in diameter [22]. The reason of using the present dimension in this study is that the dynamical response of the system, e.g. the acceleration of the inner mass and the displacement of the capsule, can be properly measured at this scale, so analysis becomes easier. Thereafter, forward and backward motion control of the capsule system was studied in [23] by using a position feedback control method, and optimisation of the system was considered from the viewpoint of an engineering application by using computational fluid dynamics simulation [24]. Páez Chávez et al. studied the directional control and energy consumption of the capsule system by means of path-following techniques [25]. A typical period-1 trajectory was followed for maximizing the rate of progression, and it was found that the capsule achieved its maximal rate when it oscillated without sticking phases. Selection of multistability in the capsule system for directional control was considered in [6], and the MATLAB-based numerical platform COCO, which supported the continuation and bifurcation detection of periodic orbits of non-smooth dynamical systems, was employed to study the robustness of the proposed control method. In [26], the concept of the vibro-impact self-propulsion was implemented on a capsule prototype which was driven by a push-type solenoid with a periodically excited rod, and the prototype was successfully tested in a fluid pipe in [27]. Later on, capsule’s dynamics in the small intestine was studied in [28], and a standard-sized capsule prototype for endoscopy was developed in [29]. For the capsule with two-sided constraints, Yan et al. studied its dynamics and compared it with the capsule with one-sided constraint [30]. In [31], an experimental rig of the capsule with two-sided constraints was studied through mathematical modelling and verification. However, the bifurcations in the dynamics of the rig was still not fully investigated. Therefore, in this paper, we will carry out a bifurcation analysis for the same experimental rig, particularly focusing on its bistability and directional control.
To gain a deeper understanding of the dynamical response of the capsule model we will employ path-following (continuation) methods for nonsmooth dynamical systems, implemented via the continuation platform COCO [32]. COCO (abbreviated form of Computational Continuation Core) is a MATLAB-based analysis and development platform for the numerical treatment of continuation problems. The software provides the users with a set of toolboxes that covers, to a good extent, the functionality of available continuation packages, such as AUTO [33] and MATCONT [34]. In our investigation, we will employ the COCO-toolbox ‘hspo’ to analyze the bifurcation structure of the model, which will reveal the presence of certain dynamical phenomena such as multistability and hysteresis. For this purpose, we will introduce a mathematical formulation for the model that will allow us to clearly identify all possible operation modes (18 in total), which poses certain difficulties for the numerical continuation analysis due to the system complexity.
The novelty of the present work is to employ path-following methods for analysing the complex dynamics of a nonsmooth dynamical system involving two nonlinearities, i.e. impact and friction, while the work studied in [31] only concentrates on model verification and optimisation in terms of progression speed and energy efficiency. Furthermore, it is worth noting that bifurcation analysis of the nonsmooth systems encoutering both nonlinearities using path-following methods is limited in the literature, and experimental studies are even rare. The rest of this paper is organized as follows. Section 2 presents the system’s main components and the experimental apparatus of the capsule rig. In Sect. 3, the vibro-impact capsule is formulated as a piecewise-smooth dynamical system for the path-following analysis via COCO. Then a detailed bifurcation analysis of the system is carried out in Sect. 4, followed by a further experimental investigation in Sect. 5. Finally, the paper finishes with some discussions and concluding remarks, given in Sect. 6.
2 Experimental apparatus
2.1 Experimental set-up
The experimental apparatus of the vibro-impact capsule system with a two-sided constraint is presented in Fig. 1a, where a solenoid is mounted inside a capsule with the coil fixed to the inner surface of the capsule and the shaft acting as an inner vibrating mass excited by an on-off rectangular waveform signal. The shaft is connected with the coil via a pre-compressed helical spring at one end, and a nylon nut and an iron washer are fixed on the other end of the shaft. When the coil is powered on, the shaft moves forward and compresses the spring. Impact will occur when the washer hits the front constraint. When the coil is switched off, the shaft moves backward due to the elastic force provided by the compressed spring. The secondary impact will happen when the nut hits the coil, i.e. the back constraint of the experimental rig. The capsule will drift forward or backward when the interaction force between the capsule and the shaft exceeds the environmental resistance. A linear variable differential transformer (LVDT) is attached to the capsule, and an accelerometer is fixed to the shaft, measuring the capsule displacement and the acceleration of the shaft, respectively. As shown in Fig. 1b, both shaft acceleration and capsule displacement are collected by a data acquisition card through a graphic user interface (GUI) in LabView with the sampling frequency of 1 kHz. The GUI also sends command (CMD) to a signal generator to control the solenoid drive circuit by using the pulse-width modulation (PWM) signal, characterised by the amplitude \(P_\mathrm {d}\), frequency f and duty cycle ratio D. Here, the duty cycle ratio is the fraction of one period (1/f) in which the on-off rectangular waveform signal is active. For more detailed description of the experimental set-up, interested readers can refer to [31].
a Photograph and b schematics of the experimental apparatus. A solenoid is mounted inside a capsule with the coil fixed to the inner surface of the capsule and the shaft acting as an inner vibrating mass excited by an on-off rectangular waveform signal. The shaft is connected with the coil via a pre-compressed helical spring at one end, and a nylon nut and an iron washer are fixed on the other end of the shaft. Impact will occur when the washer hits either the front or the back constraint. A linear variable differential transformer (LVDT) is attached to the capsule, and an accelerometer is fixed to the shaft, measuring the capsule displacement and the acceleration of the shaft, respectively. Both shaft acceleration and capsule displacement are collected by a data acquisition card through a graphic user interface (GUI) in LabView with the sampling frequency of 1 kHz. The GUI also sends command (CMD) to a signal generator to control the solenoid drive circuit by using the pulse-width modulation (PWM) signal [31]
2.2 Samples of periodic motion
In order to study the capsule’s dynamics under various friction environments, two different contacting surfaces, an aluminium bench and a cut-open synthetic small intestine, were used for experimental testing. Two samples of the obtained periodic time histories testing on the aluminium bench are presented in Fig. 2, where the signals of the excitation force, shaft acceleration and capsule displacement are shown. As can be seen from Fig. 2a, the capsule has an average forward progression, and both front and back impacts are encountered leading to forward and backward motion of the capsule in every period, respectively. It can be observed that the front impacts occur at the end of the interval when the excitation force is switched on, and the back impacts take place when the excitation is off and the shaft is pushed back to its original position by the pre-compressed spring. An average backward progression was presented in Fig. 2b, since the excitation force is insufficient to produce a front impact, and only back impacts are produced.
3 Mathematical modelling and its formulation in COCO
3.1 Equations of motion
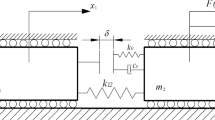
The physical model of the experimental rig is presented in Fig. 3, where \( k_1 \) and c represent the stiffness of the helical spring connecting the shaft and the capsule and the damping coefficient of the energy dissipation led by the relative speed between the capsule and the shaft, respectively. The secondary spring with stiffness \( k_2 \) and the tertiary spring with stiffness \( k_3 \) represent front and back constraints, respectively, against which front and back impacts occur. The pre-compressed displacement of the helical spring is \( G_1 \), the gap between the shaft and the front constraint is \( G_2 \), and the gap between the shaft and the back constraint is \( G_3 \). \( M_\mathrm {c} \) and \( M_\mathrm {m} \) are the masses of the capsule (including the mass of the LVDT rod) and the shaft (including the mass of the accelerometer), respectively. \( X_c \) is the displacement of the capsule, and \( X_m \) is the displacement of the shaft. The friction between the capsule and its supporting surface is modelled as Coulomb friction with the friction coefficient \( \mu \), which will be adjusted depending on the considered surface.
The considered system operates in bidirectional stick-slip phases which contain the following four modes [31]: stationary capsule without contact, moving capsule without contact, stationary capsule with contact and moving capsule with contact. All these modes can be modelled via the following equations of motion
where the interaction force acting on the shaft, \( F_\mathrm {i} \), can be written as
Here, \(X_\mathrm {r}=X_\mathrm {m}-X_\mathrm {c} \) and \( V_\mathrm {r}=V_\mathrm {m}-V_\mathrm {c} \) represent the relative displacement and velocity between the shaft and the capsule, \( F_1=k_1(X_\mathrm {r}+G_1) \), \( F_2=k_2(X_\mathrm {r}-G_2) \), \(F_3=k_3(X_\mathrm {r}+G_3)\) represent the interaction forces for the helical spring, front and back impacts, respectively. The external excitation, \( F_\mathrm {e} \), is a rectangular waveform signal, given by
where n is the period number, \( P_\mathrm {d} \), \( f=\tfrac{1}{T} \) and \( D \in (0,1) \) are the amplitude, frequency and duty cycle ratio of the signal, respectively.
Since in our experimental setup the contacting surfaces for both the aluminium and the small intestine are smooth, friction models involving Stribeck and low-speed effects were not considered. Therefore, in the capsule model we assume the following Coulomb friction law
where \( P_\mathrm {f}=\mu (M_\mathrm {m}+M_\mathrm {c})g \) is the static friction of the prototype, and g is the gravitational acceleration.
3.2 Parameter identification
The values of \(M_\mathrm {m}\) and \(M_\mathrm {c}\) were simply measured by weighting each element and kept constant throughout the experiments. For the coefficients \(k_1\), \(k_2\), \(k_3\) and c, they were identified by matching numerical simulation with each experimental run, and then averaging all the values of these coefficients. Identification of friction coefficient \(\mu \) between the capsule and the supporting surface was carried out by lifting one side of the supporting surface slowly until the stationary capsule started to move. In this way, the friction coefficient was determined by the angle of the surface slope at that moment. Finally, the identified physical parameters of the vibro-impact experimental rig are given in Table 1.
3.3 Mathematical formulation in COCO
For the numerical analysis of the capsule system (1), it is convenient to consider the following nondimensional parameters and variables:
In what follows, we will denote by \(\mathbf{z} =(v_{\mathrm {m}},x_{\mathrm {r}},v_{\mathrm {r}},s)^T\in {{\,\mathrm{\mathbb {R}}\,}}^4\) and \(\lambda =(\widetilde{T},D,\alpha ,\gamma ,\kappa _{2},\kappa _{3},\xi ,g_{1},g_{2},g_{3})\in \left( {{\,\mathrm{\mathbb {R}}\,}}^+\right) ^7\times \left( {{\,\mathrm{\mathbb {R}}\,}}^+_{0}\right) ^3\) the state variables and parameters of the system, respectively, where \({{\,\mathrm{\mathbb {R}}\,}}^+_{0}\) stands for the set of nonnegative numbers. In this framework, the capsule motion can be described by the equation (cf. (1))
where the prime symbol denotes derivative with respect to the nondimensional time \(\tau \) and \(f_{0}=(x_{\mathrm {r}}+g_{1})+2\xi v_{\mathrm {r}}\), \(f_{2}=\kappa _{2}(x_{\mathrm {r}}-g_{2})\), \(f_{3}=\kappa _{3}(x_{\mathrm {r}}+g_{3})\), while \(x_{\mathrm {r}}=x_{\mathrm {m}}-x_{\mathrm {c}}\) and \(v_{\mathrm {r}}=v_{\mathrm {m}}-v_{\mathrm {c}}\) represent the (nondimensional) mass displacement and velocity relative to those of the capsule, respectively. Note that system (6) does not include an equation describing explicitly the capsule motion. This motion, however, can be recovered from system (6) via
where \(x^*_{\mathrm {c}}\in {{\,\mathrm{\mathbb {R}}\,}}\) represents the position of the capsule at \(t=0\). By using this formula, we introduce the quantity
which gives the (nondimensional) average velocity per period of the capsule. According to formulae (5), the dimensional average velocity will be then given by \(V_{ \text{ avg }}=\Omega _{0}P_\mathrm {f}\widetilde{V}_{ \text{ avg }}/k_{1}\). Its sign indicates whether the capsule moves forwards (\(V_{ \text{ avg }}>0\)) or backwards (\(V_{ \text{ avg }}<0\)).
In model (6), s is an additional variable used to embed the time into the state space. This variable will be kept within the interval \([0,\widetilde{T}]\) according to the reset scheme
Furthermore, the symbols \(H_{\mathrm {k_{2}}}\) ,\(H_{\mathrm {k_{3}}}\), \(H_{\mathrm {vel}}\), and \(f_{\mathrm {e}}\) are discrete variables defining the operation modes of the system, according to the rules
Note that in the expressions above, the term \(f_{\mathrm {mc}}=\alpha f_{\mathrm {e}}-f_{0}-H_{\mathrm {k_{2}}}f_{2}-H_{\mathrm {k_{3}}}f_{3}\) represents the force acting on the capsule from the internal mass. Therefore, if the capsule is stationary, whenever the force \(f_{\mathrm {mc}}\) becomes smaller than \(-1\) or larger than 1, the capsule will move forward or backward, respectively. For the numerical implementation, the discrete variables defined in (8)–(11) will be used to identify the specific operation mode of the capsule. Every operation mode will be associated to a triple \(\left\{ \Sigma ,\Delta ,\Theta \right\} \), where \(\Sigma \in \left\{ \text{ NC },\text{ Ck2 },\text{ Ck3 }\right\} \) (no contact, contact with \(k_{2}\), contact with \(k_{3}\)), \(\Delta \in \left\{ \text{ Vc0 },\text{ Vcp },\text{ Vcn }\right\} \) (capsule stationary, forward motion, backward motion) and \(\Theta \in \left\{ \text{ ON },\text{ OFF }\right\} \) (forcing on, forcing off). For instance, the operation mode \(\left\{ \text{ Ck2 },\text{ Vcp },\text{ OFF }\right\} \) means that the capsule is moving forward with the internal mass in contact with the spring \(k_{2}\) and the external forcing is off (i.e. \(f_{\mathrm {e}}=0\)). In this way, the capsule system can operate under 18 different modes, as listed in Table 2.
4 Bifurcation analysis of the capsule system
In this section we will carry out a numerical continuation study of the periodic response of the capsule system (1), via the continuation platform COCO [32]. To this end, we will employ the mathematical formulation introduced in the previous section, see Eqs. (6)–(11). Although the model is formulated using nondimensional parameters and variables, the numerical results will be presented in dimensions so as to compare the predictions with the experimental observations.
4.1 Multistability
The first scenario was carried out on the aluminium bench under the variation of excitation period, which is presented in Fig. 4. The excitation period in experiment was varied from 50 to 200 ms, and both stationary and forward motions were observed. For numerical simulation, these two motions coexist when the excitation period is small (grey area), and the response for the stationary motion disappears as the excitation period increases, where the system becomes monostable. Additional windows demonstrate the time histories of shaft acceleration and capsule displacement at \(T=62.5\) ms and 76.9 ms, where Attractor 1 (red lines) has no impact and no progression, and coexists with Attractor 2 (blue lines), which has both front and back impacts and an average forward progression. Time histories of experimental results were plotted in green lines, which are consistent with the numerical simulation. The small discrepancy in capsule displacement could be due to measurement inaccuracies, such as friction coefficient and the intrinsic errors in the parameter estimation.
Average speeds of the experimental rig on the aluminium bench under different excitation periods for \(P_\mathrm {d}=183.3\) mN and \(D=0.5\), obtained by numerical simulation (blue and red dots) and experiment (green triangles). The grey area indicates the region of multistability of the rig, where two stable solutions, Attractor 1 (blue dots) and Attractor 2 (red dots), coexist. The upper panels depict the time histories of shaft acceleration and capsule displacement for \(T=62.5\) ms and 76.9 ms, as indicated by the arrows. (Color figure online)
a Numerical continuation of the periodic response of the capsule system (1) on the aluminium bench with respect to the excitation period T, computed for \(P_\mathrm {d}=172.4\) mN and \(D=0.5\), and the parameter values given in Table 1. The vertical axis \(T_\mathrm {c}\) shows the total time the mass is in contact with the constraints. The points Fi and GRi represent fold and grazing bifurcations of limit cycles, while the labels Pi denote test points along the bifurcation diagram at \(T=72.2\) ms. Dashed and solid lines represent unstable and stable solutions, respectively. The closed curve D\(_{1}\)–D\(_{2}\) shows schematically a hysteresis loop of the system. b Blow-up of the boxed region shown in panel a. Panels c–e depict phase plots of three coexisting attractors computed for \(T=72.2\) ms. Here, the vertical red lines stand for the impact boundaries \(X_\mathrm {r}=0\) mm and \(X_\mathrm {r}=3.4\) mm
To take a deeper insight into this multistable region, we will carry out the numerical continuation of the periodic response of the capsule system with respect to excitation period T. The result is shown in Fig. 5a and the blow-up given in panel (b). The vertical axis \(T_\mathrm {c}\) shows the total time the mass is in contact with the constraints, i.e. the springs \(k_{2}\) or \(k_{3}\). It should be noted that there is a difference, 10.9 mN, between the amplitude of excitation \(P_\mathrm {d}\) used in experiment (Fig. 4) and the one used for numerical continuation (Fig. 5). Since the experiment involved a lot of noise, an averaged \(P_\mathrm {d}\) was used in Fig. 4, while we found that the amplitude \(P_\mathrm {d}\) used for numerical continuation can better reveal the bifurcations in the system, so was adopted. However, such a difference can be considered as minor for comparing experimental and numerical studies in general. From the bifurcation diagram it can be seen that if the period is small, then the internal mass will oscillate without touching the constraints, see for instance the (stable) solution plotted in Fig. 5e. According to the operation modes defined in the previous section, this solution operates under the following cyclic sequence \(\left\{ \text{ NC },\text{ Vc0 },\text{ OFF }\right\} \), \(\left\{ \text{ NC },\text{ Vc0 },\text{ ON }\right\} \), see Table 2. As the period of excitation is increased, the resulting periodic orbit becomes closer and closer to the constraint given by the spring \(k_{2}\), until a grazing solution is found at \(T\approx 72.3409\) ms (GR1, see Fig. 7c). From this point on, the capsule system presents stable periodic solutions making intermittent contact with the spring \(k_{2}\). However, the stability of these solutions is lost at \(T\approx 72.3468\) ms, where the system undergoes a fold bifurcation of limit cycles (F1). Here, a branch of impacting unstable solutions is born, along which a grazing bifurcation GR3 is detected (\(T\approx 72.2450\) ms). At this point, the capsule leaves its stationary regime and starts moving forward. As the period decreases, another fold bifurcation (F3) is found for \(T\approx 72.1802\) ms, where the periodic solution becomes stable. From this point a branch of stable periodic solutions impacting the constraint \(k_{2}\) emanates, until a grazing bifurcation GR2 is detected (\(T\approx 72.7958\) ms). Here, the resulting periodic solution makes grazing contact with the other spring \(k_{3}\), as shown in Fig. 7d. Very close to this point, a fold bifurcation is detected (not shown in the diagram) where the periodic orbit loses stability, hence giving rise to a larger branch of unstable solutions. This branch, however, terminates at the point labeled F2 (\(T\approx 57.2925\) ms), where another fold bifurcation takes place. From this point onwards, the resulting periodic solutions are stable and remain so for larger values of the excitation period T. Fig. 7a depicts the same bifurcation diagram, but this time showing the average capsule velocity on the vertical axis.
Basins of attraction of the coexisting attractors shown in Fig. 5 computed for a \(T=72.2\) ms and b \(T=72.6\) ms. Blue dot with yellow basin, green dot with orange basin and red dot with grey basin denote the test points, P1, P2 and P3 in Fig. 5b at \(T=72.2\) ms, respectively. (Color figure online)
Another important feature of the bifurcation diagram discussed above is the interplay between the fold bifurcations F1 and F2, which gives rise to hysteresis in the system, schematically represented by the closed curve D\(_{1}\)–D\(_{2}\) plotted in Fig. 5a. As a result, we can determine a parameter window \(T\in [57.30,72.34]\) where the system exhibits coexisting attractors. In particular, due to the geometry of the resulting bifurcation curves, we find a smaller window defined by the bifurcation points F3 and F1 (approximately [72.18, 72.34]) where the system presents three coexisting attractors, see for instance Fig. 5, panels (c)–(e). Basins of attraction of these three coexisting attractors computed at \(T=72.2\) ms are plotted in Fig. 6a, where the blue dot with yellow basin represents P1 response with front and back impacts, the green dot with orange basin represents P2 response with front impact, and the red dot with grey basin denotes the near-grazing response P3. Figure 6b presents the basin evolution for these attractors computed at \(T=72.6\) ms, where the basin of the near-grazing response disappears and the basin of the response with front impact shrinks. As the excitation period increases, the basin of the response with front impact disappears completely, and the system becomes monostable. It should be noted that since the full dimension of the system is greater than two, Fig. 6 presents the projections of basins of attractions on the phase plane of the relative displacement and velocity between the shaft and the capsule. In our simulation, capsule’s displacement and velocity were set to zero, and shaft’s displacement and velocity were varied for basin computation. If capsule’s displacement and velocity are changed, it will not affect the obtained basins, since they were computed using the relative displacement and velocity between the shaft and the capsule.
a Numerical continuation computed in Fig. 5a showing the behavior of average capsule velocity \(V_{ \text{ avg }}\). The bifurcation labels are the same as in Fig. 5a. b Two-parameter continuation of the F1 (red curve) and F2 (black curve) bifurcation points with respect to the excitation period T and duty cycle D. The grey region represents parameter values producing multistability, where two or three attractors coexist (see Fig. 5). Panels (c) and (d) show phase plots of solutions making grazing contact with the impact boundary \(X_\mathrm {r}=3.4\) mm and \(X_\mathrm {r}=0\) mm, respectively. (Color figure online)
The phenomenon of multistability can be further investigated by performing a two-parameter continuation of the bifurcation points F1 and F2 found before, using the excitation period T and the duty cycle D. The result is shown in Fig. 7b. In this picture, the red and black curves give the two-parameter continuation of the fold points F1 and F2, respectively. These curves define a region in the parameter space (in gray) denoting combinations of T and D producing multistability in the system. In particular, these curves allows a classification of the system behavior in terms of multistability and capsule average motion, see the regions given in Fig. 7b.
4.2 Period-doubling bifurcation
The second scenario for the comparison between experiment and numerical simulation is shown in Fig. 8, where the duty cycle D is the main control parameter. It can be seen from Fig. 8a that the capsule has a period-1 backward motion at \(D=0.3\), while for \(D=0.4\) the system presents a period-2 solution with forward motion, which gives an indication of the presence of two phenomena, namely, a period-doubling bifurcation and a critical point where the capsule changes its direction of average progression. Some sample solutions related to these observations are given in Fig. 8, for \(D=0.45\), \(D=0.47\) and \(D=0.5\). It is worth noting that the values of the velocities obtained numerically are three times higher than those recorded experimentally as presented in the figure, and also the period-doubling bifurcation occurs at very different values of parameter D. These two discrepancies are due to the friction coefficient and the step size used in experiment. Since our model adopted Coulomb friction, its coefficient was a constant for which numerical continuation can be conducted, while this coefficient should increase with capsule’s speed as measured in our experiment [29]. In the experiment, we can only change the duty cycle D at the minimum step of 0.1, so any intervals between 0.1 cannot be observed. This leads our experimental observations of the period-1 backward, period-2 forward and period-1 forward motion at \(D=0.3\), 0.4 and 0.5, respectively.
Average speeds of the experimental rig on the small intestine under different duty cycle D for \(P_\mathrm {d}=275.8\) mN and \(f=18.5\) Hz obtained by a experiment and b numerical simulation. Additional windows in a demonstrate that the experimental rig bifurcates from a period-1 backward motion at \(D=0.3\) to a period-2 forward motion at \(D=0.4\), and then to a period-1 forward motion at \(D=0.5\). Additional windows in b recorded for \(D=0.45\), 0.47 and 0.5 demonstrate the same bifurcations observed in numerical simulation
In order to investigate in detail the observations described above, we will carry out the numerical continuation of the periodic response of the capsule with respect to the duty cycle D. The result is shown in Fig. 9a. Here, we show in the vertical axis the average capsule velocity. If we start the study with the duty cycle close to the symmetric case (\(D=0.5\)), we can observe that the capsule presents forward motion, as can be seen for instance at the test point P2, see Fig. 9b. As we decrease the duty cycle, the average capsule velocity \(V_{ \text{ avg }}\) decreases as well. During this continuation process, a period-doubling bifurcation of limit cycles (PD2) is found at \(D\approx 0.4734\), where the original period-1 solution becomes unstable and a stable branch of period-2 solutions is born. For these stable period-2 solutions the average capsule velocity becomes smaller as the duty cycle decreases, until a critical point P3 (\(D\approx 0.4651\)) is found where \(V_{ \text{ avg }}\) becomes zero, see Fig. 9d. For smaller duty cycles, the capsule start moving backwards, as can be seen for instance at the test point P1 (\(D=0.3\)) depicted in panel (c).
a Numerical continuation of the periodic response of the capsule system (1) on the small intestine with respect to the duty cycle D, computed for \(P_\mathrm {d}=275.8\) mN, \(f=18.5\) Hz, and the parameter values given in Table 1. The vertical axis shows the average capsule velocity. The points PDi represent period-doubling bifurcations of limit cycles, while the labels P1 and P2 denote test points at \(D=0.3\) and \(D=0.5\), respectively. The label P3 (\(D\approx 0.46514\)) gives the point for a period-2 solution with zero average capsule velocity. Panels b–d depict time plots of periodic solutions with negative (at P1), positive (at P2) and zero (at P3) average capsule velocity. Here, grey and blank areas indicate that the excitation is on and off, respectively
a Two-parameter continuation of period-2 solutions with zero average capsule velocity (see Fig. 9d) with respect to the excitation period T and duty cycle D. The resulting curve divides locally the parameter space into two regions corresponding to forward and backward capsule progression. Panels (b) and (c) show time plots of periodic solutions computed at the test points P1 (\(D=0.453\), \(T=56.5\) ms, forward progression) and P2 (\(D=0.465\), \(T=53.5\) ms, backward progression), respectively
Therefore, the critical point P3 found above can be used to define a boundary between forward and backward capsule motion, via two-parameter continuation of this critical point with respect to the excitation period T and the duty cycle D. The result of this process is shown in Fig. 10a. This curve then gives combinations of T and D producing period-2 solutions with zero average capsule velocity. Hence, this curve can be used to divide locally the parameter space into two regions: one for parameter values producing forward motion (above the curve) and one for backward motion (below the curve). This classification can be verified with the test points given in panels (b) and (c). Note that although the test points are quantitatively close to each other (P1 at \(D=0.453\), \(T=56.5\) ms, and P2 at \(D=0.465\), \(T=53.5\) ms), the precise knowledge of the critical curve allows us to identify which one will produce the desired type of motion. According to the discrepancies shown in Fig. 8, such a critical curve for the experimental rig will appear on the left of the curve obtained through two-parameter continuation. The result presented in Fig. 10a give an accurate boundary for numerical simulation, but a rough prediction for experiment. However, this numerical result do give us an indication of parameter selection in experiment. For example, by using Figs. 8 and 10, we could predict in experiment that a low frequency of external excitation with a large duty cycle will produce forward progression, while a high frequency of external excitation with a small duty cycle could generate backward progression.
5 Experimental investigation of the capsule system
In this section we will further analyse the dynamics of the experimental rig under different control parameters and contact surfaces based on experimental observations.
Figure 11 compares the movement of the rig on the aluminium bench and the small intestine under the same control parameters, \(P_\mathrm {d}=300\) mN, \(f=9\) Hz and \(D=0.5\). It can be seen from Fig. 11a that the rig moving on the aluminium bench was faster than the one moving on the small intestine. As backward drift occurred at every period of excitation, greater friction on the aluminium bench forced the rig to have less backward drift than the small intestine, so leading to a faster overall progression. This also caused different amplitudes of acceleration for the shaft when both front and back impacts were encountered as presented in Fig. 11b. As can be seen from the figure, although impacts occurred at the same time for both surfaces, and most of the amplitudes of back impacts for the small intestine (red dash line) were smaller than the aluminium bench (black solid line), the rig still had larger backward drifts on the small intestine due to smaller friction on the surface.
To investigate the influence of the impact on capsule’s motion, a comparison of capsule’s displacements on the aluminium bench under different duty cycles is presented in Fig. 12. It can be seen from the right panel that as the duty cycle is small (\(D=0.1\)), the shaft only had back impacts so leading to backward progression of the system. When \(D=0.2\), front impact was encountered which caused large forward drift. As the duty cycle was increased to \(D=0.7\), two front impacts were encountered in every period of excitation. However, such a large duty cycle seems inefficient in driving the system as the shaft stuck with the front constraint causing less forward progression.
Finally, a comparison of capsule’s response on the small intestine under different excitation forces is presented in Fig. 13. It can been seen from Fig. 13a that when \(P_\mathrm {d}=185\) mN, no impact was encountered, so the rig had chaotic motion oscillating at its original position. When \(P_\mathrm {d}=300\) mN as shown in Fig. 13b, both front and back impacts were recorded, and the rig bifurcated into a period-2 forward motion.
6 Concluding remarks
The present work considered a vibro-impact rig with two-sided constraint, which was studied in detail both from a numerical and an experimental perspective. The rig was excited by an on-off rectangular waveform signal applied to its inner vibrating shaft, which intermittently impacts with the outer frame of the entire system, leading to forward and backward drifts. The purpose of development of such a rig was to understand the dynamics of the standard-sized capsule [29] (26 mm in length and 11 mm in diameter) for gastrointestinal endoscopy. For this purpose, two different contacting surfaces, an aluminium bench and a cut-open synthetic small intestine, were tested in this study. To have a better understanding of dynamics of the rig, we introduced a mathematical formulation of the model in the framework of piecewise-smooth dynamical systems, so as to later apply path-following methods for a detailed bifurcation analysis via the continuation platform COCO [32].
Our analysis focused on the multistability and the period-doubling phenomena in the system. Through numerical continuation, it was revealed that the existence of parameter windows for which two and three attractors coexist, consisting of a combination of non-impacting solutions and solutions with front and back impacts, caused after grazing bifurcations with the motion constraints. It is also a transitional region for the system moving from stationary to forward progression. In addition, basins of attractions for the coexisting solutions were computed, showing the complex dynamical scenario of the system. Furthermore, a two-parameter continuation of the critical bifurcation points allowed the identification of a parameter region for which multistability can be observed, considering the period of the external excitation and the duty cycle as the main control parameters.
By using path-following methods a detailed bifurcation study was carried out, showing the presence of period-doubling bifurcations of limit cycles. During this study, it was observed that stable period-2 solutions produce the transition from forward to backward average motion of the capsule. This transition can be traced in two parameters (period and duty cycle) via continuation methods, which allowed the computation of a critical curve representing the boundary between forward and backward progression. This curve then enables the implementation of control strategies that can be tested in further investigations related to directional control of the vibro-impact capsule system.
Experimental observations in this work revealed that it was challenging to control the progression of the system on slippy surface as less friction may present causing excessive backward drifts. The studies also confirmed the role of front and back impacts on contributing the overall progression of the system. Front and back impacts can generate sufficiently large forces for the experimental rig to overcome environmental resistance leading to forward and backward progression, respectively.
Our future work will focus on the development of a standard-sized capsule prototype, which is 26 mm in length and 11 mm in diameter, design optimisation, mathematical modelling, numerical continuation analysis, and experimental verification.
Data availability
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.
References
Nguyen VD, Woo KC (2008) Nonlinear dynamic responses of new electro-vibroimpact system. J Sound Vib 310:769–775
Liu Y, Páez Chávez J, Pavlovskaia E, Wiercigroch M (2018) Analysis and control of the dynamical response of a higher order drifting oscillator. Proc R Soc A 474:20170500
de Souza SLT, Caldas IL, Viana RL, Balthazar JM (2008) Control and chaos for vibro-impact and non-ideal oscillators. J Theor Appl Mech Pol 46:641–664
Páez Chávez J, Hamaneh VV, Wiercigroch M (2015) Modelling and experimental verification of an asymmetric Jeffcott rotor with radial clearance. J Sound Vib 334:86–97
Liu Y, Wiercigroch M, Pavlovskaia E, Yu H (2013) Modeling of a vibro-impact capsule system. Int J Mech Sci 66:2–11
Liu Y, Páez Chávez J (2017) Controlling multistability in a vibro-impact capsule system. Nonlinear Dyn 88:1289–1304
Pisarchik AN, Feudel U (2014) Control of multistability. Phys Rep 540:167–218
Pavlovskaia E, Hendry DC, Wiercigroch M (2015) Modelling of high frequency vibro-impact drilling. Int J Mech Sci 91:110–119
Yan Y, Xu J, Wiercigroch M (2018) Stability and dynamics of parallel plunge grinding. Int J Adv Manuf Technol 99:881–985
Armstrong-Hélouvry B (1990) Stick-slip arising from Stribeck friction. In: Proceedings of the IEEE international conference on robotics and automation (Cincinnati, Ohio, USA), pp 1377–1382
Patil P, Teodoriu C (2013) A comparative review of modelling and controlling torsional vibrations and experimentation using laboratory setups. J Petrol Sci Eng 112:227–238
Savi MA, Divenyi S, Franca LFP, Weber HI (2007) Numerical and experimental investigations of the nonlinear dynamics and chaos in non-smooth systems. J Sound Vib 301:59–73
Ing J, Pavlovskaia E, Wiercigroch M, Banerjee S (2008) Bifurcation analysis of an impact oscillator with a one-sided elastic constraint near grazing. Physica D 310:769–775
Aguiar RR, Weber HI (2011) Mathematical modeling and experimental investigation of an embedded vibro-impact system. Nonlinear Dyn 65:317–334
Zhan X, Xu J, Fang H (2018) A vibration-driven plannar locomotion robot—shell. Robotica 36:1402–1420
Duong T, Nguyen V, Nguyen H, Vu N, Ngo N, Nguyen V (2018) A new design for bidirectional autogenous mobile systems with two-side drifting impact oscillator. Int J Mech Sci 140:325–338
Ho JH, Nguyen VD, Woo KC (2011) Nonlinear dynamics of a new electro-vibro-impact system. Nonlinear Dyn 63:35–49
Pavlovskaia E, Wiercigroch M, Grebogi C (2001) Modeling of an impact system with a drift. Phys Rev E 64:056224
Rabia H (1985) A unified prediction model for percussive and rotary drilling. Min Sci Technol 2:207–216
Liu Y, Pavlovskaia EE, Hendry D, Wiercigroch M (2013) Vibro-impact responses of capsule system with various friction models. Int J Mech Sci 72:39–54
Liu Y, Pavlovskaia EE, Wiercigroch M (2016) Experimental verification of the vibro-impact capsule model. Nonlinear Dyn 83(1):1029–1041
Medtronic, PillCam\(^{\text{tm}}\)SB 3 System. Available at http://www.medtronic.com/covidien/en-us/products/capsule-endoscopy/pillcam-sb-3-system.html. Accessed 14 Feb 2020
Liu Y, Pavlovskaia EE, Wiercigroch M, Peng ZK (2015) Forward and backward motion control of a vibro-impact capsule system. Int J Non-Linear Mech 70:30–46
Liu Y, Islam S, Pavlovskaia EE, Wiercigroch M (2016) Optimization of the vibro-impact capsule system. Strojniski Vestn J Mech Eng 62(7–8):430–439
Páez Chávez J, Liu Y, Pavlovskaia EE, Wiercigroch M (2016) Path-following analysis of the dynamical response of a piecewise-linear capsule system. Commun Nonlinear Sci Numer Simul 37:102–114
Yan Y, Liu Y, Páez Chávez J, Yusupov A (2018) Proof-of-concept prototype development of the self-propelled capsule system for pipeline inspection. Meccanica 53:1997–2012
Yan Y, Liu Y, Jiang H, Peng Z, Crawford A, Williamson J, Thomson J, Kerins G, Yusupov A, Islam S (2019) Optimization and experimental verification of the vibro-impact capsule system in fluid pipeline. Proc Inst Mech Eng C 233:880–894
Yan Y, Liu Y, Manfredi L, Prasad S (2019) Modelling of a vibro-impact self-propelled capsule in the small intestine. Nonlinear Dyn 96:123–144
Guo B, Ley E, Tian J, Zhang J, Liu Y, Prasad S. Experimental and numerical studies of intestinal frictions for propulsive force optimisation of a vibro-impact capsule system. Nonlinear Dyn (under review)
Yan Y, Liu Y, Liao M (2017) A comparative study of the vibro-impact capsule systems with one-sided and two-sided constraints. Nonlinear Dyn 89:1063–1087
Guo B, Liu Y, Rauf B, Prasad S (2020) Self-propelled capsule endoscopy for small-bowel examination: proof-of-concept and model verification. Int J Mech Sci 174:105506
Dankowicz H, Schilder F (2013) Recipes for continuation. Computational science and engineering. SIAM, Philadelphia
Doedel EJ, Champneys AR, Fairgrieve TF, Kuznetsov YA, Sandstede B, Wang, X-J (1997) Auto97: continuation and bifurcation software for ordinary differential equations (with HomCont). Computer Science, Concordia University, Montreal, Canada. Available at http://cmvl.cs.concordia.ca
Dhooge A, Govaerts W, Kuznetsov YA (2003) MATCONT: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans Math Softw 29(2):141–164
Acknowledgements
This work has been supported by EPSRC under Grant No. EP/P023983/1 and EP/R043698/1. The second author has been supported by the DAAD Visiting Professorships programme at the University of Koblenz-Landau, Germany.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest concerning the publication of this manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, Y., Páez Chávez, J., Guo, B. et al. Bifurcation analysis of a vibro-impact experimental rig with two-sided constraint. Meccanica 55, 2505–2521 (2020). https://doi.org/10.1007/s11012-020-01168-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-020-01168-4