A novel brush-model with flexible carcass for transient interactions

Abstract

In this investigation, a double brush model, which aims at predicting both the longitudinal and the lateral tyre characteristics during transient phases, is developed. The solution of the tyre-road contact equation is provided by using the method of characteristics and a time delay of the bristles deformation with respect to the time is also introduced by modelling both the tyre tread and the carcass by means of viscoelastic and elastic elements, respectively. The temporal trend of some quantities of interest such as the adherence length and the critical slip value is then obtained as explicit function of the time or, equivalently, of the travelled distance. A preliminary analysis is carried out with reference to the transition from a pure rolling condition to accelerating or braking ones. The tyre response to a constant lateral slip input is also comprehensively discussed. Finally, in the case of consecutive manoeuvre, the model shows that all the generalised forces exerted by the road on the tyre vary continuously by introducing a finite increase in the slip parameter. Several examples are presented in order to demonstrate the applicability of the proposed model to severe braking or handling dynamic scenarios.

1 Introduction

In the recent years, a significant amount of research has focused on traffic safety and in particular on investigating physical model-based control systems to be employed in emergency braking and handling dynamic scenarios [1]. From the perspective of emergency braking, there are two main factors influencing the braking capacity of a vehicle: tyre-road friction and available braking torque. Both are difficult to determine precisely due to modelling complexities and variations in the operating conditions. Indeed, the first step to achieve and the fundamental obstacle to overcome consists in tyre-road friction modelling and correct estimation for individual vehicles.

Some very sophisticated FEM or Multibody models [2,3,4] are able to capture with great accuracy many phenomena related to the tyre dynamics, but they are characterised by extremely long calculation times because of their intrinsic complexity. The need for real-time tyre models, on the other hand, makes them unsuitable for braking and handling applications, and, as a consequence, they are mainly adopted to evaluate static characteristics, as stiffness, resonant frequencies and vibration modes.

In order to meet the real-time requirement, several simpler approaches for tyre modelling have been proposed in the literature. Nowadays, the most widespread technique is Pacejka’s “Magic Formula”, adopting a large set of parameters to be identified for each tyre with a potential risk to completely misunderstand the physical interpretation of the tyre behaviour even in case of a good fitting towards experimental results. In contrast, the so-called “brush models” [5, 6] are based on purely physical considerations, require a small number of parameters and can be used to investigate qualitatively different phenomena connected with the tyre-road interaction problem. The first versions were based on rather limiting simplifying assumptions, but still allowed to obtain a fully analytical formulation of the generalised forces arising in the contact patch versus the slip parameters. The main drawback was a possible mismatch to the experimental data due to the approximations introduced in the modelling.

Relatively recent efforts have been aimed at a more detailed modelling of the contact patch in order to obtain more satisfying results. In particular, in [7], the effect of an asymmetrical contact pressure distribution on the longitudinal force has been studied extensively. In [8], a three-dimensional model which aims to reproduce the longitudinal characteristics of the tyre in steady-state conditions is presented; the contact patch outlier is also calculated from footprint measurements and tyre data. In [9], the author, starting from a semi-analytical model normally employed in wheel-rail contact representations, successfully extended Kalker’s theory to rubber tyres. In [10] the effect of the thermal and frictional effects on ground vehicle performance has been studied by employing a simplified model for tire wear estimation. Finally, other studies [11,12,13] were substantially aimed at estimating the road friction coefficient from forces and slip measurements by assuming the tyre behaviour following some improved brush models.

At the same time, several attempts have been made in order to include dynamic properties capable of predicting some phenomena occurring during transient phases. Among the dynamic models, the best known are perhaps the “LuGre” [1] and the Single Point Contact Model developed by Pacejka [14]. In the first model, the shear stresses exerted at the tyre-road interface and the friction-induced hysteresis are described in terms of an internal friction parameter which can be identified with the deformation of the bristles schematising the tyre tread. Some specially developed functions are also included in order to fit Pacejka’s curves.

The latter is an enhanced brush model which takes into account the deformation of the tyre carcass and it is able to provide a transient solution for both the lateral force and the self-aligning moment resulting from a first order differential equation. Lastly, other authors have proposed solutions based on finite difference approximations [15], or on interconnected bristle models [16].

However, an extremely simple model capable of exhaustively describing the main transient phenomena occurring in the contact patch has not yet been developed. Hence, in this paper, a novel double brush model with flexible carcass is presented. In this model, the tread and the carcass are schematised by means of viscoelastic elements whose deformations vary with both the slip and the travelled distance. The need to include a flexible carcass is motivated by the possibility of obtaining a variable trend over time, since the tyre-road contact equations are based on purely kinematic considerations, and do not allow to introduce a time delay of the bristle deformation with respect to a constant slip input.

The main advantage of this formulation is the possibility to obtain an analytical solution for the generalised forces resulting from the tyre-road interaction, allowing the model to be easily employed in real-time simulation for braking and handling applications.

This paper is organised as follows: in Sect. 2, the derivation of the tyre-road contact equations is given; a transient solution for the longitudinal interaction is then provided in Sect. 3. In Sect. 4, the analysis is extended to the lateral problem, while the case of consecutive manoeuvres is discussed in 5. Simulations results are finally presented in Sect. 6, and conclusions and further developments are drawn in Sect.7.

2 Tyre-road contact equations

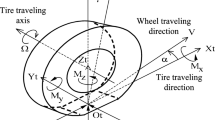
The tyre-road contact equations are derived by using the Eulerian approach. Let us consider a finite control area $\varGamma (x,y, 0)= \{(x,y,z) \in \mathbb {R} : -l/2 \le x \le l/2, -b/2 \le y \le b/2, z = 0\}$ in the absolute reference frame $({\hat{\mathbf{e}}}_x, {\hat{\mathbf{e}}}_y, {\hat{\mathbf{e}}}_z)$, where l and b are the length of the contact patch and the tyre width, respectively (Fig. 1). The vertical dimension is also assumed to be zero since the carcass and the tread only undergoes deformations in the longitudinal and lateral directions. The relative micro-slippage speed between the point of a carcass bristle attached to the rigid body and the one of the tread bristle contacting the road reads

Fig. 1

Brush model reference system

$$\begin{aligned} {\varvec{v}}({\varvec{r}},t) = {\varvec{V}}_{{\varvec{s}}}(t)+{\varvec{\omega }} \wedge {\varvec{r}} + \frac{d}{dt}({\varvec{u}}^b+{\varvec{u}}^c), \end{aligned}$$

(1)

where ${\varvec{V}}_{\varvec{s}}$ is the slippage speed defined as the difference between the speed of the rigid equivalent tyre and that of the road, ${\varvec{\omega }} ={\varvec{\omega }}_{\mathbf{1}}-{\varvec{\omega }}_{\mathbf{2}}$ is the spin angular speed, ${\varvec{\omega }}_{\mathbf{1}}$ is the normal component of the rolling speed due to camber, ${\varvec{\omega }}_{\mathbf{2}}$ is the steering speed (which in this model is attributed to the road), and ${\varvec{u}}^b(x, y, z, t)$ and ${\varvec{u}}^c(x, y, z, t)$ are the displacement fields associated with the Kelvin-Voigt element and the linear spring modelling the bristles of the tyre tread and the carcass, respectively. Introducing the operator $\nabla$, Eq. (1) can be rewritten as

$$\begin{aligned} {\varvec{v}}({\varvec{r}},t) = {\varvec{V}}_{\varvec{s}}(t)+{\varvec{\omega }} \wedge {\varvec{r}} + \frac{\partial }{\partial t}({\varvec{u}}^b+{\varvec{u}}^c) + \mathbf{v} \cdot \nabla ({\varvec{u}}^b+{\varvec{u}}^c), \end{aligned}$$

(2)

where the quantity $\mathbf{v}$ is

$$\begin{aligned} \mathbf{v}= \frac{d {\varvec{r}}}{dt} = {\varvec{\varOmega }} \wedge {\varvec{R}} +{\varvec{\omega }}_{\mathbf{1}} \wedge {\varvec{r}} \simeq {\varvec{\varOmega }} \wedge {\varvec{R}}, \end{aligned}$$

(3)

with

$$\begin{aligned} {\varvec{\varOmega }} \wedge {\varvec{R}} = \begin{bmatrix} {\hat{\mathbf{e}}}_x&{\hat{\mathbf{e}}}_y&{\hat{\mathbf{e}}}_z\\ 0&-\varOmega&0\\ 0&0&R \end{bmatrix} = -\begin{bmatrix} \varOmega R \\ 0 \\ 0 \end{bmatrix} = \mathbf{v}_{\mathbf{r}}. \end{aligned}$$

(4)

Dividing Eq. (2) by $|{\varvec{\varOmega }} \wedge {\varvec{R}}|$ yields

$$\begin{aligned} \begin{aligned} \bar{{\varvec{v}}}({\varvec{r}},t)&= \frac{{\varvec{v}}({\varvec{r}},t)}{|{\varvec{\varOmega }}\wedge {\varvec{R}}|}= \frac{{\varvec{V}}_{{\varvec{s}}}(t)}{\varOmega R}+\frac{{\varvec{\omega }}}{\varOmega } \wedge \frac{{\varvec{r}}}{R} \\&\quad + \frac{\partial }{\varOmega R \partial t}({\varvec{u}}^b+{\varvec{u}}^c) -\frac{\mathbf{v}_\mathbf{r}}{\varOmega R} \cdot \nabla ({\varvec{u}}^b+{\varvec{u}}^c). \end{aligned} \end{aligned}$$

(5)

Now we rename ${{\varvec{V}}}_{{{\varvec{s}}}}/\varOmega R = {\varvec{\varepsilon }}$, ${\varvec{\omega }}/\varOmega R = {\varvec{\psi }}$ and $\varOmega R \partial t = \partial \eta$, so that the above equation can be rewritten as

$$\begin{aligned} \bar{{\varvec{v}}}({\varvec{r}},t) = {\varvec{\varepsilon }}+{\varvec{\psi }} \wedge \frac{{\varvec{r}}}{R} + \frac{\partial }{\partial \eta }({\varvec{u}}^b+{\varvec{u}}^c) -\frac{\mathbf{v}_{\mathbf{r}}}{\varOmega R} \cdot \nabla ({\varvec{u}}^b+{\varvec{u}}^c). \end{aligned}$$

(6)

Specifying the above quantities as follows

$$\begin{aligned} {\varvec{\varepsilon }}&= \begin{bmatrix} \varepsilon _x \\ \varepsilon _y\\ 0\end{bmatrix} \end{aligned}$$

(7)

$$\begin{aligned} {\varvec{\psi }}\wedge \frac{{\varvec{r}}}{R}&= \begin{bmatrix} {\hat{\mathbf{e}}}_x&{\hat{\mathbf{e}}}_y&{\hat{\mathbf{e}}}_z\\ 0&0&\psi \\ x/R&y/R&0 \end{bmatrix} = \frac{\psi }{R}\begin{bmatrix} -y\\ x\\ 0 \\ \end{bmatrix} \end{aligned}$$

(8)

$$\begin{aligned} {\varvec{u}}^{b}&= \begin{bmatrix} u_x^b \\ u_y^b \\ 0\end{bmatrix}\end{aligned}$$

(9)

$$\begin{aligned} {\varvec{u}}^{c}&= \begin{bmatrix} u_x^c \\ u_y^c \\ 0 \end{bmatrix} \end{aligned}$$

(10)

the new dimensionless tyre-road contact equations in scalar form read

$$\begin{aligned} \bar{v}_x&= \varepsilon _x - \psi \frac{y}{R} +\frac{\partial }{\partial \eta }(u_x^b + u_x^c) - \frac{\partial }{\partial x}(u_x^b + u_x^c) \end{aligned}$$

(11a)

$$\begin{aligned} \bar{v}_y&= \varepsilon _y + \psi \frac{x}{R} +\frac{\partial }{\partial \eta }(u_y^b + u_y^c) - \frac{\partial }{\partial x}(u_y^b + u_y^c). \end{aligned}$$

(11b)

Introducing the new variable $\xi = l/2 - x$, (11) finally become

$$\begin{aligned} \bar{v}_x&= \varepsilon _x - \psi \frac{y}{R} +\frac{\partial }{\partial \eta }(u_x^b + u_x^c) + \frac{\partial }{\partial \xi }(u_x^b + u_x^c) \end{aligned}$$

(12a)

$$\begin{aligned} \bar{v}_y&= \varepsilon _y + \psi \frac{x}{R} +\frac{\partial }{\partial \eta }(u_y^b + u_y^c) + \frac{\partial }{\partial \xi }(u_y^b + u_y^c) . \end{aligned}$$

(12b)

3 Longitudinal interaction

The pure longitudinal interaction problem is studied by hypothesising a constant value of the slip parameter over the time and assigning $\psi =0$. In the adherence zone, Eq. (12) can be also particularised as

$$\begin{aligned} \frac{\partial (u_x^b+u_x^c)}{\partial \xi } + \frac{\partial (u_x^b+u_x^c)}{\partial \eta } = -\varepsilon _x. \end{aligned}$$

(13)

Equation (13) can be solved with the method of characteristics, leading to

$$\begin{aligned} u_x^b(\xi , \eta ) + u_x^c(\xi , \eta ) = -\varepsilon _x \eta + g(\eta -\xi ) . \end{aligned}$$

(14)

Imposing the spontaneous entrance condition $u_x^b(0, \eta )=0$ also gives

$$\begin{aligned} g(\eta ) = u_x^c(0, \eta ) + \varepsilon _x \eta , \end{aligned}$$

(15)

which implies

$$\begin{aligned} g(\eta -\xi ) = u_x^c(0, \eta -\xi ) + \varepsilon _x(\eta -\xi ) . \end{aligned}$$

(16)

Substituting the above relation into Eq. (14) yields

$$\begin{aligned} u_x^b(\xi , \eta ) = -\varepsilon _x \xi + u_x^c(0, \eta -\xi )-u_x^c(\xi , \eta ) . \end{aligned}$$

(17)

However, if the deformation of the bristle at the leading edge results in nothing at each value of the distance $\eta$, the function $u_x^c(0, \eta -\xi )$ must also be zero because no force acts on the carcass at the entrance point. Hence, it can be finally written

$$\begin{aligned} u_x^b(\xi , \eta ) = -\varepsilon _x \xi - u_x^c(\xi , \eta ) . \end{aligned}$$

(18)

The force per unit of area acting on the bristle at the the coordinate $\xi$ is thus

$$\begin{aligned} f_x(\xi , \eta ) = -k_x^b(\varepsilon _x\xi + u_x^c(\xi , \eta ))-\varOmega R \sigma _x \frac{\partial u_x^c(\xi , \eta )}{\partial \eta } . \end{aligned}$$

(19)

This force must equal the force acting on the spring-damper element representing the tyre carcass

$$\begin{aligned} k_x^c u_x^c=-k_x^b(\varepsilon _x\xi + u_x^c(\xi , \eta ))-\varOmega R \sigma _x \frac{\partial u_x^c(\xi , \eta )}{\partial \eta } . \end{aligned}$$

(20)

Solving equation (20) gives

$$\begin{aligned} u_x^c(\xi , \eta ) = -\frac{k_x^b}{k_x^c+k_x^b}\varepsilon _x\xi + g(\xi ) \exp \left( -\frac{\eta }{\varOmega R} \frac{k_x^c + k_x^b}{\sigma _x} \right) . \end{aligned}$$

(21)

Renaming

$$\begin{aligned} k_{x}^{eq}&= \frac{k_x^c k_x^b}{k_x^c + k_x^b} \end{aligned}$$

(22a)

$$\begin{aligned} \tau _x&= \frac{\sigma _x}{k_x^c + k_x^b} \end{aligned}$$

(22b)

Equation (21) can be rewritten as

$$\begin{aligned} u_x^c(\xi , \eta ) = -\frac{k_x^{eq}}{k_x^c}\varepsilon _x\xi + g(\xi ) \exp \left( -\frac{\eta }{\varOmega R \tau _x} \right) . \end{aligned}$$

(23)

The unknown function $g(\xi )$ can be found by conjecturing that, at the time $t=0$, the carcass is undeformed. This also implies that the shear stress acting on each bristle must result in nothing at the initial time and the tyre tread undergoes a deformation due only to the sudden change of the force. Imposing $u_x^c(\xi , 0) = 0$ gives

$$\begin{aligned} u_x^c(\xi , \eta ) = -\frac{k_x^{eq}}{k_x^c}\varepsilon _x\xi \left[ 1- \exp \left( -\frac{\eta }{\varOmega R \tau _x} \right) \right] . \end{aligned}$$

(24)

Substituting (24) into (18) leads to

$$\begin{aligned} u_x^b(\xi , \eta ) = -\frac{k_x^{eq}}{k_x^b}\varepsilon _x\xi \left[ 1+\frac{k_x^b}{k_x^c}\exp \left( -\frac{\eta }{\varOmega R \tau _x} \right) \right] \end{aligned}$$

(25)

and

$$\begin{aligned} f_x(\xi , \eta ) = -k_x^{eq}\varepsilon _x\xi \left[ 1- \exp \left( -\frac{\eta }{\varOmega R \tau _x}\right) \right] . \end{aligned}$$

(26)

Equations (24) and (25) highlight that the deformation of the element representing the tread and the carcass vary differently with the time, or, equivalently, with the travelled distance $\eta$ (Fig. 2). More specifically, while the deformation of the tread decreases with the distance, that one of the carcass increases.

Fig. 2

The deformation of the bristles schematising the tyre tread and carcass vary with the travelled distance. a Double brush scheme. b Trend of the bristles deformation is depicted for three different values of the travelled distance during a pure longitudinal interaction. At $\eta =0$, the carcass (black bristle) is undeformed, and the tread bristle (blue bristle) completely absorbs the total deformation equalling $-\varepsilon _x \xi$. Then, the carcass deformation gradually increases, and the one of the tread decreases, until they reach their steady-state value for $\eta = \infty$. (Color figure online)

This result can be interpreted in two different ways: if the series system composed by the linear spring of the carcass and the Kelvin-Voigt element schematising the tread is considered, the initial null value of force acting on the system can be explained with the fact that the carcass is undeformed at the distance $\eta = 0$; instead, if the tread and the carcass are considered together as a linear solid element, the total dynamics of the system can be described by the following equation

$$\begin{aligned} \begin{aligned}&f_x(\xi , \eta ) + \varOmega R \frac{\sigma _x}{k_x^c+k_x^b}\frac{\partial f_x(\xi , \eta )}{\partial \eta } = \frac{k_x^c k_x^b}{k_x^c+k_x^b}u_x(\xi , \eta ) \\&\quad +\varOmega R \frac{\sigma _x k_x^c}{k_x^c+k_x^b}\frac{\partial u_x(\xi , \eta )}{\partial \eta }, \end{aligned} \end{aligned}$$

(27)

in which $u_x = u_x^c+u_x^b = -\varepsilon _x \xi$.

More specifically, since the quantity $u_x$ is constant with the time or, equivalently, with the travelled distance, an initial zero stress $f_x$ in the above relation (27) necessarily implies that the total deformation for $\eta = 0$ must be related to the temporal derivative of the friction force. From the initial time, the shear stress tends then to increase and to reach asymptotically its steady-state value; the two opposite trends of the friction force and of its derivative ensure the constant total deformation prescribed by the adherence condition.

This occurs as long as the shear force acting on the bristles does not equal the vertical pressure value multiplied by the static friction coefficient.

Hence, in order to obtain the position of the breakaway point, a pressure trend must be introduced. In this paper, the vertical pressure distribution in the contact patch is modelled with the following formula [17]:

$$\begin{aligned} p_z(\xi , N, \nu ) = \frac{6N}{bl} A_1 \frac{\xi }{l}\left( 1-\frac{\xi }{l}\right) \left[ 1-A_2\frac{\xi }{l} \left( 1-\frac{\xi }{l}\right) \right] , \end{aligned}$$

(28)

with N the normal load applied at the rim centre and $A_1$ and $A_2$ defined as

$$\begin{aligned} A_1&= \frac{1+a}{1+a/5} \end{aligned}$$

(29a)

$$\begin{aligned} A_2&= \frac{4a}{1+a} \end{aligned}$$

(29b)

with

$$\begin{aligned} a(N, \bar{p}_0)= a_0(\bar{p}_0)(1-e^{-k(\bar{p}_0)N}), \end{aligned}$$

(30)

in which $\bar{p}_0$ is the dimensionless inflation pressure. This function of the parameter a is a formulation resulting from a good agreement between accuracy and formal simplicity.

The analytical expression for the friction coefficient is given as

$$\begin{aligned} \mu _d(\varepsilon ) = \mu _\infty + \frac{\mu _s-\mu _\infty }{M_1\varepsilon ^2 + M_2|\varepsilon | + 1}, \end{aligned}$$

(31)

where $\mu _s$ is the static friction coefficient, $\mu _d$ is the dynamic one varying with the slip parameter, and $\mu _\infty$ is its asymptotical value.

Introducing the following dimensionless variables

$$\begin{aligned} \bar{\xi }&= \frac{\xi }{l} \end{aligned}$$

(32a)

$$\begin{aligned} \bar{\eta }&= \frac{\eta }{l} \end{aligned}$$

(32b)

the shear stress acting on the bristles can be rewritten as

$$\begin{aligned} f_x(\bar{\xi }, \bar{\eta }) = -k_x^{eq} l\varepsilon _x\bar{\xi }\left[ 1-\exp \left( -\bar{\eta }\frac{l}{\varOmega R \tau _x} \right) \right] . \end{aligned}$$

(33)

Now the position of the breakaway point can be found by imposing the following equivalence

$$\begin{aligned} f_x(\bar{\xi }, \bar{\eta }) = - \mu _s p_z(\bar{\xi }) sign(\varepsilon _x) \end{aligned}$$

(34)

which, for $a \not = 0$, leads to

$$\begin{aligned} \begin{aligned} \lambda (|\varepsilon _x|, \bar{\eta })&= -\frac{\root 3 \of {2}(3A_2-A_2^2)}{3 A_2 (A_3 + 3 \sqrt{3} \sqrt{A_4})^{1/3}} \\&\quad + \frac{(A_3 + 3 \sqrt{3} \sqrt{A_4})^{1/3}}{3 \root 3 \of {2}A_2}+\frac{2}{3}, \end{aligned} \end{aligned}$$

(35)

with

$$\begin{aligned} A_3&= -2A_2^3-27A_2^2A_5+9A_2^2 \end{aligned}$$

(36a)

$$\begin{aligned} A_4&= 4A_2^5 A_5 + 27A_2^4 A_5^2 - 18 A_2^4 A_5 - A_2^4 + 4A_2^3 \end{aligned}$$

(36b)

$$\begin{aligned} A_5&= k_x^{eq}l|\varepsilon _x|\left[ 1-\exp \left( -\bar{\eta }\frac{l}{\varOmega R \tau _x} \right) \right] /\left( \mu _{sx}\frac{6N}{bl} A_1\right) . \end{aligned}$$

(36c)

For $a=0$ the adherence length is given by

$$\begin{aligned} \lambda = 1 - \frac{bl}{\mu _{sx} 6N} k_x^{eq} l|\varepsilon _x|\left[ 1-\exp \left( -\bar{\eta }\frac{l}{\varOmega R \tau _x } \right) \right] . \end{aligned}$$

(37)

Equations (35) and (36) highlight that the adherence length varies with both the slip parameter and the distance. The critical value of $\varepsilon _x$ for which the whole contact length is in slippage condition can be sought by imposing $\lambda = 0$

$$\begin{aligned} |\varepsilon _x^{crit}| = \frac{3\mu _{sx} N}{C_x(\bar{\eta })}A_1 , \end{aligned}$$

(38)

where $C_x(\bar{\eta })$ is defined as follows

$$\begin{aligned} C_x(\bar{\eta }) = \frac{1}{2}bl^2 k_x^{eq} \left[ 1-\exp \left( -\bar{\eta }\frac{l}{\varOmega R \tau _x} \right) \right] . \end{aligned}$$

(39)

The above equation states that the critical value of the slip parameter changes with the distance; more specifically, since the denominator grows with the time, the critical value of $|\varepsilon _x|$ becomes smaller. This occurs because the damping of both the carcass and the bristle tend to reduce the portion of the contact patch that is in slippage condition. In other words, at a fixed time, even if the slip parameter equals its asymptotical value $\varepsilon _x^{crit}$, the tyre is not in slippage condition at any finite distances. This also implies that the tyres slips only for higher value of $\varepsilon _x$ than the critical asymptotical value, depending on the travelled distance.

The total longitudinal force developed at the tyre-road interface can now be written as

$$\begin{aligned} F_x(\lambda (|\varepsilon _x|,\bar{\eta }), \bar{\eta }) = F_x^a(\lambda (|\varepsilon _x|,\bar{\eta }), \bar{\eta }) +F_x^s(\lambda (|\varepsilon _x|,\bar{\eta }), \bar{\eta }), \end{aligned}$$

(40)

where $F_x^a$ is the force contribution in the adherence zone and $F_x^s$ is the force related to the slippage one.

The first rate is defined as

$$\begin{aligned} F_x^{a} = bl\int _{0}^{\lambda } f_x^a (\bar{\xi },\bar{\eta }) \, d \bar{\xi } \end{aligned}$$

(41)

and reads

$$\begin{aligned} F_x^{a} = -\frac{1}{2}bl^2 \lambda ^2 k_x^{eq}|\varepsilon _x| \left[ 1-\exp \left( -\frac{\eta }{\varOmega R \tau _x} \right) \right] sign(\varepsilon _x). \end{aligned}$$

(42)

Substituting Eq. (39) into (42) yields

$$\begin{aligned} F_x^{a}= - C_x |\varepsilon _x| \lambda ^2 sign(\varepsilon _x). \end{aligned}$$

(43)

Specifying the product $C_x|\varepsilon _x|$ also gives

$$\begin{aligned} F_x^{a} = -3\mu _{sx} N A_1 \lambda ^2 (1-\lambda )\left[ 1-A_2\lambda (1-\lambda )\right] sign(\varepsilon _x). \end{aligned}$$

(44)

The second term of Eq. (40) is

$$\begin{aligned} F_x^{s} = bl\int _{\lambda }^{1} f_x^s (\bar{\xi }) \, d \bar{\xi } = -bl\int _{\lambda }^{1} \mu _{dx} p_z(\bar{\xi })sign(\varepsilon _x) \, d \bar{\xi } \end{aligned}$$

(45)

which is still function of the variable $\bar{\eta }$ because the position of the breakaway point changes with the travelled distance. Developing the integral in the above leads to

$$\begin{aligned} F^s_{x}&= - \mu _{dx} N A_1 \left[ \left( 1-\frac{A_2}{5}\right) -\lambda ^2 \left( 3-2\lambda (1+A_2)\right. \right. \nonumber \\&\left. \left. +A_2\left( 3\lambda ^2-\frac{6}{5}\lambda ^3 \right) \right) \right] sign(\varepsilon _x). \end{aligned}$$

(46)

Finally, the total force reads

$$\begin{aligned} F_x&= -N A_1\left[ 3\mu _{sx}\lambda ^2 (1-\lambda )\left( 1-A_2\lambda (1-\lambda )\right) \right. \nonumber \\&\left. +\mu _{xd}\left( 1-\frac{A_2}{5}\right) -\mu _{dx} \lambda ^2\left( 3-2\lambda (1+A_2)\right. \right. \nonumber \\&\left. \left. +A_2\left( 3\lambda ^2-\frac{6}{5}\lambda ^3 \right) \right) \right] sign(\varepsilon _x), \end{aligned}$$

(47)

where the adherence length $\lambda$ is function of both the slip parameter and the distance $\bar{\eta }$.

Combining Eq. (35) with (47) gives the total longitudinal force as explicit function of the slip parameter $|\varepsilon _x|$ and the travelled distance $\bar{\eta }$.

4 Lateral interaction

The determination of the lateral force due to a steering manoeuvre can be performed as in the previous section. It results

$$\begin{aligned} \begin{aligned} F_{y\alpha } &=-N A_1 \left[ 3\mu _{sy}\lambda ^2 (1-\lambda )\left( 1-A_2\lambda (1-\lambda )\right) \right. \\&\left. +\mu _{dy}\left( 1-\frac{A_2}{5}\right) -\mu _{dy}\lambda ^2\left( 3-2\lambda \left( 1+A_2\right) \right. \right. \\&\left. \left. +A_2\left( 3\lambda ^2-\frac{6}{5}\lambda ^3 \right) \right) \right] sign(\varepsilon _{y}), \end{aligned} \end{aligned}$$

(48)

with $\lambda$ as in Eq. (35) or (37) and $A_5$ now defined as

$$\begin{aligned} A_5 = k_y^{eq}l|\varepsilon _y|\left[ 1-\exp \left( -\bar{\eta }\frac{l}{\varOmega R \tau _y} \right) \right] /\left( \mu _{sy}\frac{6N}{bl} A_1\right) , \end{aligned}$$

(49)

with

$$\begin{aligned} k_y^{eq}&= \frac{k_y^c k_y^b}{k_y^c+k_y^b} \end{aligned}$$

(50a)

$$\begin{aligned} \tau _y&= \frac{\sigma _y}{k_y^c+k_y^b} \end{aligned}$$

(50b)

The self-aligning moment is given by

$$\begin{aligned} \begin{aligned} M_z = \frac{1}{2}bl \int _{0}^{l} f_{y\alpha } \, d\xi - b \int _{0}^{l} f_{y\alpha } \xi \, d\xi , \end{aligned} \end{aligned}$$

(51)

where first integral is

$$\begin{aligned} \frac{1}{2}bl \int _{0}^{l} f_{y\alpha } \, d\xi = \frac{l}{2} F_{y\alpha } \end{aligned}$$

(52)

and the total moment can be written as

$$\begin{aligned} M_z = \frac{l}{2} F_{y\alpha } - bJ, \end{aligned}$$

(53)

with

$$\begin{aligned} J = \int _{0}^{l} f_{y\alpha } \xi \, d\xi = l^2 \int _{0}^{\lambda } f^a_{y\alpha } \bar{\xi } \, d\bar{\xi } + l^2 \int _{\lambda }^{1} f^s_{y\alpha } \bar{\xi } \, d\bar{\xi }. \end{aligned}$$

(54)

Developing the above integrals yields

$$\begin{aligned} \begin{aligned} J&= -\frac{l}{b} N A_1 \left[ 2\mu _{sy} \lambda ^3 (1-\lambda ) \left( 1-A_2\lambda (1-\lambda )\right) \right. \\&\quad \left. + \frac{1}{10} \mu _{dy}\left( 5-A_2\right) -\frac{1}{10}\mu _{dy}\lambda ^3 \left( 20-15\lambda \left( 1+ A_2\right) \right. \right. \\&\quad \left. \left. +24 A_2\lambda ^2 -10 A_2 \lambda ^3 \right) \right] sign(\varepsilon _y). \end{aligned} \end{aligned}$$

(55)

Finally, combining Eqs. (48), (53) and (55) leads to

$$\begin{aligned} \begin{aligned} M_z&= -\frac{l}{2} N A_1\left[ \mu _{sy}\lambda ^2 (3-4\lambda )(1-\lambda )\left( 1-A_2\lambda (1-\lambda )\right) \right. \\&\quad \left. -\mu _{dy}\lambda ^2\left( 3-2\lambda \left( 3+A_2\right) + 3\lambda ^2\left( 1+2A_2\right) \right. \right. \\&\quad \left. \left. -\lambda ^3 2A_2 (3-\lambda )\right) \right] sign(\varepsilon _y). \end{aligned} \end{aligned}$$

(56)

5 Analysis for consecutive manoeuvres

In the previous sections we assumed that the bristles did not oppose any resistance to the deformation at $t=0$, since the initial value of the interaction forces and moments resulted in nothing at the initial time. Now we want to investigate the response of the carcass-tread system for repeated manoeuvres. Firstly, we suppose that the time between two consecutive manoeuvres is always the same $t^*$; furthermore, the increase in the slip parameter is assumed to be constant for each manoeuvre.

Hence, for the nth manoeuvre, the total slip will be

$$\begin{aligned} \varepsilon _{x} = n \varDelta \varepsilon _x. \end{aligned}$$

(57)

The problem can be solved by searching for function $g(\xi )$ in Eq. (21). From $n=1$ it is also known that it results

$$\begin{aligned} g_1(\xi ) = \frac{k_x^{eq}}{k_x^c} \varepsilon _x \xi . \end{aligned}$$

(58)

The value of the coefficient c for the nth manoeuvre can be easily deduced by imposing n times the continuity of the shear force:

$$\begin{aligned} g_n(\xi ) = \frac{k_x^{eq}}{k_x^c}\varDelta \varepsilon _x \xi \sum _{i=0}^{n-1}\exp \left( -\frac{it^*}{\tau _x}\right) , \end{aligned}$$

(59)

which can be rearranged as

$$\begin{aligned} \displaystyle g_n(\xi ) = \frac{k_x^{eq}}{k_x^c}\varDelta \varepsilon _x \xi \frac{1-\exp (-nt^*/\tau _x)}{1-\exp (-t^*/\tau _x)}. \end{aligned}$$

(60)

Renaming

$$\begin{aligned} G_n = \frac{1-\exp (-nt^* /\tau _x)}{1-\exp (-t^*/\tau _x)}, \end{aligned}$$

(61)

it can be finally written

$$\begin{aligned} u_{x,n}^b(\xi , \eta )&= -\frac{k_x^{eq}}{k_x^b}\varDelta \varepsilon _x\xi \left[ n + G_n\frac{k_x^b}{k_x^c}\exp \left( -\frac{t}{\tau _x} \right) \right] ,\end{aligned}$$

(62a)

$$\begin{aligned} u_{x,n}^c(\xi , \eta )&= -\frac{k_x^{eq}}{k_x^c}\varDelta \varepsilon _x\xi \left[ n - G_n\exp \left( - \frac{t}{\tau _x} \right) \right] , \end{aligned}$$

(62b)

$$\begin{aligned} f_{x,n}(\xi , t)&= -k_x^{eq}\varDelta \varepsilon _x\xi \left[ n-G_n \exp \left( -\frac{t}{\tau _x}\right) \right] . \end{aligned}$$

(62c)

Equation (62) states that the deformation of both the carcass and the bristle vary in a such different way in the case of consecutive manoeuvres. More specifically, because $G_n$ is a decreasing function in $t^*$, the carcass tends to deform more at the initial time, while the bristle tends to deform less; of course, the steady-state rates of deformation are the same of those obtained starting from the pure-rolling condition. The longitudinal force per unit of area also increases more rapidly in absolute value.

All these phenomena are due to the predeformation of the carcass that exists before the introduction of the slip variation. More specifically, the less is the time between two consecutive manoeuvres, the less is the change in the behaviour of the carcass-tread system.

In particular, it results

$$\begin{aligned} \lim _{t^* \rightarrow 0} G_n = \lim _{t^* \rightarrow 0} \frac{1-\exp \left( -nt^*/\tau _x \right) }{1-\exp \left( -t^*/\tau _x\right) } = n. \end{aligned}$$

(63)

Combining Eq. (62) with (63) yields

$$\begin{aligned} u_{x,n}^b(\xi , \eta )&= -\frac{k_x^{eq}}{k_x^b}n\varDelta \varepsilon _x\xi \left[ 1 + \frac{k_x^b}{k_x^c}\exp \left( -\frac{t}{\tau _x} \right) \right] , \end{aligned}$$

(64a)

$$\begin{aligned} u_{x,n}^c(\xi , \eta )&= -\frac{k_x^{eq}}{k_x^c}n\varDelta \varepsilon _x\xi \left[ 1 - \exp \left( -\frac{t}{\tau _x} \right) \right] ,\end{aligned}$$

(64b)

$$\begin{aligned} f_{x,n}(\xi , t)&= -k_x^{eq} n\varDelta \varepsilon _x\xi \left[ 1 - \exp \left( -\frac{t}{\tau _x}\right) \right] , \end{aligned}$$

(64c)

which, recalling (57), are almost identical to the Eqs. (24)–(26).

6 Simulation results

Some simulations have carried out in the MATLAB environment in order to investigate the tyre behaviour according to the model developed in this paper and the results have been compared with those ones provided by preexisting models. However, preexisting transient models are not generally able to deal with the local deformation of the tyre carcass because they are mainly based on the simplifying assumption of the single-point contact.

Figure 3 shows the qualitative deformations of the bristles schematising the tyre tread and carcass due to a pure longitudinal interaction versus the travelled distance for different values of the slip parameter. The distance from the entrance has also been fixed at $\bar{\xi }=1$. This condition virtually corresponds to a complete adherence scenario. It can be noticed that the two quantities are characterised by opposite trends over the time, since the total deformation must always equal the slip parameter value multiplied by distance from the entrance.

Fig. 3

The bristles schematising the tyre carcass and tread undergo variable deformations with the travelled distance $\eta$ (m). The two trends are opposite because the total derivative of the global deformation must always equal the slip parameter in absolute value ($k_y^b = k_y^c = 2 \times 10^7$ ($\hbox {N/m}^3$), $\sigma _y = 5 \times 10^4$ ($\hbox {N/m}^3 \,\mathrm{s}$))

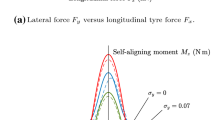
The trend of the lateral force and the self-aligning moment versus the travelled distance is shown in Fig. 4. Generally speaking, it can be highlighted that both the force and the moment go trough a transient period and then they tend asymptotically to their steady-state values. However, while the trend of the lateral force is quasi-monotonous, that one of the self-aligning moment is characterised by a peak for bigger values of the lateral slip (in the example, for values $\varepsilon _y \ge 1.0$).

Fig. 4

The lateral force increases monotonically in absolute values for the lateral slip parameter $\varepsilon _y \le \varepsilon _y^{crit}$, where $\varepsilon _y^{crit}$ is referred to its steady-state value. In contrast, at the highest slip ratios, the trend of the self-aligning moment shows a maximum and then tends to its asymptotical value

The adherence length and the critical slip values for different steering manoeuvres are also depicted in Fig. 5. More specifically, the adherence length $\lambda$ is plotted in Fig. 5a for different vertical forces and different values of the nondimensioanl travelled distance $\bar{\eta } = 0.1$ and 0.2 (dash-dotted and dashed line, respectively).

In Fig. 5b, the time trend of the absolute value of the critical slip against the travelled distance is shown for three different normal loads. The dashed lines refer to the corresponding steady-state values.

Fig. 5

The adherence length $\lambda$ increases for growing vertical loads and decreases with the time; in contrast, the critical value of the lateral slip parameter $|\varepsilon _y^{crit}|$ ideally tends to infinite the initial times and than quickly reaches its asymptotical value

Fig. 6

Both the trends of the force (longitudinal or lateral) and of the moment are coherent with the ones obtained by employing simpler models. For values of the (lateral) slip parameter $\varepsilon _y \le |\varepsilon _y^{crit}|$, the values of the generalised forces are always smaller than those obtained for the steady-state cases (solid lines), which correspond to the solution obtained by employing a brush model without carcass compliance. The dash-dotted and dashed lines refer to a nondimensional value of the travelled distance $\bar{\eta } = 0.1$ and 0.2, respectively

Fig. 7

a Compares the tangential force obtained by instantly varying the slip ratio from zero to its final value (light gray, with $t^* = 0$ (s)) with that one obtained by gradually imposing smaller increments (dark gray) after a fixed time between two consecutive manoeuvres $t^* = 2$ (s). Of course, the steady-state values obtained for the two cases coincide. The same occurs for the self aligning moment in b

In particular, it can be noticed that both the adherence length and the critical slip tend to decrease with the time (or, equivalently, with the travelled distance) for a fixed value of the slip parameter; this occurs because, in contrast, the stresses arising in the contact patch increase monotonically. Roughly speaking, this means that the static friction curve is intercepted at a point closer to the entrance, and consequently both the adherence length and the maximum value of the slip decrease over the time.

Finally, the $F_{y\alpha }-\varepsilon _y$ and the $M_z-\varepsilon _y$ curves are given in Fig. 6. Again, the dashed and the dash-dotted lines are referred to $\bar{\eta } = 0.1$ and $\bar{\eta } = 0.2$, respectively, while the solid ones represent the forces reported at their steady-state values. The asymptotical trend of both the generalised forces is exactly that one obtained by employing the common steady-state brush models. The transient behaviour of both the lateral (or longitudinal) force and the self-aligning moment is due to the deformation of the tyre carcass, which results in nothing starting from a free-rolling scenario.

Results for consecutive manoeuvres are shown in Fig. 7. In both cases, the introduction of a finite slip difference does not bring about a discontinuity in the trend of the forces. This is also in accordance with the results obtained by Pacejka with the Single Point Contact Model.

7 Conclusion

In an age when a large part of the vehicle design phase is carried out via off-line computer modelling and virtual test driving in simulators, an exhaustive understanding of the physical behaviour of each vehicle subsystem and component is crucial. Among others, the tyre has definitely the biggest impact on the overall vehicle performance, since on its dynamics depend stability, comfort, handling and NVH.

At present, while relatively complex multibody and FEM models allow to comprehensively study several phenomena concerning the tyre dynamics, they are not appropriate to be employed in real-time simulation because of their intrinsic computational burden.

In the present paper an enhanced transient brush model has been developed. Unlike the pre-existing models, it can deal with the tyre-road interaction problem without neglecting some crucial aspects such as the local deformation of the tyre carcass and the variation of both the adherence length and the critical slip value with the travelled distance. A preliminary study has been carried out with reference to the transition from the pure-rolling condition to accelerating and braking ones. Simulation outputs show a good agreement with the results obtained by employing simpler models.

Finally, in the case of consecutive manoeuvre, it has been highlighted that both the forces and the moments arising in the contact patch vary continuously by introducing a finite increase of the slip parameter. This result is consistent with those ones obtained by Pacejka by using the Single Point Contact model.

The next phase consists on the validation of the model. The possibility of integrating the presented analysis with more advanced tyre models must still be assessed. Further developments could also be geared towards removing the one-dimensionality hypothesis, by modelling the shape of the contact patch in a more accurate way.