Stochastic response determination of structural systems modeled via dependent coordinates: a frequency domain treatment based on generalized modal analysis

Abstract

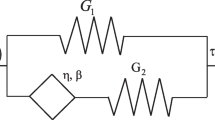
Generalized independent coordinates are typically utilized within an analytical dynamics framework to model the motion of structural and mechanical engineering systems. Nevertheless, for complex systems, such as multi-body structures, an explicit formulation of the equations of motion by utilizing generalized, independent, coordinates can be a daunting task. In this regard, employing a set of redundant coordinates can facilitate the formulation of the governing dynamics equations. In this setting, however, standard response analysis techniques cannot be applied in a straightforward manner. For instance, defining and determining a transfer function within a frequency domain response analysis framework is challenging due to the presence of singular matrices, and thus, the machinery of generalized matrix inverses needs to be employed. An efficient frequency domain response analysis methodology for structural dynamical systems modeled via dependent coordinates is developed herein. This is done by resorting to the Moore–Penrose generalized matrix inverse in conjunction with a recently proposed extended modal analysis treatment. It is shown that not only the formulation is efficient in drastically reducing the computational cost when compared to a straightforward numerical evaluation of the involved generalized inverses, but also facilitates the derivation and implementation of the celebrated random vibration input–output frequency domain relationship between the excitation and the response power spectrum matrices. The validity of the methodology is demonstrated by considering a multi-degree-of-freedom shear type structure and a multi-body structural system as numerical examples.

Appendix

1.1 Moore–Penrose theory elements

In this Appendix, some elements of the generalized matrix inverse theory pertaining to the Moore–Penrose (M–P) matrix inverse are provided for completeness [13, 14].

Definition: If ${\mathbf{A}} \in {\mathbb{C}}^{m\,x\,l} \,$ then ${\mathbf{A}}^{ + } \,$ is the unique matrix in ${\mathbb{C}}^{l\,x\,m} \,$ so that

$$ {\mathbf{A}}\,{\mathbf{A}}^{ + } {\mathbf{A}} = {\mathbf{A}},\;{\mathbf{A}}^{ + } {\mathbf{A}}\,{\mathbf{A}}^{ + } = {\mathbf{A}}^{ + } \;,\;\left( {{\mathbf{A}}\,{\mathbf{A}}^{ + } } \right)^{T} = {\mathbf{A}}\,{\mathbf{A}}^{ + } \;,\left( {{\mathbf{A}}^{ + } {\mathbf{A}}} \right)^{T} = {\mathbf{A}}^{ + } {\mathbf{A}}. $$

(29)

The matrix ${\mathbf{A}}^{ + } \,$ is known as the M-P inverse of ${\mathbf{A}}$ and satisfies all Eq. (29). In general, the M-P inverse of a square matrix exists for any arbitrary ${\mathbf{A}} \in {\mathbb{C}}^{m\,x\,m} \,$, and if ${\mathbf{A}}$ is non-singular, ${\mathbf{A}}^{ + } \,$ coincides with ${\mathbf{A}}^{ - 1}$. Further, the M-P inverse of any m x l matrix ${\mathbf{A}}$ can be determined, for instance, via a number of recursive formulae (e.g., [13, 14]), and provides a tool for solving equations of the form

$$ {\mathbf{A}}\,{\mathbf{x}} = {\mathbf{b}} $$

(30)

where ${\mathbf{A}}$ is a rectangular (m x l) matrix, ${\mathbf{x}}$ is an l vector and ${\mathbf{b}}$ is an m vector. For a singular square matrix ${\mathbf{A}}$, utilizing the M-P inverse, Eq. (2) yields

$$ \,{\mathbf{x}} = {\mathbf{A}}^{ + } {\mathbf{b}} + \left( {{\mathbf{I}} - {\mathbf{A}}^{ + } {\mathbf{A}}} \right){\mathbf{y}} $$

(31)

where y is an arbitrary n vector and ${\mathbf{I}}$ is the identity matrix.