Skip to main content
SpringerLink
Log in

Modeling and analysis of an axially acceleration beam based on a higher order beam theory

  • Published:
Meccanica Aims and scope Submit manuscript

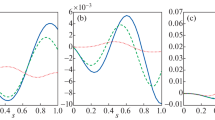
Abstract

In this paper, a higher order model equation is presented for an axially accelerating beam. Based on a new kinematic frame of the beam and continuum mechanics theory, the coupled governing equations of nonlinear vibration for axially accelerating beam are obtained with the aid of the generalized Hamilton principle. The governing equations take into account the characteristic of the material, the shear strain, the rotation strain and the effect of longitudinally varying tension due to the axial acceleration. The equations are decoupled into a nonlinear partial-integro-differential equations when the transverse nonlinear vibration is small. For the principal parametric resonances, the steady-state frequency responses are obtained by the multiple scales method. The stable and unstable interval are analyzed for the trivial and nontrivial steady-state response. Effects of the system parameters on the amplitude have been investigated. The results show that the material parameter (i.e, in-plane Poisson ratio) has a significant effect on the amplitude and the nonlinear vibration behavior type. The amplitude decrease with the growth of the in-plane Poisson ratio. The total potential energy has play a very important role in determining the amplitude of frequency response according to model analysis. Lastly, comparisons among the analytical solutions and numerical solutions are made and good agreements for the amplitude are found.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Wickert JA, Mote CD (1990) Classical vibration analysis of axially moving continua. Trans ASMW 57:738–743

    Article  MATH  Google Scholar 

  2. Moon J, Wickert JA (1997) Non-linear vibration of power transmission belts. J Sound Vib 4:419–431

    Article  ADS  Google Scholar 

  3. Pakdemirli M, Ulsoy AG (1997) Stability analysis of an axially accelerating string. J Sound Vib 203:815–832

    Article  ADS  Google Scholar 

  4. Öz HR, Parkdemirli M (1999) Vibrations of an axially moving beam with time-dependent velocity. J Sound Vib 227(2):239–257

    Article  ADS  Google Scholar 

  5. Chen L-Q, Tang Y-Q, Lim CM (2010) Dynamic stability in parameteric resonance of axially accelerating viscoelastic Timoshenko beams. J Sound Vib 329:547–565

    Article  ADS  Google Scholar 

  6. Chen L-Q, Tang Y-Q (2011) Combination and principal parameteric resonances of axially accelerating viscoelastic beam: recognition of longitudinally varying tensions. J Sound Vib 330:5598–5614

    Article  ADS  Google Scholar 

  7. Chen L-Q, Tang Y-Q (2012) Parametric stability of axially accelerating viscoelastic beam with recognition of longitudinally varying tensions. J Vib Acoust 134:011008-1–011008-11

    Google Scholar 

  8. Rezaee M, Lotfan S (2015) Non-linear nonlocal vibration and stability analysis of axially moving nanoscale beams with time-dependent velocity. Int J Mech Sci 96:36–46

    Article  Google Scholar 

  9. Sahoo B, Panda LN, Pohit G (2015) Two-frequency parametric excitation and internal resonance of a moving viscoelastic beam. Nonlinear Dyn 82:1721–1742

    Article  MathSciNet  Google Scholar 

  10. Sahoo B, Panda LN, Pohit G (2017) Stability, bifurcation and chaos of a traveling viscoelastic beam tuned to 3:1 internal resonance and subjected to parametric excitation. Int J Bifurc Chaos 27:1750017-1–1750017-20

    Article  MathSciNet  MATH  Google Scholar 

  11. Lee U, Oh H (2005) Dynamics of an axially moving viscoelastic beam subjected to axial tension. Int J Solids Struct 42:2381–2398

    Article  MATH  Google Scholar 

  12. Öz HR (2001) On the vibrations of an axially traveling beam on fixed supports with variable speed. J Sound Vib 64:556–564

    Article  Google Scholar 

  13. Jaksic N (2009) Numerical algorithm for natural frequencies computation of an axially moving beam model. Meccanica 44:687–695

    Article  MathSciNet  MATH  Google Scholar 

  14. Seddighi H, Eipakchi H (2013) Natural frequency and critical speed determination of an axially moving viscoelastic beam. Mech Time Depend Mater 17:529–541

    Article  ADS  Google Scholar 

  15. Ahmadian MT, Nasrabadi VY, Mohammadi H (2010) Nonlinear transversal vibration of an axially moving viscoelastic string on a viscoelastic guide subjected to mono-frequency excitation. Acta Mech 214:357–373

    Article  MATH  Google Scholar 

  16. Pellicano F, Zirilli F (1998) Boundary layers and non-linear vibrations in an axially moving beam. Int J Non-Linear Mech 33:691–711

    Article  MathSciNet  MATH  Google Scholar 

  17. Pellicano F, Vestroni F (2000) Nonlinear dynamics and bifurcations of an axially moving beam. J Vib Acoust 122:21–30

    Article  Google Scholar 

  18. Pellicano F, Vestroni F (2002) Complex dynamics of high-speed axially moving systems. J Sound Vib 258:31–44

    Article  ADS  Google Scholar 

  19. Parker RG (1999) Supper critical speed stability of the trivial equilibrium of an axially moving string on an elastic foundation. J Sound Vib 221:205–219

    Article  ADS  MATH  Google Scholar 

  20. Ponomareva SV, van Horssen WT (2009) On the transversal vibrations of an axially moving continuum with a time-varying velocity: transient from string to beam behavior. J Sound Vib 325:959–973

    Article  ADS  Google Scholar 

  21. Ghayesh MH, Amabili M (2013) Parametric stability and bifurcations of axially moving viscoelastic beams with time-dependent axial speed. Mech Based Des Struct Mach 41:359–381

    Article  Google Scholar 

  22. Ghayesh MH, Amabili M, Farokhi H (2013) Two-dimensional nonlinear dynamics of an axially moving viscoelastic beam with time-dependent axial speed. Chaos Solitons Fractals 52:8–29

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Ghayesh MH, Khadem SE (2008) Rotary inertia and temperature effects on non-linear vibration, steady-state response and stability of an axially moving beam with time- dependent velocity. Int J Mech Sci 50:389–404

    Article  MATH  Google Scholar 

  24. Marynowski K, Kapitaniak T (2007) Zener internal damping in modelling of axially moving viscoelastic beam with time-dependent tension. Int J Non-Linear Mech 42:118–131

    Article  MATH  Google Scholar 

  25. Chakraborty G, Mallik A (1999) Stability of an accelerating beam. J Sound Vib 227:309–320

    Article  ADS  Google Scholar 

  26. Chen LH, Zhang W, Yang FH (2010) Nonlinear dynamics of higher-dimensional system for an axially accelerating viscoelastic beam with in-plane and out-of-plane vibrations. J Sound Vib 25:5321–5345

    Article  ADS  Google Scholar 

  27. Bozkurt Burak özhan (2014) Vibration and stability analysis of axially moving beams with variable speed and axial force. Int J Struct Stab Dyn 6:1450015-1–1450015-23

    MathSciNet  MATH  Google Scholar 

  28. Mao XY, Ding H, Chen LQ (2017) Forced vibration of axially moving beam with internal resonance in the supercritical regime. Int J Mech Sci 131–132:81–94

    Article  Google Scholar 

  29. Kumar CPS, Sujatha C, Shankar K (2015) Vibration of simply supported beams under a single moving load: a detail study of cancellation phenomenon. Int J Mech Sci 99:40–47

    Article  Google Scholar 

  30. Kumar CPS, Sujatha C, Shankar K (2017) Vibration of nonuniform beams under moving point load: an approximate analytical soltuion in time domain. Int J Struct Stab Dyn 17:1750035-1–1750035-17

    Google Scholar 

  31. Ferretti M, Piccardo G, Luongo A (2017) Weakly nonlinear dynamics of taut strings traveled by a single moving force. Meccanica. https://doi.org/10.1007/s11012-017-0690-5

    MathSciNet  MATH  Google Scholar 

  32. Piccardo G, Tubino F (2012) Dynamic response of Euler–Bernoulli beams to resonant harmonic moving loads. Struct Eng Mech 44:681–704

    Article  Google Scholar 

  33. Bersani A, Corte AD, Piccardo G, Rizzi N (2016) An explicit solution for the dynamics of a taut string of finite length carrying a traveling mass: the subsonic case. Z Angew Math Phys 67:1–17

    Article  MathSciNet  MATH  Google Scholar 

  34. Amabili M, Pellicano F, Paidoussis MP (1999) Nonlinear dynamics and stability of circular cylindrica shell containing fowling fluid part I: stability. J Sound Vib 225:655–699

    Article  ADS  Google Scholar 

  35. Amabili M, Pellicano F, Paidoussis MP (1999) Nonlinear dynamics and stability of circular cylindrica shell containing fowling fluid part II: large-amplitude vibration without flow. J Sound Vib 228:1103–1124

    Article  ADS  Google Scholar 

  36. Amabili M, Pellicano F, Paidoussis MP (2000) Nonlinear dynamics and stability of circular cylindrica shell containing fowling fluid part III: truncation effect without flow and experiments. J Sound Vib 237:617–640

    Article  ADS  Google Scholar 

  37. Amabili M, Pellicano F, Paidoussis MP (2000) Nonlinear dynamics and stability of circular cylindrica shell containing fowling fluid part IV: large-amplitude vibrations with flow. J Sound Vib 237:641–666

    Article  ADS  Google Scholar 

  38. Mao XY, Ding H, Chen LQ (2016) Steady-state response of a fluid-conveying pip with 3:1 internal resonance in supercritical regime. Nonlinear Dyn 86:795–809

    Article  Google Scholar 

  39. Sinir BG, Demir DD (2015) The analysis of nonlinear vibrations of pipe conveying an ideal fluid. Eur J Mech B Fluids 52:38–44

    Article  MathSciNet  Google Scholar 

  40. Alfosail FK, Nayfeh AH, Younis MI (2017) An analytic solution of the static problem of inclined resers conveying fluid. Meccanica 52:1175–1187

    Article  MathSciNet  MATH  Google Scholar 

  41. Hu K, Wang YK, Dai HL, Wang L, Qian Q (2016) Nonlinear and chaotic vibrations of cantilevered micropipes conveying fluid based on modified coupled stress theory. Int J Eng Sci 105:93–107

    Article  Google Scholar 

  42. Semnani AMD, Bahrami MN, Yazdi MRH (2017) On nonlinear vibrations of micropipes conveying fluid. Int J Eng Sci 117:20–33

    Article  MathSciNet  Google Scholar 

  43. Arani AG, Dashti P, Amir S, Yousefi M (2015) Nonlinear vibration of coupled nano- and microstructures conveying fluid based on Timoshenko beam model under two-dimensional magnetic field. Acta Mech 226:2729–2760

    Article  MathSciNet  MATH  Google Scholar 

  44. Carrera E, Pagani A, Zangallo F (2015) Comparison of various 1D, 2D and 3D FE models for the analysis of thin-walled box with transverse ribs subjected to load factors. Finite Elem Anal Des 95:1–11

    Article  Google Scholar 

  45. Pagani A, Zangallo F, Carrera E (2014) Influence of non-structural localized inertia on free vibration response of thin-walled structures by variable kinematic beam formulations. Shock Vib 2014: Article ID 141982

  46. Carrera E, Pagani A, Zangallo F (2014) Thin-walled beams subjected to load factors and non-structural masses. Int J Mech Sci 81:109–119

    Article  Google Scholar 

  47. Carrera E, Pagani A (2016) Accurate response of wing structures to free-vibration, load factors and non-structural masses. AIAA J 54(1):227–241

    Article  ADS  Google Scholar 

  48. Bozyigit B, Yesilce Y (2016) Dynamic stiffness approach and differential transformation for free vibration analysis of a moving Reddy-Brickford beam. Struct Eng Mech 58:847–868

    Article  Google Scholar 

  49. Chang JR, Lin WJ, Huang CJ, Choi ST (2010) Vibration and stability of an axially moving Rayleigh beam. Appl Math Model 34:1842–1497

    MathSciNet  MATH  Google Scholar 

  50. Zhu XW, Wang YB, Lou ZM (2016) A study of the critical strain of materials: a new kinematic frame and the leading order term. Mech Res Commun 78:20–24

    Article  Google Scholar 

  51. Wickert JA (1992) Non-linear vibration of a traveling tensioned beam. Int J Non-Linear Mech 27:503–517

    Article  MATH  Google Scholar 

  52. Wang L, Zhendong H, Zhong Z (2013) Non-linear dynamical analysis for an aixally moving beam with finite deformation. Int J Non-Linear Mech 54:5–21

    Article  Google Scholar 

Download references

Acknowledgements

This project was supported by the State Key Program of National natural Science Foundation of China (No. 11232009) and the Natural Science Foundation of China (Nos. 11372171, 11422214 and 11472177)

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai, 200072, People’s Republic of China

    Yuanbin Wang, Hu Ding & Li-Qun Chen

  2. Department of Mathematics, ShaoXing University, Shaoxing, 312000, Zhejiang, People’s Republic of China

    Yuanbin Wang

  3. Department of Mechanics, Shanghai University, Shanghai, 200444, People’s Republic of China

    Li-Qun Chen

Authors
  1. Yuanbin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hu Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Li-Qun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li-Qun Chen.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Y., Ding, H. & Chen, LQ. Modeling and analysis of an axially acceleration beam based on a higher order beam theory. Meccanica 53, 2525–2542 (2018). https://doi.org/10.1007/s11012-018-0840-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-018-0840-4

Keywords

Search

Navigation