Circuit implementation of a piezoelectric buckled beam and its response under fractional components considerations

Abstract

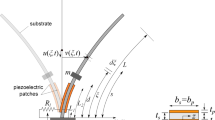
In this paper, an analog testing circuit and determinist averaging method for a vibration energy harvesting system with fractional derivative and nonlinear damping under a sinusoidal vibration source is proposed in order to predict the system response and its stability. The objective of this paper is to show that there is a possibility to make a pre-experimental design of the structure by using analog circuit and discussing the performance of a system with fractional derivative. Bifurcation diagram, poincaré maps and power spectral density are provided to deeply characterize the dynamic of the system. These results are corroborated by using 0–1 test. By using the Melnikov method, we find the necessary condition for which homoclinic bifurcation occurs. Understanding and predicting this bifurcation is very judicious in the energy harvesting field because it may lead to different types of motion in the perturbed system. The appearance of chaotic vibrations increases the frequency’s bandwidth of the harvester thereby, allowing to harvest more energy. The pre-experimental investigation is carried out through appropriate software electronic circuit (Multisim^®). The corresponding electronic circuit is designed exhibiting transient to chaos in accord with numerical simulations. The impact of fractional derivatives is presented upon the power generated by the system. In addition, by combining the harmonic force and a random excitation, the stochastic resonance appears, giving rise to large amplitude of vibration and consequently, enhancing the performance of the system. The results obtained in this work show the interest of using the electronic circuit to make the experiment analysis of the physical structure and also, the effects of the use of piezoelectric material exhibiting fractional properties in this research field.

Appendix: Analog circuit for the energy harvester

In order to build an analog circuit of Eq. (10), first write it in the form:

$$\begin{aligned} x^{\prime }&=u \nonumber \\ {u^{\prime }}&=\alpha {x^{3}}-{\mu }_{{2}}{ux^{2}}{-\eta }_{{2}}{y} \nonumber \\& \quad -\,{\omega }_{{0}}x-{\mu }_{{1}}{u}-{\sigma u}+F_{0}\cos \left( \varOmega \,\tau \right) \nonumber \\ y^{\prime }&=-\,{\omega }_{{e}}y+{\eta }_{{3}}{u}\, \end{aligned}$$

(75)

Without loss of generality, $\cos \left( \varOmega \,\tau \right)$ is replaced by $\sin \left( \varOmega \,\tau \right)$ since such a change will not affect the qualitative behavior of the system and it is conventional to denote the external sinusoidal force in an electronic circuit as $\sin \left( \varOmega \,\tau \right)$. The integration of Eq. (75) gives rise to the following system:

$$\begin{aligned} x&=\int ud \tau \nonumber \\ {u}&=\int (\alpha {x^{3}}-{\mu }_{{2}}{ux^{2}}{-\eta }_{{2}}{y} \nonumber \\& \quad -\,{\omega }_{{0}}x-{\mu }_{{1}}{u}-{\sigma u}+F_{0}\cos \left( \varOmega \,\tau \right) )d\tau \nonumber \\ y&=\int \left( -{\omega }_{{e}}y+{\eta }_{{3}}{u}\,\right) d\tau \end{aligned}$$

(76)

For the analog circuit, we use the variables $v_{x}$, $v_{y}$ and $v_{u}$ instead of x, u and y

$$\begin{aligned} v_{x}&=\int v_{u}d\tau \nonumber \\ v_{{u}}&=\int (\alpha v_{{x}}^{{3}}-{\mu }_{{2}}v_{{u}}{v}_{{x}}^{2}{ -\eta }_{{2}}v_{{y}} \nonumber \\&- \quad \,{\omega }_{{0}}v_{x}-{\mu }_{{1}}v_{{u}}-{\sigma v}_{{u}}+F_{0}\cos \left( \varOmega ^{\prime }\,\tau \right) )d\tau \nonumber \\ v_{y}&= \int \left( -{\omega }_{{e}}v_{y}+{\eta }_{{3}}v_{{u}}\,\right) d\tau \end{aligned}$$

(77)

The analog circuit for Eq. (10) is depicted in Fig. 2. From the outputs of the three integrators characterized by the capacitor $C_{1}$, $C_{2}$ and $C_{3}$, one can build the equation of the circuit. The outputs of the three integrators are denoted $v_{x}$, $v_{y}$ and $v_{u}$, respectively, are given by:

$$\begin{aligned} v_{x}&=\int {\displaystyle }\frac{1}{R_{1}C_{1}}v_{u}d\tau \nonumber \\ v_{{u}}&=\int \left( -{\displaystyle \frac{\,1}{100R_{3}C_{2}}}v_{x}^{{3}}-{ \displaystyle \ \frac{\,1}{100R_{4}C_{2}}v_{u}v_{x}^{{2}}-\,\displaystyle \frac{1 }{R_{6}C_{2}}}v_{y} \right. \nonumber \\&\left. \quad +{\displaystyle }\frac{1}{R_{5}C_{2}}v_{x}-{\ \displaystyle \frac{\,1}{ R_{2}C_{2}}}v_{u}-{\displaystyle \frac{\,1}{R_{7}C_{2}}}v_{u}+{\displaystyle \frac{v_{0}\cos \left( \varOmega \,t\right) }{R_{8}C_{2}}}\right) d\tau \nonumber \\ v_{y}&=\int \left( -{\displaystyle }\frac{1}{R_{9}C_{3}}v_{y}+{ \displaystyle }\frac{1}{R_{10}C_{3}}v_{u}\,\right) d\tau \end{aligned}$$

(78)

Differentiation of Eq. (78) with respect to the time gives:

$$\begin{aligned} v_{x}^{\prime }&={\displaystyle }\frac{1}{R_{1}C_{1}}v_{u} \nonumber \\ v_{u}^{\prime }&=\left( -{\displaystyle \frac{\,1}{100R_{3}C_{2}}}v_{x}^{{3}}-{ \displaystyle \ \frac{\,1}{100R_{4}C_{2}}v_{u}v_{x}^{{2}}-\,\displaystyle \frac{1 }{R_{6}C_{2}}}v_{y} \right. \nonumber \\&\left. +{\displaystyle }\frac{1}{R_{5}C_{2}}v_{x}-{\ \displaystyle \frac{\,1}{ R_{2}C_{2}}}v_{u}-{\displaystyle \frac{\,1}{R_{7}C_{2}}}v_{u}+\displaystyle \frac{v_{0}\cos \left( \varOmega \,t\right) }{R_{8}C_{2}}\right) \nonumber \\ v_{y}^{\prime }&=-{\displaystyle }\frac{1}{R_{9}C_{3}}v_{y}+{\displaystyle } \frac{1}{R_{10}C_{3}}v_{u} \end{aligned}$$

(79)