The effects of wall transpiration on the unsteady free convection boundary-layer flow near a stagnation point in a heat generating porous medium

Abstract

The natural convection boundary-layer flow near a stagnation point on a permeable surface embedded in a porous medium is considered when there is local heat generation within the boundary layer at a rate proportional to $(T-T_\infty )^p,\ p \ge 1$, where T is the fluid temperature and $T_\infty$ the ambient temperature. There is mass transfer through the surface characterized by the dimensionless parameter $\gamma$, with $\gamma >0$ for fluid injection and $\gamma <0$ for fluid withdrawal. The steady states are considered where it is found that, for $p >1$, there is a critical value $\gamma _c$ of $\gamma$ with solutions existing for $\gamma \ge \gamma _c$ if $1<p<2$ and for $\gamma \le \gamma _c$ if $p>2$. The initial-value problem reveals that, for $1 \le p<2$, the nontrivial steady states are stable and the solution evolves to this state at large times. However, for $p>2$ these steady states are unstable and the solution either approaches the trivial state with the local heating dying out or a finite-time singularity develops for sufficiently large initial inputs.

1 Introduction

During the transport and storage of a porous material heat can be generated locally within the medium. This can set up a convective flow within the material which may help to dissipate the heat or alternatively can lead to enhanced heat generation and even thermal runaway with possibly disastrous consequences. Examples include the spontaneous ignition in stock piles of coal [1,2,3,4], in bagasse (the cellulose waste left after the extraction of sugar from sugar cane) [5, 6] or in the wetting of cellulosic materials [7,8,9]. Previously we have modelled this problem assuming local heat generation at a rate proportional to $(T-T_\infty )^p$, where $T_\infty$ is the (constant) ambient temperature and the exponent $p \ge 1$ [10, 11]. We have assessed how the effects of the input of heat from the boundary [12] and of an outer flow [13] control the local heat generation, finding that this depended critically on the exponent p and the magnitude of the initial heat input. More recently we have considered modified form of Arrhenius kinetics [14], again seeing that the evolution of the local internal heat generation depended on the initial heat input as well as the local heating rate, finding conditions under which the local heating died away or produced a finite-time blow up in the solution.

The power-law expression for localised heat generation has been used previously in several other contexts as a model for Arrhenius kinetics. These studies have shown at least qualitative agreement with those using the more general Arrhenius form, as seen for a specific case by comparing [12] and [14]. The use of a power-law model is motivated in part by its analytic simplicity as compared to the Arrhenius function and to avoid the ‘cold boundary problem’. In this, if an inert outer region is required, as is the case here, the Arrhenius form has to be modified, as in [14]. This can, perhaps, to lead to some artificiality in the kinetic scheme used. An alternative form for the local heating has been suggested, based more on fluid flow, is to model the local heat generation as a source term with a particular spatial variation [15,16,17,18]. However, this approach has the drawback, at least for the present case of spontaneous combustion within a porous material, in that it does not allow the local heat generation to vary with the evolving temperature and velocity fields.

Here we consider how the input from the boundary influences the heat generation within the flow. We again take the above power-law term to model the heat generation within the boundary layer and allow for fluid injection or withdrawal from a thermally insulated surface. Previously, without any flow through the wall [12] and without an outer flow, we found that, when $1 \le p<2$, the local heating died away. However, for $p>2$ a finite-time blow up in the solution could occur for a sufficiently large initial input, otherwise the local heating also died out. Our aim here is to determine how this behaviour is influenced by the fluid input or withdrawal from the wall. We find that, when $p=1$, a nontrivial steady state is attained giving a balance between the rate of local heat generation and the wall mass transfer. A similar situation applies when $1<p<2$ provided now the rate of mass transfer through the wall is greater than some critical value, dependent on p. Otherwise the heat generation is inhibited. For $p>2$ there is a either finite-time thermal runaway if the initial input is above some threshold value or otherwise the local heating dies away. We start by deriving our model.

2 Model

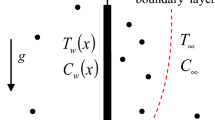
We consider the unsteady, two-dimensional natural convection boundary-layer flow that can arise near a forward stagnation point in a fluid-saturated porous material in which there is local heat generation within the boundary layer at a rate proportional to $(T-T_\infty )^p$, where T is the fluid temperature and $T_\infty$ is the ambient temperature. We assume that the bounding surface is thermally insulated and that there is normal wall velocity $v_w$, where $v_w$ can be either positive or negative. We further assume the flow is given by Darcy’s law and we make the standard Boussinesq approximation. The basic equations for our model are, see [12, 19,20,21] for example,

$$\begin{aligned}&\frac{\displaystyle \partial u}{\displaystyle \partial x}+\frac{\displaystyle \partial u}{\displaystyle \partial x}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u=\frac{g\beta K}{\nu }\,(T-T_\infty )\,S(x), \end{aligned}$$

(2)

$$\begin{aligned}&\sigma \,\frac{\displaystyle \partial T}{\displaystyle \partial t}+u\,\frac{\displaystyle \partial T}{\displaystyle \partial x}+v\,\frac{\displaystyle \partial T}{\displaystyle \partial y}=\alpha _m\,\frac{\displaystyle \partial ^2 T}{\displaystyle \partial y^2}+H_0\,(T-T_\infty )^p, \end{aligned}$$

(3)

on $0 \le y<\infty , \, t>0$, subject to the boundary conditions

$$\begin{aligned} v=v_w, \ \ \frac{\displaystyle \partial T}{\displaystyle \partial y}=0 \ \text{ on } \ y=0, \quad \ u \rightarrow 0, \ T \rightarrow T_\infty \ \text{ as } y \rightarrow \infty \quad (t >0), \end{aligned}$$

(4)

together with some initial condition and where we assume that $p \ge 1$. Here x measures distance along the body surface and y normal to it, u and v are respectively the velocity components in the x and y directions. Also K is the permeability of the porous media, $\nu$ the kinematic viscosity of the fluid, $\beta$ the coefficient of thermal expansion, g the acceleration due to gravity, $\alpha _m$ the effective thermal diffusivity and $\sigma$ the heat capacity ratio of the fluid-filled porous medium to that of the fluid. In Eq. (2), S(x) is the sine of the angle between the outward normal and the downward vertical and for a stagnation-point flow $\displaystyle S(x)=\frac{x}{\ell }$ for some length scale $\ell$.

To make Eqs. (1–4) dimensionless we write

$$\begin{aligned} \overline{x}=\frac{x}{\ell }, \ \ \overline{y}=R^{1/2}\frac{y}{\ell }, \ \ \overline{t}=\frac{U_s}{\sigma \ell }\, t, \ \ u=U_s\,\overline{u}, \ \ v=U_s\,R^{-1/2}\,\overline{v}, \ \ T-T_\infty =T_s\,\theta , \end{aligned}$$

(5)

where $T_s, U_s$ are respectively temperature and velocity scales given by

$$\begin{aligned} T_s=\left( \frac{g\beta K}{\nu H_0\ell }\right) ^{ 1/{p-2}}, \ \ \ U_s=H_0\ell \,T_s^{p-1}, \ \ (p\ne 2) \ \ \text{ and } \ \ R=\frac{U_s\ell }{\alpha _m}. \end{aligned}$$

(6)

Equation (2) becomes (on dropping the overbars) $u=x\,\theta$ and the continuity Eq. (1) is satisfied by introducing a streamfunction $\psi$ defined so that $u=\psi _y, \ v=-\psi _x$. We then write $\psi =x\,f(y,t)$, and consequently $\theta =\theta (y,t)$, to obtain

$$\begin{aligned} \frac{\displaystyle \partial ^3 f}{\displaystyle \partial y^3}+\left( \frac{\displaystyle \partial f}{\displaystyle \partial y}\right) ^{ p}+\,f\, \frac{\displaystyle \partial ^2 f}{\displaystyle \partial y^2}=\frac{\displaystyle \partial ^2 f}{\displaystyle \partial y\displaystyle \partial t}, \end{aligned}$$

(7)

subject to the boundary conditions

$$\begin{aligned} f=-\gamma , \quad \ \frac{\displaystyle \partial ^2 f}{\displaystyle \partial y^2}=0, \quad \ \frac{\displaystyle \partial f}{\displaystyle \partial y} \rightarrow 0 \ \ \text{ as } \ y \rightarrow \infty , \end{aligned}$$

(8)

where $\gamma =v_w\,R^{1/2}/U_s$. In (8), $\gamma >0$ gives fluid injection from the boundary (blowing) and $\gamma <0$ gives fluid withdrawal from the boundary (suction).

We find different behaviour depending on whether $p=1, 1<p<2$ or $p>2$, treating these cases, as well as the transition case when $p=2$, see expression (6), separately. We start by considering the steady states of Eq. (7) as these can represent the possible large time behaviour of the full initial-value problem.

3 Steady states

These represent possible large time limit of the initial-value problem (7, 8) and, for a general value of p, are given by

$$\begin{aligned} f'''+f\,f''+(f')^{\, p}=0, \quad f(0)=-\gamma , \ \ f''(0)=0, \ \ f' \rightarrow 0 \ \ \text{ as } \ y \rightarrow \infty , \end{aligned}$$

(9)

where primes denote differentiation with respect to y. We note that, for $p=2$, Eq. (9) can be integrated to give

$$\begin{aligned} f''+f\,f'=0, \end{aligned}$$

(10)

on satisfying the boundary condition as $y \rightarrow \infty$. Applying the boundary conditions on $y=0$ then shows that the only possibility when $\gamma \ne 0$ is the trivial solution $f \equiv -\gamma$ with a nontrivial solution only for $\gamma =0$.

Fig. 1

Steady states: plot of $f'(0)$ against $\gamma$ obtained from the numerical solution to (9) for $p=1$

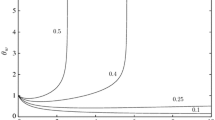
In Fig. 1 we plot $f'(0)$ against $\gamma$ for $p=1$ obtained from the numerical solution of Eq. (9). The numerical solution terminated at $\gamma =-2$, where $f'(0)$ becomes zero (we were only able to obtain the trivial solution $f \equiv -\gamma$ for $\gamma <-2$), and proceeded to large positive values of $\gamma$ with the values of $f'(0)$ increasing as $\gamma$ is increased.

Fig. 2

Steady states: plot of $f'(0)$ against $\gamma$ obtained from the numerical solution to (9) for $p=1.5$

We plot $f'(0)$ against $\gamma$ in Fig. 2 for $p=1.5$, representative of values of p in the range $1<p<2$. In this case we see that there is a critical value $\gamma _c$ of $\gamma$, where $\gamma _c \simeq -0.5085$ giving two solution branches in $\gamma _c<\gamma$. The upper branch solution continues to large positive $\gamma$, with $f'(0)$ increasing as $\gamma$ is increased, and we find only the trivial solution for $\gamma <\gamma _c$. This leads us to consider the critical values in more detail. To calculate $\gamma _c$ numerically we follow the approach given in [22], for example, whereby we make a linear perturbation to Eq. (9) resulting in a linear homogeneous equation subject to homogeneous boundary conditions and it is the solution to this eigenvalue problem that determines $\gamma _c$. We plot $\gamma _c$ against p in Fig. 3 where we see that $\gamma _c \rightarrow 0$ as $p \rightarrow 2$, as perhaps might be expected, and approaches a finite negative value as $p \rightarrow 1$, with our numerical results suggesting that $\gamma _c$ is approaching $-2$.

Fig. 3

Steady states: plot of the critical values $\gamma _c$ against p for $1<p<2$. Asymptotic expression (15) is shown by a broken line

We now consider the nature of the solution as $p \rightarrow 2$ from below. We put $p=2-\epsilon$, with then $\gamma =\mu \,\epsilon$, and look for a solution valid for $\epsilon$ small by expanding

$$\begin{aligned} f(y;\epsilon )=f_0(y)+\epsilon \,f_1(y)+\cdots . \end{aligned}$$

(11)

At leading order we obtain $f_0=2b_0\,\tanh (b_0 y)$ for some constant $b_0>0$ to be found. At $O(\epsilon )$ we have

$$\begin{aligned}&f_1'''+f_0\,f_1''+f_1\,f_0''+2f_0'\,f_1'=f_0'^{\, 2}\,\log {(f_0')},\nonumber \\&f_1(0)=-\mu , \ \ f_1''(0)=0, \ \ f_1' \rightarrow 0 \ \ \text{ as } y \rightarrow \infty . \end{aligned}$$

(12)

We can integrate Eq. (12) to obtain, on applying the boundary conditions and the expression for $f_0$,

$$\begin{aligned} 2b_0^2\,\mu= & {} \int _0^\infty f_0'^{\, 2}\log {(f_0')}dy =\frac{16b_0^3}{3}\,(\log {b_0}+\beta ) \ \ \text{ where } \ \nonumber \\ \beta= & {} \frac{3}{4}\left( 2\log {2}-\frac{10}{9}\right) \simeq 0.206387, \end{aligned}$$

(13)

on using a result given in [12]. From (13) we have

$$\begin{aligned} \mu =\frac{8b_0}{3}\,(\log {b_0}+\beta ). \end{aligned}$$

(14)

Expression (14) gives $\mu =0$ at $b_0=0$, has $b_0>0$ for $b_0>\text{ e }^{-\beta }$ and has a turning point (local minimum) at $b_0=\text{ e }^{-(1+\beta )}, \displaystyle \mu =\mu _c= -\frac{8}{3}\,\text{ e }^{-(1+\beta )}\simeq -0.79807$. Hence

$$\begin{aligned} \gamma _c \sim -0.79807\,(2-p)+\cdots \quad \text{ as } \ p \rightarrow 2. \end{aligned}$$

(15)

Asymptotic expression (15) is shown in Fig. 3 by a broken line showing good agreement with the numerically determined values as $p \rightarrow 2$.

Fig. 4

Steady states: plot of $f'(0)$ against $\gamma$ obtained from the numerical solution to (9) for $p=3.0$

We now take a value of $p=3.0$ as representative of the case when $p>2$ and in Fig. 4 we plot $f'(0)$ against $\gamma$. In this case there is a positive value critical value $\gamma _c \simeq 0.6082$ with nontrivial solutions now only for $\gamma \le \gamma _c$. This is different to the previous case when $1<p<2$, compare this figure with Fig. 2. The upper solution branch for this case continues to large negative values of $\gamma$ and the lower solution branch terminates as $\gamma \rightarrow 0$ with $f'(0) \rightarrow 0$. We can again calculate the critical values $\gamma _c$ and in Fig. 5 we plot $\gamma _c$ against p when $p>2$. We see that $\gamma _c$ is positive throughout for this case, approaching zero as $p \rightarrow 2$ from above, and that $\gamma _c$ increases as p is increased. The above discussion for the asymptotic behaviour as $p \rightarrow 2$ follows directly for this case on putting $p=2+\epsilon$. The result is that

$$\begin{aligned} \gamma _c \sim 0.79807\,(2+p)+\cdots \quad \text{ as } \ p \rightarrow 2. \end{aligned}$$

(16)

This asymptotic result is shown in Fig. 5 by a broken line, again showing good agreement with the numerically determined values.

Fig. 5

Steady states: plot of the critical values $\gamma _c$ against p for $p>2$. Asymptotic expression (16) is shown by a broken line

We next consider how the solution behaves with p for a fixed value of $\gamma$, taking $\gamma =1.0$ representative of blowing and $\gamma =-1.0$ representative of suction. We plot $f'(0)$ against p in Fig. 6 for these two cases, in Fig. 6a for p in the range $1 \leqslant p<2$ and in Fig. 6b for $p>2$. In Fig. 6a both curves start with their values at $p=1$ as shown in Fig. 1 with, for $\gamma =1.0, f'(0)$ increasing and becoming large and the boundary-layer thickness decreasing as p is increased with our numerical integrations suggesting that $f'(0) \rightarrow \infty$ as $p \rightarrow 2$. For $\gamma =-1.0$, however, $f'(0)$ decreases to the critical point at $p=p_c \simeq 1.220$ for $\gamma _c=-1.0$ shown in Fig. 3, leading to a lower solution branch in $p<p_c$, not particularly clear in the figure.

Fig. 6

Steady state: plots of $f'(0)$ against p for a $1 \leqslant p<2$, b for $p>2$ and $\gamma =1.0, \, -1.0$, obtained from the numerical solution to (9)

For $p>2$, Fig. 6b, there is now a critical value for $\gamma =1.0$ at $p=p_c \simeq 3.938$ giving rise to solutions only in $p \geqslant p_c$ and also a lower solution branch in $p>p_c$. For $\gamma =-1.0$ the values of $f'(0)$ increase rapidly as $p \rightarrow 2$, similar to that seen for $\gamma =1.0$ in Fig. 6a. In both cases the values of $f'(0)$ appear to be approaching the same limit as p is increased.

To see how the solution for $\gamma >0$ in Fig. 6a behaves as $p \rightarrow 2$ from below we put $p=2-\delta$ and look for a solution for $\delta \ll 1$ by writing $f=a(\delta )\, F, \, \zeta =a(\delta )\,y$ for some $a(\delta )$ to be determined, expecting that $a \gg 1$ for $\delta$ small. Equation (9) becomes

$$\begin{aligned}&F'''+F\,F''+\bigl (F'\bigr )^{2-\delta }\,a^{-2\delta }=0, \ \ \nonumber \\&F(0)=-\frac{\gamma }{a}, \ F''(0)=0, \ F' \rightarrow 0 \ \ \text{ as } \zeta \rightarrow 0. \end{aligned}$$

(17)

Primes now denote differentiation with respect to $\zeta$. Since $a^{-2\delta }\sim 1-2\delta \,\log a+\cdots$, we look for a solution by expanding

$$\begin{aligned} F(\zeta ;\delta )=F_0(\zeta )+(\delta \log a)\, F_1(\delta )+\cdots . \end{aligned}$$

(18)

At leading order we have

$$\begin{aligned} F_0'''+F_0\,F_0''+F_0'^2=0 \ \ \text{ giving } \ \ F_0=2c_0\tanh (c_0\zeta ), \end{aligned}$$

(19)

for some constant $c_0>0$ to be found. To obtain a solution at next order we require

$$\begin{aligned} \delta \,\log (a) \sim \frac{1}{a} \ \ \ \text{ giving } \ \ \ a \sim \frac{1}{\delta \,(-\log \delta )}+\cdots . \end{aligned}$$

(20)

This then gives at $O(\delta \,\log a)$, on integrating the equation once and applying the boundary conditions as $\zeta \rightarrow \infty$,

$$\begin{aligned} F_1''+F_0\,F_1'+F_1\,F_0'=-\int _\zeta ^\infty F_0'(s)^2\, ds. \end{aligned}$$

(21)

If we now apply the boundary conditions on $\zeta =0$, particularly that $F_1(0)=-\gamma$, and the above expression for $F_0$ we obtain

$$\begin{aligned} \gamma \,c_0^2=\int _0^\infty \text{ sech }^4(c_0\zeta )d\zeta =\frac{8c_0^3}{3} \ \ \text{ so } \text{ that } \ c_0=\frac{3\gamma }{8}. \end{aligned}$$

(22)

Hence

$$\begin{aligned} f'(0) \sim \frac{9\gamma ^2}{32}\,a^2+\cdots \ \ \text{ or } \ \ f'(0) \sim \frac{9\gamma ^2}{32}\,\frac{1}{\delta ^2\,(-\log \delta )^2}+\cdots \ \ \text{ as } \ p \rightarrow 2. \end{aligned}$$

(23)

We can readily adapt this analysis to the case when $\gamma <0$ and $p \rightarrow 2$ from above, Fig. 6b. We now put $p=2+\delta$ and make the above transformation. We then follow the above discussion, the only difference being in a sign change on the right-hand side of Eq. (21). This in turn leads to, on applying the boundary conditions on $\zeta =0$,

$$\begin{aligned} c_0=\frac{3}{8}\,(-\gamma ), \end{aligned}$$

(24)

with the expression for $f'(0)$ being the same as that given in (23).

3.1 Strong fluid withdrawal, $|{\varvec{\gamma }}|$ large

We have seen that, when $p > 2$, the solution proceeds to large negative values of $\gamma$ and to obtain a solution valid in this limit we put $f=|\gamma |+|\gamma |^{(3-p)/(p-1)}\,G, \, Y=|\gamma |\,y$. Equations (9) become

$$\begin{aligned}&G'''+(1+|\gamma |^{2(2-p)/(p-1)})\,G''+G'^{\,p}=0, \quad \nonumber \\&G(0)=G''(0)=0, \ \ G' \rightarrow 0 \ \ \text{ as } \ Y \rightarrow \infty . \end{aligned}$$

(25)

This gives, at leading order, on writing $u=G'$,

$$\begin{aligned} u''+u'+u^{\,p}=0, \ \quad u'(0)=0, \ \ u \rightarrow 0\ \ \text{ as } \ Y \rightarrow \infty . \end{aligned}$$

(26)

Now suppose $u(0)=u_0$. We then put $u=u_0\,U$ to obtain the eigenvalue problem for $u_0$ as

$$\begin{aligned} U''+U'+u_0^{p-1}\,U^{\,p}=0, \ \quad U(0)=1, \ \ U \rightarrow 0\ \ \text{ as } \ Y \rightarrow \infty . \end{aligned}$$

(27)

A plot of $u_0$ against p is shown in Fig. 7 obtained from the numerical integration of Eq. (27). The graph increases from its value of $u_0=0.8587$ at $p=2$, has a maximum value of $u_0 \simeq 1.2418$ at $p \simeq 4.9$ before decreasing slowly to $u_0=1$ as $p \rightarrow \infty$. We note that the numerical integration of (27) continues smoothly through $p=2$ into $1<p<2$ though this asymptotic solution is valid only for $p >2$. Hence

$$\begin{aligned} f'(0) \sim |\gamma |^{2/(p-1)}\,u_0+ \cdots \ \ \text{ as } \ |\gamma |\rightarrow \infty . \end{aligned}$$

(28)

Fig. 7

Steady state, solution for $|\gamma |$ large a plot of $u_0$ against p for $p > 2$ obtained from the numerical solution of Eq. (27)

4 Initial-value problem

Our discussion of the steady states suggests that we should treat the cases $p=1, 1<p<2$ and $p>2$ separately. We solved initial-value problem (7, 8) numerically using the scheme described in [10, 12] for example, taking as our initial condition $\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial y}=a_0\,\text{ e }^{-y}$ and prescribing a value for $a_0>0$.

Fig. 8

Initial-value problem: plots of the wall temperature $\theta _w$ against t for $p=1$ and $\gamma =-1.0, \, 0.0, \, 1.0, \, 2.0$, taking $a_0=1.0$ in the initial condition

4.1 ${{p}=1}$

Here we took $a_0=1.0$ and in Fig. 8 we plot values of the wall temperature $\theta _w \equiv \theta (0,t)$ against t obtained from the numerical solution of initial-value problem (7, 8) for representative values of $\gamma$. We see that these curves approach at large times the constant, nontrivial value given by the corresponding steady state solution shown in Fig. 1. For values of $\gamma \le -2$ the numerical solutions approached the trivial state $f \equiv -\gamma$ as t increased.

4.2 ${1<{p}<2}$

Here we took $p=1.5$, as in Fig. 2, and in Fig. 9 we plot the wall temperature $\theta _w$ for representative values of $\gamma$. In this case, for $\gamma <0$, there is the possibility of two steady states. Our numerical integrations indicate that it is the solution on the upper solution branch that is approached at large times, indicating that the saddle-node bifurcation at $\gamma =\gamma _c$ changes the temporal stability from stable on the upper branch to unstable on the lower branch. For values of $\gamma <\gamma _c \simeq -0.5085$ we found only the trivial solution $f \equiv -\gamma$ at large times.

Fig. 9

Initial-value problem: plots of the wall temperature $\theta _w$ against t for $p=1.5$ and $\gamma =-0.4, \, 0.0, \, 1.0, \, 2.0$, taking $a_0=1.0$ in the initial condition

4.3 ${{p}>2}$

In this case we found different behaviour to the previous cases in that now the solution either becomes singular at a finite time or approaches the trivial state at large times. We illustrate this in Fig. 10 for $p=3.0$, taking values of $\gamma <\gamma _c\simeq 0.6082$. In Fig. 10a we plot the wall temperature $\theta _w$ for representative values of $\gamma$, here taking $a_0=3.0$ in the initial condition. In each case we find that $\theta _w$ increases very rapidly as the singularity at $t=t_s$ is approached, finally becoming unbounded. To attain this finite-time singularity require a sufficiently large initial input, i.e. having $a_0$ greater than some threshold value. We illustrate this in Fig. 10b with plots of $\theta _w$ for $\gamma =-1.0$, again with $p=3.0$. With $a_0=2.18$ we again see the the development of the finite-time singularity. However, with $a_0=2.17$ the solution approaches the trivial state at large times.

Fig. 10

Initial-value problem: a plots of the wall temperature $\theta _w$ against t for $p=3.0$ and $\gamma =-1.0, \, 0.0, \, -0.4, \, -1.0$ with $a_0=3.0$, b plots of $\theta _w$ against t for $\gamma =-1.0$ and $a_0=2.17, \, 2.18$. c A plot of the time $t_s$, when there is a finite-time singularity, against $\gamma$ for $p=3.0$, taking $a_0=3.0$ in the initial condition

In Fig. 10c we plot the times $t_s$ at which the finite-time singularity occurred, at the values of $\gamma$ shown by $+$. The numerical method involved a procedure for halving the time step $\Delta t$ to maintain accuracy, with the numerical integration terminating when $\Delta t< 5\times 10^{-6}$. The values of $t_s$ in Fig. 10c are the values of t at this final time step. The values of $t_s$ depend on the value of $a_0$ taken, as well as whether a finite-time singularity occurs, Fig. 10b. For Fig. 10c we took $a_0=3.0$, noting that, for example, with $\gamma =-3.0$ the solution approached the trivial state, however, with $a_0=5.0$ a finite time singularity was seen. Thus it appears from our numerical investigation that, even though nontrivial steady states exist for $p>2$, these are unstable with the result that the solution evolves to either the trivial state or becomes singular at a finite time. This latter case gives thermal runaway with the wall temperature, as well as the temperature field within the boundary layer, becoming increasingly larger.

4.4 Solution near the singularity

The nature of the singularity as $t \rightarrow t_s$ has been discussed for related cases in [12, 13] for a general value of p. Here we restrict attention to $p=3$ in line with the results shown in Figs. 10 and 11. We start by putting $\tau =t_s-t$ and looking for a solution for $\tau$ small. There is an inner region where we put, following [12, 13],

$$\begin{aligned} f=-\gamma +\phi (\eta ,\tau ), \quad \eta =y\,\tau ^{-1/2}, \end{aligned}$$

(29)

with Eqs. (7, 8) becoming

$$\begin{aligned}&\frac{\displaystyle \partial ^3 \phi }{\displaystyle \partial \eta ^3}+\left( \frac{\displaystyle \partial \phi }{\displaystyle \partial \eta }\right) ^{ 3}+\tau ^{1/2}(-\gamma +\phi )\,\frac{\displaystyle \partial ^2 \phi }{\displaystyle \partial \eta ^2}=\frac{1}{2}\,\frac{\displaystyle \partial \phi }{\displaystyle \partial \eta }+\frac{\eta }{2}\,\frac{\displaystyle \partial ^2 \phi }{\displaystyle \partial \eta ^2}-\tau \,\frac{\displaystyle \partial ^2 \phi }{\displaystyle \partial \eta \displaystyle \partial \tau }, \ \ \nonumber \\&\phi =\frac{\displaystyle \partial ^2 \phi }{\displaystyle \partial \eta ^2}=0 \ \ \text{ on } \ \eta =0. \end{aligned}$$

(30)

Equation (30) leads to an eigenfunction expansion, following [13],

$$\begin{aligned} \phi (\eta ,\tau )=\phi _0(\eta )+\tau \, \phi _1(\eta )+\cdots , \end{aligned}$$

(31)

where

$$\begin{aligned} \phi _0=u_0\,\eta , \quad \phi _1=-u_1(\eta ^5-20\eta ^3+60\eta ), \ \ \text{ where } u_0=\frac{\sqrt{2}}{2} \ \text{ and } \ u_1>0. \end{aligned}$$

(32)

There is then a middle region where we put

$$\begin{aligned} f=\tau ^{-1/4}\, g(\xi ,\tau ), \quad \xi =y\,\tau ^{-1/4}. \end{aligned}$$

(33)

Matching with the inner region given by (31, 32) suggests an expansion in powers of $\tau ^{1/4}$, the leading-order term $g_0$ being given by

$$\begin{aligned} g_0'=\frac{u_0}{\left( 1+\frac{10u_1\eta ^4}{u_0}\right) ^{1/2}}. \end{aligned}$$

(34)

There is then an outer region in which f and y are left unscaled and in which there is a regular expansion for f, the leading-order term $f_0$ being indeterminate in the expansion, as could be expected from Stewartson [23]. On matching with the middle region,

$$\begin{aligned} \frac{\displaystyle \partial f}{\displaystyle \partial y} \sim \frac{u_0^{3/2}}{\sqrt{10u_1}}\, y^{-2}+\cdots \ \ \text{ as } \ y \rightarrow 0, \quad \frac{\displaystyle \partial f}{\displaystyle \partial y} \rightarrow 0 \ \text{ as } \ y \rightarrow \infty . \end{aligned}$$

(35)

This outer region is unaffected by the singularity developing near the wall and depends essentially on how the solution evolves from its initial input.

Fig. 11

Initial-value problem: a plots of $\theta$ against y for $p=3.0, \, \gamma =-1.0$ taking $a_0=3.0$ in the initial condition and with a space step size $\Delta y=0.005$, taken at times $t=0.12124, \, 0.12179, \, 0.12191, \, 0.12198, \, 0.12203, \, 0.12207$, b a plot of $\theta _w^{-2}$ against t, data points shown by $+$

We can see this structure in Fig. 11a where we plot $\theta$ profiles taken at times close to $t_s$, the outer boundary condition in this numerical integration was taken at $y=10.0$, much greater than used to plot the figure. The increasingly larger temperatures developing near the wall as $t \rightarrow t_s$ can clearly be seen with the temperature field essentially the same at relatively small distances from the wall. From (29), $\theta _w \sim u_0\,(t_s-t)^{-1/2}$ so that a plot of $\theta _w^{-2}$ against t should be a straight line, at least close to $t_s$. We can see this in Fig. 11b where we estimate the slope to be approximately $-1.702$ giving $u_0 \simeq 0.767$, a little greater than the theoretical value of 0.707. This difference could be accounted for by the difficulty in maintaining accuracy in integrating numerically very close to a singularity.

5 Conclusions

We have considered the effect that fluid transfer through the wall, both injection and withdrawal, can have on the development the boundary layer near a forward stagnation point when there is local heat generated at a rate proportional to $(T-T_\infty )^p$ within the boundary layer. Previously we have seen [12, 13] that, without the fluid transfer, how the solution evolved depended on whether $1 \leqslant p<2$ or $p>2$, respectively approaching a nontrivial steady state, or either dying away or having a finite-time singularity. A similar situation arises here though the injection/withdrawal of fluid through the wall can have significant effects. For $1 \leqslant p<2$, the solution approaches a nontrivial steady state provided the dimensionless parameter $\gamma$ measuring the wall transfer is such that it is greater than some critical value $\gamma _c$, dependent on p. Otherwise only the trivial state is attained at large times. When there is fluid injection, i.e. $\gamma >0$, large temperatures can be achieved within the boundary layer, increasing as $\gamma$ is increased, see Figs. 1, 2, 7 and 8. These critical values depend on the exponent p increasing from $-2$ for $p=1$ to zero as $p\rightarrow 2$, see Fig. 3. Thus if fluid withdrawal is sufficiently large the effect is to inhibit boundary layer development. However fluid injection can greatly increase both the heat transfer and the fluid flow.

The situation is essentially different when the exponent $p>2$. Here the effect of fluid injection is to limit the range of existence of any nontrivial steady state, see Figs. 4 and 5, whereas it is now fluid withdrawal that increases the temperatures seen within the boundary layer. However, these nontrivial steady states are unstable and the time dependent solution either evolves to the trivial state or reaches a finite-time singularity, see Fig. 10a. Which of these states is achieved depends strongly on the initial temperature input, see Fig. 10b.