Revisited modelling and multimodal nonlinear oscillations of a sagged cable under support motion

Abstract

Sagged cable vibrations caused by support motion and possible external loading are investigated via the four-degree-of-freedom model proposed in Benedettini et al. (J Sound Vib 182(5):775–798, 1995). The model has a considerable potential in terms of forcing cases to be possibly addressed, with the physical motion of the supports naturally giving rise to a variety of external and parametric excitation terms. Dynamics of the system is studied close to the multiple internal resonance at cable crossover, which involves two in-plane and two out-of plane vibration modes. Solutions are found by the multiple time scale method. In the numerical investigation, attention is focused on the effects of planar support motion (symmetric and/or antisymmetric) at primary resonance, with the addition of planar symmetric external excitation entailing a nice cancellation phenomenon in the system response. Results are discussed also in the background of theoretical and experimental outcomes available in the literature. Comparison with a computer simulation of original equations of motion shows that analytical results are correct for moderately large oscillations, whereas a different scenario of multimodal responses may occur at higher excitation amplitudes. The nonlinear modal coupling is investigated through bifurcation scenarios and other dynamics tools, showing also transitions to complex response regimes.

1 Introduction

In the last three decades, nonlinear dynamics of sagged cables has been studied in many papers under various aspects, via analytical, numerical, and geometrical approaches, as well as experimental techniques. The interest to cable nonlinear dynamics is motivated both by the richness of its theoretical behaviour, which has entitled the suspended cable to be considered as a meaningful archetypical model for the analysis of response of monodimensional elastic systems with initial curvature, and by the wide range of potential applications in civil, mechanical, aerospace and marine engineering. A review of nonlinear models and of the main dynamical phenomena which may appear in sagged cables under different resonance conditions is presented in [2, 3], while some more recent achievements are summarized in [4].

Among the features of specific interest there are the crossover points in the spectrum of cable natural frequencies, where conditions of multiple internal resonance involving symmetric and antisymmetric, in-plane and out-of-plane, modes occur and meaningfully affect the nonlinear dynamic response. Within the discretized, Galerkin-based, modelling perspective commonly pursued for the investigation of nonlinear response of continuous systems (for the sagged cable, see [2]), a complete four-degree-of-freedom model at first crossover was formulated in Benedettini et al. [1] by considering external loading distributed along the cable and support motion. Later on, in the framework of the direct perturbation approach which also allows one to capture the spatial dependence of cable motion, a four-mode model was formulated and used in [5, 6] by considering external loading. Sole external loading was indeed considered also in the perturbation analyses of the four-d.o.f. model accomplished in [1, 7] at primary and ½-subharmonic resonance, respectively, for dealing with the case of symmetric planar excitation and showing an already meaningful variety of classes of unimodal and multimodal responses.

Excitation through support motion was instead at the basis of a considerable amount of experimental work on horizontally hanging cable dynamics performed around the turn of the millennium. Refined investigations allowed to identify a multitude of classes of cable regular and non-regular motions under different kinds of support motions and associated resonance conditions [8, 9], to characterize in-depth the diverse involved mechanisms of transition to complex dynamics [10–12], and to explore features of control strategies [13]. Further experimental studies on resonant vibrations under support motion are reported in [14].

The effect of support motion on cable regular and non-regular vibrations was indeed addressed in several theoretical/numerical (and also experimental) papers since about mid-nineties [15], however mostly with reference to the nearly taut inclined cables of cable-stayed bridges subject to horizontal motion of the upper anchorage and/or to (prevailingly vertical) motion of the lower deck support, which originate simultaneous external and parametric excitations. Besides earlier minimal-order models [16–19], higher-order models accounting for three, four, or more modes have been considered as well [20–25], mostly if performing numerical simulations and using continuation techniques. Theoretical treatments under combined external and parametric excitations have been sometimes accomplished in the literature by considering also the self-excitation due, e.g., to air flow in helicopter dynamics [26, 27] or wind flow in cable-stayed bridge dynamics [28]. Experimental and numerical investigation of nonlinear vibrations of actually sagged inclined cables has been performed in [29].

For horizontally suspended cables, the effect of simultaneous external and parametric excitations, first addressed in [30], was considered later, e.g., in [31, 32], mostly for highlighting some global dynamics aspects of system response, even though, sometimes, with weak reference to an actual physical excitation in the background. Two-d.o.f. models accounting for one in-plane and one out-of-plane modes have been considered. Yet, a richer model is likely needed to observe the possible richness of interactions among vibration modes occurring around crossover due to multiple internal resonances and general nonlinear coupling, mostly in the presence of a combination of forcing terms also possibly corresponding to involved conditions of multifrequency excitation.

It is thus worth resuming the four-d.o.f general model in Benedettini et al. [1], with which no specific theoretical/numerical work has been done yet to evaluate the effect of support motion on cable nonlinear dynamics, also in view of a possible confirmation and cross-validation with the independently obtained experimental outcomes. Indeed, in this model, physical motion of the supports naturally gives rise to a meaningful variety of additional excitation terms, of both external and parametric nature, within the four relevant ordinary differential equations (ODEs) of motion. One more aspect of interest is that the ensuing parametric excitation is acting on both linear and nonlinear modal variables, the latter occurrence being a tricky issue which is receiving attention only in recent literature and for simpler models of continuous systems [33].

The model has a considerable potential in terms of excitation cases to be possibly addressed. However, in this paper, just a few of them will be actually investigated to get some hints about the effects of support motion on cable nonlinear response, looking at the results also in the background of behaviours previously observed theoretically/numerically in the absence of support motion or experimentally under their sole action. The main paper aims are summarized as follows:

• 1. revisiting and extending the model and its third-order multiple scale solution, with inclusion of planar/nonplanar support motion and with proper reconstitution of the modulation equations versus the incomplete one [34] accomplished in [1];

• 2. exploiting the model and solutions to investigate the effects of planar support motion (symmetric and/or antisymmetric) at primary resonance, with possible addition of planar symmetric external excitation;

• 3. highlighting worth specific effects on the dynamics, ensuing from the combination of excitations;

• 4. cross-validating results obtained with multiple scale analysis and numerical simulation of the original ODEs for relatively low vibration amplitudes, while detecting actual multimodal classes of motion for larger excitation and response amplitudes with the latter, along with some relevant transitions to complex dynamics.

The paper is organized as follows. Section 2 is devoted to discussing the reduced order model of a suspended cable, mostly in view of the worth simplifications which naturally arise for the physical problem, and to shortly dwelling on its considerable potential for a thorough investigation of nonlinear dynamic phenomena. The third-order multiple scale solution is presented in Sect. 3. Nonlinear response under planar excitations is illustrated and discussed in Sect. 4, distinguishing among symmetric excitations—external loading or support motion (Sect. 4.1), as well as their combination which produces an interesting cancellation effect (Sect. 4.2) –, antisymmetric support motion (Sect. 4.3), and combined symmetric and antisymmetric support motion (Sect. 4.4), with also possible presence of (symmetric) external loading (Sect. 4.5). A section of conclusions and future developments ends the paper.

2 Reduced-order model of a suspended cable

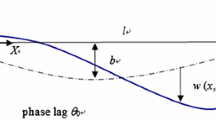
The model of the considered d-sagged cable is presented in Fig. 1, with the initial static equilibrium in-plane configuration $\mathscr{C}$ ^I and the varied dynamic 3D configuration $\mathscr{C}$ ^V attained through the displacement field components u, v, w. It is assumed that the cable supports are at the same level and can move only in the y and z directions.

Fig. 1

Physical model of a sagged cable with static equilibrium and dynamic configurations

According to [1], the following assumptions are made: (1) The dynamic extensional strain is expressed through the Lagrangian strain measure; (2) the static equilibrium configuration is defined by the parabola $y = 4d\left[ {\frac{x}{l} - \left( {\frac{x}{l}} \right)^{2} } \right]$, which entails $ds \approx dx$ and allows to approximate the cable initial tension $T^{I}$ with its horizontal component H; (3) the gradient of the longitudinal (u) in-plane displacement component is negligible with respect to unity (moderately large rotations in the cable motion); (4) $H/EA \ll 1$, where EA is the cable axial stiffness per unit length. In the absence of excitations in the longitudinal direction, and neglecting the corresponding inertia and viscous forces, the following two integro-partial differential equations of motion are obtained via a kinematic condensation procedure:

$$\begin{aligned} m\ddot{v} & = \left\{ {Hv^{{\prime }} + \frac{EA}{l}\left( {y^{{\prime }} + v^{{\prime }} } \right)\int\limits_{0}^{l} {\left[ {y^{{\prime }} v^{{\prime }} + \frac{1}{2}\left( {v^{{{\prime }^{2} }} + w^{{{\prime }^{2} }} } \right)} \right]} dx} \right\}^{{\prime }} - \mu_{v} \dot{v} + p_{v} \\ m\ddot{w} & = \left\{ {Hw^{{\prime }} + \frac{EA}{l}w^{{\prime }} \int\limits_{0}^{l} {\left[ {y^{{\prime }} v^{{\prime }} + \frac{1}{2}\left( {v^{{{\prime }^{2} }} + w^{{{\prime }^{2} }} } \right)} \right]} dx} \right\}^{{\prime }} - \mu_{v} \dot{w} + p_{w} \\ \end{aligned}$$

(1)

where the dot and prime mean $\partial /\partial t$ and $\partial /\partial x$, respectively, m and μ _v , μ _w are mass and viscous damping coefficients per unit length, and p _v , p _w are vertical and horizontal out-of-plane components of the external load distributed along the cable. The boundary conditions read

$$v(0,t) = \tilde{v}_{0} (t),\,w(0,t) = \tilde{w}_{0} (t),\,v(l,t) = \tilde{v}_{l} (t), \,w(l,t) = \tilde{w}_{l} (t)$$

(2)

where $\tilde{v}_{0} (t)$, $\tilde{w}_{0} (t)$ $\tilde{v}_{l} (t)$, $\tilde{w}_{l} (t)$ represent prescribed motion of the supports at x = 0 and x = l cable ends.

Taking into account two in-plane and two out-of-plane vibration modes of the cable with fixed supports (see Appendix 1, where physical cable data and values of all coefficients and parameters later on considered in the numerical investigation are also reported), the Galerkin reduction procedure leads to the following set of four dimensionless ODEs [1]

$$\begin{aligned} & \ddot{q}_{1} + \mu_{v}^{ * } \dot{q}_{1} + \lambda_{1}^{2} q_{1} + \sum\limits_{i = 1}^{4} {c_{i} } q_{i}^{2} + \sum\limits_{i = 2,4} c_{i}^{p} q_{i0} q_{i} + \sum\limits_{i = 1}^{4} {d_{1i} } q_{1} q_{i}^{2} + \sum\limits_{i = 2,4} {\left( {e_{1i}^{p} q_{i0}^{2} q_{1} + g_{1i}^{p} q_{i0} q_{i} q_{1} } \right)} \\ & \quad = c_{1}^{e} p_{1} (t) + c_{1}^{s} \left( {\ddot{q}_{10} + \mu_{v}^{ * } \dot{q}_{10} } \right) + \sum\limits_{i = 2,4} {h_{1i}^{s} q_{i0}^{2} } \\ & \ddot{q}_{2} + \mu_{v}^{ * } \dot{q}_{2} + \lambda_{2}^{2} q_{2} + c_{21} q_{2} q_{1} + c_{21}^{p} q_{20} q_{1} + \sum\limits_{i = 1}^{4} {d_{2i} } q_{2} q_{i}^{2} + \sum\limits_{i = 1}^{4} {d_{2i}^{p} q_{20} q_{i}^{2} } + \sum\limits_{i = 2,4} {e_{2i}^{p} q_{i0}^{2} q_{2} } + g_{24}^{p} q_{40} q_{2} q_{4} \\ & \quad + m_{24}^{p} q_{40} q_{20} q_{4} = c_{2}^{e} p_{2} (t) + c_{2}^{s} \left( {\ddot{q}_{20} + \mu_{v}^{ * } \dot{q}_{20} } \right) + n_{2}^{s} q_{20} + \sum\limits_{i = 2,4} {r_{2i}^{s} q_{i0}^{2} q_{20} } \\ & \ddot{q}_{3} + \mu_{w}^{ * } \dot{q}_{3} + \lambda_{3}^{2} q_{3} + c_{31} q_{3} q_{1} + \sum\limits_{i = 1}^{4} {d_{3i} } q_{3} q_{i}^{2} + \sum\limits_{i = 2,4} {\left( {e_{3i}^{p} q_{i0}^{2} q_{3} + g_{3i}^{p} q_{i0} q_{i} q_{3} } \right)} = c_{3}^{e} p_{3} (t) + c_{3}^{s} \left( {\ddot{q}_{30} + \mu_{w}^{ * } \dot{q}_{30} } \right) \\ & \ddot{q}_{4} + \mu_{w}^{ * } \dot{q}_{4} + \lambda_{4}^{2} q_{4} + c_{41} q_{4} q_{1} + c_{41}^{p} q_{40} q_{1} + \sum\limits_{i = 1}^{4} {d_{4i} } q_{4} q_{i}^{2} + \sum\limits_{i = 1}^{4} {d_{4i}^{p} q_{40} q_{i}^{2} } + \sum\limits_{i = 2,4} e_{4i}^{p} q_{i0}^{2} q_{4} + g_{42}^{p} q_{20} q_{4} q_{2} \\ & \quad + m_{42}^{p} q_{40} q_{20} q_{2} = c_{4}^{e} p_{4} (t) + c_{4}^{s} \left( {\ddot{q}_{40} + \mu_{v}^{ * } \dot{q}_{40} } \right) + n_{4}^{s} q_{40} + \sum\limits_{i = 2,4} {r_{4i}^{s} q_{i0}^{2} q_{40} } \\ \end{aligned}$$

(3)

where q _j is a dimensionless, generalized coordinate for in-plane symmetric (j = 1) and antisymmetric (j = 2) mode, out-of-plane symmetric (j = 3) and antisymmetric (j = 4) mode.

The support motion is defined by functions $q_{j0} \left( t \right)$, j = 1…4, which are related to the original boundary conditions (2) in the following way:

• for in-plane motion

  $$\begin{aligned} \tilde{v}_{0} \left( t \right) = q_{10} \left( t \right) + q_{20} \left( t \right) \hfill \\ \tilde{v}_{l} \left( t \right) = q_{10} \left( t \right) - q_{20} \left( t \right) \hfill \\ \end{aligned}$$

  (4)

• for out-of-plane motion

  $$\begin{aligned} \tilde{w}_{0} \left( t \right) = q_{30} \left( t \right) + q_{40} \left( t \right) \hfill \\ \tilde{w}_{l} \left( t \right) = q_{30} \left( t \right) - q_{40} \left( t \right) \hfill \\ \end{aligned}$$

  (5)

Selecting functions $q_{j0} (t)$ we can activate symmetric or antisymmetric, in-plane or out-of-plane modes. Superscripts introduced for the coefficients in Eq. (3) denote terms related to direct external excitation (index e), support motion producing external-like excitation (index s), support motion producing parametric-like excitation (index p).

The explicit expressions of all coefficients in Eq. (3) are given in the Appendix B of [1] and are not reproduced here for the sake of brevity. Looking at them, it can be easily verified analytically that a substantial number of coefficients vanishes, i.e., all of those depending on the identically vanishing integrals (I ^dp₂ and I ^dp₄ in the mentioned Appendix B) of the second in-plane (j = 2) and second out-of-plane (j = 4) cable modes, which are antisymmetric.

In particular, vanishing coefficients are related to the following terms of Eq. (3) linked to antisymmetric (in-plane or out-of-plane) support motions (see details in Appendix 1):

• some of those producing linear parametric excitation (c ^p _i , c ^p _i1 , m ^p _ji are equal to zero);

• all of those producing nonlinear parametric excitation (d ^p _ji , g ^p _ji are equal to zero);

• some of those producing external excitation (n ^s _i , r ^s _ji are equal to zero).

Equations of motion (3) thus reduce to

$$\begin{aligned} & \ddot{q}_{1} + \mu_{v} \dot{q}_{1} + \lambda_{1}^{2} q_{1} + \sum\limits_{i = 1}^{4} {c_{i} } q_{i}^{2} + \sum\limits_{i = 1}^{4} {d_{1i} q_{1} q_{i}^{2} } + \sum\limits_{i = 2,4} {e_{1i}^{p} q_{i0}^{2} q_{1} } = c_{1}^{e} p_{1} (t) + c_{1}^{s} (\ddot{q}_{10} + \mu_{v} \dot{q}_{10} ) + \sum\limits_{i = 2,4} {h_{1i}^{s} q_{i0}^{2} } , \\ & \ddot{q}_{2} + \mu_{v} \dot{q}_{2} + \lambda_{2}^{2} q_{2} + c_{21} q_{2} q_{1} + \sum\limits_{i = 1}^{4} {d_{2i} q_{2} q_{i}^{2} } + \sum\limits_{i = 2,4} {e_{2i}^{p} q_{i0}^{2} q_{2} } = c_{2}^{e} p_{2} (t) + c_{2}^{s} (\ddot{q}_{20} + \mu_{v} \dot{q}_{20} ), \\ & \ddot{q}_{3} + \mu_{w} \dot{q}_{3} + \lambda_{3}^{2} q_{3} + c_{31} q_{3} q_{1} + \sum\limits_{i = 1}^{4} {d_{3i} q_{3} q_{i}^{2} } + \sum\limits_{i = 2,4} {e_{3i}^{p} q_{i0}^{2} q_{3} } = c_{3}^{e} p_{3} (t) + c_{3}^{s} (\ddot{q}_{30} + \mu_{w} \dot{q}_{30} ), \\ & \ddot{q}_{4} + \mu_{w} \dot{q}_{4} + \lambda_{4}^{2} q_{4} + c_{41} q_{4} q_{1} + \sum\limits_{i = 1}^{4} {d_{4i} q_{4} q_{i}^{2} } + \sum\limits_{i = 2,4} {e_{4i}^{p} q_{i0}^{2} q_{4} } = c_{4}^{e} p_{4} (t) + c_{4}^{s} (\ddot{q}_{40} + \mu_{w} \dot{q}_{40} ), \\ \end{aligned}$$

(6)

Notwithstanding the ensuing simplification, besides quadratic and cubic terms due to cable geometric nonlinearities (governed by coefficients c _i , c _i1 and d _ji , respectively) and external excitation terms (governed by coefficients c ^e _i ), Eq. (6) still exhibit the following terms arising from support motion:

• linear parametric excitation (governed by coefficients e ^p _j2 , e ^p _j4 ), present in all four equations; these terms exist only in the case of non-vanishing antisymmetric in-plane (q ₂₀ ≠ 0) or out-of-plane (q ₄₀ ≠ 0) support motion;

• additional external excitation (governed by coefficients h ^s₁₂ , h ^s₁₄ ), occurring in the sole first equation in the case of non-vanishing antisymmetric in-plane (q ₂₀ ≠ 0) or out-of-plane (q ₄₀ ≠ 0) support motion;

• additional external excitation (governed by coefficients c ^s _i ), existing in each one of the four equations if the corresponding component of support motion is different from zero.

Thus, within a great variety of possible cable physical excitations, the reduced-order model exhibits excitation conditions of different dynamical nature also in its simplified version, with likely meaningful related effects. By way of example, even if limiting ourselves to the solely planar support motion (q ₃₀ = q ₄₀ = 0) and a direct, symmetrically distributed, vertical external excitation (p ₂ = p ₃ = p ₄ = 0), the following basic situations can be distinguished.

• 1. If considering only symmetric harmonic motion of the supports (q ₁₀ = A ₁₀cosΩ _s t, q ₂₀ = 0), no parametric excitation occurs, but the resulting external excitation in the first equation may come from the summation of up to three terms, one due to the possibly coexisting external excitation $c_{1}^{e} p_{1} (t)$ of frequency Ω, and the other two ensuing from the symmetric support motion of frequency Ω _s :

  $$c_{1}^{e} p_{1} (t) + c_{1}^{s} (\ddot{q}_{10} + \mu_{v} \dot{q}_{10} ) = P_{1} { \cos }\Omega t - c_{1}^{s} A_{10} \Omega_{s} (\Omega_{s} { \cos }\Omega_{s} t + \mu_{v} { \sin }\Omega_{s} t)$$

  (7)

  This is a situation of multifrequency excitation in the first (symmetric in-plane) equation, which may meaningfully affect the occurrence of the various classes of motion (from the unimodal q ₁ to multimodal also involving other components of motion) already highlighted in the case of sole direct external excitation $c_{1}^{e} p_{1} (t)$ of frequency Ω [1].

• 2. If considering only antisymmetric harmonic motion of the supports (q ₁₀ = 0, q ₂₀ = A ₂₀cosΩ _s t), indirect (i.e., support motion-originated) external excitations exist both in the first equation

  $$h_{12}^{s} q_{20}^{2} = h_{12}^{s} A_{20}^{2} { \cos }^{2} \Omega_{s} t = h_{12}^{s} A_{20}^{2} [(1 + { \cos }2\Omega_{s} t)/2]$$

  (8)

  and in the second equation

  $$c_{2}^{s} (\ddot{q}_{20} + \mu_{v} \dot{q}_{20} ) = - c_{2}^{s} A_{20} \Omega_{s} (\Omega_{s} { \cos }\Omega_{s} t + \mu_{v} { \sin }\Omega_{s} t),$$

  (9)

  even in the absence of any direct external excitation $c_{1}^{e} p_{1} (t)$, giving rise to a situation of multifrequency external excitation spread over the first two equations; moreover, there is parametric excitation due to q ₂₀, which includes products of the coordinate and harmonic functions with frequency 2Ω _s ,

  $$e_{j2}^{p} q_{20}^{2} q_{j} = e_{j2}^{p} q_{j} A_{20}^{2} \cos^{2} \Omega_{s} t = e_{j2}^{p} q_{j} A_{20}^{2} \left[ {\left( {1 + \cos 2\Omega_{s} t} \right)/2} \right],\quad j = 1 \ldots 4$$

  (10)

  in all four equations.

  If, in addition, there is the direct external excitation $c_{1}^{e} p_{1} (t)$ of frequency Ω, multifrequency external excitation (different from the one in Eq. (7)) occurs already in the first equation

  $$c_{1}^{e} p_{1} (t) + h_{12}^{s} q_{20}^{2} = P_{1} { \cos }\Omega t + h_{12}^{s} A_{20}^{2} [(1 + { \cos }2\Omega_{s} t)/2]$$

  (11)

  whereas nothing changes in the second and remaining equations.

• 3. Of course, if considering a generic harmonic support motion—to be expressed as a combination of proper symmetric and antisymmetric components—further distinct sub-cases of possible dynamic interest can arise.

• 4. All of this without considering neither direct, antisymmetrically distributed, external excitation $c_{2}^{e} p_{2} (t)$—which could indeed be somehow unrealistic from the physical viewpoint—, nor out-of-plane direct excitation and/or support motion, which would instead be physically meaningful and would add further worth perspectives.

Overall, it is clear how a great richness of nonlinear dynamic responses is indeed possible, even in the sole regular regime, with the relevant comparison in the diverse cases having a remarkable interest.

3 Multiple scale solution

To determine approximate analytical solutions of Eq. (6) we use the multiple time scale method [35] with support of ‘Wolfram Mathematica^®10’ package for symbolic computations. We consider the 1:1:1/2:1 multiple internal resonance condition occurring at first crossover, with the symmetric planar and anti-symmetric planar and non-planar modes having the same frequency and the symmetric non-planar mode having half frequency (Appendix 1). This means that, for some set of excitation and damping values all modes can be involved in the response. The solutions of Eq. (6) are sought in the form of power series expansion of the small parameter ε

$$q_{j} (t,\varepsilon ) = \varepsilon q_{j1} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{2} q_{j2} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{3} q_{j3} (T_{0} ,T_{1} ,T_{2} ) + \cdots$$

(12)

where $q_{j1} \left( {T_{0} ,T_{1} ,T_{2} } \right)$, $q_{j2} \left( {T_{0} ,T_{1} ,T_{2} } \right)$, $q_{j3} \left( {T_{0} ,T_{1} ,T_{2} } \right)$ are the first, second and third order approximation of the j-th mode, respectively. Independent time scales are introduced according to:

$$T_0=t,\quad T_1=\varepsilon t, \quad T_2=\varepsilon^2 t$$

(13)

where $T_{0}$ is the fast and $T_{1}$, $T_{2}$ are slow time scales. Such time definitions result in m order partial derivatives with respect to different (n) time-scales, $D_n^m(\, .\,)=\frac{\partial^m}{\partial T_n^m}(\, .\,)$.

We also assume that direct external loading and motion of supports are harmonic functions taken at the first order of perturbation, respectively

$$p_{j} (t) = \varepsilon \tilde{p}_{j1} \cos \Omega T_{0},\quad q_{j0} (t) = \varepsilon \tilde{A}_{j0} \cos \Omega_{s} T_{0} ,\quad j = 1 \ldots 4,$$

(14)

along with parameters related to damping, direct external excitation, and support motion

$$\mu_{v}^{*} = \varepsilon \tilde{\mu }_{11} = \varepsilon \tilde{\mu }_{21} ,\quad \mu_{w}^{*} = \varepsilon \tilde{\mu }_{31} = \varepsilon \tilde{\mu }_{41} , \quad c_{j}^{e} = \varepsilon \tilde{c}_{j}^{e} ,\quad c_{j}^{s} = \varepsilon \tilde{c}_{j}^{s} .$$

Substituting solution (12) into Eq. (6), taking into account the derivative definitions, and grouping terms with respect to order $\varepsilon$, we get a set of linear differential equations at the successive perturbation orders

• ε ¹-order

  $$\begin{aligned} & D_{0}^{2} q_{11} + \lambda_{1}^{2} q_{11} = 0 \\ & D_{0}^{2} q_{21} + \lambda_{2}^{2} q_{21} = 0 \\ & D_{0}^{2} q_{31} + \lambda_{3}^{2} q_{31} = 0 \\ & D_{0}^{2} q_{41} + \lambda_{4}^{2} q_{41} = 0 \\ \end{aligned}$$

  (15)

• ε ²-order

  $$\begin{aligned} & D_{0}^{2} q_{12} + \lambda_{1}^{2} q_{12} + \mu_{11} D_{0} q_{11} + 2D_{0} D_{1} q_{11} + \sum\limits_{j = 1}^{4} {c_{j} } q_{j1}^{2} = c_{1}^{e} p_{11} \cos \Omega T_{0} - c_{1}^{s} A_{10} \Omega_{s}^{2} \cos \Omega_{s} T_{0} \\ & \quad - \sum\limits_{j = 2,4} {h_{1j}^{s} A_{20}^{2} \Omega_{s}^{2} \cos^{2} \Omega_{s} T_{0} } \\ & D_{0}^{2} q_{22} + \lambda_{2}^{2} q_{22} + \mu_{21} D_{0} q_{21} + 2D_{0} D_{1} q_{21} + c_{21} q_{21} q_{11} = c_{2}^{e} p_{21} \cos \Omega T_{0} - c_{2}^{s} A_{20} \Omega_{s}^{2} \cos \Omega_{s} T_{0} \\ & D_{0}^{2} q_{32} + \lambda_{3}^{2} q_{32} + \mu_{31} D_{0} q_{31} + 2D_{0} D_{1} q_{31} + c_{31} q_{31} q_{11} = c_{3}^{e} p_{31} \cos \Omega T_{0} - c_{3}^{s} A_{30} \Omega_{s}^{2} \cos \Omega_{s} T_{0} \\ & D_{0}^{2} q_{42} + \lambda_{4}^{2} q_{42} + \mu_{41} D_{0} q_{41} + 2D_{0} D_{1} q_{41} + c_{41} q_{41} q_{11} = c_{4}^{e} p_{41} \cos \Omega T_{0} - c_{4}^{s} A_{40} \Omega_{s}^{2} \cos \Omega_{s} T_{0} \\ \end{aligned}$$

  (16)

• ε ³-order

  $$\begin{aligned} & D_{0}^{2} q_{13} + \lambda_{1}^{2} q_{13} + \mu_{11} \left( {D_{0} q_{12} + D_{1} q_{11} } \right) + 2D_{0} D_{1} q_{12} + 2D_{0} D_{2} q_{11} + D_{1}^{2} q_{11} + \sum\limits_{j = 1}^{4} {2c_{j} } q_{j1} q_{j2} \\ & \quad + \sum\limits_{j = 1}^{4} {d_{1j} } q_{11} q_{j1}^{2} + \sum\limits_{j = 2,4} {e_{1j}^{p} q_{11} A_{j0}^{2} \cos^{2} \Omega_{s} T_{0} = - c_{1}^{s} A_{10} \mu_{11} \Omega_{s} \sin \Omega_{s} T_{0} } \\ & D_{0}^{2} q_{23} + \lambda_{2}^{2} q_{23} + \mu_{21} \left( {D_{0} q_{22} + D_{1} q_{21} } \right) + 2D_{0} D_{1} q_{22} + 2D_{0} D_{2} q_{21} + D_{1}^{2} q_{21} + c_{21} \left( {q_{11} q_{22} + q_{12} q_{21} } \right) \\ & \quad + \sum\limits_{j = 1}^{4} {d_{2j} } q_{21} q_{j1}^{2} + \sum\limits_{j = 2,4} {e_{2j}^{p} q_{21} A_{j0}^{2} \cos^{2} \Omega_{s} T_{0} = - c_{2}^{s} \mu_{21} A_{20} \Omega_{s} \sin \Omega_{s} T_{0} } \\ & D_{0}^{2} q_{33} + \lambda_{2}^{2} q_{23} + \mu_{31} \left( {D_{0} q_{32} + D_{1} q_{31} } \right) + 2D_{0} D_{1} q_{32} + 2D_{0} D_{2} q_{31} + D_{1}^{2} q_{31} + c_{21} \left( {q_{11} q_{32} + q_{12} q_{31} } \right) \\ & \quad + \sum\limits_{j = 1}^{4} {d_{3j} } q_{31} q_{j1}^{2} + \sum\limits_{j = 2,4} {e_{3j}^{p} q_{31} A_{j0}^{2} \cos^{2} \Omega_{s} T_{0} = - c_{3}^{s} \mu_{31} A_{30} \Omega_{s} \sin \Omega_{s} T_{0} } \\ & D_{0}^{2} q_{43} + \lambda_{4}^{2} q_{43} + \mu_{41} \left( {D_{0} q_{42} + D_{1} q_{41} } \right) + 2D_{0} D_{1} q_{42} + 2D_{0} D_{2} q_{41} + D_{1}^{2} q_{41} + c_{41} \left( {q_{11} q_{42} + q_{12} q_{41} } \right) \\ & \quad + \sum\limits_{j = 1}^{4} {d_{4j} } q_{41} q_{j1}^{2} + \sum\limits_{j = 2,4} {e_{4j}^{p} q_{41} A_{j0}^{2} \cos^{2} \Omega_{s} T_{0} = - c_{4}^{s} \mu_{41} A_{40} \Omega_{s} \sin \Omega_{s} T_{0} } \\ \end{aligned}$$

  (17)

To study the interaction of direct external excitation, external and parametric excitations due to support motion, and geometrically nonlinear terms, we have to solve the perturbation problem at least up to the third order.

Besides the multi-internal resonance condition (λ ₁ = λ ₂ = λ ₄ = 1, λ ₃ = 1/2), we consider primary external resonance ($\Omega \approx 1$), and assume frequency of support motion to be equal to the external loading one, i.e., Ω_s = Ω, for the sake of simplicity. To account for internal resonances we introduce the detuning parameters σ₁, ρ₂, ρ ₃, ρ ₄, and express the dimensionless natural frequencies of each mode with respect to that of the first mode (λ ₁). Therefore we write the following conditions for the external and internal resonances

$$\lambda_{1}^{2} = \Omega^{2} - \varepsilon \sigma_{1} , \, \lambda_{2}^{2} = \lambda_{1}^{2} - \varepsilon \rho_{2} , \, \lambda_{3}^{2} = \frac{{\lambda_{1}^{2} }}{4} - \varepsilon \rho_{3} ,\, \lambda_{4}^{2} = \lambda_{1}^{2} - \varepsilon \rho_{4}$$

(18)

Conditions (18) are inserted into perturbation Eqs. (15)–(17) and the solutions of the ensuing ε-order system of equations are expressed in the form

$$\begin{aligned} q_{11} (T_{0} ,T_{1} ,T_{2} ) & = A_{1} (T_{1} ,T_{2} )\exp (i\Omega T_{0} ) + \overline{A}_{1} (T_{1} ,T_{2} )\exp ( - i\Omega T_{0} ) \\ q_{21} (T_{0} ,T_{1} ,T_{2} ) & = A_{2} (T_{1} ,T_{2} )\exp (i\Omega T_{0} ) + \overline{A}_{2} (T_{1} ,T_{2} )\exp ( - i\Omega T_{0} ) \\ q_{31} (T_{0} ,T_{1} ,T_{2} ) & = A_{3} (T_{1} ,T_{2} )\exp \left(i\frac{\Omega }{2}T_{0} \right) + \overline{A}_{3} (T_{1} ,T_{2} )\exp \left( { - i\frac{\Omega }{2}T_{0} } \right) \\ q_{41} (T_{0} ,T_{1} ,T_{2} ) & = A_{4} (T_{1} ,T_{2} )\exp (i\Omega T_{0} ) + \overline{A}_{4} (T_{1} ,T_{2} )\exp ( - i\Omega T_{0} ) \\ \end{aligned}$$

(19)

where i is the imaginary unit, $A_{j}$ is the complex amplitude, and $\bar{A}_{j}$ its complex conjugate. Solutions (19) are substituted into Eq. (16) and, upon eliminating secular generating terms, we get the complex form of modulation equations on the T ₁ slow time scale

$$\begin{aligned} & 2i\Omega D_{1} A_{1} - \sigma_{1} A_{1} + i\mu_{11} A_{1} \Omega + c_{3} A_{3}^{2} + \frac{1}{2}c_{1}^{s} \Omega^{2} A_{10} - \frac{1}{2}c_{1}^{e} p_{11} = 0 \\ & 2i\Omega D_{1} A_{2} - \rho_{2} A_{2} + i\mu_{21} A_{2} \Omega + \frac{1}{2}c_{2}^{s} \Omega^{2} A_{20} - \frac{1}{2}c_{2}^{e} p_{21} = 0 \\ & i\Omega D_{1} A_{3} - \rho_{3} A_{3} + \frac{1}{2}i\mu_{31} A_{3} \Omega + c_{31} A_{1} \overline{A}_{3} = 0 \\ & 2i\Omega D_{1} A_{4} - \rho_{4} A_{4} + i\mu_{41} A_{4} \Omega + \frac{1}{2}c_{4}^{s} \Omega^{2} A_{40} - \frac{1}{2}c_{4}^{e} p_{41} = 0 \\ \end{aligned}$$

(20)

Then, determining particular solutions of second order Eq. (16) without secular generating terms, substituting them into the third order Eq. (17), and imposing vanishing of the new set of secular generating terms, provide the complex form of modulation equations on the T ₂ scale

$$\begin{aligned} & D_{1}^{2} A_{1} + 2i\Omega D_{2} A_{1} + \mu_{11} D_{1} A_{1} + F_{10}^{s} + \left( {\bar{F}_{1}^{s} + \bar{F}_{1}^{p} } \right)\bar{A}_{1} + F_{111} A_{1}^{2} \bar{A}_{1} \\ & \quad + F_{221} A_{2}^{2} \bar{A}_{1} + F_{441} A_{4}^{2} \bar{A}_{1} + \left( {F_{1}^{s} + F_{1}^{p} } \right)A_{1} + F_{122} A_{1} A_{2} \bar{A}_{2} + F_{133} A_{1} A_{3} \bar{A}_{3} + F_{144} A_{1} A_{4} \bar{A}_{4} = 0 \\ & D_{1}^{2} A_{2} + 2i\Omega D_{2} A_{2} + \mu_{21} D_{1} A_{2} + F_{20}^{s} + F_{112} A_{1} \bar{A}_{1} A_{2} + \left( {\bar{F}_{2}^{s} + \bar{F}_{2}^{p} } \right)\bar{A}_{2} + F_{222} A_{2}^{2} \bar{A}_{2} \\ & \quad + \bar{F}_{112}^{{}} A_{1}^{2} \bar{A}_{2} + F_{442} A_{4}^{2} \bar{A}_{2} + \left( {F_{2}^{s} + F_{2}^{p} } \right)A_{2} + F_{233} A_{2} A_{3} \bar{A}_{3} + F_{244} A_{2} A_{4} \bar{A}_{4} = 0 \\ & D_{1}^{2} A_{3} + i\Omega D_{2} A_{3} + \mu_{31} D_{1} A_{3} + F_{113} A_{1} \bar{A}_{1} A_{3} + F_{223} A_{2} \bar{A}_{2} A_{3} + F_{333} A_{3}^{2} \bar{A}_{3} \\ & \quad + \left( {F_{3}^{s} + F_{3}^{p} } \right)A_{3} + F_{344} A_{3} A_{4} \bar{A}_{4} = 0 \\ & D_{1}^{2} A_{4} + 2i\Omega D_{2} A_{4} + \mu_{41} D_{1} A_{4} + F_{40}^{s} + F_{114}^{{}} A_{1} \bar{A}_{1} A_{4} + F_{334} A_{3} \bar{A}_{3} A_{4} + \left( {\bar{F}_{4}^{s} + \bar{F}_{4}^{p} } \right)\bar{A}_{4} \\ & \quad + F_{224} A_{2}^{2} \bar{A}_{4} + F_{242} A_{2} \bar{A}_{2} A_{4} + F_{444} A_{4}^{2} \bar{A}_{4} + \bar{F}_{114} A_{1}^{2} \bar{A}_{4} + \left( {F_{4}^{s} + F_{4}^{p} } \right)A_{4} = 0, \\ \end{aligned}$$

(21)

with the definitions of F coefficients being given in Appendix 2.

It is worth noting that in the multiple scale analysis of the sole external load case pursued in [1], the $D_{1}^{2 } A_{j } , j = 1,4$, contributions occurring in the secular generating terms at T ₂ time scale were neglected, based on the assumption of vanishing of underlying $D_{1}^{ } A_{j } , j = 1 ,4$ terms to be independently imposed at the T ₁ time scale when looking for only steady state solutions. This was one of the alternative ways to deal with the matter previously discussed in the literature [36]. Following studies have clarified that this is indeed an inconsistent procedure since singular points of the modulation equations, corresponding to steady state solutions, have to be unitarily looked for on their complete and consistent reconstituted version [34, 37]. Indeed, applying the reconstitution method, we may formulate the modulation equations in terms of complex amplitudes A _j , with the amplitude derivative with respect to dimensionless time taking the form

$$\frac{{dA_{j} }}{dt} = \varepsilon D_{1} A_{j} + \varepsilon^{2} D_{2} A_{j} \quad j = 1 \div 4$$

(22)

To determine modulation equations in the form (22) we have to do some additional computations. At first we find $D_{1} A_{j}$ and $D_{2} A_{j}$ from Eqs. (20) and (21), then substituting them into (22) we get four complex amplitude modulation equations (AMEs) up to the second order

$$\begin{aligned} \frac{{dA_{1} }}{dt} & = \varepsilon \left[ {\frac{1}{4}iA_{10} c_{1}^{s} \Omega - \frac{1}{2}\left( {\mu_{11} + \frac{{i\sigma_{1} }}{\Omega }} \right)A_{1} + \frac{{ic_{3} }}{2\Omega }A_{3}^{2} - \frac{{iP_{11} }}{4\Omega }} \right] \\ & \quad + \varepsilon^{2} \left[ {\frac{{P_{11} }}{{16\Omega^{3} }}\left( {\mu_{11} \Omega - i\sigma_{1} } \right) + G_{01}^{s} + } \right.G_{33} A_{3}^{2} + \left( {\bar{G}_{1}^{s} + \bar{G}_{1}^{p} } \right)\bar{A}_{1} + \bar{G}_{111} A_{1}^{2} \bar{A}_{1} + G_{221} A_{2}^{2} \bar{A}_{1} \\ & \quad + G_{441} A_{4}^{2} \bar{A}_{1} + \left( {G_{1}^{p} + G_{1}^{s} + G_{1} } \right)A_{1} + G_{122} A_{1} A_{2} \bar{A}_{2} + G_{133} A_{1} A_{3} \bar{A}_{3} \left. { + G_{144} A_{1} A_{4} \bar{A}_{4} } \right] \\ \frac{{dA_{2} }}{dt} & = \varepsilon \left[ { - \frac{1}{2}\left( {\mu_{21} + \frac{{i\rho_{2} }}{\Omega }} \right)A_{2} + \frac{1}{4}ic_{2}^{s} \Omega A_{20} - \frac{{iP_{21} }}{4\Omega }} \right] \\ & \quad + \varepsilon^{2} \left[ {\frac{1}{{16\Omega^{3} }}} \right.P_{21} \left( {\mu_{21} \Omega - i\rho_{2} } \right) + G_{02}^{s} + \bar{G}_{121} A_{1} A_{2} \bar{A}_{1} + \left( {\bar{G}_{2}^{p} + \bar{G}_{2}^{s} } \right)\bar{A}_{2} + \bar{G}_{112} A_{1}^{2} \bar{A}_{2} \\ & \quad + \bar{G}_{222} A_{2}^{2} \bar{A}_{2} + \bar{G}_{442} A_{4}^{2} \bar{A}_{2} + \left( {G_{2}^{p} + G_{2}^{s} + G_{2} } \right)A_{2} + \bar{G}_{233}^{{}} A_{2} A_{3} \bar{A}_{3} \left. { + \bar{G}_{244} A_{2} A_{4} \bar{A}_{4} } \right] \\ \frac{{dA_{3} }}{dt} & = \varepsilon \left[ { - \frac{1}{2}\left( {\mu_{31} + \frac{{i\rho_{3} }}{\Omega }} \right)A_{3} + \frac{{ic_{31} }}{\Omega }A_{1} \bar{A}_{3} } \right] + \varepsilon^{2} \left[ {G_{232} A_{2} A_{3} \bar{A}_{2} } \right. + \frac{{ic_{31} }}{{4\Omega^{3} }}P_{11} \bar{A}_{3} + \bar{G}_{3}^{s} \bar{A}_{3} \\ & \quad + \bar{G}_{333} A_{3}^{2} \bar{A}_{3} + \bar{G}_{131} A_{1} A_{3} \bar{A}_{1} + \bar{G}_{13} A_{1} \bar{A}_{3} + \left( {G_{3}^{p} + G_{3}^{s} + G_{3} } \right)A_{3}^{{}} + \left. {\bar{G}_{344} A_{3} A_{4} \bar{A}_{4} } \right] \\ \frac{{dA_{4} }}{dt} & = \varepsilon \left[ { - \frac{1}{2}\left( {\mu_{41} + \frac{{i\rho_{4} }}{\Omega }} \right)A_{4} + \frac{1}{4}ic_{4}^{s} \Omega A_{40} - \frac{{iP_{41} }}{4\Omega }} \right] \\ & \quad + \varepsilon^{2} \left[ {\frac{{P_{41} }}{{16\Omega^{3} }}\left( {\mu_{41} \Omega - i\rho_{4} } \right) + G_{04}^{s} + } \right.\bar{G}_{141} A_{1} A_{4} \bar{A}_{1} + \bar{G}_{343} A_{3} A_{4} \bar{A}_{3} + \left( {\bar{G}_{4}^{s} + \bar{G}_{4}^{p} } \right)\bar{A}_{4} \\ & \quad + \bar{G}_{114} A_{1}^{2} \bar{A}_{4} + \bar{G}_{224} A_{2}^{2} \bar{A}_{4} + \bar{G}_{444} A_{4}^{2} \bar{A}_{4} + \left( {G_{4}^{s} + G_{4}^{p} + G_{4} } \right)A_{4} \left. { + G_{242} A_{2} A_{4} \bar{A}_{2} } \right] \\ \end{aligned}$$

(23)

with the G coefficients being defined in Appendix 3.

Expressing the complex amplitude $A_{j}$ in the polar form

$$A_{j} = \frac{1}{2}a_{j} e^{{i\phi_{j} }} ,$$

(24)

with amplitude and phase $a_{j}$, $\phi_{j}$, substituting (24) into (23) and separating real and imaginary parts, we get eight modulation equations for the amplitude and pha

se. For the perfect tuning of frequencies, $\rho_{2} = \rho_{3} = \rho_{4} = \sigma_{1}$, they read

$$ \begin{aligned} \Omega^{3} \dot{a}_{1} & = \varepsilon \left\{{- \frac{1}{2}a_{1} \mu_{11} \Omega^{3} + \frac{1}{8}\left({\lambda_{1}^{2} - 5\Omega^{2}} \right)\left[{P_{11} - A_{10} c_{1}^{s} \Omega^{2}} \right]\sin \phi_{1} + \left. {\frac{{a_{3}^{2} c_{3}}}{16}\left({6\Omega^{2} - \lambda_{1}^{2} - 4\lambda_{3}^{2}} \right)\sin (\phi_{1} - 2\phi_{3})} \right\}} \right. \\ & \quad + \varepsilon^{2} \left[{\frac{1}{8}\mu_{11} \Omega \left({P_{11} + 3A_{10} c_{1}^{s} \mu_{11} \Omega^{2}} \right)\cos \phi_{1} + \frac{1}{4}a_{1} \sum\limits_{j = 2,4} {A_{j0}^{2}} \left({- \frac{1}{3}c_{1} h_{1j}^{s} + \frac{1}{2}e_{1j}^{p} \Omega^{2}} \right)\sin 2\phi_{1}} \right. \\ & \quad + \frac{{a_{3}^{2} c_{3} \Omega}}{16}\left({2\mu_{31} - \mu_{11}} \right)\cos (\phi_{1} - 2\phi_{3})\left. {+\frac{1}{4}a_{1} \sum\limits_{j = 2,4} {a_{j}^{2}} \left({\frac{1}{3}c_{1} c_{j} - c_{j} c_{j1} + \frac{1}{2}d_{1j}\Omega^{2}} \right)\sin 2(\phi_{1} - \phi_{j})} \right] \\ a_{1} \Omega^{3} \dot{\phi}_{1} & = \frac{1}{8}a_{1} \left[{\lambda_{1}^{2} \left({6\Omega^{2} - \lambda_{1}^{2}} \right) - 5\Omega^{4}} \right] \\ & \quad + \varepsilon \left[{\frac{1}{8}\left({\lambda_{1}^{2} - 5\Omega^{2}} \right)\left({P_{11} - A_{10} c_{1}^{s} \Omega^{2}} \right)\cos \phi_{1} + \frac{{a_{3}^{2} c_{3}}}{16}\left({6\Omega^{2} - \lambda_{1}^{2} - 4\lambda_{3}^{2}} \right)\cos (\phi_{1} - 2\phi_{3})} \right] \\ & \quad + \varepsilon^{2} \left[{\frac{1}{4}a_{1} \left({- \frac{5}{3}a_{1}^{2} c_{1}^{2} - \frac{1}{2}\mu_{11}^{2} \Omega^{2} + \frac{3}{4}a_{1}^{2} d_{11} \Omega^{2}} \right) + \frac{1}{2}a_{1} a_{3}^{2} \left({\frac{1}{2}d_{13} \Omega^{2} - c_{1} c_{3}} \right)} \right. \\ & \quad - \frac{1}{2}a_{1} \sum\limits_{j = 2,4} {a_{j}^{2}} \left({c_{1} c_{j} + \frac{1}{3}c_{j} c_{j1} - \frac{1}{2}d_{1j} \Omega^{2}} \right) + \frac{1}{2}a_{1} \sum\limits_{j = 2,4} {A_{j0}^{2} \left({c_{1} h_{1j}^{s} + \frac{1}{2}e_{1j}^{p} \Omega^{2}} \right)} \\ & \quad + \frac{1}{4}a_{1} \sum\limits_{j = 2,4} {A_{j0}^{2} \left({- \frac{1}{3}c_{1} h_{1j}^{s} + \frac{1}{2}e_{1j}^{p} \Omega^{2}} \right)} \cos 2\phi_{1} + \frac{1}{4}a_{1} \sum\limits_{j = 2,4} {a_{j}^{2} \left({\frac{1}{3}c_{1} c_{j} - c_{j} c_{j1} + \frac{1}{2}d_{1j} \Omega^{2}} \right)} \cos 2(\phi_{1} - \phi_{j}) \\ & \quad - \frac{1}{8}\mu_{11} \Omega \left({P_{11} + 3A_{10} c_{1}^{s} \Omega^{2}} \right)\sin \phi_{1} \left. {+ \frac{1}{8}\Omega c_{3} a_{3}^{2} \left({\frac{1}{2}\mu_{11} - \mu_{31}} \right)\sin (\phi_{1} - 2\phi_{3})} \right] \\ \Omega^{3} \dot{a}_{2} & = \varepsilon \left[{- \frac{1}{2}a_{2} \mu_{21} \Omega^{3} + \frac{1}{8}\left({\lambda_{2}^{2} - 5\Omega^{2}} \right)\left({P_{21} - A_{20} c_{2}^{s} \Omega^{2}} \right)\sin \phi_{2}} \right] \\ & \quad + \varepsilon^{2} \left[{\frac{1}{8}\mu_{21} \Omega \left({P_{21} + 3A_{20} c_{2}^{s} \Omega^{2}} \right)\cos \phi_{2}} \right. + \frac{{a_{2} a_{1}^{2}}}{24}\left({3c_{21}^{2} - c_{21} c_{1} - 3d_{21} \Omega^{2}} \right)\sin 2(\phi_{1} - \phi_{2}) \\ & \quad + \frac{1}{8}a_{2} \sum\limits_{j = 2,4} {A_{j0}^{2}} \left({- \frac{1}{3}c_{21} h_{1j}^{s} + e_{2j}^{p} \Omega^{2}} \right)\sin 2\phi_{2} \left. {+ \frac{{a_{2} a_{4}^{2}}}{24}\left({c_{21} c_{4} + 3d_{24} \Omega^{2}} \right)\sin 2(\phi_{2} - \phi_{4})} \right] \\ a_{2} \Omega^{3} \dot{\phi}_{2} & = \frac{{a_{2}}}{8}\left({6\lambda_{2}^{2} \Omega^{2} - \lambda_{2}^{4} - 5\Omega^{4}} \right) \\ & \quad + \varepsilon \left[{\frac{1}{8}\left({\lambda_{2}^{2} - 5\Omega^{2}} \right)\left({P_{21} - A_{20} c_{2}^{s} \Omega^{2}} \right)\cos \phi_{2}} \right] \\ & \quad + \varepsilon^{2} \left[{\frac{1}{8}a_{2}^{3} \left({3d_{22} \Omega^{2} - \frac{{5c_{21} c_{2}}}{3}} \right) + \frac{1}{4}a_{2}\sum\limits_{j = 1,3,4} {a_{j}^{2} \left({d_{2j} \Omega^{2} -c_{21} c_{j}} \right) - \frac{{c_{21}^{2}}}{12}a_{1}^{2} a_{2} -\frac{1}{8}a_{2} \mu_{21}^{2} \Omega^{2}}} \right. \\ & \quad +\frac{1}{4}a_{2} \sum\limits_{j = 2,4} {A_{j0}^{2} \left({c_{21}h_{1j}^{s} + e_{2j}^{p} \Omega^{2}} \right) - \frac{1}{8}\mu_{21}\Omega \left({P_{21} + 3A_{20} \Omega^{2} c_{2}^{s}} \right)\sin\phi_{2} + \frac{1}{8}a_{2} \sum\limits_{j = 2,4}A_{j0}^{2}\left(-\frac{1}{3} c_{21}h^{s}_{1j}+ e_{2j}^{p}\Omega^2\right)\cos 2\phi_2 }\\ & \quad \left. {-\frac{1}{8}c_{21}^{2}a_{2}a_{1}^{2} \cos 2\left(\phi_{1} -\phi_{2} \right)+\frac{1}{8}a_{2}\sum\limits_{j = 1,4} {a_{j}^{2}\left({\frac{{c_{j} c_{21}}}{3} + d_{2j} \Omega^{2}} \right)\cos2(\phi_{j} - \phi_{2})}} \right] \\ \Omega^{3} \dot{a}_{3} & =\varepsilon \left[{- \frac{1}{2}a_{3} \mu_{31} \Omega^{3} +\frac{1}{4}a_{3} a_{1} c_{31} \left({\lambda_{1}^{2} -3\Omega^{2}} \right)\sin (\phi_{1} - 2\phi_{3})} \right] \\ & \quad + \varepsilon^{2} \left[{\frac{1}{4}a_{3} c_{31}\left({P_{11} - A_{10} c_{1}^{s} \Omega^{2}} \right)\sin 2\phi_{3}+ \frac{1}{4}a_{3} a_{1} c_{31} \mu_{11} \Omega \cos (\phi_{1} -2\phi_{3})} \right] \\ a_{3} \Omega^{3} \dot{\phi}_{3} & = a_{3}\left[{\lambda_{3}^{2} \left({\frac{3}{2}\Omega^{2} -\lambda_{3}^{2}} \right) - \frac{5}{16}\Omega^{4}} \right] +\varepsilon \left[{\frac{1}{4}a_{1} a_{3} c_{31} \left({-\lambda_{1}^{2} + 3\Omega^{2}} \right)\cos (\phi_{1} - 2\phi_{3})}\right] \\ & \quad + \varepsilon^{2} \left[{\frac{3}{8}c_{31}^{2}a_{1}^{2} a_{3} + \frac{1}{4}a_{3}^{3} \left({- \frac{5}{2}c_{31}c_{3} + 3d_{33} \Omega^{2}} \right) + \frac{1}{2}a_{3} c_{31}\sum\limits_{j = 1,2,4} {\left({- a_{j}^{2} c_{j} + d_{3j}\Omega^{2}} \right)} - \frac{1}{4}\mu_{31}^{2} \Omega^{2} a_{3}}\right. \\ & \quad + \frac{1}{2}a_{3} \sum\limits_{j = 2,4}{A_{j0}^{2} \left({c_{31} h_{1j}^{s} + e_{3j}^{p} \Omega^{2}}\right)} + \frac{1}{4}a_{3} c_{31} \left({P_{11} - A_{10}c_{1}^{s} \Omega^{2}} \right)\cos 2\phi_{3} + \left.{\frac{1}{4}a_{1} a_{3} c_{31} \mu_{11} \Omega \sin (\phi_{1} -2\phi_{3})} \right] \\ \Omega^{3} \dot{a}_{4} & = \varepsilon\left[{- \frac{1}{2}a_{4} \mu_{41} \Omega^{3} +\frac{1}{8}\left({\lambda_{4}^{2} - 5\Omega^{2}} \right)}\right.\left. {\left({P_{41} - A_{40} c_{4}^{s} \Omega^{2}}\right)\sin \phi_{4}} \right] \\ & \quad + \varepsilon^{2}\left[{\frac{1}{8}\mu_{41} \Omega \left({P_{41} + 3A_{40}c_{4}^{s} \Omega^{2}} \right)\cos \phi_{4}} \right. + \frac{1}{8}a_{4} a_{1}^{2} c_{41}^{2} \sin 2(\phi_{1} - \phi_{4}) \\ & \quad + \frac{1}{8}a_{4} \sum\limits_{j = 2,4} {A_{j0}^{2} \left({- \frac{1}{3}c_{41} h_{1j}^{s} + e_{4j}^{p} \Omega^{2}} \right)\sin 2\phi_{4}} \left. {- \frac{1}{8}a_{4} \sum\limits_{j = 1,2} {a_{j}^{2} \left({\frac{1}{3}c_{j} c_{41} + d_{4j} \Omega^{2}} \right)\sin 2(\phi_{j} - \phi_{4})}} \right] \\ a_{4} \Omega^{3} \dot{\phi}_{4} & =\frac{{a_{4}}}{8}\left({6\lambda_{4}^{2} \Omega^{2} -\lambda_{4}^{4} - 5\Omega^{4}} \right) \\ & \quad + \varepsilon\left[{\frac{1}{8}\left({\lambda_{4}^{2} - 5\Omega^{2}}\right)\left({P_{41} - A_{40} c_{4}^{s} \Omega^{2}} \right)\cos\phi_{4}} \right] \\ & \quad + \varepsilon^{2}\left[{\frac{1}{4}a_{4} \sum\limits_{j = 1,2,3} {a_{j}^{2}\left({d_{4j} \Omega^{2} - c_{41} c_{j}} \right)}} \right. +\frac{1}{8}a_{4}^{3} \left({\frac{- 5}{3}c_{41} c_{4} + 3d_{44}\Omega^{2}} \right) - \frac{1}{8}a_{4} \mu_{41}^{2} \Omega^{2} -\frac{1}{12}c_{41}^{2} a_{1}^{2} a_{4} \\ & \quad +\frac{1}{4}a_{4} \sum\limits_{j = 2,4} {A_{j0}^{2} \left({c_{41}h_{1j}^{s} + e_{4j}^{p} \Omega^{2}} \right)} - \frac{1}{8}\mu_{41}\Omega \left({P_{41} + 3A_{40} \Omega^{2} c_{4}^{s}} \right)\sin\phi_{4} + \frac{1}{8}a_{4} \sum\limits_{j = 2,4} {A_{j0}^{2}\left({- \frac{1}{3}c_{41} h_{1j}^{s} + e_{4j}^{p} \Omega^{2}}\right)} \cos 2\phi_{4} \\ & \left. \quad - \frac{1}{8}c_{41}^{2}a_{4} a_{1}^{2} \cos 2(\phi_{1} - \phi_{4}) + \frac{1}{8}a_{4}\sum\limits_{j = 1,2} {a_{j}^{2} \left({\frac{1}{3}c_{j} c_{41} +d_{4j} \Omega^{2}} \right)\cos 2(\phi_{j} - \phi_{4})} \right] \\ \end{aligned} $$

(25)

where $P_{j1} = c_{j}^{e} p_{j1}$ is the amplitude of the direct external loading.

Taking into account generating solutions (19) and second order particular solutions, and expressing the complex amplitudes in the polar form (24), according to Eq. (12) we obtain the complete solutions up to the second order approximation

$$\begin{aligned} q_{1} & = \varepsilon a_{1} \cos \left( {\Omega T_{0} + \phi_{1} } \right) \\ & \quad + \varepsilon^{2} \frac{1}{{2\Omega^{2} }}\left[ { - c_{3} a_{3}^{2} + \sum\limits_{j = 1,2,4} {c_{j} a_{j}^{2} \left( { - 1 + \frac{1}{3}\cos \left( {2\Omega T_{0} + 2\phi_{1} } \right)} \right)} + \sum\limits_{j=2,4} {h_{1j}^{s} A_{j0}^{2} \left( {1 - \frac{1}{3}\cos 2\Omega T_{0} } \right)} } \right] \\ q_{2} & = \varepsilon a_{2} \cos \left( {\Omega T_{0} + \phi_{2} } \right) + \varepsilon^{2} \frac{1}{{2\Omega^{2} }}\left[ {c_{21} a_{1} a_{2} \left( { - \cos \left( {\phi_{1} - \phi_{2} } \right) + \frac{1}{3}\cos \left( {2\Omega T_{0} + \phi_{1} + \phi_{2} } \right)} \right)} \right] \\ q_{3} & = \varepsilon a_{3} \cos \left( {\frac{\Omega }{2}T_{0} + \phi_{3} } \right) + \varepsilon^{2} \frac{4}{{3\Omega^{2} }}\left[ {\left( {c_{3}^{s} \Omega^{2} A_{30} - P_{31} } \right)\cos \Omega T_{0} + \frac{1}{3}c_{31} a_{1} a_{3} \cos \left( {\frac{3}{2}\Omega T_{0} + \phi_{1} + \phi_{3} } \right)} \right] \\ q_{4} & = \varepsilon a_{4} \cos \left( {\Omega T_{0} + \phi_{4} } \right) + \varepsilon^{2} \frac{1}{{2\Omega^{2} }}\left[ {c_{41} a_{1} a_{4} \left( { - \cos \left( {\phi_{1} - \phi_{4} } \right) + \frac{1}{3}\cos \left( {2\Omega T_{0} + \phi_{1} + \phi_{4} } \right)} \right)} \right] \\ \end{aligned}$$

(26)

Amplitudes a _j and phases ϕ _j are found from modulation equations (25), or in the steady state from the algebraic equations obtained by equating Eq. (25) to zero.

4 Nonlinear response to planar symmetric/antisymmetric excitations

To limit the amount of numerical investigations, the strong variety of possible harmonic excitation conditions due to external loads distributed along the cable and due to support motions is restricted to cases of sole in-plane excitations (P ₃ = P ₄ = A ₃₀ = A ₄₀ = 0). In particular, sole symmetrically distributed load (P ₁₁ ≠ 0, P ₂₁ = 0) and symmetric (A ₁₀ ≠ 0) and/or antisymmetric (A ₂₀ ≠ 0) support motions are considered, along with some relevant combinations. Moreover, whether coexisting, distributed loads and support motions are assumed to have the same frequency (Ω = Ω_s), thus considering only cases of monofrequency excitations; this strongly reduces the number of dynamical conditions of possible interest to be addressed, mostly as regards combination resonances. System response will be analyzed in five distinct excitation cases:

• Symmetric excitation

  • (i) External loading or symmetric support motion (P ₁₁ ≠ 0 or A ₁₀ ≠ 0, A ₂₀ = 0)

  • (ii) Combined external loading and symmetric support motion (P ₁₁ ≠ 0 and A ₁₀ ≠ 0, A ₂₀ = 0)

• Antisymmetric excitation

  • (i) Antisymmetric support motion (P ₁₁ = 0, A ₁₀ = 0, A ₂₀ ≠ 0)

• Mixed excitation

  • (i) Symmetric plus antisymmetric support motion (P ₁₁ = 0, A ₁₀ ≠ 0, A ₂₀ ≠ 0)

  • (ii) Combined external loading and symmetric plus antisymmetric support motion (P ₁₁ ≠ 0, A ₁₀ ≠ 0, A ₂₀ ≠ 0)

Numerical solution of the AMEs is obtained via continuation in terms of (frequency or amplitude) excitation parameters by means of AUTO^® [38]. Direct numerical simulation of the four simplified ODEs of motion (Eq. (6)) is also performed with AUTO^®, and the ensuing system response with Dynamics^® [39], illustrating the results through frequency- and force-response curves, phase portraits, Poincaré maps, and bifurcation diagrams [40]. In the ODE simulation, excitation amplitude values such to allow for a comparison with the results provided by the multiple scale analysis, which are solely valid in the weakly nonlinear regime, are first considered. However, higher excitation amplitudes possibly entailing quasiperiodic and chaotic responses typical of strongly nonlinear regimes are also investigated.

Before addressing the results, it is worth noting that no parametric terms actually exist in the ODEs in the case of solely symmetric excitation, since they are only activated by the presence of antisymmetric support motion (see points 1. and 2. in Sect. 2). In the following, the nature of excitation terms occurring in the various ODEs will be pointed out in the selected cases, to help analyzing and/or interpreting numerical results.

4.1 Direct external loading or symmetric support motion (P ₁₁ ≠ 0 or A ₁₀ ≠ 0, A ₂₀ = 0)

For the sake of comparison with results available in the literature [1], we start by considering direct external excitation of amplitude P ₁₁ and frequency Ω. The softening a ₁ frequency–response curve obtained at primary resonance via the modulation equations (25) is shown in Fig. 2a.

Fig. 2

Frequency–response curves under direct external excitation: a mode 1, b mode 2, c mode 3, mode 4 equal to zero. Analytical results: P ₁₁ = 0.0015, A ₁₀ = 0, A ₂₀ = 0. (Color figure online)

In the strict neighbourhood of $\Omega \approx 1$, the directly excited planar unimodal response a ₁ (continuous black line) becomes unstable (dashed line) and the third mode a ₃ is activated (green line in Fig. 2c) via period doubling (PD) bifurcations, owed to the 2:1 internal resonance. The in-plane antisymmetric mode a ₂ is also activated via pitchfork bifurcations (PB) but it is unstable (dashed red lines in Fig. 2a, b), so that the response is symmetric bimodal (a ₁, a ₃), with nearly comparable amplitude values of the two participating components. Within the considered range of values of the excitation amplitude, this confirms the results in Fig. 3a, b of [1], thus showing the relatively minor effect, at least for low excitation amplitudes, of the partially inconsistent calculation of the modulation equations on the T ₂ time scale therein pursued and later on embedded in the reconstitution process.

Fig. 3

Frequency–response curves under direct external excitation: a mode 1, b mode 2, c mode 3; d q ₁–q ₃ phase portrait. Numerical simulation of the original ODEs: P ₁₁ = 0.0015, A ₁₀ = 0, A ₂₀ = 0

Frequency–response results obtained through numerical simulation of the original ODEs (Fig. 3a–c) fully validate analytical results in terms of values of both response amplitudes and bifurcations points. The eight shaped response typically occurring for a great variety of 2:1 internally resonant oscillators, and herein depicting the transverse physical motion of the cable mid-span point, is shown in the phase portrait of Fig. 3d. In the following, both AMEs and ODEs are used for detailed bifurcation analyses to highlight the agreement occurring at medium–low response amplitudes as well as some different response scenarios characterizing stronger nonlinear regimes.

Force-response curves are presented in Fig. 4 for two different values of excitation frequency. Instability of the unimodal a ₁ solution and onset of the stable nonplanar bimodal solution (a ₁, a ₃), with the classical saturation of planar response, occurs at both the perfect primary resonance (Ω = 1, Fig. 4a, b) and for a slightly detuned frequency value (Ω = 1.04545, Fig. 4c, d). However, the a ₃ component is activated via supercritical PB (Fig. 4b) in the former case versus subcritical PB (Fig. 4d) in the latter case, where it is initially unstable and then turns out to be stable via a (strictly neighbouring) saddle-node (SN) bifurcation (see also [1]).

Fig. 4

Force-response curves of first in-plane mode a ₁ and first out-of-plane mode a ₃ with varying P ₁₁, for Ω = 1 (a, b) and for Ω = 1.04545 (c, d). Analytical results: A ₁₀ = 0, A ₂₀ = 0

Let us now move to consideration of the sole in-plane A ₁₀ support motion, which results in indirect external terms of kinematic and inertial nature exciting the first planar mode, as shown in Eq. (7) (where P ₁₁ is assumed to be equal to zero). Analytical frequency- and force-response curves companion of those previously obtained with direct external load (Figs. 2, 4a, b) are reported in Figs. 5, 6a, c, respectively. In obtaining the former, the amplitude value A ₁₀ is selected in such a way to get responses of the same level as those provided by the direct external force. Due to the effect of indirect kinematic and inertial excitations, frequency–response curves in Fig. 5 are very similar to those in Fig. 2: there are again two alternative stable solutions, a ₁ unimodal in-plane (continuous black line in Fig. 5a) or a ₁, a ₃ bimodal involving in-plane and out-of-plane modes (continuous green line in Fig. 5a, c), with a small frequency range of coexistence and competition (which depends on the initial conditions in the relevant basins of attraction) in the neighbourhood of the left PD bifurcation. The curves in Fig. 5a look slightly more involved than those under direct excitation due to the presence of also the a ₄ component (therein absent), but both the bimodal solutions involving the antisymmetric a ₂ or a ₄ modes are again unstable (dashed red (a, b) and blue (a, d) lines in Fig. 5).

Fig. 5

Frequency–response curves under in-plane support motion: a mode 1, b mode 2, c mode 3, d mode 4. Analytical results: P ₁₁ = 0, A ₁₀ = 0.001, A ₂₀ = 0. (Color figure online)

Fig. 6

Force-response curves with varying A ₁₀, for Ω = 1: a mode 1, b mode 2, c mode 3, d mode 4. Analytical results: P ₁₁ = 0, A ₂₀ = 0. (Color figure online)

Overall, the dynamic effect of a symmetric support motion is substantially equivalent to that of a symmetrically distributed external loading, as expected. Yet, considering the support amplitude (A ₁₀ = 0.001) lower than the loading amplitude (P ₁₁ = 0.0015) in the corresponding Fig. 2, higher values of all modal amplitudes are herein obtained, which is due to the value of the cable coefficient c ^s₁  = 2.66667 (see Appendix 1) multiplying the cosine term in Eq. (7).

In turn, the force-response curves obtained analytically at perfect primary resonance (Fig. 6) for amplitudes of support motion lower than those of the external load in Fig. 4a, b (as per their higher mentioned effect) are qualitatively similar to the latter in the initial and intermediate range, with transition from unimodal a ₁ (Fig. 6a) to bimodal a ₁,a ₃ (Fig. 6a, c) solutions through PD bifurcation, and partial saturation of a ₁. However, with further increasing A ₁₀ value, the antisymmetric a ₂ component (absent in Fig. 4) enters the response, too, via a subcritical PB, ending up to the stable trimodal a ₁, a ₂, a ₃ (green lines in Fig. 6a–c) with the full saturation of a ₃. In contrast, the fourth mode a ₄ later on originated via another subcritical PB remains unstable (Fig. 6d).

Force-response curves obtained through numerical simulation of the ODEs are reported in Fig. 7 over a range of nearly doubled values of A ₁₀ and ensuing higher amplitudes of response components. Agreement with the analytical results in Fig. 6 occurs only in the initial part of the range, where the bimodal solution q ₁, q ₃ arises from the unimodal one, however with a considerably lower saturation of the q ₁ component. For increasing excitation amplitudes, no stable bifurcated trimodal q ₁, q ₂, q ₃ has been found, contrary to analytical results. Yet, a new stable, large amplitude, unimodal q ₁ solution is seen to exist over nearly the whole considered range of A ₁₀. To grasp the actual robustness of possibly competing solutions, both in this case and in forward investigations, basins of attraction should be constructed; however, this is not only computationally demanding but also quite complicated in terms of geometrical representation and interpretation, even if limiting ourselves to consider suitable cross-sections (with, e.g., null values of $q_{4}$ and $\dot{q}_{4}$) of the actual eight-dimensional attractor-basin portrait.

Fig. 7

Force-response curves with varying A ₁₀, for Ω = 1: a mode 1, b mode 2, c mode 3, (mode 4 is always zero). Numerical simulation of the original ODEs: P ₁₁ = 0, A ₂₀ = 0

4.2 Direct external loading P ₁₁ and symmetric support motion A ₁₀: cancellation effect

When combining external loading P ₁₁ and symmetric support motion A _10, we have three kinds of external excitation terms in Eq. (7), i.e., direct forcing plus kinematic and inertial excitations. Being c ^s₁  > 0, direct and indirect excitations are seen to compete with each other, thus possibly giving rise to some interaction in the system response for selected values of amplitudes and frequencies. The matter is investigated at the perfect resonance (Ω = 1) by fixing the amplitude (P ₁₁ = 0.0015) of external loading while varying the amplitude of support motion.

In Fig. 8 we observe three possible solutions: unimodal a ₁, bimodal a ₁,a ₃ and trimodal a ₁,a ₂,a ₃. Again, two saturation phenomena are observed for different A ₁₀ levels, one (at about A ₁₀ = 0.001, Fig. 8a) when the mode a ₃ is activated and the other (at about A ₁₀ = 0.005, Fig. 8c) when the mode a ₂ is activated, too. This corresponds to results in Fig. 6 relevant to the sole support motion. However, a cancellation effect consisting of a vanished contribution of the internally resonant excited out-of-plane mode a ₃ and an essential reduction of the amplitude a ₁ of the directly excited in-plane mode is herein observed for small amplitudes of A ₁₀.

Fig. 8

Force-response curves with varying A ₁₀ in the presence of external loading, for Ω = 1: a mode 1, b mode 2, c mode 3, d mode 4. Analytical results: P ₁₁ = 0.0015, A ₂₀ = 0

In Fig. 9, the cancellation effect is presented in the 3D diagram of amplitude a ₁ versus support motion A ₁₀, for different values of external loading P ₁₁. The phenomenon takes place for all P ₁₁ amplitudes, but it is greater for smaller amplitudes of external loading.

Fig. 9

Force-response curve of amplitude a ₁ against support motion A ₁₀ for different external loading P ₁₁. Analytical results: Ω = 1, A ₂₀ = 0

If we slightly change the excitation frequency to Ω = 1.04545, the cancellation effect exists as well but with only the bifurcation involving mode a ₃ taking place in the considered A ₁₀ window (Fig. 10). The phenomenon is further highlighted in Fig. 11 by the frequency–response plots of the variable a ₁, for fixed P ₁₁ = 0.0015 and A ₁₀ values respectively below (a), inside (b) and above (c) the cancellation region: considerably lower values of a ₁ are observed in Fig. 11b, down to nearly vanishing in the left neighbourhood of the perfect resonance.

Fig. 10

Force-response curves with varying A ₁₀ in the presence of external loading, for Ω = 1.04545: a mode 1, b mode 3. Analytical results: P ₁₁ = 0.0015, A ₂₀ = 0

Fig. 11

Frequency–response curves of amplitude a ₁ for different in-plane support motion. Analytical results: P ₁₁ = 0.0015, A ₂₀ = 0, A ₁₀ = 0.00025 (a), A ₁₀ = 0.0007 (b), A ₁₀ = 0.0015 (c)

The analyses show that in a certain range of amplitude A ₁₀ the cable response is meaningfully reduced, due to the interaction of excitations. The cancellation effect has been detected numerically by using the second order modulation equations (25). Yet, it is worth checking whether it can be also highlighted to the first order approximation of the multiple scale solution via simpler equations. Based on the results in Figs. 8, 11, cancellation of a ₁ is complemented by vanishing of a ₃, with the thresholds of the relevant zone corresponding to points of a ₃ activation (see Fig. 8a, c). Thus, we limit ourselves to considering the a ₁, ϕ ₁, a ₃, ϕ ₃ subset of Eq. (25), taking into account the sole $\varepsilon^{0}$ and $\varepsilon^{1}$ order terms. Assuming a ₂ = 0, a ₄ = 0, considering steady state response ($\dot{a}_{1} = 0$, $\dot{a}_{3} = 0$), and eliminating $\sin \phi_{1}$, $\cos \phi_{1}$, $\sin (\phi_{1} - 2\phi_{3} )$, $\cos (\phi_{1} - 2\phi_{3} )$ provides an algebraic equation involving amplitude a ₃ only

$$\begin{aligned} & a_{3}^{4} \frac{{c_{3}^{2} \left[ {1 + \left( {4\mu_{31}^{2} - 2} \right)\Omega^{2} + \Omega^{4} } \right]}}{{4\left( {P_{11} - A_{10} c_{1s} \Omega^{2} } \right)^{2} \left[ {\left( {1 - 2\Omega } \right)^{2} + 4\mu_{31}^{2} \Omega^{2} } \right]}} - a_{3}^{2} \frac{{c_{3}^{{}} \left[ {1 - 2\left( {1 + \mu_{11} \mu_{31} } \right)\Omega^{2} + \Omega^{4} } \right]}}{{2c_{31} \left( {P_{11} - A_{10} c_{1s} \Omega^{2} } \right)^{2} }} \\ & \quad + \frac{{\left[ {1 + \left( {\mu_{11}^{2} - 2} \right)\Omega^{2} + \Omega^{4} } \right]\left[ {\left( {1 - 2\Omega } \right)^{2} + 4\mu_{31}^{2} \Omega^{2} } \right]}}{{4c_{31}^{2} \left( {P_{11} - A_{10} c_{1}^{s} \Omega^{2} } \right)^{2} }} - 1 = 0 \\ \end{aligned}$$

(27)

Solving Eq. (27) we determine the resonance curve for a ₃ plotted in Fig. 12a against the A ₁₀ amplitude of support motion, for $\Omega = 1$. Substituting a ₃ = 0 into Eq. (27) we get the bifurcation points from trivial (a ₃ = 0) to nontrivial (a ₃ > 0) solutions to the first order approximation:

Fig. 12

Cancellation zone in the force-response curves with varying A ₁₀, for Ω = 1: a amplitude a ₃, b amplitude a ₁ for Ω = 1, black, for Ω = 0.95, red, for Ω = 1.05, blue. Analytical results, first order approximation: P ₁₁ = 0.0015, A ₂₀ = 0. (Color figure online)

$$A_{10} = \frac{{ \mp 2c_{31} P_{11} + \sqrt {\left[ {1 + \left( {\mu_{11}^{2} - 2} \right)\Omega^{2} + \Omega^{4} } \right]\left[ {1 + 2\left( {\mu_{31}^{2} - 2} \right)\Omega^{2} + \Omega^{4} } \right]} }}{{2c_{1}^{s} c_{31} \Omega^{2} }}$$

(28)

With the assumed data, Eq. (28) provides values $A_{10} = 0.00032$ and $A_{10} = 0.00081$ of bifurcation points to nontrivial a ₁, a ₃ solutions which are in a very good agreement with those obtained with the second order approximation and direct numerical simulations. Having solutions for a ₃ and limits of the cancellation zone we can then use the a ₁,ϕ ₁ subset of Eq. (25) (with a ₂ = 0, a ₃ = 0, a ₄ = 0) to find the first order approximation of a ₁ in the cancellation zone

$$a_{1} = \frac{{\left( {P_{11} - A_{10} c_{1s} \Omega^{2} } \right)}}{{\sqrt {1 + \left( {\mu_{11}^{2} - 2} \right)\Omega^{2} + \Omega^{4} } }},$$

(29)

which is presented in Fig. 12b for three different frequency values. Cancellation of the bimodal a ₁, a ₃ around $\Omega = 1$ is accompanied by an increasingly steeper decrease of the unimodal a ₁ down to zero.

The phenomenon is summarized in the overall behaviour chart of Fig. 13, which shows the bifurcation loci delimiting from above and below the cancellation region of the coupled a ₁, a ₃ solution where, in addition, the unimodal response a ₁ is reduced down to zero, with the steepest descent occurring for Ω = 1 in-between the two folds at about A ₁₀ = 0.0003 and A ₁₀ = 0.0008, as shown by the relevant contour lines calculated with Eq. (29). Thus, apart from a slight overestimation of the a ₁ reduction, the cancellation zone, which can have important practical meaning, may be determined with good accuracy in closed-form by Eqs. (28) and (29).

Fig. 13

Behaviour chart for P ₁₁ = 0.0015, showing in the Ω-A ₁₀ plane the loci of PD bifurcation points (red line) which trigger the a ₁,a ₃ solution (in the red-shadowed region), with contour plot of the unimodal a ₁ solution (black lines) vanishing within the (white, in-between) cancellation region. (Color figure online)

Numerical confirmation of the cancellation effect is given in Fig. 14, where time series of q ₁ and q ₃ directly obtained from integration of the original ODEs (6) are shown for P ₁₁ = 0.0015, Ω = 1, and A ₁₀ = 0.00025 (green line), A ₁₀ = 0.0007 (orange line), A ₁₀ = 0.0015 (blue line).

Fig. 14

Time series of q ₁(a) and q ₃(b) obtained from the original ODEs for P ₁₁ = 0.0015, A ₂₀ = 0, A ₁₀ = 0.00025 (green line), A ₁₀ = 0.0007 (orange line), A ₁₀ = 0.0015 (blue line). (Color figure online)

4.3 Antisymmetric support motion (P ₁₁ = 0, A ₁₀ = 0, A ₂₀ ≠ 0)

In contrast to symmetric support motion A₁₀, the antisymmetric one leads to external excitation terms with frequency Ω_s and 2Ω_s and also to parametric terms with frequency 2Ω_s (see Eqs. (8)–(10)). Different resonant excitation conditions occur for the various modes at Ω = Ω_s = 1, namely: (a) principal parametric and ½-subharmonic external for planar symmetric mode, (b) principal parametric and primary external for planar antisymmetric mode, and (c) principal parametric for nonplanar antisymmetric mode, while the nonplanar symmetric mode with half-frequency is non-resonantly parametrically excited. In modulation equations (25), this entails occurrence of non-vanishing external $A_{20}$ terms and parametric terms with products of $A_{20}$ and $a_{j}$, $j = 1 \ldots 4$, amplitudes. Overall, the nonlinear response is more involved than under symmetric excitations, with combined parametric and external excitation arising due to support motion only. Actually, it is not easy to distinguish between the roles played by two kinds of excitation, whose effects mixed up with also those ensuing from system geometric nonlinearities. Nonetheless, in the following, activation of the various response components is also tentatively referred to the excitation conditions in their background.

Different from symmetric excitation, the a ₂ frequency–response curve (black line in Fig. 15a) of the externally and parametrically excited planar antisymmetric mode, obtained with the modulation equations, is hardening. A new branch originates from the a ₂ resonant branch via PB due to the activation of a ₄ component (Fig. 15b), which is excited right of perfect resonance also due to parametric excitation (see the a ₄ A ²₂₀ term in Eq. (25). A stable in-plane/out-of-plane antisymmetric solution a ₂, a ₄, with nearly comparable values of the two participating amplitudes (see also Fig. 16b forward), is established; it has been previously detected experimentally and named antisymmetric ballooning [8]. Following the bifurcated branch, a Hopf bifurcation occurs.

Fig. 15

Frequency–response curves with varying A ₂₀: a ₂ (a) and a ₄ (b). Analytical results: P₁₁ = 0, A₁₀ = 0, A₂₀ = 0.003

Fig. 16

Time histories obtained from the analytical calculations, for a Ω = 0.9, b Ω = 1.1, c Ω = 1.3; q ₁—black line, q ₂—blue line, q ₄—red line; P₁₁ = 0, A₁₀ = 0, A₂₀ = 0.003. (Color figure online)

The resonance curves are computed directly from the modulation equations. However, the associated q _j , $j = 1 \ldots 4$, solution (26) highlights coupling of also other components to the $\varepsilon^{2}$-order of perturbation. With the sole A ₂₀ support motion, solution (26) reads

$$\begin{aligned} q_{1} & = \varepsilon a_{1} \cos \left( {\Omega t + \phi_{1} } \right) + \varepsilon^{2} \frac{1}{{2\Omega^{2} }}\left[ { - \sum\limits_{j = 1}^{4} {c_{j} a_{j}^{2} + A_{20}^{2} h_{12}^{s} \left( {1 - \frac{1}{3}\cos 2\Omega t} \right) + \frac{1}{3}\sum\limits_{j = 1,2,4} {a_{j}^{2} c_{j} \cos 2\left( {\Omega t + \phi_{j} } \right)} } } \right] \\ q_{2} & = \varepsilon a_{2} \cos \left( {\Omega t + \phi_{2} } \right) + \varepsilon^{2} \frac{1}{{2\Omega^{2} }}a_{1} a_{2} c_{21} \left[ {\frac{1}{3}\cos \left( {2\Omega t + \phi_{1} + \phi_{2} } \right) - \cos \left( {\phi_{1} - \phi_{2} } \right)} \right] \\ q_{3} & = \varepsilon a_{3} \cos \left( {\frac{1}{2}\Omega t + \phi_{3} } \right) + \varepsilon^{2} \frac{1}{{4\Omega^{2} }}a_{1} a_{3} c_{31} \cos \left( {\frac{3}{2}\Omega t + \phi_{1} + \phi_{2} } \right) \\ q_{4} & = \varepsilon a_{4} \cos \left( {\Omega t + \phi_{4} } \right) + \varepsilon^{2} \frac{1}{{2\Omega^{2} }}a_{1} a_{4} c_{41} \left[ {\frac{1}{3}\cos \left( {2\Omega t + \phi_{1} + \phi_{4} } \right) - \cos \left( {\phi_{1} - \phi_{4} } \right)} \right] \\ \end{aligned}$$

(30a–d)

Although the a ₁ amplitude computed from modulation equations is equal to zero, the q ₁ component (Eq. 30a) is also entrained in the overall response via the non-vanishing a ₂ and a ₄ amplitudes and the A ₂₀ term associated with ½-subharmonic external excitation in Eq. (8), all of them existing at $\varepsilon^{2}$-order; in contrast, q ₃ identically vanishes (Eq. 30c) because a ₁ = 0.

Thus, due to couplings, the in-plane symmetric component q ₁ is also activated, besides q ₂ and q ₄. Taking into account analytical solutions (30) and results presented in Fig. 15 we plot time histories for selected Ω values. In Fig. 15a, for Ω = 0.9 there is only the a ₂ amplitude which however, due to coupling, also activates the q ₁ component (Fig. 16a). Trimodal q ₁, q ₂, q ₄ (Fig. 16b) and in-plane bimodal q ₁, q ₂ (Fig. 16c) responses are obtained for Ω = 1.1 and Ω = 1.3, respectively. In all cases, q ₁ is activated in the overall response by higher order terms in Eq. (30a), though with a considerably lower importance. Shift of its time history from the reference abscissa axis is basically due to constant quadratic terms in Eq. (30a).

In Fig. 17 we present the q-components obtained by continuation performed directly on the original ODEs (6). Figure 17b corresponds to Fig. 15a and Fig. 17c to Fig. 15b, with very good quantitative agreement, while in Fig. 17a the q ₁ component directly obtained by numerical simulation is presented. It confirms what already observed through the time histories in Fig. 16.

Fig. 17

Frequency–response curves with varying A ₂₀: q ₁(a), q ₂(b), q ₄(c). Numerical simulation of the original ODEs: P₁₁ = 0, A₁₀ = 0, A₂₀ = 0.003

The Hopf bifurcation point in the modulation equations corresponds to torus bifurcation (TB) in the original ODEs. The transition through TB is shown in the bifurcation diagrams of Fig. 18, computed in relevant zoomed area. After the torus bifurcation the system exhibits quasiperiodic oscillations and then goes to chaotic motion. The Poincaré cross-sections computed for q ₁, q ₂, and q ₄ (with q ₃ = 0) at the selected frequency Ω = 1.17 are presented in Fig. 19a–c. For comparison, one more Poincaré map is plotted at Ω = 1.19 for the sole q ₄ (Fig. 19d). For this attractor, the first three Lyapunov exponents take the values λ ₁ = 0.050707, λ ₂ = 0.017823, λ ₃ = −0.016674, meaning that a transition to chaotic oscillations has occurred. A q ₄, q ₂ Poincaré map corresponding to the actual motion of cable quarter span points in the vertical configuration plane is also reported in Fig. 19e. It exhibits a chaotic, horizontally-shrunk, circumferential loop showing the different, yet somehow comparable, contributions of the two participating components, and evidencing the complex, prevailingly antisymmetric, ballooning response into which the regular one existing at Ω = 1.1 (Fig. 19f) has evolved. Such a kind of complex response has been highlighted also experimentally [8], with the relevant transition mechanism from the underlying regular one being referred to an involved homoclinic bifurcation scenario [11].

Fig. 18

Bifurcation diagrams with varying Ω near the torus bifurcation point (TB): q ₁ (a), q ₂ (b), q ₄ (c). Numerical simulation of original ODEs: P ₁₁ = 0, A ₁₀ = 0, A ₂₀ = 0.003

Fig. 19

Poincaré maps of q ₁ (a), q ₂ (b), q ₄ at Ω = 1.17 (c) and Ω = 1.19 (d), and q ₂–q ₄ map (e) at Ω = 1.19 and phase diagram (f) at Ω = 1.1; P ₁₁ = 0, A ₁₀ = 0, A ₂₀ = 0.003

The effect of antisymmetric support motion on system response is also investigated for varying A ₂₀ amplitude at the selected frequency Ω = 1.1, where q ₁, q ₂, q ₄ solution is activated. In Fig. 20 we present force-response curves of a ₂ and a ₄ obtained from modulation Eq. (25). The corresponding diagrams based on the ODEs are presented in Fig. 21a, b, respectively. The agreement between analytical and numerical solutions is very good. Figure 21c shows the presence of also the q ₁ component, which could indeed be obtained analytically, too, because vanishing of a ₁ in the modulation equations does not entail vanishing of q ₁, as previously discussed. The branching of a ₄ occurs via PB in Fig. 20a, b. The q ₄ component grows up rapidly and then remains almost constant (Figs. 20b and 21b). Contrary to analytical curves, numerical ones exhibit also two TB points with the unstable branch in-between. Indeed, as shown by the time histories in Fig. 21d, system response after the TB is almost periodic with slowly modulated amplitudes, yet with the average maximum values corresponding to those obtained analytically.

Fig. 20

Force-response curves with varying A ₂₀: amplitudes a ₂ (a) and a ₄ (b). Analytical results: Ω = 1.1, P ₁₁ = 0, A ₁₀ = 0

Fig. 21

Force-response curves with varying A ₂₀: q ₂ (a), q ₄ (b), q ₁ (c), and corresponding time histories for A ₂₀ = 0.0018 (d). Numerical simulation of original ODEs: Ω = 1.1, P ₁₁ = 0, A ₁₀ = 0

4.4 Symmetric plus antisymmetric support motion (P ₁₁ = 0, A ₁₀ ≠ 0, A ₂₀ ≠ 0)

The concurrent presence of both A ₁₀ and A ₂₀, namely symmetric and antisymmetric support motion, is analyzed for two case-studies. The analyses are carried out directly on the original equations of motion (6), being the induced dynamics already close to strongly nonlinear behaviour. In the first analyzed case, the symmetric support motion is kept prevalent than the antisymmetric one (A ₁₀ = 0.002, A ₂₀ = 0.001), and frequency–response curves are shown in Fig. 22a–c. The basic bimodal response (q ₁, q ₂) (black line in Fig. 22a, b), directly induced by the two excitation components loses stability through a PD bifurcation giving rise to a trimodal response branch (q ₁, q ₂, q ₃) (green line in Fig. 22a–c). Doubling of the solution period is due again to the onset of q ₃, which has a fundamental (linear) frequency ½. Close to Ω = 1.09, the trimodal solution shows a TB, and for slightly lower excitation frequencies, trimodal quasiperiodic responses are found (see Fig. 22d, where a phase portrait is reported in the q ₁–q ₂–q ₃ space, superimposed to its Poincaré section).

Fig. 22

Frequency–response curves under (higher) in-plane symmetric plus anti-symmetric support motion: a mode 1, b mode 2, c mode 3. Phase portrait (blue line) and Poincaré section (red points) for Ω = 1.08 (d). Original ODEs: P ₁₁ = 0, A ₁₀ = 0.002, A ₂₀ = 0.001. (Color figure online)

As a general comment, the prevailing role of the A ₁₀ excitation is evident, being the ensuing dynamics similar to what happens for P ₁₁ = 0, A ₂₀ = 0 (see Fig. 5), apart from the significant contribution of the antisymmetric support motion which directly induces, in all responses, the q ₂ component too.

A second case study is reported in Fig. 23a–d, where frequency–response plots for P ₁₁ = 0, A ₁₀ = 0.001, A ₂₀ = 0.002 are shown. Here, the prevailing role of A ₂₀ makes the dynamics more cumbersome than in the previous case. In fact, bimodal (q ₁, q ₂, black line), trimodal (q ₁, q ₂, q ₃, green line, and q ₁, q ₂, q ₄, red line) as well as quadrimodal responses (blue line) are involved. In particular, the reference bimodal solution—which shows a combination of softening q ₁ and hardening q ₂ components, as per the underlying mixed support motion—loses stability in correspondence of a PB, where a branch of trimodal q ₁, q ₂, q ₄ (red) arises. Moreover, two PD on the same bimodal solution cause the occurrence of the trimodal q ₁, q ₂, q ₃ (green) solution. The two trimodal branches are connected with one another by a branch of stable quadrimodal solution (blue), which exists in-between two PB points. Trimodal quasiperiodic evolutions are found after the TB which is found on the trimodal q ₁, q ₂, q ₄ (red) branch, and a phase portrait with Poincaré section is shown in Fig. 23e for Ω = 1.1, with the relevant Fourier spectrum in Fig. 23f, to confirm the non-regular properties of the solution. As a remark, the dominating effect of A ₂₀ is evident, being the dynamical response similar to what happens in Fig. 17, even if the participation of a non-null symmetric support motion causes, as a major result, the involvement of also the q ₃ component.

Fig. 23

Frequency–response curves under (higher) in-plane anti-symmetric plus symmetric support motion: a mode 1, b mode 2, c mode 3, d mode 4. Phase portrait (blue line) and Poincaré section (red points) for Ω = 1.1 (e), relevant Fourier spectrum (f). Original ODEs: P ₁₁ = 0, A ₁₀ = 0.001, A ₂₀ = 0.002. (Color figure online)

4.5 External loading and symmetric plus antisymmetric support motion (P ₁₁ ≠ 0, A ₁₀ ≠ 0, A ₂₀ ≠ 0)

Here, the concurrent application of the three sources of excitation is considered, for the case study in which their values are assumed as P ₁₁ = 0.002, A ₁₀ = 0.002, A ₂₀ = 0.001. Symmetric and antisymmetric support motions are the same as in the first case of the previous section, but with the addition of an apparently significant contribution of symmetric external loading.

As a result of the analysis, which is still performed by considering the original ODEs (6) and is summarized in Fig. 24, a dynamic behaviour very similar to the case P ₁₁ = 0, A ₁₀ = 0.002, A ₂₀ = 0.001, shown in Fig. 22, is found: the basic (q ₁, q ₂) bimodal solution (black curve) becomes unstable through two PD, giving rise to a trimodal branch (q ₁, q ₂, q ₃), characterized by a TB, close to which trimodal quasiperiodic solutions occur, as shown in the phase portrait in Fig. 24d. The contribution of P ₁₁ seems to be almost inconsequential, but the amplitude of both the q ₁ and q ₃ components is significantly smaller here than in the case with P ₁₁ = 0. Therefore, the cancellation effect owed to the interaction between P ₁₁ and A ₁₀, occurs also here, in the presence of A ₂₀ excitation. The non-vanishing q ₃ component (contrary to the case with sole symmetric excitations of Sect. 4.2) is herein driven in the response by the (q ₁, q ₂) bimodal solution, with the ensuing q ₂ component—activated by the low, yet unopposed, antisymmetric support motion A ₂₀—reaching the same maximum values as in Fig. 22b and the q ₁ one being solely reduced with respect to values in Fig. 22a owing to the competing symmetric excitations.

Fig. 24

Frequency–response curves under external loading and (higher) in-plane symmetric plus anti-symmetric support motion: a mode 1, b mode 2, c mode 3. Phase portrait (blue line) and Poincaré section (red points) for Ω = 1.08 (d). Original ODEs: P ₁₁ = 0.002, A ₁₀ = 0.002, A ₂₀ = 0.001. (Color figure online)

5 Conclusions and further developments

The four-degree-of-freedom model of a sagged cable proposed in Benedettini et al. [1] has been resumed to evaluate the effect of support motion on system nonlinear response at first crossover, also in combination with distributed loading. The model embeds external and parametric forcing terms arising from the physical excitations. A general third-order multiple scale solution at primary resonance and 1:1:1/2:1 multiple internal resonance has been accomplished, to deal with weakly nonlinear planar/nonplanar multimodal oscillations. In the numerical investigation of the ensuing modulation equations attention has been focused on the effect of solely planar excitations, by considering symmetric and/or antisymmetric support motions, in possible combination with symmetric external excitation, which entails an interesting cancellation phenomenon in the system response. Numerical simulation of the original ordinary differential equations of motion has validated analytical results for medium–low excitation amplitudes, and has highlighted a higher multimodal contents of the regular response at higher excitation amplitudes, along with involved transitions to regimes of complex response. The results have been discussed in the background of the analytical/numerical ones already available for the sagged cable under sole symmetric external excitation, as well as of the experimental outcomes previously obtained for a companion cable-mass system under sole support motion, by also possibly referring some observed behaviours to the presence of external and/or parametric excitations. Anyway, no meaningful effects to be specifically ascribed to the latter excitation have been detected in the response.

The considered four-d.o.f. cable model has a meaningful potential in terms of excitation cases to be possibly addressed. However, just a few of them have been investigated in this paper, thus leaving room for possible future developments in different directions. Still in the monofrequent planar excitation perspective herein pursued, analyses with symmetric/antisymmetric support motion could be extended to the ½-subharmonic resonance range, via systematic numerical investigations aimed at obtaining the response charts highlighting some main regions of regular and non-regular response in the excitation control parameters, thus complementing and possibly cross-validating the parallel, yet independent, experimental outcomes. Moreover, the effect of general multifrequency excitations (ensuing from distributed loading and support motion with different frequencies) on system response could be considered, also in order to check the actual robustness of the observed cancellation effect and the possibility to exploit it for control purposes. Of course, consideration of also out-of-plane excitations would further increase the richness of observable nonlinear responses.

Appendices

Appendix 1

1.1 Physical cable data

distance between the supports: l = 600.6 mm,

cable cross-section: A = 0.1257 mm²

gravity acceleration: g = 9.81 m/s²

sag: d = 30.5 mm

mass per unit length: m = 4.96014 × 10⁻⁴ kg/m

horizontal force (initial tension): $H = mg\frac{{l^{2} }}{8d} = 0.719117$ N

First natural frequency of the taut string: $\omega_{0} = \frac{\pi }{l}\sqrt {\frac{H}{m}} = 19.92$ rad/s

1.2 Vibration modes

• in-plane, symmetric (f ₁) and antisymmetric (f ₂):

  $$f_{1} (x) = B_{1} \left( {1 - \tan \frac{\beta l}{2}} \right)\sin \frac{\beta l}{2}x - \cos \frac{\beta l}{2}x,\quad f_{2} (x) = \sin 2\pi x,$$

• out-of-plane, symmetric (f ₃) and antisymmetric (f ₄):

  $$f_{3} (x) = \sin \pi x,\quad f_{4} (x) = \sin 2\pi x,$$

with $\frac{\beta l}{2} = \pi ,B_{1} = - 0.25.$

1.3 Natural frequencies of a sagged cable

$$\omega_{1} = \frac{{\omega_{0} }}{\pi }\sqrt {\frac{1}{{I_{1,m} }}\left( {I_{1,d} + \frac{{\varLambda^{2} }}{64}I_{1,y}^{2} } \right)} ,\quad \omega_{2} = \frac{{\omega_{0} }}{\pi }\sqrt {\frac{{I_{2,d} }}{{I_{2,m} }}} ,\quad \omega_{3} = \frac{{\omega_{0} }}{\pi }\sqrt {\frac{{I_{3,d} }}{{I_{3,m} }}} ,\quad \omega_{4} = \frac{{\omega_{0} }}{\pi }\sqrt {\frac{{I_{4,d} }}{{I_{4,m} }}}$$

Dimensionless cable frequencies: λ ² _i  = ω ² _i /ω ²₁ , i = 1÷4

At first crossover (1:1:1/2:1 internal resonance):

$$\omega_{1} = 39.83\,{\text{rad}}/{\text{s,}}\quad \omega_{2} = 39.84\,{\text{rad}}/{\text{s}},\quad \omega_{3} = 19.92\,{\text{rad}}/{\text{s,}}\quad \omega_{4} = 39.84\,{\text{rad}}/{\text{s}}$$

where $\varLambda = \sqrt {64\left( EA/H \right) {\left(d/l\right)}^{2} } = 6.28012$, with EA/H = 239.16

$$I_{j,m} = \int_{0}^{1} {f_{j}^{2} (x)dx} , \quad I_{j,d} = \int_{0}^{1} {\left[ {f_{j}^{{\prime }} (x)} \right]^{2} dx} , \quad I_{j,y} = \int_{0}^{1} {y^{{\prime }} f_{j}^{{\prime }} (x)dx}$$

1.4 Modal damping coefficients

$$\mu_{11} = \mu_{21} = 0.05,\mu_{31} = \mu_{41} = 0.08$$

1.5 Structural coefficients

$$\begin{aligned} c_{1} & = - 12.1441,\quad c_{2} = c_{4} = - 64.7893,\quad c_{3} = - 16.1973; \\ c_{21} & = c_{41} = - \, 24.3039;\quad c_{31} = - 6.07598; \\ d_{11} & = 49.1594;\quad d_{12} = d_{14} = 786.805;\quad d_{13} = 196.701; \\ d_{21} & = d_{41} = 147.574;\quad d_{22} = d_{42} = 2361.95;\quad d_{23} = d_{43} = 590.488;\quad d_{24} = d_{44} = 2361.95; \\ d_{31} & = 36.8935;\quad d_{32} = 590.488;\quad d_{33} = 147.622;\quad d_{34} = 590.488. \\ \end{aligned}$$

1.6 Coefficients associated with parametric excitation terms produced by support motion

$$\begin{aligned} c_{2}^{p} & = c_{4}^{p} = 0;\quad c_{21}^{p} = c_{41}^{p} = 0; \\ d_{21}^{p} & = d_{22}^{p} = d_{23}^{p} = d_{24}^{p} = d_{41}^{p} = d_{42}^{p} = d_{43}^{p} = d_{44}^{p} = 0; \\ e_{12}^{p} & = e_{14}^{p} = 159.44;\quad e_{22}^{p} = e_{44}^{p} = 478.631;\quad e_{24}^{p} = e_{42}^{p} = 478.631;\quad e_{32}^{p} = e_{34}^{p} = 119.658; \\ g_{12}^{p} & = g_{14}^{p} = g_{24}^{p} = g_{42}^{p} = g_{32}^{p} = g_{34}^{p} = 0; \\ m_{24}^{p} & = m_{42}^{p} = 0. \\ \end{aligned}$$

1.7 Coefficients associated with external excitation terms produced by support motion

$$\begin{aligned} c_{1}^{s} & = 2.66667;\quad c_{2}^{s} = c_{4}^{s} = - 0.63662;\quad c_{3}^{s} = - 1.27324; \\ r_{22}^{s} & = r_{24}^{s} = r_{42}^{s} = r_{44}^{s} = 0;\quad n_{2}^{s} = n_{4}^{s} = 0; \\ h_{12}^{s} & = h_{14}^{s} = 13.1291. \\ \end{aligned}$$

1.8 External load

$$P_{11} = 0.002\,({\text{reference}}\,{\text{value}},{\text{varied}}\,{\text{as}}\,{\text{a}}\,{\text{bifurcation}}\,{\text{parameter}}),\,P_{21} = P_{31} = P_{41} = 0.$$

1.9 Amplitudes of support motion

$$A_{10} = 0.002,\quad A_{20} = 0.002\,({\text{reference}}\,{\text{values}},{\text{varied}}\,{\text{as}}\,{\text{bifurcation}}\,{\text{parameters}}),\,A_{30} = 0,\quad A_{40} = 0.$$

Appendix 2

Definitions of coefficients in Eq. (21) of second order secular generating terms

• First equation

  $$\begin{aligned} F_{10}^{s} & = - \frac{1}{2}i\Omega A_{10} c_{1}^{s} \mu_{11} ,\quad \bar{F}_{1}^{s} = - \frac{{c_{1} }}{{6\Omega^{2} }}\left( {h_{12}^{s} A_{20}^{2} + h_{14}^{s} A_{40}^{2} } \right),\quad \bar{F}_{1}^{p} = \frac{1}{4}\left( {A_{20}^{2} e_{12}^{p} + A_{40}^{2} e_{14}^{p} } \right), \\ F_{111} & = 3d_{11} - \frac{{10c_{1}^{2} }}{{3\Omega^{2} }},\quad F_{221} = d_{12} + \frac{{2c_{2} }}{{\Omega^{2} }}\left( {\frac{{c_{1} }}{3} - c_{21} } \right),\quad F_{441} = d_{14} + \frac{{2c_{4} }}{{\Omega^{2} }}\left( {\frac{{c_{1} }}{3} - c_{41} } \right) ,\\ F_{1}^{p} & = \frac{1}{2}\left( {A_{20}^{2} e_{12}^{p} + A_{40}^{2} e_{14}^{p} } \right),\quad F_{1}^{s} = \frac{{c_{1} }}{{\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad F_{122} = 2d_{12} - \frac{4}{{\Omega^{2} }}c_{2} \left( {c_{1} + \frac{1}{3}c_{21} } \right), \\ F_{133} & = 2d_{13} - \frac{{c_{3} }}{{\Omega^{2} }}\left( {4c_{1} - c_{31} } \right),\quad F_{144} = 2d_{14} - \frac{{4c_{4} }}{{\Omega^{2} }}\left( {c_{1} + \frac{{c_{41} }}{3}} \right) \\ \end{aligned}$$

• Second equation

  $$\begin{aligned} F_{20}^{s} & = - \frac{1}{2}i\Omega c_{2}^{s} \mu_{21} A_{20} ,\quad F_{112} = 2d_{21} - \frac{{2c_{21} }}{{\Omega^{2} }}\left( {c_{1} + \frac{{c_{21} }}{3}} \right),\quad \bar{F}_{2}^{s} = - \frac{{c_{21} }}{{12\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right), \\ \bar{F}_{2}^{p} & = \frac{1}{4}\left( {A_{20}^{2} e_{22}^{p} + A_{40}^{2} e_{24}^{p} } \right),\quad \bar{F}_{112} = d_{21} + \frac{{c_{21} }}{{\Omega^{2} }}\left( {\frac{{c_{1} }}{3} - c_{21} } \right),\quad F_{222} = 3d_{22} - \frac{{5c_{2} c_{21} }}{{3\Omega^{2} }},\quad F_{442} = \left( {d_{24} + \frac{{c_{21} c_{4} }}{{3\Omega^{2} }}} \right), \\ F_{2}^{s} & = \frac{{c_{21} }}{{2\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad F_{2}^{p} = \frac{1}{2}\left( {A_{20}^{2} e_{22}^{p} + A_{40}^{2} e_{24}^{p} } \right),\quad F_{233} = 2\left( {d_{23} - \frac{{c_{21} c_{3} }}{{\Omega^{2} }}} \right), \\ F_{244} & = 2\left( {d_{24} - \frac{{c_{21} c_{4} }}{{\Omega^{2} }}} \right). \\ \end{aligned}$$

• Third equation

  $$\begin{aligned} F_{113} & = 2d_{31} - \frac{{c_{31} }}{{\Omega^{2} }}\left( {2c_{1} - \frac{{c_{31} }}{2}} \right),\quad F_{223} = 2\left( {d_{32} - \frac{{c_{2} c_{31} }}{{\Omega^{2} }}} \right),\quad F_{333} = 3d_{33} - \frac{{2c_{3} c_{31} }}{{\Omega^{2} }}, \\ F_{3}^{s} & = \frac{{c_{31} }}{{2\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad F_{3}^{p} = \frac{1}{2}\left( {A_{20}^{2} e_{32}^{p} + A_{40}^{2} e_{34}^{p} } \right),\quad F_{344} = 2\left( {d_{34} - \frac{{c_{31} c_{4} }}{{\Omega^{2} }}} \right) \\ \end{aligned}$$

• Fourth equation

  $$\begin{aligned} F_{40}^{s} & = - \frac{1}{2}i\Omega A_{40} c_{4}^{s} \mu_{41} ,\quad F_{114} = 2\left[ {d_{41} - \frac{{c_{41} }}{{\Omega^{2} }}\left( {c_{1} + \frac{{c_{41} }}{3}} \right)} \right],\quad F_{334} = 2\left( {d_{43} - \frac{{c_{3} c_{41} }}{{\Omega^{2} }}} \right), \\ \bar{F}_{4}^{s} & = - \frac{{c_{41} }}{{12\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad \bar{F}_{4}^{p} = \frac{1}{4}\left( {A_{20}^{2} e_{42}^{p} + A_{40}^{2} e_{44}^{p} } \right),\quad F_{224} = d_{42} + \frac{{c_{2} c_{41} }}{{3\Omega^{2} }}, \\ F_{242} & = 2\left( {d_{42} - \frac{{c_{2} c_{41} }}{{\Omega^{2} }}} \right),\quad F_{444} = 3d_{44} - \frac{{5c_{4} c_{41} }}{{3\Omega^{2} }},\quad \bar{F}_{114} = d_{41} + \frac{{c_{41} }}{{\Omega^{2} }}\left( {\frac{{c_{1} }}{3} - c_{41} } \right), \\ F_{4}^{s} & = \frac{{c_{41} }}{{2\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad F_{4}^{p} = \frac{1}{2}\left( {A_{20}^{2} e_{42}^{p} + A_{40}^{2} e_{44}^{p} } \right) \\ \end{aligned}$$

Appendix 3

Definitions of coefficients of complex amplitude modulation equation (23)

• coefficients of $\frac{{dA_{1} }}{dt}$ equation

  $$\begin{aligned} G_{01}^{s} & = \frac{{A_{10} }}{16\Omega }c_{1s} \left( {i\sigma_{1} + 3\mu_{11} \Omega } \right),\quad G_{33} = \frac{{c_{3} }}{{2\Omega^{3} }}\left( {i\rho_{3} + \frac{i}{4}\sigma_{1} - \frac{1}{4}\mu_{11} \Omega + \frac{1}{2}\mu_{31} \Omega } \right), \\ \bar{G}_{1}^{s} & = - \frac{{ic_{1} }}{{12\Omega^{3} }}\left( {h_{12}^{s} A_{20}^{2} + h_{14}^{s} A_{40}^{2} } \right),\quad \bar{G}_{1}^{p} = \frac{i}{{8\Omega^{{}} }}\left( {A_{20}^{2} e_{12}^{p} + A_{40}^{2} e_{14}^{p} } \right), \\ \bar{G}_{111} & = \frac{i}{{\Omega^{{}} }}\left( {\frac{3}{2}d_{11} - \frac{5}{3}\frac{{c_{1}^{2} }}{{\Omega^{2} }}} \right),\quad G_{221}^{{}} = \frac{i}{{2\Omega^{{}} }}d_{12} + \frac{{c_{2} i}}{{\Omega^{3} }}\left( {\frac{{c_{1} }}{3} - c_{21} } \right), \\ G_{441} & = \frac{{ic_{4} }}{{\Omega^{3} }}\left( {\frac{{c_{1} }}{3} - c_{41} } \right) + \frac{{id_{14} }}{{2\Omega^{{}} }},\quad G_{1}^{p} = \frac{i}{{4\Omega^{{}} }}\left( {A_{20}^{2} e_{12}^{p} + A_{40}^{2} e_{14}^{p} } \right), \\ G_{1}^{s} & = \frac{{ic_{1} }}{{2\Omega^{2} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad G_{1} = - \frac{i}{8\Omega }\left( {\mu_{11}^{2} + \sigma_{1}^{2} } \right),\quad G_{122}^{{}} = - \frac{{2ic_{2} }}{{\Omega^{3} }}\left( {c_{1} + \frac{1}{3}c_{21} } \right) + \frac{i}{\Omega }d_{12} , \\ G_{133} & = \frac{i}{\Omega }\left( {d_{13} - \frac{{2ic_{1} c_{3} }}{{\Omega^{2} }}} \right),\quad G_{144} = - \frac{{2ic_{4} }}{{\Omega^{3} }}\left( {c_{1} + \frac{1}{3}c_{41} } \right) + \frac{{id_{14} }}{{\Omega^{{}} }} \\ \end{aligned}$$

• coefficients of $\frac{{dA_{2} }}{dt}$ equation

  $$\begin{aligned} G_{02}^{s} & = \frac{{c_{2}^{s} }}{16\Omega }A_{20} \left( {3\mu_{21} \Omega + i\rho_{2} } \right),\quad \bar{G}_{121} = - \frac{{ic_{21} }}{{\Omega^{3} }}\left( {c_{1} + \frac{1}{3}c_{21} } \right) + \frac{{id_{21} }}{\Omega },\quad \bar{G}_{2}^{p} = \frac{i}{8\Omega }\left[ {A_{20}^{2} e_{22}^{p} + A_{40}^{2} e_{24}^{p} } \right], \\ \bar{G}_{2}^{s} & = - \frac{{ic_{21} }}{{24\Omega^{3} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad \bar{G}_{112} = - \frac{{ic_{21} }}{{2\Omega^{3} }}\left( {c_{21} - \frac{1}{3}c_{1} } \right) + \frac{{id_{21} }}{2\Omega },\quad \bar{G}_{222} = \frac{i}{2\Omega }\left( {3d_{22} - \frac{{5c_{2} c_{21} }}{{3\Omega^{2} }}} \right), \\ \bar{G}_{442} & = \frac{i}{2\Omega }\left( {d_{24} + \frac{{c_{21} c_{4} }}{{3\Omega^{2} }}} \right),\quad G_{2}^{p} = \frac{i}{4\Omega }\left[ {A_{20}^{2} e_{22}^{p} + A_{40}^{2} e_{24}^{p} } \right],\quad G_{2}^{s} = \frac{{ic_{21} }}{{4\Omega^{3} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right), \\ G_{2} & = - \frac{i}{8\Omega }\left( {\mu_{21}^{2} + \frac{{\rho_{2}^{2} }}{{\Omega^{2} }}} \right),\quad \bar{G}_{233} = \frac{i}{\Omega }\left( {d_{23} - \frac{{c_{21} c_{3} }}{{\Omega^{2} }}} \right),\quad \bar{G}_{244} = \frac{i}{\Omega }\left( {d_{24} - \frac{{c_{21} c_{4} }}{{\Omega^{2} }}} \right) \\ \end{aligned}$$

• coefficients of $\frac{{dA_{3} }}{dt}$ equation

  $$\begin{aligned} G_{232} & = \frac{2i}{\Omega }\left( {d_{23} - \frac{{c_{2}^{{}} c_{31} }}{{\Omega^{2} }}} \right),\quad \bar{G}_{3}^{s} = - \frac{{ic_{1}^{s} c_{31} }}{4\Omega }A_{10} ,\quad \bar{G}_{333} = \frac{i}{\Omega }\left( {3d_{33} - \frac{{5c_{3} c_{31} }}{{2\Omega^{2} }}} \right), \\ \bar{G}_{131} & = \frac{{ic_{31} }}{{\Omega^{3} }}\left( {\frac{3}{2}c_{31} - 2c_{1} } \right) + \frac{2i}{\Omega }d_{31} ,\quad \bar{G}_{13} = \frac{{c_{31} }}{{2\Omega^{2} }}\left( {\mu_{11} + \frac{{i\sigma_{1} }}{\Omega }} \right),\quad G_{3}^{p} = \frac{i}{2\Omega }\left( {A_{20}^{2} e_{32}^{p} + A_{40}^{2} e_{34}^{p} } \right), \\ G_{3}^{s} & = \frac{{ic_{31} }}{{2\Omega^{3} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad G_{3} = - \frac{i}{{\Omega^{3} }}\left( {\rho_{3}^{2} + \frac{{\mu_{31}^{2} \Omega^{2} }}{4}} \right),\quad \bar{G}_{344} = \frac{2i}{\Omega }\left( {d_{34} - \frac{{c_{4} c_{31} }}{{\Omega^{2} }}} \right) \\ \end{aligned}$$

• coefficients of $\frac{{dA_{4} }}{dt}$ equation

  $$\begin{aligned} G_{04}^{s} & = A_{40} \frac{{c_{4}^{s} }}{16\Omega }\left( {i\rho_{4} + 3\mu_{41} \Omega } \right),\quad \bar{G}_{141} = - \frac{{ic_{41} }}{{\Omega^{3} }}\left( {c_{1} + \frac{1}{3}c_{41} } \right) + \frac{{id_{41} }}{\Omega },\quad \bar{G}_{343} = \frac{i}{\Omega }\left( {d_{43} - \frac{{c_{3} c_{41} }}{{\Omega^{2} }}} \right), \\ \bar{G}_{4}^{s} & = - \frac{{ic_{41} }}{{24\Omega^{3} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right),\quad \bar{G}_{4}^{p} = \frac{i}{8\Omega }\left[ {A_{20}^{2} e_{42}^{p} + A_{40}^{2} e_{44}^{p} } \right],\quad \bar{G}_{114} = \frac{i}{2\Omega }\left[ {d_{41} + \frac{{c_{41} }}{{\Omega^{2} }}\left( {\frac{1}{3}c_{1} - c_{41} } \right)} \right], \\ \bar{G}_{224} & = \frac{i}{2\Omega }\left( {d_{42} + \frac{{c_{2} c_{41} }}{{3\Omega^{2} }}} \right),\quad \bar{G}_{444} = \frac{i}{2\Omega }\left( {3d_{44} - \frac{{5c_{4} c_{41} }}{{3\Omega^{2} }}} \right),\quad G_{4}^{s} = \frac{{ic_{41} }}{{4\Omega^{3} }}\left( {A_{20}^{2} h_{12}^{s} + A_{40}^{2} h_{14}^{s} } \right), \\ G_{4}^{p} & = \frac{i}{4\Omega }\left( {A_{20}^{2} e_{42}^{p} + A_{40}^{2} e_{44}^{p} } \right),\quad G_{4} = - \frac{i}{8\Omega }\left( {\mu_{41}^{2} + \frac{{\rho_{4}^{2} }}{{\Omega^{2} }}} \right),\quad G_{242} = \frac{i}{\Omega }\left( {d_{42} - \frac{{c_{2} c_{41} }}{{\Omega^{2} }}} \right) \\ \end{aligned}$$