On the use of a pendulum as mass damper to control the rocking motion of a rigid block with fixed characteristics

Abstract

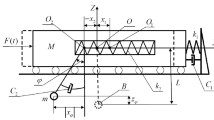
Many works have been focused on the use of the base isolation to improve the dynamic response of the rigid blocks, avoiding the overturning of these systems. In this paper the effects of a mass damper on the rocking motion of a non-symmetric rigid block, subject to one-sine pulse type excitation, is investigated. The damper is modelled as a pendulum, hinged at the top of the block, with the mass lumped at the end. The equations of rocking motion, the uplift and the impact conditions are derived and the results are obtained by numerical integration of these equations. An extensive parametric analysis is performed, by taking as variable parameters the eccentricity of the centre of mass, the frequency and the amplitude of the excitation and the characteristics of the mass damper. Here the geometrical parameters characterizing the block are taken as fixed quantities, since the main objective of the study is understand if it is possible to find the optimal properties of the pendulum, capable to make more difficult the overturning of the body. The results show that the presence of the mass damper, if correctly designed, leads to a general improvement of the response of the system, since the overturning of the block occurs for values, of the amplitude of the base excitation, higher than those observed where no mass damper is used. Curves providing the optimum value of the characteristics of the mass damper versus the parameters characterizing the excitation, are finally obtained.

Appendix: Rocking around the right corner

This section shows the expressions of all the quantities required to define the equations of motion for rocking around the right corner B.

1.1 Equations of motion

The position of the center of mass M of the rigid body with respect to an inertial reference frame with origin initially coincident with the point B are:

$$\begin{aligned} \left\{ {\begin{array}{l} x_{MB} =x_g+R_{BG}\, \cos \left( \pi -\alpha _{BG}+\vartheta \right) \\ y_{MB} =R_{BG}\, \sin \left( \pi -\alpha _{BG}+\vartheta \right) \end{array}} \right. \end{aligned}$$

(13)

while the position of the center of the mass pendulum m read:

$$\begin{aligned} \left\{ {\begin{array}{l} x_{mB} =x_{g}+R_{BC}\, \cos \left( \pi -\alpha _{BC}+\vartheta \right) +l\,\sin \left( \psi \right) \\ y_{mB}= R_{BC}\, \sin \left( \pi -\alpha _{BC}+\vartheta \right) -l\,\cos \left( \psi \right) \\ \end{array}} \right. \end{aligned}$$

(14)

The expression of the kinetic energy of the system reads:

$$\begin{aligned} {\begin{array}{l} T=\frac{1}{2} J_{G} {{\dot{\vartheta }}} + \frac{1}{2}M\left( {{\dot{x}}}^2_{MB} + {{\dot{y}}}^2_{MB}\right) + \frac{1}{2}m\left( {{\dot{x}}}^2_{mB}+ {{\dot{y}}}^2_{mB}\right) \end{array}} \end{aligned}$$

(15)

while the expression of the potential energy of the system reads:

$$\begin{aligned} {U = Mg\left( y_{MB}-{{\hat{y}}}_{MB}\right) + mg\left( y_{mB} - {{\hat{y}}}_{mB}\right) } \end{aligned}$$

(16)

The equations of motion are obtained by following the Lagrangian approach:

$$\begin{aligned} \left\{ {\begin{array}{l} -g m R_{BC} \cos (\alpha _{BC}-\vartheta )-g M R_{BG} \cos (\alpha _{BG}-\vartheta )+J_{G} {{\ddot{\vartheta }}}+\\ -l m R_{BC} {{\ddot{\psi }}} \sin (\alpha _{BC}-\vartheta +\psi )-l m R_{BC} {{\dot{\psi }}}^2 \cos (\alpha _{BC}-\vartheta +\psi )+\\ -{{\ddot{x}}}_{g} (m R_{BC} \sin (\alpha _{BC}-\vartheta )+M R_{BG} \sin (\alpha _{BG}-\vartheta ))+\\ +m R_{BC}^2 {{\ddot{\vartheta }}}+M R_{BG}^2 {{\ddot{\vartheta }}}=0\\ l\,m \left( g \sin (\psi )+l {{\ddot{\psi }}}-R_{BC} {{\ddot{\vartheta }}} \sin (\alpha _{BC}-\vartheta +\psi )\right) +\\ +\,l\,m \left( R_{BC} {{\dot{\vartheta }}}^2 \cos (\alpha _{BC}-\vartheta +\psi )+{{\ddot{x}}}_{g} \cos (\psi )\right) =0 \end{array}}\right. \end{aligned}$$

(17)

1.2 Uplift conditions

With reference to Fig. 3, the uplift condition around the right corner B reads:

$$\begin{aligned} {\begin{array}{l} {{\ddot{x}}}_{g}\ge -\frac{2 }{H}\left[ g\,b_{2}+\mu \left( {{\ddot{y}}}_{m}\,\frac{B}{2}+{{\ddot{x}}}_{m}\,H\right) \right] \end{array}} \end{aligned}$$

(18)

1.3 Impact conditions

With reference to an impact that happens when the body is rocking around the left corner A and successively re-uplifts around the right corner B, the conservation of the angular momentum evaluated with respect to the right corner B, reads:

$$\begin{aligned} \begin{array}{l} \left( {{J_B} + BM{R_{BG}}cos(\pi - {\alpha _{BG}})} \right) {{{\dot{\vartheta }} }^ + } \\ + m\left( { - \frac{{{B^2}{{{\dot{\vartheta }} }^ + }}}{4} + \frac{1}{2}Bl{{{\dot{\vartheta }} }^ + }\sin (\psi ) + {H^2}{{{\dot{\vartheta }} }^ + } - H l {{{\dot{\vartheta }} }^ + }\cos (\psi )} \right) \\ = {J_B}{{{\dot{\vartheta }} }^ - } + m\left( {\frac{{{B^2}{{{\dot{\vartheta }} }^ - }}}{4} - \frac{1}{2}B l {{{\dot{\vartheta }} }^ - }\sin (\psi ) + {H^2}{{{\dot{\vartheta }} }^ - } - H l {{{\dot{\vartheta }} }^ - }\cos (\psi )} \right) \end{array} \end{aligned}$$

(19)

where $J_{B}=J_{G}+R_{BG}^2 M$ is the polar momentum evaluated with respect to the right corner B.