A mathematically consistent stochastic simulation of a 3D pendulum tuned mass damper and tuning

Abstract

This work proposes an Itō calculus-based mathematical framework for the optimal design of a nonlinear passive control arrangement. Traditional numerical methods make use of ordinary differential integration schemes to study such nonlinear systems, thereby failing to account for the stochastic nature of the input excitation. Furthermore, such integration schemes require finer time steps for accurate analysis of stochastically excited nonlinear systems, therefore, rendering these schemes to be computationally expensive. Towards this, the present work proposes a new approach employing stochastic differential calculus for the optimal design of a stochastically excited three-dimensional nonlinear pendulum tuned mass damper (PTMD) system. The proposed approach comprises of Itō-Taylor expansion-based framework for deriving the displacement mean-square response of the primary structure. Three different approaches for the determination of the mean-square response are shown. The first approach is based on numerical simulation by employing Itō-Taylor 1.5 integration scheme and the other two premises on the formulation of Itō-Taylor-based mean-square differential equations. The accurate mean-square response obtained from different approaches is then utilised for the optimal design of the PTMD system. The optimal parameters resulted in amplitude reduction of around 75 % in terms of displacement mean-square response and about 85 % at peak frequency. Further, the optimal parameters were utilised to carry out stability analysis of the nonlinear PTMD system.

Appendices

Appendix A Closed form expression results from mean-square derivation

1.1 A.1 Moment derivatives for approaches #2 and #3

Five of the 55 mean-square derivatives are listed here.

• 1.
  $$\begin{aligned} \begin{aligned} \frac{d E[y_1^2]}{dt} = 2 E[y_1 y_2] \end{aligned} \end{aligned}$$
• 2.
  $$\begin{aligned} \begin{aligned} \frac{d E[y_2^2]}{dt} = \frac{l b_1^2 + 2 m_s h^2 E[y_2 y_8] - 2 c_s l m_s E[y_2^2] - 2 k_s l m_s E[y_1 y_2] + 2 l m_s m_p E[y_2 y_7]}{m_s^2 l^2} \end{aligned} \end{aligned}$$
• 3.
  $$\begin{aligned} \begin{aligned} \frac{d E[y_3^2]}{dt}= 2 E[y_3 y_4] \end{aligned} \end{aligned}$$
• 4.
  $$\begin{aligned} \begin{aligned} \frac{d E[y_4^2]}{dt} = \frac{l b_2^2 + 2 m_s h^2 E[y_4 y_{10}] - 2 c_s l m_s E[y_4^2] - 2 k_s l m_s E[y_3 y_4] + 2 l m_s m_p E[y_4 y_9]}{m_s^2 l^2} \end{aligned} \end{aligned}$$
• 5.
  $$\begin{aligned} \frac{d E[y_1 y_2]}{dt} = \frac{m_s l E[y_2^2] - k_s l E[y_1^2] - c_s l E[y_1 y_2] + h^2 E[y_1 y_8] + m_p l E[y_1 y_7]}{m_s l} \end{aligned}$$

  (44)

1.2 A.2 Moment equations for approaches #2 and #3

The mean-square equations of the structure in the u and v directions is obtained as,

$$\begin{aligned}&\sigma ^2_{\mathrm {num}} = c_s \alpha ^4 g^2+ k_s m_s c^3 h^6+ k_s c^3 h^6 m_p \nonumber \\&\quad + k_s^2 l^2 \alpha ^2 c h^2+ m_s^2 \alpha ^2 c g^2 h^2+ \alpha ^2 c g^2 h^2 m_p^2\nonumber \\&\quad + k_s \alpha ^3 c g h^2+ c_s k_s l \alpha c^2 h^4+ c_s m_s \alpha c^2 g h^4\nonumber \\&\quad + c_s \alpha c^2 g h^4 m_p + c_s^2 l \alpha ^2 c g h^2+ 2 m_s \alpha ^2 c g^2 h^2 m_p\nonumber \\&\quad - 2 k_s l m_s \alpha ^2 c g h^2- 2 k_s l \alpha ^2 c g h^2 m_p \end{aligned}$$

(45)

$$\begin{aligned}&\sigma ^2_{\mathrm {denom}} = c_s^2 \alpha ^4 g^2+ k_s^2 \alpha ^2 c^2 h^4+ c_s k_s m_s c^3 h^6\nonumber \\&\quad + c_s k_s c^3 h^6 m_p + c_s m_s^2 \alpha ^2 c g^2 h^2\nonumber \\&\quad + c_s \alpha ^2 c g^2 h^2 m_p^2+ 2 c_s k_s \alpha ^3 c g h^2+ c_s^2 k_s l \alpha c^2 h^4\nonumber \\&\quad + c_s^3 l \alpha ^2 c g h^2\nonumber \\&\quad + c_s^2 m_s \alpha c^2 g h^4+ c_s^2 \alpha c^2 g h^4 m_p + c_s k_s^2 l^2 \alpha ^2 c h^2\nonumber \\&\quad + 2 c_s m_s \alpha ^2 c g^2 h^2 m_p - 2 c_s k_s l m_s \alpha ^2 c g h^2\nonumber \\&\quad - 2 c_s k_s l \alpha ^2 c g h^2 m_p \end{aligned}$$

(46)

$$\begin{aligned}&\quad \sigma _{2,3}^2 = \frac{b_1^2}{2 k_s} \frac{\sigma ^2_{\mathrm {num}}}{\sigma ^2_{\mathrm {denom}}} \end{aligned}$$

(47)

where $\alpha = m_pl$, $u=m_s+m_p$, $c_s=c_u=c_v=c_w$ and $k_s=k_u=k_v=k_w$. g is the acceleration due to gravity.

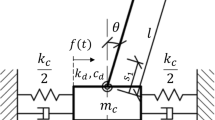
Appendix B Equations of motion of the 2D-PTMD system

This system comprises of the same primary structure as the 3D-PTMD system described in the main body of this article.

Consequently, the kinetic energy, potential energy and dissipation energies can be formulated as,

$$\begin{aligned} V&=\frac{1}{2}m_s\left[ {{\dot{x}}}^2 + {{\dot{y}}}^2 + {{\dot{z}}}^2\right] \\&\quad +\frac{1}{2}m_p\left[ {{\dot{x}}}^2+{{\dot{y}}}^2+{{\dot{z}}}^2+2l{\dot{x}}\cos {\theta }{\dot{\theta }}\right. \\&\quad \left. +2l{\dot{y}}\cos {\varphi }{\dot{\varphi }}+2l{\dot{z}}\left( \sin {\theta }{\dot{\theta }}+\sin {\varphi }{\dot{\varphi }}\right) +l^2{({\dot{\theta }}}^2+{{\dot{\varphi }}}^2) \right] \\ E&=\frac{1}{2}k_s\left[ x^2+y^2+z^2\right] +m_pg\left( z-l\left( \cos {\theta }+\cos {\varphi }\right) \right) \\ R&=\frac{1}{2}c_s\left[ {{\dot{x}}}^2 + {{\dot{y}}}^2 +{{\dot{z}}}^2\right] +\frac{1}{2}ch^2\left( \cos ^2{\theta }{{\dot{\theta }}}^2+\cos ^2{\varphi }{{\dot{\varphi }}}^2\right) \end{aligned}$$

Deriving the equations of motion using Lagrange’s equation leads to,

$$\begin{aligned}&\begin{pmatrix} m_s + m_p &{} 0 &{} 0 &{} m_p l\cos {\theta } &{} 0\\ 0 &{} m_s + m_p &{} 0 &{} 0 &{} m_p l\cos {\varphi }\\ 0 &{} 0 &{} m_s + m_p &{} m_p l\sin {\theta } &{} m_p l\sin {\varphi }\\ m_p l\cos {\theta } &{} 0 &{} m_p l\sin {\theta } &{} m_p l^2 &{} 0\\ 0 &{} m_p l\cos {\varphi } &{} m_p l\sin {\varphi } &{} 0 &{} m_p l^2 \end{pmatrix}\\&\begin{pmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \\ \ddot{\theta } \\ \ddot{\varphi } \end{pmatrix} + \begin{pmatrix} c_u &{} 0 &{} 0 &{} -m_p l\sin {\theta }{\dot{\theta }} &{} 0\\ 0 &{} c_v &{} 0 &{} 0 &{} -m_p l\sin {\varphi }{\dot{\varphi }}\\ 0 &{} 0 &{} c_w &{} m_p l\cos {\theta }{\dot{\theta }} &{} m_p l\cos {\varphi }{\dot{\varphi }}\\ 0 &{} 0 &{} 0 &{} ch^2\cos ^2{\theta } &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} ch^2\cos ^2{\varphi } \end{pmatrix}\\&\begin{pmatrix} {\dot{x}} \\ {\dot{y}} \\ {\dot{z}} \\ {\dot{\theta }} \\ {\dot{\varphi }} \end{pmatrix} + {\mathbf {K}} \begin{pmatrix} x \\ y \\ z \\ \theta \\ \varphi \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -2m_pg \\ -m_p g l\sin {\theta }\\ -m_p g l \sin {\varphi } \end{pmatrix} \end{aligned}$$

Table 6 Displacement

Note that deriving the SAA simplified version of this system and keeping all terms up to the second-order results in Eq. (33). This signifies that both systems under study have identical behaviours when small angular displacements are considered (Table 6).