1 Introduction

Considerable deformation and change of shape is one of the inherent features of slender structures such as lines, cables and risers. Much research has been carried out into both linear and nonlinear dynamics of such systems. Benedettini et al. [1, 2] intensively studied linear and nonlinear vibrations of cables and devoted their attention especially to the problem of coupling “in-plane” and “out-of plane” vibrations. Two further papers [3, 4] present the experimental set-up which enables such coupling to be investigated for a cable with eight lumped masses. Results of experimental measurements are compared with those of numerical simulations. Moreover, the authors assumed that nonlinear vibrations can be induced by motion of the supports.

Slender systems undergoing large base motion occur in offshore engineering systems where there is a coupling between the dynamics of a vessel or platform and attached risers or mooring lines and cables. In such cases not only bending and longitudinal flexibilities of slender systems but also large deflections have to be considered. Moreover, in the marine environment uplift pressure, drag force, added mass water and, in the case of risers, internal flow of hydrocarbons (petroleum and gas) has to be taken into account. An extensive discussion on the state of the art in modeling and on problems in total dynamic analysis of offshore systems is presented by Chakrabarti [5]. Although Patel and Seyed [6] report many different modelling methods, the most popular methods used are the lumped mass [7, 8] and the finite element methods [9–11]. Those methods are used in commercial packages not only specialized in offshore engineering (Riffex, Orcaflex or Offpipe) but also of general use such as Abaqus. The Flexible Segment Model (FSM) presented in [12] is another similar approach. Nevertheless, new methods of modeling slender systems used in offshore engineering are still being sought [13–15], and this paper follows this trend by presenting a modified formulation of the rigid finite element method (RFEM).

The RFEM has been successfully used for dynamic analysis of flexible systems containing beam-like links [16, 17] or plates and shells [18, 19]. Considerations of both bending and longitudinal flexibilities of slender links are presented in [20]. This paper presents the model which is derived using a modified formulation of RFEM in absolute coordinates [20, 21]; this model is supplemented with relations describing the influence of hydrodynamic forces. The validation of the method concerned with: deflections of a catenary line; vibrations with large amplitudes of a line several hundred meters long; frequencies of free vibrations of a vertical riser additionally loaded with tension; vibrations of a vertical riser with the upper end moving periodically, is presented in [21]. The comparisons indicate the correctness of the models obtained by means of the rigid finite element method even when the influence of the water environment (drag forces, hydrodynamic resistance or added mass and currents) is considered.

This paper is concerned with dynamics of risers, especially vibrations due to which there is a significant increase in bending moments. First, the results are compared with those presented by Chatjigeorgiu [22] obtained by means of the finite element and finite difference methods. Numerical simulations show that acceptable exactness of the results is obtained even when the riser is divided into less than a hundred elements, so due to the numerical effectiveness of the method it is possible to use it in order to solve a dynamic optimization task. The aim of the optimization is such a choice of vertical displacement of the upper end of the riser attached to a vessel or platform that despite its horizontal displacements the magnitude of the bending moment in the riser does not exceed its static counterpart. The solution of the optimization problem requires integration of the nonlinear equations of motion at each optimization step. The solution consists of the parameters defining the function describing the motion of the upper end of the riser. The results can be used when at a certain point of the riser the bending moment has to be restricted to a certain value, for example when there is a risk of failure.

2 Model of a riser

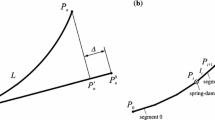
The Rigid Finite Element Method (RFEM) is used in order to formulate the model of a riser. Detailed description of the modified formulation of RFEM used for modelling is presented in [21]. A flexible link is divided into rigid elements (rfe) reflecting mass features of the link connected by means of dimensionless spring-damping elements (sde) reflecting bending ⊗ and longitudinal ⊠ flexibilities (Fig. 1). The vector of generalized coordinates takes the following form:

$${\mathbf{q}}_{i} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{i} } & {y_{i} } \\ \end{array} } & {\begin{array}{*{20}c} {\Delta _{i} } & {\varphi_{i} } \\ \end{array} } \\ \end{array} } \right]^{T}$$
(1)

where \(x_{i} , y_{i}\) are coordinates of point A i , \(\Delta _{i}\) is the elongation of sde ⊠, φ i is the declination angle of rfe i towards the axis x of the global coordinate system.

Fig. 1
figure 1

System of rigid finite and spring-damping elements

Full size image

In the paper the hydrodynamic forces are taken into account according to Morison’s law. This approach is appropriate for nonlinear analysis presented in this paper, although more complicated fluid-structure interaction can be also considered [23]. Having omitted the detailed derivations [21], the equations of motion describing the dynamics of the system can be written in the form

$${\mathbf{M}}{\ddot{\mathbf{q}}} - {\mathbf{DR}} = {\mathbf{F}}$$
(2)
$${\mathbf{D}}^{T} {\ddot{\mathbf{q}}} = {\mathbf{G}}$$
(3)

where \({\mathbf{q}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{q}}_{0}^{T} } & {{\mathbf{q}}_{1}^{T} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {{\mathbf{q}}_{n}^{T} } \\ \end{array} } \\ \end{array} } \right]^{T}\) is the vector of generalized coordinates of the system with 4(n + 1) elements, \({\mathbf{R}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{R}}_{0}^{T} } & {{\mathbf{R}}_{1}^{T} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {{\mathbf{R}}_{n}^{T} } \\ \end{array} } \\ \end{array} } \right]^{T}\) is the vector of constraint reactions with 2(n + 1) elements, \({\mathbf{M}} = {\mathbf{M}}\left( {\mathbf{q}} \right) = diag\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{M}}_{0} } & {{\mathbf{M}}_{1} } & \ldots \\ \end{array} } & {\begin{array}{*{20}c} {{\mathbf{M}}_{i} } & \ldots & {{\mathbf{M}}_{n} } \\ \end{array} } \\ \end{array} } \right)\) is the mass matrix with variable elements together with the mass of added water, and \({\mathbf{D}} = {\mathbf{D}}\left( {\mathbf{q}} \right)\), \({\mathbf{F}} = {\mathbf{F}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}}} \right)\), \({\mathbf{G}} = {\mathbf{G}}\left( {t,{\mathbf{q}},{\dot{\mathbf{q}}}} \right)\), and x A (t), y A (t) are known functions defining the motion of point A 0.

Equations (2) and (3) are nonlinear due to large deflections and nonlinear terms when forces caused by the water environment are considered.

Since matrix \({\mathbf{M}}\) has a block diagonal form, it is easy to calculate the inverse matrix \({\mathbf{M}}^{ - 1}\). The following can be obtained from (2)

$${\ddot{\mathbf{q}}} = {\mathbf{M}}^{ - 1} \left( {{\mathbf{F}} + {\mathbf{DR}}} \right) = {\mathbf{f}}\left( {t,{\mathbf{q}}} \right)$$
(4)

where \({\mathbf{M}}\) is calculated by solving the system of linear algebraic equations:

$$\left( {{\mathbf{D}}^{T} {\mathbf{M}}^{ - 1} {\mathbf{D}} } \right){\mathbf{R}} = {\mathbf{G}} - {\mathbf{D}}^{{T}} {\mathbf{M}}^{ - 1} {\mathbf{F}}$$
(5)

3 Numerical simulations

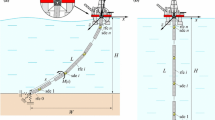
Dynamics of a catenary riser (Fig. 2) are analysed in [22] by means of the finite difference method. Three models of risers with different lengths are considered in order to investigate the influence of heave motion on bending moments and tension or shear forces.

Fig. 2
figure 2

Catenary riser

Full size image

Axial excitations can have a considerable influence on dynamic behaviour of risers and catenary moorings and are especially important in practical applications. For the purpose of comparative analysis presented in this section only one of the models is used. The parameters of the analysed model of the riser are presented in Table 1.

Table 1 Parameters of the catenary riser
Full size table

Two types of harmonic motion are analysed:

W1—vertical motion with period 60 s and amplitude 5 m.

W2—vertical motion with period 12 s and amplitude 2 m.

It is assumed that horizontal motion of a vessel or platform is described by the following function:

$$x_{E} = - a + a\cos \omega t$$
(6)

where a is the amplitude of motion, ω = 2π/T, T is the period of the harmonic motion.

Comparison of maximal and minimal values of bending moments as well as tension at the top of the riser and static top tension are presented in Table 2. The results obtained with the rigid finite element m method (RFEM) are compared with those presented in [22] obtained using RIFLEX (RF) and the finite difference method (FD).

Table 2 Comparison of results obtained by RFEM and those presented in [22]
Full size table

The results obtained using the rigid finite element method for n = 101 elements are very close to those obtained with a nonlinear model (FD). More discrepancies can be seen when the results by the RFEM are compared with those from the linear model (RF—by commercial package RIFLEX). Figure 3a shows the static configuration of the riser and static bending moment obtained using the authors’ model and those presented by [22]. It is important to note that the rigid finite element method takes into account rotational inertia of the elements and this explains the differences in maximal values of bending moments presented in Table 2. Consideration of rotational inertia results in larger hydraulic damping. Courses of the tension and shear forces, and of the bending moment along the riser are presented in Fig. 3b–d.

Fig. 3
figure 3

Comparative analysis for static equilibrium: a configuration of the riser, b tension force, c bending moment, d shear force

Full size image

The rigid finite element method enables us to calculate displacements, inclination angles of the elements and forces at discrete points. Values at intermediate points (for an arbitrary s) can be calculated by means of spline functions. Figure 4 shows the influence of the number of elements n into which the riser is divided on the results of the bending moment calculated at selected points for harmonic motion W2.

Fig. 4
figure 4

Maximal and minimal values of the bending moment at selected points (W2)

Full size image

It can be seen that even for n = 40 the results are acceptable. The simulation time for one instance of simulations does not exceed 5 s on a medium class personal computer.

4 Optimisation

Numerical effectiveness of the method enables it to be used in solving dynamic optimisation problems [24, 25]. In the papers the method is used for modelling ropes in order to solve the problem of stabilisation of a load at a given depth despite vertical and horizontal movements of the base vessel. The task is solved by definition of the rotation angle of a hoisting winch, which is responsible for keeping the load at a set distance from the seabed.

For the purpose of this paper the optimisation task is formulated as follows (Fig. 5).

Fig. 5
figure 5

Riser configuration during optimisation: a without compensation, b with compensation

Full size image

The horizontal motion of a vessel (platform) is defined by (6). Such movements cause a significant increase in bending moments in the riser presented in Fig. 2, which finally can lead to damage of the structure. This means that the problem is very important from the practical point of view. Thus, the vertical motion of point E (the upper end of the riser) should be chosen in such a way that the bending moment at a given point of the riser is as close as possible to the static bending moment. For further analysis it is assumed that the riser parameters are the same as those presented in Table 1. The course of the bending moment calculated at given points for a = 3 m and T = 12 s in formula (6) is presented in Fig. 6.

Fig. 6
figure 6

Courses of the bending moment at selected points

Full size image

Courses of minimal and maximal values of the bending moment along the riser for the second type of harmonic motion (W2) are presented in Fig. 7.

Fig. 7
figure 7

Course of the maximal and minimal values of the bending moment

Full size image

The optimisation task is formulated using the spline functions of the third order as follows:

Find function y E (t) for t ∊ 0, T defined by means of parameters:

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {p_{1} = y_{E} \left( {t_{1} } \right)} \\ \vdots \\ {p_{i} = y_{E} \left( {t_{i} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {p_{m} = y_{E} \left( {t_{m} } \right)} \\ \end{array} } \\ \end{array} } \right.$$
(7)

where \(t_{i} = i\Delta t\) for i = 1, 2,…,m, \(\Delta t = \frac{T}{m}\), so that the function:

$$\Omega \left( {p_{1} , \ldots ,p_{m} } \right) = \frac{1}{T}\mathop \smallint \limits_{0}^{t} \left[ {M\left( {s^{*} ,t} \right) - M_{stat}^{*} } \right]^{2} dt$$
(8)

where M(s*, t) is the bending moment at the selected point of the riser, M stat * is the value of this moment for the static equilibrium problem, reaches its minimum while fulfilling the following:

$$y_{Emin} \le p_{i} \le y_{Emax}$$
(9)

where \(y_{Emin} ,y_{Emax}\) are minimal and maximal accepted values of function y E (t).In order to calculate the value of functional (8) for a specific combination of parameters p i (i = 1,…,m), bending moment M(s*, t) has to be known. Thus, the equations of motion of the riser have to be integrated at each optimisation step. The downhill simplex method is used for solving the optimisation task.

The parameters occurring in the optimisation problem have to be chosen properly in order to obtain correct results, especially the number of time intervals \(m\) in formula (7), and y Emin and y Emax in inequalities (9). A large number of decisive variables m significantly increases simulation time, but too small a number leads to a limitation of function classes describing vertical displacements of point E of the riser. Figure 8 presents the courses of function y E (t) for m = 5, 10, 15.

Fig. 8
figure 8

Courses of function y E (t) with respect to number of time intervals m

Full size image

It can be seen that the difference between values of y E obtained for m =  5 and 10 is large, while for m = 10 and 15 it is small. Calculation times were T * = 202 s for m =  5, \(T^{*}\) = 1220 s for m = 10 and T* = 1825 s for m = 15. The calculations were carried out for s* = 75 m, y Emin  = 1.5 m and y Emax  = 1.5 m. The simulations did not show that values y Emin and y Emax have a significant influence on the exactness of results obtained. The choice of y Emin and y Emax was made on the assumption that they should be proportional to the amplitude of the input motion a, but should not exceed ±50 % of this value.

Figures 9, 10 and 11 present the results of optimisation for a = 3, 4, 5 m. It can be seen that, by means of technically possible vertical motion of the upper end of the riser, the bending moment at any selected point of the riser can be stabilized despite the horizontal movements of the base (vessel or platform). The numerical simulations were carried out for \(s^{*} = 75,\, 150\,{\text{m}}\), and the number of discretization points of function y E (t) m = 10.

Fig. 9
figure 9

Courses of: a moment M(s*, t), b top tension T(L, t) before and after the optimisation, c function y E (t)

Full size image
Fig. 10
figure 10

Courses of: a moment M(s*, t), b top tension T(L, t) before and after the optimisation, c function y E (t)

Full size image
Fig. 11
figure 11

Courses of: a moment M(s*, t), b top tension T(L, t) before and after the optimisation, c function y E (t)

Full size image

It can be seen that the reduction of maximal values of bending moments down to the value of M * stat at a selected point of the riser is correctly realised. As a result of the optimisation task, the courses of the bending moments are close to the values of bending moment at initial time \(t = 0 {\text{s}}\). Table 3 presents maximal and minimal values of the bending moments and top tension force before and after optimisation.

Table 3 Maximum and minimum of values of the bending moment and top tension before and after optimisation
Full size table

Reduction of the bending moment at a chosen point and top tension of the riser was achieved by the use of function (8) for the optimisation task. The difference between the maximal and minimal values of the bending moment on average was about 25 kNm and after optimisation this difference was <10 kNm.

Realizing optimal displacements y E (t) involves applying the appropriate top tension at point E of the riser. From Figs. 9b, 10b and 11b it can be seen that realization of displacements of point E requires a characteristic force which is not larger than ±5 % of the tangential force. Special devices are necessary for technical realization of the optimal displacement (y E (t) or force \(T\left( {L,t} \right)\)) Information about the method of realizing displacements at point E and about devices used can be found in papers dealing with “heave compensation systems” [26, 27].

5 Final remarks

The paper presents an application of the modification of the rigid finite element method to modeling of dynamics of ropes and risers. The basic advantage of the method is its simple physical interpretation. A flexible link is divided into rigid segments which represent mass features of the link and spring-damping elements responsible for its flexible and damping features. The essential aspect of the method is the possibility of accounting for large deflections of links. The formulation using absolute coordinates gives reliable results both in the range of static and dynamic analysis. The static analysis concerned with a catenary line shows that the largest differences obtained using the RFEM are less than 0.5 % in comparison to the analytically calculated values of deflections. Free vibrations can be also calculated using the method without the necessity of special formulations. The results obtained using the modified rigid finite element method are compared with those presented by other authors and obtained using commercial software, and very good compatibility is obtained. Thus the models and programs formulated are reliable and numerically efficient. Calculation time is considerably shorter than that necessary for simulations by means of commercial software. The simple physical interpretation and the numerical efficiency of the method enables the method to be applied in engineering design of offshore equipment, especially in dynamic analysis of flexible structures, dynamic optimization problems and control. An exemplary optimisation problem is presented and solved in the paper. However, the problem can be generalized by including several points along the riser in the functional Ω. Since the method enables us to calculate forces in the connections of the elements (as constraint reactions) it is possible to formulate tasks in which the limitations are imposed not only on the bending moment but also longitudinal or transversal forces. Solution of several optimisation tasks (for example for different parameters of waves, length of risers) can be used for training an artificial neural network, which then can be used in control.