1 Introduction

Problems concerned with static, kinematic and dynamic analysis of devices used for extracting and transporting hydrocarbons from the seabed are extremely complex. In the case of risers the difficulties are due to the fact that it is necessary to consider large deflections and the interaction of the sea, which lead to nonlinear equations of dynamics. In order to consider the influence of the sea, base motion caused by waves, currents, buoyancy forces, hydrodynamic drag as well as change in the added mass have to be taken into account.

The most popular methods used for modelling risers are the finite element method [1, 2], finite difference method [3, 4], lumped mass method [5, 6], finite segment method [7,8,9] and the rigid finite element method [10,11,12,13,14,15,16,17]. The professional software packages both for general purpose (Abaqus, Ansys) and specifically for marine applications (Orcaflex) generally use the finite element method. A review of models and methods used for statics and dynamics of risers, including different excitation problems, is presented in [18]. More recent discussions of models and methods used for dynamics as well as control techniques can be found in [19].

Longitudinal flexibility is usually omitted in dynamic analysis of risers due to the fact that elongation of typical risers of 2 to 3 km length is usually less than 1 m. Torsional flexibility is also rarely considered [6, 20,21,22,23,24,25,26,27], but even then is usually examined only when the multi-layered structure of pipes is taken into account [22,23,24,25,26,27]. Geometric and bending stiffness are dominant although torsional vibrations may cause damage due to material fatigue. Some research is devoted to stability of risers under torsion and bending-torsion coupling [23, 24] as well as structural analysis of the layer pipes and axial–torsional coupling [22, 25, 26]. Analysis of different modelling approaches to flexible pipes with layers under tension, torsion and bending loads is presented in [27].

The finite segment method (FSM) and the rigid finite element method (RFEM) are popular not only due to their simple physical interpretation. Customised formulations of these methods can be numerically effective and thus easy to apply for solution of optimisation problems [15,16,17, 28,29,30]. The main idea of both methods is to divide a flexible link into rigid finite elements (rfe) reflecting mass features, and spring-damping elements (sde) reflecting flexible and damping features of the link. The motion of the subsequent elements is usually described in relation to the previous element [7, 31, 32]. The Euler angles are used in order to describe the motion, and continuity of displacements in connections of the elements is assumed. Such an approach means that the generalised coordinates defining the motion of element \(i\) depend not only on its own coordinates but also on generalised coordinates of all preceding elements and coordinates of a chosen point of the first segment. As a consequence the mass matrix of a segment not only depends on all these coordinates but is also full [32], whereas the stiffness matrix of the system has a simple form for linear physical and geometrical relations.

This paper further develops models described in [30, 31]. Paper [30] describes the segment method using joint coordinates and its application to analysis of spatial bending vibrations, while torsional vibrations are omitted. The models presented there are numerically effective and they are used for the solution of the dynamic optimisation problem for stabilisation of forces and moments in the connection of the riser with a wellhead.

The model used in this paper is described in detail in [31] and it takes into consideration both bending and torsional flexibilities. The essential difference between the model presented here and the model presented in [31] is a different method of calculating bending and torsional moments acting at spring-damping elements. In paper [31], generalised forces reflecting bending and torsion are calculated by means of the energy of spring deformations, while in this paper special formulae for calculating moments are presented. Thus, the paper presents a nonlinear model of a riser including bending-torsional coupling, influence of the marine environment such as buoyancy, drag forces and sea current, and also motion of the platform or vessel that the riser is attached to. The model is validated by comparing the authors’ results with those presented by other researchers. Finally, the influence of riser twisting on natural frequencies and on riser vibrations during the motion caused by the surface vessel is examined.

2 Riser model

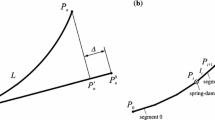
The main idea of the finite segment method is to replace a continuous link with a system of rigid segments (rfe) connected by means of spring-damping elements (sde). The division is carried out in two steps: first the discretised link is divided into elements of equal length reflecting mass features of the link and then spring-damping elements are placed in the middle of primary elements (points \(A_{1} \ldots A_{n} )\) reflecting flexible features of the segment.

According to [32, 33] coefficients characterising an sde for a homogenous beam can be calculated from the following formulae:

$$c^{\left( b \right)} = \frac{EJ}{\Delta }$$
(1.1)
$$c^{\left( t \right)} = \frac{{GJ_{0} }}{\Delta }$$
(1.2)

where \(E\), \(G\) are Young and Kirchoff moduli, respectively, \(J\) is the inertial moment of cross-sectional area with respect to the bending axis, \(J_{0}\) is the inertial moment of cross-sectional area with respect to the torsional axis (lengthwise).

Thus a flexible link is replaced by a system of \(n + 1\) rigid elements (segments \(S_{0} \div S_{n} )\) connected at points (\(A_{1} \div A_{n} )\) by spring-damping elements (\(e_{1} \div e_{n} )\).

As a result, the motion of the divided link, presented in Fig. 1, is described by \(m = 3 + 3\left( {n + 1} \right)\) generalised coordinates, which are the components of the following vector:

$${\mathbf{q}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{r}}_{0} } \\ {{{\varvec{\alpha}}}_{0} } \\ {{{\varvec{\alpha}}}_{0} } \\ \end{array} } \\ \vdots \\ {{{\varvec{\alpha}}}_{i} } \\ \vdots \\ {{{\varvec{\alpha}}}_{n} } \\ \end{array} } \right]$$
(2)
Fig. 1
figure 1

Notation: a set of segments of the flexible link, b rotations—ZYX Euler angles

Full size image

where \({\mathbf{r}}_{0} = \left[ {\begin{array}{*{20}c} {x_{0} } \\ {y_{0} } \\ {z_{0} } \\ \end{array} } \right]\) is the vector of coordinates of point \(A_{0}\), \({\varvec{\alpha }}_{i} = \left[ {\begin{array}{*{20}c} {\psi_{i} } \\ {\theta_{i} } \\ {\varphi_{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\alpha_{i,1} } \\ {\alpha_{i,2} } \\ {\alpha_{i,3} } \\ \end{array} } \right]\) (Fig. 1b).

The model used in this paper is derived in [31] and thus its description here is limited to parts which are relevant for the present discussion. Coordinate system \(\left\{ i \right\}^{\prime}\) is assigned to segment \(S_{i}^{{}}\). As shown in Fig. 2b, angles \(\psi_{i}\), \(\theta_{i}\), \(\varphi_{i}\), called heading, attitude and bank angles [34], are ZYX Euler angles, the name of which describes the order of rotations assumed for the model. Coordinates of point \(A\) of segment \(i\) in global coordinate system {} can be calculated according to the formula:

$${\mathbf{r}} = {\mathbf{r}}_{0} + \mathop \sum \limits_{j = 0}^{i - 1} l_{j}{\varvec{ \phi}}_{j} + {\mathbf{R}}_{i} {\mathbf{r^{\prime}}}$$
(3)
Fig. 2
figure 2

Notations for calculations of moments caused by bending and torsion

Full size image

where \(l_{j}\) is the distance between points \(A_{j}\) and \(A_{j + 1}\), \({\varvec{\phi}}_{j} = \left[ {\begin{array}{*{20}c} {c\theta_{j} c\psi_{j} } \\ {c\theta_{j} c\psi_{j} } \\ { - s\theta_{j} } \\ \end{array} } \right]\), \(c\beta = \cos \beta\); \(s\beta = \sin \beta\); \(\beta \in \left\{ {\psi_{i} ,\theta_{i} ,\varphi_{i} { }} \right\}\), \({\mathbf{R}}_{i}\) is the rotation matrix; \({\mathbf{r}}_{i}\) defines coordinates of point \(A_{i}\) and \({\mathbf{r^{\prime}}}\) is the coordinate vector of point \(A\) in local system \(\left\{ i \right\}^{\prime}\).

The equations of motion are derived from the Lagrange equations of the second order. Having omitted detailed derivations, for which we refer the reader to [31], the first variational derivative can be written in the following block-matrix form:

$${{\varvec{\upvarepsilon}}}_{{\mathbf{q}}} \left( T \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{rr} } & {{\mathbf{M}}_{r\alpha } } \\ {{\mathbf{M}}_{r\alpha }^{T} } & {{\mathbf{M}}_{\alpha \alpha } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{r}}}_{0} } \\ {{\mathbf{\ddot{\varvec{\alpha} }}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{h}}_{r} } \\ {{\mathbf{h}}_{\alpha } } \\ \end{array} } \right]$$
(4)

where \({\mathbf{M}}_{rr}\), \({\mathbf{M}}_{r\alpha }\), \({\mathbf{M}}_{\alpha \alpha }\), \({\mathbf{h}}_{r}\), \({\mathbf{h}}_{\alpha }\) are mass matrices and vectors referring to respective generalised coordinates \({{\varvec{\alpha}}} = \left[ {{{\varvec{\alpha}}}_{0}^{T} \;\;{{\varvec{\alpha}}}_{i}^{T} \;\;{{\varvec{\alpha}}}_{n}^{T} } \right]^{T}\).

Bending and torsional moments induced by spring damping elements are calculated as follows. Using stiffness coefficients defined in Eq. (1) we introduce subscript \(i\) to denote an sde, and thus \(c_{i}^{\left( b \right)}\) is the bending stiffness coefficient of sde \(i\) connecting segments \(i - 1\) and \(i\). The bending moments acting on segments \(i - 1\) and \(i\) are then expressed in the form:

$$M_{i - 1}^{{{^{\prime}}\left( \psi \right)}} = - M_{i}^{{{^{\prime}}\left( \psi \right)}} = c_{i}^{\left( b \right)} \frac{{{\Delta }\gamma_{i} }}{{\sin {\Delta }\gamma_{i} }}\sin {\Delta }\theta_{i} \cos {\Delta }\psi_{i}$$
(5.1)
$$M_{i - 1}^{{{^{\prime}}\left( \theta \right)}} = - M_{i}^{{{^{\prime}}\left( \theta \right)}} = c_{i}^{\left( b \right)} \frac{{{\Delta }\gamma_{i} }}{{\sin {\Delta }\gamma_{i} }}\cos {\Delta }\theta_{i} \sin {\Delta }\psi_{i}$$
(5.2)

where \(\cos {\Delta }\gamma_{i} = \cos {\Delta }\theta_{i} \cos {\Delta }\psi_{i}\).

Moments caused by torsion can be calculated according to the formula:

$$M_{i - 1}^{{{^{\prime}}\left( \varphi \right)}} = - M_{i}^{{{^{\prime}}\left( \varphi \right)}} = c_{i}^{\left( t \right)} \Delta \varphi_{i}$$
(6)

Angles \({\Delta }\psi_{i}\), \({\Delta }\theta_{i}\), \(\Delta \varphi_{i}\) denote relative rotations of segment \(i\) with respect to segment \(i - 1\) and for general discussion we assume that they are not small (Fig. 2). They can be calculated using formulae:

$$\Delta \varphi_{i } = {\rm{arctg}}\frac{{\left( {{\mathbf{R}}_{i,\Delta } } \right)_{3,2} }}{{\left( {{\mathbf{R}}_{i,\Delta } } \right)_{3,3} }}$$
(7.1)
$$\Delta \theta_{i} = - {\rm{arcsin}}\left( {{\mathbf{R}}_{i,\Delta } } \right)_{3,1}$$
(7.2)
$${\Delta }\psi_{i} = {\rm{arctg}}\frac{{\left( {{\mathbf{R}}_{i,\Delta } } \right)_{2,1} }}{{\left( {{\mathbf{R}}_{i,\Delta } } \right)_{1,1} }}$$
(7.3)

where \(\left( {{\mathbf{R}}_{i,\Delta } } \right)_{i,j}\) denotes element of the \(i\)-th row and \(j\)-th column of matrix \({\mathbf{R}}_{i,\Delta }\):

$${\mathbf{R}}_{i,\Delta } = {\mathbf{R}}_{i - 1}^{T} {\mathbf{R}}_{i} = \left[ {\begin{array}{*{20}c} {c\Delta \theta_{i} c\Delta \psi_{i} } & \cdots & \cdots \\ {c\Delta \theta_{i} s\Delta \psi_{i} } & \cdots & \cdots \\ { - s\Delta \theta_{i} } & {s\Delta \varphi_{i} c\Delta \theta_{i} } & {c\Delta \varphi_{i} c\Delta \theta_{i} } \\ \end{array} } \right]$$
(8)

Due to the deformation of sde \(i\), the generalised forces in the form of the following vector will occur in the equations of motion:

$${\mathbf{f}}^{\left( s \right)} = \left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{M}}_{0} } \\ {\begin{array}{*{20}c} { - {\mathbf{M}}_{0} + {\mathbf{M}}_{1} } \\ \vdots \\ {\begin{array}{*{20}c} { - {\mathbf{M}}_{i} + {\mathbf{M}}_{i + 1} } \\ { \vdots { }} \\ {\begin{array}{*{20}c} { - {\mathbf{M}}_{n - 1} + {\mathbf{M}}_{n} } \\ { - {\mathbf{M}}_{n} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]{\rm{respective}}\;{\rm{to}}\;\begin{array}{*{20}c} {{\mathbf{r}}_{0} { }} \\ {{{\varvec{\alpha}}}_{0} { }} \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{{\varvec{\alpha}}}_{{1{ }}} } \\ {{ } \vdots } \\ \end{array} } \\ {{{\varvec{\alpha}}}_{i} { }} \\ {\begin{array}{*{20}c} \vdots \\ {\begin{array}{*{20}c} {{{\varvec{\alpha}}}_{n - 1} } \\ {{{\varvec{\alpha}}}_{n} { }} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array}$$
(9)

where \({\mathbf{M}}_{i}={\mathbf{U}}_{i}{\mathbf{M}}_{i}^{{^{\prime}}}\); \({\mathbf{M}}_{i}^{{^{\prime}}}=\left[\begin{array}{c}{M}_{i}^{{^{\prime}}\left(\psi \right)}\\ {M}_{i}^{{^{\prime}}\left(\theta \right)}\\ {M}_{i}^{{^{\prime}}\left(\varphi \right)}\end{array}\right]\); \({\mathbf{U}}_{i}=\left[\begin{array}{ccc}c{\varphi }_{i}c{\theta }_{i}& s{\varphi }_{i}c{\theta }_{i}& -s{\theta }_{i}\\ -s{\varphi }_{i}& c{\varphi }_{i}& 0\\ 0& 0& 1\end{array}\right]\).

Gravity, buoyancy forces and hydrodynamic drag forces can be incorporated into the model by means of the generalised forces as described in [31], and finally the equations of motion take the form:

$${\mathbf{M\ddot{q}}} = - {\mathbf{h}} + {\mathbf{Q}}^{\left( g \right)} + {\mathbf{Q}}^{\left( w \right)} + {\mathbf{Q}}^{\left( H \right)} = {\mathbf{f}}$$
(10)

Reactions have to be introduced and equations of motion have to be supplemented with constraint equations.

3 Reactions and constraint equations

Numerical simulations are carried out for a riser (Fig. 3) whose motion at the top point \({(A}_{0}\)) is known and whose coordinates are known functions of time:

$${\mathbf{r}}_{0} = {\overline{\mathbf{r}}}_{0} \left( t \right)$$
(11)
Fig. 3
figure 3

Rigid connection of the riser with a wellhead

Full size image

In this case the coordinates of point \({A}_{0}\) can be eliminated as generalised coordinates, and the equations of motion can be written as follows:

$${\mathbf{M}}_{rr} {\mathbf{\ddot{r}}}_{0} + {\mathbf{M}}_{r\alpha } {\varvec{\ddot{\alpha }}} = {\mathbf{f}}_{r} + {\mathbf{F}}_{0}$$
(12.1)
$${\mathbf{M}}_{r\alpha }^{T} {\mathbf{\ddot{r}}}_{0} + {\mathbf{M}}_{\alpha \alpha } {\varvec{\ddot{\alpha }}} = {\mathbf{f}}_{\alpha }$$
(12.2)

where \({\mathbf{F}}_{0}\) is the vector of reactions at point \(A_{0}\).

Equation (12.2) takes the form:

$${\mathbf{M}}_{\alpha \alpha } {\varvec{\ddot{\alpha }}} = {\mathbf{f}}_{\alpha } - {\mathbf{M}}_{r\alpha }^{T} {\mathbf{\ddot{r}}}_{0}$$
(13)

from which acceleration vector \(\ddot{{\varvec{\upalpha}}}\) can be calculated. Then from (12.1) the vector of reactions at \({A}_{0}\) can be calculated in the form:

$${\mathbf{F}}_{0} = {\mathbf{M}}_{rr} {\mathbf{\ddot{r}}}_{0} + {\mathbf{M}}_{r\alpha } {\varvec{\ddot{\alpha }}} - {\mathbf{f}}_{r}$$
(14)

In the case when there are constraints imposed on point \(E = A_{n + 1}\) (Fig. 2), for example when this end of the riser is connected with a wellhead, it is assumed that this connection is rigid (Fig. 3).

In such a case the influence of force \({\mathbf{F}}_{E}\) on the riser has to be considered and the respective constraint equations have to be formulated. Due to reaction \({\mathbf{F}}_{E}\) at point \(E\), coordinates \({\mathbf{r}}_{E}\) are defined as follows:

$${\mathbf{r}}_{E} = {\mathbf{r}}_{0} + \mathop \sum \limits_{j = 0}^{n} l_{j} {\varvec{\phi}}_{j} = {\mathbf{r}}_{E,0}$$
(15)

and the vector of reactions occurs in the equations of motion in the following form:

$${\mathbf{M}}_{\alpha \alpha } {\varvec{\ddot{\alpha }}} - {\mathbf{D}}_{E} {\mathbf{F}}_{E} = {\mathbf{f}}_{\alpha } - {\mathbf{M}}_{r\alpha }^{T} {\mathbf{\ddot{r}}}_{0}$$
(16.1)
$${\mathbf{F}}_{0} = {\mathbf{M}}_{rr} {\mathbf{\ddot{r}}}_{0} + {\mathbf{M}}_{r\alpha } {\varvec{\ddot{\alpha }}} - {\mathbf{f}}_{r} - {\mathbf{F}}_{E}$$
(16.2)

where \({\mathbf{D}}_{E} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{E,0} } \\ \vdots \\ {{\mathbf{D}}_{E,n} } \\ \end{array} } \right]\); \({\mathbf{D}}_{E,i} = l_{i} \left[ {\begin{array}{*{20}c} {\varvec{\phi}_{i,1}^{T} } \\ {\varvec{\phi}_{i,2}^{T} } \\ {\varvec{\phi}_{i,3}^{T} } \\ \end{array} } \right]\).

The constraint equations can take the acceleration form:

$${\mathbf{D}}_{E}^{T} {\varvec{\ddot{\alpha }}} = {\mathbf{p}}_{E}$$
(17)

where \({\mathbf{p}}_{E} = {\mathbf{p}}_{E} \left( {{\dot{\varvec{\alpha }}},{\dot{\mathbf{r}}}_{E,0} ,{\mathbf{\ddot{r}}}_{E,0} } \right)\).

Initial conditions are defined after assuming \({\dot{\mathbf{q}}} = {\mathbf{\ddot{q}}} = 0\) and solving equations of statics resulting from (15,16).The nonlinear set of algebraic equations is solved by the iterative Newton method.

Equations (13, 17) are integrated using the Runge–Kutta method of the fourth order with a constant integration step. If it is necessary to calculate frequencies of free vibrations, we apply a procedure described in [14]. The Baumgarte method [35] is applied for stabilisation of the constraint equations.

4 Validation of the model

In order to prove the correctness of the models and computer programmes elaborated on the basis of these models, a validation is carried out. This involves comparing frequencies of free vibrations calculated from the authors’ own models with the results presented in [36] obtained by the differential transformation method. It is important to note that the results of Chen et al. [36] are compatible with those presented by other researchers obtained by means of five different methods. As for large deflections and forced vibrations of risers, we compare our results with those presented in [37].

Natural frequency analysis is concerned with vibrations of the riser shown in Fig. 4, with parameters given in Table 1.

Fig. 4
figure 4

Riser for free vibration analysis a load, b support types

Full size image
Table 1 Parameters assumed for natural frequency analysis
Full size table

It is assumed that the riser is submerged in water, and vibration analysis takes into account the gravity force, drag force, buoyancy force and fluid inside the riser. Extensibility is omitted and bending in plane \(xy\) as well as torsional vibrations are analysed.

In order to calculate the free vibrations, we use an approach inspired by [38] and described in detail in [14] for a system with geometrical constraints. Table 2 contains the first five frequencies of the riser calculated for various numbers of segments \(n = 25, 50, 100\) and \(200\) and results presented in [36]. Four different supports shown in Fig. 4b are analysed.

Table 2 Comparison of natural frequencies [rad/s]
Full size table

Analysis of the results presented in Table 2 shows that the segment method proposed in this paper gives results compatible with those obtained by means of different methods, especially those from [36]. The differences are not larger than 1.5% even for the number of segments as small as \(n = 25\).

We also compare results obtained by means of the segment method (SM) with analytical values calculated according to the following formula [39]:

$$\omega_{i}^{\left( b \right)} = \frac{i\pi }{L}\sqrt {\frac{T}{{m^{*} }} + \frac{{i^{2} \pi^{2} }}{{L^{2} }}\frac{EI}{{m^{*} }}}$$
(18)

where \(L\) is the length of the riser, \(i\) is the mode, \(T\) is the top tension, \({m}^{*}\) is the mass per unit length. This formula is valid for H–H boundary conditions and buoyancy forces acting along the whole length of the riser. The comparison of the first five frequencies calculated for \(n=100\) is presented in Table 3. Very good correspondence of results is achieved.

Table 3 Comparison of bending natural frequencies with analytical solution
Full size table

Table 4 presents torsional frequencies calculated by means of the segment method and using an analytical formula. The results refer to the riser with both ends fixed; rotation about axis \(x{^{\prime}}\) at points \(O\) and \(E\) is eliminated. The analytical formula for bending natural frequencies is as follows [40, 41]:

$$\omega_{i}^{\left( t \right)} = \frac{i\pi }{L}\sqrt {\frac{{G\left( {A_{{{\rm{out}}}} - A_{{{\rm{inn}}}} } \right)}}{{m^{* } }}}$$
(19)
Table 4 Comparison of torsional natural frequencies with analytical solution [rad/s]
Full size table

where \(G\) is Kirchoff’s modulus, \(A_{{{\rm{out}}}} = \frac{{\pi D_{{{\rm{out}}}}^{2} }}{4}\), \(A_{{{\rm{inn}}}} = \frac{{\pi D_{{{\rm{inn}}}}^{2} }}{4}\).

The results presented in Table 4 are obtained for the riser described in Table 1.

Analysis of the results implies the compatibility of the segment method with the analytical solution; the error smaller than 1% for the first natural frequencies is achieved even for \(n \ge 25\). One can also see stabilisation of the results as the number of segments \(n\) increases. It is important to emphasise that the values of torsional natural frequencies for the riser described in Table 1 are two orders of magnitude larger than frequencies of bending vibrations.

Paper [37] presents a riser shown in Table 5, since it is an important example for validating the finite element method in analysis of large vibrations of slender systems. The curve of the bending moment and values of reactions at point \(B\) for static deflections in the final configuration are shown in Fig. 5. Albino et al. [37] compare their results with those presented by McNamara et al. [42], who use cable theory, and with those obtained by Yazdchi and Crisfield [43] by means of a beam model. Very good compatibility of the results is achieved.

Table 5 Parameters of the riser in analysis of forced vibrations
Full size table
Fig. 5
figure 5

Static bending moment along the riser

Full size image

For the dynamic analysis the top of the riser is excited with a horizontal (along \(x\) axis) harmonic function whose amplitude is \(a = 2.01{ }\left[ {\rm{m}} \right]\) and period \(T = 14{ }\left[ {\rm{s}} \right]\). Time series of vertical reactions at points \(O\) and \(B\) are displayed in Fig. 6.

Fig. 6
figure 6

Vertical reactions at the ends of the riser a top \(V_{O} = F_{Oy}\) b bottom \(V_{B} = F_{By}\)

Full size image

Compatibility of results is satisfactory. Reaction \(V_{O}\) calculated by means of the segment method changes from \(35.75\) to \(36.00{ }\left[ {{\rm{kN}}} \right]\), while in [37] value \(V_{O} \in \left<35.73{\rm{ kN}},{ }35.94{\rm{ kN}}\right>\) and in [43] \(V_{O} \in \left<36.64{\rm{ kN}},{ }36.7{\rm{ kN}}\right>\).

5 Numerical simulations

This section presents numerical simulations based on the method described above and concerned with both statics and dynamics of the riser with parameters presented in Table 6.

Table 6 Parameters of the riser for static and dynamic analysis
Full size table

Both ends of the riser are fixed by means of springs with stiffness coefficients \(c_{0}^{\left( t \right)} ,c_{E}^{\left( t \right)}\) equal to \(10^{8} {\rm{Nm}}/{\rm{rad}}\). Analysis carried out in this paper also includes the influence of different sea currents on the riser. Three cases are analysed:

C0 – without current;

C1 – current changing (Fig. 7a) according to the formula:

$$V_{w} \left( y \right) = \left\{ {\begin{array}{*{20}l} {V_{{{\rm{nom}}}} + 0.5yV_{{{\rm{nom}}}} /200{ }} \hfill & {{\rm{for}}\quad y > - 200\;{\rm{m}}} \hfill \\ {0.5V_{{{\rm{nom}}}} { }} \hfill & {{\rm{for}}\quad y \le - 200\;{\rm{m}}} \hfill \\ \end{array} } \right.\left[ {\frac{{\rm{m}}}{{\rm{s}}}} \right]$$
(20)
Fig. 7
figure 7

Profiles of the sea currents

Full size image

C2 – constant current (Fig. 7b)

$$V_{w} = V_{{{\rm{nom}}}} \quad \left[ {\frac{{\rm{m}}}{{\rm{s}}}} \right]$$
(21)

For the simulations carried out it is assumed that the coordinates of point \({A}_{0}\) are \((0{\rm{ m}}, 0{\rm{ m}}, 0{\rm{ m}})\) and coordinates of point \(E\) are chosen so that \({x}_{E}=-250 {\rm{m}}\), \({y}_{E}=-400{\rm{m}}\), \(z_{E} = 0\). The current speed \(V_{{{\rm{nom}}}} = 1 \left[ {\frac{{\rm{m}}}{{\rm{s}}}} \right]\). Coordinate \(y_{E}\) depends on the deflection of the riser due to the sea current acting in the direction of \(z\) axis.

Figures 8 and 9 show how the static deflection of the riser is influenced by sea currents. It can be seen that the differences are considerable when different profiles of currents are taken into account.

Fig. 8
figure 8

Shape of the riser affected by different sea currents a C0, b C1, c C2

Full size image
Fig. 9
figure 9

Projection of statically deformed riser for different sea currents on planes a \(xy\), b \(zy\), c \(xz\)

Full size image

Figure 10 exemplifies how the profile of the sea current influences the torsion angle and bending moment along the riser in the static problem.

Fig. 10
figure 10

Influence of the sea current profile on a torsion angle \(\varphi\) b bending moment \(M_{B}\)

Full size image

The influence of torsional loading on the riser is also examined by introducing initial twisting at the bottom end of the riser. The change of coordinate \(z\) with respect to different twisting angles when there is no current is shown in Fig. 11.

Fig. 11
figure 11

Displacement in \(z\) direction for different twisting angles

Full size image

The model presented enables us to carry out dynamic analysis for displacements occurring at discretisation points. The vibration analysis of a riser connected to a moving vessel is presented below. It is assumed that the hang-off point of the vessel moves in the horizontal \(xz\) plane along the trajectory shown in Fig. 12a, and its velocity changes in directions \(x\) and \(z\) in the way presented in Fig. 12b.

Fig. 12
figure 12

Vessel movement a trajectory of point \(A_{0}\), b velocity in \(x\) and \(z\) direction

Full size image

The functions assumed are similar to the harmonic functions:

$$\begin{array}{*{20}c} {x\left( t \right) = a_{x} \cos \omega t} \\ {z\left( t \right) = a_{z} \sin \omega t} \\ \end{array}$$
(22)

where \(a_{x} = 5{ }\left[ {\rm{m}} \right],a_{z} = 4 \left[ m \right],\omega = 2\pi /T_{\omega }\) and period \(T_{\omega } = 10 \left[ s \right]\).

These functions are changed for \(t = 0\) and \(t = 2T_{\omega }\) in order to both fulfil homogenous initial conditions for the equations of motion of the riser and to stop the motion of the riser for \(t = 2T_{\omega }\):

$$\begin{aligned} & x^{\prime}\left( 0 \right) = z^{\prime}\left( 0 \right) = x^{\prime\prime}\left( 0 \right) = z^{\prime\prime}\left( 0 \right) = 0 \\ & x^{\prime}\left( {2T_{\omega } } \right) = z^{\prime}\left( {2T_{\omega } } \right) = x^{\prime\prime}\left( {2T_{\omega } } \right) = z^{\prime\prime}\left( {2T_{\omega } } \right) = 0 \\ \end{aligned}$$
(23)

This causes deformation of the trajectory of point \(A_{0}\), as seen in Fig. 12a.

The period of functions \(x\left( t \right)\) and \(z\left( t \right)\) is close to the most common frequencies of surface waves. The period of vibrations of the riser considered is about 0.4 s.

The calculations are carried out for a riser with the data from Table 6 over period \(t \in \left<0,30{\rm{s}}\right>\) with integration step \(h = 0.0005{\rm{s}}\) and number of segments \(n = 25\). Figure 13 presents how the profile of the sea current influences torsion angle \(\varphi\) and torsion moment \(M_{T}\) in the middle of the riser (\(s = 250{\rm{m}}\)), while Fig. 14 shows this influence on displacements of the middle point of the riser.

Fig. 13
figure 13

Influence of the sea current profile on a torsion angle \(\varphi\) b torsion moment \(M_{T}\)

Full size image
Fig. 14
figure 14

Influence of the sea current profile on displacements a \(x\) b \(y\) c \(z\)

Full size image

The influence of additional loading on the riser either in the form of sea currents or twisting is important when stress analysis is concerned. Figure 15 shows the differences in values of the torsional moment in the middle of the riser under different current profiles and twisting angles acting at the bottom end of the riser.

Fig. 15
figure 15

Differences in torsion moment in the middle of the riser \(\Delta M_{T} = M_{T} |_{t = 0} - M_{T}\) for a sea currents b twisting angles

Full size image

It can be seen that initial twisting results in smaller increase in the moment than the sea current does. Analysis of the results from Figs. 10, 11, 13, 14 and 15 indicates that the intensity of sea currents and initial twist of the riser have an essential influence both on the displacements of the riser and on the loading. Thus, consideration of torsional stiffness in the mathematical model is important since this can change both bending and torsional stress in the riser.

6 Final remarks

The paper presents a spatial model of a riser for static and dynamic analysis with consideration of bending and torsional stiffness. The finite segment method is used for discretisation of a flexible link. The computer programme developed on the basis of the model presented can be used for nonlinear static analysis of displacements and loads as well as for analysis of both free and forced vibrations caused by the motion of the base (vessel or platform) to which the riser is attached. The authors’ own results concerned with free and forced vibrations in water, when buoyancy, drag forces and added mass are taken into account, are compared with those presented in the literature, and good agreement is obtained. Static and dynamic analysis is concerned with the influence of sea currents and initial twisting of the riser on bending and torsional displacements. The results obtained show a considerable influence of the presence and intensity of the sea currents as well as initial torsional loading. Dynamic analysis deals with vibrations of a riser caused by the horizontal motion of the base along almost an elliptical path with diameters of 10 m and 8 m. The influence of the sea current and twisting is illustrated by vibrations of a point in the middle of the riser length. Time series of the torsional angle and torsion moment also show the considerable influence of the sea current and twisting. A strong sea current acting in a direction perpendicular to the riser causes a torsion of between ten and twenty degrees. Thus the stress due to torsion may be considerable.

Calculation time for simulation of dynamics of the riser over a time period of 30 s with an integration step of 0.0005 s are less than 3 min on an average PC computer. This means that the programs developed can be very useful in designing such devices.