Abstract
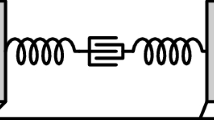
We formulate and solve the locomotion problem for a bio-inspired crawler consisting of two active elastic segments (i.e., capable of changing their rest lengths), resting on three supports providing directional frictional interactions. The problem consists in finding the motion produced by a given, slow actuation history. By focusing on the tensions in the elastic segments, we show that the evolution laws for the system are entirely analogous to the flow rules of elasto-plasticity. In particular, sliding of the supports and hence motion cannot occur when the tensions are in the interior of certain convex regions (stasis domains), while support sliding (and hence motion) can only take place when the tensions are on the boundary of such regions (slip surfaces). We solve the locomotion problem explicitly in a few interesting examples. In particular, we show that, for a suitable range of the friction parameters, specific choices of the actuation strategy can lead to net displacements also in the direction of higher friction.









Similar content being viewed by others
References
Arroyo M, Heltai L, Milan D, DeSimone A (2012) Reverse engineering the euglenoid movement. Proc Nat Acad Sci USA 109:17874–17879. doi:10.1073/pnas.1213977109
Bolotnik N, Pivovarov M, Zeidis I, Zimmermann K (2015) On the motion of lumped-mass and distributed-mass self-propelling systems in a linear resistive environment. Z Angew Math Mech. doi:10.1002/zamm.201500091
Borisenko IN, Figurina TYu, Chernousko FL (2014) The quasi-static motion of a three body system on a plane. J Appl Math Mech 78:220–227. doi:10.1016/j.jappmathmech.2014.09.003
DeSimone A, Tatone A (2012) Crawling motility through the analysis of model locomotors: two case studies. Eur Phys J E 35:85. doi:10.1140/epje/i2012-12085-x
DeSimone A, Guarnieri F, Noselli G, Tatone A (2013) Crawlers in viscous environments: linear vs non-linear rheology. Int J Non-Linear Mech 56:142–147. doi:10.1016/j.ijnonlinmec.2013.02.007
DeSimone A, Gidoni P, Noselli G (2015) Liquid crystal elastomer strips as soft crawlers. J Mech Phys Solids 85:254–272. doi:10.1016/j.jmps.2015.07.017
Gidoni P, Noselli G, DeSimone A (2014) Crawling on directional surfaces. Int J Non-Linear Mech 61:65–73. doi:10.1016/j.ijnonlinmec.2014.01.012
Hirose S (1993) Biologically inspired robots: snake-like locomotors and manipulators. Oxford University Press, Oxford
Ikuta K, Hasegawa T, Daifu S (2003) Hyper redundant miniature manipulator Hyper Finger for remote minimally invasive surgery in deep area. In: Proceeding of IEEE International Conference on Robotics and Automation, Vol. 1, Taipei, pp 1098–1102
Magnasco MO (1993) Forced thermal ratchets. Phys Rev Lett 71:1477–1481. doi:10.1103/PhysRevLett.71.1477
Menciassi A, Dario P (2003) Bio-inspired solutions for locomotion in the gastrointestinal tract: background and perspectives. Phil Trans R Soc Lond A 361:2287–2298. doi:10.1098/rsta.2003.1255
Menciassi A, Accoto D, Gorini S, Dario P (2006) Development of a biomimetic miniature robotic crawler. Auton Robot 21:155–163. doi:10.1007/s10514-006-7846-9
Mielke A, Theil F (2004) On rate-independent hysteresis models. NoDEA Nonlinear Differ Equ Appl 11(2):151–189. doi:10.1007/s00030-003-1052-7
Mielke A (2005) Evolution of rate-independent systems. In: Dafermos C, Feireisl E (eds) Handbook of Differential Equations, evolutionary equations. Elsevier, Amsterdam
Mielke A, Roubíček T (2015) Rate-independent systems. Theory and application. Springer, Berlin
Montino A, DeSimone A (2015) Three-sphere low-Reynolds-number swimmer with a passive elastic arm. Eur Phys J E 38:42. doi:10.1140/epje/i2015-15042-3
Noselli G, DeSimone A, Tatone A (2013) Discrete one-dimensional crawlers on viscous substrates: achievable net displacements and their energy cost. Mech Res Commun 58:73–81. doi:10.1016/j.mechrescom.2013.10.023
Noselli G, DeSimone A (2014) A robotic crawler exploiting directional frictional interactions: experiments, numerics, and derivation of a reduced model. Proc Roy Soc Lond A 470:20140333. doi:10.1098/rspa.2014.0333
Recho P, Truskinovsky L (2016) Maximum velocity of self-propulsion for an active segment. Math Mech Solids 21:263–278. doi:10.1177/1081286515588675
Sheshka R, Recho P, Truskinovsky L (2015) Pseudo energy wells in active systems. Preprint arXiv:1509.02753v1
Steigenberger J, Behn C (2012) Worm-like locomotion systems. An intermediate theoretical approach. Oldenbourg Wissenschaftsverlag, Berlin
Zimmermann K, Zeidis I, Behn C (2009) Mechanics of terrestrial locomotion. Springer, Berlin
Acknowledgments
This work has been supported by the ERC Advanced Grant 340685-MicroMotility.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gidoni, P., DeSimone, A. Stasis domains and slip surfaces in the locomotion of a bio-inspired two-segment crawler. Meccanica 52, 587–601 (2017). https://doi.org/10.1007/s11012-016-0408-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-016-0408-0