1 Introduction

A periodic pattern of shape changes is the keystone in the description of most biological and robotic locomotion strategies. Common examples are the flapping of fins in fishes or wings in birds, a peristaltic wave in a crawler, as well as the rotations of a ship’s propeller. Periodicity brings a clear design advantage, since a long-term and complex task, such as going from A to B, can be decomposed as the iteration of a much simpler and brief input. Indeed, not only a periodic input can be easily implemented in a robotic device, but also several biological organisms are known to employ basic mechanisms called central pattern generators to produce cyclic shape-change patterns, without recurring to any movement-related sensory feedback [26].

To fully describe a locomotion strategy, identifying what is usually called a gait, a specific periodic shape-changing pattern must be associated with a corresponding movement of the locomotor in a given environment. More abstractly, a gait can be identified as a relative-periodic evolution of the system [15, 27].

Relative-periodicity is based on the decomposition of the configuration space of the locomotor into the product of a shape space and a position space. The shape space describes, as predictable, the shape of the body of the locomotor and is where a periodic evolution is expected. In the models discussed in our paper, the shape space will be an Euclidean space in discrete models and a Sobolev space in continuous ones; but, for instance, in the presence of a rotating body part a manifold, such as \(\mathbb {R}^n\times \mathcal S^1\), would be a suitable choice.

The position space describes the location and orientation of the locomotor and, usually, is a Lie group. To each gait, we would like to associate an element \(\gamma \) of the position space, called geometric phase whose action on the group describes the movement of the locomotor. Given an initial position \(y_0\), a single iteration of the gait will displace the locomotor to \(\gamma y_0\).

However, while relative-periodicity is an extremely useful structure to study locomotion, it is also a sort of ideal behaviour that can be consistently observed only in a limited set of models. Examples where periodic inputs always produce relative-periodic evolutions are swimming at low-Reynolds number [29] and some special models of wheeled locomotion [27] and of crawling [2, 13, 37].

Often, instead, a relative-periodic behaviour might be expected to emerge as an asymptotic behaviour of the system. The Reader might get an intuitive description of this phenomenon by considering the following examples. The first is a degenerate example of crawling: a passive object lying on a surface, subject to friction but without any actuation. It is easy to identify its associated relative-periodic behaviour: a constant shape and a stationary position, so that \(\gamma \) is the identity of the group. However, this behaviour is instantly reached only if the initial condition is also stationary. An analogous phenomenon is produced by an elastic body with an initial deformation different from the rest configuration. In such cases, the stationary asymptotic behaviour can be showed by noticing that the mechanical energy of the system is a Lyapunov function, decreasing in time.

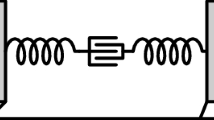
A more relevant situation appears when the crawler is active: consider, for instance, a robotic device such as that idealized in Fig. 1, programmed to repeat a given periodic shape change. If the locomotion were relatively periodic and the device were deployed with an advantageous “rolling start” so fast that all the body parts were sliding forward at the time of deployment, then they would all simultaneously slide forward, again and again, during each repetition of the initial stage of the actuation pattern. If, instead, even for the same actuation pattern, the “rolling start” were unfavorable, with the whole crawler initially sliding backwards, then the crawler would slide backwards for some time interval during each actuation cycle. Thus, if the locomotion were always relatively periodic, the initial state would be as important as the shape change pattern in determining the evolution of the system at all times. In concrete situations, this is usually not the case. We expect the advantage of a “rolling start” to be depleted during the first few cycles, or an initial disadvantage to be soon recovered, with the long time behaviour depending only on the actuation pattern. Relative periodic evolutions occur only for some specific—usually unique—initial velocity. In the other cases, instead, relative periodicity emerges as a limit behaviour, with the shape periodically changing as assigned and the geometric phase \(\gamma \) corresponding to the asymptotic shift over a period of any point of the crawler.

The aim of this paper is to rigorously investigate such an asymptotic behaviour for some general families of models of dynamic crawling locomotion with prescribed shape. Mathematically, the case of a true locomotion model is much more challenging than the example of the passive crawler, since, due to the work produced by the actuation, the mechanical energy of the system is no longer decreasing. We emphasize that our work is not limited to proving the convergence of each solution of the system to a relative periodic behaviour. For practical applications, it is also necessary to show that the (asymptotic) shape change and geometric phase do not depend on the initial conditions. As we will show, counterexamples are possible and the uniqueness of the limit behaviour requires stronger assumptions than convergence alone.

This kind of investigation is pivotal in the design, operation and optimization of robotic devices. As we mentioned, the possibility to rely just on a small toolbox of periodic patterns, without any dedicated sensor or feedback mechanism, reduces the complexity of the device, with advantages for manufacturing, cost and miniaturization. This is however possible only if the behaviour of the locomotor is not affected in a relevant way by uncontrolled factors, such as the state of the locomotor when a new gait is applied, or a temporary external perturbation. The fact that a locomotion strategy do not involve a full control of the state of the locomotor can be interpreted as a basic form of morphological computation [31], meaning that the ability to adapt to the external conditions is partially delegated to structural properties of the robot, reducing the complexity of the actuation.

A rigorous proof of the well-posedness and uniqueness of the asymptotic behaviour of the system is not only relevant per se, but can also be seen as a preliminary step to gait optimization. Indeed, since gaits can be properly defined only as an asymptotic property of a periodic input, gait optimization must also be evaluated in the long-time limit [23], so that optimality is considered only among limit-cycles. Example of this limit-cycle optimization have been discussed, for instance, for the Chaplygin sleigh [16, 36] and for a model of quasistatic crawling [9].

Whereas asymptotic stabilization is usually observed numerically or experimentally for a specific choice of the actuation (e.g. [39]), in this paper we undertake a more theoretical approach, providing rigorous results on the existence and structure of a global attractor for the dynamics. Such an analytical approach allows in general to explore the effects (or lack thereof) of the different elements in a locomotion model: the actuation pattern, the geometry of the locomotor, the rheology of the interaction with the substrate, the relevance of inertial effects and the possible elasticity of the body. In this paper, our focus will be on the effect of the rheology in a dynamic framework for general actuation strategies. Thus, we will restrict ourselves to rectilinear models of crawlers—although highlighting the qualitative differences between discrete and continuous models—and neglect elastic deformations, so that the shape of the crawler is directly controlled by the actuation.

A prescribed shape allows to reduce the dynamics to the position space \(\mathbb {R}\). In particular, an asymptotically relative-periodic behaviour corresponds to a limit cycle for the velocity \(v=\dot{\bar{x}}\) of the position of the locomotor. Accordingly, the geometric phase \(\gamma \) identifies the asymptotic limit of the Poincaré time-map, with its value describing the asymptotic average velocity \(\gamma /T\) of the locomotor.

For this reason, we start in Sect. 2 by discussing some general results for a special class of scalar time-periodic differential inclusions \(\dot{v}\in G(t,v)\). This framework allows to deal also with set-valued friction forces such as dry friction. For the class considered, we prove that the dynamics is asymptotically periodic and that the periodic limit of a solution lies on a global attractor. Strengthening in two alternative ways the assumptions on G, we prove that such attractor is a unique limit cycle.

In Sect. 3, we apply these general results to discrete models of crawling locomotion, considering various friction laws. We show that, under mild dissipativity assumptions, the system will always converge to a relative-periodic behaviour, which however might depend on the initial state. The uniqueness of the asymptotic velocity is obtained either for strictly monotone friction forces, extending the results in [18], or for dry friction if the actuation is sufficiently smooth in time (continuous friction coefficients and a \(\mathcal {C}^1 \) shape change). Several examples and counterexamples are included, illustrating the sharpness of our assumptions.

In Sect. 4, we repeat the same analysis for continuous models of crawlers, obtaining analogous results. The only difference is in the case of dry friction, for which uniqueness of the limit cycle does not require any additional time-regularity. We remark that, both in the discrete and in the continuous case, dry friction provides only the (weak) monotonicity of G in v, that is not by itself sufficient for uniqueness: its proof relies specifically on the intrinsic structure of our locomotion models.

Finally, in Sect. 5 we discuss the results obtained in the paper in the context of the existing literature, together with possible future developments.

2 Theoretical results for first-order differential equations and inclusions

2.1 Structural assumptions

Since we plan to describe the locomotion of crawlers under general friction forces, including also dry friction, our framework should accomodate also set-valued maps. Hence, we denote by \(\mathcal {P}(E)\) the power set of a set E. Moreover, with a slight abuse of notation, given \(B\in \mathcal {P}(\mathbb {R})\) and \(a\in \mathbb {R}\), we identify \(B+a\in \mathcal {P}(\mathbb {R})\) as the set of the elements \(b+a\) with \(b\in B\). Let us also recall some monotonicity properties for set-valued maps \(F:\mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\).

Definition 2.1

We say that the set-valued map \(F:\mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\) is monotone increasing (resp. decreasing) if

$$\begin{aligned} \begin{aligned} (y_2 - y_1)(u_2-u_1)\ge 0 \qquad \text{ for } \text{ every }\, (u_1,u_2)\in \mathbb {R}^2,\, u_1\ne u_2,\, y_1\in F(u_1),\, y_2\in F(u_2) \end{aligned} \end{aligned}$$

(resp. if \((y_2 - y_1)(u_2-u_1)\le 0 \) on the same domain).

We say that a monotone map is strictly monotone if the corresponding inequality is always strict.

Definition 2.2

We say that a set-valued monotone map \(F:\mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\) is maximal monotone [7] if it is maximal among the set of monotone set-valued maps, with the respect to the relation of graph inclusion, i.e. if there is no monotone map \(\widetilde{F}:\mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\) such that \({{\,\textrm{graph}\,}}F \subsetneqq {{\,\textrm{graph}\,}}{\widetilde{F}}\).

Notice that, given a convex function \(V:\mathbb {R}\rightarrow \mathbb {R}\) then its subdifferential \(\partial V\) is a maximal monotone increasing map, with strict monotonicity corresponding to a strictly convex V.

Set-valued friction forces, however, also bring a favourable structure to the problem, providing, for instance, existence and forward-in-time uniqueness of solution. For this reason, we will focus on a special class of differential inclusions \(\dot{u}\in G(t,u)\) satisfying the following assumptions on G, which will be referred to in the rest of the paper as structural assumptions:

  1. (S1)

    The set-valued map \(G:\mathbb {R}\times \mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\) is of the following form

    $$\begin{aligned} G(t,u)=-\mathcal {A}(t,u)+p(t,u) \end{aligned}$$
    (2.1)

    where

    • \(\mathcal {A}:\mathbb {R}\times \mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\setminus \emptyset \) is a set-valued map, locally bounded by a measurable function, T-periodic in t, maximal monotone increasing in u for every t and measurable in t for every u.

    • \(p:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}\) is a single-valued Carathéodory function, T-periodic in t, locally Lipschitz continuous in the variable u uniformly in t.

  2. (S2)

    There exist a positive constant \(R>0\) and two T-periodic measurable functions \(\ell _d^\pm (t):\mathbb {R}\rightarrow \mathbb {R}\) such that \(\int _0^T\ell _d^\pm (s)\mathop {}\!\textrm{d}s<0\) and

    $$\begin{aligned} \begin{aligned} y&\ge -\ell _d^-(t){}&{} \textit{for almost every }t\in \mathbb {R},\, u\in (-\infty , -R],\,y\in G(t,u),\\ y&\le \ell _d^+(t){}&{} \textit{for almost every }t\in \mathbb {R},\, u\in [R,+\infty ),\,y\in G(t,u). \end{aligned} \end{aligned}$$

Notice that in (S1) we require G to be nowhere empty-valued. Moreover, for every t, \(G(t,\cdot )\) is convex- and compact-valued, upper semi-continuous, single-valued outside a set of null measure.

We plan to study the differential problem

$$\begin{aligned} \dot{u}\in G(t,u). \end{aligned}$$
(2.2)

We will call solution of (2.2) an absolutely continuous function such that (2.2) is satisfied at almost every t on the domain of the solution. In particular, we observe that we have local existence [11, Corollary 5.2, pag. 59] and right uniqueness (using the same argument as [17, Theorem 1, pag. 106]) of solution for the Cauchy problems associated with (2.2); see also [38].

2.2 Existence of periodic solutions and attractors

We now investigate the existence and qualitative properties of periodic solutions and global attractors for the dynamics of (2.2), assuming that G satisfies the structural assumptions (S1) and (S2).

The existence of periodic solution and attractors has been studied by several authors in the generalized framework of Hilbert spaces, both in the cases when the maximal monotone term is autonomous [3, 19, 25] and time-periodic [28, 34, 35]. For our purposes, we restrict ourselves to the scalar case. If, on one hand, this simplifies the problem, on the other hand it allows us to relax the assumptions on the system and to obtain additional qualitative properties of the set of periodic solutions. For instance, the scalar setting together with the structure of the crawling problem will allow us to obtain uniqueness of the periodic solution also for a monotone G (Theorem 4.3), which is not to be expected in the general case. Some proofs in this subsection follow classical lines of reasoning, used also for scalar periodic ordinary differential equations (see, for example, [33]). However, unlike the ODEs case, it is worth to stress that the lack of uniqueness of solutions in the past for (2.2) can lead to asymptotically periodic motions which attain the periodic regime in finite time (as it happens in Examples 3.1 and 3.3).

Firstly, we observe that our structural assumptions guarantee global forward existence and boundedness of the solutions. Indeed, let us set

$$\begin{aligned} v_-:=-R-\left\Vert \ell _d^-\right\Vert _{L^1(0,T)},{} & {} v_+:=R+\left\Vert \ell _d^+\right\Vert _{L^1(0,T)}. \end{aligned}$$

From the bounds in (S2), we easily deduce the following statement:

Proposition 2.3

Let G satisfy the structural assumptions. Then the solution of the Cauchy problem \(v(t_0)=v_0\) is bounded between \(\min \{v_0-\left\Vert \ell _d^-\right\Vert _{L^1(0,T)},v_-\}\) and \(\max \{v_0+\left\Vert \ell _d^+\right\Vert _{L^1(0,T)},v_+\}\) for every \(t\ge t_0\). In particular, this implies global forward existence of solutions.

Since we have global forward existence and uniqueness of solution, we can define the Poincaré map, \(\Phi _T:\mathbb {R}\rightarrow \mathbb {R}\), that associates to every initial datum \(x_0\) at time \(t=0\) the value \(\Phi _T(x_0)=x(T;x_0)\) of the solution at time \(t=T\) of the corresponding Cauchy problem for (2.2). Existence and forward uniqueness of solutions also imply that this map is monotone, while (S1) implies continuous dependence of solutions. However, unlike for the ODEs case, \(\Phi _T\) may fail to be injective. Nevertheless, we can translate many properties of the dynamics of (2.2) into the discrete dynamics associated to \(\Phi _T\), given by the difference equation \(v_{n+1}=\Phi _T(v_n)=\Phi _T^n(v_0)\). For example, a fixed point \(v_*\) of \(\Phi _T\) corresponds to a T periodic solution \(v(t,v_*)\) of (2.2).

The next result establishes the asymptotic behaviour of \(\Phi _T.\)

Theorem 2.4

Suppose that G satisfies the structural assumptions. Then the interval

$$\begin{aligned} K:=[\alpha ,\beta ]=\bigcap _{i\in \mathbb {N}}\Phi ^i_T([v_-,v_+]) \end{aligned}$$
(2.3)

is a global attractor for the discrete dynamics induced by \(\Phi _T\). Moreover, \(\Phi _T(\alpha )=\alpha \), \(\Phi _T(\beta )=\beta \) and for any \(v_0\in \mathbb {R},\, \lim _{i\rightarrow +\infty }\Phi ^i_T(v_0)=v^*= \Phi _T(v^*)\in [\alpha ,\beta ]\,. \)

Proof

First of all, we observe that, since we have forward uniqueness of solution and our dynamics is in dimension one, then the map \(\Phi _T\) is monotone increasing, else two orbits would cross each other. Since by (S2) we have \(\Phi _T(v_-)> v_-\) and \(\Phi _T(v_+)< v_+\), using the monotonicity of \(\Phi _T\) we deduce that the sequences \(\Phi _T^i(v_-)\) and \(\Phi _T^i(v_+)\) are, respectively, increasing and decreasing. Thus, there exist the limits

$$\begin{aligned} \alpha :=\lim _{i\rightarrow +\infty } \Phi _T^i(v_-),{} & {} \beta :=\lim _{i\rightarrow +\infty } \Phi _T^i(v_+). \end{aligned}$$
(2.4)

Notice that the set \([v_-,v_+]\) is forward invariant for the map \(\Phi _T\) and that, by monotonicity, \(v_-<\alpha \le \beta <v_+\). Therefore, equality in (2.3) holds with \(\alpha \) and \(\beta \) defined by (2.4). By monotonicity, we also deduce that K is an attractor for all the orbits starting in \([v_-,v_+]\). Hence, it remains to show that every other orbit enters the forward invariant set \([v_-,v_+]\). Let us consider the solution of a general Cauchy problem \(v(t_0)=v_0\). We discuss the case \(v_0>v_+\); if \(v_0<v_-\) the argument is analogous. Suppose by contradiction that \(v(t_0+kT)>v_+\) for every \(k\in \mathbb {N}\). Hence, by construction, \(v(t)>R\) for every \(t\in [t_0,+\infty )\). By (S2) we have \(\dot{v}(t)\le \ell _d^+(t)\) for every \(t\ge t_0\). Then, for every \(k\in \mathbb {N}\) it holds

$$\begin{aligned} v(t_0+kT)=v_0+\int \limits _{t_0}^{t_0+kT} \dot{v}(s)\mathop {}\!\textrm{d}s\le v_0+k\Lambda \qquad \text {where}\qquad \Lambda = \int \limits _{0}^T\ell _d^+(s)\mathop {}\!\textrm{d}s<0 . \end{aligned}$$

Taking any integer \(k>(v_0-v_+)/\left|\Lambda \right|,\) we get \(v(t_0+kT)<v_+\), and we arrive to a contradiction. Hence, each orbit reaches the forward invariant set \([v_-,v_+]\) in a finite time (depending on the orbit), therefore K is a global attractor.

Since \(\Phi _T\) is continuous, then \(\Phi _T(\alpha )=\alpha \) and \(\Phi _T(\beta )=\beta \) follow from (2.4). Moreover, since all the orbits are monotone and belong eventually to K,  by the continuity of \(\Phi _T\) we get immediately the last part of the statement. \(\square \)

Since a point \(v_0\) whose orbit \(\{\Phi _T^n(v_0)\}_{n\in \mathbb {N}}\) converges to a fixed point of \(\Phi _T\) corresponds to an asymptotically periodic solution of (2.2), we get immediately the following:

Theorem 2.5

Suppose that G satisfies the structural assumptions. Then, for any solution v of (2.2) there exists a T-periodic solution \(v^*(t)\) of (2.2) such that \(v^*(0)\in K\) and \(\lim _{t\rightarrow +\infty } (v(t)-v^*(t))=0\).

In particular, we get:

Corollary 2.6

Suppose that G satisfies the structural assumptions. If (2.2) admits only one T-periodic solution \(v^*\), then \(v^*\) is a global attractor for the dynamics in the following sense: given \(v_0\), the solution \(v(t;v_0)\) of (2.2) such that \(v(t_0;v_0)=v_0\) satisfies

$$\begin{aligned} \lim _{t\rightarrow +\infty } (v(t; v_0)-v^*(t))=0 . \end{aligned}$$
(2.5)

A monotonicity assumption on G allows us to better characterize the attractor K.

Theorem 2.7

Suppose that G satisfies the structural assumptions and is monotone decreasing in v. Then, in addition to the conclusions of Theorem 2.4, the set K is the (non-empty) set of all the fixed points of \(\Phi _T\), each corresponding to a T-periodic solution of (2.2). Furthermore, denoting with \(v_\alpha (t)\) the T-periodic solution with \(v_\alpha (t_0)=\alpha \), all T-periodic solutions of (2.2) are given by \(v_\alpha (t)+(\gamma -\alpha )\) with \(\gamma \in [\alpha ,\beta ]\).

Proof

Let us consider two solutions u(t), v(t) of (2.2). We observe that, by monotonicity, for almost every t we have

$$\begin{aligned} (\dot{u}(t) -\dot{v}(t) )(u(t) -v(t) ) \le 0 . \end{aligned}$$
(2.6)

Assume in addition that \(u(t^*)=u^*\) and \(v(t^*)=v^*\), with \(u^*\ge v^*\). Then, for every \(t>t^*\) it holds

$$\begin{aligned} \begin{aligned} \left| u(t)-v(t)\right| = u(t)-v(t)=u(t^*)-v(t^*)+\int \limits _{t^*}^{t}(\dot{u}(s)-\dot{v}(s))\mathop {}\!\text {d}s\le u(t^*)-v(t^*)= \left| u(t^*)-v(t^*)\right| \end{aligned} \end{aligned}$$
(2.7)

where the integral term is non-positive by (2.6), since \(u-v\ge 0\) due to the forward uniqueness of solutions. If \(\alpha =\beta \) the proof is completed by noticing that, by Theorem 2.4, all the fixed points of \(\Phi _T\) must be in K. Suppose now that \(\alpha \ne \beta \) and denote with \(v_\gamma \) the solution of the Cauchy problem \(v(t_0)=\gamma \) for some \(\gamma \in K\). We show that \(v_\gamma -v_\alpha \) is constant, and therefore \(v_\gamma \) is T-periodic. Let \(v_\beta \) be the solution of the Cauchy problem \(v(t_0)=\beta \). Being \(v_\beta \) and \(v_\alpha \) T-periodic, we deduce that \(v_\beta =v_\alpha +\beta -\alpha \), since \(v_\beta -v_\alpha \) is nonincreasing by (2.7) and therefore must be constant. By (2.7) we also obtain that \(v_\gamma -v_\alpha \) and \(v_\beta -v_\gamma \) are both nonincreasing. Since \(v_\beta -v_\gamma =v_\alpha -v_\gamma +\beta -\alpha \) we deduce that \(v_\gamma -v_\alpha \) is both nondecreasing and nonincreasing, and therefore it is constant and equal to \(\gamma -\alpha \). \(\square \)

Example 3.3 will illustrate a case where G satisfies the assumptions of Theorem 2.4 but is not monotone. In this case, the set K is a nontrivial interval but the dynamics has exactly three periodic solutions.

We now investigate sufficient conditions for the uniqueness of the periodic solution. The first one is strict monotonicity.

Theorem 2.8

Suppose that G satisfies the structural assumptions and is strictly monotone decreasing in v. Then (2.2) admits exactly one T-periodic solution \(v^*\), which is a global attractor for the dynamics in the sense of (2.5).

Proof

First of all, let us notice that Theorem 2.7 applies, so that, by Corollary 2.6 we only need to verify that \(\beta =\alpha \). Let us denote by \(v_\alpha \) and \(v_\beta \) their corresponding solutions. By Theorem 2.7, we have \(\dot{v}_\beta =\dot{v}_\alpha \) almost everywhere, which by strict monotonicity is possible if and only if \(v_\alpha =v_\beta \). \(\square \)

In general, however, uniqueness of the periodic solution might be achieved also when G is only monotone, provided that it satisfies some additional structural assumptions. We present now a first result of this type in Theorem 2.9; a different structure with set-valued maps will be considered in Theorem 3.4.

Theorem 2.9

Let \(G:\mathbb {R}^2\rightarrow \mathbb {R}\) be a single-valued, continuous function, monotone decreasing in the second variable u, satisfying (S2) and, moreover, suppose that for every t there exists an unique \(u_t\) such that \(G(t,u_t)=0\). Then (2.2) admits exactly one T-periodic solution \(v^*\), which is a global attractor for the dynamics in the sense of (2.5).

Proof

Noticing that the assumptions of Theorem 2.7 are satisfied, let us denote by \(v_\alpha \) and \(v_\beta \) the solutions with initial values \(\alpha \) and \(\beta \). By Corollary 2.6, we only need to verify that \(\beta =\alpha \). We observe that \(v_\alpha \) is periodic and continuously differentiable, hence there exists \(t^*\in [0,T]\) such that \(\dot{v}_\alpha (t^*)=0\). By Theorem 2.7, we have \(\dot{v}_\beta (t^*)=\dot{v}_\alpha (t^*)=0\), which by the assumptions of the Theorem is possible only if \( v_\beta (t^*)=v_\alpha (t^*)\), implying \(\beta =\alpha \) since we have forward uniqueness of solution. \(\square \)

2.3 A lemma

This technical result will be a fundamental tool to prove the existence of a global limit cycle in the case of dry friction (see Theorem 3.4).

Definition 2.10

Given n functions \(\alpha _1,\dots \alpha _n:\mathbb {R}\rightarrow \mathbb {R}\), for every index \(1\le j\le n\) we denote with \(\Gamma ^\alpha _j(t)\) the unique value belonging to \(\{\alpha _1(t),\cdots ,\alpha _n(t)\}\) such that

  • \(\Gamma ^\alpha _j(t)\ge \alpha _i(t)\) for at least j distinct indices \(i\in \{1,\dots n\}\);

  • \(\Gamma ^\alpha _j(t)\le \alpha _k(t)\) for at least \(n-j+1\) distinct indices \(k\in \{1,\dots n\}\).

That is, \(\Gamma ^\alpha _j(t)\) is the jth smallest value (counting multiplicity) at time t of the collection of functions.

Lemma 2.11

Let \(\alpha _1(t),\dots \alpha _n(t):\mathbb {R}\rightarrow \mathbb {R}\) be continuous functions, T-periodic, and such that

$$\begin{aligned} \int _{0}^T\alpha _i(t)\mathop {}\!\textrm{d}t=0 \quad \text {for every }i. \end{aligned}$$

Then the functions \(\Gamma ^\alpha _j(t)\) are continuous and T-periodic. Moreover, for every \(\delta >0\) and index \(j\in \{1,\dots n-1\}\) there exists a measurable set \(U_{j,\delta }\subseteq [0,T)\) with positive measure such that \(\Gamma ^\alpha _{j+1}(t)-\Gamma ^\alpha _j(t)<\delta \) for every \(t\in U_{j,\delta }\).

Proof

Continuity and T-periodicity of the functions \(\Gamma ^\alpha _j\) follow from the corresponding property of the functions \(\alpha _j\). To verify the last property, suppose by contradiction that there exist an index k and a \(\delta >0\) such that \(\Gamma ^\alpha _{k+1}(t)-\Gamma ^\alpha _k(t)\ge \delta \) at almost every t. By the continuity of the \(\Gamma ^\alpha _j\) functions, we deduce that \(\Gamma ^\alpha _{k+1}(t)>\Gamma ^\alpha _k(t)\) for every \(t\in [0,T)\). Thus, there exists two non-empty set of indexes \(J_k^-\) and \(J_k^+\) such that \(\alpha _i\le \Gamma ^\alpha _{k}\) for every \(i\in J_k^-\), while \(\alpha _j\ge \Gamma ^\alpha _{k+1}\) for every \(j\in J_k^+\). Taking any \(i\in J_k^-\) and \(j\in J_k^+\) we get the contradiction

$$\begin{aligned} 0=\int _0^T\alpha _i(t)\mathop {}\!\textrm{d}t<\int _0^T\alpha _j(t)\mathop {}\!\textrm{d}t=0 . \end{aligned}$$

\(\square \)

3 Discrete models of crawler

Fig. 1
figure 1

The discrete model of crawler studied in Sect. 3

Full size image

We consider a system composed of n linked point masses \(m_1,\dots m_n\) on a line, illustrated in Fig. 1. Similar models have been considered, for instance, in [4, 6, 18, 22, 30, 39], and in [10, 20] at the quasistatic regime. We assume that each mass is non-negative, but we require the total mass of the system \(M:=\sum m_i\) to be positive. We assume that all masses are placed on a line, and denote with the vector \(x(t)=(x_1(t),x_2(t),\dots ,x_n(t))\in \mathbb {R}^{n}\) their position at any time t. The shape of the locomotor is prescribed, namely the relative distances between the position of the masses are assigned. This means that the vector x can be decomposed in an unknown scalar value indicating the overall position of the crawler and a prescribed \((n-1)\)-dimensional vector describing its shape. Several choices of the reference point are possible, e.g. the barycentre, the average position, the head, the tail; clearly this does not affect the qualitative behaviour of the system. In the following, we identify the position of the locomotor with its barycentre \({\bar{x}}(t)\) and denote with \(z_i(t)\) the position of the ith mass relative to the barycentre, namely

$$\begin{aligned} {\bar{x}}(t)=\frac{1}{M}\sum _{i=1}^n m_ix_i(t) ,{} & {} z_i(t):=x_i(t)-{\bar{x}}(t) . \end{aligned}$$

Notice that that the vector \(z(t)\in \mathbb {R}^n\) is actually contained in the \((n-1)\)-dimensional subspace defined by the constraint \(\sum m_i z_i=0\). Moreover, assigning an input z(t) is equivalent to controlling the (signed) distance between consecutive masses, since \(x_i-x_j=z_i-z_j\).

In what follows, unless stated differently, we will always assume that the following holds for the shape functions:

  1. (D1)

    the functions \(z_i(t)\) are T-periodic and Lipschitz continuous.

Each mass is subject to a time-dependent friction force \(F_i(t,\dot{x}_i)\). In concrete situation, time-dependence can be produced by various mechanisms: a change in the normal force on the contact surfaces (e.g. due to an expansion while crawling in a tube) or in their properties (e.g. a change in the tilt angle of bristles or scales on the body of the crawler [21, 30]) or more complex phenomena (cf. [37]). We assume that each friction force \(F_i\) is T-periodic in time; the possible types of friction force-velocity law will be discussed below. Notice that, in general, the functions \(F_i\) may be set-valued, in order to account for discontinuous forces such as dry friction, for which a yield force has to be reached in order to slide. This implies that, in general, the dynamics of the system is described by a differential inclusion.

Finally, we also allow an external force B(t) acting on the system. Since we are in a one-dimensional setting and the shape of the locomotor is predetermined, the force might be considered as applied to the barycentre. We assume

  1. (D2)

    the function B(t) is T-periodic, bounded and measurable.

We point out that locomotion is, per se, driven by an internal actuation, in our case represented by shape change \(z_i\), so in our examples we will focus on \(B\equiv 0\). External forces may however be relevant to describe additional effects: for instance, crawling on a slope with angle \(\theta \) corresponds to \(B\equiv -Mg\sin \theta \), where g denotes gravity.

Since the shape of the locomotor is prescribed, to study its evolution we just have to consider that of its barycenter \(\bar{x}(t)\), that is determined by the sum of the external forces B and \(F_i\). Denoting \(v:=\dot{{\bar{x}}}\) and \(w:=\dot{z}\), we can rewrite the dynamics of the barycenter as

$$\begin{aligned} \dot{v}\in G(t,v):=\frac{1}{M}\left( B(t)+\sum _{i=0}^n F_i(t,v+w_i(t))\right) . \end{aligned}$$
(3.1)

Notice that G(t, v) is defined up to a set of zero measure (which corresponds to the points of non-differentiability of the given shape functions \(z_i\)). However, we can redefine arbitrarily G on such set without changing the set of solutions. Also, note that the functions \(x_i={\bar{x}}+z_i\) are the sum of \({\bar{x}}\in W^{2,1}([0,T],\mathbb {R})\) and \(z\in W^{1,\infty }([0,T],\mathbb {R})\), so that, in general, the evolution of the material points \(x_i\) is less regular. This corresponds to the exchange of impulsive internal forces at the times at which \(z_i\) is not differentiable, so that the dynamics of a single material point can be expressed only in a distributional sense.

We will discuss several classes of friction forces, providing increasingly stronger convergence properties of the dynamics. We look for limit cycles of Eq. (3.1): indeed, a periodic solution \({\bar{v}}\) of (3.1) corresponds to a relative-periodic evolution of the state x, with geometric phase \(\gamma =\int _0^T{\bar{v}}(t)\mathop {}\!\textrm{d}t\).

Generic friction force (possibly non-monotone). We begin by discussing the situation of a generic friction force.

  1. (D3)

    For every index i, the function \(F_i\) is a set-valued map T-periodic in t and locally bounded by a measurable function. Moreover, it can be decomposed as \(F_i(t,u)=A_i(t,u)+\psi _i(t,u)\), where \(A_i\) is maximal monotone decreasing in u for every t and measurable in t for every u, while \(\psi _i\) is a Carathéodory function locally Lipschitz continuous in the variable u uniformly in t.

  2. (D4)

    There exists \(R>0\) and, for every index i, two T-periodic measurable functions \(\ell _i^\pm (t):\mathbb {R}\rightarrow \mathbb {R}\) such that, for almost every \(t\in \mathbb {R}\)

    $$\begin{aligned} F_i(t,u)&\ge -\ell _i^-(t){} & {} \text {for every } u\le -R,\\ F_i(t,u)&\le \ell _i^+(t){} & {} \text {for every } u\ge R, \end{aligned}$$

    with

    $$\begin{aligned} \int \limits _{0}^T \left( B(s)+\sum _{i=1}^n\ell _i^+(s)\right) \mathop {}\!\textrm{d}s<0<\int \limits _{0}^T \left( B(s)-\sum _{i=1}^n\ell _i^-(s)\right) \mathop {}\!\textrm{d}s . \end{aligned}$$

The regularity condition (D3) allows to include \(F_i(t,\cdot )\) that are, in general, non-monotone, hence accounting for a Stribeck effect [1, 32]. Notice, however, that the left limit of \(F_i(t,\cdot )\) at discontinuity points is always greater than the right one, due to the monotonicity of \(A_i\).

In concrete cases, we expect the forces \(F_i\) to act always against the direction of motion. We would like, however, to include also situations in which one point-mass is not in contact with the surface during a certain phase of the period, for instance due to lifting or shrinking of the corresponding part of the body, resulting in a temporarily null \(F_i\). On the other hand, this should be a constrained phenomenon, avoiding a perpetual frictionless sliding in one direction. This is, intuitively, the meaning of condition (D4) for \(B\equiv 0\), although, for mathematical generality, such property is required only at sufficiently large speeds. For \(B\ne 0\), (D4) also guarantees that the external load does not overcome friction forces, i.e. the locomotion component of the dynamics. For instance, in the case of crawling on a slope, it guarantees that an inactive crawler would not slide downward accelerating endlessly.

Theorem 3.1

Let us consider a discrete model of crawler as above, satisfying (D1), (D2), (D3) and (D4). Then all the solutions v of (3.1) are asymptotically T-periodic. Moreover, there exists two, possibly identical, T-periodic solutions \(v_\alpha ,v_\beta \) of the dynamics such that every solution v of (3.1) satisfies

$$\begin{aligned} \lim _{t\rightarrow +\infty }{{\,\textrm{dist}\,}}(v(t),[v_\alpha (t),v_\beta (t)])=0 . \end{aligned}$$
(3.2)

Proof

We observe that the function G in (3.1) is, by (D3), of the form (2.1); furthermore, by (D4) and the Lipschitz continuity of the \(z_i\), it satisfies (S2). Indeed, denoting by \(\Lambda _z\) the Lipschitz constant of the \(z_i\), and taking \(R:=r+\Lambda _z+1\) we get, for every \(v\ge R\) and \(t\in \mathbb {R}\),

$$\begin{aligned} G(t,v)=\frac{1}{M}\left( B(t)+\sum _{i=0}^n F_i(t,v+w_i(t))\right) \le \frac{1}{M}\left( B(t)+\sum _{i=0}^n \ell _i^+(t)\right) =:\ell _d^+(t) \end{aligned}$$

where the function \(\ell _d^+(t)\) thus defined satisfies, by (D4), the requirements of (S2). The other bound in (S2) can be deduced analogously. We can therefore apply Theorem 2.5 and conclude. \(\square \)

Monotone friction forces. Most of the classical examples of friction forces, for instance viscous or dry friction, are however monotone with respect to velocity. This means that in (D3) we can set \(\psi _i\equiv 0\); namely

  1. (D5)

    For every index i, the function \(F_i:\mathbb {R}\times \mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\setminus \emptyset \) is a set-valued map, locally bounded by a measurable function, T-periodic in t, maximal monotone decreasing in u for every t and measurable in t for every u.

The most important example of this family, excluding strictly monotone ones, is that of dry friction, defined by \(F_i(t,u)=-\alpha \, \partial _u \left|u\right|\).

Theorem 3.2

Let us consider a discrete model of crawler as above, satisfying (D1), (D2), (D4) and (D4). Then, for every solution v(t) of (3.1) there exists a T-periodic solution \({\bar{v}}\) such that

$$\begin{aligned} \lim _{t\rightarrow +\infty } (v(t)-{\bar{v}}(t))=0{.} \end{aligned}$$

Moreover, there exists an interval [a, b], possibly degenerate, such that \({\bar{v}}\) is a T-periodic solution if and only if \(\bar{v}=v^*+c\) for some \(c\in [a,b]\).

Proof

The function G in (3.1) is, by (D4), of the form (2.1) and monotone decreasing in v; furthermore, by (D4) and the Lipschitz continuity of the \(z_i\), it satisfies (S2). The conclusion follows by Theorem 2.7. \(\square \)

Fig. 2
figure 2

The function G in Examples 3.1, 3.2 and 3.3. In Examples 3.1 and 3.3, the resulting function G(t, v) does not depend on time t. In Example 3.2 the function G switches every half-period. The behaviour for \(t\in (0,T/2)\) is illustrated by the solid green line, whereas for \(t\in (T/2,T)\) it is given by the dashed blue one

Full size image

Example 3.1

Let us consider the following example with \(n=2\), \(M=1\) and \(B\equiv 0\), characterized by isotropic dry friction, constant in time and equal on both point masses, and a T-periodic triangular wave actuation on shape; more precisely we set

$$\begin{aligned} F_1(t,u)=F_2(t,u)=-\partial _u \left|u\right| \qquad \qquad w_1(t)=-w_2(t)={\left\{ \begin{array}{ll} -\alpha &{}\text {for } t\in (0,T/2)\\ \alpha &{}\text {for }t\in (T/2,T) \end{array}\right. } \end{aligned}$$

for some \(\alpha \ne 0\). The function G from (3.1) is constant in time (except for times of the form \(t=kT/2\), \(k\in \mathbb {Z}\), where we can extend it by continuity), with values

$$\begin{aligned} G(t,u)=-\partial _u \left( \left|u-\alpha \right|+\left|u+\alpha \right|\right) \end{aligned}$$

(see Fig. 2A). We notice that G is monotone decreasing in u, with \(0\in G(t,u)\) if and only if \(u\in [-\alpha ,\alpha ]\). Hence the set of periodic solutions provided by Theorem 3.2 consists of the constant functions \({\bar{v}}\in [-\alpha ,\alpha ]\).

We emphasize that, in this example, different initial conditions might lead to a different asymptotic velocities of the crawler, even having opposite sign.

In the previous example, all periodic solution have constant velocity \(\dot{v}\) of the barycenter, so we might ask ourselves whether this is a necessary feature for multiplicity. The issue is furthermore relevant since the friction configuration considered in the example is problematic at the quasistatic regime, violating uniqueness condition \((*)\) in [20], leading to multiplicity of solutions (to the initial value problem) with the same shape change but different velocity [20, Example 3.2]. The answer is negative, as we show with the following example satisfying \((*)\), which therefore plays no role in the dynamic regime.

Example 3.2

Let us modify Example 3.1 just by doubling the friction on the first point mass, namely \(F_1(t,u)=-2 \partial _u\left|u\right|\), and setting \(T<4\alpha \). Considering only the relevant part, we have

$$\begin{aligned} \begin{aligned} G(t,u)={\left\{ \begin{array}{ll} 1 &{}{}\text{ for } t\in (0,T/2), u\in (-\alpha ,\alpha )\\ -1 &{}{}\text{ for } t\in (T/2,T), u\in (-\alpha ,\alpha ) \end{array}\right. } \end{aligned} \end{aligned}$$

(see Fig. 2B). Hence, for each \(u_0\in [-\alpha , \alpha -T/2]\) we have a parametric set of periodic solutions

$$\begin{aligned} u={\left\{ \begin{array}{ll} u_0 +t &{}\text {for }t\in (0,T/2)\\ u_0 +(T-t) &{}\text {for }t\in (T/2,T) \end{array}\right. } \end{aligned}$$
(3.3)

of the dynamics, each with average velocity \(u_0+T/4\).

Example 3.3

We now consider a variation of Example 3.1 with the addition of a Stribeck effect on friction. We set

$$\begin{aligned} F_1(t,u)=F_2(t,u)=-\partial _u \left|u\right|+\psi (u) \qquad \qquad \psi (u)={\left\{ \begin{array}{ll} \frac{1}{2}\sin (\frac{\pi }{\alpha } u ) &{}\text {for }u\in (-\alpha ,\alpha )\\ 0 &{}\text {elsewhere} \end{array}\right. } \end{aligned}$$

with \(\alpha , w_1, w_2, B\) as in Example 3.1. Hence

$$\begin{aligned} \begin{aligned} G(t,u)=-\partial _u \left( \left| u-\alpha \right| +\left| u+\alpha \right| \right) +\psi (u-\alpha )+\psi (u+\alpha ) \end{aligned} \end{aligned}$$

(see Fig. 2C). The dynamics (3.1) admits exactly three T-periodic solutions: the constant solutions \(v^*\equiv -\alpha \) and \(v^{**}\equiv \alpha \) are semistable, with basins of attraction given respectively by \((-\infty ,-\alpha ]\) and \([\alpha ,+\infty )\), whereas the constant solution \(v^0\equiv 0\) is stable with basin of attraction \((-\alpha , \alpha )\). All the solutions of the basins of attractions of \(v^*\) and \(v^{**}\) attain the corresponding periodic regime in finite time.

Strictly monotone friction forces. We strengthen the assumptions of the previous case, requiring strict monotonicity of the functions \(F_i(t,\cdot )\).

  1. (D6)

    For every index i, the function \(F_i:\mathbb {R}\times \mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\setminus \emptyset \) is a set-valued map, locally bounded by a measurable function, T-periodic in t, maximal strictly monotone decreasing in u for every t and measurable in t for every u.

The most important example in this family is that of viscous friction \(F_i(t,u)=-\mu u\). For set-valued maps, we mention the case of Bingham friction, defined by \(F_i(t,u)=-\mu u -\alpha \, \partial _u\left|u\right|\).

Theorem 3.3

Let us consider a discrete model of crawler as above, satisfying (D1), (D2), (D4) and (D6). Then the dynamics (3.1) admits exactly one T-periodic solution \(v^*\), which is a global attractor for the dynamics, i.e. every solution v(t) of (3.1) satisfies

$$\begin{aligned} \lim _{t\rightarrow +\infty } (v(t)- v^*(t))=0 . \end{aligned}$$
(3.4)

Proof

The function G in (3.1) is, by (D6), of the form (2.1) and strictly monotone decreasing in v; furthermore, by (D4) and the Lipschitz continuity of the \(z_i\), it satisfies (S2). The conclusion follows by Theorem 2.8. \(\square \)

Example 3.4

(Asymptotically incompetent crawler) Let us consider the case with \(n\ge 2\), \(B\equiv 0\) and (constant, isotropic) viscous friction, namely \(F_i(t,u)=-\mu _i u\), with \(\mu _i>0\). The unique T-periodic solution \(v^*\) of (3.1) satisfies

$$\begin{aligned} 0=\int \limits _0^T \dot{v}^*(t)\mathop {}\!\textrm{d}t=-\sum _{i=1}^n\frac{\mu _i}{M}\int \limits _0^T v^*(t)\mathop {}\!\textrm{d}t -\sum _{i=1}^n\frac{\mu _i}{M}\int \limits _0^Tw_i(t)\mathop {}\!\textrm{d}t . \end{aligned}$$

Since the \(w_i\) are the derivatives of the T-periodic functions \(z_i\), we deduce that \(\int \limits _0^Tw_i(t)\mathop {}\!\textrm{d}t=0\) and therefore

$$\begin{aligned} \int \limits _0^T v^*(t)\mathop {}\!\textrm{d}t =0 . \end{aligned}$$

The fact that, in discrete models, constant, isotropic viscous friction leads to an “incompetent” crawler, with a null net displacement, was observed, in a quasi-static setting, in [13]. Here we see that, considering also inertia, such a crawler is still incompetent, but in an asymptotic sense.

The issue in Example 3.4 can be overcome still in a viscous setting, if we consider anisotropic viscosity or time-dependent viscosity. We illustrate this second possibility with the following example, that can be seen a viscous adaptation of two-anchor crawling.

Example 3.5

Let us set \(n=2\), \(M=2\), \(B\equiv 0\) and

$$\begin{aligned} F_1(t,u)=-(2+\sin t)u \qquad F_2(t,u)=-(2-\sin t)u \qquad z_1(t)=-z_2(t)=2+\cos t \end{aligned}$$

so that the dynamics (3.1) reads

$$\begin{aligned} \dot{v}=-2v+\sin ^2 t \end{aligned}$$

whose solutions have the form

$$\begin{aligned} v(t)=\frac{\sin ^2 t}{2}+\frac{\cos 2t-\sin 2t}{8}+c e^{-2t} \end{aligned}$$

with \(c\in \mathbb {R}\). Clearly the solution \(v^*\) associated with \(c=0\) is the unique T-periodic solution of the system and a global attractor for the dynamics. Unlike the previous case, however, it is easily verified that, in the asymptotic regime, each actuation cycle of duration \(2\pi \) produces a forward net displacement of the crawler of \(2\pi /4\).

Dry friction forces with additional time-regularity

Theorem 3.4

We make the following assumptions:

  1. (i)

    Each mass is affected by dry friction with nonzero coefficients continuous in time, i.e.

    $$\begin{aligned} F_i(t,u)= {\left\{ \begin{array}{ll} \{-\mu _i^+(t)\} &{} \text {for }u>0\\ \{\mu _i^-(t)\} &{} \text {for } u<0\\ {[}-\mu _i^+(t),\mu _i^-(t){]} &{} \text {for }u=0 \end{array}\right. } \end{aligned}$$

    where the \(\mu _i^\pm \) are continuous, T-periodic and positive;

  2. (ii)

    the shape functions \(z_i(t)\) are continuously differentiable and T-periodic;

  3. (iii)

    the external load B(t) is continuous, T-periodic and such that

    $$\begin{aligned} \int \limits _0^T \left( B(s)-\sum _{i=1}^n \mu _i^+(s)\right) \mathop {}\!\textrm{d}s<0< \int \limits _0^T \left( B(s)+\sum _{i=1}^n \mu _i^-(s)\right) \mathop {}\!\textrm{d}s \end{aligned}$$

Then the dynamics (3.1) admits exactly one T-periodic solution \(v^*\), which is a global attractor for the dynamics in the sense of (3.4).

Proof

We observe that the assumptions of Theorem 3.2 are satisfied, hence there exists at least a T-periodic solution \(v^*\) and, if the dynamics admits additional T-periodic solutions, they are of the form \({\bar{v}}(t)=v^*(t)+\delta \) for some constant \(\delta \). To show that \(v^*\) is unique, we suppose by contradiction that there exists a second T-periodic solution \({\bar{v}}(t)=v^*(t)+\delta \), assuming without loss of generality \(\delta >0\).

We notice that by (i) the function G in (3.1) is such that for every t and for every \(u_a,u_b\) satisfying \(u_a<-w_i(t)<u_b\) we have \(G(t,u_a)>G(t,u_b)\).

Recalling that \(w_i(t)=\dot{z}_i(t)\), so that \(\int _0^T w_i(t)=0\), we consider the functions \(\Gamma ^{-w}_j\) as in Definition 2.10 with \(\alpha _i=-w_i\). Since \(v^*\) is continuous, we must be in one of the following cases.

  • there exists a set \(U\subset [0,T)\) with positive measure and an index \(k\in \{1,\dots n\}\) such that \(v^*(t)<\Gamma ^{-w}_k(t)<{\bar{v}}(t)\) for every \(t\in U\). This implies \(G(t,v^*(t))>G(t,{\bar{v}}(t))\) for \(t\in U\), and therefore \(\dot{v}^*>\dot{{\bar{v}}}\) almost everywhere on U. On the other hand, by \({\bar{v}}(t)=v^*(t)+\delta \) we deduce that \(\dot{v}^*=\dot{{\bar{v}}}\) almost everywhere, obtaining a contradiction.

  • there exists an index \(k\in \{1,\dots n-1\}\) such that \(\Gamma ^{-w}_k(t)\le v^*(t)<{\bar{v}}=v^*(t)+\delta \le \Gamma ^{-w}_{k+1}(t)\) for every t. This is in contradiction with the final proposition in Lemma 2.11.

  • \(v^*(t)<{\bar{v}}(t)\le \Gamma ^{-w}_1(t)\) for almost every t. Then by (i) we deduce that \(\dot{v}^*(t)\in G(t,v^*(t))>0\) for almost every t, which is a contradiction with \(v^*\) being absolutely continuous and T-periodic.

  • \({\bar{v}}(t)>v^*(t)\ge \Gamma ^{-w}_n(t)\) for almost every t. Then by (i) we deduce that \(\dot{\bar{v}}(t)\in G(t,v^*(t))<0\) for almost every t, which is a contradiction with \({\bar{v}}\) being absolutely continuous and T-periodic.

Since in each case the existence of a second T-periodic solution \({\bar{v}}=v^*+\delta \) leads to a contradiction, we deduce that \(v^*\) is the unique T-periodic solutions of (3.1) and therefore a global attractor for the dynamics in the sense of (3.4). \(\square \)

4 Continuous models of crawler

Fig. 3
figure 3

The continuous model of crawler studied in Sect. 4

Full size image

Let us now consider that the body of our crawler is, in the reference configuration, the interval \(\Omega =[\xi _a,\xi _b]\), so that its position at time t is described by a function \(x(t,\xi ):[0,T] \times \Omega \rightarrow \mathbb {R}\), cf. Fig. 3. Similar models have been considered, for instance, in [5], and, at the quasistatic regime, in [2, 12, 13, 20]. We assume that the crawler has a total mass \(M>0\) distributed according to a non-negative mass density \(\rho \in L^\infty (\Omega ,[0,+\infty ))\), and define \(\bar{x}(t):=\int _\Omega x(t,\xi )\mathop {}\!\textrm{d}\rho (\xi )\) as the position of the barycentre. Analogously to the discrete case, the shape of the crawler is prescribed. To do so, we prescribe the deformation gradient \(\nabla _\xi x(t,\xi )=\phi (t,\xi )\) where

  1. (C1)

    \(\phi \in W^{1,\infty }(\mathbb {R},L^\infty (\Omega ,\mathbb {R}))\) is T-periodic in t; moreover we assume that there exist \(\phi _\textrm{max},\phi _\textrm{min}\) such that \(0<\phi _\textrm{min}\le \phi (t,\xi )\le \phi _\textrm{max}\) for almost every \((t,\xi )\in \mathbb {R}\times \Omega \).

As in the discrete case, we we denote the relative position of an element \(\hat{\xi }\in \Omega \) with respect to the barycentre as \(z(t,\hat{\xi })=x(t,\hat{\xi })-{\bar{x}}(t)\). We observe that

$$\begin{aligned} z(t,\hat{\xi })=x(t,\hat{\xi })-{\bar{x}}(t)=\frac{1}{M}\int \limits _\Omega \rho (\xi )(x(t,\hat{\xi })-x(t,\xi ))\mathop {}\!\textrm{d}\xi =\frac{1}{M}\int \limits _\Omega \rho (\xi )\int \limits _\xi ^{\hat{\xi }}\phi (t,s)\mathop {}\!\textrm{d}s\mathop {}\!\textrm{d}\xi \end{aligned}$$
(4.1)

so that \(z\in W^{1,\infty }(\mathbb {R},W^{1,\infty }(\Omega ,\mathbb {R}))\). We also notice that \(\int _\Omega z(t,\xi )\mathop {}\!\textrm{d}\rho (\xi )=0\).

The crawler is subject to a time-dependent friction force per unit length \(f(t,\xi , \dot{x}_i)\) acting along the body. We assume that \(t\mapsto f(t,\xi ,\eta )\) is T-periodic. The possible types of friction force-velocity law will be discussed below, analogously to the discrete case.

As in the discrete case, we also allow an external force B(t) acting on the system, which, without loss of generality, is considered as applied to the barycentre. We assume

  1. (C2)

    the function B(t) is T-periodic, bounded and measurable.

The equation of motion reads

$$\begin{aligned} M\ddot{{\bar{x}}} -B(t) \in \int \limits _\Omega f\bigl (t,\xi ,\dot{x}(t,\xi )\bigr )\mathop {}\!\textrm{d}\xi = \int \limits _\Omega f\bigl (t,\xi ,\dot{{\bar{x}}}(t) +\dot{z}(t,\xi )\bigr )\mathop {}\!\textrm{d}\xi . \end{aligned}$$
(4.2)

Recalling that z is assigned, so that the problem has to be solved only for \({\bar{x}}\), we proceed as in the previous section and set \(v(t)=\dot{{\bar{x}}}(t)\), \(w(t,\xi )=\dot{z}(t,\xi )\) and obtain

$$\begin{aligned} \dot{v}(t) \in G(t,v):=\frac{1}{M}\left( B(t)+\int \limits _\Omega f\bigl (t,\xi ,v(t) +w(t,\xi )\bigr )\mathop {}\!\textrm{d}\xi \right) . \end{aligned}$$
(4.3)

As in discrete case, we study limit cycles for (4.3), since its periodic solutions correspond to relative-periodic evolutions of the state x.

Generic friction force (possibly non-monotone). We begin by discussing the situation of a generic friction force. For simplicity, we will consider friction forces possibly multivalued only in zero, which includes all the physically relevant cases. More precisely, we consider friction density f of the form

$$\begin{aligned} f(t,\xi ,u)=h(t,\xi ,u)+q(t,\xi ,u) \end{aligned}$$
(4.4)

where h and q are as follows:

  1. (C3)

    the function \(h:\mathbb {R}\times \Omega \times \mathbb {R}\rightarrow \mathcal {P}(\mathbb {R})\) is of the form

    $$\begin{aligned} h(t,\xi ,u):={\left\{ \begin{array}{ll} \{-\mu ^+(t,\xi )\} &{} \text {for }u>0\\ \{\mu ^-(t,\xi )\} &{} \text {for }u<0\\ {[}-\mu ^+(t,\xi ),\mu ^-(t,\xi ){]} &{} \text {for } u=0 \end{array}\right. } \end{aligned}$$
    (4.5)

    where the functions \(\mu ^\pm \in L^\infty (\mathbb {R},L^\infty (\Omega ,[0,+\infty ))\) are T-periodic in t.

  2. (C4)

    the function \(q=q(t,\xi ,u):\mathbb {R}\times \Omega \times \mathbb {R}\) satisfies

    • \(q(t,\xi , \cdot )\) is locally Lipschitz continuous uniformly in \((t,\xi )\);

    • for every \(u\in \mathbb {R}\), \(q(\cdot ,\cdot ,u)\) is measurable, bounded and T-periodic in t.

  3. (C5)

    There exist \(R>0\) and two T-periodic measurable functions \(\ell ^\pm :\mathbb {R}\rightarrow \mathbb {R}\) such that, for every \(t\in \mathbb {R}\)

    $$\begin{aligned} \int \limits _\Omega f(t,\xi ,u) \mathop {}\!\textrm{d}\xi&\ge -\ell ^-(t){} & {} \text {for every } u\le -R\\ \int \limits _\Omega f(t,\xi ,u)\mathop {}\!\textrm{d}\xi&\le \ell ^+(t){} & {} \text {for every } u\ge R \end{aligned}$$

    with

    $$\begin{aligned} \int \limits _{0}^T \left( B(s)-\ell ^+(s)\right) \mathop {}\!\textrm{d}s<0< \int \limits _{0}^T \left( B(s)+\ell ^-(s)\right) \mathop {}\!\textrm{d}s . \end{aligned}$$

For such forces we have immediately the following result:

Theorem 4.1

Let us consider a continuous model of crawler as above, satisfying (C1), (C2), (C3), (C4) and (C5). Then the same conclusions of Theorem 3.1 hold.

Proof

The theorem follows from Theorem 2.5. In particular, we notice that the maximal monotonicity required by (S1) follows by the convexity of \(u\rightarrow \int _\Omega H(t,\xi ,u+w(t,\xi ))\mathop {}\!\textrm{d}\xi \), where \(H(t,\xi ,v)=\int _0^v h(t,\xi ,u)\mathop {}\!\textrm{d}u\). \(\square \)

Strictly monotone friction. In the case of strictly monotone friction forces we also have a result analogous to the discrete case:

Theorem 4.2

Let us consider a continuous model of crawler as above, satisfying (C1), (C2), (C3), (C4) and (C5). Assume moreover that \(f(t,\xi ,u)\) is strictly monotone decreasing in u for every \(t,\xi \). Then the same conclusions of Theorem 3.3 hold.

The result is a straightforward consequence of Theorem 2.8.

Dry friction In the continuous case, differently from the discrete one, for dry friction we have uniqueness of the periodic solution also without requiring additional regularity in time of the shape function \(z(t,\xi )\), assuming positive friction coefficients. We prove this in a generalized case for q monotone, but requiring that the inequalities in (C5) are satisfied also for \(q\equiv 0\), meaning:

  1. (C6)

    \(q(t,\xi ,u)\) is monotone decreasing in u for every \(t,\xi \), with \(q(t,\xi ,0)\equiv 0\) and

    $$\begin{aligned} \int \limits _{0}^T \left( B(s)-\int \limits _\Omega \mu ^+(t,\xi )\mathop {}\!\textrm{d}\xi \right) \mathop {}\!\textrm{d}s<0< \int \limits _{0}^T \left( B(s)+\int \limits _\Omega \mu ^-(t,\xi )\mathop {}\!\textrm{d}\xi \right) \mathop {}\!\textrm{d}s \end{aligned}$$

and assuming that

  1. (C7)

    the functions \(\mu ^\pm (t,\xi )\) satisfy for almost every t

    $$\begin{aligned} \mu ^+(t,\xi )+\mu ^-(t,\xi )>0 \end{aligned}$$

    almost everywhere in \(\Omega \).

As showed by Examples 3.1 and 3.2, analogous assumptions in the discrete case do not guarantee the uniqueness of the T-periodic orbit in that framework, but in the continuous setting we have the following:

Theorem 4.3

Let us consider a continuous model of crawler as above, satisfying (C1), (C2), (C3), (C4), (C6) and (C7). Then the same conclusions of Theorem 3.4 hold.

Proof

By (C1), (C2), (C3), (C4) and (C6), G satisfies (S1).

We observe that, for almost every t, \(\dot{z}(t,\cdot )\in W^{1,\infty }(\Omega ,\mathbb {R})\). Thus, for almost every t, we can define the T-periodic functions

$$\begin{aligned} \zeta ^-(t):=\min _{\xi \in \Omega } -\dot{z}(t,\xi )\le 0\le \max _{\xi \in \Omega } -\dot{z}(t,\xi )=:\zeta ^+(t) . \end{aligned}$$

The inequalities follow from the fact that \(\dot{z}(t,\cdot )\) has zero average weighted with the measure \(\rho \). Note that \(\zeta ^\pm (\cdot )\in L^\infty [0,T]\). By (C6) we have that \(G(t,\cdot )\) is decreasing in u and verifies

$$\begin{aligned} G(t,u)\ge -l^-_d(t):=\frac{1}{M}\left( B(t)+\int \limits _\Omega \mu ^-(t,\xi ) d\xi \right) \qquad \text {for }u\le \zeta ^-(t) \end{aligned}$$
(4.6)

and

$$\begin{aligned} G(t,u)\le l^+_d(t):=\frac{1}{M}\left( B(t)-\int \limits _\Omega \mu ^+(t,\xi ) d\xi \right) \qquad \text {for }u\ge \zeta ^+(t). \end{aligned}$$
(4.7)

In particular, this implies that (S2) holds for \(R=\max \{\left\Vert \zeta ^+\right\Vert _\infty , \left\Vert \zeta ^-\right\Vert _\infty \}\).

Since the structural assumptions hold, by Theorem 2.7 we have that the nonempty attractor of the dynamics of Eq. (4.3) is made by periodic orbits with the same derivative.

We show now that for almost every t and every \(v\in [\zeta ^-(t),\zeta ^+(t)]\) we have

$$\begin{aligned} G(t,u_1)>G(t,u_2) \qquad \text {for every } u_1<v<u_2. \end{aligned}$$
(4.8)

We consider two cases:

  • If \(\zeta ^-(t)<\zeta ^+(t)\), we begin by proving that \(G(t, \cdot )\) is strictly decreasing on \(J=[\zeta ^-(t),\zeta ^+(t)]\). Consider \(v\in J\) and \(u_1<v<u_2\). By the continuity of \(\dot{z}(t,\cdot )\) there exists an interval \(I\subset \Omega \) with positive measure such that \(-\dot{z}(t,\xi )\in (\zeta ^-(t),\zeta ^+(t))\cap (v_1,v_2) \) for any \(\xi \in I\). Then, by (C7) we have

    $$\begin{aligned} \int \limits _I h(t,\xi ,u_1+\dot{z}(t,\xi ))\mathop {}\!\textrm{d}\xi =\int \limits _I\mu ^+(t,\xi )\mathop {}\!\textrm{d}\xi >\int \limits _I-\mu ^-(t,\xi )\mathop {}\!\textrm{d}\xi =\int \limits _I h(t,\xi ,u_2+\dot{z}(t,\xi )) \mathop {}\!\textrm{d}\xi \end{aligned}$$
    (4.9)

    while by the monotonicity of h

    $$\begin{aligned} \int \limits _{\Omega \setminus I} h(t,\xi ,u_1+\dot{z}(t,\xi ))\mathop {}\!\textrm{d}\xi \ge \int \limits _{\Omega \setminus I} h(t,\xi ,u_2+\dot{z}(t,\xi )) \mathop {}\!\textrm{d}\xi . \end{aligned}$$

    Since also q is monotone decreasing in u we get (4.8).

  • If \(\zeta ^-(t)=\zeta ^+(t)=0\), and hence \(\dot{z}=0\), then (4.8) is obtained directly, since it must be verified only for \(v=0\) and we know by (C3), (C6) and (C7) that \(f(t,\xi ,u_1)<f(t,\xi ,u_2)\) for \(u_1<0<u_2\).

In order to prove the uniqueness of the T-periodic orbit of (4.3), we observe first that, if \(\alpha (t)\) is any T-periodic solution of (4.3), then it cannot be neither

$$\begin{aligned} \begin{aligned} \alpha (t)< \zeta ^-(t)\quad \text{ almost } \text{ everywhere } \text{ on } [0,T] \end{aligned} \end{aligned}$$
(4.10)

nor

$$\begin{aligned} \begin{aligned} \alpha (t)> \zeta ^+(t)\quad \text{ almost } \text{ everywhere } \text{ on } [0,T]. \end{aligned} \end{aligned}$$
(4.11)

In fact, if (4.10) holds, we get a contradiction since

$$\begin{aligned} \begin{aligned} 0=\int \limits _0^T\dot{\alpha }(t) \mathop {}\!\text {d}t=\int \limits _0^T G(t,\alpha (t)) \mathop {}\!\text {d}t\ge \int \limits _0^T -l_d^-(t) \mathop {}\!\text {d}t>0 \,. \end{aligned} \end{aligned}$$

Inequality (4.11) is ruled out analogously.

We conclude that, given any T-periodic solution \(\alpha (t)\) of (4.3), it must be

$$\begin{aligned} \begin{aligned} \alpha (t)\in [\zeta ^-(t),\zeta ^+(t)] \qquad \text{ on } \text{ a } \text{ subset } \text{ of } \text{ positive } \text{ measure } \text{ of } \, [0,T]. \end{aligned} \end{aligned}$$
(4.12)

Assume now by contradiction that there exist two distinct T-periodic solutions \(v^*\) and \({\bar{v}}\) of (4.3) with \(v^*(t)<{\bar{v}}(t)\) on [0, T].

By the first part of the proof, we know that \(\dot{v}^*(t)=\dot{{\bar{v}}}(t)\) almost everywhere on [0, T]. But then, by (4.12) and (4.8) we have

$$\begin{aligned} \dot{v}^*(t)\in G(t,v^*(t))>G(t, {\bar{v}}(t))\ni \dot{{\bar{v}}}(t) \end{aligned}$$

on a set of positive measure in [0, T], a contradiction. Our proof is concluded. \(\square \)

We remark that assumption (C7) is necessary for uniqueness, as we show in the following example where we reconstruct the discrete model of Example 3.1 in a continuous setting.

Example 4.1

Let us set \(\Omega =[0,3]\), \(\rho \equiv 1/3\), \(B\equiv 0\), \(q\equiv 0\) and

$$\begin{aligned} \begin{aligned} \mu ^\pm (t,x)={\left\{ \begin{array}{ll} 0 &{}{} \text{ if } \zeta \in [1,2]\\ 1 &{}{} \text{ if } \zeta \in [0,1)\cup (2,3] \end{array}\right. } \qquad \dot{\phi }(t,x)={\left\{ \begin{array}{ll} 2 w_2(t)&{}{} \text{ if } \zeta \in [1,2]\\ 0 &{}{} \text{ if } \zeta \in [0,1)\cup (2,3] \end{array}\right. } \end{aligned} \end{aligned}$$

where \(w_2(t)\) is the same as in Example 3.1, with \(\phi (0,\cdot )\equiv 1\) and \(\alpha >0\). Then we obtain the same function G of Example 3.1, so that the asymptotic average velocity is not unique.

5 Discussion

In this work we have studied the asymptotic gait of discrete as well as continuous crawlers with prescribed shape moving on a line subject to different classes of frictions and possibly to an additional external forcing, such as that due to gravity when crawling on a slope.

Our aim was to make evident how a well-posed notion of gait as asymptotic behaviour, although it can be reasonably expected, requires some special care in the mathematical formulation of the model. Smooth and strictly monotone friction laws guarantee a unique asymptotic behaviour. However, as we have shown with Example 3.4, in discrete models with viscous friction the velocity of the crawler converges to zero. This implies that, to effectively achieve locomotion, nonlinearities should be highly relevant in the dynamics: for smooth friction laws, this often corresponds to large velocity variations, which usually is not a realistic case. A natural way to introduce strong nonlinearities, also at low velocities, is to consider set-valued friction laws. While, as proved in Theorem 3.3, set-valued strictly monotone friction laws still produce an unique limit gait, the situation becomes more problematic in the case of dry friction, which is monotone, but not strictly. As we show with Examples 3.1 and 3.2, a shape change generated by a triangular wave might produce different asymptotical average velocity of the crawler, depending on the initial velocity. Uniqueness is instead recovered if the shape is continuously differentiable in time (Theorem 3.4) or in models with a continuous body (Theorem 4.3). While we do not expect this issue to arise in experimental observations (small viscosities are always present and shape changes will always be smooth), it becomes relevant on the theoretical side. Triangular waves are not only one of the easiest ways to define a periodic contraction-elongation cycle, but are also very likely to emerge as the solution of a control problem. Indeed, defining the control set in terms of derivatives of the shape, triangular waves in shape are produced by bang-bang controls. Such possibility must therefore be deliberately avoided when studying controllability or optimality problems on the limit cycles.

To better illustrate our contribution to the topic and possible future developments, we now make a brief comparison with the related results in [10, 14, 18]. In [18], the asymptotic behaviour of the discrete locomotor of Sect. 3 has been studied in the special case of continuous, autonomous, single-valued and strictly monotone friction forces, for a \(\mathcal {C}^1\) shape change, in the absence of external forces and for a more restrictive dissipative condition than (D4). We generalized all these assumptions and provided various examples on when they become sharp for the uniqueness of the limit behaviour. In particular, our results on dry friction show that monotonicity alone is not sufficient to prove sharp results on the uniqueness of the limit cycle, but the intrinsic structure of a crawling model (compared to a general periodically forced system) must also be exploited.

In such framework, [18] also discusses the rate of convergence of the system to the limit cycle characterizing the gait. We did not address this in our work, but the topic is certainly worth of further investigation. Indeed, we observe that, in the case of set-valued forces, and in particular of dry friction, the behaviour becomes more complex: we can observe finite-time convergence, possibly coexisting with asymptotic-only convergence for a different initial state (see e.g. Example 3.3). Such a coexistence in related problems with set-valued dissipation forces has been studied also in [8, 10, 24].

Two further directions of investigation are suggested by [14], which studies the locomotion on the plane of a tetrahedral crawler with elastic links. All friction forces in the model are viscous. The paper proved the stability of relative periodic solutions for a small actuation with perturbative methods starting from the (stable) steady state of a passive (i.e. non-actuated) crawler. Both a more complex geometry of the crawler and an elastic body imply that the asymptotic stabilization can no longer be reduced to a scalar problem, but has to be studied in a higher dimensional setting, where we expect a more complex phenomenology.

To make a comparison in the case of dry friction, which is the most valuable contribution in our work, a meaningful perspective comes from [10], where the analogous of our discrete models of Sect. 3 were studied assuming an elastic body, but only for dry friction at a quasistatic regime. At the quasistatic regime, an additional balance-breaking condition on the friction coefficients is necessary for the uniqueness of solution of the initial value problems (notice that the uniqueness argument of [20, Theorem 2.2] and [20, Example 3.2] can be straightforwardly adapted also to the case of prescribed shape). Yet, once uniqueness of solution is provided, uniqueness of the asymptotic average velocity of the crawler follows [10, Theorem 11]. In this work, we show instead that, at a dynamic regime, uniqueness of solutions always holds, but uniqueness of the asymptotic average velocity for a gait is true only for smooth inputs (Theorem 3.4).

We conclude highlighting, once more, how an intuitive concept such as the characterization of a gait as an asymptotic behaviour poses theoretical issues and open problems, even in simple models. We hope that our work will clarify this picture, encourage further investigations on the topic and support the study of more complex issues, such as optimal control, which, as explained, must be based on a well-posed notion of asymptotic behaviour.