Postbuckling behavior of functionally graded nanobeams subjected to thermal loading based on the surface elasticity theory

Abstract

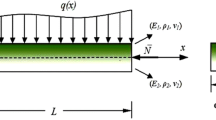
In the present investigation, an analytical solution is proposed to predict the postbuckling characteristics of nanobeams made of functionally graded materials which are subjected to thermal environment and surface stress effect. To this end, a non-classical beam model on the basis of Gurtin–Murdoch elasticity theory in the framework of Euler–Bernoulli beam theory and concept of physical neutral surface is utilized which has the capability to consider the effect of surface stress and von Karman-type of kinematic nonlinearity. The size-dependent nonlinear governing equations are solved analytically for different end supports. The postbuckling equilibrium paths corresponding to various boundary conditions are given in the presence of surface stress corresponding to various beam thicknesses, material gradient indexes, temperature changes and buckling mode numbers. It is found that by increasing the values of temperature change, the equilibrium path is shifted to right and the normalized applied axial load decreases indicating that the effect of surface stress diminishes.

Appendix

The resultant forces and bending moments corresponding to the bulk and surface parts can be introduced as

$$N_{xx} = A_{11} \left( {U_{0}^{{\prime }} + \frac{1}{2}\left( {W^{{\prime }} } \right)^{2} } \right) - B_{11} W^{{{\prime \prime }}} - N_{T} + \left( {\frac{{A_{44} \Delta \tau^{s} }}{2} + \frac{{B_{44} \bar{\tau }^{s} }}{h}} \right)W^{{{\prime \prime }}}$$

(27)

$$M_{xx} = B_{11} \left( {U_{0}^{{\prime }} + \frac{1}{2}\left( {W^{{\prime }} } \right)^{2} } \right) - D_{11} W^{{{\prime \prime }}} - M_{T} + \left( {\frac{{B_{44} \Delta \tau^{s} }}{2} + \frac{{D_{44} \bar{\tau }^{s} }}{h}} \right)W^{{{\prime \prime }}}$$

(28)

$$N_{xx}^{s} = \left( b \bar{\mathcal{A}}^{s} + 2A_{11}^{s} \right)\left( U_{0}^{\prime} + \frac{1}{2}\left( W^{\prime} \right)^{2} \right) - \left( \frac{bh}{2}\Delta {\mathcal{A}}^{s} + 2B_{11}^{s} \right)W^{\prime \prime } + \left( b \bar{\tau}^{s} + 2 \theta_{11}^{s} \right)\left( 1 - \frac{1}{2}\left( W^{\prime} \right)^{2} \right)$$

(29)

$$M_{xx}^{s} = \left( {\frac{bh}{2}\Delta {\mathcal{A}}^{s} + 2B_{11}^{s} } \right)\left( {U_{0}^{{\prime }} + \frac{1}{2}\left( {W^{{\prime }} } \right)^{2} } \right) - \left( {\frac{{bh^{2} }}{4}{\bar{\mathcal{A}}}^{s} + 2D_{11}^{s} } \right)W^{{{\prime \prime }}} + \left( {\frac{bh}{2}\Delta \tau^{s} + 2\theta_{22}^{s} } \right)\left( {1 - \frac{1}{2}\left( {W^{{\prime }} } \right)^{2} } \right)$$

(30)

in which

$$\bar{\tau }^{s} = \tau^{s + } + \tau^{s - } ,\quad\Delta \tau^{s} = \tau^{s + } - \tau^{s - } ,\quad{\bar{\mathcal{A}}}^{s} = \lambda^{s + } + 2\mu^{s + } + \lambda^{s - } + 2\mu^{s - } ,\quad\Delta {\mathcal{A}}^{s} = \lambda^{s + } + 2\mu^{s + } - \lambda^{s - } - 2\mu^{s - }$$

and

$$\left\{ {\begin{array}{*{20}c} {A_{11} } \\ {B_{11} } \\ {D_{11} } \\ \end{array} } \right\} = \mathop \int \limits_{A} \left( {\lambda + 2\mu } \right)\left\{ {\begin{array}{*{20}c} 1 \\ {\bar{z}} \\ {\bar{z}^{2} } \\ \end{array} } \right\}dA, \quad \left\{ {\begin{array}{*{20}c} {A_{44} } \\ {B_{44} } \\ {D_{44} } \\ \end{array} } \right\} = \mathop \int \limits_{A} \frac{\nu }{{\left( {1 - \nu } \right)}}\left\{ {\begin{array}{*{20}c} 1 \\ {\bar{z}} \\ {\bar{z}^{2} } \\ \end{array} } \right\}dA$$

(31)

$$\left\{ {\begin{array}{*{20}c} {A_{11}^{s} } \\ {B_{11}^{s} } \\ {D_{11}^{s} } \\ \end{array} } \right\} = \mathop \int \limits_{A} \left( {\lambda^{s} + 2\mu^{s} } \right)\left\{ {\begin{array}{*{20}c} 1 \\ {\bar{z}} \\ {\bar{z}^{2} } \\ \end{array} } \right\}dz,\quad \left\{ {\begin{array}{*{20}c} {\theta_{11}^{s} } \\ {\theta_{22}^{s} } \\ \end{array} } \right\} = \mathop \int \limits_{A} \tau^{s} \left\{ {\begin{array}{*{20}c} 1 \\ {\bar{z}} \\ \end{array} } \right\}dz,$$

(32)

Furthermore, the resultant thermal force can be defined as

$$N_{T} = \mathop\int \limits_{A} \beta \left( {T\left( z \right) - T_{0} } \right)dA,\quad M_{T} = \mathop \int \limits_{A} \beta \left( {T\left( z \right) - T_{0} } \right)\bar{z}dA$$

(33)

where U ₀ and W are the displacement of neutral axis in the x and lateral directions, respectively. Also, $\bar{z} = z - z_{0}$ and z ₀ denote the z coordinate associated with the physical neutral surface. Moreover, $\lambda = E\nu /\left( {1 - \nu^{2} } \right)$ and $\mu = E/\left( {2\left( {1 + \nu } \right)} \right)$ are Lame constants, $\beta = \alpha E/\left( {1 - \nu } \right)$ is the stress–temperature modulus and α is the thermal expansion coefficient, $\Delta T = T - T_{0}$, where Trepresents the temperature distribution through the FG beam and T ₀ is reference temperature. Moreover, it is noted that the position of neutral line z ₀ can be obtained by the following equation

$$z_{0} = \frac{{\mathop\int \nolimits_{A} z\left( {\lambda \left( z \right) + 2\mu \left( z \right)} \right)dA}}{{\mathop \int \nolimits_{A} \left( {\lambda \left( z \right) + 2\mu \left( z \right)} \right)dA}}$$

(34)

In this work, the initial uniform temperature (T ₀ = 300° K) is assumed to be a stress free state.