Skip to main content
SpringerLink
Log in

Nonlocal effects on the longitudinal vibration of a complex multi-nanorod system subjected to the transverse magnetic field

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

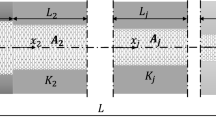
In this communication we examine the free longitudinal vibration of a complex multi-nanorod system (CMNRS) using the nonlocal elasticity theory. Discussion is limited to the cases of two types of boundary conditions, namely, clamped–clamped (C–C) and clamped–free (C–F), where nanorods are coupled in the “Free-Chain” system by an elastic medium. Each nanorod in CMNRS is subjected to the influence of transversal magnetic field. The longitudinal vibration of the system are described by a set of m partial differential equations, derived by using D’Alembert’s principle and classical Maxwell’s relation, which includes Lorentz magnetic force. Analytical expressions for the nonlocal natural frequencies are obtained in closed-form by using the method of separations of variables and trigonometric method. Results for the nonlocal natural frequencies are compared for the special cases of a single and double-nanorod system with the existing results in the literature. Numerical examples are given in order to examine the effects of nonlocal parameter, stiffness coefficient and transversal magnetic field on nonlocal natural frequencies of axially vibrating CMNRS.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Payton OD, Picco L, Miles MJ, Homer ME, Champneys AR (2012) Modeling oscillatory flexure modes of an atomic force microscope cantilever in contact mode whilst imaging at high speed. Nanotechnology 23(265702):1–7

    Google Scholar 

  2. Adhikari S, Chowdhury R (2012) Zeptogram sensing from gigahertz vibration: graphene based nanosensor. Physica E 44:1528–1534

    Article  ADS  Google Scholar 

  3. Calleja M, Kosaka PM, San Paulo A, Tamayo J (2012) Challenges for nanomechanical sensors in biological detection. Nanoscale 4:4925–4938

    Article  ADS  Google Scholar 

  4. Menicke O, Kaempfer D, Weickmann H, Friedrich C, Vathauer M, Warth H (2004) Mechanical properties and electrical conductivity of carbon-nanotube filled polyamide-6 and its blends with acrylonitrile/butadiene/styrene. Polymer 45(3):739–748

    Article  Google Scholar 

  5. Che JW, Cagin T, Goddard WA (2000) Thermal conductivity of carbon nanotubes. Nanotechnology 11:65–69

    Article  ADS  Google Scholar 

  6. Lin Q, Rosenberg J, Chang D, Camacho R, Eichenfield M, Vahala KJ, Painter O (2010) Coherent mixing of mechanical excitations in nano-optomechanical structures. Nat Photonics 4(4):236–242

    Article  ADS  Google Scholar 

  7. Arash B, Wang Q (2012) A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput Mater Sci 51:303–313

    Article  Google Scholar 

  8. Roque CMC, Fidalgo DS, Ferreira AJM, Reddy JN (2013) A study of a microstructure-dependent composite laminated Timoshenko beam using modified couple stress theory and a meshless method. Compos Struct 96:532–537

    Article  Google Scholar 

  9. Aifantis EC (2011) On the gradient approach–relation to Eringen’s nonlocal theory. Int J Eng Sci 49:1367–1377

    Article  MathSciNet  Google Scholar 

  10. Reddy JN (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48:1507–1518

    Article  MATH  Google Scholar 

  11. Lu P, Zhang PQ, Lee HP, Wang CM, Reddy JN (2007) Non-local plate theories. Proc R Soc A A463:3225–3240

    Article  ADS  MathSciNet  Google Scholar 

  12. Pradhan SC, Phadikar JK (2009) Nonlocal elasticity theory for vibration of nanoplates. J Sound Vib 325:206–223

    Article  ADS  Google Scholar 

  13. Lei Y, Adhikari S, Frishwell MI (2013) Vibration of nonlocal Kelvin–Voigt viscoelastic damped Timoshenko beams. Int J Eng Sci 66–67:1–13

    Article  Google Scholar 

  14. Narendar S, Gopalakrishnan S (2012) Scale effects on buckling analysis of orthotropic nanoplates based on nonlocal two-variable refined plate theory. Acta Mech 223:395–413

    Article  MATH  MathSciNet  Google Scholar 

  15. Hosseini-Hashemi S, Nahas I, Fakher M, Nazemnezhad R (2014) Surface effects on free vibration of piezoelectric functionally graded nanobeams using nonlocal elasticity. Acta Mech 225(6):1555–1564

  16. Kozić P, Pavlović R, Karličić D (2014) The flexural vibration and buckling of the elastically connected parallel-beams with a Kerr-type layer in between. Mech Res Commun 56:83–89

    Article  Google Scholar 

  17. Ansari R, Rajabiehfard R, Arash B (2010) Nonlocal finite element model for vibrations of embedded multi-layered graphene sheets. Comput Mater Sci 49(4):831–838

    Article  Google Scholar 

  18. Manevich A, Kolakowski Z (2011) Free and forced oscillations of Timoshenko beam made of viscoelastic material. J Theor Appl Mech 49:3–16

    Google Scholar 

  19. Oniszczuk Z (2011) Free transverse vibrations of an elastically connected complex beam-string system. J Theor Appl Mech 49:3–16

    Google Scholar 

  20. Oniszczuk Z (2003) Forced transverse vibrations of an elastically connected complex double-beam system. J Sound Vib 264:273–286

    Article  ADS  Google Scholar 

  21. Kelly SG, Srinivas S (2009) Free vibrations of elastically connected stretched beams. J Sound Vib 326:883–893

    Article  ADS  Google Scholar 

  22. Rašković D (1953) On some characteristics of the frequency equation of torsional vibrations of light shafts with several disks. Publications de l’Institut Mathématique V (05) 155–164. http://elib.mi.sanu.ac.rs/files/journals/publ/11/16.pdf

  23. Rašković D (1957) Uber die eigenschaften der frequenzgleichungen eines schwingenden systems. Z Angew Math Mech 37:278–279. doi:10.1002/zamm.19570370729

    Article  MATH  Google Scholar 

  24. Stojanović V, Kozić P, Janevski G (2013) Exact closed-form solutions for the natural frequencies and stability of elastically connected multiple beam system using Timoshenko and high-order shear deformation theory. J Sound Vib 332:563–576

    Article  ADS  Google Scholar 

  25. Karličić D, Kozić P, Pavlović R (2014) Free transverse vibration of nonlocal viscoelastic orthotropic multi-nanoplate system (MNPS) embedded in a viscoelastic medium. Compos Struct 115:89–99

    Article  Google Scholar 

  26. Karličić D, Adhikari S, Murmu T, Cajić M (2014) Exact closed-form solution for non-local vibration and biaxial buckling of bonded multi-nanoplate system. Compos B Eng 66:328–339

    Article  Google Scholar 

  27. Rossikhin YA, Shitikova MV (2010) Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl Mech Rev 63(010801):1–52

    Google Scholar 

  28. Lao JY, Wen JG, Ren ZF (2012) Hierarchical ZnO nanostructures. Nano Lett 2(11):1287–1291

    Article  ADS  Google Scholar 

  29. Xing YJ, Xi ZH, Xue ZQ, Zhang XD, Song JH, Wang RM, Xu J, Song Y, Zhang SL, Yu DP (2003) Optical properties of the ZnO nanotubes synthesized via vapor phase growth. Appl Phys Lett 83(9):1689–1691

    Article  ADS  Google Scholar 

  30. Liu B, Zeng HC (2003) Hydrothermal synthesis of ZnO nanorods in the diameter regime of 50 nm. J Am Chem Soc 125:4430–4431

    Article  Google Scholar 

  31. Park WI, Kim DH, Jung S-W, Yi G-C (2002) Metalorganic vapor-phase epitaxial growth of vertically well-aligned ZnO nanorods. Appl Phys Lett 80:4232–4234

    Article  ADS  Google Scholar 

  32. Duan WH, Wang CM, Zhang YY (2007) Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J Appl Phys 101(024305):1–7

    Google Scholar 

  33. Arash B, Ansari R (2010) Evaluation of nonlocal parameter in the vibrations of single-walled carbon nanotubes with initial strain. Physica E 42:2058–2064

    Article  ADS  Google Scholar 

  34. Danesh M, Farajpour A, Mohammadi M (2012) Axial vibration analysis of a tapered nanorod based on nonlocal elasticity theory and differential quadrature method. Mech Res Commun 39:23–27

    Article  MATH  Google Scholar 

  35. Aydogdu M (2012) Axial vibration analysis of nanorods (carbon nanotubes) embedded in an elastic medium using nonlocal elasticity. Mech Res Commun 43:34–40

    Article  Google Scholar 

  36. Narendar S, Gopalakrishnan S (2011) Axial wave propagation in coupled nanorod system with nonlocal small scale effects. Mech Res Commun Compos Part B Eng 42:2013–2023

    Article  Google Scholar 

  37. Hsu J-C, Lee H-L, Chang W-J (2011) Longitudinal vibration of cracked nanobeams using nonlocal elasticity theory. Curr Appl Phys 11:1384–1388

    Article  ADS  Google Scholar 

  38. Kiani K (2013) Longitudinal, transverse, and torsional vibrations and stabilities of axially moving single-walled carbon nanotubes. Curr Appl Phys 13:1651–1660

    Article  ADS  Google Scholar 

  39. Şimşek M (2012) Nonlocal effects in the free longitudinal vibration of axially functionally graded tapered nanorods. Comput Mater Sci 61:257–265

    Article  Google Scholar 

  40. Huang Z (2012) Nonlocal effects of longitudinal vibration in nanorod with internal long-range interactions. Int J Solids Struct 49:2150–2154

    Article  Google Scholar 

  41. Chang T-P (2012) Small scale effect on axial vibration of non-uniform and non-homogeneous nanorods. Comput Mater Sci 54:23–27

    Article  Google Scholar 

  42. Filiz S, Aydogdu M (2010) Axial vibration of carbon nanotube heterojunctions using nonlocal elasticity. Comput Mater Sci 49:619–627

    Article  Google Scholar 

  43. Karličić D, Cajić M, Murmu T, Adhikari S (2014) Nonlocal longitudinal vibration of viscoelastic coupled double-nanorod systems. Eur J Mech Solids. doi:10.1016/j.euromechsol.2014.07.005

    Google Scholar 

  44. Murmu T, Adhikari S (2010) Nonlocal effects in the longitudinal vibration of double-nanorod systems. Physica E 43:415–422

    Article  ADS  Google Scholar 

  45. Murmu T, McCarthy MA, Adhikari S (2013) In-plane magnetic field affected transverse vibration of embedded single-layer graphene sheets using equivalent nonlocal elasticity approach. Compos Struct 96:57–63

    Article  Google Scholar 

  46. Kiani K (2014) Vibration and instability of a single-walled carbon nanotube in a three-dimensional magnetic field. J Phys Chem Solids 75(1):15–22

    Article  MathSciNet  Google Scholar 

  47. Murmu T, McCarthy MA, Adhikari S (2012) Nonlocal elasticity based magnetic field affected vibration response of double single-walled carbon nanotube systems. J Appl Phys 111(113511):1–7

    Google Scholar 

  48. Murmu T, McCarthy MA, Adhikari S (2012) Vibration response of double-walled carbon nanotubes subjected to an externally applied longitudinal magnetic field: a nonlocal elasticity approach. J Sound Vib 331(23):5069–5086

    Article  ADS  Google Scholar 

  49. Arani AG, Maboudi MJ, Arani AG, Amir S (2013) 2D-magnetic field and biaxiall in-plane pre-load effects on the vibration of double bonded orthotropic graphene sheets. J Solid Mech 5(2):193–205

    Google Scholar 

  50. Narendar S, Gupta SS, Gopalakrishnan S (2012) Wave propagation in single-walled carbon nanotube under longitudinal magnetic field using nonlocal Euler–Bernoulli beam theory. Appl Math Model 36(9):4529–4538

    Article  MATH  MathSciNet  Google Scholar 

  51. Kiani K (2014) Elastic wave propagation in magnetically affected double-walled carbon nanotubes. Meccanica. doi:10.1007/s11012-014-9957-2

    Google Scholar 

  52. Kiani K (2014) Magnetically affected single-walled carbon nanotubes as nanosensors. Mech Res Commun 60:33–39

    Article  ADS  Google Scholar 

  53. Kiani K (2014) Longitudinally varying magnetic field influenced transverse vibration of embedded double-walled carbon nanotubes. Int J Mech Sci 87:179–199

    Article  Google Scholar 

  54. Murmu T, Adhikari S, McCarthy MA (2014) Axial vibration of embedded nanorods under transverse magnetic field effects via nonlocal elastic continuum theory. J Comput Theor Nanosci 11(5):1230–1236

    Article  Google Scholar 

  55. Eringen CA (1972) Nonlocal polar elastic continua. Int J Eng Sci 10:11–16

    Google Scholar 

  56. Eringen CA (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54:4703–4710

    Article  ADS  Google Scholar 

  57. Murmu T, Adhikari S (2011) Nonlocal vibration of carbon nanotubes with attached buckyballs at tip. Mech Res Commun 38(1):62–67

    Article  MATH  Google Scholar 

  58. Cao G, Chen X, Kysar JW (2006) Thermal vibration and apparent thermal contraction of single-walled carbon nanotubes. J Mech Phys Solids 54:1206–1236

    Article  ADS  MATH  Google Scholar 

Download references

Acknowledgments

This research was supported by the research grants of the Serbian Ministry of Education, Science and Technological Development under the numbers ON 174001 and ON 174011.

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, University of Niš, A. Medvedeva 14, 18000, Nis, Serbia

    Danilo Karličić & Predrag Kozić

  2. Mathematical Institute, Serbian Academy of Sciences and Arts, Kneza Mihaila 36, 11001, Belgrade, Serbia

    Milan Cajić

  3. School of Engineering, University of the West of Scotland, Paisley, PA1 2BE, UK

    Tony Murmu

  4. College of Engineering, Swansea University, Singleton Park, Swansea, SA2 8PP, UK

    Sondipon Adhikari

Authors
  1. Danilo Karličić
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Milan Cajić
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tony Murmu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Predrag Kozić
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Sondipon Adhikari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Danilo Karličić.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Karličić, D., Cajić, M., Murmu, T. et al. Nonlocal effects on the longitudinal vibration of a complex multi-nanorod system subjected to the transverse magnetic field. Meccanica 50, 1605–1621 (2015). https://doi.org/10.1007/s11012-015-0111-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-015-0111-6

Keywords

Search

Navigation