Explicit solutions for multi-layered wide plates and beams with perfect and imperfect bonding and delaminations under thermo-mechanical loading

Abstract

Explicit expressions, for efficient application in engineering practice, are derived for generalized displacements and stresses in simply supported multi-layered wide plates and beams subjected to steady-state thermal and mechanical loading. The expressions are general and apply to plates composed of an arbitrary number of layers, of arbitrary thickness and elastic/thermal properties, and where the interfaces between the layers may be imperfect and allow relative sliding. The closed-form solutions are obtained using a multiscale homogenized model which depends on only three displacement variables and overcomes limitations of current models based on discrete-layer approaches. The accuracy of the expressions in predicting the highly complex and discontinuous fields, which characterize the response of thick and highly anisotropic plates with interlayer damage and delaminations, is verified using exact 2D thermo-elasticity solutions. The asymptotic limits of the model/solution correspond to the problems of an intact and a multiply delaminated plate. They are derived using a perturbation technique, which also explains the multiscale dependence of the model on the parameters.

Appendices

Appendix 1: Thermo-mechanical equilibrium equations

1.1 Uncoupled homogenized equilibrium equations

$$ \begin{aligned} & w_{{0,222222}} - aw_{{0,2222}} \\ & \quad + \left\{ {b_{1} \left( {f_{3} + f_{{2m,2}} - \frac{{C_{{22}}^{1} }}{{C_{{22}}^{0} }}f_{{2,2}} } \right) - \left( {b_{2} + b_{3} } \right)f_{{3,22}} + \left( {\frac{{b_{2} C_{{22}}^{1} - b_{3} C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}} \right)f_{{2,222}} - b_{2} f_{{2m,222}} } \right\} \\ & \quad - \left\{ {b_{1} \left( {M_{{22,22}}^{{bT}} - \frac{{C_{{22}}^{1} }}{{C_{{22}}^{0} }}N_{{22,22}}^{T} } \right) + b_{3} \left( {M_{{22}}^{{zT}} + M_{{22}}^{{ST}} } \right)_{{,2222}} } \right. \\ & \quad + \left. {\left( {\frac{{b_{2} C_{{22}}^{1} - b_{3} C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}} \right)N_{{22,2222}}^{T} - b_{2} M_{{22,2222}}^{{bT}} } \right\} = 0 \\ \end{aligned} $$

(62)

$$ \begin{aligned} \varphi_{2,2} & = - w_{0,22} + \frac{1}{ac}\,w_{0,2222} - \frac{1}{ac}\left\{{(b_{2} + b_{3})\;f_{3} - \left({\frac{{b_{2} C_{22}^{1} - b_{3} C_{22}^{0S}}}{{C_{22}^{0}}}} \right)f_{2,2} + \;b_{2} f_{2m,2}} \right\}\\ & \quad + \frac{1}{ac}\left\{{- b_{3} \left({M_{22,22}^{zT} + M_{22,22}^{ST}} \right) - \left({\frac{{b_{2} C_{22}^{1} - b_{3} C_{22}^{0S}}}{{C_{22}^{0}}}} \right)N_{22,22}^{T} + b_{2} M_{22,22}^{bT}} \right\} \\ \end{aligned} $$

(63)

$$ \begin{aligned} v_{{02,22}} & = \frac{{C_{{22}}^{1} }}{{C_{{22}}^{0} }}w_{{0,222}} - \frac{{C_{{22}}^{1} + C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}\frac{1}{{ac}}w_{{0,22222}} - \frac{1}{{C_{{22}}^{0} }}f_{2} \\ & \quad + \frac{{C_{{22}}^{1} + C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}\frac{1}{{ac}}\left\{ {(b_{2} + b_{3} )f_{{3,2}} - \left( {\frac{{b_{2} C_{{22}}^{1} - b_{3} C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}} \right)f_{{2,22}} + b_{2} f_{{2m,22}} } \right\} + \frac{1}{{C_{{22}}^{0} }}N_{{22,2}}^{T} \\ & \quad \left. { - \frac{{C_{{22}}^{1} + C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}\frac{1}{{ac}}\left\{ { - b_{3} \left( {M_{{22,222}}^{{zT}} + M_{{22,222}}^{{ST}} } \right) - \left( {\frac{{b_{2} C_{{22}}^{1} - b_{3} C_{{22}}^{{0S}} }}{{C_{{22}}^{0} }}} \right)N_{{22,222}}^{T} } \right. + b_{2} M_{{22,222}}^{{bT}} } \right\} \\ \end{aligned} $$

(64)

1.2 Geometrical and mechanical boundary conditions

$$ \delta v_{02} : \left[{v_{02,2} C_{22}^{0} + \varphi_{2,2} \left({C_{22}^{1} + C_{22}^{0S}} \right) + w_{0,22} C_{22}^{0S} - N_{22}^{T}} \right]n_{2} = \tilde{N}_{2}^{B} \,\,\text{or}\,\, v_{02} = \tilde{v}_{02} $$

(65)

$$ \begin{aligned} \delta w_{0} :\left\{{- v_{02,22} C_{22}^{0S} - \varphi_{2,22} \left({C_{22}^{1S} + C_{22}^{S2}} \right) + \left({w_{0,2} + \varphi_{2}} \right)\left[{K^{2} C_{55}^{P} + C_{22}^{S}} \right]} \right. \hfill \\ \left. {- w_{0,222} C_{22}^{S2} + C_{22}^{C} + \left({M_{22,2}^{zT} + M_{22,2}^{ST}} \right) - f_{2mbc}} \right\}n_{2} = \tilde{N}_{3}^{B} \,\;{\text{or}}\;\,w_{0} = \tilde{w}_{0} \hfill \\ \hfill \\ \end{aligned} $$

(66)

$$ \delta \varphi_{2} : \left[{v_{02,2} C_{22}^{1} + \varphi_{2,2} \left({C_{22}^{2} + C_{22}^{1S}} \right) + w_{0,22} C_{22}^{1S} - M_{22}^{bT}} \right]n_{2} = \tilde{M}_{2}^{bB} \,\,\text{or}\,\, \varphi_{2} = \tilde{\varphi}_{2} $$

(67)

$$ \delta w_{0,2} : \left[{v_{02,2} C_{22}^{0S} + \varphi_{2,2} \left({C_{22}^{1S} + C_{22}^{S2}} \right) + w_{0,22} C_{22}^{S2} - \left({M_{22}^{zT} + M_{22}^{ST}} \right)} \right]n_{2} = \tilde{M}_{2}^{zB} + \tilde{M}_{2}^{SB} \,\text{or}\, w_{0,2} = \tilde{w}_{0,2} $$

(68)

Additional condition needed to define the constants of integration when using the uncoupled Eqs. (62)–(64):

$$ \begin{aligned} \left({C_{22}^{1} + C_{22}^{0S}} \right)\,v_{02,22} + \left({C_{22}^{2} + 2C_{22}^{1S} + C_{22}^{S2}} \right)\,\varphi_{2,22} + \left({C_{22}^{1S} + C_{22}^{S2}} \right)\,w_{0,222} + \hfill \\ - \left({K^{2} \;C_{55}^{P} + C_{22}^{S}} \right)\left({\varphi_{2} + w_{0,2}} \right) - C_{22}^{C} + f_{2m} = M_{22,2}^{bT} + M_{22,2}^{zT} + M_{22,2}^{ST} \end{aligned} $$

(69)

1.3 Coefficients: geometry, layup, status of the interfaces

$$ C_{22}^{r} = \sum\limits_{k = 1}^{n} {{}^{\left(k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {\left({x_{3}} \right)^{r} dx_{3}}}, $$

(70)

$$ C_{22}^{rS} = \sum\limits_{k = 1}^{n} {{}^{\left(k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {\left({x_{3}} \right)^{r} R_{S22}^{k} dx_{3}}}, $$

(71)

$$ C_{22}^{S2} = \sum\limits_{k = 1}^{n} {{}^{\left(k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {\left({R_{S22}^{k}} \right)^{2} dx_{3}}} $$

(72)

$$ C_{22}^{S} = \sum\limits_{k = 1}^{n - 1} {{{\left({\Psi_{22}^{k}} \right)^{2}} \mathord{\left/{\vphantom {{\left({\Psi_{22}^{k}} \right)^{2}} {B_{S}^{k}}}} \right. \kern-0pt} {B_{S}^{k}}}} $$

(73)

$$ C_{55}^{P} = \sum\limits_{k = 1}^{n} {{}^{(k)}C_{55}^{{}} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {\left({1 + \sum\limits_{i = 1}^{k - 1} {\Lambda_{22}^{{\left({1;i} \right)}}}} \right)^{2}} dx_{3}} $$

(74)

$$ C_{22}^{C} = \mathop \sum \limits_{k = 1}^{n - 1} \,t_{S}^{(k)} \,\Psi_{22}^{(k)} $$

(75)

$$ a = \frac{{\left({K^{2} C_{55}^{P} + C_{22}^{S}} \right)\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)\,^{2}} \right]C_{22}^{0}}}{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S} \,} \right)^{2}} \right]\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)\,^{2}} \right] - \left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right)^{2}}} $$

(76)

$$ b_{1} = \frac{{\left({K^{2} C_{55}^{P} + C_{22}^{S}} \right)\left({C_{22}^{0}} \right)^{2}}}{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S}} \right)^{2}} \right]\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right] - \left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right)^{2}}} $$

(77)

$$ b_{2} = \frac{{\left\{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S}} \right)\,^{2}} \right] + \left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right)} \right\}C_{22}^{0}}}{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S}} \right)\,^{2}} \right]\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right] - \left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right)^{2}}} $$

(78)

$$ b_{3} = \frac{{\left\{{\left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right) + \left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right]} \right\}C_{22}^{0}}}{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S}} \right)^{2}} \right]\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right] - \left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right)^{2}}} $$

(79)

$$ c = \frac{{\left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right) + \left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right]}}{{\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right]}} $$

(80)

$$ d = \frac{a}{{b_{1}}} = \frac{{\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right]}}{{C_{22}^{0}}} $$

(81)

$$ \frac{1}{ac} = \frac{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S}} \right)^{2}} \right]\left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right] - \left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right)^{2}}}{{\left({K^{2} C_{55}^{P} + C_{22}^{S}} \right)C_{22}^{0} \,\left\{{\left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right) + \left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right]} \right\}}} $$

(82)

$$ \frac{{b_{2} + b_{3}}}{a} = \frac{{\left[{C_{22}^{S2} C_{22}^{0} - \left({C_{22}^{0S}} \right)^{2}} \right] + 2\left({C_{22}^{0} C_{22}^{1S} - C_{22}^{1} C_{22}^{0S}} \right) + \left[{C_{22}^{2} C_{22}^{0} - \left({C_{22}^{1}} \right)^{2}} \right]}}{{\left({K^{2} C_{55}^{P} + C_{22}^{S}} \right)\left({C_{22}^{2} C_{22}^{0} - (C_{22}^{1})\,^{2}} \right)}} $$

(83)

1.4 Coefficients: thermal loads

$$ N_{22}^{T} = \sum\limits_{k = 1}^{n} {{}^{\left(k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{(k)}\tilde{\varepsilon}_{22}^{t}} dx_{3}}, $$

(84)

$$ M_{22}^{bT} = \sum\limits_{k = 1}^{n} {{}^{\left( k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1} }}^{{x_{3}^{k} }} {{}^{(k)}\tilde{\varepsilon }_{22}^{t} } x_{3} dx_{3} } $$

(85)

$$ M_{22}^{ST} = \sum\limits_{k = 1}^{n} {{}^{\left(k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{(k)}\tilde{\varepsilon}_{22}^{t} \sum\limits_{i = 1}^{k - 1} {\Psi_{22}^{i}}} dx_{3}}, $$

(86)

$$ M_{22}^{zT} = \sum\limits_{k = 1}^{n} {{}^{\left(k \right)}\bar{C}_{22} \int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{(k)}\tilde{\varepsilon}_{22}^{t}} \sum\limits_{i = 1}^{k - 1} {\Lambda_{22}^{{\left({1;i} \right)}} \left({x_{3} - x_{3}^{i}} \right)} dx_{3}} $$

(87)

1.5 Coefficients: prescribed forces and moments at the plate ends

$$ \tilde{N}_{i}^{B} = \sum\limits_{k = 1}^{n} {\int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{\left(k \right)}F_{i}^{B}} dx_{3}},\quad {\text{for}}\;i = 2,3\quad \tilde{M}_{2}^{bB} = \sum\limits_{k = 1}^{n} {\int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{\left(k \right)}F_{2}^{B} x_{3}} dx_{3}}, $$

$$ \tilde{M}_{2}^{SB} = \sum\limits_{k = 1}^{n} {\int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{\left(k \right)}F_{2}^{B} \sum\limits_{i = 1}^{k - 1} {\Psi_{22}^{i}} d} x_{3}},\quad \tilde{M}_{2}^{zB} = \sum\limits_{k = 1}^{n} {\int_{{x_{3}^{k - 1}}}^{{x_{3}^{k}}} {{}^{\left(k \right)}F_{2}^{B} \sum\limits_{i = 1}^{k - 1} {\Lambda_{22}^{{\left({1;i} \right)}} \left({x_{3} - x_{3}^{i}} \right)}} dx_{3}}, $$

$$ f_{2mbc} = F_{2}^{S +} \left. {R_{S22}^{n}} \right|_{{x_{3}^{n}}} $$

(88)

1.6 Order of the coefficients in the asymptotic limits of fully bonded and fully debonded plates

The coefficients of the differential Eqs. (62)–(64) and (32)–(34) can be expanded into power series of $\delta$. The tables below defines the dominant orders of the coefficients in the two asymptotic limits.

Table 1 Fully bonded multilayered plate, $\delta = 1/K_{S}^{k}\,<\!\!< 1$ for $k = 1,\ldots,n - 1$

Table 2 Fully bonded unidirectionally reinforced plate, $\delta = 1/K_{S}^{k}\, <\!\!< 1$ for $k = 1,\ldots,n - 1$

Table 3 Fully debonded plate, $\delta = K_{S}^{i} \,<\!\!< 1$ for at least one interface i

Appendix 2: Explicit solution for simply supported plate subjected to sinusoidal transverse load

In a simply supported plate subjected to a sinusoidal transverse load, $f_{3} (x_{2}) = q_{m} \sin \left({px_{2}} \right)$, with $p = m\pi/L$ and $m \in {\mathbb{N}}$, Fig. (3a), the generalized displacements are:

(89)

$$ \begin{aligned}{\varphi }_{2} (x_{2} ) = -\frac{{q_{m} }}{{p^{3} d}}\left\{ 1 + \left[ 1 + \left( c-1 \right)\left( {b_{2} + b_{3}} \right)d \right]\frac{{p^{2} }}{ac} \right\}\left( {1 + \frac{{p^{2} }}{a}} \right)^{ - 1} {\cos \left( {px_{2} } \right)} \end{aligned} $$

(90)

$$ \begin{aligned} v_{02} (x_{2} ) & = \frac{{q_{m} }}{{p^{3} d}}\left\{ {\frac{{C_{22}^{1} }}{{C_{22}^{0} }} + \left[ {\frac{{C_{22}^{1} + C_{22}^{0S} + \left( {cC_{22}^{1} - C_{22}^{1} - C_{22}^{0S} } \right)\left( {b_{2} + b_{3} } \right)d}}{{C_{22}^{0} }}} \right]\frac{{p^{2} }}{ac}} \right\} \\ & \left( {1 + \frac{{p^{2} }}{a}} \right)^{ - 1} \left[ {\cos \left( {px_{2} } \right) - 1} \right] \\ \end{aligned} $$

(91)

Appendix 3: Asymptotic limits of the macro-scale generalized displacements in simply supported plates

3.1 Uniform transverse load: fully bonded limit

When $\delta = 1/K_{S}^{k} \to 0$ for $k = 1,\ldots,n - 1$, $1/a \to 0$, $d = O(1) = \bar{C}_{22} h^{3}/12$, $C_{22}^{1}/C_{22}^{0} = O(1)$ and the zero order expansions of the other coefficients in the solutions (35)–(37) are finite and given by $\mathop c\limits^{0} = 1$ and $\mathop {[(b_{2} + b_{3})/(ac)]}\limits^{0} = 1/(K^{2} C_{55} h)$. In the zero-order expansion in integral powers of $\delta = 1/K_{S}^{k}$ of Eqs. (35)–(37), the terms with the hyperbolic functions vanish and the two terms with the curved line on top cancel each other, . The zero-order expansion define the global displacements, which coincide with the solution of classical first order shear deformation single-layer theory. The resulting zero-order displacements are:

$$ {\mathop {w}\limits^{0}}_{0} (x_{2} ) = \frac{{qL^{4} }}{{2\bar{C}_{22} h^{3} }}\left[ {\frac{{x_{2} }}{L}\left( {1 - \frac{{x_{2} }}{L}} \right)\left( {1 + \frac{{x_{2} }}{L} - \left( {\frac{{x_{2} }}{L}} \right)^{2} } \right)} \right] + \frac{{qL^{2} }}{{2K^{2} C_{55} h}}\frac{{x_{2} }}{L}\left( {1 - \frac{{x_{2} }}{L}} \right) $$

(92)

$$ {\mathop {\varphi }\limits^{0}}_{2} (x_{2} ) = \frac{{qL^{3} }}{{2\bar{C}_{22} h^{3} }}\left[ {\left( {1 + 2\frac{{x_{2} }}{L} - 2\left( {\frac{{x_{2} }}{L}} \right)^{2} } \right)\left( {\frac{{2x_{2} }}{L} - 1} \right)} \right] $$

(93)

$$ {\mathop {v }\limits^{0}}_{02} (x_{2} ) = \frac{{qL^{3} }}{{\bar{C}_{22} h^{3} }}\frac{{C_{22}^{1} }}{{C_{22}^{0} }}\left( {\frac{{x_{2} }}{L}} \right)^{2} \left( {\frac{{2x_{2} }}{L} - 3} \right) $$

(94)

The maximum deflection at $x_{2} = L/2$ is ${\mathop {w}\limits^{0}}_{0} (x_{2} = L/2) = \frac{{5qL^{4} }}{{32\bar{C}_{22} h^{3} }} + \frac{{qL^{2} }}{{8K^{2} C_{55} h}}$ with $\bar{C}_{22}$ the reduced longitudinal stiffness, Eq. (1).

3.2 Uniform transverse load: fully debonded limit

When $\delta = K_{S}^{i} \to 0$ for at least one interface i, the finite coefficients in the solutions (35)–(37) are $a \to 0$, $b_{3} \to 0$, $d = O(1)$, $C_{22}^{1},C_{22}^{0} = O(1)$, $1/(ac) \to \mathop {1/(ac)}\limits^{0}$, $b_{2} \to {\mathop {b}\limits^{0}}_{2}$, $C_{22}^{0S}/c \to \mathop {\left({C_{22}^{0S}/c} \right)}\limits^{0}$; while $c \to \infty$ is unbounded. The zero- and first-order terms of the expansion in integral power of $\delta$ of Eqs. (35)–(37), define the global displacements and the small-scale enrichments, respectively. Up to a rigid longitudinal translation, which depend on the position of the assumed reference surface and vanishes when $x_{3}^{0} = - {}^{(1)}h/2$, the first order expansions , $\varphi_{2} = {\mathop \varphi \limits^{0}}_{2}$ and $v_{02} = {\mathop v\limits^{0}}_{02}$, define the generalized displacements of a stack of Timoshenko beams free to slide over each other: ${\mathop w\limits^{0}}_{0}$, ${\mathop \varphi \limits^{0}}_{2}$ and ${\mathop v\limits^{0}}_{02}$ are the solutions of classical Euler–Bernoulli single-layer theory; accounts for shear deformations. The first-order expansions $w_{0} = {\mathop {w}\limits^{0}}_{0} + \delta {\mathop {w}\limits^{1}}_{0}$ and $\varphi_{2} = {\mathop {\varphi}\limits^{0}}_{2} + \delta {\mathop {\varphi}\limits^{1}}_{2}$ are instead needed to derive the longitudinal displacements in the layers and to fully describe the small-scale behavior (jumps, stresses and displacements in the layers) using Eqs. (5), (11), (38) and (40). The expansions are:

(95)

$$ {\mathop w\limits^{1}}_{0} (x_{2})\delta = - \left[{\frac{{q L^{6}}}{240} \left({\mathop {b_{2}}\limits^{0} - \frac{1}{d}} \right) \left({\frac{{x_{2}}}{L} - \frac{5}{3}\left({\frac{{x_{2}}}{L}} \right)^{3} + \left({\frac{{x_{2}}}{L}} \right)^{5} - \frac{1}{3}\left({\frac{{x_{2}}}{L}} \right)^{6}} \right)} \right][\mathop a\limits^{1}]\delta $$

(96)

$$ {\mathop \varphi \limits^{0}}_{2} (x_{2}) = \frac{{q L^{3}}}{24}\mathop {b_{2}}\limits^{0} \left({1 + 2\frac{{x_{2}}}{L} - 2\left({\frac{{x_{2}}}{L}} \right)^{2}} \right) \left({\frac{{2 x_{2}}}{L} - 1} \right) $$

(97)

$$ {\mathop \varphi \limits^{1}}_{2} (x_{2})\delta = - \left({\mathop {b_{2}}\limits^{0} - \frac{1}{d}} \right)\left({\frac{{2 x_{2}}}{L} - 1} \right)\left[{\frac{{q L^{3}}}{24}\mathop {\left(\frac{1}{ac} \right)}\limits^{0} \left({1 + 2\frac{{x_{2}}}{L} - 2\left({\frac{{x_{2}}}{L}} \right)^{2}} \right) + \frac{{q L^{5}}}{240} \left({1 + \frac{{x_{2}}}{L} - \left({\frac{{x_{2}}}{L}} \right)^{2}} \right)^{2} } \right][\mathop a\limits^{1}]\delta $$

(98)

$$ {\mathop v\limits^{0}}_{02} (x_{2}) = - \frac{{q L^{3}}}{6}\left[{\mathop {b_{2}}\limits^{0} \frac{{C_{22}^{1}}}{{C_{22}^{0}}} + \left({\frac{1}{d} - \mathop {b_{2}}\limits^{0}} \right)\left({\mathop {\frac{{C_{22}^{0S}}}{{c C_{22}^{0}}}}\limits^{0}} \right)} \right]\left({\frac{{x_{2}}}{L}} \right)^{2} \left({\frac{3}{2} - \frac{{x_{2}}}{L}} \right) $$

(99)

where $1/{\mathop {b}\limits^{0}}_{2}$ is the flexural stiffness of the layer assembly ($1/{\mathop {b}\limits^{0}}_{2} \to h^{3} \bar{C}_{22}/(12 n^{2})$ in a unidirectionally reinforced laminate with n equal thickness fully delaminated layers).

The maximum deflection at $x_{2} = L/2$ is ${\mathop w\limits^{0}}_{0} (x_{2} = L/2) = \frac{{5{\mathop {b}\limits^{0}}_{2} q L^{4}}}{384} + \frac{{q L^{2}}}{{8K^{2} C_{55} h}}$ which becomes ${\mathop w\limits^{0}}_{0} (x_{2} = L/2) = \frac{{5q L^{4} }}{{32 \bar{C}_{22} h^{3} }} + \frac{{q L^{2} }}{{8K^{2} C_{55} h}}$ in a plate with n equal thickness layers.

The need of using the first order expansions of the transverse displacement and rotation to define the small-scale behavior is made clear by looking at the asymptotic expansion of Eq. (11) $\hat{v}_{2}^{k} = \mathop {\hat{v}_{2}^{k} }\limits^{0} + O(\delta ) = \left[ {\left( {{\mathop {w }\limits^{0}}_{0,2} + {\mathop {\varphi }\limits^{0} }}_{2} \right) + \left( {{\mathop {w}\limits^{1}}_{0,2} + {\mathop {\varphi }\limits^{1} }}_{2} \right)\delta } \right]B_{S}^{k} \left( {1 + \sum\limits_{j = 1}^{k} {\Lambda_{22}^{{\left( {1;j} \right)}} } } \right)\,{}^{{\left( {k + 1} \right)}}{C_{55} }+ O(\delta )$; the term $({\mathop w\limits^{0} }_{0,2} + {\mathop \varphi \limits^{0} }_{2}) = 0$, after Eqs. (96) and (97); then, since $\delta = 1/B_{S}^{k}$, the zero order expansion of the jump is finite and given by $\mathop {\hat{v}_{2}^{k}}\limits^{0} = \left({{\mathop w\limits^{1} }_{0,2} + {\mathop \varphi \limits^{1} }_{2}} \right)\left({1 + \sum\limits_{j = 1}^{k} {\Lambda_{22}^{{\left({1;j} \right)}}}} \right){}^{{\left({k + 1} \right)}}C_{55}$.

3.3 Uniform thermal load: fully debonded limit

When $\delta = K_{S}^{i} \to 0$ for at least one interface i, the finite coefficients in the solutions (41)–(43) are $a \to 0$, $d = O(1)$, $C_{22}^{1},C_{22}^{0} = O(1)$, ${{C_{22}^{0S}}/ {c \to \mathop {\left({C_{22}^{0S}/c} \right)}\limits^{0}}}$; while $c \to \infty$ is unbounded. As explained above for the asymptotic limit of the case with uniform transverse load, the zero- and first-order terms of the expansion in integral power of $\delta$ of Eqs. (41)–(43) define the global displacements (assembly of Timoshenko layers free to slide over each other) and the small-scale enrichment, respectively. The zero order expansions are:

$$ \begin{aligned} {\mathop{w}\limits^{0}}_{0} (x_{2}) &= \frac{1}{{C_{22}^{0} d}}\frac{{x_{2} (x_{2} - L)}}{2}\left\{ \mathop{\left({\frac{{a\left({C_{22}^{S2} C_{22}^{1} - C_{22}^{0S} C_{22}^{1S}} \right)}}{{C_{22}^{S}}}} \right)}\limits^{0}N_{22}^{T} + \mathop{\left({\frac{{a\left({\left({C_{22}^{0S}} \right)^{2} - C_{22}^{0} C_{22}^{S2}} \right)}}{{C_{22}^{S}}}} \right)}\limits^{0} M_{22}^{bT} \right. \hfill \\ & \quad \left. + C_{22}^{0} {\mathop {d\left({\frac{ac}{{C_{22}^{S}}}\left({M_{22}^{zT} + M_{22}^{ST}} \right)} \right)}\limits^{0}} \right\} \hfill \\ \end{aligned} $$

(100)

$$ \begin{aligned} {\mathop {\varphi}\limits^{0}}_{2} (x_{2}) &= \frac{1}{{C_{22}^{0} d}}\frac{{L - 2x_{2}}}{2}\left\{{\mathop {\left({\frac{{a\left({C_{22}^{1} C_{22}^{S2} - C_{22}^{0S} C_{22}^{1S}} \right)}}{{C_{22}^{S}}}} \right)}\limits^{0} N_{22}^{T}} \right. + \mathop {\left({\frac{{a\left({\left({C_{22}^{0S}} \right)^{2} - C_{22}^{0} C_{22}^{S2}} \right)}}{{C_{22}^{S}}}} \right)}\limits^{0} M_{22}^{bT} \hfill \\ & \quad \left. {+\,C_{22}^{0} d\mathop {\left({\frac{ac}{{C_{22}^{S}}}\left({M_{22}^{zT} + M_{22}^{ST}} \right)} \right)}\limits^{0}} \right\} \hfill \\ \end{aligned} $$

(101)

$$ \begin{aligned}{ \mathop v\limits^{0} }_{02} (x_{2}) & = \frac{{x_{2}}}{{C_{22}^{0} d}}\left\{{\mathop {\left({\frac{{a\left({C_{22}^{S2} C_{22}^{2} - \left({C_{22}^{1S}} \right)^{2}} \right)}}{{C_{22}^{S}}}} \right)}\limits^{0}} \right.N_{22}^{T} + \mathop {\left({\frac{{a\left({C_{22}^{0S} C_{22}^{1S} - C_{22}^{S2} C_{22}^{1}} \right)}}{{C_{22}^{S}}}} \right)}\limits^{0} M_{22}^{bT} \\ & \quad + \left. {\mathop {\left({\frac{{a\left({cC_{22}^{1} - C_{22}^{0S}} \right)}}{{C_{22}^{S}}}(M_{22}^{zT} + M_{22}^{ST})} \right)}\limits^{0}} \right\} \\ \end{aligned} $$

(102)

And the first order expansions:

$$ \begin{aligned} {\mathop {w}\limits^{1}}_{0} (x_{2} ) & = \frac{1}{{C_{{22}}^{0} d}}\frac{{x_{2} (x_{2} - L)}}{{24}}\left\{ {\mathop {\left( {\frac{{ac\left( {C_{{22}}^{{S0}} C_{{22}}^{2} - C_{{22}}^{{1S}} C_{{22}}^{1} } \right)}}{{C_{{22}}^{S} }}\left( {L^{2} + x_{2} L - x_{2}^{2} } \right) + \frac{{12K^{2} C_{{55}}^{P} C_{{22}}^{1} }}{{aC_{{22}}^{S} }}} \right)}\limits^{0} } \right.N_{{22}}^{T} \\ & \quad + \mathop {\left( {\frac{{ac^{2} dC_{{22}}^{0} }}{{C_{{22}}^{S} }}\left( {L^{2} + x_{2} L - x_{2}^{2} } \right) + \frac{{12C_{{22}}^{0} \left( {K^{2} C_{{55}}^{P} - acd} \right)}}{{aC_{{22}}^{S} }}} \right)}\limits^{0} M_{{22}}^{{bT}} \\ & \quad \left. { - C_{{22}}^{0} d\left( {L^{2} + x_{2} L - x_{2}^{2} } \right)\mathop {\left( {\frac{{ac}}{{C_{{22}}^{S} }}\left( {M_{{22}}^{{zT}} + M_{{22}}^{{ST}} } \right)} \right)}\limits^{0} } \right\} \\ \end{aligned} $$

(103)

$$ \begin{aligned} {\mathop {\varphi}\limits^{1}}_{2} (x_{2} ) & = \frac{1}{{C_{{22}}^{0} d}}\frac{{L - 2x_{2} }}{{24}} \\ & \quad \left\{ {\mathop {\left( {\frac{{ac(C_{{22}}^{{S0}} C_{{22}}^{2} - C_{{22}}^{{1S}} C_{{22}}^{1} )}}{{C_{{22}}^{S} }}\left( {L^{2} + 2x_{2} L - 2x_{2}^{2} } \right) + \frac{{12\left( {a\left( {C_{{22}}^{{S0}} C_{{22}}^{2} - C_{{22}}^{{1S}} C_{{22}}^{1} } \right) + K^{2} C_{{55}}^{P} C_{{22}}^{1} } \right)}}{{aC_{{22}}^{S} }}} \right)}\limits^{0} } \right.N_{{22}}^{T} \\ & \quad + \mathop {\left( {\frac{{ac^{2} dC_{{22}}^{0} }}{{C_{{22}}^{S} }}\left( {L^{2} + 2x_{2} L - 2x_{2}^{2} } \right) + \frac{{12C_{{22}}^{0} \left( {2acd - K^{2} C_{{55}}^{P} } \right)}}{{aC_{{22}}^{S} }}} \right)}\limits^{0} M_{{22}}^{{bT}} \\ & \quad \left. { - C_{{22}}^{0} d\mathop {\left( {\left( {\frac{{ac\left( {L^{2} + 2x_{2} L - 2x_{2}^{2} } \right) + 12}}{{C_{{22}}^{S} }}} \right)\left( {M_{{22}}^{{zT}} + M_{{22}}^{{ST}} } \right)} \right)}\limits^{0} } \right\} \\ \end{aligned} $$

(104)

Appendix 4: 2D thermo-elasticity solutions for multi-layered wide plates with thermally and mechanically imperfect interfaces subjected to steady-state thermal gradients

Exact solutions have been obtained in [2, 23] for temperature and stress/strain fields in simply supported, fully bonded, multilayered plates subjected to steady-state thermal loading with sinusoidal in-plane distribution. The derivation is based on the preliminary definition of the three-dimensional temperature field, through the solution of the heat conduction equation in each layer and the imposition of thermal boundary and continuity conditions at the interfaces; this is followed by the solution of Navier’s thermo-elasticity equations in each layer and the imposition of interfacial boundary conditions to define the constants of integration.

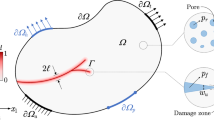
Here the formulation proposed in [2] is particularized to plates deforming in cylindrical bending, with $x_{2} - x_{3}$ the bending plane, and extended to account for interfaces which may be mechanically and/or thermally imperfect or fully debonded. The plates, of length L and thickness h in the bending plane, are made of orthotropic layers with the material axes parallel to the reference axes (cross-ply layup); the layers have arbitrary thickness, ${}^{(k)}h$, elastic constants and stacking sequence (Fig. 1). The plane-strain thermo-elastic constitutive equations of the layer k are derived from the 3D thermoelasticity relationships [26]:

(105)

with ${}^{(k)}C_{ij}$ (for i, j = 2,3) the coefficients of the 3D stiffness matrix in engineering notation, ${}^{(k)}\alpha_{i}$ the coefficient of thermal expansion along the $x_{i}$ principal material direction and ${}^{(k)}T = {}^{(k)}T(x_{2},x_{3})$ the temperature increment in the layer k. Equation (105) assumes that the coupling between elastic deformations in the layer and heat transfer can be neglected and that the temperature distribution is prescribed.

The mechanical behavior of the interfaces is described by the interfacial tractions laws, $\hat{\sigma}_{S}^{k} (x_{2}) = \left. {\left[{{}^{(k)}\sigma_{23} (x_{2},x_{3} = x_{3}^{k})} \right]n_{3}^{k}} \right|_{{^{(k)} \fancyscript{S}^{+} }} = K_{S}^{k} \hat{v}_{2}^{k} (x_{2})$ and $\hat{\sigma}_{N}^{k} (x_{2}) = \left. {\left[{{}^{(k)}\sigma_{33} (x_{2},x_{3} = x_{3}^{k})} \right]n_{3}^{k}} \right|_{{^{(k)} \fancyscript{S}^{+} }} = K_{N}^{k} \hat{v}_{3}^{k} (x_{2})$ with $n_{3}^{k}$ the component of the outward normal to the surface; the laws relates the interfacial tractions to the relative sliding and opening displacements, $\hat{v}_{2}^{k} (x_{2}) = {}^{(k + 1)}v_{2} \left({x_{2},x_{3} = x_{3}^{k}} \right) - {}^{(k)}v_{2} \left({x_{2},x_{3} = x_{3}^{k}} \right)$ and $\hat{v}_{3}^{k} (x_{2}) = {}^{(k + 1)}v_{3} \left({x_{2},x_{3} = x_{3}^{k}} \right) - {}^{(k)}v_{3} \left({x_{2},x_{3} = x_{3}^{k}} \right)$.

Following [3], the thermal behavior of the interface $^{(k)} \fancyscript{S}^{+}$ at the coordinate $x_{3} = x_{3}^{k}$ is controlled by an interfacial thermal resistance $R^{k} = 1/H^{k}$, which is defined as the reciprocal of the interlayer thermal conductance $H^{k}$ and relate the heat flux through the interface, ${}^{(k)}q_{3}^{k} = - {}^{(k)}K_{3} {}^{(k)}T^{k} ,_{3}$, to the interfacial temperature variation, ${}^{(k)}q_{3}^{k} = - \frac{1}{{R^{k}}}\left[{{}^{(k + 1)}T^{k} - {}^{(k)}T^{k}} \right]$, where ${}^{(k)}q_{3}^{k} = {}^{(k)}q_{3} (x_{3}^{{}} = x_{3}^{k} )$ and ${}^{(k)}T^{k} = {}^{(k)}T(x_{3} = x_{3}^{k} )$; when the layers are in perfect thermal contact, $R^{k} = 0$ and the temperature becomes continuous at the interface, ${}^{(k)}T^{k} = {}^{(k + 1)}T^{k}$; when $H^{k} = 0$, the interface becomes impermeable and there is no heat flux, ${}^{(k)}q_{3}^{k} = 0$ .

Exact solutions are found for a simply supported plate with boundary conditions given by $v_{3} ,\sigma_{22} = 0$ at $x_{2} = 0,L$. The plate is subjected to applied temperatures onto the upper and lower surfaces $\fancyscript{S}^{+}$ and $\fancyscript{S}^{-}$ at $x_{3} = x_{3}^{n}$ and $x_{3} = x_{3}^{0}$:

$$ T\left( {x_{2} ,x_{3} = x_{3}^{n} } \right) = T_{m1} \sin ( {px_{2} }), \quad T\left( {x_{2} ,x_{3} = x_{3}^{0} } \right) = T_{m2} \sin \left( {px_{2}} \right) $$

(106)

with $p = m\pi /L$ and $m \in {\mathbb{N}}$ (Fig. 3c). Solutions for applied temperatures other than Eq. (106) can be obtained from the results obtained here using superposition and Fourier’s series expansions. A uniform temperature field applied to the upper surface, $T\left( {x_{3} = x_{3}^{n} } \right) = T_{1}$, for instance, is approximated using the distribution (106) and the expansion:

$$ T\left( {x_{2} ,x_{{3}} = x_{3}^{n} } \right) = T_{1} \sum\limits_{{k = 1}}^{{k{\text{max}}}} {\frac{4}{{\pi \left( {2k - 1} \right)}}\sin \left[ {\left( {2k - 1} \right)\frac{\pi }{L}x_{2} } \right]} \quad {\text{for}}\;0 \le x_{2} \le L $$

(107)

For large values of $k_{\hbox{max} }$, the series (107) defines an applied temperature which is approximately constant over the domain but for some boundary regions near $x_{2} = 0,L$, whose sizes are proportional to the wave length of $k_{\hbox{max} }$ and decrease on increasing $k_{\hbox{max} }$; there the Fourier sum overshoots by an amount which does not vanishes on increasing $k_{\hbox{max} }$ and for the square half wave of height $T_{1}$ of Eq. (107) the error in the approximation is around 18 %.

4.1 Heat conduction problem

The thermal boundary conditions and continuity conditions at the n − 1 interfaces are:

$$ {}^{(n)}T\left({x_{2},x_{3} = x_{3}^{n}} \right) = T_{m1} \sin \left({px_{2}} \right) $$

$$ {}^{(1)}T\left({x_{2},x_{3} = x_{3}^{0}} \right) = T_{m2} \sin \left({px_{2}} \right) $$

$$ {}^{(k)}q_{3}^{k} \left({x_{2}^{{}}} \right) = - \frac{1}{{R^{k}}}\left[{{}^{(k + 1)}T^{k} \left({x_{2}} \right) - {}^{(k)}T^{k} \left({x_{2}} \right)} \right],\quad {}^{(k)}q_{3}^{k} \left({x_{2}^{{}}} \right) = {}^{(k+1)}q_{3}^{k} \left({x_{2}^{{}}} \right),\quad {\text{for}}\;k = 1..n - 1 $$

(108)

In the special cases of perfect thermal contact and impermeable interfaces, the continuity conditions in Eq. (108) become:

$$ {}^{(k)}T^{k} \left({x_{2}^{{}}} \right) = {}^{(k + 1)}T^{k} \left({x_{2}^{{}}} \right),\;{\text{when}}\;R^{k} = 0\quad,{\text{for}}\;k = 1 \ldots n - 1 $$

$$ ^{{(k)}} q_{3}^{k} \left( {x_{2}^{{}} } \right) = 0,\quad {\text{when}}\quad H^{k} = 0,\quad {\text{for}}\;k = 1 \ldots n - 1 $$

(109)

The steady state heat conduction equation for a homogeneous orthotropic solid, where all the fields variable depend on $x_{2} \,{\text{and}}\,x_{3}$ only, is given by:

$$ K_{2} \frac{{\partial^{2} T\left({x_{2},x_{3}} \right)}}{{\partial x_{2}^{2}}} + K_{3} \frac{{\partial^{2} T\left({x_{2},x_{3}} \right)}}{{\partial x_{3}^{2}}} = 0 $$

(110)

where $K_{i}$ is the thermal conductivity in the $x_{i}$ principal material direction which coincides with a geometrical axis. The temperature field:

$$ {}^{\left(k \right)}T\left({x_{2},x_{3}} \right) = {}^{\left(k \right)}F\left({x_{3}} \right)\sin \left({px_{2}} \right) $$

(111)

with

$$ {}^{\left(k \right)}F\left({x_{3}} \right) = {}^{\left(k \right)}\left({\bar{c}_{1} e^{{s_{1} x_{3}}} + \bar{c}_{2} e^{{s_{2} x_{3}}}} \right) $$

$$ {}^{\left(k \right)}s_{1,2} = \pm \sqrt {\frac{{{}^{\left(k \right)}K_{2} p^{2}}}{{{}^{\left(k \right)}K_{3}}}} \quad {\text{and}} \quad {}^{\left(k \right)}s_{2} = - {}^{\left(k \right)}s_{1} $$

(112)

solves the Eq. (110) and the imposition of the 2n boundary and continuity conditions, Eq. (108), leads to an algebraic system of 2n equations in the 2n unknown constants ${}^{\left( k \right)}\bar{c}_{1,2}$, for $k = 1,\ldots,n$ [2]. Since the ${}^{\left( k \right)}s_{1,2}$ are real, Eq. (112) can be written as:

$$ {}^{\left(k \right)}F\left({x_{3}^{{}}} \right) = {}^{\left(k \right)}c_{1} cosh\left({{}^{\left(k \right)}s_{1} x_{3}} \right) + {}^{\left(k \right)}c_{2} sinh\left({{}^{\left(k \right)}s_{2} x_{3}} \right) $$

(113)

with the 2n unknown constants ${}^{\left( k \right)}c_{1} = {}^{\left( k \right)}\bar{c}_{1} + {}^{\left( k \right)}\bar{c}_{2}$ and ${}^{\left( k \right)}c_{2} = {}^{\left( k \right)}\bar{c}_{1} - {}^{\left( k \right)}\bar{c}_{2}$ for k = 1,…,n.

If the applied temperatures are uniform and described by the Fourier expansion, Eq. (107), the temperature field in each layer is approximated over most of the plate domain, away from the boundaries at $x_{2} = 0,L$, by

$$ \begin{aligned} {}^{\left(k \right)}T\left({x_{2},x_{3}} \right) = \sum\limits_{j = 1}^{j\max} {\frac{4}{m\pi}\left[{{}^{\left(k \right)}c_{1} cosh\left({{}^{\left(k \right)}s_{1} x_{3}} \right) + {}^{\left(k \right)}c_{2} sinh\left({{}^{\left(k \right)}s_{2} x_{3}} \right)} \right]\sin \left({\frac{m\pi}{L}x_{2}} \right)} \hfill \\ {\text{where}}\,\,m = 2j - 1 \hfill \\ \end{aligned} $$

(114)

The temperature distribution in the plate will depend on the relative thermal conductivity of the layers, the interface thermal resistance and the assigned temperature distribution. The sinusoidal temperature of Eq. (106) originates piecewise nonlinear temperature fields, which become piecewise linear in the central portion of the plate when $p = m\pi /L$ is small, e.g. in thin plates. If the applied temperatures are uniform along $x_{2}$, $T\left( {x_{2} ,x_{3} = x_{3}^{n} } \right) = T_{1}$ and $T\left( {x_{2} ,x_{3} = x_{3}^{0} } \right) = T_{2}$, the temperature distribution in the layers is piece-wise linear, Eq. (110), with jumps at the interfaces which are not in perfect thermal contact; the slope of the pieces varies between layers characterized by different values of thermal conductivity ${}^{\left( k \right)}K_{3}$ or by interfacial thermal contact resistance. In a classical cross-ply laminate made of n unidirectionally reinforced plies of equal thickness, ${}^{\left( k \right)}h = h/n$, where ${}^{\left( k \right)}K_{3} = K_{3}$ is the same in all layers, and thermal contact is imperfect, the temperature distribution in the layer k is:

$$ {}^{\left(k \right)}T\left({x_{3}} \right) = {}^{\left(k \right)}c_{1} + {}^{\left(k \right)}c_{2} \frac{{\left({x_{3} - x_{3}^{0}} \right)}}{h} $$

(115)

with

$$ {}^{\left(k \right)}c_{1} = T_{2} + \frac{{T_{1} - T_{2}}}{{1 + K_{3} \sum\limits_{i = 1}^{n - 1} {\frac{{R^{i}}}{h}}}}K_{3} \sum\nolimits_{i = 1}^{k - 1} {\frac{{R^{i}}}{h}},\quad {}^{\left(k \right)}c_{2} = \frac{{T_{1} - T_{2}}}{{1 + K_{3} \sum\nolimits_{i = 1}^{n - 1} {\frac{{R^{i}}}{h}}}} . $$

(116)

4.2 Thermo-elastic problem

Using the thermo-elastic constitutive Eq. (105) and the compatibility equations relating strain and displacements, the equilibrium equations for the generic layer k are given in terms of the displacement variables, ${}^{(k)}v_{2}$ and ${}^{(k)}v_{3}$, by Navier’s equations:

(117)

The 2n differential equations, in the 2n variables, are complemented by 4n boundary and continuity conditions. The boundary conditions are:

$$ {}^{\left(n \right)}\sigma_{23} \left({x_{2},x_{3}^{n}} \right) = {}^{\left(n \right)}\sigma_{33} \left({x_{2},x_{3}^{n}} \right) = {}^{\left(1 \right)}\sigma_{23} \left({x_{2},x_{3}^{0}} \right) = {}^{\left(1 \right)}\sigma_{33} \left({x_{2},x_{3}^{0}} \right) = 0 $$

(118)

and the continuity conditions at the imperfect interfaces, which impose traction continuity and relative jumps controlled by the interfacial traction laws, are:

$$ \begin{aligned}^{\left( k \right)}\sigma_{23} \left( {x_{2} ,x_{3}^{k} } \right) & =^{{\left( {k + 1} \right)}}\sigma_{23} \left( {x_{2} ,x_{3}^{k} } \right) \\^{\left( k \right)}\sigma_{33} \left( {x_{2} ,x_{3}^{k} } \right) & =^{{\left( {k + 1} \right)}}\sigma_{33} \left( {x_{2} ,x_{3}^{k} } \right) \\ \end{aligned} $$

$$ \begin{aligned} {}^{\left(k \right)}\sigma_{23} \left({x_{2},x_{3}^{k}} \right) = K_{S}^{k} \left[{{}^{{\left({k + 1} \right)}}v_{2} \left({x_{2},x_{3}^{k}} \right) - {}^{\left(k \right)}v_{2} \left({x_{2},x_{3}^{k}} \right)} \right], \hfill \\ {}^{\left(k \right)}\sigma_{33} \left({x_{2},x_{3}^{k}} \right) = K_{N}^{k} \left[{{}^{{\left({k + 1} \right)}}v_{3} \left({x_{2},x_{3}^{k}} \right) - {}^{\left(k \right)}v_{3} \left({x_{2},x_{3}^{k}} \right)} \right] \quad {\text{for}}\;k = 1 ,\ldots, n - 1\end{aligned} $$

(119)

The displacement variables in the kth layer are defined by the sum of a complementary and a particular solution, ${}^{(k)}v_{2} (x_{2},x_{3}) = {}^{(k)}v_{2c} (x_{2},x_{3}) + {}^{(k)}v_{2p} (x_{2},x_{3})$ and ${}^{(k)}v_{3} (x_{2},x_{3}) = {}^{(k)}v_{3c} (x_{2},x_{3}) + {}^{(k)}v_{3p} (x_{2}^{{}},x_{3}^{{}})$.

4.2.1 Particular solution

A particular solution of the system (117), with ${}^{(k)}T\left({x_{2},x_{3}} \right)$ given by Eqs. (111) and (113), which satisfies the boundary conditions, is:

$$ \begin{aligned} {}^{\left(k \right)}v_{2p} \left({x_{2},x_{3}} \right) = {}^{\left(k \right)}\left({B_{1} e^{{s_{1} x_{3}}} + B_{2} e^{{- s_{1} x_{3}}}} \right)\cos \left({px_{2}} \right) \hfill \\ {}^{\left(k \right)}v_{3p} \left({x_{2},x_{3}} \right) = {}^{\left(k \right)}\left({D_{1} e^{{s_{1} x_{3}}} + D_{2} e^{{- s_{1} x_{3}}}} \right)\sin \left({px_{2}^{{}}} \right) \hfill \\ p = m\pi/L\,\,{\text{and}}\,\,{}^{\left(k \right)}s_{1} = + \sqrt {\frac{{{}^{\left(k \right)}K_{2} p^{2}}}{{{}^{\left(k \right)}K_{3}}}} \hfill \\ \end{aligned} $$

(120)

where ${}^{(k)}B_{1},{}^{(k)}B_{2},{}^{(k)}D_{1},{}^{(k)}D_{2}$ are unknown constants. Substituting Eqs. (120) into (117) and collecting the terms multiplying $e^{{s_{1} x_{3}}}$ and $e^{{- s_{1} x_{3}}}$, leads to four algebraic equations in the unknown ${}^{(k)}B_{1},{}^{(k)}B_{2},{}^{(k)}D_{1},{}^{(k)}D_{2}$:

$$ {}^{(k)}\left[{C_{22} p^{2} B_{1} - \left({C_{23} + C_{55}} \right)ps_{1} D_{1} - C_{55} s_{1}^{2} B_{1} + pc_{1} \left({C_{12} \alpha_{1} + C_{22} \alpha_{2} + C_{23} \alpha_{3}} \right)} \right] = 0 $$

$$ {}^{(k)}\left[{C_{22} p^{2} B_{2} + \left({C_{23} + C_{55}} \right)ps_{1} D_{2} - C_{55} s_{1}^{2} B_{2} + pc_{2} \left({C_{12} \alpha_{1} + C_{22} \alpha_{2} + C_{23} \alpha_{3}} \right)} \right] = 0 $$

$$ {}^{(k)}\left[{C_{33} s_{1}^{2} D_{1} - \left({C_{23} + C_{55}} \right)ps_{1} B_{1} - C_{55} p_{{}}^{2} D_{1} - s_{1} c_{1} \left({C_{13} \alpha_{1} + C_{23} \alpha_{2} + C_{33} \alpha_{3}} \right)} \right] = 0 $$

$$ {}^{(k)}\left[{C_{33} s_{1}^{2} D_{2} + \left({C_{23} + C_{55}} \right)ps_{1} B_{2} - C_{55} p_{{}}^{2} D_{2} + s_{1} c_{2} \left({C_{13} \alpha_{1} + C_{23} \alpha_{2} + C_{33} \alpha_{3}} \right)} \right] = 0 $$

(121)

4.2.2 Complementary solution

An appropriate solution of the complementary problem, which satisfies the simply support conditions is:

$$ \begin{aligned} & ^{{\left( k \right)}} v_{{2c}} \left( {x_{2} ,x_{3} } \right) =\,{}^{{\left( k \right)}}V\left( {x_{3} } \right)\cos \left( {px_{2} } \right) \\ & ^{{\left( k \right)}} v_{{3c}} \left( {x_{2} ,x_{3} } \right)= {}^{{\left( k \right)}}W\left( {x_{3} } \right)\sin \left( {px_{2} } \right) \\ & p = m\pi /L \\ \end{aligned} $$

(122)

with

$$ \left[{{}^{\left(k \right)}V\left({x_{3}} \right),{}^{\left(k \right)}W\left({x_{3}} \right)} \right] = \left[{{}^{\left(k \right)}V_{0},{}^{\left(k \right)}W_{0}} \right]e^{{tx_{3}}} $$

(123)

Substituting Eq. (123) into the homogeneous part of Eq. (117) yields a homogeneous system of algebraic equations whose non-trivial solution is defined by the characteristic equation [24]:

$$ A_{0} t^{4} + A_{1} t^{2} + A_{2} = 0 $$

(124)

with

$$ A_{0} = C_{33} C_{55}, \quad A_{1} = p^{2} \left[{\left({C_{23} + C_{55}} \right)^{2} - C_{22} C_{33} - C_{55}^{2}} \right], \quad A_{2} = p^{4} C_{22} C_{55} $$

(125)

Equation (124) can be written in the form of a quadratic equation with

$$ A_{0} \gamma^{2} + A_{1} \gamma + A_{2} = 0 $$

$$ \gamma = t^{2} $$

$$ \Delta = A_{1}^{2} - 4A_{0} A_{2} $$

(126)

The nature of the solution depends on the elastic constants of the layer through the discriminant $\Delta$. In [2] only solutions corresponding to positive discriminants were examined, since they correspond to typical orthotropic layers used in laminated systems. Here, following what done in [24, 30], solutions are presented also for the case of zero discriminant, which describe isotropic layers, and for negative discriminants [24], which could describe orthotropic layers which are stiffer in the transverse direction, e.g. sandwich cores.

4.2.2.1 Positive discriminant

When $\Delta$ is positive, Eq. (126) has two real and unequal roots, $\gamma_{1,2} = {{(- A_{1} \pm \sqrt \Delta)} \mathord{\left/{\vphantom {{(- A_{1} \pm \sqrt \Delta)} {2A_{0}}}} \right. \kern-0pt} {2A_{0}}}$. By setting $m_{j} = \sqrt {\left| {\gamma_{j}} \right|}$ for j = 1,2, if $\gamma_{j} > 0$ then the roots of Eq. (126) are real, $t_{j} = \pm m_{j}$, so that:

$$ \begin{aligned} {}^{\left(k \right)}V\left({x_{3}} \right) & = \sum\limits_{j = 1}^{2} {a_{1j} \cosh \left({m_{j} x_{3}} \right)} + a_{2j} \sinh \left({m_{j} x_{3}} \right) \\ {}^{\left(k \right)}W\left({x_{3}} \right) & = \sum\limits_{j = 1}^{2} {b_{1j} \cosh \left({m_{j} x_{3}} \right)} + b_{2j} \sinh \left({m_{j} x_{3}} \right) \\ \end{aligned} $$

(127)

where four of the eight constants are derived substituting (127) into the equilibrium Eq. (117),

$$ b_{1j} = \beta_{j} a_{2j}, \quad b_{2j} = \beta_{j} a_{1j}, $$

$$ \beta_{j} = \frac{{\left({C_{23} + C_{55}} \right)pt_{j}}}{{C_{33} t_{j}^{2} - C_{55} p_{{}}^{2}}} $$

(128)

(formulas (128) corrects a sign omission in the derivation in [24]).

If $\gamma_{j} < 0$, the roots of Eq. (126) are complex and $t_{j} = \pm im_{j}$ so that:

$$ \begin{aligned} {}^{\left(k \right)}V\left({x_{3}} \right) & = \sum\limits_{j = 1}^{2} {a_{1j} \cos \left({m_{j} x_{3}} \right)} + a_{2j} \sin \left({m_{j} x_{3}} \right) \\ {}^{\left(k \right)}W\left({x_{3}} \right) & = \sum\limits_{j = 1}^{2} {b_{1j} \cos \left({m_{j} x_{3}} \right)} + b_{2j} \sin \left({m_{j} x_{3}} \right) \\ \end{aligned} $$

(129)

Where four of the eight constants are derived substituting (129) into the equilibrium Eq. (117),

$$ b_{1j} = - \alpha_{j} a_{2j}, \quad b_{2j} = \alpha_{j} a_{1j}, $$

$$ \alpha_{j} = \frac{{\left({C_{23} + C_{55}} \right)pt_{j}}}{{C_{33} t_{j}^{2} + C_{55} p_{{}}^{2}}} $$

(130)

The remaining four constants for each layer are determined through boundary and continuity conditions (119).

4.2.2.2 Zero discriminant

When the layer is isotropic, $\Delta = 0$, Eq. (126) has two real and equal roots, $\gamma_{1,2} = {{- A_{1}} \mathord{\left/{\vphantom {{- A_{1}} {2A_{0}}}} \right. \kern-0pt} {2A_{0}}} = p^{2}$ and Eq. (124) has two repeated roots $t_{j} = \pm p$, for j = 1, 2. The displacement functions are:

$$ \begin{aligned} {}^{\left(k \right)}V\left({x_{3}} \right) & = \left({a_{1} + c_{1} x_{3}} \right)e^{{px_{3}}} + \left({a_{2} + c_{2} x_{3}} \right)e^{{- px_{3}}} \\ {}^{\left(k \right)}W\left({x_{3}} \right) & = \left({b_{1} + d_{1} x_{3}} \right)e^{{px_{3}}} + \left({b_{2} + d_{2} x_{3}} \right)e^{{- px_{3}}} \\ \end{aligned} $$

(131)

where four of the eight constants are derived substituting (131) into the equilibrium Eq. (117):

$$ \begin{aligned} d_{1} = c_{1}, \quad d_{2} = - c_{2}, \quad \hfill \\ b_{1} = a_{1} - \left[{\frac{{2C_{55}}}{{\left({C_{23} + C_{55}} \right)p}} + \frac{1}{p}} \right]c_{1}, \quad b_{2j} = - a_{2} - \left[{\frac{{2C_{55}}}{{\left({C_{23} + C_{55}} \right)p}} + \frac{1}{p}} \right]c_{2}, \hfill \\ \end{aligned} $$

(132)

The remaining four constants for each layer are determined through boundary and continuity conditions (119).

4.2.2.3 Negative discriminant

When $\Delta < 0$, Eq. (126) has two complex conjugate roots, $\gamma_{1,2} = \mu_{r} \pm i\mu_{c} = r\left( {{ \cos }\,\theta \pm i\,{ \sin }\,\theta } \right)$, where $\mu_{r} = {{- A_{1}} \mathord{\left/{\vphantom {{- A_{1}} {2A_{0}}}} \right. \kern-0pt} {2A_{0}}}$ and $\mu_{c} = {{\sqrt {\left| \Delta \right|}} \mathord{\left/{\vphantom {{\sqrt {\left| \Delta \right|}} {2A_{0}}}} \right. \kern-0pt} {2A_{0}}}$, $r = \sqrt {\mu_{c}^{2} + \mu_{r}^{2}}$ and $\theta = \arctan \left({{{\mu_{c}} \mathord{\left/{\vphantom {{\mu_{c}} {\mu_{r}}}} \right. \kern-0pt} {\mu_{r}}}} \right)$. The corresponding roots of Eq. (126) are $t_{1,2,3,4} = \pm \left({\rho_{1} \pm i\rho_{2}} \right)$, where $\rho_{1} = \sqrt r \,{ \cos }(\theta /2)$ and $\rho_{2} = \sqrt r { \sin }(\theta /2)$. The displacement functions are:

$$ \begin{aligned} {}^{\left(k \right)}V\left({x_{3}} \right) & = a_{1} e^{{\rho_{1} x_{3}}} \cos \left({\rho_{2} x_{3}} \right) + a_{2} e^{{\rho_{1} x_{3}}} \sin \left({\rho_{2} x_{3}} \right) + a_{3} e^{{- \rho_{1} x_{3}}} \cos \left({\rho_{2} x_{3}} \right) + a_{4} e^{{- \rho_{1} x_{3}}} \sin \left({\rho_{2} x_{3}} \right) \\ {}^{\left(k \right)}W\left({x_{3}} \right) & = b_{1} e^{{\rho_{1} x_{3}}} \cos \left({\rho_{2} x_{3}} \right) + b_{2} e^{{\rho_{1} x_{3}}} \sin \left({\rho_{2} x_{3}} \right) + b_{3} e^{{- \rho_{1} x_{3}}} \cos \left({\rho_{2} x_{3}} \right) + b_{4} e^{{- \rho_{1} x_{3}}} \sin \left({\rho_{2} x_{3}} \right) \\ \end{aligned} $$

(133)

where four of the eight constants are derived substituting Eq. (133) into the equilibrium Eq. (117):

$$ \begin{aligned} b_{1} = r_{1} a_{1} - r_{2} a_{2}, \quad b_{2} = r_{2} a_{1} + r_{1} a_{2}, \hfill \\ b_{3} = - r_{1} a_{3} - r_{2} a_{4}, \quad b_{4} = r_{2} a_{3} - r_{1} a_{4} \hfill \\ \end{aligned} $$

(134)

where

$$ r_{1} = \frac{{\rho_{1} \left[{C_{22} p^{2} - C_{55} \left({\rho_{1}^{2} + \rho_{2}^{2}} \right)} \right]}}{{p\left({C_{23} + C_{55}} \right)\left({\rho_{1}^{2} + \rho_{2}^{2}} \right)}}, \quad r_{2} = \frac{{\rho_{2} \left[{C_{22} p^{2} + C_{55} \left({\rho_{1}^{2} + \rho_{2}^{2}} \right)} \right]}}{{p\left({C_{23} + C_{55}} \right)\left({\rho_{1}^{2} + \rho_{2}^{2}} \right)}} $$

(135)

The remaining four constants are determined through boundary and continuity conditions (119).