Assessment and correction of theories for multilayered plates with imperfect interfaces

Abstract

The response of multilayered plates with imperfectly bonded interfaces and delaminations to quasi static and dynamic loadings is conveniently studied by assuming the displacements as two length-scales fields, given by global displacements, which are continuous in the thickness, and local perturbations or enrichments, which account for the multilayered structure and the jumps at the interfaces. The a priori imposition of interfacial continuity conditions then leads to a homogenized field defined by the global variables only. The number of displacement unknowns is independent of the number of layers and is equal to five or six, for sliding or mixed mode interfaces, respectively. Dynamic equilibrium equations are derived using variational principles. This effective idea, which was originally proposed in the zigzag theories for fully bonded plates, was first applied to plates with imperfect interfaces by Cheng et al. (J Appl Mech, 63:1019–1026, 1996), Schmidt and Librescu (Nova J Math Game Theory Algebra, 5:131–147, 1996), and Di Sciuva (AIAA J, 35(11):1753–1759, 1997). These pioneering models, as all subsequent models which extend the theories to various problems, suffer from a common omission in the treatment of the interfacial energy in the derivation of the equilibrium equations, which leads to solutions which are accurate only for fully bonded/debonded plates. In this paper a linear, first order model which resolves the inaccuracy and extends the theories to more general interfacial traction laws is presented along with the corrected formulations of the original models. The formulations are validated using exact 2D elasticity solutions for multilayered plates in cylindrical bending.

Appendices

Appendix 1

Consider the schematic shown in Fig. 9, which represents a 1D element of thickness h and unit cross-sectional area, subjected to uniform traction F ₃, in series with a 1D spring of stiffness K _N .

Fig. 9

Schematic of a 1D element in series with a 1D spring, used to verify the validity of the proposed approach

The spring defines a zero thickness interface between the external constraint and the 1D element. In accordance with the theory proposed in this paper, Eq. (4), the displacement field in the element is assumed as:

$$ w(x_{3} ) \, = \varphi_{3} x_{3} + \, \hat{w} $$

(36)

where φ ₃ is the constant axial strain in the bar ɛ ₃₃ = w,₃ = φ ₃, Eq. (5), which is related to the axial stress by σ ₃₃ = E ₃ φ ₃, Eq. (6b), with E ₃ the Young modulus. The traction at the interface with unit positive normal vector n is given by the spring reaction $\hat{\sigma }_{33} = K_{N} \hat{w}$, Eq. (2). The interfacial relative displacement, $\hat{w}$, is obtained by imposing $\hat{\sigma }_{33} = \sigma_{33} n_{3}$, which yields $\hat{w} = {{\varphi_{3} E_{3} } \mathord{\left/ {\vphantom {{\varphi_{3} E_{3} } {K_{N} }}} \right. \kern-0pt} {K_{N} }}$, Eq. (10b). The homogenized displacement, Eq. (13), then becomes:

$$ w(x_{3} ) = \varphi_{3} \left( {x_{3} + \frac{{E_{3} }}{{K_{N} }}} \right) $$

(37)

and depends on the global variable φ ₃ only.

Direct imposition of equilibrium conditions at the upper surface of the element at x ₃ = h, F ₃ = σ ₃₃ n ₃, yields

$$ F_{3} = \varphi_{3} E_{3} . $$

(38)

The equilibrium equation can also be found particularizing to this problem the principle of virtual works, Eq. (16):

(39)

where the term with the line on top accounts for the strain energy of the spring. This term was erroneously omitted in the original models formulated in [14–17]. Substitution of virtual strains and displacements, leads to:

(40)

which yields the equilibrium equation in terms of stresses, Eqs. (17):

(41)

and in terms of homogenized displacements:

(42)

The terms in brackets in the equation above cancel and the equation coincides with that obtained by imposing direct equilibrium, Eq. (38). In the absence of the term with the line on top in the principle of virtual works, Eq. (39), the terms in brackets would not cancel and equilibrium won’t be satisfied.

Appendix 2: Revision and correction of original models. Cheng, Jemah and Williams’s model (1996) [14] revised

Cheng et al. formulated in [14] a pioneering model which extends to plates with imperfect, sliding interfaces the homogenized approach of the zigzag theories originally formulated for perfectly bonded plates. An efficient linear, third order theory was proposed which is revised and corrected here.

2.1 Displacement field (Eqs. 13a, b in [14])

$$ v_{\alpha }^{{}} (x_{i} ,t) = u_{\alpha } + \psi_{\alpha } x_{3} + \varphi_{\alpha } x_{3}^{2} + \eta_{\alpha } x_{3}^{3} + \sum\limits_{m = 1}^{k - 1} {\left[ {{}^{\left( m \right)}\Delta v_{\alpha } + {}^{\left( m \right)}u_{\alpha } \left( {x_{3} - {}^{\left( m \right)}h} \right)} \right]H\left( {x_{3} - {}^{\left( m \right)}h} \right)} $$

(43)

$$ v_{3}^{{}} (x_{i} ,t) = u_{3} $$

with $H ( {x_{3} - {}^{( m )}h} ) = \{ {1{\text{ for }}( {x_{3} - {}^{( m )}h} ) \ge 0; \, 0 \;{\text{for }}( {x_{3} - {}^{( m )}h} ) < 0} \}$, ^(m)Δv _α the jump at the ^(m)Ω interface and ^(m) u _α the mth zigzag function.

2.2 Interfacial tractions law (Eq. 6 in [14])

$$ \Delta {\mathbf{v}} \equiv \left[ {{\mathbf{v}}(\Omega ^{ + } ) - {\mathbf{v}}(\Omega ^{ - } )} \right] = {\mathbf{R}} \cdot {\varvec{\upsigma}} \cdot {\mathbf{n}} $$

(44)

with ${\mathbf{R}}$ the compliance tensor of the spring layer interface and ${\mathbf{n}}$ the unit positive normal vector of the interface.

2.3 Stress and strain components (Eqs.14,15 in [14])

$$ e_{ij} = \frac{1}{2}\left( {v_{i,j} + v_{j,i} } \right), \quad \sigma_{\alpha \beta } = H_{\alpha \beta \omega \rho } e_{\omega \rho } , \quad \sigma_{\alpha 3} = 2E_{\alpha 3\omega 3} e_{\omega 3} $$

(45)

$$ H_{\alpha \beta \omega \rho } = E_{\alpha \beta \omega \rho } - \frac{{E_{\alpha \beta 33} E_{33\omega \rho } }}{{E_{3333} }} $$

where negligible normal tractions have been assumed in the thickness direction.

2.4 Compatibility of transverse shear strains on bounding surfaces (Eqs. 16 in [14])

$$ \psi_{\alpha } = - u_{3,\alpha } $$

(46)

$$ \eta_{\alpha } = - \frac{2}{3}\left( {\frac{1}{h}\varphi_{\alpha } + \frac{1}{{2h^{2} }}\sum\limits_{m = 1}^{k - 1} {{}^{\left( m \right)}u_{\alpha } } } \right) $$

2.5 Continuity conditions on transverse shear tractions at interfaces (Eq. 17, 18 in [14])

$$ \begin{gathered} \frac{1}{2}{}^{(i)}E_{\alpha 3\omega 3} {}^{\left( i \right)}u_{\omega } + \left( {{}^{(i + 1)}E_{\alpha 3\omega 3} - {}^{(i)}E_{\alpha 3\omega 3} } \right)\left[ {\left( {{}^{\left( i \right)}h - \frac{1}{h}{}^{\left( i \right)}h^{2} } \right)\varphi_{\omega } + \frac{1}{2}\sum\limits_{m = 1}^{i} {{}^{\left( m \right)}u_{\omega } } - \frac{1}{{2h^{2} }}{}^{\left( i \right)}h^{2} \sum\limits_{m = 1}^{k - 1} {{}^{\left( m \right)}u_{\omega } } } \right] = 0 \hfill \\ (i = 1, \ldots k - 1) \hfill \\ \end{gathered} $$

(47)

from which:

$$ ^{\left( i \right)} u_{\alpha } =^{\left( i \right)} a_{\alpha \lambda } \varphi_{\lambda } \quad (i = 1, \ldots, k - 1) $$

(48)

where the ⁽ⁱ⁾ a _αλ are constants to be derived using the previous equation.

2.6 Homogenized displacement jumps (Eq. 22 in [14])

$$ {}^{\left( m \right)}\Delta v_{\alpha } = {}^{\left( m \right)}R_{\alpha \beta } (x_{\rho } ){}^{{\left( {m + 1} \right)}}E_{\beta 3\omega 3} f_{\omega \lambda ,3} ({}^{\left( m \right)}h^{ + } )\varphi_{\lambda } $$

(49)

where

$$ \begin{aligned} f_{\omega \lambda } & = f_{\omega \lambda } (x_{3} ) = \delta_{\omega \lambda } x_{3}^{2} + c_{\omega \lambda } x_{3}^{3} + \sum\limits_{m = 1}^{k - 1} {{}^{\left( m \right)}a_{\omega \lambda } \left( {x_{3} - {}^{\left( m \right)}h} \right)H\left( {x_{3} - {}^{\left( m \right)}h} \right)} \\ c_{\omega \lambda } & = - \frac{2}{3h}\left( {\delta_{\omega \lambda } + \frac{1}{2h}\sum\limits_{m = 1}^{k - 1} {{}^{\left( m \right)}a_{\omega \lambda } } } \right) \\ \end{aligned} $$

(50)

2.7 Homogenized displacement field (Eq. 23, 24 in [14])

$$ v_{\alpha }^{{}} = u_{\alpha } - x_{3} u_{3,\alpha } + h_{\alpha \lambda } \varphi_{\lambda } $$

(51)

where

$$ h_{\alpha \lambda } = h_{\alpha \lambda } (x_{i} ) = f_{\alpha \lambda } (x_{3} ) + \sum\limits_{m = 1}^{k - 1} {{}^{\left( m \right)}R_{\alpha \beta } (x_{\rho } ){}^{{\left( {m + 1} \right)}}E_{\beta 3\omega 3} f_{\omega \lambda ,3} ({}^{\left( m \right)}h^{ + } )H\left( {x_{3} - {}^{\left( m \right)}h} \right)} $$

(52)

2.8 Hamilton equation (Eq. 25 [14] revised)

(53)

(Note terms with line on top correct original equations).

2.9 Dynamic equilibrium equations (Eqs. 26 [14] revised)

(54)

where

(55)

(Note terms with line on top correct original equations).

2.10 Boundary conditions (Eqs. 27 [14])

$$ \begin{aligned} \delta u_{\alpha } {:}& \, n_{\beta } N_{\alpha \beta } = 0\,\,{\text{or }}\delta u_{\alpha } = 0 \hfill \\ \delta u_{3} {:}& \, n_{\beta } \left( {M_{\alpha \beta ,\alpha } - J\ddot{\it{u}}_{\beta } + K\ddot{\it{u}}_{3,\beta } - J_{\beta \alpha } \ddot{\varphi }_{\alpha } } \right) = 0\,\,{\text{or }}\delta u_{ 3} = 0 \\ \delta \varphi_{\lambda } {:}& \, n_{\beta }^{{}} P_{\alpha \beta } = 0\,\,{\text{or }}\delta \varphi_{\alpha } = 0 \\ \delta u_{3,\alpha } {:}& \, n_{\beta } M_{\alpha \beta } = 0\,\,{\text{or }}\delta u_{ 3,\alpha } = 0 \\ \end{aligned} $$

(56)

where N _αβ , M _αβ , P _αβ and R _λ are given in Eqs. (28, 29) in Cheng et al. [14]; I, J, K, I _αβ , J _αβ , K _λβ in Eqs. (30, 31).

Appendix 3: Revision and correction of original models. Schmidt and Librescu’s model (1996, 1999, 2001) [15, 17, 24] revised

Schmidt and Librescu proposed different models for plates and shells with interlaminar bonding imperfection based on the derivation of a homogenized displacement field with a reduced number of unknowns. The models were formulated for geometrically nonlinear multilayered plates [15] and shells [24], using a first order shear approximation and assuming sliding only interfaces, and for linear multilayered shells with mixed-mode interfaces [17]. A revised formulation is presented here for the linear model proposed in [17]; the equations will be derived for the special case of shallow shell or flat plate, sliding only interfaces (mixed mode interfaces can be treated using the model presented in this paper) and zero body forces. The terminology used in [17] will be maintained, including vectors and tensors components, but for the differentiations which will be given as regular partial differentiations as allowed by the particularization to a flat plate presented here.

3.1 Displacement field (Eqs. 19a, b in [17])

$$ \begin{aligned} V_{\alpha }^{\left( k \right)} (x^{\omega } ,x^{3} ,t) & = v_{\alpha } + x^{3} \psi_{\alpha } + \sum\limits_{l = 1}^{k - 1} {\left[ {x^{3} - {}^{\left( l \right)}Z^{ + } } \right]\Omega _{\alpha }^{\left( l \right)} Y\left( {x^{3} - {}^{\left( l \right)}Z^{ + } } \right)} + \sum\limits_{l = 1}^{k - 1} {{}^{\left( l \right)}\hat{v}_{\alpha } Y\left( {x^{3} - {}^{\left( l \right)}Z^{ + } } \right)} \\ V_{3}^{\left( k \right)} (x^{\omega } ,x^{3} ,t) & = v_{3} \\ \end{aligned} $$

(57)

with $Y ( {x^{3} - {}^{ ( l )}Z^{ + } } ) = \{ {1{{ for }}( {x^{3} - {}^{( l )}Z^{ + } } ) \ge 0; \, 0{\text{ for }} ( {x^{3} - {}^{ ( l )}Z^{ + } } ) < 0} \}$

3.2 Interfacial tractions law (Eqs. 15a, 16a, 17a in [17])

$$ \begin{aligned} \hat{\sigma }_{{}}^{\alpha 3} =&\,\Gamma _{\lambda }^{\alpha } \left[\kern-0.15em\left[ {V^{\lambda } } \right]\kern-0.15em\right] \\ \left[\kern-0.15em\left[ {V^{\lambda } } \right]\kern-0.15em\right] =&\, V^{\lambda } \left( {0^{ - } } \right) - V^{\lambda } \left( {0^{ + } } \right) =& \hat{V}^{\lambda } (x^{\omega } ) \\ \left( {\Gamma ^{ - 1} } \right)_{\lambda }^{\alpha } B_{\alpha }^{\omega } =& \,\delta_{\lambda }^{\omega } \\ \end{aligned} $$

(58)

3.3 Transverse shear and normal strain components (Eqs. 20, 22, 21a, 21b, 23a in [17])

$$ \begin{aligned} E_{\alpha \beta }^{\left( k \right)} =&\, \mathop {e_{\alpha \beta } }\limits^{{0^{\left( k \right)} }} + x^{3} \mathop {e_{\alpha \beta } }\limits^{{1^{\left( k \right)} }} \\ E_{\alpha 3}^{\left( k \right)} =&\, \mathop {e_{\alpha 3} }\limits^{{0^{\left( k \right)} }} \\ \end{aligned} $$

(59)

with:

$$ \begin{aligned} 2\mathop {e_{\alpha \beta } }\limits^{{0^{\left( k \right)} }} & = v_{\alpha ,\beta } + v_{\beta ,\alpha } - \sum\limits_{l = 1}^{k - 1} {{}^{\left( l \right)}Z^{ + } \left( {\Omega _{\alpha ,\beta }^{\left( l \right)} +\Omega _{\beta ,\alpha }^{\left( l \right)} } \right)} + \sum\limits_{l = 1}^{k - 1} {\left( {{}^{\left( l \right)}\hat{v}_{\alpha ,\beta } + {}^{\left( l \right)}\hat{v}_{\beta ,\alpha } } \right)} \\ 2\mathop {e_{\alpha \beta } }\limits^{{1^{\left( k \right)} }} & = \psi_{\alpha ,\beta } + \psi_{\beta ,\alpha } + \sum\limits_{l = 1}^{k - 1} {\left( {\Omega _{\alpha ,\beta }^{\left( l \right)} +\Omega _{\beta ,\alpha }^{\left( l \right)} } \right)} \\ \mathop {2e_{\alpha 3} }\limits^{{0^{\left( k \right)} }} & = \psi_{\alpha } + v_{3,\alpha } + \sum\limits_{l = 1}^{k - 1} {\Omega _{\alpha }^{\left( l \right)} } \\ \end{aligned} $$

(60)

3.4 Transverse shear stress (Eqs. 33a in [17])

$$ {}^{\left( k \right)}\sigma^{\beta 3} = 2{}^{\left( k \right)}E^{\beta 3\alpha 3} E_{\alpha 3}^{\left( k \right)} $$

(61)

where E ^β3α3 are components of the elastic tensor.

3.5 Omega functions (Eqs. 40, 35b in [17])

$$ \Omega _{\alpha }^{\left( k \right)} = {}^{{\left( {1;k} \right)}}\Lambda _{ \cdot \alpha }^{\omega } \left( {\psi_{\omega } + v_{3,\omega } } \right) $$

(62)

with:

$$ {}^{{\left( {l;k} \right)}}\Lambda _{ \cdot \sigma }^{\omega } = 4{}^{\left( l \right)}E^{\beta 3\omega 3} \left( {{}^{{\left( {k + 1} \right)}}F_{\beta 3\sigma 3} - {}^{\left( k \right)}F_{\beta 3\sigma 3} } \right) $$

(63)

where F _β3α3 are components of the compliance tensor.

3.6 Displacement jumps (Eqs. 43, 45a in [17])

$$ {}^{(k)}\hat{v}_{\alpha }^{{}} = {}^{\left( k \right)}\Psi _{ \cdot \alpha }^{\rho } \left( {v_{3,\rho } + \psi_{\rho } } \right) $$

(64)

where:

$$ {}^{\left( k \right)}\Psi _{ \cdot \alpha }^{\rho } = {}^{\left( k \right)}B_{\lambda }^{\beta } {}^{{\left( {k + 1} \right)}}E^{\lambda 3\omega 3} \left( {\delta_{\omega }^{\rho } + \sum\limits_{l = 1}^{k} {{}^{{\left( {1;l} \right)}}\Lambda _{ \cdot \omega }^{\rho } } } \right) $$

(65)

3.7 Homogenized displacement field

$$ \begin{aligned} V_{\alpha }^{\left( k \right)} (x^{\omega } ,x^{3} ,t) & = v_{\alpha } + x^{3} \psi_{\alpha } + \left( {\psi_{\omega } + v_{3,\omega } } \right)\sum\limits_{l = 1}^{k - 1} {\left\{ {\left[ {\left( {x^{3} - {}^{\left( l \right)}Z^{ + } } \right){}^{{\left( {1;l} \right)}}\Lambda _{ \cdot \alpha }^{\omega } + {}^{\left( l \right)}\Psi _{ \cdot \alpha }^{\omega } } \right]Y\left( {x^{3} - {}^{\left( l \right)}Z^{ + } } \right)} \right\}} \\ V_{3}^{\left( k \right)} (x^{\omega } ,x^{3} ,t) & = v_{3} \\ \end{aligned} $$

(66)

3.8 Homogenized strain components

$$ 2\mathop {e_{{\alpha \beta }} }\limits^{{0^{{(k)}} }} = v_{{\alpha ,\beta }} + v_{{\beta ,\alpha }} + \left( {\psi _{{\omega ,\beta }} + v_{{3,\omega \beta }} } \right)\sum\limits_{{l = 1}}^{{k - 1}} {\left( { - {}^{{\left( l \right)}}Z^{ + } {}^{{\left( {1;l} \right)}}\Lambda _{{ \cdot \alpha }}^{\omega } + {}^{{\left( l \right)}}\Psi _{{ \cdot \alpha }}^{\omega } } \right) + \left( {\psi _{{\omega ,\alpha }} + v_{{3,\omega \alpha }} } \right)\sum\limits_{{l = 1}}^{{k - 1}} {\left( { - {}^{{\left( l \right)}}Z^{ + } {}^{{\left( {1;l} \right)}}\Lambda _{{ \cdot \beta }}^{\omega } + {}^{{\left( l \right)}}\Psi _{{ \cdot \beta }}^{\rho } } \right)} } \sum\limits_{{l = 1}}^{{k - 1}} {\left( { - {}^{{\left( l \right)}}Z^{ + } \;{}^{{\left( {1;l} \right)}}\Lambda _{{ \cdot \beta }}^{\omega } + {}^{{\left( l \right)}}\Psi _{{ \cdot \beta }}^{\omega } } \right)} 2\mathop {e_{{\alpha \beta }} }\limits^{{1(k)}} = \psi _{{\alpha ,\beta }} + \psi _{{\beta ,\alpha }} + \sum\limits_{{l = 1}}^{{k - 1}} {\left( {{}^{{\left( {1;l} \right)}}\Lambda _{{ \cdot \alpha }}^{\omega } \left( {\psi _{{\omega ,\beta }} + v_{{3,\omega \beta }} } \right){\text{ }}{}^{{\left( {1;l} \right)}}\Lambda _{{ \cdot \beta }}^{\omega } \left( {\psi _{{\omega ,\alpha }} + v_{{3,\omega \alpha }} } \right)} \right)} \mathop {2e_{{\alpha 3}} }\limits^{{0^{{(k)}} }} = \left( {\psi _{\omega } + v_{{3,\omega }} } \right)\left( {\delta _{{\alpha \omega }} + \sum\limits_{{l = 1}}^{{k - 1}} {{}^{{\left( {1;l} \right)}}\Lambda _{{ \cdot \alpha }}^{\omega } } } \right) $$

(67)

3.9 Hamilton equation (Eqs. 48 [17] revised)

(68)

(Note terms with line on top correct original equations).

3.10 Dynamic equilibrium equations (Eqs. 50a, b, c [17] revised)

(69)

where

(70)

(Note terms with line on top correct original equations).

where $\mathop {L^{\alpha \beta } }\limits^{0}$ , Q ^β3, $\, \mathop {L^{\alpha \beta } }\limits^{1}$ are given in Eqs. (51a, b, c), (A1), (A2) in Librescu and Schmidt [17]; $\mathop {p^{\alpha } }\limits^{0} ,\;\mathop {p^{3} }\limits^{0} ,\;\mathop {p^{\alpha } }\limits^{1}$ in Eqs. (52a, b, c); $\mathop {I^{\alpha } }\limits^{0} ,\;\mathop {I^{3} }\limits^{0} ,\;\mathop {I^{\alpha } }\limits^{1}$ in Eqs. (53a–c) as explained.

3.11 Static boundary conditions (Eqs. 56a–h [17] revised)

$$ \delta v_{\nu } {:} \, \mathop {L^{\alpha \beta } }\limits^{0} v_{\alpha } v_{\beta } = \mathop {{\mathop{L}\limits_{\sim}}^{\alpha \beta }}\limits^{0} v_{\alpha } v_{\beta } $$

$$ \delta v_{\tau } {:} \, \mathop {L^{\alpha \beta } }\limits^{0} \tau_{\alpha } \nu_{\beta } = \mathop {{\mathop{L}\limits_{\sim}}^{\alpha \beta } }\limits^{0} \tau_{\alpha } \nu_{\beta } $$

$$ \delta \psi _{\nu } {:}\left( {\mathop {L^{{\alpha \beta }} }\limits^{1} - K^{{\alpha \beta }} } \right)v_{\alpha } v_{\beta } = \left( {\mathop {{\mathop{L}\limits_{\sim}}^{{\alpha \beta }} }\limits^{1} - {\mathop{K}\limits_{\sim}}^{{\alpha \beta }} } \right)v_{\alpha } v_{\beta } $$

(71)

$$ \delta \psi _{\tau } :{\text{ }}\left( {\mathop {L^{{\alpha \beta }} }\limits^{1} - K^{{\alpha \beta }} } \right)\tau _{\alpha } v_{\beta } = \left( {\mathop {{\mathop{L}\limits_{\sim}}^{{\alpha \beta }} }\limits^{1} - {\mathop{K}\limits_{\sim}}^{{\alpha \beta }} } \right)\tau _{\alpha } v_{\beta } $$

$$ \delta v_{3,\alpha } {:} \, K^{\alpha \beta } \nu_{\beta } = {\mathop{K}\limits_{\sim}}^{\alpha \beta } \nu_{\beta } $$

where

and ${\varvec{\tau}}$ and ${\varvec{\upnu}}$ are unit tangent and outward normal vectors along the boundary curve of the plate; $\mathop {{\mathop{L}\limits_{\sim}}^{\alpha \beta } }\limits^{0}$, $\mathop {{\mathop{L}\limits_{\sim}}^{\alpha \beta } }\limits^{1}$, $\mathop {{\mathop{Q}\limits_{\sim}}^{\alpha 3} }\limits^{0}$, ${\mathop{P}\limits_{\sim}}^{\alpha }$ and ${\mathop{K}\limits_{\sim}}^{\alpha \beta }$ are given in Appendix B of [17].

Appendix 4: Revision and correction of original models. Di Sciuva model (1997) [16] revised

Di Sciuva formulated in [16] a general theory for geometrically nonlinear plates featuring interlayer slips where no a priori assumption is made on the order of the thickness expansion of the in-plane displacements. The theory is a development of the results obtained by the author in [12, 13] for multilayered fully bonded plates and for fully bonded shells in [42]. The linearized version of the theory is revised and corrected here.

4.1 Displacement field (Eqs. 7–10 in [16])

$$ \tilde{u}_{\alpha } (x_{j} ) = u_{\alpha } (x_{j} ) + U_{\alpha } (x_{j} ) + \hat{U}_{\alpha } (x_{j} ) $$

(72)

$$ \tilde{u}_{3} (x_{j} ) = u_{3}^{(0)} (x_{\beta } ) $$

where

$$ \begin{aligned} u_{\alpha } (x_{j} ) =&\, \sum\limits_{r = 0}^{R} {L^{(r)} \left( {x_{3} } \right)} \, u_{\alpha }^{(r)} (x_{\beta } ) \\ U_{\alpha } (x_{j} ) =&\, \sum\limits_{k = 1}^{N - 1} {{}^{(k)}\phi_{\alpha }^{{}} (x_{\beta } )\left( {x_{3} - {}^{(k)}Z_{{}}^{ + } } \right)H_{k} } \\ \hat{U}_{\alpha } (x_{j} ) =&\, \sum\limits_{k = 1}^{N - 1} {{}^{(k)}\hat{U}_{\alpha }^{{}} (x_{\beta } )H_{k} } \end{aligned}$$

(73)

with $H_{k} = H ( {x_{3} - {}^{ ( k )}Z^{ + } } ) = \{ {1{\text{ for }} ( {x_{3} - {}^{ ( k )}Z^{ + } } ) \ge 0; \, 0{\text{ for }} ( {x_{3} - {}^{ ( k )}Z^{ + } } ) < 0} \}$, ${}^{(k)}\hat{U}_{\alpha } (x_{\beta } )$ the jump at the interface with x ₃ = ^(k) Z ⁺ and ^(k) ϕ _α (x _β ) the kth zigzag function.

4.2 Interfacial tractions law (Eq. 22 in [16])

$$ {}^{(k)}\hat{U}_{\alpha } (x_{\tau } ,x_{3} = {}^{(k)}Z^{ + } ) = {}^{(k)}T_{\alpha \beta } (x_{\tau } ,x_{3} = {}^{(k)}Z^{ + } ) \times {}^{(k)}\tilde{\sigma }_{\beta 3} (x_{\tau } ,x_{3} = {}^{(k)}Z^{ + } )\, $$

(74)

with ${\mathbf{T}}$ the compliance tensor of the spring layer interface.

4.3 Stress and strain components (linearized problem) (Eqs. 2, 3 in [16])

$$ \tilde{e}_{ij} = \frac{1}{2}\left( {\tilde{u}_{i,j} + \tilde{u}_{j,i} } \right), \quad \tilde{\sigma }_{\alpha \beta } = Q_{\alpha \beta \gamma \delta } \tilde{e}_{\gamma \delta } , \quad \tilde{\sigma }_{\alpha 3} = 2Q_{\alpha 3\gamma 3} \tilde{e}_{\gamma 3} $$

(75)

where negligible normal tractions are assumed in the thickness direction and Q _αβγδ are the transformed reduced components of the stiffness tensor.

4.4 Zigzag functions from continuity on transverse shear tractions at interfaces (Eqs. 12–15 in [16])

$$ {}^{(k)}\phi_{\alpha }^{{}} (x_{\beta } ) = {}^{(k)}a_{\alpha \beta }^{{}} u_{3,\beta }^{(0)} + \sum\limits_{r = 0}^{R} {{}^{(k)}a_{\alpha \beta }^{(r)} u_{\beta }^{(r)} } $$

(76)

where:

$$ {}^{(k)}a_{\alpha \beta }^{{}} = {}^{(k)}A_{\alpha \beta }^{{}} + {}^{(k)}A_{\alpha \delta }^{{}} \sum\limits_{q = 1}^{k - 1} {{}^{(q)}a_{\delta \beta }^{{}} } $$

$$ {}^{(k)}a_{\alpha \beta }^{(r)} = {}^{(k)}A_{\alpha \beta }^{{}} \left. {L_{,3}^{(r)} } \right|_{{x_{3} = {}^{\left( k \right)}Z^{ + } }} + {}^{(k)}A_{\alpha \delta }^{{}} \sum\limits_{q = 1}^{k - 1} {{}^{(q)}a_{\delta \beta }^{(r)} } $$

$$ {}^{(k)}A_{\alpha \beta }^{{}} = - {}^{(k + 1)}S_{\alpha 3\gamma 3}^{{}} \left( {{}^{(k + 1)}Q_{\gamma 3\beta 3}^{{}} - {}^{(k)}Q_{\gamma 3\beta 3}^{{}} } \right) $$

(the last equation corrects a wrong sign in Eq. (15) in [16]).

4.5 Homogenized displacement jumps (Eqs. 23, 19, 20 in [16])

$$ {}^{(k)}\hat{U}_{\alpha }^{{}} = {}^{(k)}T_{\alpha \lambda }^{{}} (x_{\omega } ){}^{(k)}Q_{\lambda 3\gamma 3}^{{}} \times \left[ {\sum\limits_{r = 0}^{R} {P_{\gamma \beta ,3}^{(r)} u_{\beta }^{(r)} + \left( {\delta_{\gamma \beta }^{{}} + h_{\gamma \beta ,3}^{{}} } \right)u_{3,\beta }^{(0)} } } \right]_{{x_{3} = {}^{\left( k \right)}Z^{ + } }} $$

(77)

where:

$$ P_{\gamma \beta }^{(r)} = \delta_{\gamma \beta }^{{}} L_{{}}^{(r)} (x_{3} ) + \sum\limits_{k = 1}^{N - 1} {{}^{(k)}a_{\gamma \beta }^{(r)} \left( {x_{3} - {}^{\left( k \right)}Z^{ + } } \right)H_{k}^{{}} } $$

(78)

$$ h_{\gamma \beta }^{{}} = \sum\limits_{k = 1}^{N - 1} {{}^{(k)}a_{\gamma \beta }^{{}} \left( {x_{3} - {}^{\left( k \right)}Z^{ + } } \right)H_{k}^{{}} } $$

4.6 Homogenized displacement field (Eqs. 24, 25, 26 in [16])

$$ \tilde{u}_{\alpha } (x_{j} ) = \sum\limits_{r = 0}^{R} {\hat{P}_{\alpha \beta }^{(r)} (x_{3} )u_{\beta }^{(r)} (x_{\tau } ) + \hat{h}_{\alpha \beta } (x_{3} )u_{3,\beta }^{(0)} } (x_{\tau } ) $$

(79)

where

$$ \hat{P}_{\alpha \beta }^{(r)} (x_{3} ) = P_{\alpha \beta }^{(r)} (x_{3} ) + \sum\limits_{k = 1}^{N - 1} {{}^{(k)}T_{\alpha \lambda }^{{}} {}^{(k)}Q_{\lambda 3\gamma 3}^{{}} P_{\gamma \beta ,3}^{(r)} \left( {{}^{\left( k \right)}Z^{ + } } \right)H_{k}^{{}} } $$

(80)

$$ \hat{h}_{\alpha \beta }^{{}} (x_{3} ) = h_{\alpha \beta }^{{}} (x_{3} ) + \sum\limits_{k = 1}^{N - 1} {{}^{(k)}T_{\alpha \lambda }^{{}} {}^{(k)}Q_{\lambda 3\gamma 3}^{{}} } \left[ {\delta_{\gamma \beta }^{{}} + h_{\gamma \beta ,3}^{{}} \left( {{}^{\left( k \right)}Z^{ + } } \right)H_{k}^{{}} } \right] $$

4.7 Principle of virtual displacements equation (Eq. 29 [16] revised)

(81)

(Note terms with line on top correct original equations).

4.8 Dynamic equilibrium equations (Eqs. 37, 38 [16] revised)

(82)

(Note terms with line on top correct original equations).

4.9 Static boundary conditions (Eqs. 49b, 50b, 51b [16] revised)

$$ \delta u_{\gamma }^{(r)} : \, \hat{S}_{\gamma n}^{(r)} = \overline{{\hat{S}_{\gamma n}^{(r)} }} $$

$$ \delta u_{3,n}^{(0)} : \, \hat{M}_{nn} = \overline{\hat{M}}_{nn} $$

(83)

where $\hat{S}_{\alpha \gamma }^{(s)}$ and $\hat{M}_{\alpha \gamma }$ are given in Eq. (33) in [16], $\hat{V}_{3}$ in Eq. (31), T _γ , Q _γ and T ^(r) _γ in Eq. (34), m ⁽ⁱ⁾, $\hat{m}_{\gamma \beta }^{{}}$, $\hat{m}_{\gamma \beta }^{(r)}$, $\hat{m}_{\gamma \beta }^{(r,s)}$ in Eq. (35) and $\overline{{\hat{S}_{\gamma n}^{(r)} }}$, $\overline{\hat{M}}_{\gamma n}$ and $\overline{V}_{3}$ in Eq. (36).

Appendix 5: Equilibrium equations and boundary conditions in multilayered plates with sliding interfaces, subjected to transverse loading and deforming in cylindrical bending

Equilibrium equations in terms of generalized displacements:

$$ \delta v_{0 2} {:}\,w_{0, 2 2 2} C_{ 2 2}^{0S} + v_{0 2, 2 2} C_{ 2 2}^{0} + \varphi_{ 2, 2 2} \left( {C_{ 2 2}^{ 1} + C_{ 2 2}^{0S} } \right) = 0, $$

(84)

(85)

(86)

where:

$$ \begin{aligned} C_{22}^{r} &= \sum\limits_{k = 1}^{n} {{}^{\left( k \right)}\overline{C}_{2222} \int_{{x_{3}{}^{k - 1} }}^{{x_{3}^{k} }} {\left( {x_{3} } \right)^{r} dx_{3} } }, \\ C_{22}^{rS} &= \sum\limits_{k = 1}^{n} {{}^{\left( k \right)}\overline{C}_{2222}\int_{{x_{3}{}^{k - 1}} }^{{x_{3}{}^{k} }} {\left( {x_{3} } \right)^{r} R_{S22}^{k} dx_{3} } } , \end{aligned}$$

(87)

$$\begin{aligned} C_{22}^{S2} &= \sum\limits_{k = 1}^{n} {{}^{\left( k \right)}\overline{C}_{2222} \int_{{x_{3}{}^{k - 1} }}^{{x_{3}{}^{k} }} {\left( {R_{S22}^{k} } \right)^{2} } dx_{3}, } \\ C_{23}^{P} &= \sum\limits_{k = 1}^{n} {\int_{{x_{3}^{k - 1} }}^{{x_{3}{}^{k} }} {{}^{(k)}C_{2323}^{{}} \left( {1 + \sum\limits_{i = 1}^{k - 1} {\Lambda _{22}^{{\left( {1;i} \right)}} } } \right)^{2} } dx_{3} } \end{aligned} $$

(88)

Mechanical boundary conditions in terms of displacements:

$$ \delta v_{0 2} :\left[ {v_{02,2} C_{22}^{0} + \varphi_{2,2} \left( {C_{22}^{1} + C_{22}^{0S} } \right) + w_{0,22} C_{22}^{0S} } \right]n_{2} = \tilde{N}_{2}^{B} $$

(89)

(90)

$$ \delta \varphi_{ 2} :\left[ {v_{02,2} C_{22}^{1} + \varphi_{2,2} \left( {C_{22}^{2} + C_{22}^{1S} } \right) + w_{0,22} C_{22}^{1S} } \right]n_{2} = \tilde{M}_{2}^{B} - \tilde{M}_{2}^{zB} $$

(91)

(92)

In the definition of the equations above, the transverse shear resultant, Eq. (28a), and strain, Eq. (15b), have been related through $Q_{{\text{2}}} = K^{{\text{2}}} C_{{23}}^{P} \left( {w_{{0,{\text{2}}}} + \varphi _{{\text{2}}} } \right)$, where $\left( {w_{{0,2}} + \varphi _{2} } \right) = 2\varepsilon _{{23}} (1 + \sum\limits_{{i = 1}}^{{k - 1}} {\Lambda _{{22}}^{{\left( {1;i} \right)}} } )^{{ - 1}},\; C^{P}_{23}$ is the shear stiffness given in Eq. (88) and K ² is a shear correction factor, which is needed in this first order theory to properly account for the contribution of the shear deformations to the displacement field, as a consequence of the approximation in the distribution of the shear stresses in the thickness. In a unidirectionally reinforced, perfectly bonded plate, C ^P₂₃  = C ₂₃₂₃ h with C ₂₃₂₃ the transverse shear modulus, Q ₂ = σ ₂₃ h, and K ² is that appropriate for a single-layer plate, i.e. K ² = 5/6. In a perfectly bonded, multilayered plate, K ² becomes a problem dependent parameter (e.g. [37]); in [12] it was shown that, for simply supported plates with common layups and geometrical/loading conditions, the homogenized theory with K ² = 1 leads to accurate predictions of the displacement field. In a plate with imperfect interfaces, the difference between the transverse shear strain, 2ɛ ₂₃, and the generalized shear strain, 2ɛ _23g , introduced in Sect. 6, which is the actual measure of the shear deformations in the plate, can be very large, especially in thick plates with very compliant interfaces. The transverse displacements of the plates, obtained through the solution of the system of differential equations (84)–(86), which depend on 2ɛ ₂₃ only, are then underestimated. To overcome this problem, we are currently working on a modification of the shear factor that could be made dependent on the interfacial properties. Work on this problem is in progress and the results presented in Sect. 8 refer to K ² = 5/6 (unidirectionally reinforced plate) and K ²  = 1 (multilayered plate).

Appendix 6: Extension of Pagano’s model [33] to plates with linearly elastic interfaces

The exact 2D elasticity solution for a multilayered plate with perfectly bonded interfaces deforming in cylindrical bending was obtained by Pagano in [33]. Pagano’s approach was extended to model multilayered plates with linearly elastic interfaces in [34]. The strategy proposed in [34] is briefly recalled here.

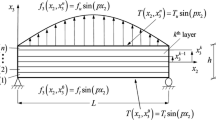
The solution refers to plates of length L with linearly elastic interfaces, subjected to a quasi-static transverse load q = q ₀ sin (πx ₂/L), simply supported at the edges at x ₂ = 0 and x ₂ = L and deforming in cylindrical bending (Fig. 3). A system of local axes of material symmetry ^(k) x ₂ and ^(k) x ₃ is introduced with the origin at the kth layer mid-plane and the axis ^(k) x ₂ longitudinal and parallel to the global mid-plane longitudinal axis x ₂. The solution is based on a stress function approach, where the stress function for the kth layer is:

$$ {}^{\left( k \right)}\Phi \left( {{}^{\left( k \right)}x_{2} ,{}^{\left( k \right)}x_{3} } \right) = {}^{\left( k \right)}f\left( {{}^{\left( k \right)}x_{3} } \right)\sin \left( {{{\pi {}^{\left( k \right)}x_{2} } \mathord{\left/ {\vphantom {{\pi {}^{\left( k \right)}x_{2} } L}} \right. \kern-0pt} L}} \right) , $$

(93)

which is related to the stress components by:

$$ {}^{\left( k \right)}\sigma_{22} = {}^{\left( k \right)}\Phi ,_{33}{;} \, {}^{\left( k \right)}\sigma_{33} = {}^{\left( k \right)}\Phi ,_{22}{;} \, {}^{\left( k \right)}\sigma_{23} = - {}^{\left( k \right)}\Phi ,_{23} $$

(94)

Compatibility and constitutive equations (${}^{(k)}{\varvec{\upvarepsilon}} \, = \, {}^{(k)}{\tilde{\mathbf{A}}}{}^{(k)}{\varvec{\upsigma}}$) yield the fourth order ordinary differential equation :

$$ {}^{(k)}\tilde{A}_{22} {}^{(k)}f_{,3333} - \left( {{}^{(k)}\tilde{A}_{55} + 2{}^{(k)}\tilde{A}_{23} } \right)\left( {\frac{\pi }{L}} \right)^{2} {}^{(k)}f_{,33} + {}^{(k)}\tilde{A}_{33} \left( {\frac{\pi }{L}} \right)^{4} {}^{(k)}f = 0 \, , $$

(95)

where the tilde indicates compliance coefficients which account for plane strain conditions parallel to the plane ^(k) x ₂-^(k) x ₃. The general solution for an orthotropic layer is:

$$ {}^{\left( k \right)}f = \sum\limits_{j = 1}^{4} {c_{jk} } \exp (m_{jk} {}^{\left( k \right)}x_{3} ) $$

(96)

where the c _jk are constants, provided the m _jk are all distinct. The m _jk are functions of the compliance coefficients [33], $m_{1k} ,m_{2k} = \pm {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}\sqrt {{{(a_{k} + b_{k} )} \mathord{\left/ {\vphantom {{(a_{k} + b_{k} )} {c_{k} }}} \right. \kern-0pt} {c_{k} }}}$ and $m_{3k} ,m_{4k} = \pm {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}\sqrt {{{(a_{k} - b_{k} )} \mathord{\left/ {\vphantom {{(a_{k} - b_{k} )} {c_{k} }}} \right. \kern-0pt} {c_{k} }}}$, with $a_{k} = {}^{(k)}\tilde{A}_{55} + 2{}^{(k)}\tilde{A}_{23}$, $b_{k} = \sqrt {a_{k}^{2} - 4{}^{(k)}\tilde{A}_{22} {}^{(k)}\tilde{A}_{33} }$ and $c_{k} = 2{}^{(k)}\tilde{A}_{22}$. If a _k  > b _k and $a_{k}^{2} > 4{}^{(k)}\tilde{A}_{22} {}^{(k)}\tilde{A}_{33}$, then the m _jk are all real and distinct and the c _jk are all real. For materials that do not satisfy the above condition, the solution for a fully bonded plate is given in [43]. The displacement field is:

$$ \begin{aligned} {}^{\left( k \right)}v_{2} & = {\rm cos}\left( {{{\pi {}^{\left( k \right)}x_{2} } \mathord{\left/ {\vphantom {{\pi {}^{\left( k \right)}x_{2} } L}} \right. \kern-0pt} L}} \right)\frac{L}{\pi }\left[ { - \tilde{A}_{22} {}^{(k)}f_{,33} + \tilde{A}_{23} \left( {\frac{\pi }{L}} \right)^{2} {}^{(k)}f} \right] \\ {}^{\left( k \right)}w & = {\rm sin}\left( {{{\pi {}^{\left( k \right)}x_{2} } \mathord{\left/ {\vphantom {{\pi {}^{\left( k \right)}x_{2} } L}} \right. \kern-0pt} L}} \right)\left[ {\tilde{A}_{23} {}^{(k)}f_{,3} - \tilde{A}_{33} \left( {\frac{\pi }{L}} \right)^{2} \int {{}^{(k)}f} d{}^{\left( k \right)}x_{3} } \right] \\ \end{aligned} . $$

(97)

The boundary conditions at the plate ends are identically satisfied by the functions (94) and (97). The 4 × n arbitrary constants in Eq. (96) are determined by imposing the remaining boundary conditions at the upper and lower surfaces of the plate, continuity conditions at the interfaces between layers and the constitutive laws of the interfaces:

$$ \begin{aligned} {}^{\left( k \right)}\sigma_{23} \left( {x_{3}^{k} } \right) & = K_{2}^{k} \left[ {{}^{{\left( {k + 1} \right)}}v_{2} \left( {x_{3}^{k} } \right) - {}^{\left( k \right)}v_{2} \left( {x_{3}^{k} } \right)} \right], \, \\ {}^{\left( k \right)}\sigma_{33} \left( {x_{3}^{k} } \right) & = K_{N}^{k} \left[ {{}^{{\left( {k + 1} \right)}}w\left( {x_{3}^{k} } \right) - {}^{\left( k \right)}w\left( {x_{3}^{k} } \right)} \right], \\ \end{aligned} $$

(98)

where the global coordinate x ^k₃ defines the interface k between the layers k and k + 1.