1 Introduction

A queue where the customers that cannot be served within a fixed time leave the system is usually referred to as a queue with impatient customers or a queue with bounded waiting time. To describe such systems balking and reneging have also been used as denominations, see Ancker and Gafarian (1963).

The motivation for studying such queues has often been problems in telecommunication where the main challenge is to dimension the system so that on the one hand not too many calls are lost and on the other hand not having too many servers, which means that more equipment than necessary is used. An early contribution with the possibility that the customers hang up and leave the system is Palm (1957). Also notice that bounding the waiting time can act as a simple load control.

Another field where models allowing impatient customers arise is perishable inventory theory. In blood banks the supply of blood portions is random and shelf time is limited, see Perry and Stadje (2022) for some discussion and also the monographs of Nahmias (2012) and Karaesmen et al. (2011). In contrast to the previous situation the impatience time is usually less manageable and must often be considered as fixed.

The operation of call centers is a third area where impatience has to be taken into account. This is stressed in several papers by Mandelbaum and coauthors, see e.g. Mandelbaum and Zeltyn (2009). The crucial question here is to avoid that the center is understaffed, rejecting too many customers, or overstaffed such that the proportion of time the servers are unoccupied is larger than necessary.

In all areas of application mentioned above there is a trade-off between loosing too many customers and having too many idle servers. Knowledge of the distribution of the waiting times and loads is helpful for choosing an appropriate impatience time, when that is possible. For managerial decisions and design of this kind of systems, especially deciding on the number of servers, such insight is crucial.

In this note we will consider a first-come first-served queue with c servers where the service times are independent exponential random variables with expectation \(1/\mu\). The arrivals of new customers follow a renewal process where the distribution of the inter-arrival times is of the phase type. Customers whose waiting time exceeds the fixed non-random impatience time \(\tau\) leave the system. This system is often denoted as PH/M/c+D.

The main contribution of the present note is that in a PH/M/c queue with impatient customers where the impatient time is deterministic, explicit solutions, up to some matrix inversions, exist for the stationary asymptotic distribution of the remaining loads and consequently for the virtual and the actual waiting time. It turns out that the procedure proposed by Swensen (1986) with a Coxian distribution describing the renewal input process, can be extended, with some adjustments, to the more general case where a phase type distribution is used. The key result for the generalization can be found in Lemma 2 in Appendix B.

Relevant papers dealing with impatient customers are Choi et al. (2004) and Kawanishi and Takine (2016) who considered the more general Markovian arrival process, MAP/M/c queue with bounded waiting or impatience time. He and Wu (2020) treated the situation where the impatience time is not constant. Kawanishi and Takine (2015) derived the stationary distribution for the virtual waiting time in a PH/M/c queues with impatient customers. It is worth noticing that the results in Choi et al. (2004) and Kawanishi and Takine (2015, 2016) are complementary to the results in the present paper. The distribution of the virtual waiting time in those papers is derived directly by solving a second order differential equation. The distributions of the waiting times, virtual and actual, in Swensen (1986) are derived as an implication of the distribution of the loads of the servers. Thus, the results and methods of proof are different and a natural question is how they are related. We will discuss this issue. In particular we compare the density for the virtual waiting time derived by Kawanishi and Takine (2015) with the expression of the present note.

Although the distribution of the virtual waiting time is important, knowledge of the simultaneous distribution of the remaining loads of the servers represents an additional value. For example, one can focus on the simultaneous remaining loads of a particular group of servers, cf. the famous Palm-Jacobæus formula in the telecommunication literature.

It is also worth remarking that the methods for the numerical computations of the distributions in the two cases are quite different. In papers by Choi et al. (2004) and Kawanishi and Takine (2015, 2016) the expressions that are used involve matrix exponentials. On the other hand, the formula for the probability density of the remaining loads in the present paper is quite easy to evaluate when a procedure for computing matrix eigenvalues and eigenvectors is available.

The note is organized as follows. The distribution of the remaining loads for phase type distributed arrival times is derived in the next section. In section 3 the relation between the implied distribution of the virtual waiting time relying on the distribution of the remaining load and the more direct version in Kawanishi and Takine (2015) is discussed. In section 4 the solution of a linear equation which is important for finding the asymptotic distribution of the remaining loads is considered. In section 5 we discuss how the results on the distribution of the remaining loads can be used to find distributions for fixed particular servers and carry out the actual computations in an exampel. In the Appendices the necessary modifications of the Kolmogorov forward equations for the remaining loads for phase type distributed inter-arrival times are explained. The stationary solution to these equations is found and some lemmas crucial for the derivation are proved.

We use the following notation, as in Swensen (1986): a phase type distribution is described by the pair \((\boldsymbol{\gamma },T)\) where \(\boldsymbol{\gamma }= (\gamma _{1},\ldots ,\gamma _{m})\) is a probability vector, i.e. \(\gamma _{1},\ldots ,\gamma _{m} \ge 0\), \(\sum _{i=1}^m=1\), and T is a non-singular \(m \times m\) matrix with negative diagonal elements and nonnegative off-diagonal elements. The Coxian distributions define the subclass of the phase type distributions where \(\boldsymbol{\gamma } =(1,0,\ldots ,0)\) and the only nonnegative elements of the matrix \(T=\{t_{ij}\}\) are the elements \(t_{i(i+1)},\; i=1,\ldots ,m-1\).

To a large extent the arguments used in the treatment of the Coxian case carry over to the phase type case. Therefore there will be some overlap with Swensen (1986) when the arguments are verified in the phase type setup.

In the following we consider the scalar field of complex numbers and matrices whose elements also are complex numbers.

2 Distribution of Remaining Loads

Consider the process \((Y(t),V_1(t),\ldots ,V_c(t))\) where \(V_i(t)\) is the unfinished work, i.e. the remaining load, for sever \(i\;=1,\dots ,c\) and Y(t) is the phase of the arrival process. Under the assumptions that the service times are independent, exponentially distributed and that the arrival process is a renewal process where the distribution of the inter-arrival times is of the phase type, the process is Markovian.

The phase type distribution of the inter-arrival times satisfies

Assumption 1

  1. (i)

    The m solutions \(\{\eta _1,\ldots ,\eta _m\}\) of \(\det [c\mu \textbf{e}\cdot \boldsymbol{\gamma } +T-c\eta I_m] = 0\) are distinct and are not equal to any of the eigenvalues of T/c.

  2. (ii)

    The matrix \(T+\textbf{T}\cdot \boldsymbol{\gamma }\) where \(\textbf{T}=-T\textbf{e}, \textbf{e}=(1,\cdots ,1)'\), is irreducible and has distinct eigenvalues.

Remark 1. The claim in Assumption 1 that there are no equal eigenvalues of \(\mu \textbf{e}\cdot \boldsymbol{\gamma } +T/c\) and no equal eigenvalues of \(T+\textbf{T}\cdot \boldsymbol{\gamma }\) simplifies the derivations since there is only one eigenvector associated with each eigenvalue. We therefore exclude the situation where the dimension of the eigenspace of an eigenvalue is strictly less than the algebraic multiplicity of the eigenvalue, i.e. where the geometric multiplicity is less than the algebraic multiplicity, see Horn and Johnson (2013).

The m solutions \(\{\eta _1,\ldots ,\eta _m\}\) are sorted in decreasing order according to size of the moduli. For a conjugate pair the number with positive imaginary part is counted first. Also, define B as the matrix where the rows are the left normalized eigenvectors of \(T+ \textbf{T}\cdot \boldsymbol{\gamma }\). Let D be the diagonal matrix with diagonal elements \((c\mu -\kappa _{\ell })^{-1},\;\ell =1,\ldots ,m\) where \(\kappa _{\ell },\;\ell =1,\ldots ,m\) are the eigenvalues of \(T+ \textbf{T}\cdot \boldsymbol{\gamma }\) and where one, \(\kappa _1\) say, is equal to 0. Let E be the diagonal matrix with diagonal elements \(\exp (-\tau c \eta _{\ell }),\;\ell =1,\ldots ,m\).

The following theorem is a description of the density of the asymptotic distribution of the remaining loads.

Theorem 1

Consider a first-come first-served GI/M/c queuing model with waiting time bounded by \(\tau\), service rate \(\mu\) and inter-arrival distribution of the phase type \((\boldsymbol{\gamma },T)\). Under Assumption 1 the stationary asymptotic distribution of the remaining loads \(V_1,\ldots , V_c\) has density

$$\begin{aligned} \mu ^{c-1}\exp (-\mu (v_1+\cdots +v_c) + c\mu (\tau \wedge \min v_i)) \sum _{k=1}^m \delta _k \underline{y}_{c}^k\textbf{e} \exp (-c\eta _{k}(\tau \wedge \min v_i)) \end{aligned}$$
(1)

for \(\min V_i >0\) where \(\boldsymbol{\delta }=(\delta _1,\ldots ,\delta _m)\) is the solution of

$$\begin{aligned} \boldsymbol{\delta }EY_{c-1}[c\mu \textbf{T}\cdot \boldsymbol{\gamma } B^{-1}DB-(c-1)\mu I_m+(c-1)\mu \textbf{e} \cdot \boldsymbol{\gamma } + T]=0 \end{aligned}$$
(2)

and

$$\begin{aligned} \sum _{k=1}^m \delta _k \{ \sum _{i=0}^{c-1}\left( {\begin{array}{c}c\\ i\end{array}}\right) \underline{y}_{i}^k \textbf{e} + \underline{y}_{c}^k\textbf{e} [(\frac{1}{\mu }-\frac{1}{\eta _k})\exp {(-c\eta _k \tau ) + \frac{1}{\eta _k}}]\}=1. \end{aligned}$$
(3)

The matrix \(Y_{c-1}\) has rows \(\underline{y}_{c-1}^1,\ldots , \underline{y}_{c-1}^m\) where \(\underline{y}_{c-1}^k\) is the solution of the homogenous linear equation

$$\begin{aligned} \underline{y}_{c-1}^k[(c-1)\mu I_m -(c-1) \mu \textbf{e}\cdot \boldsymbol{\gamma }-T- c \mu R_{k}] =0 \end{aligned}$$

with \(y_{c-1 1}^k =1\) and the \(m \times m\) matrix \(R_{k} =\textbf{T} \cdot \boldsymbol{\gamma } [c\eta _k I_m -T]^{-1},\; k=1,\ldots ,m\).

Furthermore, when \(c=1\), \(\underline{y}_{1}^k=c\mu \underline{y}_{0}^kR_{k}\). When \(c > 1\), \(\underline{y}_{c}^k=c\mu \underline{y}_{c-1}^k R_{k}\) and \(\underline{y}_{0}^k,\ldots ,\underline{y}_{c-2}^k,\) \(k=1,\ldots ,m\) are defined by the recursion

$$\begin{aligned} \begin{array}{l} \underline{y}_{i}^k=(c-i)\mu \underline{y}_{i+1}^k( i\mu I_m - i \mu \textbf{e}\cdot \boldsymbol{\gamma }-T)^{-1}, \; i=c-2,\ldots ,1 \\ \underline{y}_0^k=-c\mu \underline{y}_1^k T^{-1}. \end{array} \end{aligned}$$

Remark 2. From Lemma 3 it follows that the matrices \([(c-1)\mu I_m -(c-1) \mu \textbf{e}\cdot \boldsymbol{\gamma }-T- c \mu R_{k}]\) have rank m-1 such that \(\underline{y}_{c-1}^k,\; k=1,\ldots ,m\) are determined up to a normalizing constant. Also it follows frem Lemma 1 in Neuts (1982) that when \(c>1\), the matrices \(( i\mu I_m - i \mu \textbf{e}\cdot \boldsymbol{\gamma }-T), \; i=1,\ldots ,c-2\) are nonsingular.

The proof of the theorem is an elaboration of Swensen (1986) for the case where the inter-arrival distribution is Coxian. In the first step to prove the main result we show, in Appendix A, that when \(t \rightarrow \infty\) the functions

$$\begin{aligned} q_{k0j}= & {} y_{0j}^k,\;j=1,\ldots ,m, \end{aligned}$$
(4)
$$\begin{aligned} q_{kij}(v_1,\ldots ,v_i)= & {} \mu ^{i}y_{ij}^k\exp (-\mu (v_1+\cdots +v_i)),\;i=1,\ldots , c-1,\;j=1,\ldots ,m, \end{aligned}$$
(5)
$$\begin{aligned} q_{kcj}(v_1,\ldots ,v_c)= & {} \mu ^{c-1}y_{cj}^k\exp (-\mu (v_1+\cdots +v_c) +c(\mu -\eta _k)v_{(1)}),\;j=1,\ldots ,m, \end{aligned}$$
(6)

for \(k=1,\ldots ,m\), satisfy the differential equation defined by the Kolmogorov forward equations in the region \(v_{(1)}=\min v_i \le \tau\). Since \(\eta _1,\ldots ,\eta _m\) are distinct the solutions are independent and the general solution in this region therefore has the form \(\textbf{Q} =\sum _{k=1}^m \delta _k \textbf{Q}_k\).

As a second step, the function \(\textbf{Q}\) is inserted in the Kolmogorov forward equation to obtain a differential equation for values in the region \(\min v_i > \tau\). In Appendix A it is shown that the solution has the form

$$\begin{aligned} K\exp (-\mu (v_1+\cdots +v_c))\boldsymbol{\gamma } B^{-1}D B \end{aligned}$$

where \(K= \sum _{k=1}^m \delta _k c \mu ^c\underline{y}_{c-1}^k \textbf{T}\exp (c(\mu -\eta _k)\tau )\).

Finally, in the third step the distribution of the remaining loads is determined by requiring that the solutions for \(\min v_i \le \tau\) and \(\min v_i > \tau\) are continuous at \(\min v_i = \tau\).

3 Distribution of the Virtual Waiting Time

Building on the results in Choi et al. (2004) and Kawanishi and Takine (2015) found an explicit expression for the stationary joint distribution of the phase of the arrival process and the virtual waiting time. The density of the stationary virtual waiting time has the form

$$\begin{aligned} \textbf{v}(v)\textbf{e}=(v_1(v),\ldots ,v_m(v))\textbf{e}=p {\hat{\textbf{v}}}\exp [(c\mu \textbf{e}\cdot \boldsymbol{\gamma } +T)(\tau -v) ]\textbf{e},\; 0<v< \tau \end{aligned}$$
(7)

where \({\hat{\textbf{v}}}=(\hat{v}_1,\ldots ,\hat{v}_m)= \boldsymbol{\gamma }(c\mu I-T)^{-1}/\boldsymbol{\gamma }(c\mu I-T)^{-1}\textbf{e}\), and p is the normalizing constant given in Kawanishi and Takine (2015).

However, an expression for the density of the stationary virtual waiting time can also be obtained from the density of the remaining loads. Differentiating the expression for the complimentary distribution function in Swensen (1986) one gets the probability density of virtual waiting time when Assumption 1 is satisfied

$$\begin{aligned} f(v)= \sum _{k=1}^m\delta _k (y_c^k \textbf{e})\;c\exp {(-c\eta _kv)}, \; 0<v <\tau \end{aligned}$$
(8)

where \(\boldsymbol{\delta }=(\delta _1,\ldots ,\delta _m)\) is defined in Theorem 1. By the same arguments as in the next section it follows that the expression (8) has an imaginary part equal to zero.

The following proposition summarizes the relation between the two expressions of the density.

Proposition 1

If Assumption 1 holds the coefficients of (8) are given by

$$\begin{aligned} \delta _k (y_c^k \textbf{e})= p\exp (c \eta _k \tau )\sum _{j,\ell =1}^m \hat{v}_j f_{j,k}\, f^{k\ell }/c,\;k=1,\ldots ,m \end{aligned}$$
(9)

where \(c\eta _1,\ldots , c\eta _m\) are the eigenvalues of \(c\mu \textbf{e}\cdot \mathbf {\gamma }+T\), \(F=\{\,f_{j\ell }\}_{j,\ell =1}^m\) is the matrix where the columns are the right eigenvectors of the matrix \(c\mu \textbf{e}\cdot \mathbf {\gamma }+T\) and \(F^{-1} = \{\,f^{j\ell }\}_{j,\ell =1}^m\).

Also

$$\begin{aligned} p=c\sum _{k=1}^m\delta _k (y_c^k\textbf{e}) \exp (- c \eta _k \tau ). \end{aligned}$$
(10)

Proof. Assumption 1i) implies that \(c\mu \textbf{e}\cdot \boldsymbol{\gamma } +T\) is diagonalizable, that is \(c\mu \textbf{e}\cdot \boldsymbol{\gamma } +T= F \text{ diag }(c\eta _1,\ldots ,c\eta _m ) F^{-1}\) where the m eigenvalues \(\{c\eta _1,\ldots ,c\eta _m\}\) are sorted in decreasing order according to the size of the moduli. From elementary properties of the exponential matrix it follows that

$$\begin{aligned} \begin{aligned} p {\hat{\textbf{v}}}\exp&\; [(c\mu \textbf{e}\cdot \boldsymbol{\gamma } +T)(\tau -v) ]\textbf{e}\\ {}&=p {\hat{\textbf{v}}}F\exp [ \text{ diag } ({c\eta _1(\tau -v)},\ldots ,{c\eta _m(\tau -v))}]F^{-1}\textbf{e}\\ {}&=p {\hat{\textbf{v}}}F\text{ diag } (\exp (c\eta _1(\tau -v)),\ldots , \exp (c\eta _m(\tau -v)))F^{-1}\textbf{e}\\ {}&=p \sum _{k=1}^m[ \exp (c \tau \eta _k)\sum _{j,\ell =1}^m \hat{v}_j f_{j,k}\,f^{k\ell }]\exp (-c\eta _k v),\; 0<v<\tau . \end{aligned} \end{aligned}$$

Hence by comparing the coefficients of \(\exp (-c\eta _1),\ldots , \exp (-c\eta _m),\)

$$\begin{aligned} \delta _k(y_c^k \textbf{e})= p\exp ( c\tau \eta _k )\sum _{j,\ell =1}^m \hat{v}_j f_{j,k}\,f^{k\ell }/c,\;k=1,\ldots ,m \end{aligned}$$

which is (9). This shows how the density (8) for the virtual waiting time can be expressed using the results (7) from Kawanishi and Takine (2015).

Furthermore, summing over k, since \(\sum _{k=1}^m f_{j,k}\,f^{k\ell } =1\) if \(j=\ell\) and 0 if \(j\ne \ell\),

$$\begin{aligned} \begin{aligned} \sum _{k=1}^m\delta _k (y_c^k \textbf{e})\exp (- c\tau \eta _k )&= p\sum _{j,\ell =1}^m \hat{v}_j \sum _{k=1}^m f_{j,k}\,f^{k\ell }/c= p\sum _{j=1}^m \hat{v}_j/c= p {\hat{\textbf{v}}}\textbf{e}/c\\ {}&=\frac{1}{c}p\boldsymbol{\gamma }(c\mu I-T)^{-1}\textbf{e}/\boldsymbol{\gamma }(c\mu I-T)^{-1}\textbf{e}= p/c \end{aligned} \end{aligned}$$

which is (10). \(\blacksquare\)

Remark 3. For numerical computations the representation in (8) yields an alternative to the approach using matrix exponentials suggested by Kawanishi and Takine (2015). With a procedure computing eigenvalues and eigenvectors the quantities \(\delta _1,\ldots ,\delta _m\) can be found as described in Theorem 1.

4 Solution of the Linear Equations (2) and (3)

The linear equations (2) and (3) can be solved directly by writing them on the form \(A\boldsymbol{\delta }'=e_{m+1}\) where A is a \((m+1)\times m\) matrix and \(e_{m+1}\) is a \((m+1)\)-dimensional vector with all elements equal to 0 except the last which equals 1. Then, using a QR factorization, as described in Theorem 2.1.14 in Horn and Johnson (2013), there exist a \((m+1)\times m\) matrix Q with orthonormal columns and an upper triangular \(m\times m\) matrix R such that the linear equations may be expressed as \(QR\boldsymbol{\delta }'=e_{m+1}\) from which \(\boldsymbol{\delta }\) is easily found.

But there is an alternative way to obtain a solution starting with solving

$$\begin{aligned} \boldsymbol{\phi }[c\mu \textbf{T}\cdot \boldsymbol{\gamma } B^{-1}DB-(c-1)\mu I_m+(c-1)\mu \textbf{e} \cdot \boldsymbol{\gamma } + T]=0 \end{aligned}$$
(11)

which is determined up to a normalization by Lemma 4. Normalizing the first element of \(\boldsymbol{\phi }\) as 1, it follows from Lemma 1 that all elements of \(\boldsymbol{\phi }\) are real.

Lemma 1

The solutions of Eq. (11) have real elements.

Proof. If \(\boldsymbol{\kappa }\) is the diagonal matrix with diagonal elements \(\kappa _1,\ldots ,\kappa _m\),

\(B(T+ \textbf{T}\cdot \boldsymbol{\gamma })B^{-1}= \boldsymbol{\kappa }\). Furthermore, \(B c\mu I_m B^{-1} = c\mu I_m\). Subtracting \(B(-T- \textbf{T}\cdot \boldsymbol{\gamma }+c\mu I_m)B^{-1}= c\mu I_m-\boldsymbol{\kappa }\). Then \(B(c\mu I_m -T- \textbf{T}\cdot \boldsymbol{\gamma })^{-1}B^{-1}= (c\mu I_m-\boldsymbol{\kappa })^{-1}\) and \((c\mu I_m -T- \textbf{T}\cdot \boldsymbol{\gamma })^{-1}= B^{-1}(c\mu I_m-\boldsymbol{\kappa })^{-1}B=B^{-1}DB\). Thus since the matrix \((c\mu I_m -T- \textbf{T}\cdot \boldsymbol{\gamma })\) has real elements, so has the matrix \(B^{-1}DB\) and the matrix \(c\mu \textbf{T}\cdot \boldsymbol{\gamma } B^{-1}DB-(c-1)\mu I_m+(c-1)\mu \textbf{e} \cdot \boldsymbol{\gamma } + T\). Therefore also the solutions of (11) must be real. \(\blacksquare\)

Remark that \(\boldsymbol{\phi }=\boldsymbol{\delta }EY_{c-1}\). The matrix \(Y_{c-1}\) defined in Theorem 1 has rows corresponding to \(\eta _1,\ldots ,\eta _m\). Then \(\bar{Y}_{c-1}\) is the rows corresponding to \(\bar{\eta }_1,\ldots ,\bar{\eta }_m\) where \(\bar{\eta }_i\) is the conjugate of \(\eta _i\) if this number is not real. Let \(\boldsymbol{\delta }\) and \({\tilde{\boldsymbol{\delta}}}\) be the solutions of equation (2). Since the elements of \(\boldsymbol{\phi }\) are real

$$\begin{aligned} \boldsymbol{\phi }=\boldsymbol{\delta }Y_{c-1}E= {\tilde{\boldsymbol{\delta}}}\bar{Y}_{c-1}\bar{E}. \end{aligned}$$

The matrices \(\bar{Y}_{c-1}\) and \(\bar{E}\) are nonsingular, such that \({\bar{\boldsymbol{\delta}}}= {\tilde{\boldsymbol{\delta}}}\). This means that in the solutions of equation (3) the complex elements occur in conjugate pairs. But then

$$\begin{aligned} \begin{array}{r} \sum _{k=1}^m \delta _k \{ \sum _{i=0}^{c-1}\left( {\begin{array}{c}c\\ i\end{array}}\right) \underline{y}_{i}^k \textbf{e} + \underline{y}_{c}^k\textbf{e} [(\frac{1}{\mu }-\frac{1}{\eta _k})\exp {(-c\eta _k \tau ) + \frac{1}{\eta _k}}]\} \\ =\sum _{k=1}^m \delta _k \underline{y}_{c-1}^k\{ \sum _{i=0}^{c-1}\left( {\begin{array}{c}c\\ i\end{array}}\right) \prod _{\ell =i}^{c-2} (c-\ell )\mu ^{c-\ell +1} ( \ell \mu I_m -\ell \mu \textbf{e} \cdot \boldsymbol{\gamma }-T)^{-1}\\ +cI_m+ c\mu R_{k} [(\frac{1}{\mu }-\frac{1}{\eta _k})\exp {(-c\eta _k \tau ) + \frac{1}{\eta _k}}] \}\textbf{e} \end{array} \end{aligned}$$
(12)

must be a real number, since conjugate pairs of \(\delta _i\) correspond to conjugate pairs of other terms in the sum (12).

But the sum of a complex number and its conjugate must be real. Therefore (12) is real and can be used for normalizing \(\boldsymbol{\delta }\).

5 Computation of the Loads for a Particular Group of Servers

Theorem 1 describes the distribution of the remaining load of the c servers on the open set \(<0,\infty >^c\). As pointed out in Remark 1 in Swensen (1986) the distribution on \([0,\infty >^c\) can easily be obtained. This result can be used to find expressions for probabilities and distributions for particular fixed servers. In addition to the distribution of the load we will consider two such probabilities as a function of the threshold \(\tau\): the probability that a particular server is occupied and the probability that customers are rejected at the particular server. Denote the load of this server by \(V_{p1}\). The main argument for finding the distribution is, for \(V_{p2}\) the load at another fixed particular server,

$$\begin{aligned} P(V_{p1}>v) & = P(V_{p1}=\min _{1\le i \le m}V_i>v) + P(V_{p1}>v, V_{p1}> \min _{1\le i \le m}V_i) \\&= \frac{1}{c}P(\min _{1\le i \le m}V_i>v)+ (c-1)P(V_{p1}>v, V_{p2}=\min _{1\le i \le m}V_i>v)\\&+ P(V_{p1}>v, \min _{1\le i\le m}V_i=0). \end{aligned}$$

The probabilities on the right-hand side follow from Theorem 1. More details can be found in Lemma A.7 in Swensen (1986).

Fig. 1
figure 1

Probability of server 1 being occupied as function of \(\tau\). Exponential inter-arrivals: solid line, PH1 inter-arrivals: dashed line, PH2 inter-arrivals: dotted line, PH3 inter-arrivals: dot-dashed line

Full size image

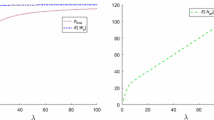
In Fig. 1 the probability that a particular server is busy, i.e. \(P(V_{p1}>0)\), is shown as a function of the bound \(\tau\) for a queue with 4 servers.

Fig. 2
figure 2

Probability of customer being rejected at server 1 as function of \(\tau\). Exponential inter-arrivals: solid line, PH1 inter-arrivals: dashed line, PH2 inter-arrivals: dotted line, PH3 inter-arrivals: dot-dashed line

Full size image

The distributions of the inter-arrival distributions which are considered are an exponential distribution and three phase type distributions with intensity matrix

$$\begin{aligned} \left( \begin{array}{rrr} -16.0 &{} 4.0 &{}b \\ d &{} -2.0 &{} a \\ c &{} 0 &{}-0.4 \end{array} \right) . \end{aligned}$$

The case with \(a=0.4, b=c=d=0.0\) corresponds to the Coxian distribution considered in Swensen (1986).

The probability is plotted in Fig. 1 for four distributions which all have expectation 0.3125. In addition to the exponential distribution there are 3 phase type distributions; PH1: \(a=0.346, b=d=0.0, c=0.5\) with coefficient of variation 2.98, PH2: \(a=0.07, b=0.5, c=0.8, d=0.0\) with coefficient of variation 2.84, PH3: \(a=0.05, b=0.5, c=0.0,d=0.8\) with coefficient of variation 2.59. The intensity of the server distribution, \(\mu\), is taken equal to 1.

As one can see in Fig. 1, \(P(V_{p1}>0)\), the probability of server 1 being busy, is, not surprisingly, increasing in \(\tau\). This follows from the fact that larger value of \(\tau\) means that there are more customers in the system. Therefore the probability that the server is idle is less and the probability of being busy is larger.

In Fig. 2 the probability that a particular server has a load such that no new customer is allowed at this server, i.e. \(P(V_{p1}>\tau )\), is shown as a function of the bound \(\tau\) for the a queue with 4 servers for the same queuing systems as those used in Fig. 1. The decreasing probability is due to the fact that as \(\tau\) increases fewer customer are rejected, and the probability of being rejected therefore becomes smaller.

As \(\tau \rightarrow 0\), \(\lim P(V_{p1}>\tau ) =P(V_{p1}>0)\) for all inter-arrival distributions. In particular, in the situation displayed in Figs. 1 and 2 for the exponential distribution, the system reduces to Erlang’s loss system when \(\tau =0\). The probability that a fixed server is busy is then given by the Palm-Jacobæus formula which in this case equals 0.617, see page 63 in Asmussen (1987).

The calculations were done using the software package R, R Core Team (2020).