From port-based teleportation to Frobenius reciprocity theorem: partially reduced irreducible representations and their applications

Abstract

In this paper, we present the connection of two concepts as induced representation and partially reduced irreducible representations (PRIR) appear in the context of port-based teleportation protocols. Namely, for a given finite group G with arbitrary subgroup H, we consider a particular case of matrix irreducible representations, whose restriction to the subgroup H, as a matrix representation of H, is completely reduced to diagonal block form with an irreducible representation of H in the blocks. The basic properties of such representations are given. Then as an application of this concept, we show that the spectrum of the port-based teleportation operator acting on n systems is connected in a very simple way with the spectrum of the corresponding Jucys–Murphy operator for the symmetric group $S(n-1)\subset S(n)$. This shows on the technical level relation between teleporation and one of the basic objects from the point of view of the representation theory of the symmetric group. This shows a deep connection between the central object describing properties of deterministic PBT schemes and objects appearing naturally in the abstract representation theory of the symmetric group. In particular, we present a new expression for the eigenvalues of the Jucys–Murphy operators based on the irreducible characters of the symmetric group. As an additional but not trivial result, we give also purely matrix proof of the Frobenius reciprocity theorem for characters with explicit construction of the unitary matrix that realizes the reduction in the natural basis of induced representation to the reduced one.

1 Introduction

Port-based teleportation (PBT) [1, 2] is a remarkable protocol possessing a counter-intuitive emanating in that the teleported state requires no unitary correction and is ready for use after the sender performs a measurement and sends classical communication. No-unitary correction property has attracted wide attention from the community resulting in intensive research in the field of the PBT resulting in the development of quantum information theory. First, the PBT scheme offers a model of a universal programmable quantum processor [1], it gives a connection with quantum cryptography and instantaneous non-local computation [3]. PBT protocols were instrumental in establishing a link between interaction complexity and entanglement in non-local computation and holography [4], between quantum communication complexity advantage and a violation of a Bell inequality [5], deriving fundamental bounds for quantum channels discrimination by designing PBT stretching protocols [6], and many other interesting results [7,8,9]. Describing the efficiency of the PBT protocol was a very complex task and for a long time satisfactory description, in particular, a description in higher dimensions and asymptotic behavior was missing. Difficulties came mostly from the point of view of mathematical methods and much effort was put into optimizing the protocol and its variants by developing a proper mathematical tool-kit [10,11,12,13,14,15,16] and recently in [17].

In this paper, we start from Sect. 2 with a general description of the basic properties of PBT operator, an object crucial for describing the efficiency of the deterministic PBT. We shortly remind its connection with the representation theory of the symmetric group. In particular, we focus on the aspect of the occurrence of induced representation and connection of the PBT operator with Jucys–Murphy elements and partial transposition. We focus here also on the case of the multi-port-based teleportation protocols [18] where we have to consider many layers of the induction process. Next, in Sect. 3 we on the above-mentioned connection more formal. We present rigorously the concept of Partially Reduced Irreducible Representations (PRIRs)—a notion related to subgroup-adapted basis [19]—and we discuss their properties and their role in induced representation. As an application of developed techniques, we show how the spectrum of famous Jucys–Murphy elements [20, 21] acting on $n-1$ systems is connected with the spectrum of the PBT operator acting on n systems. In particular, in Corollary 11 we present new expressions for the spectrum of the Jucys–Murphy of the symmetric group by use of the irreducible characters. In this regard in Proposition 9, we present fully analytical expressions for the mentioned eigenvalues, in the natural representation of the Jucys–Murphy elements, when the dimension of the underlying space is 2. This is possible, since then we have analytical expressions for corresponding irreducible characters which are labeled by Young frames with up to two rows, see Lemma 8. In the same section, we also contain, up to our best knowledge, a completely unknown previously orthogonality relation. It is contained in Proposition 3. Finally, we present purely matrix proof of the celebrated Frobenius reciprocity theorem for characters which was not known earlier in the literature. As an additional result, we give the explicit form of the unitary matrix $U(\beta )$ which realizes the reduction in the natural basis of induced representation to the reduced one. These results are contained in Theorem 1, preceded by auxiliary considerations.

2 From PBT operator to induced representation and PRIR

In this section, we will show (based on our previous papers) how the two concepts: the induced representation and PRIR appears in the context of port-based teleportation. We shall then show how this leads to the proof of the Frobenius reciprocity theorem for a subgroup of the symmetric group.

2.1 Algebra of the symmetric group and partial transposition

For the symmetric group S(n), we can define its natural representation $V^n_d:S(n)\rightarrow ({\mathbb {C}}^{d})^{\otimes n}$ by the following action on the set of basis vectors $\{|i\rangle \}_{i=1}^{d}$, where d stand for the local dimension:

$$\begin{aligned} \forall \sigma \in S(n)\qquad V^n_d(\sigma ).|i_{1}\rangle \otimes |i_{2}\rangle \otimes \cdots \otimes |i_{n}\rangle =|i_{\sigma ^{-1}(1)}\rangle \otimes |i_{\sigma ^{-1}(2)}\rangle \otimes \cdots \otimes |i_{\sigma ^{-1}(n)}\rangle . \nonumber \\ \end{aligned}$$

(1)

The representation $V^n_d(S(n))$ is defined in a given basis of the space ${\mathbb {C}}^d$, so it is a matrix representation, and operators $V^n_d(\sigma )$ just permute basis vectors according to the given permutation $\sigma$. Whenever the numbers n, d are clear from the context, we will write just simply $V(\sigma )$ instead of $V^n_d(\sigma )$ to simplify the notation.

For later purposes, we can introduce a matrix algebra ${\mathcal {A}}_d(n)$ spanned by the operators $V(\sigma )$ as follows:

$$\begin{aligned} {\mathcal {A}}_n(d):={\text {span}}_{{\mathbb {C}}}\{V(\sigma ) \ | \ \sigma \in S(n)\}. \end{aligned}$$

(2)

The above matrix algebra is just a natural representation of an abstract algebra ${\mathbb {C}}[S(n)]$ of the symmetric group S(n). Having definition of the group algebra ${\mathbb {C}}[S(n)]$ in Eq. (2), we can naturally introduce the algebra of partially transposed operators with respect to the last subsystem ${\mathcal {A}}_{n}^{t_{n}}(d)$ in the following way:

Definition 1

For ${\mathcal {A}}_{n}(d):= {\text {span}}_{{\mathbb {C}}}\{V(\sigma ):\sigma \in S(n)\}$ we define a new complex algebra

$$\begin{aligned} {\mathcal {A}}_{n}^{T_{n}}(d):= {\text {span}}_{{\mathbb {C}}}\{V^{T_{n}}(\sigma ) \ | \ \sigma \in S(n)\}, \end{aligned}$$

(3)

where the symbol $T_{n}$ denotes the partial transposition with respect to the last subsystem in the space ${\text {Hom}}(({\mathbb {C}}^{d})^{\otimes n})$.

Fig. 1

The left-hand side graphic presents an element from the walled Brauer algebra ${\mathcal {B}}^{\delta }_{3,2}$. On the right-hand side, we illustrate the composition of two diagrams $\sigma ,\pi \in {\mathcal {B}}^{\delta }_{3,2}$. When we identify a closed loop (red color), we multiply the resulting diagram by a scalar $\delta \in {\mathbb {C}}$. We see that the resulting composition $\sigma \pi$ also belongs to ${\mathcal {B}}^{\delta }_{3,2}$

Fig. 2

Graphic presents the procedure of partial transposition $T_{34}$ applied to a diagram from ${\mathcal {B}}^{\delta }_{3,2}$. Notice that the resulting diagram is no longer an element of ${\mathcal {B}}^{\delta }_{3,2}$. The resulting diagram is an element of Brauer algebra ${\mathcal {B}}^{\delta }_{3+2}$ introduced in [27] and graphically represents permutation from $S(3+2)=S(5)$. The walled Brauer algebra ${\mathcal {B}}^{\delta }_{p,q}$ is subalgebra of the Brauer algebra ${\mathcal {B}}^{\delta }_{p+q}$. We can say that $\pi \in {\mathcal {B}}^{\delta }_{p+q}$ if and only if $\pi ^T \in S(p+q)$

Definition 1 can be extended to a larger number of partial transpositions, see for example [17, 18]. The considered algebra ${\mathcal {A}}_{n}^{T_{n}}(d)$ is in fact a matrix representation of a diagram algebra called walled Brauer algebra ${\mathcal {B}}^{\delta }_{p,q}$, where $p,q\le 0$, $p+q=n$, and $\delta \in {\mathbb {C}}$, introduced and analyzed in an abstract way in [22,23,24,25,26]. The abstract algebra ${\mathcal {B}}^{\delta }_{p,q}$ is composed of formal combinations of diagrams. Each diagram has two rows with $p+q$ nodes, associated with a vertical wall between the first p and the last q nodes. These nodes are connected up in pairs in such a way that:

• 1. if both nodes are in the same row, they must lie on different sides of the wall,

• 2. if both nodes are in different rows, they must lie on the same side of the wall.

We illustrate the above construction with the notion of composition of such diagrams in Fig. 1. For any diagram from ${\mathcal {B}}^{\delta }_{p,q}$, the partial transposition T can be understood by exchanging the nodes on the right-hand side of the wall. This procedure is illustrated in Fig. 2. To get matrix representation (3) we set $p=n-1,q=1$, and $\delta =d$. In this case of two systems the following relation between transposition V((1, 2)) and unnormaalised projector on maximally entangled state $P_+=|\phi _+\rangle _{1,2}\langle \phi _+|$ between systems 1 and 2:

$$\begin{aligned} V^{T_2}((1,2))=dP_+,\qquad V^{T_2}((1,2))V^{T_2}((1,2))=dV^{T_2}((1,2))=dP_+, \end{aligned}$$

(4)

where $|\phi _+\rangle =\sum _{i=1}^d|i_1\rangle |i_2\rangle$. This relation will be exploited extensively in the further parts of this manuscript. This particular case is illustrated on the diagram level also in Fig. 3.

Fig. 3

Graphic illustrates on the diagram-level relation given in Eq. (4). This is a special case of the walled Brauer algebra ${\mathcal {B}}^{\delta }_{p,q}$ with $p=q=1$ and $\delta =d$, where d is the local dimension

2.2 PBT operator and induced representation

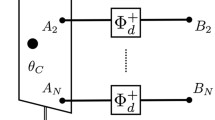
One of the key ingredients of most of the results on port-based teleportation was understanding an operator that can be called PBT operator. For standard port-based teleportation it acts on $n=N+1$ systems, where N is the number of shared ports, and it is of the form:

$$\begin{aligned} \rho =\sum _{a=1}^N V((a,N)) \left( \textbf{1}^{\otimes N-1} \otimes P_+\right) V((a,N)), \end{aligned}$$

(5)

where $V(\sigma )$ is the operator that permutes systems according to permutation $\sigma$, $P_+=|\phi _+\rangle _{N,N+1}\langle \phi _+|$ is unnormalized projector on the unnormalized maximally entangled state between systems N and $N+1$,

$$\begin{aligned} |\phi _+\rangle =\sum _{i=1}^d |i\rangle _N|i\rangle _{N+1}, \end{aligned}$$

(6)

and $\textbf{1}^{\otimes N-1}$ is the identity operator on rest of the systems.

For generalization of the port-based teleportation for sending composite quantum systems [11, 28,29,30] the relevant operator is a direct generalization of the above one:

$$\begin{aligned} \rho =\frac{1}{(N-l)!}\sum _{\sigma \in S(N)} V(\sigma )\left( \textbf{1}^{\otimes N-l} \otimes P_+^{\otimes l}\right) V(\sigma ^{-1}), \end{aligned}$$

(7)

where l is the number of systems to be teleported, and S(N) is the symmetric group over N elements. From Fig. 4 it is easy to see on what systems identities and are acting. The factor $1/(N-l)!$ is to remove overcounting.

Fig. 4

For $l=1$ the operator $\rho$ is a sum of the depicted operators in (a); here $N=4$. For $l>1$, $\rho$ is the sum of operators of type of those depicted in (b). Here $N=7$ and $l=3$

Thus the operator $\rho$ is sum of operators, for which $N-l$ systems are identity, while the other 2l are occupied by maximally entangled states. In [14] it was noted that the operator is tightly related to the notion of induced representation as well as with PRIR (“partially reduced irreducible representation”).

To see how they arise, let us first notice how permutation from S(N) acts on the state. For each particular constituent of $\rho$ an effect will be the following: the ends of maximally entangled states that lie to the left of the “wall” will be redistributed, and permuted, and the same happens to the free systems. Let us start with one constituent of the state—the one where all free systems are on the left:

$$\begin{aligned} I^{\otimes N-l}\otimes P_+^{\otimes l} \end{aligned}$$

(8)

Let us split the identity into projectors onto irreps of $S(N-l)$:

$$\begin{aligned} I^{\otimes N-l}=\bigoplus _\alpha P_\alpha , \end{aligned}$$

(9)

where $\alpha$ are all irreps of $S(N-l)$ which are present in the representation that permutes the “free” systems. Now, if we apply some permutation $\sigma$ from S(N), then we see that $P_\alpha$ is put to different systems, but still it becomes $P_\alpha$ as it is invariant under permutations. The same happens to any other constituent of $\rho$. Thus we can split $\rho$ into a direct sum of $\rho _\alpha$’s which instead of identity will have $P_\alpha$:

$$\begin{aligned} \rho =\bigoplus _\alpha \rho _\alpha \end{aligned}$$

(10)

with

$$\begin{aligned} \rho _\alpha =\frac{1}{(N-l)!}\sum _{\sigma \in S(N)}V(\sigma ) P_\alpha \otimes P_+^{\otimes l} V(\sigma ^{-1}). \end{aligned}$$

(11)

Thus $\rho$ is block diagonal, and the blocks are subspaces ${{{\mathcal {H}}}}_\alpha$, that are spanned by vectors of the form

$$\begin{aligned} V(\sigma ) |\phi _i^\alpha \rangle |\phi _+\rangle ^{\otimes l}, \end{aligned}$$

(12)

where $i=1,\ldots ,d_\alpha$ with $d_\alpha$ being dimension of irrep $\alpha$; $\sigma \in S(N)$. However, in the above equation we have much more vectors than needed to span ${{{\mathcal {H}}}}_\alpha$. Indeed, a permutation $\sigma$ acting on $|\phi _i^\alpha \rangle |\phi _+\rangle ^{\otimes l}$ does the following: it changes the configuration of legs and applies some permutation on the free systems, see Fig. 5.

Fig. 5

How permutation from S(N) acts on exemplary constituent of $\rho$: it re-configures legs

We see, that if we have some permutation $\sigma$ then all other permutations $\sigma '$ which have the same permutation on free systems are not needed—as the resulting vectors will have the same configuration of legs, and will differ only by permutation on free systems, which will enlarge dimension. Indeed on free systems, we have anyway full irrep basis, and permuting it we shall not go outside of the space.

Thus since we are not interested in action instead of all $\sigma$ from S(N) it is enough to take only ones from transversal, the quotient $S(N)/S(N-l)$, which we shall denote by $t_k, k=1,\ldots , N!/(N-l)!$:

$$\begin{aligned} V(t_k)|\phi ^\alpha _i\rangle |\phi _+\rangle ^{\otimes l} \equiv |t_k,\phi _i^\alpha \rangle . \end{aligned}$$

(13)

We are now in a position to examine the action of our group S(N) on the space ${{{\mathcal {H}}}}_\alpha$. For $\sigma \in S(N)$ We write

$$\begin{aligned} V(\sigma ) |t_k,\phi _i^\alpha \rangle = V(\sigma ) V(t_k) |\phi _i^\alpha \rangle |\phi _+\rangle ^{\otimes l}. \end{aligned}$$

(14)

Now we use that there is unique element $t_p$ of transversal, which satisfies:

$$\begin{aligned} \sigma t_k = t_p h, \end{aligned}$$

(15)

where $h\in S(N-l)$, so that

$$\begin{aligned} V(\sigma ) V(t_k) |\phi _i^\alpha \rangle |\phi _+\rangle ^{\otimes l}&= V(t_p) V(h)|\phi _i^\alpha \rangle |\phi _+\rangle ^{\otimes l}=\sum _{j} \varphi ^\alpha _{ji}(h) V(t_p)|\phi _j^\alpha \rangle | \phi _+\rangle ^{\otimes l} \nonumber \\&=\sum _j \varphi ^\alpha _{ji}(h) |t_p,\phi _j^\alpha \rangle . \end{aligned}$$

(16)

However this is nothing but one of the definitions of the induced representation: it permutes elements of transversal, and applies an element from the subgroup to the irrep $\alpha$ (cf. (68))

Thus we have seen that if we apply permutation $\sigma \in S(N)$ to the total system, on the space ${{{\mathcal {H}}}}_\alpha$ it acts as the induced representation by irrep $\alpha$. Such representation is reducible, and the Frobenius reciprocity theorem says that the multiplicity of each irrep $\mu$ is equal to the multiplicity of the so-called, reduced representation $\alpha$ in $\mu$ (see below for definition of reduced representation).

2.3 PRIR and proof of Frobenius theorem for symmetric group

Suppose now that we do not know the Frobenius theorem, and let us proceed with setting orthonormal basis in ${\mathcal {H}}_\alpha$. Such basis was derived in [18] in the form of matrix basis, on space ${\mathcal {H}}_\alpha$ including multiplicity, which is given by $m_\alpha$—the multiplicity of irrep $\alpha$ in the natural representation of the symmetric group in $N-l$ systems (by natural we mean that it is given by operators $V(\sigma )$ which permute the systems, i.e., this is Schur-Weyl setup). To write it down we need a bit of preparation. First, for irrep $\mu$ of S(N) we define the natural representation of the matrix basis (or matrix units) for the irrep $\mu$ including multiplicities as follows

$$\begin{aligned} E_{ij}^\mu = \frac{d_{\mu }}{N!}\sum _{\sigma \in S(N)} \varphi ^\mu _{ji}(\sigma ^{-1})V(\sigma ). \end{aligned}$$

(17)

Here $\varphi ^\mu _{ji}(\sigma ^{-1})$ are matrix elements of irrep of $\sigma ^{-1}\in S(N)$ and $i,j=1,\ldots , d_{\mu }$, where $d_{\mu }$ is dimension of the irrep $\mu$. Now consider subgroup $S(N-l)\subset S(N)$. If in our irrep $\mu$ we restrict to this subgroup, we obtain representation called reduced representation. It is reducible, and let $\alpha$ labels its irreducible components within irrep $\mu$, determining blocks. Further, each copy of irrep $\alpha$ can appear with multiplicity, which we shall denote by $m_{\alpha /\mu }$. Now we can always assume that the basis in which the matrix elements of $\varphi ^\mu (\sigma )$ are written are chosen in such a way that the basis of (17) is compatible with the $\alpha$ blocks. This is what we call partially reduced irreducible representation. Now the label $i_\mu$ can be alternatively written by means of a triple $i_\mu =(\alpha ,r_{\mu /\alpha }, i_\alpha$). Namely, the index $\alpha$ tells in which irrep $\alpha$ we are, the index $r_{\mu /\alpha }$ tells in which copy of irrep $\alpha$ we are, and finally, the index $i_\alpha$ denotes the position in that copy (in the same way as $i_\mu$ denotes position in irrep $\mu$). One can use even shorter notation $i_\mu =(r_{\mu /\alpha },i_\alpha )$. We are now prepared to write the promised basis that appeared earlier in Theorem 11 [18]

$$\begin{aligned} F^{r_{\mu /\alpha } r_{\nu /\alpha }}_{i_{\mu }\quad j_{\nu }}:= d^k \frac{m_{\alpha }}{\sqrt{m_{\mu }m_{\nu }}}E_{i_{\mu } \ 1_{\alpha }}^{\quad r_{\mu /\alpha }} P_+^{\otimes k}E^{r_{\nu /\alpha }}_{1_{\alpha }\quad j_{\nu }} \end{aligned}$$

(18)

where $m_\alpha$ is multiplicity of irrep $\alpha$ in natural representation of $S(N-l)$ and $m_\mu$, $m_\nu$ are multiplicities of natural representation of S(N), and we have written one of the index of the operators E in the partially reduced notation:

$$\begin{aligned} E_{i_{\mu } \ 1_{\alpha }}^{\quad r_{\mu /\alpha }}\equiv E^\mu _{i_{\mu }i'_\mu } \end{aligned}$$

(19)

with $i'_\mu =(r_{\mu /\alpha },1_\alpha )$. Here $1_\alpha$ represents some arbitrarily fixed label—the operator does not depend on its choice. Now [18] the operator

$$\begin{aligned} \sum _{i_\mu } F^{r_{\mu /\alpha } r_{\mu /\alpha }}_{i_{\mu }\quad i_{\mu }} \end{aligned}$$

(20)

projects onto irrep $\mu$ within $H_\alpha$, which is the space for representation of S(N) induced by irrep $\alpha$ of its subgroup $S(N-l)$. Thus we see here explicitly, how the indices r that originally count multiplicity of $\alpha$ within reduced representation of $\mu$, now count multiplicity of $\mu$ within the induced representation. Equation (18) is a special case of the more general result presented in Theorem 1.4 in [31].

This is just the contents of the Frobenius reciprocity theorem in the special case for the symmetric group. In the following, inspired by this example, we shall prove the Frobenius reciprocity theorem for general group and subgroup.

2.4 Duality between induced and reduced representation via PBT operator versus Jucys–Murphy operator for $l=1$

The dualism of reduced and induced representation manifested by the Frobenius theorem is indeed very directly seen in our above derivation of the theorem. In this section, we shall present this dualism in yet another way. To do so let us define the Jucys–Murphy operator [20, 21, 32], which in the natural representation, is given by

$$\begin{aligned} J_N=\sum _{a=1}^{N-1} V((a,N)), \end{aligned}$$

(21)

where V((a, N)) are as before operators that permute N systems according to permutation (a, N). It is clear from its definition that the operator $J_N$ belongs to the matrix algebra ${\mathcal {A}}_N(d)$ defined through (2). Due to the discussion presented in Sect. 2.1, the operator $J_N$ is the matrix representation of the element from the Brauer algebra ${\mathcal {B}}^d_{N}$. The Jucys–Murphy elements play an important role in the representation theory of the symmetric group. In principle, they have found an application to an alternative approach in the construction of irreducible representations of S(n) called Okounkov–Vershik approach [32,33,34]. The spectrum of the Jucys–Murphy elements is known and discussed for example in Section 4.5 of [17]. Now let us consider the operator $J_{N+1}$ and apply to it partial transpose on $(N+1)-$th system. Now, since the partially transposed swap operator is equal to $dP_+$ we see that PBT operator $\rho$ is just a partially transposed Jucys–Murphy operator on $N+1$ systems

$$\begin{aligned} \rho =(J_{N+1})^{T_{N+1}}. \end{aligned}$$

(22)

Clearly, the above operator belongs to the algebra of partially transposed permutation operators ${\mathcal {A}}_{N+1}^{T_{N+1}}(d)$ defined through Definition 1. In other words, the operator $\rho$ is the matrix representation of the element from the walled Brauer algebra ${\mathcal {B}}^d_{N,1}$, according to the discussion presented in Sect. 2.1. The eigenvalues of this operator were found in [12] and are given by

$$\begin{aligned} \lambda _\mu (\alpha )=N\frac{m_\mu d_\alpha }{m_\alpha d_\mu } \end{aligned}$$

(23)

and multiplicity of the eigenvalue is $d_\mu m_\alpha$. In the rest of the paper, we shall find eigenvalues of ordinary Jucys–Murphy operator $J_N$ (see Corollary 15). They are given by

$$\begin{aligned} \gamma _\mu (\alpha ) =N\frac{m_\mu d_\alpha }{m_\alpha d_\mu } - d \end{aligned}$$

(24)

and multiplicity of the eigenvalue is $m_\mu d_\alpha$. We have summarized this in Table 1. The discussion in the previous section shows how the multiplicity for transposed Jucys–Murphy element $\rho =(J_{N+1})^{T_{N+1}}$ is related to induced representation. Namely, $m_\alpha$ term in multiplicity comes from the fact that space ${{{\mathcal {H}}}}_\alpha$ is labeled by $\alpha$, which repeats $m_\alpha$ times. And the multiplicity $m_\mu$ comes from the fact, that $\rho$ is invariant under $\mu$, hence by Schur lemma, is proportional to identity on irreps of $\mu$.

Table 1 Table collects relations between the eigenvalues of Jucys–Murphy operator $J_N$ and partially transposed Jucys–Murphy operator $(J_{N+1})^{T_{N+1}}$, or equivalently the PBT operator $\rho$, see (22)

Similarly, it is easy to understand the opposite formula for the multiplicity of the Jucys–Murphy operator $J_N$. First, since it is a combination of permutations, it is a direct sum over irreps $\mu$ with multiplicity $m_\mu$. Next, within irrep $\mu$, it is constant on irrep $\alpha$ of subgroup $S(N-1)$, hence we have term $d_\alpha$.

3 The concept of PRIR for an arbitrary group G and its subgroup $H\subset G$

Let $H\subset G$ be an arbitrary subgroup of G with transversal $T=\{t_{k}:k=1,\ldots ,\frac{|G|}{|H|}\equiv s\}$, i.e., we have a coset decomposition

$$\begin{aligned} G=\bigcup _{k=1}^{s}t_{k}H, \quad \quad \forall g\in G\quad g=t_{k}h:h\in H, \end{aligned}$$

(25)

where the last decomposition of $g\in G$ is unique. Now, let us consider an arbitrary unitary irreducible representation (irrep) $\psi ^{\mu }$ of G, which also will be denoted briefly as $\mu \in \widehat{G}$ where the latter is the set of all irreps of the group G. The irrep $\psi ^{\mu }$ can be always unitarily transformed to a partially reduced form, such that

$$\begin{aligned} {\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu })=\bigoplus _{\alpha \in \mu ,a_{\alpha }}\varphi ^{\alpha (a_{\alpha })},\quad a_{\alpha }=1,\ldots ,m_{\alpha }^{\mu }, \end{aligned}$$

(26)

where $\alpha$ labels the type of irrep of H and $a_{\alpha }$ is a number of irrep type $\alpha$ in the decomposition (26), and $m_{\alpha }^{\mu }$ is the multiplicity of irrep $\varphi ^{\alpha }$ in ${\text {Res}}\downarrow _{H}^{G}(\phi _{R}^{\mu })$. Decomposition (26) is not unique. We will assume that irreps $\varphi ^{\beta (b_{\beta })}$ of subgroup H are identical, i.e., we have

$$\begin{aligned} \varphi ^{\alpha (a_{\alpha })}=\varphi ^{\alpha },\quad \forall a_{\alpha }=1,\ldots ,m_{\alpha }^{\mu }. \end{aligned}$$

(27)

Definition 2

A unitary matrix irrep $\psi ^{\mu }$ of G, with partially reduced form (26), i.e., which on the subgroup H has block diagonal form, we call Partially Reduced Irreducible Representation (PRIR).

From the above, it follows that the diagonal blocks in the decomposition (26) are labeled and in fact ordered by the index $\alpha (a_{\alpha })$ and inside diagonal blocks the matrix elements are labeled by indices $j_{\alpha }=1,\ldots ,\dim \varphi ^{\alpha }=d_{\alpha }$ of irrep $\varphi ^{\alpha (a_{\alpha })}$ of the subgroup H, which is included in irrep $\psi ^{\mu }$ of G, so in matrix notation we have

$$\begin{aligned} \forall h\in H\quad (\psi _{R}^{\mu })_{i_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(h)=\delta ^{\alpha \beta }\delta ^{a_{\alpha }b_{\beta }}\varphi _{i_{\alpha }j_{\alpha }}^{\alpha (a_{\alpha })}(h). \end{aligned}$$

(28)

The block structure of this reduced representation allows us to introduce such a block indexation for irrep $\psi ^{\mu }$ for all elements of G

$$\begin{aligned} \forall g\in G\quad \psi _{R}^{\mu }(g)=((\psi _{R}^{\mu })_{k_{\mu }l_{\mu }}(g))=\bigl ((\psi _{R}^{\mu })_{i_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(g)\bigr ), \end{aligned}$$

(29)

where the indices $k_{\mu },l_{\mu }$ are standard matrix indices, so in PRIR the standard matrix indices are replaced by indexation directly connected with irreps of subgroup H included in irrep $\psi ^{\mu }$ of G. Note that the diagonal blocks are square, whereas the off-diagonal blocks in general need not be square. Thus we see that $PRIR^{\prime }s$ have two main features:

• 1. They are partially reduced on subgroup H.

• 2. The matrix elements of irrep $\psi ^{\mu }$ of G are labeled by multi-indices $\left( {\begin{array}{c}\alpha (a_{\alpha })\\ i_{\alpha }\end{array}}\right) ,$ $\left( {\begin{array}{c}\beta (b_{\beta })\\ j_{\beta }\end{array}}\right) .$

Note that in definition of PRIR we do not assume that ${\text {Res}} \downarrow _{H}^{G}(\psi ^{\mu })$ is simply reducible, which is important because it allows us to give a new proof of the Frobenius reciprocity theorem (see Thm. 1). Actually, if we have an inclusion chain of subgroups so that each inclusion is multiplicity-free, then we obtain a chain of PRIRs which are multiplicity-free, which leads to the well-known Gelfand-Tsetlin basis. As said, we are interested in PRIR that is not necessarily multiplicity-free. As a matter of fact, PRIR is strictly related to subgroup-adapted basis [19]. The latter is the basis in the irreducible representation of a group whose elements are basis vectors from individual irreps of the subgroup (which are subspaces of the irrep of the group). Now PRIR is simply irreducible representation of the group written in subgroup-adapted basis. On the level of matrices, this is equivalent to saying that PRIRs are block diagonal on the subgroup as in Eq. (26).

The above-introduced indexation of PRIRs is more complicated than the standard one but, for example, it allows to derive some important new relations among matrix elements of PRIRs which would be difficult to rewrite in standard indexation—see Proposition 3 below).

Using Eq. (28) we get

$$\begin{aligned} (\psi _{R}^{\mu })_{i_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(t_{k}h)=\sum _{k_{\beta }}(\psi _{R}^{\mu })_{i_{\alpha }\quad \quad k_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(t_{k})\varphi _{k_{\beta }j_{\beta }}^{\beta (b_{\beta })}(h),\quad \forall h\in H\quad \forall t_{k}\in T. \end{aligned}$$

(30)

From this, it follows that multiplication by a matrix representing elements of subgroup H is simpler than in non-PRIR representations.

Now we may formulate the first important property of PRIRs, which is a kind of orthogonality relation for matrix elements of transversal T.

Proposition 3

Suppose that

$$\begin{aligned} \varphi ^{\beta }\in {\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu })\quad and\quad \varphi ^{\beta }\in {\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\nu }). \end{aligned}$$

(31)

Then the matrix elements of $PRIR^{\prime }s$ $\psi _{R}^{\mu }$ and $\phi _{R}^{\nu }$ of G satisfy the following sum rule

$$\begin{aligned} \sum _{k=1}^{s}\sum _{k_{\beta }=1}^{|\beta |}(\psi _{R}^{\mu })_{i_{\alpha }\quad \quad k_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(t_{k}^{-1})(\psi _{R}^{\nu })_{k_{\beta }\quad \quad j_{\gamma }}^{(\beta ,b_{\beta }^{\prime })(\gamma ,c_{\gamma })}(t_{k})=\frac{|G|}{|H| }\frac{d_{\beta }}{d_{\mu }}\delta ^{\mu \nu }\delta ^{b_{\beta }b_{\beta }^{\prime }}\delta ^{\alpha \gamma }\delta ^{a_{\alpha }c_{\gamma }}\delta _{i_{\alpha }j_{\gamma }},\nonumber \\ \end{aligned}$$

(32)

where $\varphi ^{\alpha }\in {\text {Res}}\downarrow _{H}^{G}(\phi _{R}^{\mu })\quad and\quad \varphi ^{\gamma }\in {\text {Res}}\downarrow _{H}^{G}(\phi _{R}^{\nu })$.

Proof

The proof is based on the classical orthogonality relations for irreps, which in PRIR notation takes the form

$$\begin{aligned} \sum _{g\in G}(\psi _{R}^{\mu })_{i_{\alpha }\quad \quad k_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(g^{-1})(\psi _{R}^{\nu })_{k_{\beta }\quad \quad j_{\gamma }}^{\beta (b_{\beta }^{\prime })\gamma (c_{\gamma })}(g)= \frac{|G|}{d_{\mu }}\delta ^{\mu \nu }\delta ^{b_{\beta }b_{\beta }^{\prime }}\delta ^{\alpha \gamma }\delta ^{a_{\alpha }c_{\gamma }}\delta _{i_{\alpha }j_{\gamma }}, \end{aligned}$$

(33)

which means, that even if $\alpha =\gamma$, i.e., these representations are of the same type, but $a_{\alpha }\ne c_{\gamma }$, the RHS of (33) is equal to zero. Similarly, if the indices $b_{\beta },b_{\beta }^{\prime }$ which enumerate irreps $\beta$ are not equal, then RHS of (33) is equal to zero. This follows from the fact that in the classical orthogonality relations if corresponding indices of irreps are not equal, then the RHS of the orthogonality relations is equal to zero, and in PRIR notation the irreps $\varphi ^{\alpha }$ of subgroup H and their indices $i_{\alpha }$ play the role of indices in irrepss $\psi _{R}^{\mu }$. The next part of the proof is a simple generalization of the proof of Proposition 17 in [14]. $\square$

Remark 1

From the form of LHS of Eq. (33) in the thesis of Proposition 3, in particular from the fact that the second sum in LHS runs over a lower part of multi-index $\left( {\begin{array}{c}\beta (b_{\beta })\\ k_{\beta }\end{array}}\right)$ only (over $k_{\beta }$) it is clear that PRIR multi-index notation is essential to formulate and prove this result.

Next result concerns properties of the transversal $T=\{t_{k}:k=1,\ldots ,\frac{ |G|}{|H|}\equiv s\}$ of the subgroup $H\subset G$ and transversal element $\Upsilon =\sum _{k=1}^{s}t_{k}$ in the group algebra ${\mathbb {C}}[G].$ It is well known that any irrep of any group G is also an irrep the corresponding group algebra ${\mathbb {C}}[G]$, so we may use the concept of $PRIR^{\prime }s$ in the group algebra.

Proposition 4

Suppose that $\{t_k\}$ is any transversal of a group G with respect to subgroup H (25), $\psi _{R}^{\mu }$ is PRIR of a group algebra ${\mathbb {C}}[G]$, such that

• 1. ${\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu })$ is simply reducible,

• 2. and we have

  $$\begin{aligned} \forall h\in H\quad h\left( \sum _{k=1}^{s}t_{k}\right) h^{-1}=\left( \sum _{k=1}^{s}t_{k}\right) , \end{aligned}$$

  (34)

then

$$\begin{aligned} \sum _{k=1}^{s}(\psi _{R}^{\mu })(t_{k})=\bigoplus _{\alpha \in \mu }\eta _{\mu }(\alpha )\textbf{1}_{\alpha }, \end{aligned}$$

(35)

i.e., on RHS we have a block diagonal matrix, such that the diagonal blocks are unit matrices multiplied by numbers $\eta _{\mu }(\alpha )$. These numbers do not depend on the form of PRIR $\psi _{R}^{\mu }$, i.e., for all possible choices of PRIR representation, satisfying the above assumptions, these numbers are the same.

Proof

We give here a sketch of the proof. The assumption of simple reducibility and condition (34) together with classical Schur Lemma for irreps implies that Eq. (35) must hold. This result is easy to see due to the PRIR blocks indexation of PRIR $\psi _{R}^{\mu }$. $\square$

From Proposition 4 we get immediately:

Corollary 5

For any PRIR $\psi _{R}^{\mu }$ transversal element $\Upsilon =\sum _{k=1}^{s}t_{k}\in {\mathbb {C}}[G]$ takes in $\psi _{R}^{\mu }$ diagonal form

$$\begin{aligned} \psi _{R}^{\mu }(\Upsilon )=\bigoplus _{\alpha \in \mu }\eta _{\mu }(\alpha ) \textbf{1}_{\alpha } \end{aligned}$$

(36)

and the numbers $\eta _{\mu }(\alpha )$ form the spectrum of the operator $\psi _{R}^{\mu }(\Upsilon )$. Multiplicity of eigenvalue $\eta _{\mu }(\alpha )$ is equal to $\dim \varphi ^{\alpha }=d_{\alpha }$. Decomposing arbitrary representation $\Psi$ of the group G into $PRIR^{\prime }s$ $\psi _{R}^{\mu }$ and using Proposition 4 we get the spectral decomposition of the transversal operator $\Psi (\Upsilon )$.

As an important example of application of PRIRs we have the following:

Proposition 6

Let $G=S(n)$ and $H=S(n-1)$ with standard transversal $T=\{(an):a=1,\ldots ,n\}$, which satisfy the assumptions of Proposition 4. Then for any PRIR $\psi _{R}^{\mu }$ of the group S(n) we have

$$\begin{aligned}{} & {} \sum _{a=1}^{n}(\psi _{R}^{\mu })(an)=\psi _{R}^{\mu }(\Upsilon )=\bigoplus _{\alpha \in \mu }\eta _{\mu }(\alpha )\textbf{1}_{\alpha }, \end{aligned}$$

(37)

$$\begin{aligned}{} & {} \eta _{\mu }(\alpha )=\left( \begin{array}{c} n \\ 2 \end{array} \right) \frac{\chi ^{\mu }(12)}{d_{\mu }}-\left( \begin{array}{c} n-1 \\ 2 \end{array} \right) \frac{\chi ^{\alpha }(12)}{d_{\alpha }}+1,\quad \end{aligned}$$

(38)

where $\chi ^{\mu }$ is the character of $\psi _{R}^{\mu }$ and $\chi ^{\alpha }$ s the character of $\varphi ^{\alpha }$. We see that numbers $\eta _{\mu }(\alpha )$ depend only on the pure characteristics of irreps $\psi _{R}^{\mu }$ and $\varphi ^{\alpha }\in {\text {Res}}\downarrow _{H}^{G}(\phi _{R}^{\mu })$ (for brevity $\alpha \in \mu )$.

Proof

The starting point in this proof is the following equation

$$\begin{aligned} \sum _{a<b}^{n}(\psi _{R}^{\mu })(ab)=\left( \begin{array}{c} n \\ 2 \end{array} \right) \frac{\chi ^{\mu }(12)}{d_{\mu }}\textbf{1}_{d_{\mu }}, \end{aligned}$$

(39)

where $\textbf{1}_{d_{\mu }}$ is the unit matrix of dimension $d_{\mu }$ and on LHS we have the sum of all transpositions in S(n) which forms an equivalence class. This equation follows from the fact that the famous Schur lemma implies that the sum of all elements of any the equivalence class of an arbitrary group in any irrep is proportional to the unit matrix. Taking trace we derive the coefficient of proportionality. Next we rewrite LHS as follows

$$\begin{aligned} \sum _{a<b}^{n}(\psi _{R}^{\mu })(ab)=\sum _{a=1}^{n-1}(\psi _{R}^{\mu })(an)+\sum _{a<b}^{n-1}(\psi _{R}^{\mu })(ab), \end{aligned}$$

(40)

so in the second sum on RHS the summation is over all equivalence class of transpositions but in the subgroup $S(n-1)$. Therefore, from definition of PRIRs matrix of the second sum is block diagonal matrix and in the diagonal blocks we have irreps of $S(n-1)$ included in $\psi _{R}^{\mu }$. Again from the Schur lemma we get in each diagonal block in the last sum

$$\begin{aligned} \sum _{a<b}^{n}(\varphi ^{\alpha })(ab)=\left( \begin{array}{c} n-1 \\ 2 \end{array} \right) \frac{\chi ^{\alpha }(12)}{d_{\alpha }}\textbf{1}_{d_{\alpha }} \end{aligned}$$

(41)

for any irrep $\varphi ^{\alpha }$ of $S(n-1)$ included in $\psi _{R}^{\mu }$, so we see that diagonal blocks in matrix $\sum _{a<b}^{n-1}(\psi _{R}^{\mu })(ab)$ are also diagonal. Shifting the diagonal matrix $\sum _{a<b}^{n-1}(\psi _{R}^{\mu })(ab)$ on RHS of the first equation we get the result. $\square$

In the above proof, we see that the defining property of PRIRs, i.e., partial reduction plays an essential role in it.

Example 7

In the simplest case, i.e., for identity irrep $\mu =id$, we have

$$\begin{aligned} \eta _{id}(id)=n. \end{aligned}$$

(42)

In general the above formulae for eigenvalues $\eta _{\mu }(\alpha )$ of the transversal operator $\Upsilon$ are not entirely analytical because for natural characteristics of irreps characters $\chi ^{\mu }$ and corresponding dimension $d_{\mu }$ there are not analytical expressions. However, for particular irreps of group S(n) there exists purely analytical formulae for these quantities. Namely, we have

Lemma 8

(see [35]) Let $\mu \equiv \mu _{k}=(n-k,k):1\le k\le \frac{1}{2}n$ be a two-row partition of irrep of S(n), then

$$\begin{aligned} \chi ^{\mu _{k}}(12)=\left( {\begin{array}{c}n-2\\ k\end{array}}\right) +\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) -\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-2 \\ k-3\end{array}}\right) , \end{aligned}$$

(43)

and

$$\begin{aligned} \dim \mu _{k}=d_{\mu _{k}}=\left( {\begin{array}{c}n\\ k\end{array}}\right) -\left( {\begin{array}{c}n\\ k-1\end{array}}\right) . \end{aligned}$$

(44)

When $k=1$ we set $\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) \equiv 0\equiv \left( {\begin{array}{c}n-2\\ k-3\end{array}}\right)$, and when $k=2$ we set $\left( {\begin{array}{c}n-2\\ k-3\end{array}}\right) \equiv 0$ in (43).

Next, we have for $n-k>k$

$$\begin{aligned} {\text {Res}}\downarrow _{S(n-1)}^{S(n)}(\psi ^{\mu _{k}})= \varphi ^{\alpha _{k}}\oplus \varphi ^{\alpha _{k-1}}, \end{aligned}$$

(45)

where $\alpha _k=(n-1-k,k),$ and $\alpha _{k-1}=(n-1-(k-1),k-1)$, so $\alpha _{k}, \alpha _{k-1}$ are irreps of $S(n-1)$. For $n-k=k$, we have

$$\begin{aligned} {\text {Res}}\downarrow _{S(n-1)}^{S(n)}(\psi ^{\mu _{k}})=\varphi ^{\alpha _{k-1}}, \end{aligned}$$

(46)

where $\alpha _{k-1}=(n-1-(k-1),k-1)$.

Using Lemma 8 and expressions (45), (46), we derive purely analytical formulae for the eigenvalues of the transversal operator $\Upsilon$ in two rows PRIRs of the group S(n).

Proposition 9

Let $\mu \equiv \mu _{k}=(n-k,k):1\le k\le \frac{1}{2}n$ be a two row partition of irrep of S(n), then

• 1. If $n-k>k$ the transversal operator $\Upsilon =\sum _{a=1,\ldots ,n}(an)$ takes in PRIR $\psi ^{\mu _{k}}$ diagonal form with two different eigenvalues

  $$\begin{aligned} \eta _{\mu _{k}}(\alpha _{k})=\left( {\begin{array}{c}n\\ 2\end{array}}\right) \frac{\left( {\begin{array}{c}n-2\\ k\end{array}}\right) +\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) -\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-2\\ k-3\end{array}}\right) }{\left( {\begin{array}{c}n\\ k\end{array}}\right) -\left( {\begin{array}{c}n\\ k-1\end{array}}\right) } -\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) \frac{\left( {\begin{array}{c}n-3\\ k\end{array}}\right) +\left( {\begin{array}{c}n-3\\ k-2\end{array}}\right) -\left( {\begin{array}{c}n-3\\ k-1\end{array}}\right) -\left( {\begin{array}{c} n-3\\ k-3\end{array}}\right) }{\left( {\begin{array}{c}n-1\\ k\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) }+1\nonumber \\ \end{aligned}$$

  (47)

  with multiplicity $d_{\alpha _{k}}=\left( {\begin{array}{c}n-1\\ k\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right)$, and

  $$\begin{aligned}{} & {} \eta _{\mu _{k}}(\alpha _{k-1})=\left( {\begin{array}{c}n\\ 2\end{array}}\right) \frac{\left( {\begin{array}{c}n-2\\ k\end{array}}\right) +\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) -\left( {\begin{array}{c}n-2\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-2\\ k-3\end{array}}\right) }{\left( {\begin{array}{c}n\\ k\end{array}}\right) -\left( {\begin{array}{c}n\\ k-1\end{array}}\right) } -\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) \frac{\left( {\begin{array}{c}n-3\\ k-1\end{array}}\right) +\left( {\begin{array}{c}n-3\\ k-3\end{array}}\right) -\left( {\begin{array}{c}n-3\\ k-2\end{array}}\right) - \left( {\begin{array}{c}n-3\\ k-4\end{array}}\right) }{\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-2\end{array}}\right) }+1\nonumber \\ \end{aligned}$$

  (48)

  with multiplicity $d_{\alpha _{k-1}}=\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-2\end{array}}\right)$.

• 2. If $n-k=k$ then $\psi ^{\mu _{k}}(\Upsilon )$ has only one eigenvalue equal to $\eta _{\mu _{k}}(\alpha _{k-1})$ with multiplicity $d_{\alpha _{k-1}}=\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-2\end{array}}\right) =d_{\mu _{k}}.$ In this particular case, $\psi ^{\mu _{k}}(\Upsilon )$ is proportional to unit matrix.

Definition 10

The element $J_{n}=\sum _{a=1}^{n-1}(an)$ is called Jucys–Murphy element (JM element) in the group algebra ${\mathbb {C}}[S(n)]$ and together with reduced JM element $J_{k}=\sum _{a=1}^{k-1}(ak),$ $k=2,\ldots ,n$ it plays an important role in the representation theory of symmetric group S(n) [20, 21, 33, 36].

In general, calculating analytically the spectrum of JM elements in the group algebra ${\mathbb {C}}[S(n)]$ is not easy (see [36]). Using Proposition 4 together with the above example we get

Corollary 11

In any PRIR $\psi _{R}^{\mu }$ of the symmetric group S(n) we have the following spectral decomposition JM operator $J_{n}= \sum _{a=1}^{n-1}(an)$

$$\begin{aligned} \psi _{R}^{\mu }(J_{n})=\bigoplus _{\alpha \in \mu }\gamma _{\mu }(\alpha ) \textbf{1}_{\alpha }, \end{aligned}$$

(49)

where

$$\begin{aligned} \gamma _{\mu }(\alpha )=\left( \begin{array}{c} n \\ 2 \end{array} \right) \frac{\chi ^{\mu }(12)}{d_{\mu }}-\left( \begin{array}{c} n-1 \\ 2 \end{array} \right) \frac{\chi ^{\alpha }(12)}{d_{\alpha }}=\eta _{\mu }(\alpha )-1, \end{aligned}$$

(50)

and multiplicity of the eigenvalue $\gamma _{\mu }(\alpha )$ is equal to $d_{\alpha }$.

Again, knowing the spectrum of the operator $J_{n}$ in any PRIR, one can determine the spectrum of $J_{n}$ in any representation. As an example let us consider the natural permutation representation of symmetric as it is defined in (1). It is known [35] that then for $d=2$, we have the following

$$\begin{aligned} V_{d=2}^{n}=m_{id}\psi ^{id}\oplus \left[ \bigoplus _{1\le k\le \frac{1}{2}n}m_{\mu _{k}}\psi ^{\mu _{k}}\right] , \end{aligned}$$

(51)

where $m_{id}=n+1$, and $m_{\mu _{k}}=n-2k+1$ are the multiplicities of corresponding irreps which are assumed to be PRIRs. Now using the above results we may derive the spectrum of the JM operator in the natural representation $V_{d=2}^{n}$.

Proposition 12

The spectrum of the operator $V_{d=2}^{n}(J_{n})$ acting in the space $({\mathbb {C}}^{2})^{\otimes n}$ is the following

• 1. If $\mu _k=id$, then

  $$\begin{aligned} \gamma _{id}(id)=n-1, \end{aligned}$$

  (52)

  with multiplicity $n+1$.

• 2. If $\mu _{k}$ is such that $n-k>k$, then

  $$\begin{aligned} \gamma _{\mu _{k}}(\alpha _{k})=\eta _{\mu _{k}}(\alpha _{k})-1, \end{aligned}$$

  (53)

  with multiplicity $m_{\mu _{k}}d_{\alpha _{k}}=(n-2k+1)\left( {\begin{array}{c}n-1\\ k\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right)$, and

  $$\begin{aligned} \gamma _{\mu _{k}}(\alpha _{k-1})=\eta _{\mu _{k}}(\alpha _{k-1})-1, \end{aligned}$$

  (54)

  with multiplicity $m_{\mu _{k}}d_{\alpha _{k-1}}=(n-2k+1)\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) -\left( {\begin{array}{c}n-1\\ k-2\end{array}}\right)$.

• 3. If $\mu _{k}$ is such that $n-k=k$, then

  $$\begin{aligned} \gamma _{\mu _{k}}(\alpha _{k-1})=\eta _{\mu _{k}}(\alpha _{k-1})-1 \end{aligned}$$

  (55)

  with multiplicity $m_{\mu _{k}}d_{\alpha _{k-1}}.$

It is well known that any group algebra ${\mathbb {C}}[G]$ (G is finite) has the following decomposition into irreps

$$\begin{aligned} {\mathbb {C}}[G]=\bigoplus _{\mu \in \widehat{G}}m_{\mu }\psi ^{\mu },\quad \end{aligned}$$

(56)

where $m_{\mu }=\dim \psi ^{\mu }$. From this and Corollary 11 we get:

Proposition 13

The spectrum of JM element $J_{n}=\sum _{a=1}^{n-1}(an)$, acting on the group algebra ${\mathbb {C}}[S(n)]$, i.e in regular representation is given by numbers $\gamma _{\mu }(\alpha )$ and multiplicity of eigenvalue $\gamma _{\mu }(\alpha )$ is equal to $m_{\mu }d_{\alpha }$.

We see that by using the PRIR concept one can express the eigenvalues of the JM element $J_{n}=\sum _{a=1}^{n-1}(an)$ via characters of irreps of the groups S(n) and $S(n-1)$, which are basic characteristics of irreps. Their multiplicities are also expressed by basic group representation parameters. Obtained expressions for the spectrum of the JM elements are of a different nature than in [33, 34, 36].

One very efficient application of PRIR concept was dedicated studies on PBT operator in deterministic port-based teleportation scheme, see (5) and (7). Hereunder we use original notation and we denote the total number of systems (number of ports + teleported state) by n, while the number of ports by N, and we have of course $n=N+1$. The algebraic structure of the port-based teleportation scheme is connected with the algebra of partially transposed operators ${\mathcal {A}}_{n}^{t_{n}}(d)$ acting in n-fold tensor product of $d-$dimensional vector space. This algebra is not isomorphic (except when $d=2$) with standard permutational representation of symmetric group S(n) in the Schur-Weyl construction. Due to the application of properties of PRIR’s it was possible to derive elegant expression for the spectrum of PBT operator and to derive entanglement fidelity for deterministic PBT-scheme in all variants. The result for the mentioned eigenvalues are contained in [12, 14].

Proposition 14

The eigenvalues $\lambda _{\mu }(\alpha )$ of PBT operator with $N=n-1$ ports are of the following form

$$\begin{aligned} \lambda _{\mu }(\alpha )=(n-1)\frac{m_{\mu }d_{\alpha }}{m_{\alpha }d_{\mu }} =\left( \begin{array}{c} n-1 \\ 2 \end{array} \right) \frac{\chi ^{\mu }(12)}{d_{\mu }}-\left( \begin{array}{c} n-2 \\ 2 \end{array} \right) \frac{\chi ^{\alpha }(12)}{d_{\alpha }}+d, \end{aligned}$$

(57)

where $d_{\alpha },d_{\mu }$ are dimensions of irreps $\psi ^{\mu }\in \widehat{S(n-1)}$, $\varphi ^{\alpha }\in \widehat{S(n-2)}$ and $m_{\mu },m_{\alpha }$ are corresponding multiplicities is the standard swap representation of $S(n-1)$ and $S(n-1)$, respectively.

Comparing Proposition 14 with Corollary 11 we get

Corollary 15

The eigenvalues $\lambda _{\mu }(\alpha )$ of PBT operator with $N=n-1$ ports and eigenvalues $\gamma _{\mu }(\alpha )$ of Jucys–Murphy element $J_{n-1}$ are related in a very simple way

$$\begin{aligned} \lambda _{\mu }(\alpha )-d=(n-1)\frac{m_{\mu }d_{\alpha }}{m_{\alpha }d_{\mu }}-d=\gamma _{\mu }(\alpha ). \end{aligned}$$

(58)

In this way, we get, from PBT formalism, another (up to our best knowledge not known earlier) expression for the spectrum of the JM element $J_{n-1}$. Another expression for the numbers $\eta _{\mu }(\alpha )$, so also for the eigenvalues $\gamma _{\mu }(\alpha )$ of $J_{n-1}$, is given in [14].

Remark 2

Note that although we have very simple relation between PBT operator $\rho$ and JM operator $J_{n}$:

$$\begin{aligned} J_{n} \mapsto \rho =J_n^{t_n}, \end{aligned}$$

(59)

the spectrum of the operator $\rho$ is in very simple ’shift’ relation with the spectrum of the ’shorter’ JM operator $J_{n-1}$, see Eq. (57).

Let us remind basic properties of the regular representation of a group algebra ${\mathbb {C}}[G]$ for finite a finite group G.

Proposition 16

Let $\psi ^{\mu }$ be any irrep (not necessarily PRIR) of a finite group G, then the operators

$$\begin{aligned} E_{ij}^{\mu }=\frac{d_{\mu }}{|G|}\sum _{g\in G}\psi _{ji}^{\mu }(g^{-1})g\in {\mathbb {C}}[G] \end{aligned}$$

(60)

have the following properties

$$\begin{aligned} E_{ij}^{\mu }E_{kl}^{\nu }=\delta ^{\mu \nu }E_{il}^{\mu },\quad gE_{ij}^{\mu }=\sum _{k=1}^{d_{\mu }}\psi _{ki}^{\mu }(g)E_{kj}^{\mu },\quad \forall j=1,\ldots ,d_{\mu },\quad {\mathbb {C}}[G]=\bigoplus _{\mu \in \widehat{G}}E^{\mu },\nonumber \\ \end{aligned}$$

(61)

where $E^{\mu }={\text {span}}_{{\mathbb {C}}}\{E_{ij}^{\mu }:i,j=1,\ldots ,d_{\mu }\}.$ The algebra ${\mathbb {C}}[G]$ is a direct sum of non-isomorphic matrix algebras and for any fixed $j=1,\ldots ,d_{\mu }$ set of $d_{\mu }$ vectors $E_{ij}^{\mu }:i=1,\ldots ,d_{\mu }$ form a basis of irrep $\psi ^{\mu }$ contained in ${\mathbb {C}}[G].$ Each subalgebra $E^{\mu }$ contains $d_{\mu }$ such irreps.

If the $\psi ^{\mu }\in {\mathbb {C}}[G]$ are $PRIR^{\prime }s$, then we may rewrite the expressions from Proposition 16 as follows

$$\begin{aligned}{} & {} (E_{R}^{\mu })_{i_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}=\frac{d_{\mu }}{|G|}\sum _{g\in }(\psi _{R}^{\mu }(g^{-1})_{j_{\beta }\quad \quad i_{\alpha }}^{\beta (b_{\beta })\alpha (a_{\alpha })}g,\quad \end{aligned}$$

(62)

$$\begin{aligned}{} & {} g(E_{R}^{\mu })_{j_{\beta }\quad \quad i_{\alpha }}^{\beta (b_{\beta })\alpha (a_{\alpha })}=\sum _{\gamma (c_{\gamma }),k_{\gamma }}(\psi _{R}^{\mu }(g)_{k_{\gamma }\quad \quad j_{\beta }}^{\gamma (c_{\gamma })\beta (b_{\beta })}(E_{R}^{\mu })_{k_{\gamma }\quad \quad i_{\alpha }}^{\gamma (c_{\gamma })\alpha (a_{\alpha })}, \end{aligned}$$

(63)

$$\begin{aligned}{} & {} (E_{R}^{\mu })_{i_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(E_{R}^{\mu })_{i_{\alpha }^{\prime }\quad \quad j_{\beta }^{\prime }}^{\alpha ^{\prime }(a_{\alpha }^{\prime })\beta ^{\prime }(b_{\beta }^{\prime })}=\delta ^{\beta \alpha ^{\prime }}\delta ^{b_{\beta }a_{\alpha }^{\prime }}\delta _{j_{\beta }i_{\alpha }^{\prime }}(E_{R}^{\mu })_{i_{\alpha }\quad \quad j_{\beta }^{\prime }}^{\alpha (a_{\alpha })\beta ^{\prime }(b_{\beta }^{\prime })}. \end{aligned}$$

(64)

Now we consider, in the regular representation of the group algebra ${\mathbb {C}}[G]$, a construction of induced representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\alpha })$, where $\varphi ^{\alpha }\in \widehat{H}$ is an arbitrary irrep of the subgroup $H\subset G$. We have (for simplicity we omit label $\beta$ in indices i, j):

Proposition 17

Consider the standard matrix algebra generated by the irrep $\varphi ^{\beta }=(\varphi _{ij}^{\beta })\in \widehat{H}$ (here for simplicity we write omit label $\beta$ in indices i, j)

$$\begin{aligned} E_{ij}^{\beta }=\frac{d_{\beta }}{|H|}\sum _{h\in H}\varphi _{ji}^{\beta }(h^{-1})h\in {\mathbb {C}}[H]\subset {\mathbb {C}}[G], \end{aligned}$$

(65)

and the transversal $T=\{t_{k}:k=1,\ldots ,\frac{|G|}{|H|}\equiv s\}$, then for any fixed value of $j=1,\ldots ,d_{\beta }$, the $sd_{\beta }$ vectors

$$\begin{aligned} t_{k}E_{ij}^{\beta }:k=1,\ldots ,\frac{|G|}{|H|}\equiv s,\quad i=1,\ldots ,d_{\beta } \end{aligned}$$

(66)

form a basis of the induced representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$ of the group G, embedded in the regular representation of group algebra ${\mathbb {C}}[G]$, i.e. we have

$$\begin{aligned} \forall g\in G\quad g.t_{k}E_{ij}^{\beta }=\sum _{t_{p}\in T}\sum _{l=1,\ldots ,d_{\alpha }}\varphi _{li}^{\beta }(t_{p}^{-1}gt_{k})t_{p}E_{lj}^{\beta }, \end{aligned}$$

(67)

where the summation over $t_{p}\in T$ is taken over such $t_{p}\in T$, that $t_{p}^{-1}gt_{k}\in H$ [37]. From the uniqueness of coset decomposition, Eq. (25) we get that such an element $t_{p}\in T$ is unique and we have $t_{p}^{-1}gt_{k}=h=h_{k}\in H$ so the above equation may written equivalently

$$\begin{aligned} \forall g\in G\quad g.t_{k}E_{ij}^{\beta }=\sum _{l=1,\ldots ,d_{\alpha }}\varphi _{li}^{\beta }(h_{k})t_{p}E_{lj}^{\beta }, \end{aligned}$$

(68)

where $gt_{k}=t_{p}h_{k}$ is the unique coset decomposition. Thus we see that the main feature of the induced representation is that the action of $g\in G$ on basis vectors $\{t_{k}E_{ij}^{\beta }\}$ permutes the transversal vectors $\{t_{k}:k=1,\ldots ,\frac{|G|}{|H|}\equiv s\}$ and transforms vectors $\{E_{ij}^{\beta }:i=1,\ldots ,d_{\beta }\}$ (j is fixed) according irrep $\varphi ^{\beta }$.

The subspaces

$$\begin{aligned} I_{j}^{\beta }=I_{j_{\beta }}^{\beta }={\text {span}}_{\mathbb {C}}\left\{ t_{k}E_{ij}^{\beta }:k=1,\ldots ,\frac{|G|}{|H|}\equiv s,\quad i=1,\ldots ,d_{\beta }\right\} ,\quad j_{\beta }=1,\ldots ,d_{\beta }\nonumber \\ \end{aligned}$$

(69)

are representation spaces for representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$. From the above we get

Corollary 18

We have the following decomposition of algebra ${\mathbb {C}}[G]$

$$\begin{aligned} {\mathbb {C}}[G]=\bigoplus _{\beta \in \widehat{H}} \ \bigoplus _{j_{\beta }=1,\ldots ,d_{\beta }}I_{j_{\beta }}^{\beta } \,\quad {\mathbb {C}}[G]=\bigoplus _{\mu \in \widehat{G}}E^{\mu }. \end{aligned}$$

(70)

Now it is well known that the induced representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\alpha })$ of the group G is in general reducible. It appears that the reduction of ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\alpha })$ onto the direct product of irreps of the group G may be achieved using $PRIR^{\prime }s$. Using such a PRIR matrices $\psi _{R}^{\mu }$ we define the following matrices

Definition 19

Let $\varphi ^{\beta }\in \widehat{H\text { }}$ be an irrep and all $\psi _{R}^{\mu }\equiv \psi _{R}^{\mu _{\beta }}\in \widehat{G}$ be a $PRIR^{\prime }s$, such that $\varphi ^{\beta }\in {\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu })$. For such an irreps $\varphi ^{\beta }$ and $PRIR^{\prime }s$ $\psi _{R}^{\mu _{\beta }}$ we define a matrix $U(\beta )$ with coefficients

$$\begin{aligned} U(\beta )_{b_{\beta }\quad l_{\alpha },k_{\beta }}^{\mu \alpha (a_{\alpha }),~t_{k}}=\sqrt{\frac{|H|d_{\mu }}{|G|d_{\beta }}}(\overline{\psi } _{R}^{\mu })_{l_{\alpha }\quad \quad k_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(t_{k})=U(\beta )_{RL}, \end{aligned}$$

(71)

so the left multi-index $R= \begin{array}{c} \mu _{\beta }\quad \alpha (a_{\alpha }) \\ b_{\beta }\quad l_{\alpha } \end{array}$, which includes four indices, runs over all $\mu _{\beta }$, over PRIR indices $\alpha (a_{\alpha })$, $l_{\alpha }$ inside $PRIR^{\prime }s$ $\psi _{R}^{\mu _{\beta }}$, as well over index $b_{\beta }$, which enumerates the copies of the irrep $\varphi ^{\beta }$ in $\psi _{R}^{\mu _{\beta }}$. The right muli-index $L= \begin{array}{c} t_{k} \\ k_{\beta } \end{array}$ runs over the natural indices of the induced representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$. Matrix $U(\beta )$ is of dimension $d_{\beta }[G:H]=\dim {\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$. One can check that

$$\begin{aligned} (U^{\dagger })(\beta )_{k_{\beta },\quad b_{\beta }~l_{\alpha }}^{t_{k},~~\mu \alpha (a_{\alpha })}=\sqrt{\frac{|H|d_{\mu }}{|G|d_{\beta }}}(\overline{ \psi }_{R}^{\mu })_{k_{\beta }\quad \quad l_{\alpha }}^{\beta (b_{\beta })\alpha (a_{\alpha })}(t_{k})=U^{\dagger }(\beta )_{IR}. \end{aligned}$$

(72)

Matrix $U(\beta )$ is determined by irrep $\varphi ^{\beta }\in \widehat{H}$ because, by assumption irrep $\varphi ^{\beta }$ determines all irreps $\mu _{\beta }\in \widehat{G}$, which must satisfy $\varphi ^{\beta }\in {\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu })$. Note that the matrix $U(\beta )$ is not proportional to some $PRIR^{\prime }s$ matrix $\psi _{R}^{\mu (\beta )}$, the coefficients of the matrix $U(\beta )$ are equal to corresponding coefficients of the different matrices $\psi _{R}^{\mu (\beta )}$. In general the matrices $U(\beta )$ and $\psi _{R}^{\mu (\beta )}$ have different dimension.

Directly from Definition 19 and the sum rule for PRIRs in Proposition 3 we get

Proposition 20

The matrix $U(\beta )$ is unitary with respect to the induced multi-indices $I= \begin{array}{c} t_{k} \\ k_{\beta } \end{array}$, i.e. we have

$$\begin{aligned} \sum _{t_{k},k_{\beta }}U(\beta )_{b_{\beta }\quad l_{\alpha },k_{\beta }}^{\nu \alpha (a_{\alpha }),~t_{k}}(U^{\dagger })(\beta )_{k_{\beta },~b_{\beta }^{\prime }~j_{\gamma }}^{t_{k},~~\mu ~\gamma (c_{\gamma })}=\delta ^{\mu \nu }\delta _{b_{\beta }b_{\beta }^{\prime }}\delta ^{\alpha \gamma }\gamma ^{a_{\alpha }c_{\gamma }}\delta _{l_{\alpha }j_{\gamma }} \end{aligned}$$

(73)

and it is known that if a matrix is unitary with respect to the columns, then it is also unitary with respect to the rows, so the matrix $U(\beta ):\varphi ^{\beta }\in \widehat{H}$ is unitary and has dimension $d_{\beta }\frac{|G|}{|H|}$.

Now let us consider subspace $I_{j_{\beta }}^{\beta }\subset {\mathbb {C}}[G]$ with fixed label $j_{\beta }=1,d_{\beta }$, a representation space for ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$, which in general, as representation of G is reducible. It appears that matrix $U(\beta )$ realize reduction of natural basis $\{t_{k}E_{i_{\beta }j_{\beta }}^{\beta }\}$ in $I_{j_{\beta }}^{\beta }$ to the reduced one with PRIR operators $(E^{\mu })_{l_{\alpha }\quad \quad j_\beta }^{\alpha (a_{\alpha })\beta (b_{\beta })}$ as a basis.

Lemma 21

Let $\varphi ^{\beta }\in \widehat{H}$ be an irrep and let us fix label $j_{\beta }=1,\ldots ,d_{\beta }$. Then the unitary matrix $U(\beta )$ transforms the natural basis $\{t_{k}E_{i_{\beta }j_{\beta }}^{\beta }\}$ of the subspace $I_{j_{\beta }}^{\beta }\subset {\mathbb {C}}[G],$ representation space for ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$ onto a reduced basis of this representation space, that is we have

$$\begin{aligned} \sqrt{\frac{|G|}{|H|}\frac{d_{\mu }}{d_{\beta }}}\sum _{t_{p}\in T}\sum _{k_{\beta }=1,\ldots ,d_{\beta }}U(\beta )_{b_{\beta }\quad l_{\alpha },k_{\beta }}^{\mu \alpha (a_{\alpha }),~t_{p}}t_{p}E_{k_{\beta }j_{\beta }}^{\beta (b_{\beta })}=(E^{\mu })_{l_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}, \end{aligned}$$

(74)

where

$$\begin{aligned} (E^{\mu })_{l_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}=\frac{d_{\mu }}{|G|}\sum _{g\in G}(\psi _{R}^{\mu })_{j_{\beta }\quad \quad l_{\alpha }}^{\beta (b_{\beta })\alpha (a_{\alpha })}(g^{-1})g\in I_{j_{\beta }}^{\beta } \end{aligned}$$

(75)

are standard matrix operators of the group algebra ${\mathbb {C}}[G]$, defined by the irrep $\psi _{R}^{\mu }$ in the PRIR version included in $I_{j_{\beta }}^{\beta },$ the representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$.

Proof

In order to prove the equation

$$\begin{aligned} \frac{|G|}{|H|}\frac{d_{\mu }}{d_{\beta }}\sum _{t_{p}\in T}\sum _{k_{\beta }=1,\ldots ,d_{\beta }}\overline{(\psi _{R}^{\mu })}_{l_{\alpha }\quad \quad k_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}(t_{k})t_{p}E_{k_{\beta }j_{\beta }}^{\beta (b_{\beta })}=(E^{\mu })_{l_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}, \end{aligned}$$

(76)

it is enough to use the definition of the matrix operators $E_{k_{\beta }j_\beta }^{\beta }$ and $(E^{\mu })_{l_{\alpha }\quad \quad j_\beta }^{\alpha (a_{\alpha })\beta (b_{\beta })}$ (see Eq. (65)) together with Eq. (30). $\square$

From Eq. (74) in Lemma 21 we see that each irrep $\varphi ^{\beta (b_{\beta })}$ of H, where $\beta (b_{\beta })=1,\ldots ,m_{\beta }^{\mu },$ included in ${\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu })$ defines one irrep $\psi _{R}^{\mu }\equiv \psi _{R}^{\mu (\beta )}$ (the index $j_{\beta }$ is fixed) with basis vectors indexed by the left pair of PRIR indices $\left( \begin{array}{c} \alpha (a_{\alpha }) \\ l_{\alpha } \end{array} \right)$ in the element $(E^{\mu })_{l_{\alpha }\quad \quad j_{\beta }}^{\alpha (a_{\alpha })\beta (b_{\beta })}$ and this correspondence is one-to-one from the invertibility of the matrix $U(\beta )$. From this as a corollary we get

Theorem 1

Let $\varphi ^{\beta }\in \widehat{H},$ $I_{j_{\beta }}^{\beta }\subset {\mathbb {C}}[G]$ be the corresponding representation space for ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$ with natural basis $\{t_{p}E_{k_{\beta }j_{\beta }}^{\beta }\}$ and $U(\beta )$ be an unitary PRIR matrix determined by $\varphi ^{\beta }$, then

• 1. the transformation of the natural basis of the representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$ in ${\mathbb {C}}[G]$ to the reduced one is realized by the PRIR unitary matrix $U(\beta )$ in the following way

  $$\begin{aligned} U(\beta ):t_{k}E_{i_{\beta }j_{\beta }}^{\beta }\rightarrow \sqrt{\frac{|G|}{ |H|}\frac{d_{\mu }}{d_{\beta }}}\sum _{t_{p}\in T}\sum _{k_{\beta }=1,\ldots ,d_{\beta }}U(\beta )_{b_{\beta }\quad l_{\alpha },k_{\beta }}^{\mu \alpha (a_{\alpha }),~t_{p}}t_{p}E_{k_{\beta }j_\beta }^{\beta }=(E^{\mu })_{l_{\alpha }\quad j_\beta }^{\alpha (a_{\alpha })\beta (b_{\beta })},\quad \end{aligned}$$

  (77)

• 2. from this one can deduce the following decomposition of the induced representations

  $$\begin{aligned} {\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })=\bigoplus _{\mu (\beta )}m_{\beta }^{\mu }\psi _{R}^{\mu (\beta )}, \end{aligned}$$

  (78)

  so each irrep $\psi _{R}^{\mu }$ appears in representation ${\text {Ind}}\uparrow _{H}^{G}(\varphi ^{\beta })$ with multiplicity equal to the multiplicity $m_{\beta }^{\mu }$ of irrep $\varphi ^{\beta }$ in ${\text {Res}}\downarrow _{H}^{G}(\psi _{R}^{\mu }).$

The second part of Theorem 1 is the famous Frobenius reciprocity theorem [36, 38]. This classical theorem is usually proved using group character properties and this proof seems to be the simplest. Our proof of the theorem is technically much more complicated, but its first result gives in Eq. (77) a unitary matrix $U(\beta )$ which realizes the reduction of the natural basis of induced representation to the reduced one, and this is the most complicated part of our proof. To our knowledge, this is a new result. The standard, character proof of the Frobenius theorem does not give such representation reduction (via unitary matrix) because that proof is independent of matrix form of considered representations (which is obtained by use of character theory). The second statement of Theorem 1, i.e., the Frobenius theorem itself is a relatively simple corollary from the multi-index structure of the matrix $U(\beta ).$

4 Discussion

In this paper, we discuss the appearance of induced representation in port-based teleportation protocols, focusing on its deterministic version. First, we define the concept of partially reduced irreducible representation for an arbitrary group G and its subgroup H and discuss the most important properties of the introduced concept. This part is presented on the most possible abstract level, i.e., we do not restrict ourselves to a specific choice of the group G. Afterward, we choose G to be a symmetric group S(n) with subgroup $H=S(n-1)$—groups naturally appearing in all variants of the PBT. This restriction allows us to show the relation between basic objects for representation theory for the symmetric group, so-called Jucys–Murphy elements, and the PBT operator $\rho$. In particular, we prove a linear connection between the spectra of these two objects, presenting two different expressions. Spectra of the JM element $J_{n-1}$ and n-particle PBT operator are related by a simple shift by factor d. In particular, we give new expression for the eigenvalues of the Jucys–Murphy elements based on the irreducible character of the symmetric group, and new orthogonality relations exploiting the concept of PRIRS. In the special case, when one considers the natural representation of Jucys–Murphy elements in dimension 2, we present fully analytical expressions for the mentioned spectrum. Evaluated spectra are crucial in determining entanglement fidelity in deterministic PBT schemes. At the end, we present a matrix proof of the famous Frobenius reciprocity theorem for characters, and we give the explicit construction of the unitary matrix that realizes the reduction of the natural basis of induced representation to the reduced one.