On the vertex functions of type A quiver varieties

Abstract

The goal of this paper is to better understand the quasimap vertex functions of type A Nakajima quiver varieties. To that end, we construct an explicit embedding of any type A quiver variety into a type A quiver variety with all framings at the rightmost vertex of the quiver. Then, we consider quasimap counts, showing that the map induced by this embedding on equivariant K-theory preserves vertex functions.

1 Introduction

The topic of this paper is type A Nakajima quiver varieties, see [1,2,3], and their quasimap vertex functions [4]. These varieties are of crucial importance in geometric representation theory, see for example [3,4,5,6,7]. From a physical perspective, they arise as the Higgs branch of the moduli space of vacua of 3d ${\mathcal {N}}=4$ gauge theories, which leads to their relevance in the phenomenon of 3d mirror symmetry studied, for example, in [8,9,10,11,12,13,14,15,16]. Our main goal here is to prove a statement relating the quasimap vertex functions of two different type A quiver varieties. As we will discuss later in the introduction, our results are motivated by the hope of developing a sufficient technical understanding of vertex functions needed to prove their expected duality under 3d mirror symmetry.

1.1 Embedding of quiver varieties

Fix a natural number m and consider the type $A_{m}$ quiver Q, which has vertex set $Q_{0}=\{1,2,\ldots ,m\}$ and edges $i\rightarrow i+1$ for $1 \le i \le m-1$. For a choice of ${\textsf{v}},{\textsf{w}}\in {\mathbb {Z}}_{\ge 0}^{Q_{0}}$, called the dimension vector and framing vector, respectively, and for a stability parameter $\theta \in {\mathbb {Z}}^{Q_{0}}$, Nakajima defined a quasiprojective algebraic variety ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$. To be sure, Nakajima varieties are well-defined for any choice of quiver Q, but our interest in this paper is only in the type A setting.

Assume now that ${\textsf{w}}_{i} \ne 0$ for some $i<m$. Let $k\in Q_{0}$ be the maximal vertex such that $k+1<m$ and ${\textsf{w}}_{k+1} \ne 0$. We define ${\textsf{v}}', {\textsf{w}}' \in {\mathbb {Z}}_{\ge 0}^{Q_{0}}$ by

$$\begin{aligned} {\textsf{v}}'_{i}&={\left\{ \begin{array}{ll} {\textsf{v}}_{i} &{} \quad 1 \le i \le k \\ {\textsf{v}}_{i}+i-k-1 &{}\quad k+1 \le i \le m \end{array}\right. } \\ {\textsf{w}}'_{i}&={\left\{ \begin{array}{ll} {\textsf{w}}_{k+1}-1 &{} \quad i=k+1 \\ {\textsf{w}}_{m}+m-k &{} \quad i=m \\ {\textsf{w}}_{i} &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

Theorem 1

(Theorem 3) There exists a closed embedding

$$\begin{aligned} \Phi : {\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}}) \hookrightarrow {\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}') \end{aligned}$$

(1)

Furthermore, let ${\textsf{T}}$ and ${\textsf{T}}'$ be the natural tori acting on ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ and ${\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}')$, see Sect. 2.3. Then, there is an inclusion $\iota : {\textsf{T}}\hookrightarrow {\textsf{T}}'$ such that (1) is ${\textsf{T}}$-equivariant.

We construct (1) in Sects. 3 and 4. Recall that ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ is the moduli space of $\theta$-semistable representations of the doubled framed quiver of Q with dimension vectors ${\textsf{v}}$ and ${\textsf{w}}$. In Sect. 3, we consider the data of a quiver representation corresponding to the vertices $\{k+1,k+2,\ldots ,m\} \subset Q_{0}$ and we define the map (1) explicitly in terms of this data. We then check that it respects the stability condition, descends to the quiver varieties, and is ${\textsf{T}}$-equivariant.

Applying Theorem 1 repeatedly, we can embed ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ into a quiver variety with all framings at the last vertex.

Corollary 1

Given ${\textsf{v}}, {\textsf{w}}\in {\mathbb {Z}}^{Q_{0}}_{\ge 0}$, there exists ${\textsf{v}}', {\textsf{w}}' \in {\mathbb {Z}}^{Q_{0}}_{\ge 0}$ where ${\textsf{w}}'_{i}=0$ for $i \ne m$ and a ${\textsf{T}}$-equivariant closed embedding

$$\begin{aligned} {\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}}) \hookrightarrow {\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}') \end{aligned}$$

(2)

If ${\textsf{w}}=(0,0,\ldots ,N)$, it is known that the corresponding Nakajima variety ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ is nonempty if and only if ${\textsf{v}}_{1} \le {\textsf{v}}_{2} \le \ldots \le {\textsf{v}}_{m} \le N$, [2, section 7]. Furthermore, if $\theta =\pm (1,1,\ldots ,1)$, then ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ is the cotangent bundle of a partial flag variety. It follows immediately from Corollary 1 that any type A quiver variety arising from the stability conditions $\theta ^{\pm }=\pm (1,1,\ldots ,1)$ can be embedded into the cotangent bundle of a partial flag variety.

1.2 Vertex functions

Our motivation for and construction of Theorem 1 was inspired by the work [17]. To explain the connection, we must recall some aspects of the enumerative geometry of Nakajima quiver varieties. As shown in the pioneering work of Maulik–Okounkov [5] and later in [4], enumerative invariants of Nakajima varieties are deeply related to the representation theory of certain quantum groups. In the K-theoretic setting, the relevant enumerative theory of curves is the theory of quasimaps to a GIT quotient developed in [18]. In [4], Okounkov identifies q-difference equations constraining certain K-theoretic quasimap counts with the quantum Knizhnik–Zamolodchikov equations arising from the representation theory of quantum affine algebras [19].

One of the key curve counts studied in [4] are known as vertex functions. For $d \in {\mathbb {Z}}^{Q_{0}}$, let $\text {\textsf {QM}}^{d}_{\text {ns }\infty }$ denote the moduli space of degree d stable quasimaps from ${\mathbb {P}}^{1}$ to a Nakajima variety X nonsingular at $\infty \in {\mathbb {P}}^{1}$. The usual action of ${\mathbb {C}}^{\times }$ on ${\mathbb {P}}^{1}$ gives rise to the action of a torus, denoted ${\mathbb {C}}^{\times }_{q}$, on quasimaps. Let $K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}(X)_{loc}= K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}(X) \otimes _{R} \text {Frac}(R)$ where $R=K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}(pt)$. Let $\text {ev}_{\infty }:\text {\textsf {QM}}^{d}_{\text {ns }\infty } \rightarrow X$ be the map given by evaluating a quasimap at $\infty$. Let $\hat{{\mathcal {O}}}_{\text {vir}}^{d}$ be the symmetrized virtual structure sheaf on $\text {\textsf {QM}}^{d}_{\text {ns }\infty }$¹. Then, the vertex function of X is defined to be:

$$\begin{aligned} V(z)=\sum _{d} \text {ev}_{\infty ,*}\left( \hat{{\mathcal {O}}}_{\text {vir}}^{d} \right) z^{d}\in K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}(X)_{loc}[[z]] \end{aligned}$$

where d runs over all degrees such that $\text {\textsf {QM}}^{d}_{\text {ns }\infty }$ is nonempty and $z^{d}:=\prod _{i=1}^{m} z_{i}^{d_{i}}$. The variables $z_{i}$ for $1\le i \le m$ can be though of as formal parameters and are conventionally referred to as “Kähler parameters" (or Fayet–Iliopoulos parameters in the physics literature). In section 7 of [4], Okounkov shows that V(z) satisfies a system a scalar q-difference equations with regular singularities, from which it follows that V(z) is in fact the Taylor series expansion of a meromorphic function of z. The notation [[z]] above refers to a completion of the semigroup algebra of the cone of effective curves in X. We review vertex functions in Sect. 5, but see also [4, 20,21,22] for further explanations.

In [23], Aganagic and Okounkov show how the Bethe equations can be obtained from quiver varieties. This was also explored in [22], where the Bethe equations for the XXZ spin chain were identified with the criticality conditions for the saddle point approximation of a contour integral computing the vertex functions for the cotangent bundle of the Grassmannian. The work of Koroteev–Zeitlin in [17] studied 3d mirror symmetry from the perspective of Bethe equations. There the authors show that the Bethe equations associated with ${\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}')$ recover those associated to ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ under a certain specialization of the parameters. Because the Bethe equations can be recovered from the vertex functions, which depend on the geometry of the quiver variety, it seemed desirable to us to obtain a direct geometric relationship between ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ and ${\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}')$, hence Theorem 1. Furthermore, one hopes that Theorem 1 would relate vertex functions, thus giving a broader explanation for the coincidences observed in [17].

In Sects. 5 and 6, we pursue this agenda. Let $\theta =\theta ^{-}$ and consider the pullback on equivariant K-theory

$$\begin{aligned} \Phi ^{*}: K_{{\textsf{T}}'}({\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}')) \rightarrow K_{{\textsf{T}}}({\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})) \end{aligned}$$

induced by $\Phi$.

Let $V(z) \in K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}({\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}}))_{loc}[[z]]$ and $V'(z) \in K_{{\textsf{T}}'\times {\mathbb {C}}^{\times }_{q}}({\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}'))_{loc}[[z]]$ be the vertex functions of ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$ and ${\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}')$, respectively. Then, our main theorem is the following.

Theorem 2

(Theorem 6) The map $\Phi ^{*}$ preserves vertex functions. More precisely,

$$\begin{aligned} \Phi ^{*}(V'(z))=V({\tilde{z}}) \end{aligned}$$

where ${\tilde{z}}$ stands for a shift of the parameters $z_{1},\ldots , z_{m}$ by certain powers of q.

Skipping ahead to Theorem 5, the reader can see that in the K-theoretic fixed point basis, vertex functions are certain q-hypergeometric series. In fact, vertex functions generalize many of the most important q-hypergeometric series. For the quiver variety $T^*{\mathbb {P}}^{n}$, one recovers the so-called $_{n+1} \phi _{n}$ basic hypergeometric series. Concretely, Theorem 2 gives a relationship between two different q-series under a parameter specialization. From this perspective, Theorem 2 demonstrates how the geometry of quiver varieties can be exploited to give a deeper understanding of certain special functions. Special cases of vertex functions were studied in [11, 21, 24,25,26,27,28], which considered summation formulas, symmetries under swaps of the parameters (i.e. 3d mirror symmetry), and connections with Macdonald theory.

Theorem 2 is proven in Sect. 6 by a careful analysis of the localization formula for the vertex. Although the proof involves complicated combinatorial expressions, Theorem 2 is actually a “term-by-term" result. By this we mean the following. Each term in the localization formula for $V'(z)$ corresponds to a ${\textsf{T}}' \times {\mathbb {C}}^{\times }_{q}$ fixed quasimap to ${\mathcal {M}}_{\theta }({\textsf{v}}',{\textsf{w}}')$, and similarly for V(z). Applying $\Phi ^{*}$ to $V'(z)$, some of these terms become zero, and the remaining terms can be matched in a one-to-one fashion with the terms of V(z).

For this reason, one is tempted to say that $V'(z)$ is a more complicated series than V(z). However, in the special case where ${\mathcal {M}}_{\theta }({\textsf{v}}', {\textsf{w}}')$ is the cotangent bundle to a complete flag variety, there is at least one aspect of $V'(z)$ which is better understood: the q-difference equations in the Kähler parameters. In a future work, we will exploit this fact to prove 3d mirror symmetry of the vertex functions for those cotangent bundles of partial flag varieties whose 3d mirror duals are still Nakajima quiver varieties.

In closing, we mention the work [29] of Rimányi and Botta. In the more general setting of bow varieties, they independently arrived at the same construction as Theorem 1, which they call the “D5 resolution". They prove an analog of Theorem 2 for elliptic stable envelopes and use it, along with another construction known as the “NS5 resolution", to prove 3d mirror symmetry for elliptic stable envelopes.

2 Review of quiver varieties

2.1 Definition

We review the construction of Nakajima quiver varieties from [2, 3], see also [1]. Since our interest is only in type A quiver varieties, we will specialize to that case. Consider a quiver Q with vertices $Q_{0}=\{1,2,\ldots ,n\}$ and edges from i to $i+1$ for $1 \le i \le n-1$. Choose ${\textsf{v}},{\textsf{w}}\in {\mathbb {Z}}_{\ge 0}^{Q_{0}}$. Let $\theta \in {\mathbb {Z}}^{Q_{0}}$ be the stability parameter.

For each $i \in Q_{0}$, let $V_{i}$ and $W_{i}$ be complex vector spaces of dimension ${\textsf{v}}_{i}$ and ${\textsf{w}}_{i}$, respectively. Let

$$\begin{aligned} \text {Rep}_{Q}({\textsf{v}},{\textsf{w}})= \bigoplus _{i=1}^{n-1} \text {Hom}(V_{i},V_{i+1}) \oplus \bigoplus _{i=1}^{n} \text {Hom}(W_{i},V_{i}) \end{aligned}$$

and

$$\begin{aligned} G_{{\textsf{v}}}=\prod _{i \in Q_{0}} GL(V_{i}) \end{aligned}$$

Since $G_{{\textsf{v}}}$ acts on $\text {Rep}_{Q}({\textsf{v}},{\textsf{w}})$ by change of basis, there is an induced Hamiltonian action of $G_{{\textsf{v}}}$ on $T^*\text {Rep}_{Q}({\textsf{v}},{\textsf{w}})$, with associated moment map

$$\begin{aligned} \mu _{{\textsf{v}},{\textsf{w}}}: T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}}) \rightarrow \text {Lie}(G_{{\textsf{v}}})^{*} \end{aligned}$$

The associated Nakajima quiver variety is defined as the algebraic symplectic reduction:

(3)

Here the notation stands for the GIT quotient with stability parameter $\theta$. The stability parameter corresponds to the character of $G_{{\textsf{v}}}$ given by

$$\begin{aligned} (g_{i})_{i \in Q_{0}} \mapsto \prod _{i \in Q_{0}} \det (g_{i})^{-\theta _{i}} \end{aligned}$$

By the trace pairing, we have $\text {Hom}(A,B)^{*} \cong \text {Hom}(B,A)$, so that we can denote a general element of

$$\begin{aligned} T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}})\cong \text {Rep}_{Q}({\textsf{v}},{\textsf{w}})\oplus \text {Rep}_{Q}({\textsf{v}},{\textsf{w}})^{*} \end{aligned}$$

by a quadruple $(\{X_{i}\}_{1 \le i \le n-1}, \{Y_{i}\}_{1 \le i \le n-1}, \{I_{i}\}_{i \in Q_{0}}, \{J_{i}\}_{i \in Q_{0}})$, where $X_{i} \in \text {Hom}(V_{i},V_{i+1})$, $Y_{i} \in \text {Hom}(V_{i+1},V_{i})$, $I_{i} \in \text {Hom}(W_{i},V_{i})$ and $J_{i} \in \text {Hom}(V_{i},W_{i})$, see Fig. 1. We abbreviate this by (X, Y, I, J).

Fig. 1

A graphical depiction of the data (X, Y, I, J)

Under the identification $\text {Lie}(G_{{\textsf{v}}})^{*}\cong \text {Lie}(G_{{\textsf{v}}})$ given by the trace pairing, the moment map is

$$\begin{aligned} \mu _{{\textsf{v}},{\textsf{w}}}(X,Y,I,J)=\left( X_{i-1}Y_{i-1}-Y_{i}X_{i} + I_{i} J_{i}\right) _{i \in Q_{0}} \in \bigoplus _{i \in Q_{0}} \text {End}(V_{i}) = \text {Lie}(G_{{\textsf{v}}}) \end{aligned}$$

2.2 Criterion for semistability

We will also need the well-known criterion for GIT (semi)stability. To state it, we define two conditions on (X, Y, I, J):

• 1. Let $\{S_{i}\}_{i \in I}$ be a collection of subspaces $S_{i} \subset V_{i}$ preserved by X and Y such that $S_{i} \subset \ker J_{i}$ for all i. Then,

  $$\begin{aligned} \sum _{i \in Q_{0}} \theta _{i} \dim _{{\mathbb {C}}}S_{i} \le 0 \end{aligned}$$

• 2. Let $\{T_{i}\}$ be a collection of subspaces $T_{i} \subset V_{i}$ preserved by X and Y such that $T_{i} \supset {{\,\textrm{Im}\,}}I_{i}$ for all i. Then,

  $$\begin{aligned} \sum _{i \in Q_{0}}\theta _{i} \dim _{{\mathbb {C}}}T_{i} \le \sum _{i \in Q_{0}} \theta _{i} \dim _{{\mathbb {C}}} V_{i} \end{aligned}$$

Proposition 1

([1], Proposition 5.1.5) A quadruple $(X,Y,I,J) \in \mu _{{\textsf{v}},{\textsf{w}}}^{-1}(0)$ is $\theta$-semistable if and only if conditions 1 and 2 above hold.

2.3 Torus action

There is a natural action of the torus ${\textsf{A}}:=({\mathbb {C}}^{\times })^{|{\textsf{w}}|}$ on $T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}})$ coming from the action of ${\textsf{A}}$ on each $W_{i}$. It descends to an action on ${\mathcal {M}}_{\theta }({\textsf{v}},{\textsf{w}})$. In addition, there is an action of ${\mathbb {C}}^{\times }$ on $T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}})$ given by dilation of the cotangent fibers. We denote this latter torus by ${\mathbb {C}}^{\times }_{\hbar }$. Let ${\textsf{T}}={\textsf{A}}\times {\mathbb {C}}^{\times }_{\hbar }$

3 The embedding: local case

Our goal is to define an embedding of one quiver variety inside another. Our embedding will be constructed locally on the quiver. For the basic situation, let ${\textsf{v}}\in {\mathbb {Z}}_{\ge 0}^{n}$ be arbitrary, but assume that ${\textsf{w}}_{i}=0$ if $2 \le i \le n-1$.

3.1 Notations

Points in $T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}})$ are given by diagrams of the form:

Choose a basis for each vector space $V_i$ and $W_i$ and write all linear maps in the diagram above as matrices. In particular, we write

$$\begin{aligned} I_1= \begin{pmatrix} A_1&A_2&\ldots&A_{{\textsf{w}}_1} \end{pmatrix} \end{aligned}$$

where each $A_{k}$ is a column vector in ${\mathbb {C}}^{{\textsf{v}}_{1}}$. Similarly, we write

$$\begin{aligned} J_1= \begin{pmatrix} B_1 \\ B_2 \\ \vdots \\ B_{{\textsf{w}}_1} \end{pmatrix} \end{aligned}$$

where each $B_{k}$ is a row vector in ${\mathbb {C}}^{{\textsf{v}}_{1}}$.

Let ${\textsf{v}}',{\textsf{w}}' \in {\mathbb {Z}}^{n}_{\ge 0}$ be defined by

$$\begin{aligned} {\textsf{v}}_{i}'&= {\textsf{v}}_{i}+i-1 \\ {\textsf{w}}_{i}&= {\left\{ \begin{array}{ll} {\textsf{w}}_{1}-1 &{} \quad i=1 \\ 0 &{} \quad 2 \le i \le n-1 \\ {\textsf{w}}_{n}+n &{} \quad i=n \end{array}\right. } \end{aligned}$$

Let $V_{i}'$ and $W_{i}'$ be complex vector spaces of dimension ${\textsf{v}}_{i}'$ and ${\textsf{w}}_{i}'$, respectively. We identify $V_{i}'=V_{i} \oplus {\mathbb {C}}^{i-1}$ for $1 \le i \le n$ and $W_{n}'=W_{n}\oplus {\mathbb {C}}^{n}$.

3.2 Construction of the map

To $(X,Y,I,J)\in T^{*} \text {Rep}_{Q}({\textsf{v}},{\textsf{w}})$, we associate an element $(X',Y',I',J')$ of $T^{*}\text {Rep}_{Q}({\textsf{v}}',{\textsf{w}}')$ as follows:

• The framing maps at the first node are:

  $$\begin{aligned} I'_{1}= \begin{pmatrix} A_2&A_3&\ldots&A_{{\textsf{w}}_1} \end{pmatrix}, \quad J'_{1} = \begin{pmatrix} B_2 \\ B_3 \\ \vdots \\ B_{{\textsf{w}}_1} \end{pmatrix} \end{aligned}$$

• $X'_{k}: V_k \oplus {\mathbb {C}}^{k-1} \rightarrow V_{k+1} \oplus {\mathbb {C}}^{k}$ is given by

  

  where

  $$\begin{aligned}&C_k=\begin{pmatrix} c^{1}&\quad c^{2}&\quad \ldots&\quad c^{k-1} \end{pmatrix} \qquad \quad \in \text {Mat}_{1,k-1}({\mathbb {C}}), \\ {}&c^{j} = B_1 \left( Y_1 \ldots Y_{j-1} X_{j-1} \ldots X_{1} \right) A_1 \end{aligned}$$

  and ${\mathbb {I}}_{k-1}$ is the $(k-1)\times (k-1)$ identity matrix.

  Notice that

  $$\begin{aligned} X_{k}&\in \text {Mat}_{{\textsf{v}}_{k+1},{\textsf{v}}_k}({\mathbb {C}}) \\ J_1 Y_1 \ldots Y_{k-1}&\in \text {Mat}_{1,{\textsf{v}}_{k}}({\mathbb {C}}) \end{aligned}$$

  so that $X'_{k}$ is a $({\textsf{v}}_{k+1}+1+(k-1))\times ({\textsf{v}}_{k}+(k-1))={\textsf{v}}'_{k}\times {\textsf{v}}'_{k+1}$ matrix.

• $Y'_{k}: V_{k+1} \oplus {\mathbb {C}}^{k} \rightarrow V_{k} \oplus {\mathbb {C}}^{k-1}$ is given by

  

  Notice that

  $$\begin{aligned} Y_{k}&\in \text {Mat}_{{\textsf{v}}_k,{\textsf{v}}_{k+1}}({\mathbb {C}}) \\ X_{k-1} \ldots X_1 A_1&\in \text {Mat}_{{\textsf{v}}_{k},1}({\mathbb {C}}) \end{aligned}$$

  so that $Y'_{k}$ is a $(({\textsf{v}}_k)+(k-1))\times (({\textsf{v}}_{k+1})+(k-1)+1)={\textsf{v}}'_{k}\times {\textsf{v}}'_{k+1}$ matrix.

• The new framing maps at the final node are:

  

  and

  

Fig. 2

The new quiver representation

This construction defines a map $\Phi : T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}}) \rightarrow T^{*}\text {Rep}_{Q}({\textsf{v}}',{\textsf{w}}')$.

3.3 Induced map on quiver varieties

We next check that the map $T^{*}\text {Rep}_{Q}({\textsf{v}},{\textsf{w}}) \rightarrow T^{*}\text {Rep}_{Q}({\textsf{v}}',{\textsf{w}}')$ constructed in the previous section descends to a map on quiver varieties. In the proofs below, we will freely use the notation $A_{1}$, $B_{1}$, and $C_{k}$ defined in the previous section.

Proposition 2

If $(X,Y,I,J)\in \mu _{{\textsf{v}},{\textsf{w}}}^{-1}(0)$, then $\Phi (X,Y,I,J) \in \mu _{{\textsf{v}}',{\textsf{w}}'}^{-1}(0)$.

Proof

We denote $\Phi (X,Y,I,J)=(X',Y',I',J')$. For the first vertex, we calculate

$$\begin{aligned} -Y'_1 X'_1 + I'_{1} J'_{1}&=\begin{pmatrix} Y_1&A_1 \end{pmatrix}\cdot \begin{pmatrix} -X_1 \\ B_1 \end{pmatrix} + \begin{pmatrix} A_2&\quad A_3&\quad \ldots&\quad A_{{\textsf{w}}_1} \end{pmatrix} \cdot \begin{pmatrix} B_2 \\ B_3 \\ \vdots \\ B_{{\textsf{w}}_1} \end{pmatrix} \\&= -Y_{1} X_{1}+ \sum _{j=1}^{{\textsf{w}}_{1}} A_{j} B_{j} \\&= -Y_1 X_1+I_{1} J_{1} =0 \end{aligned}$$

For the last vertex, we calculate

$$\begin{aligned} X'_{n-1} Y'_{n-1}&=\begin{pmatrix} -X_{n-1} &{}\quad 0 \\ B_1 Y_1\ldots Y_{n-2} &{}\quad C_{n-1} \\ 0 &{}\quad -{\mathbb {I}}_{n-2} \end{pmatrix}\cdot \begin{pmatrix} Y_{n-1} &{}\quad 0 &{}\quad X_{n-2} \ldots X_{1} A_{1} \\ 0 &{} \quad {\mathbb {I}}_{n-2} &{}\quad 0 \end{pmatrix} \\&=\begin{pmatrix} -X_{n-1} Y_{n-1} &{}\quad 0 &{}\quad -X_{n-1} \ldots X_1 A_1 \\ B_1 Y_1 \ldots Y_{n-1} &{}\quad C_{n-1} &{}\quad B_1 Y_1 \ldots Y_{n-2} X_{n-2} \ldots X_1 A_1 \\ 0 &{}\quad -{\mathbb {I}}_{n-2} &{}\quad 0 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} I'_n J'_n&= -\begin{pmatrix} I_{n} &{}\quad 0 &{}\quad X_{n-1} \ldots X_{1} A_{1} \\ 0 &{}\quad {\mathbb {I}}_{n-1} &{}\quad 0 \end{pmatrix} \cdot \begin{pmatrix} J_n &{}\quad 0 \\ B_1 Y_1 \ldots Y_{n-1} &{}\quad C_n \\ 0 &{}\quad -{\mathbb {I}}_{n-1} \end{pmatrix} \\&=-\begin{pmatrix} I_n J_n &{}\quad 0 &{}\quad -X_{n-1} \ldots X_1 A_1 \\ B_1 Y_1 \ldots Y_{n-1} &{}\quad C_{n-1} &{}\quad B_1 Y_1 \ldots Y_{n-2} X_{n-2} \ldots X_{1} A_{1} \\ 0 &{}\quad -{\mathbb {I}}_{n-2} &{}\quad 0 \end{pmatrix} \end{aligned}$$

which shows that

$$\begin{aligned} X'_{n-1} Y'_{n-1} + I'_{n} J'_{n} = 0 \end{aligned}$$

Now suppose that $n>2$ and fix k so that $1<k<n$. Then,

$$\begin{aligned} X'_{k} Y'_{k}&=\begin{pmatrix} -X_k &{}\quad 0 \\ B_1 Y_1 \ldots Y_{k-1} &{}\quad C_k \\ 0 &{}\quad -{\mathbb {I}}_{k-1} \end{pmatrix} \cdot \begin{pmatrix} Y_{k} &{}\quad 0 &{}\quad X_{k-1} \ldots X_{1} A_{1} \\ 0 &{}\quad {\mathbb {I}}_{k-1} &{}\quad 0 \end{pmatrix} \\&=\begin{pmatrix} -X_k Y_k &{}\quad 0 &{}\quad -X_{k} \ldots X_1 A_1 \\ B_1 Y_1 \ldots Y_{k} &{}\quad C_{k} &{}\quad B_1 Y_1 \ldots Y_{k-1} X_{k-1} \ldots X_1 A_1 \\ 0 &{}\quad -{\mathbb {I}}_{k-1} &{}\quad 0 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} Y'_{k+1} X'_{k+1}&=\begin{pmatrix} Y_{k+1} &{}\quad 0 &{}\quad X_{k} \ldots X_{1} A_1 \\ 0 &{}\quad {\mathbb {I}}_{k} &{}\quad 0 \end{pmatrix} \cdot \begin{pmatrix} -X_{k+1} &{}\quad 0 \\ B_1 Y_1 \ldots Y_{k} &{}\quad C_{k+1} \\ 0 &{}\quad -{\mathbb {I}}_{k} \end{pmatrix} \\&= \begin{pmatrix} - Y_{k+1} X_{k+1} &{}\quad 0 &{}\quad -X_{k} \ldots X_{1} A_1 \\ B_1 Y_1 \ldots Y_k &{}\quad C_k &{}\quad B_1 Y_1 \ldots Y_{k-1} X_{k-1} \ldots X_1 A_1 \\ 0 &{}\quad -{\mathbb {I}}_{k-1} &{}\quad 0 \end{pmatrix} \end{aligned}$$

So

$$\begin{aligned} X'_{k} Y'_{k} - Y'_{k+1} X'_{k+1}=0 \end{aligned}$$

which concludes the proof. $\square$

Now fix a stability parameter $\theta \in {\mathbb {Z}}^{n}$.

Proposition 3

If (X, Y, I, J) is $\theta$-semistable, then $\Phi (X,Y,I,J)$ is $\theta$-semistable.

Proof

We use Proposition 1. Suppose $(X,Y,I,J) \in T^*\text {Rep}_{Q}({\textsf{v}}, {\textsf{w}})$ is $\theta$-semistable. As above, write $\Phi (X,Y,I,J)=(X',Y',I',J')$.

Let $\{S_{i}\}$ be a collection of subspaces $S_{i} \subset V_{i}'$ preserved by the maps $X_{k}'$ and $Y_{k}'$ such that $S_{1} \subset \ker J_{1}'$ and $S_{n} \subset \ker J_{n}'$. By definition of $J_{n}'$, this forces $S_{n} \subset V_{n} \subset V_{n} \oplus {\mathbb {C}}^{n-1}$. By definition of $X_{n-1}'$, it is obvious that if $X_{n-1}'(S_{n-1}) \subset V_{n}$, then $S_{n-1} \subset V_{n-1}$. Continuing inductively, we see that $S_{i} \subset V_{i}$ for all i. Furthermore, $X_{1}'(S_{1}) \subset V_{2}$ and $S_{1} \in \ker J_{1}'$ together imply that $S_1 \subset \ker J_{1}$. Since (X, Y, I, J) is $\theta$-semistable, Proposition 1 implies that $\sum _{j=1}^{n} \theta _{j} \cdot \dim _{{\mathbb {C}}} S_{j} \le 0$.

Let $\{T_{i}\}$ be a collection of subspaces $T_{i} \subset V_{i}'$ preserved by the maps $X_{k}'$ and $Y_{k}'$ such that $T_{1} \supset {{\,\textrm{Im}\,}}I'_{1}$ and $T_{n} \supset {{\,\textrm{Im}\,}}I_{n}'$. Let $T_{i}'= T_{i} \cap V_{i}$. Since $T_{i}$ is preserved by $X_{i}'$ and $Y_{i}'$, it is clear from the definition of $X_{i}'$ and $Y_{i}'$ that $T_{i}'$ is preserved by $X_{i}$ and $Y_{i}$.

By definition of $I_{n}'$, it is clear that $T_{n} \supset U_{n} \oplus {\mathbb {C}}^{n-1}$ for some subspace $U_{n} \subset V_{n}$ and $U_{n} \supset {{\,\textrm{Im}\,}}I_{n}$. Proceeding inductively, we also see that $T_{i}\supset U_{i} \oplus {\mathbb {C}}^{i-1}$ for some subspace $U_{i} \subset V_{i}$ for all i. In particular, $T_2 \supset U_{2} \oplus {\mathbb {C}}$. Since $Y_{1}'=\begin{pmatrix} Y_{1}&A_{1}\end{pmatrix}$, we see that $T_{1} \supset {{\,\textrm{Im}\,}}A_{1}$. Thus $T_{1} \supset {{\,\textrm{Im}\,}}I_1$. From $T_{1} \supset {{\,\textrm{Im}\,}}I_1$ and $T_{n} \supset {{\,\textrm{Im}\,}}I_{n}'$, we see that $T_{1}'\supset {{\,\textrm{Im}\,}}I_{1}$ and $T_{n}'\supset {{\,\textrm{Im}\,}}I_{n}$.

Thus, we have

$$\begin{aligned} \sum _{j=1}^{n}\theta _{j} \dim _{{\mathbb {C}}} T_j&= \sum _{i} \theta _{i} (\dim _{{\mathbb {C}}} T_{i}'+i-1) \\&\le \sum _{j=1}^{n} \theta _{j} \dim _{{\mathbb {C}}} V_{j} + \sum _{i} \theta _{i}(i-1) \\&= \sum _{j=1}^{n} \theta _{j}\dim _{{\mathbb {C}}} V'_{j} \end{aligned}$$

We have verified both conditions of Proposition 1. Thus, $(X',Y',I',J')$ is $\theta$-semistable. $\square$

We denote $G_{{\textsf{v}}'}= \prod _{i=1}^{n} GL(V_i \oplus {\mathbb {C}}^{i-1})$. We consider the Nakajima quiver varieties

There is a natural inclusion $\rho$ from $G_{{\textsf{v}}}$ to $G_{{\textsf{v}}'}$, defined by inclusion into the first component. Write $g\in G_{{\textsf{v}}}$ as $g=(g_{1},g_{2},\ldots ,g_{n})$. Then,

$$\begin{aligned} \rho =(\rho _{1},\ldots , \rho _{n}), \quad \rho _{i}(g_{i})= \begin{pmatrix} g_i &{}\quad 0 \\ 0 &{}\quad {\mathbb {I}}_{i-1} \end{pmatrix} \end{aligned}$$

Proposition 4

The map $\Phi$ is $\rho$-equivariant. In particular, $\Phi$ descends to a map ${\mathcal {M}} \rightarrow {\mathcal {M}}'$, which we also denote by $\Phi$.

Proof

This follows from the block form of $\Phi (X,Y,I,J)$. For example,

$$\begin{aligned} \rho _{k+1}(g_{k+1}) X_{k}' \rho _{k}(g_{k})^{-1}&= \begin{pmatrix} g_{k+1} &{}\quad 0 \\ 0 &{}\quad {\mathbb {I}}_{k} \end{pmatrix}\begin{pmatrix} -X_k &{}\quad 0 \\ B_1 Y_1 \ldots Y_{k-1} &{}\quad C_k \\ 0 &{}\quad -{\mathbb {I}}_{k-1} \end{pmatrix} \begin{pmatrix} g_{k}^{-1} &{}\quad 0 \\ 0 &{}\quad {\mathbb {I}}_{k-1} \end{pmatrix} \\&=\begin{pmatrix} -g_{k+1} X_k g_{k}^{-1} &{}\quad 0 \\ B_1 Y_1 \ldots Y_{k-1} g_{k}^{-1} &{}\quad C_k \\ 0 &{}\quad -{\mathbb {I}}_{k-1} \end{pmatrix} \end{aligned}$$

On the other hand, the component of $\Phi (g \cdot (X,Y,I,J))$ inside $\text {Hom}(V_{k}',V_{k+1}')$ is:

$$\begin{aligned}&\begin{pmatrix} -g_{k+1}X_{k} g_{k}^{-1} &{}\quad 0 \\ (B_{1} g_{1}^{-1}) (g_1 Y_1 g_2^{-1}) \ldots (g_{k-1} Y_{k-1} g_{k}^{-1}) &{}\quad C_{k} \\ 0 &{}\quad -{\mathbb {I}}_{k-1} \end{pmatrix} \\&\quad =\begin{pmatrix} -g_{k+1} X_k g_{k}^{-1} &{}\quad 0 \\ B_1 Y_1 \ldots Y_{k-1} g_{k}^{-1} &{}\quad C_k \\ 0 &{}\quad -{\mathbb {I}}_{k-1} \end{pmatrix} \end{aligned}$$

The $C_{k}$ block is unchanged because of the formula

$$\begin{aligned}{} & {} B_{1}(Y_{1} \ldots Y_{j-1} X_{j-1} \ldots X_{1})A_{1} \\{} & {} \quad = B_{1} g_{1}^{-1}(g_{1}Y_{1} g_{2}^{-1}\ldots g_{j-1} Y_{j-1} g_{j}^{-1} g_{j} X_{j-1} g_{j-1}^{-1} \ldots g_{2} X_{1} g_{1}^{-1})g_{1} A_{1} \end{aligned}$$

Similar computations for the rest of the data show that $\Phi (g \cdot (X,Y,I,J))= \rho (g) \Phi (X,Y,I,J)$. $\square$

By the previous three propositions, $\Phi$ descends to a map of quiver varieties.

Remark 1

From now on, we will use $\Phi$ to denote the induced map

$$\begin{aligned} \Phi : {\mathcal {M}} \rightarrow {\mathcal {M}}' \end{aligned}$$

(4)

3.4 Injectivity

Proposition 5

The map (4) of quiver varieties is injective.

Proof

We must show that if $\Phi (X,Y,I,J)$ and $\Phi (X',Y',I',J')$ are in the same $G_{{\textsf{v}}'}$-orbit, then (X, Y, I, J) and $(X',Y',I',J')$ are in the same $G_{{\textsf{v}}}$-orbit. Note that in this proof $(X',Y',I',J')$ denotes a point in the domain of (4), in contrast to previous usage.

So suppose that $g \cdot \Phi (X,Y,I,J)=\Phi (X',Y',I',J')$. We write the components $g_i$ of g, where $g_i \in GL(V_i\oplus {\mathbb {C}}^{i-1})$ in $({\textsf{v}}_i+(i-1))\times ({\textsf{v}}_i+(i-1))$ block form as

$$\begin{aligned} \begin{pmatrix} g_{i,1} &{}\quad g_{i,2} \\ g_{i,3} &{}\quad g_{i,4} \end{pmatrix} \end{aligned}$$

Consider the component of the equation $g \cdot \Phi (X,Y,I,J)=\Phi (X',Y',I',J')$ lying in $\text {Hom}(W_{n}',V_{n}')$:

$$\begin{aligned} \begin{pmatrix} g_{n,1} &{}\quad g_{n,2} \\ g_{n,3} &{}\quad g_{n,4} \end{pmatrix} \cdot \begin{pmatrix} I_{n} &{}\quad 0 &{}\quad X_{n-1} \ldots X_{1} A_{1} \\ 0 &{}\quad {\mathbb {I}}_{n-1} &{}\quad 0 \end{pmatrix}&= \begin{pmatrix} g_{n,1} I_n &{}\quad g_{n,2} &{}\quad g_{n,1} X_{n-1} \ldots X_1 A_1 \\ g_{n,3} I_n &{}\quad g_{n,4} &{}\quad g_{n,3} X_{n-1} \ldots x_1 A_1 \end{pmatrix} \\&=\begin{pmatrix} I_n' &{}\quad 0 &{}\quad X_{n-1}' \ldots X_1 ' I_1' \\ 0 &{}\quad {\mathbb {I}}_{n-1} &{}\quad 0 \end{pmatrix} \end{aligned}$$

This implies that $g_{n,2}=0$ and $g_{n,4}={\mathbb {I}}_{n-1}$.

The inverse of $g_{n}$ is given as follows:

$$\begin{aligned} g_{n}^{-1}= \begin{pmatrix} g_{n,1}&{}\quad 0 \\ g_{n,3} &{}\quad {\mathbb {I}}_{n-1} \end{pmatrix}^{-1} = \begin{pmatrix} g_{n,1}^{-1} &{}\quad 0 \\ -g_{n,3} g_{n,1}^{-1} &{}\quad {\mathbb {I}}_{n-1} \end{pmatrix} \end{aligned}$$

We write this as a $({\textsf{v}}_n+(n-1))\times ({\textsf{v}}_n+(n-2)+1)$ block matrix as

$$\begin{aligned} \begin{pmatrix} g_{n,1}^{-1} &{}\quad 0 &{}\quad 0 \\ -g_{n,3} g_{n,1}^{-1} &{}\quad {\mathbb {I}}_{n-1,n-2} &{}\quad D \end{pmatrix} \end{aligned}$$

where ${\mathbb {I}}_{n-1,n-2}$ is the $(n-1)\times (n-2)$ matrix with 1’s on the main diagonal and D is the $(n-1)\times 1$ matrix with 1 in the last entry and 0 elsewhere.

Write the inverse of $g_n$ as

$$\begin{aligned} g_{n}^{-1} \begin{pmatrix} h_{n,1} &{}\quad 0 \\ h_{n,3} &{}\quad {\mathbb {I}}_{n-1} \end{pmatrix} \end{aligned}$$

and consider the component of the equation $g \cdot \Phi (X,Y,I,J)=\Phi (X',Y',I',J')$ in $\text {Hom}(V_{n}',W_{n}')$:

$$\begin{aligned}&-\begin{pmatrix} J_n &{}\quad 0 \\ B_1 Y_1 \ldots Y_{n-1} &{}\quad C_n \\ 0 &{}\quad -{\mathbb {I}}_{n-1} \end{pmatrix}\cdot \begin{pmatrix} h_{n,1} &{}\quad 0 \\ h_{n,3} &{}\quad {\mathbb {I}}_{n-1} \end{pmatrix} \\&\quad = -\begin{pmatrix} J_n h^{n}_1 &{}\quad 0 \\ B_1 Y_1 \ldots Y_{n-1} h_{n,1} + C_n h_{n,3} &{}\quad C_n {\mathbb {I}}_{n-1} \\ - h_{n,3} &{}\quad -{\mathbb {I}}_{n-1} \end{pmatrix} \\&\quad =\begin{pmatrix} J_n' &{}\quad 0 \\ B_1' Y_1' \ldots Y_{n-1}' &{}\quad C_n' \\ 0 &{}\quad -{\mathbb {I}}_{n-1} \end{pmatrix} \end{aligned}$$

So $h_{n,3}=0$, which implies that $g_{n,3}=0$.

Continuing inductively, we can show that

$$\begin{aligned} g_i = \begin{pmatrix} g_{i,1} &{}\quad 0\\ 0 &{}\quad {\mathbb {I}}_{i-1} \end{pmatrix} \end{aligned}$$

which means that $g=\rho ((g_{i,1})_{1\le i\le n})$. Letting ${\tilde{g}}=(g_{i,1})_{1 \le i \le n}$, we see that ${\tilde{g}} \cdot (X,Y,I,J)= (X',Y',I',J')$. $\square$

3.5 Torus equivariance

The varieties ${\mathcal {M}}$ and ${\mathcal {M}}'$ are acted on by tori ${\textsf{T}}$ and ${\textsf{T}}'$, respectively.

Denote the coordinates on torus ${\textsf{T}}$ by $(a_{1,1},\ldots ,a_{1,{\textsf{w}}_1},a_{n,1},\ldots ,a_{n,{\textsf{w}}_n}, \hbar )$ and the coordinates on torus ${\textsf{T}}'$ by $(b_{1,1}, \ldots , b_{1,{\textsf{w}}_1-1}, b_{n,1},\ldots b_{n,{\textsf{w}}_n},c_1,\ldots ,c_{n},\hbar ')$. We define the map

$$\begin{aligned} \iota : {\textsf{T}}\rightarrow {\textsf{T}}' \end{aligned}$$

which is given on coordinates by

$$\begin{aligned}&b_{1,j-1}\mapsto a_{1,j}, \quad \text {for} \quad j \in \{2,\ldots ,{\textsf{w}}_1\} \\&b_{n,j}\mapsto a_{n,j}, \quad \text {for} \quad j \in \{1,\ldots ,{\textsf{w}}_n\} \nonumber \\&c_{j}\mapsto \hbar ^{j-n} a_{1,1} , \quad \text {for} \quad j \in \{1,\ldots ,n\} \nonumber \\&\hbar '\mapsto \hbar \nonumber \end{aligned}$$

(5)

We will abuse notation and just write $\hbar$ instead of $\hbar '$. We will abbreviate elements of ${\textsf{T}}$ as $(a,\hbar )$ and elements of ${\textsf{T}}'$ as $(b,c,\hbar )$.

Proposition 6

The map $\Phi$ is equivariant with respect to $\iota$

Proof

We must show that $\iota (a,\hbar ) \cdot \Phi (p) = \Phi ((a,\hbar ) \cdot p)$. Let (X, Y, I, J) be a representative of p. Then, we must show that

$$\begin{aligned} \Phi ((a,\hbar ) \cdot (X,Y,I,J)) =g (\cdot \iota (a,\hbar ) \cdot \Phi (X,Y,I,J) ) \end{aligned}$$

(6)

for some $g \in G_{{\textsf{v}}'}$ (we have abused notation here, using $\Phi$ for the map on the prequotient). We will inductively define the appropriate g. Write each $g_{i} \in \text {End}(V_{i})$ in block form as

$$\begin{aligned} g_{i}=\begin{pmatrix} g_{i,1} &{}\quad g_{i,2} \\ g_{i,3} &{}\quad g_{i,4} \end{pmatrix} \end{aligned}$$

Set $g_{n,1}={\mathbb {I}}_{{\textsf{v}}_n,{\textsf{v}}_n}$ and $g_{n,4}=\text {diag}(\hbar ^{1-n} a_{1,1},\ldots ,\hbar ^{-1} a_{1,1})$. Then, the component of $g \cdot (\iota (a,\hbar ) \cdot \Phi (X,Y,I,J))$ in $\text {Hom}(W_{n},V_{n})$ is:

$$\begin{aligned}{} & {} \hbar ^{-1} \cdot \begin{pmatrix} \text {diag}(a_{n,1},\ldots ,a_{n,{\textsf{w}}_n}) J_n g_{n,1}^{-1} &{}\quad 0 \\ \hbar ^{1-n} a_{1,1} B_1 Y_1 \ldots Y_{n-1}g_{n,1}^{-1} &{}\quad \hbar ^{1-n} a_{1,1} C_n g_{n,4}^{-1} \\ 0 &{}\quad -\text {diag}(\hbar ^{2-n}a_{1,1},\ldots ,a_{1,1}) g_{n,4}^{-1} \end{pmatrix} \\{} & {} \quad \qquad = \begin{pmatrix} \hbar ^{-1} \text {diag}(a_{n,1},\ldots ,a_{n,{\textsf{w}}_n}) J_n &{}\quad 0 \\ \hbar ^{-n} a_{1,1} B_1 Y_1 \ldots Y_{n-1} &{}\quad \hbar ^{-n} a_{1,1} C_n g_{n,4}^{-1} \\ 0 &{}\quad -{\mathbb {I}}_{n-1} \end{pmatrix} \end{aligned}$$

We calculate

$$\begin{aligned} \hbar ^{-n} a_{1,1} C_n g_{n,4}^{-1} = \begin{pmatrix} \hbar ^{-1} B_1 A_1&\quad \hbar ^{-2} B_1 Y_1 X_1 A_1&\quad \ldots&\quad \hbar ^{-n+1} B_1 (Y_1 \ldots Y_{n-2} X_{n-2} \ldots X_1 ) A_1 \end{pmatrix} \end{aligned}$$

so that (6) holds for this component.

Similarly, the component of $g \cdot (\iota (a,\hbar ) \cdot \Phi (X,Y,I,J))$ in $\text {Hom}(W_{n},V_{n})$ is:

$$\begin{aligned}{} & {} \begin{pmatrix} g_{n,1} I_n \text {diag}(a_{n,1},\ldots ,a_{n,{\textsf{w}}_n})^{-1} &{}\quad 0 &{}\quad g_{n,1} X_{n-1} \ldots X_{1} A_{1} a_{1,1}^{-1} \\ 0 &{}\quad g_{n,4} \text {diag}(\hbar ^{1-n} a_{1,1},\ldots ,\hbar ^{-1}a_{1,1})^{-1} &{}\quad 0 \end{pmatrix} \\{} & {} \qquad \quad \quad =\begin{pmatrix} I_n \text {diag}(a_{n,1},\ldots ,a_{n,{\textsf{w}}_n})^{-1} &{}\quad 0 &{}\quad X_{n-1} \ldots X_1 A_1 a_{1,1}^{-1} \\ 0 &{}\quad {\mathbb {I}}_{n-1} &{}\quad 0 \end{pmatrix} \\ \end{aligned}$$

which equals the component of $\Phi ((a,\hbar )\cdot (X,Y,I,J))$ in $\text {Hom}(W_{n},V_{n})$.

Next, set $g_{n-1,1}={\mathbb {I}}_{{\textsf{v}}_{n-1},{\textsf{v}}_{n-1}}$, $g_{n-1,4}=\text {diag}(\hbar ^{2-n}a_{1,1},\ldots ,\hbar ^{-1}a_{1,1})$, $g_{n-1,2}=0$, and $g_{n-1,3}=0$. The torus $\iota ({\textsf{T}})$ acts trivially on the component of $\Phi (X,Y,I,J)$ in $\text {Hom}(V_{n-1},V_{n})$, so we must show that this component is preserved by the action of g. We compute

$$\begin{aligned} g_{n} X'_{n-1} g_{n-1}^{-1}&= \begin{pmatrix} -X_{n-1} &{}\quad 0 \\ \hbar ^{1-n}a_{1,1} B_1 Y_1 \ldots Y_{n-2} &{}\quad \hbar ^{1-n} a_{1,1} C_{n-1} g_{n-1,4}^{-1} \\ 0 &{}\quad \text {diag}(\hbar ^{2-n} a_{1,1},\ldots , \hbar ^{-1} a_{1,1}) g_{n-1,4}^{-1} \end{pmatrix} \\&= \begin{pmatrix} -X_{n-1} &{}\quad 0 \\ \hbar ^{1-n} a_{1,1} B_1 Y_1 \ldots Y_{n-2} &{}\quad \hbar ^{1-n}a_{1,1} C_{n-1} g_{n-1,4}^{-1} \\ 0 &{}\quad {\mathbb {I}}_{n-2} \end{pmatrix} \end{aligned}$$

Note that

$$\begin{aligned}{} & {} \hbar ^{1-n} a_{1,1} C_{n-1}g_{n-1,4}^{-1} \\{} & {} \quad = \begin{pmatrix} \hbar ^{-1} B_1 A_1&\quad \hbar ^{-2} B_1 Y_1 X_1 A_1&\quad \ldots&\quad \hbar ^{-(n-2)} B_1 (Y_1 \ldots Y_{n-3} X_{n-3} \ldots X_1) A_1 \end{pmatrix} \end{aligned}$$

so that (6) holds for the component in $\text {Hom}(V_{n-1},V_{n})$. For the component in $\text {Hom}(V_{n},V_{n-1})$, we have

$$\begin{aligned}{} & {} g_{n-1} \hbar ^{-1} \begin{pmatrix} Y_{n-1} &{}\quad 0 &{}\quad X_{n-2} \ldots X_{1} A_{1} \\ 0 &{}\quad {\mathbb {I}}_{n-2} &{}\quad 0 \end{pmatrix} g_n^{-1} \\{} & {} \qquad \quad \quad = \hbar ^{-1} \begin{pmatrix} Y_{n-1} &{}\quad 0 &{}\quad X_{n-2} \ldots X_1 A_1 \\ 0 &{}\quad \text {diag}(\hbar ^{2-n} a_{1,1},\ldots ,\hbar ^{-1} a_{1,1}) &{}\quad 0 \end{pmatrix} g_n^{-1} \\{} & {} \qquad \quad \quad =\begin{pmatrix} \hbar ^{-1} Y_{n-1} &{}\quad 0 &{}\quad X_{n-2} \ldots X_{1} A_1 a_{1,1}^{-1}\\ 0 &{}\quad {\mathbb {I}}_{n-2} &{}\quad 0 \end{pmatrix} \end{aligned}$$

Continuing inductively, we see that (6) holds. $\square$

Proposition 7

The largest subtorus of ${\textsf{T}}'$ that preserves $\Phi ({\mathcal {M}})$ is $\iota ({\textsf{T}})$.

Proof

The fact that $\iota ({\textsf{T}})$ preserves ${\mathcal {M}}$ follows by Proposition 6. So we only need to show that there is no larger subtorus that does.

Let $(b,c,\hbar ) \in {\textsf{T}}'$ and suppose that $\Phi ({\mathcal {M}})$ is fixed by $(b,c,\hbar )$. Let $(X,Y,I,J)\in T^{*}\text {Rep}({\textsf{v}},{\textsf{w}})$ be a representative of a point $p\in {\mathcal {M}}$. If $(b,c,\hbar ) \cdot \Phi (p)=\Phi (p') \in \Phi ({\mathcal {M}})$, then there exists a representative $(X',Y',I',J')$ of $p'$ so that

$$\begin{aligned} (b,c,\hbar ) \cdot \Phi (X,Y,I,J) = g \cdot \Phi (X',Y',I',J') \end{aligned}$$

for some $g \in \prod _{i \in Q_{0}} GL(V'_i)$. Writing $g=(g_i)_{i \in Q_{0}}$ and

$$\begin{aligned} g_i = \begin{pmatrix} g_{i,1} &{}\quad g_{i,2} \\ g_{i,3} &{}\quad g_{i,4} \end{pmatrix} \end{aligned}$$

it follows by the same reasoning as in the proof of Proposition 5 that $g_{i,2}=0$ and $g_{i,3}=0$. And we have

$$\begin{aligned}{} & {} \begin{pmatrix} I_n \text {diag}(b_{n,1},\ldots ,b_{n,{\textsf{w}}_n})^{-1} &{}\quad 0 &{}\quad X_{n-1} \ldots X_{1} A_{1} c_n^{-1} \\ 0 &{}\quad \text {diag}(c_1,\ldots ,c_{n-1})^{-1} &{}\quad 0 \end{pmatrix} \\{} & {} \qquad \quad =\begin{pmatrix} g_{n,1} I_n' &{}\quad 0 &{}\quad g_{n,1} X_{n-1}' \ldots X_1' A_1' \\ 0 &{}\quad g_{n,4} {\mathbb {I}}_{n-1} &{}\quad 0 \end{pmatrix} \end{aligned}$$

Also,

$$\begin{aligned}{} & {} \hbar ^{-1} \cdot \begin{pmatrix} \text {diag}(b_{n,1},\ldots ,b_{n,{\textsf{w}}_n}) J_n &{}\quad 0 \\ c_1 B_1 Y_1 \ldots Y_{n-1} &{}\quad c_1 C_n \\ 0 &{}\quad -\text {diag}(c_2,\ldots ,c_n) \end{pmatrix} \\{} & {} = \begin{pmatrix} J_n' (g_{n,1})^{-1} &{}\quad 0 \\ B_1' Y_1' \ldots Y_{n-1}' g_{n,1}^{-1} &{}\quad c_1 C_n' g_{n,4}^{-1} \\ 0 &{}\quad -g_{n,4}^{-1} \end{pmatrix} \end{aligned}$$

These two equations imply that

$$\begin{aligned} \text {diag}(c_1,\ldots ,c_{n-1})^{-1} = g_{n,4}= \hbar \cdot \text {diag}(c_2,\ldots ,c_n)^{-1} \end{aligned}$$

Hence,

$$\begin{aligned} c_j=\hbar ^{-1} c_{j+1} \implies c_j = \hbar ^{j-n} c_n \end{aligned}$$

which implies that $(b,c,\hbar )$ is in $\iota ({\textsf{T}})$. $\square$

We also have

Corollary 2

The embedding $\Phi$ maps the ${\textsf{T}}$-fixed locus to the $\iota ({\textsf{T}})$-fixed locus.

4 The embedding: general case

4.1 One step

Now we apply the local construction from the previous section to the case of a general type A quiver variety. So choose a natural number $m\ge 2$ and consider the $A_{m}$ quiver, i.e. the quiver with vertices $Q_{0}=\{1,2,\ldots ,m\}$ and edges $i\rightarrow i+1$ for $1 \le i \le m-1$. Let ${\textsf{v}},{\textsf{w}}\in {\mathbb {Z}}_{\ge 0}^{Q_{0}}$. Fix a stability parameter $\theta \in {\mathbb {Z}}^{Q_{0}}$. We will suppress $\theta$ from the notation. Consider the corresponding quiver variety ${\mathcal {M}}({\textsf{v}},{\textsf{w}})$. Let k be the maximal integer such that $k+1<m$ and ${\textsf{w}}_{k+1}\ne 0$. We assume that such a k exists. Let $n=m-k$. See Fig. 3.

Fig. 3

The framed quiver data for a type A quiver variety. We omit drawing the framed vertices if the corresponding framing dimension is 0

We apply (4) to the data arising from the full subquiver with vertices $\{k+1,k+2,\ldots ,k+n\}$ to deduce the following.

Theorem 3

There is a torus equivariant closed embedding

$$\begin{aligned} {\mathcal {M}}({\textsf{v}},{\textsf{w}}) \hookrightarrow {\mathcal {M}}({\textsf{v}}',{\textsf{w}}') \end{aligned}$$

(7)

where

$$\begin{aligned} {\textsf{v}}'_{i}&={\left\{ \begin{array}{ll} {\textsf{v}}_{i} &{} \quad 1 \le i \le k \\ {\textsf{v}}_{i}+i-k-1 &{} \quad k+1 \le i \le m \end{array}\right. } \\ {\textsf{w}}'_{i}&={\left\{ \begin{array}{ll} {\textsf{w}}_{k+1}-1 &{} \quad i=k+1 \\ {\textsf{w}}_{m}+m-k &{} \quad i=m \\ {\textsf{w}}_{i} &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

We view this as trading a framing at vertex $k+1$ for many framings at the last vertex.

4.2 Repeated embeddings

Repeating the procedure of the previous section ${\textsf{w}}_{k+1}$ times, we obtain an embedding

$$\begin{aligned} {\mathcal {M}}({\textsf{v}},{\textsf{w}}) \hookrightarrow {\mathcal {M}}' \end{aligned}$$

where ${\mathcal {M}}'$ is a quiver variety with ${\textsf{w}}_{k+1}=0$. Continuing inductively, we obtain an embedding of ${\mathcal {M}}({\textsf{v}},{\textsf{w}})$ into a type A quiver variety with ${\textsf{w}}_{i}=0$ for $i \ne m$.

Theorem 4

Any type $A_{m}$ Nakajima quiver variety can be equivariantly embedded into an $A_{m}$ quiver variety with all framings at the rightmost vertex.

Let $\theta ^{\pm }=\pm (1,1,\ldots ,1)$. In the special case where $\theta =\theta ^{\pm }$, we obtain the following.

Corollary 3

Any type $A_{m}$ Nakajima quiver variety with stability condition $\theta ^{+}$ or $\theta ^{-}$ can be equivariantly embedded into the cotangent bundle of an m-step partial flag variety.

4.3 Combinatorics of torus fixed points

Now we specialize to the case $\theta =\theta ^{-}$. Fixed points on the Nakajima variety ${\mathcal {M}}({\textsf{v}},{\textsf{w}})$ are indexed by certain $|{\textsf{w}}|$-tuples of partitions, see for example Proposition 4 in [30].

Let $\lambda =(\lambda _1\ge \lambda _{2} \ge \ldots )$ be a partition. The length of $\lambda$ is denoted by $l(\lambda )$, and we use the convention that $\lambda _{i}=0$ for $i > l(\lambda )$. The Young diagram of $\lambda$ is the collection of points in the plane given by $\{(i,j) \, \mid \, 1 \le i \le l(\lambda ), 1\le j \le \lambda _{i}\}$. We will refer to these points as “boxes" in the Young diagram. If $\square =(i,j)$ is such a box, we write $\square \in \lambda$. Given $\square =(i,j) \in \lambda$, the content and height of $\square$ are defined by: $\text {cont}_{\lambda }(\square )=i-j$ and $\text {ht}_{\lambda }(\square )=i+j-2$.

Definition 1

A $({\textsf{v}},{\textsf{w}})$-tuple of partitions is a $({\textsf{w}}_1+\ldots +{\textsf{w}}_{m})$-tuple of partitions

$$\begin{aligned} {\varvec{\lambda }}=\left( \lambda ^{i,j}\right) _{\begin{array}{c} 1 \le i \le m \\ 1 \le j \le {\textsf{w}}_i \end{array}} \end{aligned}$$

such that the set

$$\begin{aligned} S_{l}:=\bigcup _{\begin{array}{c} 1 \le i \le m \\ 1 \le j \le {\textsf{w}}_i \end{array}}\{\square \in \lambda ^{i,j} \, \mid \, \text {cont}_{\lambda ^{i,j}}(\square )+i=l \} \end{aligned}$$

has size ${\textsf{v}}_l$ for $l=1,\ldots m$.

Given a $({\textsf{v}},{\textsf{w}})$-tuple of partitions ${\varvec{\lambda }}$, we will write $\square \in {\varvec{\lambda }}$ to mean that $\square \in \lambda ^{i,j}$ for some i and j.

Definition 2

Let $\square \in {\varvec{\lambda }}$; in particular, $\square \in \lambda ^{i,j}$ for some i and j. We associate an equivariant parameter of the torus ${\textsf{T}}$ from Sect. 2.3 to $\square$ by

$$\begin{aligned} a_{\square }=a_{i,j} \end{aligned}$$

Proposition 8

([30], Proposition 4) ${\textsf{T}}$ fixed points on ${\mathcal {M}}({\textsf{v}},{\textsf{w}})$ are in natural bijection with $({\textsf{v}},{\textsf{w}})$-tuples of partitions.

Definition 3

Let ${\varvec{\lambda }}$ be a $({\textsf{v}},{\textsf{w}})$-tuple of partitions. Let $\square \in {\varvec{\lambda }}$, and in particular, suppose that $\square \in \lambda ^{i,j}$. Then, we define

$$\begin{aligned} \gamma (\square ):=\text {cont}_{\lambda ^{i,j}}(\square )+i \end{aligned}$$

We also define

$$\begin{aligned} \delta ^{{\varvec{\lambda }}}_{\square }=\text {ht}_{\lambda ^{i,j}}(\square ) \end{aligned}$$

The function $\gamma$ is just a shifted version of the content. The number $\delta ^{{\varvec{\lambda }}}_{\square }$ is just the height; however, we introduce this notation because in Sect. 6 we will consider subpartitions ${\varvec{\lambda }}\subset {\varvec{\mu }}$ and will need to distinguish between $\delta ^{{\varvec{\lambda }}}_{\square }$ and $\delta ^{{\varvec{\mu }}}_{\square }$.

The vector spaces $V_{i}$ in the definition of ${\mathcal {M}}({\textsf{v}},{\textsf{w}})$ give rise to tautological vector bundles ${\mathcal {V}}_{i}$ over ${\mathcal {M}}({\textsf{v}},{\textsf{w}})$. It is known that the ${\textsf{T}}$ character of the fiber of these vector bundles over a fixed point ${\varvec{\lambda }}$ is given by:

$$\begin{aligned} {\mathcal {V}}_{i}|_{{\varvec{\lambda }}}=\sum _{\begin{array}{c} \square \in {\varvec{\lambda }}\\ \gamma (\square )=i \end{array}} a_{\square } \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square }} \end{aligned}$$

(8)

See Fig. 4 for an example of a torus fixed point.

Fig. 4

An example of the torus fixed point ${\varvec{\lambda }}=((3,3,1),(2,2),(4,1,1))$ on the quiver variety ${\mathcal {M}}((2,3,4,4,3,1),(0,0,1,2,0,0))$. We have filled each box with $a_{\square } \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square }}$. The ${\textsf{T}}$ character of the tautological bundle ${\mathscr {V}}_{3}$ is $a_{3,1}+a_{3,1}\hbar +a_{4,1}\hbar +a_{4,2}\hbar$

4.4 Correspondence between torus fixed points

Let us consider the embedding (7).

Let ${\varvec{\lambda }}=\left( \lambda ^{i,j} \right) _{\begin{array}{c} 1 \le i \le m\\ 1 \le j \le {\textsf{w}}_{i} \end{array}}$ be a $({\textsf{v}},{\textsf{w}})$-tuple of partitions.

Definition 4

Let ${\varvec{\lambda }}$ be a $({\textsf{v}},{\textsf{w}})$-tuple of partitions. We define another tuple of partitions ${\varvec{\mu }}=\left( \mu ^{i,j}\right) _{\begin{array}{c} 1 \le i \le m \\ 1 \le j \le {\textsf{w}}'_{i} \end{array}}$ by

• $\mu ^{i,j}= \lambda ^{i,j}$ if $1 \le i \le k$.

• $\mu ^{k+1,j}=\lambda ^{k+1,j+1}$ if $1 \le j \le {\textsf{w}}'_{k+1}={\textsf{w}}_{k+1}-1$.

• $\mu ^{i,j}=\emptyset$ if $k+1< i <m$.

• $\mu ^{m,j}=\lambda ^{m,j}$ for $1\le j \le {\textsf{w}}_{m}$.

• $\mu ^{m,{\textsf{w}}_{m}+j}=(\lambda ^{k+1,1}_{j}+n-j)$ for $1 \le j \le n$.

Concretely, ${\varvec{\mu }}$ is obtained from ${\varvec{\lambda }}$ by removing the partition corresponding to the first framing at vertex $k+1$ and by adding certain length 1 partitions at the last vertex depending on the partition that was removed.

Proposition 9

With the notation above, ${\varvec{\mu }}$ is a $({\textsf{v}}',{\textsf{w}}')$-tuple of partitions.

Proof

This follows by direct computation from the definitions of ${\textsf{v}}'$, ${\textsf{w}}'$, and ${\varvec{\mu }}$. $\square$

Proposition 10

Let $F_{{\varvec{\lambda }}}$ be the $\iota ({\textsf{T}})$ fixed component of ${\mathcal {M}}({\textsf{v}}',{\textsf{w}}')$ containing ${\varvec{\lambda }}$. Then, ${\varvec{\mu }}\in F_{{\varvec{\lambda }}} \cap {\mathcal {M}}({\textsf{v}}',{\textsf{w}}')^{{\textsf{T}}'}$.

Proof

This follows from the construction of $\Phi$ in Sect. 3.2. $\square$

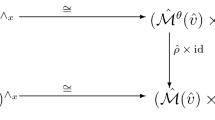
Consider the diagram

where the horizontal maps are restrictions to torus fixed points.

Lemma 1

The previous diagram commutes.

Proof

Let ${\mathcal {V}}_{i}'$ be a tautological bundle on ${\mathcal {M}}({\textsf{v}}',{\textsf{w}}')$. Formula (8) and the definition of (7) show that $\iota ^{*}({\mathcal {V}}_{i}'|_{{\varvec{\mu }}})=\Phi ^{*}({\mathcal {V}}_{i}')|_{{\varvec{\lambda }}}$. By [31], the K-theory of Nakajima varieties is generated by tautological classes. The lemma follows. $\square$

4.5 Examples

To help the read parse the constructions and notation above, we provide a few examples.

Example 1

Let ${\textsf{v}}=(1,1)$ and ${\textsf{w}}=(1,1)$. Then ${\mathcal {M}}'={\mathcal {M}}((1,2),(0,3))$. The map on fixed points from Definition 4 is as follows:

$$\begin{aligned}&((1),(1)) \mapsto ((1),(2),(0)) \\&((1,1),(0)) \mapsto ((0),(2),(1)) \\&((0),(2)) \mapsto ((2),(1),(0)) \end{aligned}$$

As in Sect. 3.5, the tori are ${\textsf{T}}={\mathbb {C}}^{\times }_{a_{1,1}} \times {\mathbb {C}}^{\times }_{a_{2,1}} \times {\mathbb {C}}^{\times }_{\hbar }$ and ${\textsf{T}}'= {\mathbb {C}}^{\times }_{b_{2,1}}\times {\mathbb {C}}^{\times }_{c_{1}} \times {\mathbb {C}}^{\times }_{c_{2}} \times {\mathbb {C}}^{\times }_{\hbar }$ and the map (5) is given by

$$\begin{aligned} (a_{1,1},a_{2,1},\hbar )\mapsto (a_{2,1},\hbar ^{-1} a_{1,1},a_{1,1},\hbar ) \end{aligned}$$

Let us next consider an example where we apply the construction (7) several times, as in Theorem 4.

Example 2

Let ${\textsf{v}}=(2,3,4,4,3,1)$ and ${\textsf{w}}=(0,0,1,2,0,0)$. The map in Theorem 4 is:

$$\begin{aligned} {\mathcal {M}}({\textsf{v}},{\textsf{w}})&\hookrightarrow {\mathcal {M}}((2,3,4,4,4,3),(0,0,1,1,0,3)) \nonumber \\&\hookrightarrow {\mathcal {M}}((2,3,4,4,5,5)),(0,0,1,0,0,6))) \nonumber \\&\hookrightarrow {\mathcal {M}}((2,3,4,5,7,8),(0,0,0,0,0,10)) \end{aligned}$$

(9)

Consider the $({\textsf{v}},{\textsf{w}})$-tuple of partitions

$$\begin{aligned} {\varvec{\lambda }}=(((3,3,2),(2,2),(4,1,1)) \end{aligned}$$

Under the first step of the embedding, Definition 4 sends ${\varvec{\lambda }}$ to the fixed point ((3, 3, 1), (2, 2), (6), (2), (1)) of ${\mathcal {M}}((2,3,4,4,4,3),(0,0,1,1,0,3))$. This is depicted in Fig. 5.

The reader can check that under the composition of all the maps in (9), Definition 4 maps ${\varvec{\lambda }}$ to the fixed point $((6),(2),(1),(4),(3),\emptyset ,(6),(5),(2),\emptyset )$ of ${\mathcal {M}}((2,3,4,5,7,8),(0,0,0,0,0,10))$.

As the picture shows, essentially what happens is that each column lengthens down and to the right as much as it needs to in order to be a partition with corner box above the last vertex.

The tori acting on the varieties in the first and last steps of (9) are ${\textsf{T}}= {\mathbb {C}}^{\times }_{a_{3,1}} \times {\mathbb {C}}^{\times }_{a_{4,1}} \times {\mathbb {C}}^{\times }_{a_{4,2}} \times {\mathbb {C}}^{\times }_{\hbar }$ and ${\textsf{T}}'= ({\mathbb {C}}^{\times })^{10}\times {\mathbb {C}}^{\times }_{\hbar }$, respectively. The map on tori (5) is

$$\begin{aligned}{} & {} (a_{3,1},a_{4,1},a_{4,2},\hbar ) \\{} & {} \quad \mapsto (\hbar ^{-2} a_{4,2},\hbar ^{-1} a_{4,2},a_{4,2},\hbar ^{-2} a_{4,1},\hbar ^{-1} a_{4,1},a_{4,1},\hbar ^{-3} a_{3,1},\hbar ^{-2} a_{3,1},\hbar ^{-1} a_{3,1},a_{3,1},\hbar ) \end{aligned}$$

Fig. 5

The fixed point on the left maps to the fixed point on the right

5 Quasimaps

We give a brief review of vertex function for Nakajima varieties. The foundational treatment of quasimap counting was given in [18], and the case of quasimaps to Nakajima quiver varieties is treated in [4]. It is also reviewed in [20, section 2.2] and [21, section 2.3].

5.1 Localization formula

Let ${\mathcal {M}}={\mathcal {M}}_{\theta ^{-}}({\textsf{v}},{\textsf{w}})$ be a type $A_{m}$ Nakajima quiver variety. The vertex function of ${\mathcal {M}}$ is an equivariant count of quasimaps from ${\mathbb {P}}^{1}$ to ${\mathcal {M}}$ nonsingular at $\infty$, see [4, section 7.2] for precise definitions. See also [20, section 2], [21, section 2], and [22, section 2]. For explicit computations of vertex functions, see [20, section 5.1.3] and [22, section 2].

A stable quasimap from ${\mathbb {P}}^{1}$ to ${\mathcal {M}}$ provides the data of

• Vector bundles ${\mathscr {V}}_{i}$ over ${\mathbb {P}}^{1}$ for $i \in Q_{0}$.

• Topologically trivial vector bundles ${\mathscr {W}}_{i}$ over ${\mathbb {P}}^{1}$ for $i \in Q_{0}$.

• A global section $s \in H^{0}\left( {\mathbb {P}}^{1}, {\mathscr {M}} \oplus \hbar ^{-1} {\mathscr {M}}^{\vee } \right)$, where

  $$\begin{aligned} {\mathscr {M}}=\bigoplus _{i \rightarrow j} \text {Hom}({\mathscr {V}}_{i},{\mathscr {V}}_{j}) \oplus \bigoplus _{i \in Q_{0}} \text {Hom}({\mathscr {W}}_{i},{\mathscr {V}}_{i}) \end{aligned}$$

such that s(p) satisfies the moment map equations for all $p \in {\mathbb {P}}^{1}$ and s(p) is a $\theta$-semistable point for all but finitely many $p \in {\mathbb {P}}^{1}$. Points p where s(p) is $\theta$-semistable are called nonsingular points of the quasimap.

The vector $d=(d_{i})_{i \in Q_{0}}=(\deg {\mathscr {V}}_{i})_{i \in Q_{0}} \in {\mathbb {Z}}^{Q_{0}}$ is called the degree of a quasimap. Let $\text {\textsf {QM}}$ be the moduli space of stable quasimaps from ${\mathbb {P}}^{1}$ to ${\mathcal {M}}$. For $d \in {\mathbb {Z}}^{Q_{0}}$, let $\text {\textsf {QM}}^{d}\subset \text {\textsf {QM}}$ be the moduli space of degree d quasimaps. It is known that $\text {\textsf {QM}}^{d}$ admits a canonical deformation-obstruction theory, which gives rise to a virtual structure sheaf ${\mathcal {O}}_{\text {vir}}^{d}$ [18]. Let $T^{1/2}{\mathcal {M}}\in K_{{\textsf{T}}}({\mathcal {M}})$ be the polarization of the tangent bundle of ${\mathcal {M}}$ given by

$$\begin{aligned} T^{1/2}{\mathcal {M}}=\sum _{i \rightarrow j} \text {Hom}({\mathcal {V}}_{i},{\mathcal {V}}_{j}) + \sum _{i \in Q_{0}} \text {Hom}({\mathcal {W}}_{i},{\mathcal {V}}_{i}) - \sum _{i \in Q_{0}} \text {Hom}({\mathcal {V}}_{i},{\mathcal {V}}_{i}) \end{aligned}$$

This induces a virtual bundle ${\mathscr {T}}^{1/2}$ on ${\mathbb {P}}^{1} \times \text {\textsf {QM}}$. As discussed in [4] and [32], it is better to study the symmetrized virtual structure sheaf, which is defined by

$$\begin{aligned} \hat{{\mathcal {O}}}_{\text {vir}}^{d} ={\mathcal {O}}^{d}_{\text {vir}}\otimes \left( {\mathscr {K}} \otimes \frac{\det {\mathscr {T}}^{1/2}|_{0}}{\det {\mathscr {T}}^{1/2}|_{\infty }}\right) ^{1/2} \end{aligned}$$

where ${\mathscr {K}}_{\text {vir}}=(\det T_{\text {vir}}\text {\textsf {QM}}^{d})^{-1}$.

Let ${\mathbb {C}}^{\times }_{q}$ act on ${\mathbb {P}}^{1}$ by

$$\begin{aligned} q \cdot [x_{0}:x_{1}] = [x_{0}:q x_{1}] \end{aligned}$$

This induces an action of ${\mathbb {C}}^{\times }_{q}$ on $\text {\textsf {QM}}$. The action of the torus ${\textsf{T}}$ on ${\mathcal {M}}$ also induces an action on $\text {\textsf {QM}}$. We will work equivariantly with respect to ${\textsf{T}}_{q}={\textsf{T}}\times {\mathbb {C}}^{\times }_{q}$. Denote $0=[0:1]$ and $\infty =[1:0]$.

Consider the open locus $\text {\textsf {QM}}^{d}_{\text {ns }\infty } \subset \text {\textsf {QM}}^{d}$ of quasimaps that are nonsingular at $\infty \in {\mathbb {P}}^{1}$. Thus there is a well-defined evaluation map $\text {ev}_{\infty }: \text {\textsf {QM}}^{d}_{\text {ns }\infty } \rightarrow {\mathcal {M}}$.

Up to normalization,² the vertex function of ${\mathcal {M}}$ is the formal series with coefficients in the localized K-theory of ${\mathcal {M}}$ defined by:

$$\begin{aligned} \sum _{d} \text {ev}_{\infty ,*}\left( \hat{{\mathcal {O}}}_{\text {vir}}^{d} \right) z^{d} \in K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}({\mathcal {M}})_{loc}[[z]] \end{aligned}$$

Localization is necessary to define the vertex function since $\text {ev}_{\infty }$ is not a proper map. The set of degrees of all quasimaps forms a cone in ${\mathbb {Z}}^{Q_{0}}$. Given $d\in {\mathbb {Z}}^{Q_{0}}$, we understand $z^{d}$ to be an element of the semigroup algebra of this cone. The notation [[z]] above stands for formal series in $z^{d}$ as d ranges over all possible quasimap degrees.

The vertex function of ${\mathcal {M}}$ can be computed by equivariant localization with respect to ${\textsf{T}}_{q}$ in the following way. Define the function ${\hat{a}}$ on weights of ${\textsf{T}}_{q}$ by ${\hat{a}}(x)=\frac{1}{x^{1/2}-x^{-1/2}}$, and extend it by multiplicativity to sums and differences of weights. This should be thought of as a symmetrized version of the function $x\mapsto \frac{1}{1-x^{-1}}$ that appears in the usual K-theoretic equivariant localization formula, see Remark 2.

By localization, the restriction of the vertex function to $p \in {\mathcal {M}}^{{\textsf{T}}}$ can be calculated as:

$$\begin{aligned} V(z)|_{p} = \sum _{\begin{array}{c} f \in (\text {\textsf {QM}}_{\text {ns }\infty })^{{\textsf{T}}_{q}} \\ f(\infty )=p \end{array}} z^{\deg f} {\hat{a}}\left( T_{\text {vir},f} \text {\textsf {QM}}- T_{p}{\mathcal {M}} \right) q^{\deg {\mathscr {T}}^{1/2}/2} \end{aligned}$$

(10)

In this formula, $T_{p}{\mathcal {M}}$ and the virtual tangent space $T_{\text {vir},f} \text {\textsf {QM}}$ are identified with their ${\textsf{T}}_{q}$ characters and hence lie in the domain of ${\hat{a}}$.

Remark 2

Tangent weights contribute to the vertex function via ${\hat{a}}$ rather than the usual K-theoretic Euler class because the vertex function is defined using the symmetrized virtual structure sheaf, see [4, section 6.1]. This is also the reason for the appearance of $q^{\deg {\mathscr {T}}^{1/2}/2}$.

Remark 3

The subtraction of $T_{p}{\mathcal {M}}$ is simply a normalization condition and has the effect of making the vertex function start with 1.

5.2 Explicit formula for vertex functions

By definition, a stable quasimap f to ${\mathcal {M}}$ provides vector bundles ${\mathscr {V}}_{i}$ and ${\mathscr {W}}_{i}$ over ${\mathbb {P}}^{1}$. Let

$$\begin{aligned} {\mathcal {T}}^{1/2}= \sum _{i=1}^{m-1} \text {Hom}({\mathscr {V}}_{i},{\mathscr {V}}_{i+1}) + \sum _{i=1}^{m} \text {Hom}({\mathscr {W}}_{i},{\mathscr {V}}_{i}) - \sum _{i=1}^{m} \text {Hom}({\mathscr {V}}_{i}, {\mathscr {V}}_{i}) \end{aligned}$$

The virtual tangent space at f of the moduli space of quasimaps is

$$\begin{aligned} T_{\text {vir},f} \text {\textsf {QM}}= H^{*}\left( {\mathbb {P}}^{1}, {\mathcal {T}}^{1/2} + \hbar ^{-1} \left( {\mathcal {T}}^{1/2}\right) ^{\vee } \right) , \end{aligned}$$

(11)

see [4]. This is an equality of representations of ${\textsf{T}}_{q}$. We compute the character of this representation.

As ${\mathscr {V}}_{i}$ is a vector bundle over ${\mathbb {P}}^{1}$, there is a decomposition

$$\begin{aligned} {\mathscr {V}}_{i}\cong \bigoplus _{j=1}^{{\textsf{v}}_{i}} x_{i,j}(p) {\mathcal {O}}(d_{i,j}) \end{aligned}$$

where $d_{i,j} \in {\mathbb {Z}}$ and $\{x_{i,j}(p)\}_{1 \le j \le {\textsf{v}}_{i}}$ is the set of ${\textsf{T}}$-weights of the tautological bundle ${\mathcal {V}}_{i}$ on ${\mathcal {M}}$. The lines bundles ${\mathcal {O}}(d)$ are linearized so that the ${\mathbb {C}}^{\times }_{q}$ character of $H^{0}({\mathbb {P}}^{1},{\mathcal {O}}(d))$ is $\sum _{j=0}^{d} q^{j}$ when $d\ge 0$. The integers $d_{i,j}$ that appear must satisfy certain linear inequalities to arise from a quasimap, see [27, section 3]. We denote this set by $C_{p} \subset {\mathbb {Z}}^{|{\textsf{v}}|}$. In fact, one can show that for each $\{d_{i,j}\} \in C_{p}$, there exists a unique ${\textsf{T}}\times {\mathbb {C}}^{\times }_{q}$ fixed quasimap in $\text {\textsf {QM}}_{\text {ns }\infty }$, see [20, section 5.1.3].

Lemma 2

([22] Lemma 1) For any weight w of ${\textsf{T}}_{q}$, we have

$$\begin{aligned}{} & {} H^{*}\left( w {\mathcal {O}}(d)+\frac{1}{\hbar w} {\mathcal {O}}(-d) \right) -w - \frac{1}{\hbar w} \\{} & {} \quad = {\left\{ \begin{array}{ll} w q (1+q+\ldots q^{d-1}) - \frac{1}{\hbar w}(1 + q^{-1} + \ldots + q^{-(d-1)}) &{} \quad d \ge 0 \\ \frac{q}{\hbar w}(1 + q + \ldots q^{-d-1}) - w(1+ q^{-1} +\ldots q^{d+1}) &{} \quad d< 0 \end{array}\right. } \\{} & {} \quad ={\left\{ \begin{array}{ll} w q \sum _{i=0}^{d-1} q^{i} - \frac{1}{\hbar w}\sum _{i=-(d-1)}^{0} q^i &{} \quad d \ge 0 \\ \frac{q}{\hbar w}\sum _{i=0}^{-d-1} q^i - w\sum _{i=d+1}^{0} q^i &{} \quad d < 0 \end{array}\right. } \end{aligned}$$

Proof

The equivariant dualizing sheaf on ${\mathbb {P}}^1$ is $q {\mathcal {O}}(-2)$, where the q means to twist ${\mathcal {O}}(-2)$ by the trivial line bundle with equivariant weight q. The result follows by Serre duality. $\square$

Lemma 3

$$\begin{aligned} {\hat{a}}\left( H^{*}\left( w {\mathcal {O}}(d)+\frac{1}{\hbar w} {\mathcal {O}}(-d) \right) -w - \frac{1}{\hbar w} \right) =\frac{(\hbar w)_{d}}{(q w)_{d}}\left( -\frac{q^{1/2}}{\hbar ^{1/2}} \right) ^{d} \end{aligned}$$

where $(x)_{d}:=\frac{(x)_{\infty }}{(x q^{d})_{\infty }}$ and $(x)_{\infty }=\prod _{i=0}^{\infty }(1-x q^{i})$.

Proof

This follows by applying the function ${\hat{a}}$ to the previous lemma. $\square$

Along with the factor of $q^{\deg {\mathscr {T}}^{1/2}/2}$, the contribution of $w {\mathcal {O}}(d)+\frac{1}{\hbar w} O(-d)$ to the vertex function is thus:

$$\begin{aligned} \frac{(\hbar w)_{d}}{(q w)_{d}}\left( -\frac{q}{\hbar ^{1/2}} \right) ^{d} \end{aligned}$$

Denote

$$\begin{aligned} \{x\}_{d}=\frac{(\hbar x)_{d}}{(q x)_{d}}\left( -\frac{q}{\hbar ^{1/2}}\right) ^{d} \end{aligned}$$

Combining Lemma 3, (10), and (11), we deduce the following.

Theorem 5

The restriction of the vertex function to p is

$$\begin{aligned} V(z)|_{p}= & {} \sum _{\{d_{i,j}\} \in C_{p}} z^{d} \prod _{i=1}^{m-1} \prod _{j=1}^{{\textsf{v}}_i} \prod _{k=1}^{{\textsf{v}}_{i+1}} \left\{ \frac{x_{i+1,k}(p)}{x_{i,j}(p)} \right\} _{d_{i+1,k}-d_{i,j}}\\{} & {} \prod _{i=1}^{m} \prod _{j=1}^{{\textsf{w}}_{i}} \prod _{k=1}^{{\textsf{v}}_{i}} \left\{ \frac{x_{i,k}(p)}{a_{i,j}}\right\} _{d_{i,k}} \prod _{i=1}^{m} \prod _{j=1}^{{\textsf{v}}_{i}} \prod _{k=1}^{{\textsf{v}}_{i}} \left\{ \frac{x_{i,k}(p)}{x_{i,j}(p)}\right\} _{d_{i,k}-d_{i,j}} \end{aligned}$$

where $z^{d}=\prod _{i=1}^{m}\prod _{j=1}^{{\textsf{v}}_{i}} z_{i}^{d_{i,j}}$.

Remark 4

As already mentioned, the set of degrees $\{d_{i,j}\}$ must satisfy certain conditions to arise from a quasimap. However, the formula in Theorem 5 turns out to be quite miraculous: it suffices to take $d_{i,j}\ge 0$ for all i and j and all terms not arising from quasimaps are automatically zero, see [25, Proposition 7].

Remark 5

When ${\mathcal {M}}=T^*{\mathbb {P}}^{n}$, Theorem 5 shows that the vertex function is equal to the usual basic q-hypergeometric function $_{n+1} \phi _{n}$ for certain values of the parameters, see [33].

Let ${\varvec{\lambda }}\in {\mathcal {M}}({\textsf{v}},{\textsf{w}})^{{\textsf{T}}}$. Recall the weights of the tautological bundle ${\mathcal {V}}_{i}$ from (8). Thus, we can write the vertex function as

$$\begin{aligned} V(z)|_{{\varvec{\lambda }}}= & {} \sum _{\{d_{\square }\} \in C_{{\varvec{\lambda }}}} z^{d} \prod _{\begin{array}{c} \square ,\square ' \in {\varvec{\lambda }}\\ \gamma (\square ')=\gamma (\square )+1 \end{array}} \left\{ \frac{a_{\square '}}{a_{\square }}\hbar ^{\delta ^{{\varvec{\lambda }}}_{\square '}-\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} \\{} & {} \prod _{\square \in {\varvec{\lambda }}} \prod _{j=1}^{{\textsf{w}}_{\gamma (\square )}} \left\{ \frac{a_{\square }}{a_{\gamma (\square ),j}} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square }} \prod _{\begin{array}{c} \square ,\square '\in {\varvec{\lambda }}\\ \gamma (\square )=\gamma (\square ') \end{array}} \left\{ \frac{a_{\square '}}{a_{\square }} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square '}-\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square '}-d_{\square }}^{-1} \end{aligned}$$

Proposition 11

([25], Proposition 7) A collection $\{d_{\square }\}_{\square \in {\varvec{\lambda }}}$ lies in $C_{{\varvec{\lambda }}}$ if and only if the following two conditions hold:

• 1. $d_{\square } \ge 0$ for all $\square \in {\varvec{\lambda }}$

• 2. If $\square ,\square ' \in \lambda ^{i,j}$ satisfy $\gamma (\square ')=\gamma (\square )\pm 1$ and $\delta ^{{\varvec{\lambda }}}_{\square '}=\delta ^{{\varvec{\lambda }}}_{\square }+1$, then $d_{\square } \le d_{\square '}$.

Definition 5

We call $C_{{\varvec{\lambda }}}$ the set of admissible degrees for ${\varvec{\lambda }}$.

5.3 Preservation of vertex functions

Recall the notation of Sect. 4.1. We have $\Phi :{\mathcal {M}}({\textsf{v}},{\textsf{w}})\hookrightarrow {\mathcal {M}}'({\textsf{v}}',{\textsf{w}}')$ as in (7). These are quiver varieties from a type A quiver with m vertices. Recall the definitions of k and n used there. There are tori ${\textsf{T}}$ and ${\textsf{T}}'$ that act on these two varieties and an embedding $\iota : {\textsf{T}}\rightarrow {\textsf{T}}'$. The map $\Phi$ is equivariant with respect to $\iota$ and hence induces a pullback

$$\begin{aligned} \Phi ^{*}:K_{{\textsf{T}}'\times {\mathbb {C}}^{\times }_{q}}({\mathcal {M}}')_{loc} \rightarrow K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}({\mathcal {M}})_{loc} \end{aligned}$$

Our main theorem is the following.

Theorem 6

Up to shifts of z, $\Phi ^{*}$ preserves vertex functions. More specifically,

$$\begin{aligned} \Phi ^{*}(V'(z))=V({\tilde{z}}) \end{aligned}$$

where ${\tilde{z}}$ stands for the shift $z_{j}\mapsto z_{j} q^{-1}$ for $k+1 \le j <m$ and $z_{m} \mapsto z_{m} q^{n-1}$.

Let

$$\begin{aligned} \iota ^{*}: K_{{\textsf{T}}' \times {\mathbb {C}}^{\times }_{q}}(pt) \rightarrow K_{{\textsf{T}}\times {\mathbb {C}}^{\times }_{q}}(pt) \end{aligned}$$

be the induced map. Let ${\varvec{\lambda }}\in {\mathcal {M}}^{{\textsf{T}}}$. Let ${\varvec{\mu }}\in {\mathcal {M}}'^{{\textsf{T}}'}$ be the fixed point constructed from ${\varvec{\lambda }}$ in Definition 4.

In view of Lemma 1, Theorem 6 is equivalent to the following.

Theorem 7

Let ${\varvec{\lambda }}\in {\mathcal {M}}^{{\textsf{T}}}$ and let ${\varvec{\mu }}\in {\mathcal {M}}'^{{\textsf{T}}'}$ be the fixed point constructed in Sect. 4.4. Then

$$\begin{aligned} \iota ^{*}(V'(z)|_{{\varvec{\mu }}})=V({\tilde{z}})|_{{\varvec{\lambda }}} \end{aligned}$$

Repeating the embedding procedure as described in 4.2, we obtain the following.

Corollary 4

Up to shifts of $z_{1},\ldots ,z_{m}$ by powers of q, the vertex function of any type A quiver variety can be obtained by a certain specialization of the equivariant parameters of the vertex function of the cotangent bundle of a partial flag variety.

We will prove Theorem 6 in Sect. 6 by a careful analysis of the localization formula in Theorem 5.

6 Proof of Theorem 7

6.1 Setup

We review the setup of Sect. 7. Let ${\textsf{v}},{\textsf{w}}\in {\mathbb {Z}}^{m}_{\ge 0}$ and let k be the maximal index such that $k+1<m$ and ${\textsf{w}}_{k+1}\ne 0$. Define n by $k+n=m$. Then

$$\begin{aligned} {\textsf{w}}&=({\textsf{w}}_{1},{\textsf{w}}_{2},\ldots ,{\textsf{w}}_{k},{\textsf{w}}_{k+1},0,\ldots ,0,{\textsf{w}}_{k+n})\\ {\textsf{v}}'&=({\textsf{v}}_{1},{\textsf{v}}_{2},\ldots ,{\textsf{v}}_{k+1},{\textsf{v}}_{k+2}+1,\ldots ,{\textsf{v}}_{k+n}+n-1) \\ {\textsf{w}}'&=({\textsf{w}}_{1},{\textsf{w}}_{2},\ldots ,{\textsf{w}}_{k+1}-1,0,\ldots ,0,{\textsf{w}}_{k+n}+n) \end{aligned}$$

Let ${\mathcal {M}}:={\mathcal {M}}_{\theta ^{-}}({\textsf{v}},{\textsf{w}})$ and ${\mathcal {M}}':={\mathcal {M}}_{\theta ^{-}}({\textsf{v}}',{\textsf{w}}')$ and consider the embedding $\Phi : {\mathcal {M}} \hookrightarrow {\mathcal {M}}'$ and the embedding $\iota : {\textsf{T}}\rightarrow {\textsf{T}}'$. Let $\iota ^*$ be the induced pullback on torus weights.

Denote the equivariant parameters of ${\textsf{T}}$ by $a_{i,j}$ where $1 \le i \le m$ and $1 \le j \le {\textsf{w}}_{i}$ and the equivariant parameters of ${\textsf{T}}'$ by $b_{i,j}$ where $1 \le i \le m$ and $1 \le j \le {\textsf{w}}'_{i}$. We will also denote $c_{j}:=b_{m,{\textsf{w}}_{m}+j}$ for $1 \le j \le n$. By (5), the map $\iota ^*$ is defined by

$$\begin{aligned} \iota ^*(b_{i,j})={\left\{ \begin{array}{ll} a_{i,j} &{} \quad 1 \le i \le k \\ a_{k+1,j+1} &{} \quad i=k+1 \text { and } 1\le j \le {\textsf{w}}_{k+1}-1 \\ a_{m,j} &{} \quad i=m \text { and } 1 \le j \le {\textsf{w}}_{m}\\ \hbar ^{j-{\textsf{w}}_{m}-n} a_{k+1,1} &{} \quad i=m \text { and } {\textsf{w}}_{m}+1 \le j \le {\textsf{w}}_{m}+n \end{array}\right. } \end{aligned}$$

We abbreviate $a:=a_{k+1,1}$ so that the last line reads $\iota ^{*}(c_{j})=\hbar ^{j-n} a$ for $1\le j \le n$.

Let ${\varvec{\lambda }}$ be a $({\textsf{v}},{\textsf{w}})$-tuple of partitions and let ${\varvec{\mu }}$ be as in Definition 4. To simplify notations below, we will denote $\lambda :=\lambda ^{k+1,1}$ and

$$\begin{aligned} \nu :=(\nu ^{1},\nu ^{2},\ldots ,\nu ^{n}):=(\mu ^{m,{\textsf{w}}_{m}+1},\ldots ,\mu ^{m,{\textsf{w}}_{m}+n}) \end{aligned}$$

Since $\mu ^{m,{\textsf{w}}_{m}+j}=(\lambda _{j}+n-j)$, we can and will canonically identify the Young diagram of $\lambda$ with a subset of the disjoint union of the Young diagrams of each $\mu ^{m,{\textsf{w}}_{m}+j}$ for $1 \le j \le n$. By Sect. 4.4, $\mu ^{i,j}=\lambda ^{i,j}$ if $i \ne m$ or if $i=m$ and $j\le {\textsf{w}}_{m}$. We identify such boxes $\square \in {\varvec{\lambda }}$ with their counterparts in ${\varvec{\mu }}$. So, we have defined an inclusion ${\varvec{\lambda }}\subset {\varvec{\mu }}$; for example, see Fig. 6.

6.2 Comparison of degrees

We denote by $V'_{{\varvec{\mu }}}$ the restriction of the vertex function of ${\mathcal {M}}'$ to ${\varvec{\mu }}$. We similarly write $V_{{\varvec{\lambda }}}$ for the restriction of the vertex function of ${\mathcal {M}}$ to ${\varvec{\lambda }}$. We will denote the coefficients of the vertex function $V'_{{\varvec{\mu }}}$ by $C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )$, so that

$$\begin{aligned} V'_{{\varvec{\mu }}}=\sum _{\{d_{\square }\} \in C_{{\varvec{\mu }}}} z^{d} C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar ) \end{aligned}$$

and similarly for $C^{{\varvec{\lambda }}}_{\{d_{\square }\}}(a,\hbar )$

Let $\{d_{\square }\}_{\square \in {\varvec{\mu }}}$ be an admissible collection of degrees appearing in the vertex function $V'_{{\varvec{\mu }}}$. By forgetting the degrees corresponding to boxes $\square \in {\varvec{\mu }}{\setminus } {\varvec{\lambda }}$, we obtain a set $\{d_{\square }\}_{\square \in {\varvec{\lambda }}}$.

Fig. 6

The identification of boxes of ${\varvec{\lambda }}$ (left) with a subset of the boxes of ${\varvec{\mu }}$ (right)

Lemma 4

If $\iota ^*\left( C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )\right) \ne 0$, then $\{d_{\square }\}_{\square \in {\varvec{\lambda }}}$ is a collection of admissible degrees for ${\varvec{\lambda }}$ and $\{d_{\square }\}_{\square \in {\varvec{\mu }}} {\setminus } \{d_{\square }\}_{\square \in {\varvec{\lambda }}}=\{0\}$.

Proof

Suppose $\{d_{\square }\}_{\square \in {\varvec{\mu }}}$ is a collection of admissible degrees for ${\varvec{\mu }}$ and satisfies $\iota ^*(C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )\ne 0$. We use the characterization of Proposition 11. We know a-priori that $d_{\square } \ge 0$. The rational function $C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )$ is a product of q-Pochhammer terms. For each $1 \le i,j \le n$ and each box $\square$ in $\nu ^{j}$ with height l, there is a term

$$\begin{aligned} A_{i,j,l}:=\frac{\left( \hbar \frac{c_{j}\hbar ^{l}}{c_{i}}\right) _{d_{\square }}}{\left( q \frac{c_{j}\hbar ^{l-1}}{c_{i}}\right) _{d_{\square }}} \end{aligned}$$

Then,

$$\begin{aligned} \iota ^{*}\left( A_{i,j,l}\right) = \frac{\left( \hbar ^{j-i+l+1}\right) _{d_{\square }}}{\left( q \hbar ^{j-i+l}\right) _{d_{\square }}} \end{aligned}$$

If $j=i-p$ for $p >1$ and $\square \in \nu ^{j}$ has height $p-1$, then the numerator is $(1)_{d'_{\square }}$. For $\iota ^{*}\left( A_{i,j,l}\right)$ to be nonzero, we must have $d'_{\square }=0$ for any such box.

This shows that $d_{\square }=0$ whenever $\square$ is a box of height less than or equal to $n+j-1$ in $\nu ^{j}$. In other words, $\{d_{\square }\}_{\square \in {\varvec{\mu }}} {\setminus } \{d_{\square }\}_{\square \in {\varvec{\lambda }}}=\{0\}$.

Now suppose that $\square \in \lambda _{j}$ and $\square ' \in \lambda _{j+1}$ satisfy $\delta ^{{\varvec{\lambda }}}_{\square }=\delta ^{{\varvec{\lambda }}}_{\square '}$, or equivalently, $\delta ^{{\varvec{\mu }}}_{\square }=\delta ^{{\varvec{\mu }}}_{\square '}+1$. We must show that $\iota ^*\left( C_{\{d_{\square }\}}(b,\hbar )\right) \ne 0 \implies d_{\square '}-d_{\square }\ge 0$. A term in $C_{\{d_{\square }\}}(b,\hbar )$ is

$$\begin{aligned} B_{\square ,\square '}:=\frac{\left( \hbar \frac{c_{j+1}}{c_{j} \hbar }\right) _{d_{\square '}-d_{\square }}}{\left( q \frac{c_{j+1}}{c_{j}\hbar }\right) _{d_{\square '}-d_{\square }}} \end{aligned}$$

And

$$\begin{aligned} \iota ^*\left( B_{\square ,\square '}\right) =\frac{\left( \hbar \right) _{d_{\square '}-d_{\square }}}{\left( q \right) _{d_{\square '}-d_{\square }}} \end{aligned}$$

which is nonzero if and only if $d_{\square '} - d_{\square } \ge 0$.

A similar argument applies for $\square ,\square ' \in \lambda _{j}$ such that $\delta ^{{\varvec{\lambda }}}_{\square '}=\delta ^{{\varvec{\lambda }}}_{\square }+1$. Thus, $\{d_{\square }\}_{\square \in {\varvec{\lambda }}}$ is a collection of admissible degrees for ${\varvec{\lambda }}$. $\square$

Lemma 5

If $\square \in \lambda _{j}$, then $\delta ^{{\varvec{\lambda }}}_{\square }=\delta ^{{\varvec{\mu }}}_{\square }+j-n$. If $\square \in {\varvec{\lambda }}\setminus \lambda$, then $\delta ^{{\varvec{\lambda }}}_{\square }=\delta ^{{\varvec{\mu }}}_{\square }$.

Proof

This follows straightforwardly from the definitions. $\square$

6.3 Comparison of localization terms

Next we start comparing $\iota ^{*}\left( C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )\right)$ with $C^{{\varvec{\lambda }}}_{\{d_{\square }\}}(a,\hbar )$. We define $X^{{\varvec{\mu }}},Y^{{\varvec{\mu }}}$, and $Z^{{\varvec{\mu }}}$ by the following:

$$\begin{aligned} C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )= & {} \underbrace{\prod _{\begin{array}{c} \square , \square ' \in {\varvec{\mu }}\\ \gamma (\square ')=\gamma (\square )+1 \end{array}} \left\{ \frac{b_{\square '}}{b_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} }_{X^{{\varvec{\mu }}}} \\{} & {} \underbrace{\prod _{\square \in {\varvec{\mu }}} \prod _{j=1}^{{\textsf{w}}_{\gamma (\square )}} \left\{ \frac{b_{\square }}{b_{\gamma (\square ),j}} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square }}}_{Y^{{\varvec{\mu }}}} \underbrace{\prod _{\begin{array}{c} \square , \square ' \in {\varvec{\mu }}\\ \gamma (\square ')=\gamma (\square ) \end{array}} \left\{ \frac{b_{\square '}}{b_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }}^{-1}}_{Z^{{\varvec{\mu }}}} \end{aligned}$$

Lemma 6

$$\begin{aligned}&\frac{ \iota ^{*}\left( X^{{\varvec{\mu }}}\right) }{X^{{\varvec{\lambda }}}} \nonumber \\&\quad =\prod _{j=1}^{n} \prod _{\begin{array}{c} \square \in (\nu \setminus \lambda )_{j} \\ \square ' \notin \nu \\ \gamma (\square ')=\gamma (\square )+1 \end{array}} \left\{ \frac{a_{\square '}}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }-j+n} \right\} _{d_{\square '}} \prod _{l=1}^{n} \prod _{\begin{array}{c} \square \notin \nu \\ \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=\gamma (\square )+1 \end{array}} \left\{ \frac{a}{a_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }+l-n}\right\} _{-d_{\square }} \nonumber \\&\qquad \prod _{j,l=1}^{n} \prod _{\begin{array}{c} \square \in (\nu \setminus \lambda )_{j} \\ \square ' \in \lambda _{l} \\ \gamma (\square ')=\gamma (\square )+1 \end{array}} \left\{ \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square } +l-j}\right\} _{d_{\square '}} \prod _{j,l=1}^{n} \prod _{\begin{array}{c} \square \in \lambda _{j} \\ \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=\gamma (\square )+1 \end{array}} \left\{ \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }+l-j} \right\} _{-d_{\square }} \end{aligned}$$

(12)

Proof

We split the term as

$$\begin{aligned} X^{{\varvec{\mu }}}=\prod _{\square , \square ' \in {\varvec{\mu }}} X^{{\varvec{\mu }}}_{\square ,\square '}, \quad X^{{\varvec{\mu }}}_{\square ,\square '}=\left\{ \frac{b_{\square '}}{b_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} \end{aligned}$$

and consider $\iota ^*(X^{{\varvec{\mu }}})$. Assuming that $\gamma (\square ')=\gamma (\square )+1$, we break the possibilities into four cases:

• 1. Suppose $\square ,\square ' \notin \nu$. By Lemma 5, we have

  $$\begin{aligned} \iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \frac{a_{\square '}}{a_{\square }} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square '}-\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square '}-d_{\square }}=X^{{\varvec{\lambda }}}_{\square ,\square '} \end{aligned}$$

• 2. Suppose $\square ' \notin \nu$ and $\square \in \nu ^{j}$. If $\square \in \lambda _{j}\subset \nu ^{j}$, then

  $$\begin{aligned} \iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})&= \left\{ \frac{a_{\square '}}{a} \hbar ^{n-j+\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} \\&=\left\{ \frac{a_{\square '}}{a} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square '}-\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} \\&= X^{{\varvec{\lambda }}}_{\square ,\square '} \end{aligned}$$

  where the second equality follows from Lemma 5. If $\square \in (\nu \setminus \lambda )_{j}$, then we get

  $$\begin{aligned} \iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})= \left\{ \frac{a_{\square '}}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }-j+n} \right\} _{d_{\square '}} \end{aligned}$$

  since $d_{\square }=0$.

• 3. Similarly, if $\square \notin \nu$ and $\square ' \in \nu ^{l}$, we obtain either $X^{{\varvec{\lambda }}}_{\square ,\square '}$ or the extra terms

  $$\begin{aligned} \iota (X^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \frac{a}{a_{\square }} \hbar ^{l-n+\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }} \end{aligned}$$

  which arise from the case when $\square ' \in (\nu {\setminus }\lambda )_{l}$.

• 4. Suppose $\square \in \nu ^{j}$ and $\square ' \in \nu ^{l}$. If $\square \in \lambda _{j} \subset \nu ^{j}$ and $\square ' \in \lambda _{l} \subset \nu ^{l}$, then

  $$\begin{aligned} \iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})&=\left\{ \hbar ^{l-j +\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} \\&=\left\{ \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square '} -\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square '}-d_{\square }} \\&= X^{{\varvec{\lambda }}}_{\square ,\square '} \end{aligned}$$

  If $\square \in (\nu {\setminus } \lambda )_{j}$ and $\square ' \in \lambda _{l} \subset \nu _{l}$, then

  $$\begin{aligned} \iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \hbar ^{l-j +\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}} \end{aligned}$$

  If $\square ' \in (\nu {\setminus }\lambda )_{l}$ and $\square \in \lambda _{j}$, then

  $$\begin{aligned} \iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \hbar ^{l-j +\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }}\right\} _{-d_{\square }} \end{aligned}$$

  If $\square ' \in (\nu {\setminus }\lambda )_{l}$ and $\square \in (\nu {\setminus }\lambda )_{j}$, then $d_{\square '}=d_{\square }=0$. So $\iota ^{*}(X^{{\varvec{\mu }}}_{\square ,\square '})=1$.

$\square$

Lemma 7

$$\begin{aligned}&\frac{ \iota ^{*}\left( Y^{{\varvec{\mu }}}\right) }{Y^{{\varvec{\lambda }}}}=\prod _{j=1}^{n} \prod _{\begin{array}{c} \square \notin \nu \\ \gamma (\square )=m \end{array}} \left\{ \frac{a_{\square }}{a} \hbar ^{n-j}\right\} _{d_{\square }} \prod _{j,l=1}^{n}\prod _{\begin{array}{c} \square \in \lambda _{l} \\ \gamma (\square )=m \end{array}} \left\{ \hbar ^{l-j} \right\} _{d_{\square }} \end{aligned}$$

(13)

Proof

We split $Y^{{\varvec{\mu }}}$ as

$$\begin{aligned} Y^{{\varvec{\mu }}}=\prod _{\square \in {\varvec{\mu }}} \prod _{j=1}^{{\textsf{w}}_{\gamma (\square )}} Y^{{\varvec{\mu }}}_{\square ,j}, \quad Y^{{\varvec{\mu }}}_{\square ,j}= \left\{ \frac{b_{\square }}{b_{\gamma (\square ),j}} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square }} \end{aligned}$$

Assuming that $\square \in {\varvec{\mu }}$ and $1 \le j \le {\textsf{w}}_{\gamma (\square )}$, we have five possibilities:

• 1. Suppose $\square \notin \nu$. Suppose also that either $\gamma (\square )\ne m$ or $\gamma (\square )=m$ and $1\le j \le {\textsf{w}}_{m}$. Then,

  $$\begin{aligned} \iota ^{*}(Y^{{\varvec{\mu }}}_{\square ,j})=\left\{ \frac{a_{\square }}{a_{\gamma (\square ),j}} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square }} = Y^{{\varvec{\lambda }}}_{\square ,j} \end{aligned}$$

• 2. Suppose $\square \notin \nu$. Suppose also that $\gamma (\square )=m$ and ${\textsf{w}}_{m}+1\le j \le {\textsf{w}}_{m}+n$, and let $i=j-{\textsf{w}}_{m}$. We necessarily have $\delta ^{{\varvec{\mu }}}_{\square }=\delta ^{{\varvec{\lambda }}}_{\square }=0$. Then

  $$\begin{aligned} \iota ^{*}(Y^{{\varvec{\mu }}}_{\square ,j})=\left\{ \frac{a_{\square }}{a}\hbar ^{n-i} \right\} _{d_{\square }} \end{aligned}$$

  (14)

• 3. Suppose $\square \in \lambda _{l} \subset \nu ^{l}$. Suppose also that $\gamma (\square )\ne m$ or $\gamma (\square )=m$ and $1 \le j \le {\textsf{w}}_{m}$. Then,

  $$\begin{aligned} \iota ^{*}(Y^{{\varvec{\mu }}}_{\square ,j})&=\left\{ \frac{a}{a_{\gamma (\square ),j}} \hbar ^{l-n+\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square }} \\&=\left\{ \frac{a}{a_{\gamma (\square ),j}} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square }} \\&= Y^{{\varvec{\lambda }}}_{\square ,j} \end{aligned}$$

  where the second equality follows by Lemma 5.

• 4. Suppose $\square \in \lambda _{l}\subset \nu ^{l}$ and $\gamma (\square )=m$. Such a box must satisfy $\delta ^{{\varvec{\mu }}}_{\square }=\delta ^{{\varvec{\lambda }}}_{\square }=0$. Suppose also that j satisfies ${\textsf{w}}_{m}+1 \le j \le {\textsf{w}}_{m}+n$. Let $i=j-{\textsf{w}}_{m}$. Then,

  $$\begin{aligned} \iota ^{*}(Y^{{\varvec{\mu }}}_{\square ,j})&=\left\{ \hbar ^{l-i} \right\} _{d_{\square }} \end{aligned}$$

  (15)

• 5. The terms from $\square \in (\nu \setminus \lambda )_{l}$ are all 1, since $d_{\square }=0$ for such a box.

$\square$

Lemma 8

$$\begin{aligned} \frac{ \iota ^{*}\left( Z^{{\varvec{\mu }}}\right) }{Z^{{\varvec{\lambda }}}}&=\prod _{j=1}^{n} \prod _{\begin{array}{c} \square \in (\nu \setminus \lambda )_{j} \\ \square ' \notin \nu \\ \gamma (\square ')=\gamma (\square ) \end{array}} \left\{ \frac{a_{\square '}}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }-j+n} \right\} _{d_{\square '}}^{-1} \prod _{j=1}^{n} \prod _{\begin{array}{c} \square ' \in (\nu \setminus \lambda )_{l} \\ \square \notin \nu \\ \gamma (\square ')=\gamma (\square ) \end{array}} \left\{ \frac{a}{a_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }+l-n} \right\} _{-d_{\square }}^{-1} \nonumber \\&\quad \prod _{j,l=1}^{n} \prod _{\begin{array}{c} \square \in (\nu \setminus \lambda )_{j} \\ \square ' \in \lambda _{l} \\ \gamma (\square ')=\gamma (\square ) \end{array}} \left\{ \hbar ^{l-j+\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }}\right\} _{d_{\square '}}^{-1} \prod _{j,l=1}^{n} \prod _{\begin{array}{c} \square \in \lambda _{j} \\ \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=\gamma (\square ) \end{array}} \left\{ \hbar ^{l-j +\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }}^{-1} \end{aligned}$$

(16)

Proof

We write

$$\begin{aligned} Z^{{\varvec{\mu }}}=\prod _{\begin{array}{c} \square ,\square ' \in {\varvec{\mu }}\\ \gamma (\square ')=\gamma (\square ) \end{array}} Z^{{\varvec{\mu }}}_{\square ,\square '}, \quad Z^{{\varvec{\mu }}}_{\square ,\square '}= \left\{ \frac{b_{\square '}}{b_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }}^{-1} \end{aligned}$$

Assuming that $\gamma (\square )=\gamma (\square ')$, we break the possibilities into four cases:

• 1. Suppose that $\square ,\square ' \notin \nu$. Then $\iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})=Z^{{\varvec{\lambda }}}_{\square ,\square '}$.

• 2. Suppose $\square \in \nu ^{j}$ and $\square ' \notin \nu$. Then

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})= \left\{ \frac{a_{\square '}}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }+n-j} \right\} _{d_{\square '}-d_{\square }}^{-1} \end{aligned}$$

  If $\square \in \lambda _{j} \subset \nu _{j}$, then

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})= \left\{ \frac{a_{\square '}}{a} \hbar ^{\delta ^{{\varvec{\lambda }}}_{\square '}-\delta ^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square '}-d_{\square }}^{-1} = Z^{{\varvec{\lambda }}}_{\square ,\square '} \end{aligned}$$

  If $\square \in (\nu \setminus \lambda )_{j}$, then

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \frac{a_{\square '}}{a}\hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square } +n-j}\right\} _{d_{\square '}}^{-1} \end{aligned}$$

  since $d_{\square }=0$.

• 3. Similarly, if $\square ' \in (\nu \setminus \lambda )_{l}$ and $\square \notin \nu$ then

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})= \left\{ \frac{a}{a_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }+l-n} \right\} _{-d_{\square }}^{-1} \end{aligned}$$

• 4. Suppose $\square \in \nu ^{j}$ and $\square ' \in \nu ^{l}$. Then

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \hbar ^{l-j +\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}-d_{\square }}^{-1} \end{aligned}$$

  If $\square \in \lambda _{j}$ and $\square ' \in \lambda _{l}$, then $\iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})=Z^{{\varvec{\lambda }}}_{\square ,\square '}$, and similarly if we switch the roles of $\square$ and $\square '$.

  If $\square \in (\nu {\setminus } \lambda )_{j}$ and $\square '\in \lambda _{l}$, then

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \hbar ^{l-j+\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square '}}^{-1} \end{aligned}$$

  With the roles of $\square$ and $\square '$ reversed, we get

  $$\begin{aligned} \iota ^{*}(Z^{{\varvec{\mu }}}_{\square ,\square '})=\left\{ \hbar ^{l-j +\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }}^{-1} \end{aligned}$$

  If $\square \in (\nu {\setminus } \lambda )_{j}$ and $\square ' \in (\nu {\setminus } \lambda )_{l}$, then we get 1.

$\square$

Theorem 8

$$\begin{aligned} \iota ^*\left( C^{{\varvec{\mu }}}_{\{d_{\square }\}}(b,\hbar )\right) = C^{{\varvec{\lambda }}}_{\{d_{\square }\}}(a,\hbar )\prod _{\begin{array}{c} \square \in {\varvec{\mu }}\\ \gamma (\square )=m \end{array}} q^{(n-1)d_{\square }}\prod _{l=1}^{n}\prod _{\begin{array}{c} \square \in {\varvec{\mu }}\\ \gamma (\square )=k+l \end{array}} q^{-d_{\square }} \end{aligned}$$

Proof

What we have shown so far is that $\iota ^{*}\left( C^{{\varvec{\mu }}}_{\{d'_{\square }\}}(b,\hbar )\right) /C^{{\varvec{\lambda }}}_{\{d_{\square }\}}(a,\hbar )$ is a product of terms appearing in the previous three lemmas. In what follows, we will often use the identity $\{ x \}_{-d}=\{\hbar ^{-1} x^{-1} \}_{d} q^{-d}$ for $d\ge 0$, which follows easily by direct computation.

First, we locate the terms in $C^{{\varvec{\lambda }}}_{\{d_{\square }\}}(a,\hbar )$ corresponding to the framing at vertex $k+1$. Let $\square ' \in (\nu {\setminus }\lambda )_{1}$ be the box such that $\gamma (\square ')=k+2$ and $\delta ^{{\varvec{\mu }}}_{\square '}=n-2$. Then inside the product in (12), there are terms

$$\begin{aligned}&\prod _{\begin{array}{c} \square \notin \nu \\ \gamma (\square ')=k+1 \end{array}} \left\{ \frac{a}{a_{\square }} \hbar ^{-1-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }}\prod _{j=1}^{n}\prod _{\begin{array}{c} \square \in \lambda _{j}\\ \gamma (\square ')=k+1 \end{array}} \left\{ \hbar ^{n-2-(n-1)+1-j} \right\} _{-d_{\square }} \\&\quad = \prod _{\begin{array}{c} \square \notin \nu \\ \gamma (\square ')=k+1 \end{array}} \left\{ \frac{a}{a_{\square }} \hbar ^{-1-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }}\prod _{j=1}^{n}\prod _{\begin{array}{c} \square \in \lambda _{j}\\ \gamma (\square ')=k+1 \end{array}} \left\{ \hbar ^{-j} \right\} _{-d_{\square }} \\&\quad =\prod _{\begin{array}{c} \square \notin \nu \\ \gamma (\square ')=k+1 \end{array}} \left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square }} q^{-d_{\square }} \prod _{j=1}^{n} \prod _{\begin{array}{c} \square \in \lambda _{j}\\ \gamma (\square ')=k+1 \end{array}} \left\{ \hbar ^{j-1} \right\} _{d_{\square }} q^{-d_{\square }} \\&\quad = \prod _{\begin{array}{c} \square \in {\varvec{\mu }}\\ \gamma (\square )=k+1 \end{array}} \left\{ \frac{a_{\square }}{a} \hbar ^{d^{{\varvec{\lambda }}}_{\square }} \right\} _{d_{\square }} q^{-d_{\square }} \end{aligned}$$

which, up to the powers of q, are exactly the missing framing terms in $V_{{\varvec{\lambda }}}$.

Next, let $\square \notin \nu$ and suppose that $\gamma (\square )=k+2$. All the contributions of this box to $\iota ^{*}\left( C^{{\varvec{\mu }}}_{\{d'_{\square }\}}(b,\hbar )\right) /C^{{\varvec{\lambda }}}_{\{d_{\square }\}}(a,\hbar )$ come from interactions of $\square$ with itself, and then from the two boxes of $\nu \setminus \lambda$ that are one place to the right of $\square$. These terms are

$$\begin{aligned}&\left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }-(n-2)-1+n} \right\} _{d_{\square }}^{-1} \left\{ \frac{a}{a_{\square }} \hbar ^{(n-3) -\delta ^{{\varvec{\mu }}}_{\square }+1-n} \right\} _{-d_{\square }} \\&\left\{ \frac{a}{a_{\square }} \hbar ^{(n-2)-\delta ^{{\varvec{\mu }}}_{\square }+1-n} \right\} _{-d_{\square }}^{-1} \left\{ \frac{a}{a_{\square }} \hbar ^{(n-3) -\delta ^{{\varvec{\mu }}}_{\square }+2-n} \right\} _{-d_{\square }} \\&\quad = \left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }+1} \right\} _{d_{\square }}^{-1} \left\{ \frac{a}{a_{\square }} \hbar ^{-2 -\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }} \left\{ \frac{a}{a_{\square }} \hbar ^{-1-\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }}^{-1} \left\{ \frac{a}{a_{\square }} \hbar ^{-1 -\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }} \\&\quad = \left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }+1} \right\} _{d_{\square }}^{-1} \left\{ \frac{a}{a_{\square }} \hbar ^{-2 -\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }} \\&\quad =\left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }+1} \right\} _{d_{\square }}^{-1} \left\{ \frac{a_{\square }}{a} \hbar ^{1 +\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{d_{\square }} q^{-d_{\square }} \\&\quad = q^{-d_{\square }} \end{aligned}$$

Next suppose that $\square \notin \nu$ satisfies $\gamma (\square )=k+j$ for $2\le j \le m$. Then, the terms involving $\square$ in (12), (13), and (16) are:

$$\begin{aligned}&\prod _{l=1}^{n}\Bigg ( \prod _{\begin{array}{c} \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=k+j \end{array}} \left\{ \frac{a_{\square }}{a}\hbar ^{\delta ^{{\varvec{\mu }}}_{\square } -\delta ^{{\varvec{\mu }}}_{\square '}-l+n} \right\} _{d_{\square }}^{-1} \prod _{\begin{array}{c} \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=k+j \end{array}} \left\{ \frac{a}{a_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '}-\delta ^{{\varvec{\mu }}}_{\square }+l-n} \right\} _{-d_{\square }}^{-1}\\&\prod _{\begin{array}{c} \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=k+j-1 \end{array}} \left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }-\delta ^{{\varvec{\mu }}}_{\square '}-l+n} \right\} _{d_{\square }} \prod _{\begin{array}{c} \square ' \in (\nu \setminus \lambda )_{l} \\ \gamma (\square ')=k+j+1 \end{array}} \left\{ \frac{a}{a_{\square }} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square '} -\delta ^{{\varvec{\mu }}}_{\square }+l-n} \right\} _{-d_{\square }} \Bigg ) \\&\quad =\prod _{l=1}^{j-1}\left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }+j-l} \right\} _{d_{\square }}^{-1} \prod _{l=2}^{j} \left\{ \frac{a}{a_{\square }} \hbar ^{-1-j+l -\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }}^{-1} \\&\qquad \prod _{l=2}^{j-1} \left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }+j-l}\right\} _{d_{\square }} \prod _{l=1}^{j} \left\{ \frac{a}{a_{\square }} \hbar ^{-1+l-j -\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }} \\&\quad =\left\{ \frac{a}{a_{\square }} \hbar ^{-j -\delta ^{{\varvec{\mu }}}_{\square }} \right\} _{-d_{\square }} \left\{ \frac{a_{\square }}{a} \hbar ^{\delta ^{{\varvec{\mu }}}_{\square }+j-1} \right\} _{d_{\square }}^{-1} \\&\quad = q^{-d_{\square }} \end{aligned}$$

Next, suppose that $\square \notin \nu$ satisfies $\gamma (\square )=m$. The terms in (12), (13), and (16) involving $\square$ are:

$$\begin{aligned}&\prod _{l=1}^{n-1}\left\{ \frac{a_{\square }}{a} \hbar ^{n-l} \right\} _{d_{\square }}^{-1} \prod _{l=2}^{n} \left\{ \frac{a}{a_{\square }} \hbar ^{-1-n+l}\right\} _{-d_{\square }}^{-1} \\&\prod _{l=2}^{n-1} \left\{ \frac{a_{\square }}{a} \hbar ^{n-l} \right\} _{d_{\square }} \prod _{l=1}^{n} \left\{ \frac{a_{\square }}{a} \hbar ^{n-l} \right\} _{d_{\square }} \\&\quad =\prod _{l=2}^{n} q^{d_{\square }} \\&\quad = q^{(n-1)d_{\square }} \end{aligned}$$

This accounts for all the terms in (12), (13), and (16) involving $\square \notin \nu$. The computation for the remaining terms (i.e. the terms involving only $\hbar$ and q) is similar, and we omit it. $\square$