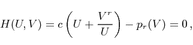Abstract
We study \(\mathrm {U}(N|M)\) character expectation value with the supermatrix Chern–Simons theory, known as the ABJM matrix model, with emphasis on its connection to the knot invariant. This average just gives the half-BPS circular Wilson loop expectation value in ABJM theory, which shall correspond to the unknot invariant. We derive the determinantal formula, which gives \(\mathrm {U}(N|M)\) character expectation values in terms of \(\mathrm {U}(1|1)\) averages for a particular type of character representations. This means that the \(\mathrm {U}(1|1)\) character expectation value is a building block for the \(\mathrm {U}(N|M)\) averages and also, by an appropriate limit, for the \(\mathrm {U}(N)\) invariants. In addition to the original model, we introduce another supermatrix model obtained through the symplectic transform, which is motivated by the torus knot Chern–Simons matrix model. We obtain the Rosso–Jones-type formula and the spectral curve for this case.




Similar content being viewed by others
Notes
Although we do not have an explicit proof of this statement, we check it with a number of examples by numerical calculations.
The spectral curve for Chern–Simons theory on the lens space \(L(r,1) = S^3/\mathbb {Z}_r\) (the r-cut Chern–Simons matrix model) is given by [29]
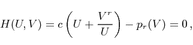
where \(p_r(V)\) is a degree r polynomial such that the coefficients of \(V^r\) and \(V^0\) are given by one, \(p_r(V) = V^r + \cdots + 1\). When the Chern–Simons gauge group is broken as \(\mathrm {U}(N_1 + \cdots + N_r) \rightarrow \mathrm {U}(N_1) \times \cdots \times \mathrm {U}(N_r)\), the parameter c corresponds to the total ’t Hooft coupling \(c = \exp g_s (N_1 + \cdots + N_r)/2\). Since the polynomial \(p_r(V)\) has \(r-1\) parameters, the total number of the parameters becomes \(1 + (r-1) = r\), which is consistent with that of the subgroups, \(\mathrm {U}(N_i)\) with \(i = 1, \ldots , r\).
Let us note that another kind of approach to the B-model description, which is in principle applicable to any knots, is discussed based on the A-polynomial [41].
When the representation does not satisfy this condition, there is no simple analogy between the matrix integral with the external fields and the Wilson loop average (2.34), because such an external field has to consist of \(N+N\) parameters for \(\mathrm {U}(N|N)\) theory. On the other hand, this analogy holds for arbitrary representations in the ordinary \(\mathrm {U}(N)\) Chern–Simons theory as (6.21). It is because even if the number of nonzero elements in the partition is less than N at the first place, it can be made N by the constant shift, since the average (2.31) is invariant under the shift of the partition
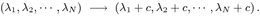
It is obvious that the \(\mathrm {U}(N|N)\) invariant (2.26) is not invariant under such a constant shift of the partition, since the corresponding external field is characterized by the Frobenius coordinates of the partition.
References
Witten, E.: Quantum field theory and the Jones polynomial. Commun. Math. Phys. 121, 351–399 (1989)
Lawrence, R., Rozansky, L.: Witten–Reshetikhin–Turaev invariants of Seifert manifolds. Commun. Math. Phys. 205, 287–314 (1999)
Beasley, C.: Localization for Wilson loops in Chern–Simons theory. Adv. Theor. Math. Phys. 17, 1–240 (2013). arXiv:0911.2687 [hep-th]
Källén, J.: Cohomological localization of Chern–Simons theory. JHEP 1108, 008 (2011). arXiv:1104.5353 [hep-th]
Brini, A., Eynard, B., Mariño, M.: Torus knots and mirror symmetry. Ann. Henri Poincaré 13, 1873–1910 (2012). arXiv:1105.2012 [hep-th]
Kapustin, A., Willett, B., Yaakov, I.: Exact results for Wilson loops in superconformal Chern–Simons theories with matter. JHEP 1003, 089 (2010). arXiv:0909.4559 [hep-th]
Aharony, O., Bergman, O., Jafferis, D.L., Maldacena, J.: \(\cal{N}=6\) superconformal Chern–Simons-matter theories, M2-branes and their gravity duals. JHEP 0810, 091 (2008). arXiv:0806.1218 [hep-th]
Drukker, N., Trancanelli, D.: A supermatrix model for \(\cal{N}=6\) super Chern–Simons-matter theory. JHEP 1002, 058 (2010). arXiv:0912.3006 [hep-th]
Bars, I.: Supergroups and their representations. Lect. Appl. Math. 21, 17 (1983)
Berele, A., Regev, A.: Hook Young-diagrams with applications to combinatorics and to representations of Lie superalgebras. Adv. Math. 64, 118–175 (1987)
Fay, J.D.: Theta Functions on Riemann Surfaces. Lecture Notes in Mathematics, vol. 352. Springer, Berlin (1973)
Borodin, A., Olshanski, G., Strahov, E.: Giambelli compatible point processes. Adv. Appl. Math. 37, 209–248 (2006). arXiv:math-ph/0505021
Bergère, M., Eynard, B.: Determinantal formulae and loop equations. arXiv:0901.3273 [math-ph]
Eynard, B., Orantin, N.: Invariants of algebraic curves and topological expansion. Commun. Num. Theor. Phys. 1, 347–452 (2007). arXiv:math-ph/0702045 [math-ph]
Dijkgraaf, R., Fuji, H., Manabe, M.: The volume conjecture, perturbative knot invariants, and recursion relations for topological strings. Nucl. Phys. B 849, 166–211 (2011). arXiv:1010.4542 [hep-th]
Borot, G., Eynard, B.: All-order asymptotics of hyperbolic knot invariants from non-perturbative topological recursion of A-polynomials. Quantum Top. 6, 39–138 (2015). arXiv:1205.2261 [math-ph]
Gukov, S., Saberi, I.: Lectures on Knot Homology and Quantum Curves. arXiv:1211.6075 [hep-th]
Gopakumar, R., Vafa, C.: On the gauge theory/geometry correspondence. Adv. Theor. Math. Phys. 3, 1415–1443 (1999). arXiv:hep-th/9811131 [hep-th]
Ooguri, H., Vafa, C.: Knot invariants and topological strings. Nucl. Phys. B 577, 419–438 (2000). arXiv:hep-th/9912123 [hep-th]
Mariño, M., Putrov, P.: Exact results in ABJM theory from topological strings. JHEP 1006, 011 (2010). arXiv:0912.3074 [hep-th]
Moens, E., Van der Jeugt, J.: A determinantal formula for supersymmetric Schur polynomials. J. Algebr. Comb. 17, 283–307 (2003)
Hatsuda, Y., Honda, M., Moriyama, S., Okuyama, K.: ABJM Wilson loops in arbitrary representations. JHEP 1310, 168 (2013). arXiv:1306.4297 [hep-th]
Dolivet, Y., Tierz, M.: Chern–Simons matrix models and Stieltjes–Wigert polynomials. J. Math. Phys. 48, 023507 (2007). arXiv:hep-th/0609167 [hep-th]
Rosso, M., Jones, V.: On the invariants of torus knots derived from quantum groups. J. Knot Theory Ramif. 2, 97–112 (1993)
Kapustin, A., Willett, B., Yaakov, I.: Nonperturbative tests of three-dimensional dualities. JHEP 1010, 013 (2010). arXiv:1003.5694 [hep-th]
Aharony, O., Bergman, O., Jafferis, D.L.: Fractional M2-branes. JHEP 0811, 043 (2008). arXiv:0807.4924 [hep-th]
Basor, E.L., Forrester, P.J.: Formulas for the evaluation of Toeplitz determinants with rational generating functions. Math. Nachr. 170, 5–18 (1994)
Aganagic, M., Klemm, A., Mariño, M., Vafa, C.: Matrix model as a mirror of Chern–Simons theory. JHEP 0402, 010 (2004). hep-th/0211098
Halmagyi, N., Yasnov, V.: The spectral curve of the lens space matrix model. JHEP 0911, 104 (2009). arXiv:hep-th/0311117
Jockers, H., Klemm, A., Soroush, M.: Torus knots and the topological vertex. Lett. Math. Phys. 104, 953–989 (2014). arXiv:1212.0321 [hep-th]
Stevan, S.: Torus knots in lens spaces and topological strings. Ann. Henri Poincaré 16, 1937–1967 (2015). arXiv:1308.5509 [hep-th]
Borot, G., Eynard, B., Orantin, N.: Abstract loop equations, topological recursion and new applications. Commun. Num. Theor. Phys. 9, 51–187 (2015). arXiv:1303.5808 [math-ph]
Borot, G., Guionnet, A., Kozlowski, K.K.: Large-\(N\) asymptotic expansion for mean field models with Coulomb gas interaction. Int. Math. Res. Not. 2015, 10451–10524 (2015). arXiv:1312.6664 [math-ph]
Aganagic, M., Klemm, A., Marino, M., Vafa, C.: The topological vertex. Commun. Math. Phys. 254, 425–478 (2005). arXiv:hep-th/0305132 [hep-th]
Klemm, A., Mariño, M., Schiereck, M., Soroush, M.: ABJM Wilson loops in the Fermi gas approach. Z. Naturforsch. A68, 178–209 (2013). arXiv:1207.0611 [hep-th]
Mariño, M.: Open string amplitudes and large order behavior in topological string theory. JHEP 0803, 060 (2008). arXiv:hep-th/0612127 [hep-th]
Bouchard, V., Klemm, A., Mariño, M., Pasquetti, S.: Remodeling the B-model. Commun. Math. Phys. 287, 117–178 (2009). arXiv:0709.1453 [hep-th]
Eynard, B., Orantin, N.: Computation of open Gromov–Witten invariants for toric Calabi–Yau 3-folds by topological recursion, a proof of the BKMP conjecture. Commun. Math. Phys. 337, 483–567 (2015). arXiv:1205.1103 [math-ph]
Aganagic, M., Vafa, C.: Mirror symmetry, D-branes and counting holomorphic discs. arXiv:hep-th/0012041 [hep-th]
Aganagic, M., Klemm, A., Vafa, C.: Disk instantons, mirror symmetry and the duality web. Z. Naturforsch. A57, 1–28 (2002). arXiv:hep-th/0105045 [hep-th]
Aganagic, M., Vafa, C.: Large \(N\) duality, mirror symmetry, and a Q-deformed A-polynomial for knots. arXiv:1204.4709 [hep-th]
Hatsuda, Y., Mariño, M., Moriyama, S., Okuyama, K.: Non-perturbative effects and the refined topological string. JHEP 1409, 168 (2014). arXiv:1306.1734 [hep-th]
Eynard, B., Orantin, N.: Topological expansion of mixed correlations in the Hermitian 2-matrix model and \(x\)-\(y\) symmetry of the \(F_g\) invariants. J. Phys. A 41, 015203 (2008). arXiv:0705.0958 [math-ph]
Eynard, B., Orantin, N.: About the \(x\)–\(y\) symmetry of the \(F_g\) algebraic invariants. arXiv:1311.4993 [math-ph]
Kimura, T.: Note on a duality of topological branes. PTEP 2014, 103B04 (2014). arXiv:1401.0956 [hep-th]
Kimura, T.: Duality and integrability of a supermatrix model with an external source. PTEP 2014, 123A01 (2014). arXiv:1410.0680 [math-ph]
Desrosiers, P., Eynard, B.: Supermatrix models, loop equations, and duality. J. Math. Phys. 51, 123304 (2010). arXiv:0911.1762 [math-ph]
Brézin, E., Hikami, S.: Characteristic polynomials of random matrices. Commun. Math. Phys. 214, 111–135 (2000). arXiv:math-ph/9910005
Harish-Chandra, : Differential operators on a semisimple lie algebra. Am. J. Math. 79, 87–120 (1957)
Itzykson, C., Zuber, J.-B.: The planar approximation. II. J. Math. Phys. 21, 411–421 (1980)
Tanaka, A.: Comments on knotted 1/2 BPS Wilson loops. JHEP 1207, 097 (2012). arXiv:1204.5975 [hep-th]
Hama, N., Hosomichi, K., Lee, S.: SUSY gauge theories on squashed three-spheres. JHEP 1105, 014 (2011). arXiv:1102.4716 [hep-th]
Deguchi, T., Akutsu, Y.: Graded solutions of the Yang–Baxter relation and link polynomials. J. Phys. A 23, 1861–1876 (1990)
Kauffman, L.H., Saleur, H.: Free fermions and the Alexander–Conway polynomial. Commun. Math. Phys. 141, 293–327 (1991)
Rozansky, L., Saleur, H.: \(S\) and \(T\) matrices for the super U(1,1) WZW model: application to surgery and three manifolds invariants based on the Alexander-Conway polynomial. Nucl. Phys. B 389, 365–423 (1993). arXiv:hep-th/9203069 [hep-th]
Kashaev, R.M.: The hyperbolic volume of knots from quantum dilogarithm. Lett. Math. Phys. 39, 269–275 (1997). arXiv:q-alg/9601025 [math.QA]
Murakami, H., Murakami, J.: The colored Jones polynomials and the simplicial volume of a knot. Acta Math. 186, 85–104 (2001). arXiv:math/9905075 [math.GT]
Gukov, S.: Three-dimensional quantum gravity, Chern–Simons theory, and the A-polynomial. Commun. Math. Phys. 255, 577–627 (2005). arXiv:hep-th/0306165 [hep-th]
Garoufalidis, S.: On the characteristic and deformation varieties of a knot. Geom. Topol. Monogr. 7, 291–309 (2004). arXiv:math/0306230 [math.GT]
Khovanov, M.: A categorification of the Jones polynomials. Duke Math. J. 101, 359–426 (2000). arXiv:math/9908171 [math.QA]
Khovanov, M., Rozansky, L.: Matrix factorizations and link homology. Fundam. Math. 199, 1–91 (2008). arXiv:math/0401268 [math.QA]
Khovanov, M., Rozansky, L.: Matrix factorizations and link homology II. Geom. Topol. 12, 1387–1425 (2008). arXiv:math/0505056 [math.QA]
Gukov, S., Schwarz, A.S., Vafa, C.: Khovanov–Rozansky homology and topological strings. Lett. Math. Phys. 74, 53–74 (2005). arXiv:hep-th/0412243 [hep-th]
Dunfield, N.M., Gukov, S., Rasmussen, J.: The superpolynomial for knot homologies. Exp. Math. 15, 129–159 (2006). arXiv:math/0505662 [math.GT]
Acknowledgements
We would like to thank G. Borot and M. Mariño for fruitful discussions. We are also grateful to A. Brini for carefully reading the manuscript and giving useful comments. BE thanks Centre de Recherches Mathématiques de Montréal, the FQRNT grant from the Québec government, Piotr Sułkowski and the ERC starting grant Fields-Knots. The work of TK is supported in part by Keio Gijuku Academic Development Funds, MEXT-Supported Program for the Strategic Research Foundation at Private Universities “Topological Science” (No. S1511006), and JSPS Grant-in-Aid for Scientific Research on Innovative Areas “Topological Materials Science” (No. JP15H05855).
Author information
Authors and Affiliations
Corresponding author
Appendix: Mirror of the torus knot ABJM partition function
Appendix: Mirror of the torus knot ABJM partition function
In this appendix, we derive the mirror description of the torus knot ABJM partition function [25]. We first expand the determinants in (3.10) as summation over permutations
Applying the formula (2.20), we have
At this moment, it is obvious that the partition function depends only on the composition of permutations \(\sigma \cdot \sigma '^{-1}\). Thus, by fixing either of them \(\sigma '\) as the trivial permutation, we obtain
This is the mirror expression of the partition function (3.10). Especially for \(k=1\), the mirror theory turns out to be \(\mathcal {N}=4\) SYM theory with a single fundamental and a single adjoint hypermultiplet. The dependence on the parameters (P, Q) becomes trivial in this mirror representation.
Rights and permissions
About this article
Cite this article
Eynard, B., Kimura, T. Toward \(\mathrm {U}(N|M)\) knot invariant from ABJM theory. Lett Math Phys 107, 1027–1063 (2017). https://doi.org/10.1007/s11005-017-0936-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-017-0936-0