1 Introduction

Efficient management and monitoring of groundwater systems require the integrated interpretation of all sources of available data during the geo-modelling workflow. For sustainable groundwater management, and better prediction of the hydrogeological behaviour of such complex systems, we need to capture the small-scale variability of the subsurface geology, producing high-resolution aquifer models, while accounting for the uncertainties related to such spatial predictions. Despite the need for better groundwater modelling, the existing numerical models are still built from a limited data set, which is often composed exclusively of sparsely distributed direct observations (i.e., borehole data). The prediction of the hydrogeological properties of interest at relevant spatial scales for locations far from the observation points (i.e., the borehole locations) is therefore challenging and uncertain.

Spatial predictions of hydrogeological properties and groundwater characterization data can be performed using simple interpolation techniques (e.g., inverse quadratic distance, kriging) or more advance methodologies based on geostatistical simulation (Deutsch and Journel 1998). Prediction of the spatial variability of groundwater level is the most frequent implementation of geostatistical modelling. Common workflows involve interpolating the primary variable of interest (e.g., groundwater level), auxiliary correlated variables where applicable, and spatiotemporal analysis (e.g., Budiman et al. 2022; Rivest et al. 2008; Ruybal et al. 2019; Varouchakis et al. 2022). Hydraulic properties of aquifers have been spatially estimated using geostatistical modelling such as hydraulic conductivity (e.g., Zhang and Yang 2010; Jiang et al. 2021), porosity (e.g., Li et al. 2021; Osorno et al. 2022) and transmissivity (e.g., Al-Murad et al. 2018; Barbosa et al. 2019). These properties are fundamental for understanding groundwater flow and are essential for various hydrogeological and environmental applications. Geostatistical modelling has been also commonly used in contamination characterization of groundwater (e.g., Júnez-Ferreira et al. 2016; Messier et al. 2019; Zhao et al. 2016) and specifically in saltwater intrusion studies (e.g., Agoubi et al. 2013; Panagiotou et al. 2022). Geostatistical modelling plays a crucial role in understanding the spatial distribution of contaminants in the subsurface environment, assessing contamination risks, and making informed decisions about groundwater remediation and management.

For hydrogeological characterization studies and saltwater intrusion modelling, existing borehole data are frequently composed of one-dimensional electrical profiles acquired along the borehole path (i.e., vertical electrical sounding (VES)). For groundwater modelling and characterization, electrical conductivity (or electrical resistivity) measurements are relevant as they can be related to the type of pore fluid (i.e., brine versus fresh water) and, to a smaller extent, the type of subsurface lithology. These data are often the conditioning data (i.e., experimental data) used to model the spatial distribution of the saltwater intrusion. Octova et al. (2020) and Abdulkadir and Fisseha (2022) applied kriging to interpolate one-dimensional VES logs to predict the spatial distribution of geoelectrical resistivity. Co-kriging of electrical resistivity data and kriging with external drift was also performed by Calamita et al. (2017) and Troisi et al (2000) to explore aquifer and groundwater properties.

Within this context, geostatistical simulation methods are often preferable as they allow imposing a priori knowledge about the expected spatial continuity pattern through a spatial covariance matrix (i.e., a variogram model), the predicted models reproduce exactly the borehole data at its locations and the statistical properties as inferred from the set of direct observations. This set of methodological tools allows assessing the spatial uncertainty about the predictions by, for example, computing the pointwise variance model from a set of geostatistical realizations (e.g., Deutsch and Journel 1998; Azevedo and Soares 2017).

Uncertainty quantification for geostatistical applications, with a focus on electrical resistivity modelling, involves addressing the challenges and methods specific to geophysical data. Some key methods for uncertainty quantification in this topic include (i) stochastic sequential simulation methods, such as sequential Gaussian simulation, which can be used to generate multiple possible resistivity distributions and assess the range of uncertainties assuming a given spatial continuity pattern and the set of available observations, and (ii) Bayesian geostatistics, which combines geostatistical techniques with Bayesian inference to estimate resistivity models and associated uncertainties by integrating prior information and observed data (Santibañez et al. 2019; Boyd et al. 2019; De Clercq et al. 2020).

Although there is potential for geostatistical simulation methods to assess the spatial uncertainty of the predictions, their application is limited to the a priori assumptions regarding the number and location of direct observations (i.e., borehole) and the imposed variogram model. Alternative scenarios can be created to increase the exploration of the model parameter space. This objective can be achieved for example by using a jackknife type of approach where multiple geostatistical realizations are generated by removing the data for one borehole at a time from the set of conditioning data. However, the combination of the multiple scenarios and associated uncertainties is not straightforward. For more informed risk assessment and decision-making, these scenarios require efficient integration into a single one.

The main contribution of this work is the proposed geo-modelling approach to integrate multiple scenarios generated from geostatistical simulation and retrieve an uncertainty envelope (e.g., the P10–P90 interval) that is weighted by the misfit between observed and predicted data (i.e., the misfit between the predictions at the borehole location excluded from the set of existing boreholes). The proposed workflow is based on two complementary methodological vectors. The first is geostatistical simulation to generate possible scenarios of the relevant subsurface properties (e.g., electrical resistivity) following a jackknife resampling method (Quenouille 1956). The second is the application of Bayesian model averaging (BMA) (e.g., Raftery et al. 2005) to integrate the multiple subsurface scenarios. This step is aimed at predicting more informed uncertainty intervals as revealed by the P10–P90 interval. Depending on the objectives of the study, alternative uncertainty envelopes could be used. The proposed methodology is illustrated with its application to a groundwater system threatened by saltwater intrusion. The aquifer is located in the Tympaki basin (Crete).

2 Methodology

The methodology proposed in this study aims to assess uncertainty when predicting the spatial distribution of the subsurface electrical resistivity from a set of resistivity borehole logs. The method is applied to characterize a complex coastal aquifer system located in the Tympaki basin (Crete). The proposed method has two main stages: (i) scenario generation with stochastic sequential simulation (Soares 2001) of electrical resistivity considering different sets of borehole data, and (ii) BMA to combine the different scenarios into one, while accounting for the uncertainty envelope of the geostatistical realizations generated in step (i) (Fig. 1). We describe below in detail each step of the proposed methodology.

Fig. 1
figure 1

Schematic representation of the proposed methodology. N represents the number of geological scenarios (i.e., number of borehole locations for the application example shown herein), Ns the number of geostatistical realizations per scenario. Multiple scenarios are combined using Bayesian model averaging (BMA). P10, P50 and P90 represent the 10th, 50th and 90th percentiles of the predicted distribution, respectively

Full size image

2.1 Scenario Generation with Stochastic Sequential Simulation

Alternative electrical resistivity scenarios are generated with geostatistical simulation (i.e., direct sequential simulation) (Soares 2001) considering different a priori information in terms of number and location of observations. The same spatial continuity pattern (i.e., variogram model) is kept constant in all the scenarios considered. Therefore, the uncertainty about the spatial continuity pattern is ignored. For each scenario, one borehole at a time is removed, following a jackknife resampling method (Quenouille 1956).

The jackknife method (Quenouille 1956) is a non-parametric resampling technique used to estimate parameter values and the corresponding variability. Given N observations in a data set, this sampling method removes a single observation from the conditioning data set and estimates the parameters considering the remaining observations. Thus, if a data set comprises N observations (i.e., boreholes in our application example), this approach will assume a total of N data sets, each one constrained by N − 1 observations.

In our application example, 16 scenarios (N = 16) were created by omitting a single, distinct borehole each time. For each scenario, a set of Ns geostatistical realizations (Ns=30) were generated. We restrict the number to 30 due to the lack of computational resources to compute the BMA in step 2 of the proposed methodology, but a larger value might be used to increase the reliability of the estimated uncertainty envelope. Per scenario, each realization is conditioned to the corresponding borehole data and to the spatial pattern imposed by a global variogram model estimated from the set of all available wells (i.e., the same variogram model was used in all the scenarios). This decision implies that no uncertainty was considered during the variogram modelling.

While in aquifer modelling studies sequential Gaussian simulation (SGS) (Deutsch and Journel 1998) is the most common stochastic sequential algorithm for modelling the spatial distribution of continuous variables, such as electrical resistivity, here we opted for direct sequential simulation (DSS) (Soares 2001) due to its implementation simplicity. SGS requires a Gaussian transform of the available direct measurement values, which might represent a drawback for multi-modal distributions. On the other hand, DSS does not require any transform, so the experimental data are used in their original domain. Briefly, in DSS, each location of the simulation grid is visited sequentially following a random path. At each location along the random path, a value of the variable to be simulated is drawn from a probability distribution function estimated directly from the experimental data and previously simulated values based on the kriging estimate and kriging variance. The stochastic sequential simulation finishes after all the locations of the random path are visited.

Each time the simulation runs, an alternative model is generated (i.e., a geostatistical realization) as the random path changes, and so the previously simulated data that are used as conditioning data for the simulation at a given location also change. Each geostatistical realization reproduces the observed data at its location, the probability distribution function of the electrical resistivity as inferred from the conditioning data set and the variogram models imposed during the stochastic sequential simulation.

2.2 Uncertainty Quantification

The set of Ns geostatistical realizations of electrical resistivity created within each scenario have limited capabilities to explore the spatial uncertainty of the subsurface electrical resistivity as the conditioning data (i.e., number of borehole data and variogram models) within each ensemble is constant. On the other hand, changing the set of conditioning data might have a great impact on the spatial prediction of the spatial distribution of subsurface electrical conductivity. To model the uncertainty jointly for all the scenarios, this work proposes BMA.

2.2.1 Bayesian Framework and Uncertainty Quantification

A Bayesian framework allows accounting for uncertainty in spatial prediction

$$ p\left( {m|O} \right) = \frac{{p\left( {O|m} \right)p\left( m \right)}}{{\mathop \smallint \nolimits_{m}^{{}} p\left( {O|m} \right)p\left( m \right){\text{d}}m}}, $$
(1)

where p(m|O) is the posterior probability distribution of the model given the observed data, p(O|m) is the data likelihood, p(m) is the initial prior probability distribution, and m is the space of the model. In our case, the likelihood of an aquifer model can be defined as the probability that the borehole data removed at a given scenario is equal to the prediction provided by the geostatistical simulation at that specific location. The likelihood is represented as

$$ p\left( {O|m} \right) = e^{ - M} , $$
(2)

where M is the misfit between simulated (i.e., predicted) and observed data. In the application example shown herein the misfit is computed between the predicted electrical resistivity from the stochastic sequential simulation and the observed borehole data at the location of the well removed from the conditioning data. M is defined as the least square norm (e.g., Arnold et al. 2013)

$$ M = \mathop \sum \limits_{L = 1}^{L} \frac{{[{\text{obs}}\left( {c_{i} } \right) - {\text{sim}}\left( {c_{i} } \right)]^{2} }}{{2\sigma_{i}^{2} }}, $$
(3)

where obs is the experimental data at model cell ci, sim is the simulated data at model cell ci, L is the number of data points, and \(\sigma_{i}^{2}\) is a representation of the observed data errors, assuming these data errors are independent and have a normal distribution.

The posterior probability distribution of the model (i.e., p(m|O)) represents the updated knowledge about the model m based on the observations O and the prior knowledge of the model. It can be numerically approximated using the neighbourhood algorithm–Bayes (NAB) approach (Sambridge 1999). NAB, which is based on the Markov chain Monte Carlo method, uses Voronoi cells to interpolate values of misfit away from the known sampled points (i.e., models in the parameter space), for which the likelihood is computed exactly, and a Gibbs sampler to estimate the posterior probability (Christie et al. 2006). The resulting ensemble of the model with their posterior probabilities can be used to estimate the confidence interval (e.g., P10–P90 interval) to describe the uncertainty envelopes for the aquifer spatial distribution.

2.2.2 Bayesian Model Averaging

BMA has been successfully applied to distinct scientific areas such as weather forecasting (Raftery et al. 2005) or oil production forecasting (Pickup et al. 2008). It is a technique applied with the purpose of inferring a single probability distribution function (PDF) that reflects the contribution of alternative PDFs as represented by the ensemble of geostatistical realizations generated under each scenario. The combination of the different PDF encompasses a weighted average of the individual predictions based on the uncertainty of predictions and variance between models. The PDF computed from BMA of a quantity y based on K models is given by

$$ p\left( {y|f_{1} , \ldots ,f_{k} } \right) = \mathop \sum \limits_{k = 1}^{k} w_{k} g_{k} (y|f_{k} ), $$
(4)

where fk is the prediction of model K, wk is the weight of model k, and \(g_{k} (y|f_{k} )\) is the PDF of y given the prediction fk. Assuming a normal distribution (Raftery et al. 2005), the BMA mean (E) is represent by

$$ E\left( {y|f_{1} , \ldots ,f_{k} } \right) = \mathop \sum \limits_{k = 1}^{k} w_{k} f_{k} . $$
(5)

The posterior weights, wk, are calculated as

$$ w_{k} = \frac{{B_{kj} }}{{\mathop \sum \nolimits_{i = 1}^{k} B_{ij} }}, $$
(6)

where \(B_{kj}\) is the Bayes factor of model k regarding the assumed best model j (i.e., maximum likelihood). The wk weight each scenario for the calculation of the models corresponding to each scenario based on the misfit between observed and predicted data.

The Bayes factor assumes independent conditional distributions and allows one to compare the validity of the different models according to their data. It can be calculated using Laplace’s method (Kass and Raftery 1995)

$$ B_{kj} = \frac{{p( {\tilde{O}} |m_{k} )}}{{p({\tilde{O}} |m_{j} )}}, $$
(7)

where \(p(\ {\tilde{O}} |m_{x} )\) is the posterior probability of model x around the maximum likelihood model.

Based on the likelihood between the omitted borehole data and the predicted data at the corresponding borehole location, BMA was used to combine the uncertainty envelopes of the predictions of spatial distribution of electrical resistivity for each scenario into a global prediction. The application example below shows the combined P10–P50–P90 interval. Alternative intervals could be used; for example, the P5–P95 interval would allow the consideration of more extreme scenarios. The P10–P90 interval explains 80% of the uncertainty through all N scenarios and encompasses the most likely areas of the models predicted in the stochastic sequential simulation of the jackknife scenarios.

The methodology proposed herein, and applied in the real case application example shown below, can be summarized by the following sequence of steps (Fig. 1):

  1. (i)

    Modelling three-dimensional global variograms from experimental variograms computed directly from the existing electrical resistivity borehole data.

  2. (ii)

    Creation of N scenarios following a jackknife resampling method. For each scenario there is the omission of a single, distinct borehole from the conditioning data set in each of them.

  3. (iii)

    Generation of a set of Ns electrical resistivity models for each scenario using DSS and the corresponding borehole data as hard data. The spatial continuity pattern of the stochastic sequential simulation was imposed by the global variogram models computed in step (i).

  4. (iv)

    Application of the BMA to combine the uncertainty envelopes associated with the predictions of the spatial distribution of electrical resistivity for each scenario into a global one.

3 Application Example

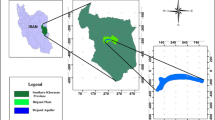
The proposed methodology was applied to model the saltwater intrusion into the groundwater system of the Tympaki basin, Crete. The aquifer is modelled from a set of 16 boreholes with electrical resistivity logs. Electrical resistivity logs are well known for their ability to distinguish water masses with different ionic composition (i.e., fresh versus salt water). These logs were acquired from a postprocessing procedure of data from an electromagnetic campaign carried out on the western and onshore area of the Tympaki basin (Greece) (Pipatpan and Blindow 2005). As the geophysical campaign did not cover the entire spatial extent of the basin, the proposed methodology was applied to the coastal region located in the western part of the full basin. The study area is defined as the spatial extent in which the borehole’s electrical resistivity logs are spatially correlated (Fig. 2).

Fig. 2
figure 2

Location of the 16 electrical resistivity wells obtained from the electromagnetic campaign carried out near the shore of Tympaki basin (Crete, Greece)

Full size image

3.1 Data Set Description

The Tympaki basin is in the southwestern tip of the Heraklion prefecture in Central Crete (Greece) and covers a surface area of about 55 km2 (Fig. 2). The basin was morphologically differentiated into a coastal plain to the west and a hilly area to the east. Its average annual rainfall is 500 mm/year, with an average temperature of about 15 °C. The resultant moisture index is in turn very low, bordering on semi-arid conditions. Despite these unfavourable climatic conditions, the basin is the centre of intense agricultural activity. More than 4000 hectares are cultivated, predominantly with olive trees and greenhouse vegetables, and most of them are irrigated.

A water reservoir of 17,000,000 m3 has been operating in the area since 2013 to cover the needs of the Tympaki basin and the Messara plane upstream. However, in Tympaki basin, irrigation is performed mainly by groundwater extraction, amounting to 7,000,000 m3 per year. Due to overpumping, the groundwater level has decreased more than 20 m in the last two decades, resulting in seawater intrusion in the aquifer and a major water supply problem in the area (Special Secretariat for Water Greece 2017).

According to recent studies (Special Secretariat for Water Greece 2020), the toe of the saltwater intrusion front lies 550 to 600 m from the coastline, while at the northern end of the coast, the toe of the saltwater intrusion front is located 1500 m from the coastline. This apparent differential behaviour of seawater intrusion between the southern and northern part of the coast is attributed to the complex hydrogeology of the northern part and effects of the Geropotamos river infiltration recharge which represents 36% of the total recharge of the basin. To balance the water pumping, a dam was constructed and recently became fully operational. Irrigation water is also supplied from surface resources (Varouchakis 2017).

4 Results and Discussion

To apply the proposed modelling methodology, the three-dimensional variogram model of the subsurface electrical resistivity was estimated directly from the electrical resistivity data for the 16 boreholes. First, experimental variograms were computed from these data along the N–S, E–W and vertical directions, representing the directions of maximum continuity. Then these experimental variograms were eye-fitted with a spherical variogram model for all directions considered (Fig. 3). Several variogram models were tested and fitted to the experimental variogram. We chose a spherical variogram model based on the experimental variograms for the horizontal direction and considering the known hydrogeological characteristics of the aquifer. The variogram model selected for the vertical direction (Fig. 3c) is a compromise with both horizontal directions. The ranges for the variogram model are 3750 m for the major direction, 3250 m for the minor direction, and 16 m for the vertical directions (Fig. 3).

Fig. 3
figure 3

Three-dimensional experimental variograms computed directly from the electrical resistivity borehole data and spherical model fitted for the a major, b minor, and c vertical directions

Full size image

Considering the available boreholes, 16 scenarios were created by omitting a distinct well in each set of geostatistical simulations (Table 1). For each scenario, we created 30 realizations of electrical resistivity models using DSS conditioned to the corresponding predefined set of borehole data (Table 1) and accounting for the spatial continuity as represented by the previously computed global variogram models (Fig. 3). The imposed variogram model is, by default, reproduced at each single realization of electrical conductivity (Deutsch and Journel 1998). The decision about the number of realizations was based on the computational power required to compute the BMA.

Table 1 Description of the 16 scenarios considered
Full size table

The second step of the proposed methodol is based on BMA to estimate the posterior probability of each scenario. First, we calculate the Bayes factor (Eq. 7) for weighting the different scenarios based on the misfit (Eq. 3) between predicted electrical resistivity for the entire ensemble of geostatistical simulations at the blind borehole location. Figure 4 shows the recorded log samples along the vertical path of the existing boreholes and the prediction of the geostatistical realizations along the same grid cells. In general, the geostatistical realizations capture the true electrical resistivity log. However, the prediction for some scenarios fails to capture the vertical trend of the true recorded values (i.e., Sc5, Sc12, Sc14).

Fig. 4
figure 4

Comparison between observed and predicted electrical resistivity at the blind borehole location for all 16 scenarios considered [from Sc1 (a) to Sc16 (p)]

Full size image

The weight of each scenario in the BMA is presented in Fig. 5 by the normalized Bayes factor. Three scenarios (i.e., Sc2, Sc9 and Sc13) contribute the most for BMA due to their larger misfit between predicted and observed electrical conductivity (Fig. 4b, i and m). The larger the misfit, the larger the contribution of the scenario towards the integrated uncertainty envelope.

Fig. 5
figure 5

Normalized Bayes factor used for Bayesian model averaging of the 16 scenarios considered

Full size image

With the Bayes factor for each scenario, the PDF accounting for all scenarios can be predicted by the BMA (Eq. 4) for each cell of the model. As an illustrative example, Fig. 6 shows the comparison between the experimental cumulative distribution function (ecdf) of each scenario and the one obtained with BMA for a single-cell model. The ecdf of the BMA does not represent the average ecdf of all the experimental ecdfs, but takes into account the Bayes factors (i.e., weights) associated with each scenario (Fig. 6). As expected, the ecdf of the BMA is closer to the experimental one resulting from scenario Sc2. The same procedure can be adopted for the full model considering all cells with the model (Fig. 7). Figure 7 compares the predicted electrical resistivity of the P10–P50–P90 interval of each scenario and the one obtained with the BMA. The effect of the computed Bayes factor in the P10–P50–P90 interval is easily interpreted for example by the difference between the P50 curve and the average curve of all P50 scenarios. As for the single-cell example (Fig. 6), the BMA cdf curves for the entire model are weighted by the Bayes factor for each scenario.

Fig. 6
figure 6

Comparison between the ecdf computed from the 30 realizations of each scenario and the one obtained by BMA for a single cell inside the aquifer model

Full size image
Fig. 7
figure 7

Comparison between the P10–P50–P90 interval computed from the 30 realizations of each scenario and the ones obtained by BMA for the full model

Full size image

Figure 8 shows horizontal slices parallel to the top of the aquifer model to illustrate the spatial distribution pattern of electrical resistivity within the uncertainty interval considered (i.e., the P10–P50–P90 interval). The spatial continuity of electrical resistivity decreases as we move from the P10 model into the P90. Note that these models do not represent a single realization but are created from the set of realizations for all the scenarios considered. As the electrical resistivity of the subsurface is directly related to the salt concentration in the water filling in the rock pore space, a 5 Ω m cutoff is applied to the P10–P50–P90 models predicted by the BMA. As expected, the spatial continuity of the saltwater intrusion predicted by the P90 model is highest.

Fig. 8
figure 8

Comparison between the top of the predicted electrical resistivity for the model represented by a P10, b P50, c P90

Full size image

The saltwater models (Fig. 9) show the distinct behaviour of the north and south areas of the model. The three scenarios include two extended sections where cells with resistivity values less than 5 Ω m can be found. In these areas, major fractures exist that facilitate the saltwater intrusion into the plane. These results agree with those published by Panagopoulos et al. (2021). Low resistivity levels in the coastal region can be attributed to seawater intrusion, originating from the increased usage of groundwater for irrigation. These models also agree with studies by Vafidis et al. (2013) that found seawater intrusion for the same location. For areas closer to the mainland, low resistivity values should be attributed to either the presence of groundwater or to clayey lithologies, which often have low values (Vafidis et al. 2013). Furthermore, the resulting electrical resistivity spatial distribution in the study basin agrees with the ones developed using the numerical models MODFLOW and FEFLOW simulation (Soupios et al. 2015; Dokou et al. 2016; Panagopoulos et al. 2021).

Fig. 9
figure 9

Three-dimensional view of the spatial distribution of electrical resistivity greater than 5 Ω m for the BMA models corresponding to a P10, b P50, c P90

Full size image

According to the comparison between the original, electrical resistivity and stochastic realizations of the corresponding field obtained using the aforementioned procedure, the BMA prediction enables the creation of reliable estimates of both the local- and regional-scale electrical resistivity distribution. Contrary to alternative weighting approaches that allow the computation of the P10–P90 interval, the BMA allows one to integrate the misfit between observed and predicted data when interpolating the ensemble of realizations to generate the pointwise probability models. This feature enables better prediction of the uncertainty envelope.

The capacity of the suggested method to produce realizations at a low computational cost in comparison to more rigorous and/or comprehensive approaches is perhaps its greatest advantage (Nussbaumer et al. 2019). Some of the benefits of adopting a three-dimensional geostatistical and simulation model in hydrogeology include the outcomes mentioned above. Even if a three-dimensional geostatistical model honours the input-real data, it is built in part using assumptions, particularly when the input data are constrained. Although three-dimensional modelling is still one of the greatest methods, the final three-dimensional model should always be considered an approximation. The predicted resistivity models were used to derive the fluid-relevant subsurface properties to create the final aquifer model. Areas of low resistivity that might be connected to seawater intrusion processes can be found using the electrical resistivity property model.

As with any Bayesian procedure, the accuracy and dependability of the previous knowledge have a significant impact on the final outcomes. The availability of more borehole data tends to increase the accuracy of such prior knowledge. However, if the prior is based, as in our case, on only a small number of borehole locations, then the uncertainty representativeness of the posterior results is the key factor in determining how efficient the prior is (Ruggeri et al. 2013). The main advantage of the proposed method is the ability to predict uncertainty bounds for each cell of the model. This uncertainty interval is dependent on the misfit between observations and predictions at specific locations within the model. More informed uncertainty bounds allow for better risk assessment and consequently better decision-making.

5 Conclusions

Sampling exhaustively complex natural systems such as the aquifer presented in this study is impossible due to administrative and technical factors. To close these gaps, a ground survey was conducted; however, the density of data gathered by ground geophysical techniques does not cover the entire area extent. Therefore, a geostatistical approach was successfully employed which estimated the electrical resistivity parameter on the unmeasured location. To achieve this objective, we created a two-step Bayesian-based sequential simulation approach that is intended for the typical situation where there are sparsely distributed borehole data (i.e., direct measurements of the property of interest) of a governing geophysical parameter such as the electrical resistivity over a large area. The results, however, are simply a preliminary step of the application of the proposed method (BMA-sequential simulation) in the extraction of subsurface data at aquifer units. The method created in this study not only offers reliable values to close the data gap, but it can also be used to cut the time and expense associated with the exploitation of geophysical data. In this work the resistivity values were combined to create the final three-dimensional property model. The spatial distribution analysis of the available data provided areas of low resistivity that might be connected to seawater intrusion processes. This work can help the development of a reliable groundwater model to investigate future electrical resistivity fluctuations at the study area under climate change scenarios.