Introduction

Groundwater, as a critical source of freshwater, has a vital role in coastal regions and needs to be assessed against threats. In coastal regions, aquifers are important sources of water supply for domestic, industrial and agricultural consumption. Nowadays, high demand from the coastal groundwater systems has increased the pressure on these resources (Oude Essink et al. 2010; Ketabchi et al. 2016b; Karamouz et al. 2017, 2020; Klassen and Allen 2017). Saltwater intrusion (SWI) is a main problem in many coastal regions (Post et al. 2018). Also, submarine groundwater discharge (SGD), which is the exchange of groundwater between the land and sea, involves the associated fluxes of nutrients. Further, high water demand causes increase in the groundwater withdrawal and the added stress to coastal aquifers and ecosystems (Small and Nicholls 2003; Moore 2010; Yao et al. 2019; Mahmoodzadeh and Karamouz 2019). In some coastal urban areas such as Nassau County in Long Island, New York (USA), groundwater is the main source of domestic water supply (Suozzi 2005). Protection of this groundwater resource is needed to guarantee a sustainable domestic water source for locals. Therefore, it is important to assess the risk of groundwater pollution in these coastal regions, which could support decision-making in the planning and management of local water resources (Zeng et al. 2016; Lal and Datta 2019; Ketabchi and Ataie-Ashtiani 2015a, b; Moreno et al. 2020).

In coastal regions, the groundwater system is usually recharged by direct infiltration from precipitation and surface-water resources. The regional flow of groundwater is commonly toward the ocean, but saltwater intrudes into the aquifers at many locations (Motallebian et al. 2019). Submarine groundwater discharge (SGD) to the ocean includes water flow on continental margins from the seabed to the ocean (Burnett et al. 2003; Moore 2010); moreover, SGD is associated with fluxes of nutrients that can damage coastal ecosystems (Slomp and Van Cappellen 2004; Moore 2010; Zhou et al. 2019). Coastal aquifers are affected by decreasing groundwater levels which can cause subsidence and serious damage to infrastructures (e.g., Minderhoud et al. 2017). Saltwater intrusion threatens the quality of fresh groundwater resources that are used for drinking water. Coastal aquifers are sensitive to natural processes, climate change effects including sea-level rise, and human interventions such as over-pumping (Oude Essink et al. 2010). A comprehensive review of factors that affect SWI and SGD is given by Moore (2010), Werner et al. (2013), and Ketabchi et al. (2016a).

Many researchers are dealing with modeling of the afore-mentioned threats to quantify their impacts on the groundwater system, while mostly they do not incorporate the risk concepts in the modeling of coastal aquifers. In this concept, risk is determined as the product of the probability of occurrence of an event and the associated consequence (Klassen and Allen 2017). Also, the modeling results are affected by simplifications and assumptions about the groundwater system that are not true for many real-world applications. For instance, considering the same hydraulic conductivity value for each geological layer of a groundwater system is a (very) simple assumption, increasing the uncertainty (Mahmoodzadeh and Karamouz 2017, 2019). Due to the inherent heterogeneity of aquifers, there are several other unavoidable sources of uncertainty such as estimates of hydraulic conductivity, recharge and pumping, in the groundwater models. Therefore, uncertainty analysis should be considered in SWI models (Rajabi and Ketabchi 2017; Mostafaei-Avandari and Ketabchi 2020); thus, the analysis of risk for coastal aquifers under present uncertainties, and quantification of potential threats to the groundwater system, is important.

The risk concept has been mostly associated with natural disasters, and a risk-based modeling framework has not typically been applied to the field of coastal hydrogeology. A few studies have considered the risk concept in the coastal groundwater field and applied the concept through different objectives. Recently, Mostafaei-Avandari and Ketabchi (2020) applied a numerical model to determine optimal net recharge rates on each groundwater management zone in a real-case coastal aquifer in Ajabshir, Iran. In that study, the uncertainty is considered only in hydraulic conductivity, and the risks under the threat of decreasing groundwater level and the existence of SWI were not considered. In this context, steps for groundwater pollution assessment were investigated by Massone and Barilari (2019). Their first step introduced the assessment of aquifer vulnerability; in the second step, methodological approaches were developed with regard to risk assessment. Technology and associated approaches were incorporated into the third step. They emphasized that the greatest challenge is to consider the risk of groundwater pollution through an integrated approach.

Eriksson et al. (2018) used a mapping method to estimate the risks of well salinization and the impacts of sea-level rise on the Baltic Sea island of Öland, Sweden. They found that hydrology, geomorphology, and climatology parameters have a significant impact on the risk of SWI. This study highlighted that a salinization risk map, could be useful for decision-makers in the planning of infrastructure. Klassen and Allen (2017) also used a mapping method for quantification of the risk of SWI under natural threats such as sea-level rise and storm surge, and human interventions such as over-pumping, in the Gulf Islands in British Columbia, Canada. They assessed the vulnerability of the aquifer to SWI spatially, by mapping threats considering the aquifer susceptibility. In their study to characterize aquifer susceptibility to SWI, distance from the coast, topographic slope, and groundwater flux were used. Risk assessment maps were useful tools for classifying areas vulnerable to SWI; however, these studies were limited to analytical methods and did not consider the uncertainty analysis of model input parameters.

Holding and Allen (2015, 2016) applied a numerical model to assess the risk to water security at low-lying Andros Island, Florida, USA. They presented areas of increasing risk to water security. The risk maps provided useful information to policy makers to identify high-risk areas. In that study, the uncertainty of the model input parameters (variables) was not considered and limited to defining only the risk under water security.

Zeng et al. (2016) used numerical modeling to assess the pollution risk to the groundwater source of western Laizhou Bay, Shandong province, China. Their modelling results demonstrated that the sampling algorithm based on Markov Chain Monte Carlo simulations was efficient and reliable to estimate the model parameters using observed data. Also, their results showed that within the 95% confidence level, the groundwater system would not be threatened by SWI within the coming 5 years. In that study, the pollution risk to a groundwater source point is assessed under some assumptions which include the simplification of the SWI model and aquifer heterogeneity. Also, the pollution risk is described only by one indicator (i.e. SWI).

Simpson et al. (2014) developed a risk assessment framework for water protection purposes in the Township of Langley, in British Columbia, Canada. They studied risk assessment with respect to groundwater quality associated with different land uses at the ground surface due to man-made interventions. They showed maps of risk to the aquifer and demonstrated that the more vulnerable areas have potential chemical and biological threats. Thorn (2011) used the measurement method to evaluate the risk of SWI on a fractured chalk aquifer in Greve, Denmark. They showed how the geochemical analysis could be used to identify areas at risk of SWI and to determine the source of salinity. Their results showed that diffusion from connate formational waters and SWI were the sources of salinity in the study area. However, these studies were limited to analytical methods and did not consider uncertainty analysis of the model input parameters.

A review of studies has shown that there has been a limited number investigation that considered the risk analysis of coastal aquifers. These studies considered the risk analysis under one numerical indicator (i.e. water security or SWI). Of these, in the studies of Holding and Allen (2016) and Nobre et al. (2007), the uncertainty of the model input parameters (variables) was not considered. Also, in the studies of Holding and Allen (2016), Zeng et al. (2016) and Nobre et al. (2007), the heterogeneity of the aquifer and quantitative indices to assess the risk to the groundwater resources under different threats were not considered.

Risk-based groundwater modeling is required to understand and manage groundwater resources with the purpose of predicting long-term and short-term impacts. The contribution of this paper is to consider the risk analysis concerning the decreasing groundwater levels, SWI based on the salinity concentration and the so-called filling ratio, and SGD, which can threaten the quality and quantity of coastal aquifers and ecosystems. SWI based on the filling ratio is a percentage of the occupied volume by saltwater (for example 50% of salinity concentration of saltwater) to the total volume of the considered aquifer. In this study, a risk-based groundwater modeling framework is developed in which the main feature is the ability to consider the uncertainty in the hydraulic conductivity and recharge rate parameters in a real-world setting. Numerical modelling is performed within a Monte Carlo framework with a Latin hypercube sampling (LHS) algorithm. Four indices are formulated to quantify the risk in the coastal groundwater system, located in Nassau County, Long Island, to obtain susceptible areas to control SWI and decreasing groundwater level. Based on the reviewed studies, such a risk-based groundwater modeling framework has not yet been applied to a real-case coastal groundwater system considering geological heterogeneity.

The rest of the paper is organized as follows: the risk-based groundwater modeling framework is described. Next, the study area, numerical simulations, and indices are described. Then, the risk to the groundwater system under decreasing groundwater level, SWI, and SGD are assessed and discussed. Finally, the main conclusions are drawn from the analysis.

Methodology

The risk-based groundwater modeling framework for this study is shown in Fig. 1. In this framework, after developing a conceptual model based on the collection of data and information, uncertainty analyses are applied to a real-case study, with a three-dimensional (3D) numerical model, simulating variable-density groundwater flow and coupled salt transport. The simulation component of the uncertainty analyses consists of Monte Carlo simulations (MCSs) followed by a risk analysis based on defined indices. All abbreviations and mathematical terms are defined in the Appendix.

Fig. 1
figure 1

The risk-based groundwater modeling framework

Full size image

Numerical simulation approach

The variation of spatial and temporal fresh and salt groundwater is simulated with a 3D variable-density groundwater model, SEAWAT code (Langevin et al. 2008). Many studies have previously applied this code to simulate variable-density, transient groundwater flow and coupled salt transport, in coastal regions (e.g., Rasmussen et al. 2013; Holding and Allen 2016; Colombani et al. 2016; Huizer et al. 2018).

SEAWAT solves the fluid and the solute equations simultaneously with a cell-centered finite difference approximation to characterize variable-density flow associated with SWI. The fluid equation (Eq. 1) demonstrates the single-phase flow in a porous medium and the solute equation (Eq. 2) describes the solute transport including advection and dispersion mechanisms (Langevin et al. 2008).

$$ \nabla \cdotp \left[\rho \frac{\mu_0}{\mu }{K}_0\left(\nabla {h}_0+\frac{\rho -{\rho}_0}{\rho_0}\nabla \mathrm{z}\right)\right]=\rho {S}_{\mathrm{s},0}\frac{{\partial h}_0}{\partial t}+\theta \frac{\partial \rho }{\partial C}\frac{\partial C}{\partial t}-{\rho}_{\mathrm{s}}{q}_{\mathrm{s}}^{\prime } $$
(1)
$$ \left(1+\frac{\rho_{\mathrm{b}}{K}_{\mathrm{d}}^k}{\theta}\right)\frac{\partial \left(\theta {C}^k\right)}{\theta t}=\nabla \cdotp \left(\theta d\cdotp \nabla {C}^k\right)-\left(q{C}^k\right)-{q}_{\mathrm{s}}^{\prime }{C}_{\mathrm{s}}^k $$
(2)

where ρ0 is the fluid density [M/ L3] at the reference concentration and reference temperature, μ is dynamic viscosity [M/L.T], K0 is the hydraulic conductivity tensor of material saturated with the reference fluid [L/T], h0 is the head [L] measured in terms of the reference fluid of a specified concentration and temperature, Ss,0 is the specific storage [1/L], θ is porosity [−], C is salt concentration [M/L3], \( {q}_{\mathrm{s}}^{\prime } \) is a source or sink [1/T] of fluid with density ρs, ρb is the bulk density [M/L3], \( {K}_{\mathrm{d}}^k \) is the distribution coefficient of species k [L3/M], D is the hydrodynamic dispersion coefficient tensor [L2 /T], Ck is the concentration of species k [M/L3], q is specific discharge [L/T], and \( {C}_{\mathrm{s}}^k \) is the source or sink concentration [M/L] of species k.

In this study, the calibration procedure is done using an automated parameter estimation code, PEST (Doherty 2005). The model is calibrated for steady-state groundwater level (head) and solute (chloride concentration). Due to limited observation information on chloride concentration, calibration and validation of the transient model are performed for groundwater level. A primary adjustment of model input parameters and variables, i.e. the hydraulic conductivity and recharge rate, is made to reduce the difference between the observed and the simulated groundwater level.

Uncertainty and risk analysis approaches

Monte Carlo simulations as a sampling-based method is most widely used for uncertainty analysis, with a wide range of applications in different fields such as SWI modeling (see Rajabi and Ketabchi 2017; Mahmoodzadeh and Karamouz 2019). In this approach, mathematical problems are solved by the simulation of random variables. MCSs have been employed to analyze the propagation of uncertainty from input variables/parameters such as hydraulic conductivity, porosity, recharge and pumping rate, to output quantities such as simulated head and concentration. The uncertainty of input is considered through the definition of a probability density function.

The limitation of the Monte Carlo method is the efficacy of the result, which depends on a large number of samples to get an acceptable representation of the distribution function. In overcoming this problem and to reduce the required number of MCSs, sampling selection methods such as LHS algorithm are used (see previous studies like Lassila et al. 1999; Baalousha 2003; Dimov 2008; Rajabi and Ataie-Ashtiani 2014). LHS is known as a stratified Monte Carlo sampling method. In this method, the domain of each random variable/parameter is divided into the interval with the same probability in all the intervals. From each interval, a value is randomly selected regarding the probability density in the interval. In this study, the hydraulic conductivity and recharge rate are considered to be uncertain input parameters. Also, the LHS algorithm is employed to generate the samples.

Based on the results of MCSs, the probability of failure is evaluated. For estimating the probability of a failure event, a realization for a random variable based on the probability distribution function is generated. Then, the performance function based on the simulation model for each random variable x is assessed. The following function can be identified by (Press et al. 1992):

$$ I(x)=\left\{\begin{array}{c}1\kern0.5em \mathrm{if}\kern0.5em G(x)<0;\kern1.25em \mathrm{The}\ \mathrm{system}\ \mathrm{has}\ \mathrm{failed}\kern3em \\ {}0\ \mathrm{if}\kern0.75em G(x)\ge 0\kern2.75em \mathrm{Otherwise}\kern7.25em \end{array}\right. $$
(3)

where I(x) is the output of the simulation model for each random variable x, and G(x) is the performance function. The probability of failure is estimated as follows:

$$ {P}_{\mathrm{f}}={\int}_{G(x)<0}{f}_x(x) dx $$
(4)

where Pf is the probability of failure and fx(x) is the probability density function of the random variables x. Based on Eqs. (3) and (4), the probability of failure is calculated for each realization as follows:

$$ E\left[{P}_{\mathrm{f}}\right]=\frac{1}{N_{\mathrm{MCS}}}\ {\int}_{n=1}^{N_{\mathrm{MCS}}}{P}_n;{P}_{\mathrm{f}}=\frac{N_{\mathrm{f}}}{N_{\mathrm{MCS}}} $$
(5)

where Nf is the number of failures and NMCS is the total number of MCSs.

The risk is determined by the product of two components (Eq. 6) which are the probability of an event and the proposed potential consequences/loss (Klassen and Allen 2017). The two components of risk, namely the probability of a failure event and the severity of a failure event, are required to be quantified for all indices.

$$ \mathrm{Risk}\left({R}_m\right)={C}_m\times P\left({C}_m\right) $$
(6)

where Cm is the indicating characteristic of potential loss and P(Cm) is the probability of the potential loss. Also, m denotes a specific event. The probability of a failure event is the exceedance of an indicator defined to monitor the groundwater resources, based on the MCSs from a certain threshold. The threshold represents the allowable level of risk and the severity of a failure event is the difference between the simulated and the allowable conditions of the index. The allowable level of risk and the severity of a failure event are described in the following subsections for each index.

Description of indices

Quantitative indices are used to assess the risk of the current state of groundwater resources considering different threats. The four indices are (1) the depletion of groundwater level (HGWL); (2) salinity concentration (Cswi) of the groundwater system; (3) volume of SWI based on the filling ratio (FRswiv); and (4) the average contamination load discharged through SGD (CLSGD). Although the second and third indices represent the SWI, different practical concepts are introduced for each location and each layer of the study area. These indices can provide a basis to develop sustainable management decisions.

Decrease of groundwater level

In the first index, the objective is defined to assess the risk of the decrease of groundwater level. The probability of exceedance of the groundwater level [−], denoted by \( P\left({H}_{\mathrm{GWL}}^{x,y}\right) \), is defined from a certain threshold as:

$$ {\displaystyle \begin{array}{c}P\left({H}_{\mathrm{GWL}}^{x,y}\right)=\frac{\int_T{N}_{MCS}^{H_t^{x,y}\le {H}_t^{\mathrm{allow}}}}{T\times {N}_{\mathrm{MCS}}}\\ {}{H}_t^{\mathrm{allow}}={H}_{\min, t,k}^{\mathrm{x},\mathrm{y}}=\min \left({H}_{t,k}^{x,y}\right)\end{array}} $$
(7)
$$ {\displaystyle \begin{array}{c}L\left({H}_{\mathrm{GWL}}^{x,y}\right)=\frac{\int_T{\int}_K\Delta {H}_{t,k}}{T\times {N}_{\mathrm{MCS}}}\\ {}\Delta {H}_{t,k}=\left\{\begin{array}{c}{H}_t^{\mathrm{allow}}-{H}_{t,k}^{x,y}\kern0.5em \mathrm{if}{H}_{t,k}^{x,y}\le {H}_t^{\mathrm{allow}}\\ {}0\kern0.5em \mathrm{if}{H}_{t,k}^{x,y}>{H}_t^{\mathrm{allow}}\end{array}\right.\end{array}} $$
(8)

where \( {N}_{\mathrm{MCS}}^{H_t^{x,y}\le {H}_t^{\mathrm{allow}}} \) is the total number of MCSs resulting [−] in the decrease of groundwater level below \( {H}_t^{\mathrm{allow}} \) in each location of the groundwater system (i.e. x,y), NMCS is the total number of MCSs, T is the total number of assumed stress periods, \( {H}_t^{\mathrm{allow}} \) represents the allowable decrease of the groundwater level [L] and is assumed to be \( \left(1\pm \alpha \right)\times {H}_{\min, t,k}^{x,y} \) where (1 ± α) is the confidence level for the interval, t is the stress period [T], and \( {H}_{\min, t,k}^{x,y} \) is the minimum groundwater level [L] among all number of realizations under the zero-extraction scenario (it comprises lower bounds that bracket a future unknown value with a certain confidence level). In this study, the zero-extraction scenario (as the natural condition without human-induced groundwater extraction) is defined as the condition whereby groundwater withdrawal using pumping wells not happen throughout the simulation period. \( L\left({H}_{\mathrm{GWL}}^{x,y}\right) \) is the severity of the failure event [−] and is defined as the difference (denoted by ∆Ht,k) between the decrease of \( {H}_t^{\mathrm{allow}} \) and the decrease of groundwater level at each location in the aquifer in the tth stress period, for the kth realization. The counter K is the total number of realizations (equal to 150).

Salinity concentration

Salinity concentration in each location of the groundwater system is calculated with a certain threshold (denoted by CTr) and defined as SWI:

$$ {\displaystyle \begin{array}{l}{C}_{\mathrm{swi},t}^{x,y,z}=\left\{\begin{array}{c}{C}_t^{x,y,z}\\ {}0\end{array}\right.\begin{array}{c}\mathrm{if}\ {C}_t^{x,y,z}\ge {C}_{\mathrm{Tr}}\\ {}\mathrm{if}\ {C}_t^{x,y,z}<{C}_{\mathrm{Tr}}\end{array}{C}_{\mathrm{Tr}}=0.002{C}_{\mathrm{SW}},0.05{C}_{\mathrm{SW}},0.5{C}_{\mathrm{SW}},\mathrm{and}\ 0.95{C}_{\mathrm{SW}}\\ {}\end{array}} $$
(9)

where\( {C}_{\mathrm{swi},t}^{x,y,z} \)is the salinity concentration [M/L3] at each location and depth in the groundwater system, i.e. x,y, and z, and CTr is a threshold for the commonly used 0.2, 5, 50, and 95% of salinity concentration of saltwater (Csw) [M/L3] (see Mahmoodzadeh and Karamouz 2019). The salinity concentration equal to 0.2% saltwater is defined as potable fresh groundwater (NYSDOH 2003).

The probability of exceedance of salinity concentrations at each location in the aquifer is defined from a certain threshold as:

$$ {\displaystyle \begin{array}{c}P\left({C}_{\mathrm{swi}}^{x,y,z}\right)=\frac{\int_T{N}_{\mathrm{MCS}}^{C_{\mathrm{swi},t}^{x,y,z}\ge {C}_{\mathrm{swi},t}^{\mathrm{allow}}}}{T\times {N}_{\mathrm{MCS}}}\\ {}{C}_{\mathrm{swi},t}^{\mathrm{allow}}={C}_{\max, \mathrm{swi},t}^{x,y,z}=\max \left({C}_{\mathrm{swi},k,t}^{x,y,z}\right)\end{array}} $$
(10)
$$ {\displaystyle \begin{array}{l}L\left({C}_{\mathrm{swi}}^{x,y,z}\right)=\frac{\int_T{\int}_K\varDelta {C}_{t,k}}{T\times {N}_{\mathrm{MCS}}}\\ {}\varDelta {C}_{t,k}=\left\{\begin{array}{cc}{C}_{\mathrm{swi}}^{x,y,z}-{C}_{\mathrm{swi},t}^{\mathrm{allow}}& \mathrm{if}\kern1em {C_{\mathrm{swi},t,k}}^{x,y,z}\ge {C}_{\mathrm{swi},t}^{\mathrm{allow}}\\ {}0& \mathrm{if}\kern2.00em {C}_{\mathrm{swi},t,k}^{x,y,z}<{C}_{\mathrm{swi},t}^{\mathrm{allow}}\end{array}\right.\end{array}} $$
(11)

where \( P\left({C}_{\mathrm{swi}}^{x,y,z}\right) \) is the probability of exceeding the SWI [−] at each location in the aquifer, i.e. x,y,z, from a certain threshold (denoted by \( {C}_{\mathrm{swi},t}^{\mathrm{allow}} \)), \( {N}_{\mathrm{MCS}}^{C_{\mathrm{swi},t}^{x,y,z}\ge {C}_{\mathrm{swi},t}^{\mathrm{allow}}} \) is the number of MCSs resulting [−] in salinity concentrations of the SWI above the threshold, \( {C}_{\mathrm{swi},t}^{\mathrm{allow}} \) represents the allowable level of risk for salinity concentrations [M/L3] of SWI and assumed to be \( \left(1\pm \alpha \right)\times {C}_{\max, \mathrm{swi},t}^{x,y,z} \) where \( {C}_{\max, \mathrm{swi},t}^{x,y,z} \) as the maximum of salinity concentration [M/L3] among all realizations under zero-extraction scenarios, and \( L\left({C}_{\mathrm{swi}}^{x,y,z}\right) \) is the magnitude of the failure event [−] which is defined as the difference (denoted by ∆Ct,k) between the salinity concentrations (\( {C}_{\mathrm{swi},t,k}^{x,y,z} \)) and the \( {C}_{\mathrm{swi},t}^{\mathrm{allow}} \) (in the kth realization and the tth stress period).

Filling ratio

The volume of SWI based on the filling ratio (FR) index (Van Camp et al. 2010), defined as the ratio of the occupied volume by saltwater to total volume of the considered aquifer layer, is calculated according to Eq. (12).

$$ {\displaystyle \begin{array}{cc}{\mathrm{FR}}_{\mathrm{sw}\mathrm{iv}}^i=\frac{\int_T{\int}_J{V}_{j,t}^i}{T\times \theta \times {\int}_J{V}_j^i}& \forall i,\forall j,\forall t\\ {}{V}_{j,t}^i=\left\{\begin{array}{c}{V}_{j,t}^i\kern-0.10em \mathrm{if}\kern0.5em {C}_{j,t}^i\\ {}\begin{array}{ccc}0& \mathrm{if}& {C}_{j,t}^i<{C}_{\mathrm{Tr}}\end{array}\end{array}\right.& {C}_{\mathrm{Tr}}=0.002{C}_{\mathrm{sw}},0.05{C}_{\mathrm{sw}},0.5{C}_{\mathrm{sw}},\mathrm{and}\ 0.95{C}_{\mathrm{sw}}\end{array}} $$
(12)

where FRiswiv is the ratio of the occupied volume by saltwater in the ith model layer [−], \( {V}_{j,t}^i \) is the volume of SWI [L3] in the ith model layer, in the jth model cell, and in the tth stress period, Vij is volume of the model cell [L3], θ is porosity [−], \( {C}_{j,t}^i \) is the salinity concentration [M/L3], and CTr is a certain threshold for the salinity concentration [M/L3]. The threshold is defined by the exceedance of the salinity concentration in each model cell from specified thresholds, i.e. 0.02, 5, 50, and 95% of salinity concentration of saltwater. The counter i is the number of model layers (equal to 14), and j is the number of model cells in each model layer. To assess the risk of SWI, based on Eqs. (13) and (14):

$$ {\displaystyle \begin{array}{l}P\left({\mathrm{FR}}_{\mathrm{swiv}}^i\right)=\frac{N_{\mathrm{MCS}}^{FR_{\mathrm{swiv}}^i\ge {FR}_{\mathrm{swiv}}^{\mathrm{allow}}}}{N_{\mathrm{MCS}}}\\ {}{\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}}={\mathrm{FR}}_{\max, \mathrm{swiv}}^{i,z}=\max \left({\mathrm{FR}}_{\mathrm{swiv},k}^{i,z}\right)\end{array}} $$
(13)
$$ {\displaystyle \begin{array}{c}L\left({\mathrm{FR}}_{\mathrm{swiv}}^i\right)=\frac{\int_K\Delta {\mathrm{FR}}_{\mathrm{swiv},k}}{N_{\mathrm{MCS}}}\\ {}\Delta {\mathrm{FR}}_{\mathrm{swiv},k}=\left\{\begin{array}{ccc}{\mathrm{FR}}_{\mathrm{swiv},k}^i-{\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}}& \mathrm{if}& {\mathrm{FR}}_{\mathrm{swiv},k}^i\ge {\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}}\\ {}0& \mathrm{if}& {\mathrm{FR}}_{\mathrm{swiv},k}^i<{\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}}\end{array}\right.\end{array}} $$
(14)

where \( P\left({\mathrm{FR}}_{\mathrm{swiv}}^i\right) \) is the probability of exceeding the ratio of the occupied volume by saltwater [−] in the ith model layer from a certain threshold (denoted by \( {\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}} \)), and\( {N}_{\mathrm{MCS}}^{{\mathrm{FR}}_{\mathrm{swiv}}^i\ge {\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}}} \)is the number of MCSs resulting [−] in the filling ratio of SWI above \( {\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}} \). The threshold represents the allowable level of risk for the filling ratio of SWI and it is assumed to be \( \left(1\pm \alpha \right)\times {\mathrm{FR}}_{\max, \mathrm{swiv}}^{i,z} \). \( {\mathrm{FR}}_{\max, \mathrm{swiv}}^{i,z} \)is the maximum of filling ratio [−] among all realizations under the zero-extraction scenario, and \( L\left({\mathrm{FR}}_{\mathrm{swiv}}^i\right) \) is the severity of the failure event [−] which is defined as the difference (denoted by ∆FRk) between the ratio of the occupied volume by saltwater (\( {\mathrm{FR}}_{\mathrm{swiv},k}^i \)) and the \( {\mathrm{FR}}_{\mathrm{swiv}}^{\mathrm{allow}} \).

Submarine groundwater discharge

The average concentration of contamination (nitrate here) load discharged through SGD [M/T] (denoted by CLSGD), as discharging flow out of the aquifers to the sea, is calculated according to Eq. (15).

$$ {\mathrm{CL}}_{\mathrm{SGD}}=\frac{\int_T\overline{C}\times {\mathrm{SGD}}_t}{T}\kern2.5em $$
(15)

where \( \overline{C} \) is the average concentration [M/L3] (the average nitrate concentration in the study area), and SGDt is discharging flow out of the aquifers to the sea in each stress period [L3/T]. The probability of exceedance of the average contamination load that discharges through SGD to the sea from a certain threshold (denoted by \( {\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}} \)) is estimated as:

$$ {\displaystyle \begin{array}{c}P\left({\mathrm{CL}}_{\mathrm{SGD}}\right)=\frac{N_{\mathrm{MCS}}^{{\mathrm{CL}}_{\mathrm{SGD}}\ge {\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}}}}{N_{\mathrm{MCS}}}\\ {}{\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}}={\mathrm{CL}}_{\max, \mathrm{SGD},\mathrm{z}}^{\mathrm{allow}}=\max \left({\mathrm{CL}}_{\mathrm{SGD},\mathrm{z}}^{\mathrm{allow}}\right)\end{array}} $$
(16)
$$ {\displaystyle \begin{array}{c}L\left({\mathrm{CL}}_{\mathrm{SGD}}\right)=\frac{\int_K\Delta {\mathrm{CL}}_{\mathrm{k}}}{N_{\mathrm{MCS}}}\\ {}\Delta {\mathrm{CL}}_k=\left\{\begin{array}{ccc}{\mathrm{CL}}_{\mathrm{SGD},k}-{\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}}& \mathrm{if}& {\mathrm{CL}}_{\mathrm{SGD},k}\ge {\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}}\\ {}0& \mathrm{if}& {\mathrm{CL}}_{\mathrm{SGD},k}<{\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}}\end{array}\right.\end{array}} $$
(17)

where \( {N}_{\mathrm{MCS}}^{{\mathrm{CL}}_{\mathrm{SGD}}\ge {\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}}} \) is the number of MCSs resulting [−] in the average contamination load higher than \( {\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}} \) of the aquifer. The threshold represents the allowable level of risk for the contamination load and is assumed to be \( \left(1\pm \alpha \right)\times {\mathrm{CL}}_{\max, \mathrm{SGD},z}^{\mathrm{allow}} \). \( {\mathrm{CL}}_{\max, \mathrm{SGD},z}^{\mathrm{allow}} \) is a maximum contamination load [M/T] among all realizations under the zero-extraction scenario. L(CLSGD) is defined as the difference (denoted by ∆CLk) between the average contamination of the aquifer in the kth realization and the \( {\mathrm{CL}}_{\mathrm{SGD}}^{\mathrm{allow}} \).

Application

The proposed methodology is applied to a part of Nassau County in the state of New York, USA.

Study area

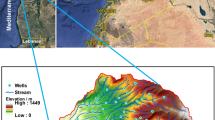
The study area has an area of 204 km2 and is located in Nassau County, on western Long Island between 40° 34′ to 40° 55′N latitude and 73° 44′ to 73° 34′E longitude (Fig. 2a). This area is dependent on groundwater meet residential, commercial, and industrial demands. The portion attributed to commercial and industrial demand is minimal (about 10%). The groundwater is critically important to the health and security of all residents (Suozzi 2005). In this area, the groundwater flows naturally towards the Atlantic Ocean and Long Island Sound on the south shore and on the north shore respectively, where it eventually encounters saltwater. Groundwater withdrawal and the decrease in groundwater levels has caused the quality of this groundwater to be threatened by SWI (Gulotta 1998; Suozzi 2005). It is important to monitor the groundwater system and to implement appropriate actions to address the SWI problem; therefore, the risk-based numerical modeling approach has been set up to understand the behavior of groundwater resources that face SWI and decreasing groundwater levels. Figure 2 shows a map of the study area and the locations of the multi-level observation wells (USGS 2019a, b, c) in Nassau County.

Fig. 2
figure 2

a map of the study area in Nassau County, New York, USA, and b the locations of the observation wells (map source: New York State, Earthstar Geographics, Esri, Garmin)

Full size image

In the study area, 36 observation wells are used to monitor groundwater levels and the extent of SWI in the three main aquifers. The main characteristics of the study area are summarized in Table 1. As shown in this table, the area’s climate is classified as humid subtropical. The long-term average (about 45 years) precipitation in Nassau County is approximately 1,117.6 mm/year. Accounting for groundwater extraction for consumption by residential, commercial, and industrial users, the net recharge to the groundwater system is estimated to be 29–57% of the average annual precipitation (Peterson 1987; Suozzi 2005).

Table 1 Main characteristics of the study area
Full size table

Geological setting

The geological units that contain fresh groundwater in Nassau County consist of three major aquifers: the Upper glacial, the Magothy, and the Lloyd. The geological layers of the study area are shown in Fig. 3. The Lloyd aquifer is a wedge of unconsolidated gravel, sand, silt and clay deposits, and it is underlain by consolidated rock. Above the Lloyd aquifer, there is a major relatively impermeable clay layer (the Raritan formation). This layer is overlain by the Magothy formation. Most of the Magothy formation consists of clay and silty fine to medium sand, some gravel, and thin clay layers. Overlying the Magothy formation, there are several units which include the Jameco gravel, the Gardiners clay, and the upper Pleistocene deposits (upper glacial formation). The Gardiners clay and Jameco in the upper part of the Magothy formation in some places cause a confining layer (Perlmutter and Geraghty 1963; Lusczynski and Swarzenski 1966). The type of material for each geological layer varies considerably from location to location and also varies considerably with depth. Generally, the Magothy and Lloyd aquifers are thickest below the south shore.

Fig. 3
figure 3

Geological setting including the geological layers, the aquifers and the aquitards as well as the average thickness values

Full size image

All geological layers and their thickness are schematized in Fig. 3. Smaller aquifers such as Jameco and clay layers such as Gardiners clay, increase the complexity of the groundwater system and affect aquifer behavior in parts of Nassau County. The geologic setting of Long Island and Nassau County is described in previous reports such as Perlmutter and Geraghty (1963); Lusczynski and Swarzenski (1966); Smolensky et al. 1989 and Suozzi (2005).

Groundwater recharge and withdrawal

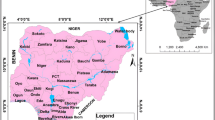
In the study area, the groundwater system is recharged by direct infiltration from precipitation as a natural source of freshwater. It is also recharged by return flows through onsite septic systems, leaking water-supply or sewer lines, and by infiltration into (mainly Magothy) aquifers by lateral flows, in the northern sections (Buxton and Smolensky 1999). The outflow from the groundwater system includes withdrawals from the aquifers through pumping wells, as well as submarine groundwater discharge. About 29–57% of the precipitation (depending on the land-cover type and degree of urban development), is recharged to the groundwater system, and the remaining water flows as surface runoff to streams or is lost through evapotranspiration (Peterson 1987; Cohen et al. 1968). The groundwater consumption is about 97% compared to surface-water supply and bottled water, and the water is delivered by the public water suppliers. As shown in Fig. 4, there are nine water districts in this area. About 20% (in the sewered areas) of the water pumped for public water supply is estimated to return to the groundwater system (Buxton and Smolensky 1999).

Fig. 4
figure 4

Water district areas in the study area (map source: New York State, Earthstar Geographics, Esri, Garmin)

Full size image

In each water districts, recharge by the infiltration of precipitation is estimated as a percentage of mean annual precipitation. Return flows are estimated and introduced into the simulation model with separate values for each water district. It is assumed that approximately 20–30% of the consumed domestic water returns to the aquifers (Suozzi 2005; Buxton and Smolensky 1999). Due to the high uncertainty associated with determining inputs and outputs, the estimates of recharge from precipitation and return flows are subjected to calibration in the simulation procedure. Fig. 5 shows the fluctuation of the average groundwater withdrawal for each month the long period of study. The average temperatures in the months of June, July and August are high (about 21–22 °C), and these conditions cause a considerably larger water demand than the base demand in the months of January, February, March, November, and December. The highest and the lowest groundwater withdrawals are about 193.5 and 350.4 million m3/year in the July and December months, respectively.

Fig. 5
figure 5

Long-term average groundwater withdrawal (Adopted from Suozzi 2005)

Full size image

Table 2 shows the average annual groundwater withdrawal from the different aquifers for the years 1990–2012. As shown, the highest and lowest groundwater withdrawals are in water districts Nos. 1–4 and water district Nos. 6, respectively.

Table 2 Average annual groundwater withdrawal in study area
Full size table

Saltwater intrusion

The historical chloride data for water sampled from SWI-monitoring wells near the shoreline show increasing chloride concentrations. Analysis of the data shows that SWI occurs at the northern shore and the southwestern part of Nassau County. In southwest Nassau, SWI occurs in both Magothy and Lloyd aquifers due to mainly groundwater withdrawal (Suozzi 2005).

SWI is quantified by means of total dissolved solids (TDS) concentration; however, in the SWI-monitoring wells, chloride concentration is measured. The measured chloride concentrations are converted to salinity (TDS) based on the relation between chloride and TDS, as reduced from data in the sea offshore Long Island, i.e. 1 g/L Cl is similar to 1.84 g/L TDS. The chloride concentration in pure saltwater is approximately 19 g/L Cl (35 g/L TDS) (Suozzi 2005; Misut and Voss 2004).

Based on Stumm et al. (2002) and Suozzi (2005) studies, fresh groundwater for Long Island can be defined as water with a concentration of less than 0.074 g/L TDS; brackish groundwater has a concentration of 0.074–0.46 g/L TDS; and (saline) saltwater has a concentration greater than 0.46 g/L TDS. The historical data from the SWI-monitoring wells in the shore aquifers of the southern part of the study area show that the average TDS concentrations is 0.11 g/L TDS in the Upper Glacial, 5.70 g/L TDS in the Magothy, and 0.031 g/L TDS in the Lloyd aquifers.

Numerical simulations

To simulate variable-density groundwater flow and coupled salt transport, the finite difference SEAWAT code (Langevin et al. 2008) is used. In this study, the impacts of coastal flooding due to storm surge, sea-level rise and variation of temperature and precipitation, are not considered. Also, in line with all previous studies (e.g. Narayan et al. 2007; Yang et al. 2013 and Xiao et al. 2019), the impacts of tidal fluctuations on the interface of saltwater and freshwater are small and are neglected. A brief description of the numerical modeling processes is presented in the following.

Spatial and temporal discretization

A slice of the 3D modeling schematization and the assigned boundary conditions is illustrated in Fig. 6. The model domain is discretized in 35 rows, 29 columns, and 14 model layers, with horizontal cell sizes of 500 m, and varying model layer thickness of 3–200 m in the vertical direction. The varying model layer thickness in the vertical direction is due to the varying thickness of geological layers and the occurrence of more intense hydrogeological processes near the ground surface. In temporal discretization, the simulation model is transient with a total simulation period of 18 years, from 2000 to 2018. A total of 288 stress periods is used in the model, each representing 1 month of the simulation period.

Fig. 6
figure 6

A slice of the schematized 3D modeling with assigned boundary conditions and the range of (horizontal and vertical) hydraulic conductivity values as well as the specific yield for each geological layer. a Gulotta (1998), Buxton and Smolensky (1999), b Buxton and Smolensky (1999)

Full size image

Boundary and initial conditions

The boundary conditions of the model are defined either as the time-dependent specified head or as the no-flow boundaries (see Fig. 6). A specified head value of zero represents the mean sea level. The inland boundaries are assigned based on the groundwater-level contour lines, derived from head observation in the observation wells (USGS 2019a, b). Fresh groundwater sources are assigned to model cells on the land surface where recharge enters the groundwater system from the top (the salinity concentration is 0 g/L TDS). A no-flow boundary is assumed at the bedrock and boundaries perpendicular to the shoreline and flow paths. A fixed salinity concentration of 35 g/L TDS (Suozzi 2005; Misut and Voss 2007) is assigned to water that enters the model from the sea boundaries.

The 3D simulations start with saltwater conditions everywhere below the land surface and continue to run for a time that is long enough to reach a steady-state equilibrium. The steady-state equilibrium is approached asymptotically, and a cutoff is therefore assumed for the purposes of this analysis, after 10,000 years of simulation time. This final situation is considered as an initial condition in the automatic calibration procedure. Table 3 presents the characteristics of the simulation model including the simulation setup, spatial and temporal discretization, and boundary conditions.

Table 3 Summary of the simulation model characteristics
Full size table

Hydrogeologic parameters

The wide range of hydraulic conductivity values for each major geological layer (aquifer) (estimated from pump tests, empirical correlations with specific capacity values and grain size distributions) are reported in previous studies (McClymonds and Franke 1972; Prince and Schneider 1989; Lindner and Reilly 1983; Getzen 1977; Franke and Getzen 1976). The hydraulic conductivity of each geological layer varies significantly from location to location. In addition, the horizontal hydraulic conductivity is often an order of magnitude or greater than the vertical hydraulic conductivity for that geological layer (Buxton and Smolensky 1999). Considering the same hydraulic conductivity value for each geological layer is a simple assumption and it has uncertainty; therefore, the uncertainty can significantly affect real-case outcomes compared to those initially expected. Figure 6 shows the range of hydraulic conductivity values for each geological layer, as well as the specific yield values, which take into account the geological heterogeneity of the unconfined aquifer system. The porosity is taken to be 0.3 (Getzen 1977; Misut and Voss 2007).

Also, the various ranges of the longitudinal dispersivity (include 20, 50, 125, and 150 m) considering the scale dependency and the model cell size are assessed, and finally, the value of the longitudinal dispersivity is set to 125 m. The ratio of the horizontal transverse dispersivity to the longitudinal dispersivity is 0.1, while the ratio of the vertical transverse to the longitudinal dispersivity is 0.01 (Lin et al. 2009). Table 4 summarizes the values of the input parameters for the numerical modeling.

Table 4 Input parameters in numerical simulations
Full size table

Considering uncertainties

To account for the uncertainty in the simulation model, the input parameters that are considered to be uncertain include (1) the hydraulic conductivity of each geological layer, and (2) recharge rates in all water district areas. The uncertainty in these parameters is represented by normal probability distributions for recharge rates and log-normal probability distributions for hydraulic conductivity, with mean (μ) and standard deviation (σ), as presented in Figs. 7 and 8. In these figures, lower and upper bound values as well as calibrated values from the simulation model are presented.

Fig. 7
figure 7

Uncertain recharge rate (mm/year) for each zone in the numerical simulation

Full size image
Fig. 8
figure 8

Uncertain hydraulic conductivity (m/day) for each geological layer in the numerical simulation

Full size image

Results and discussion

In this section, model calibration and validation are explained with regard to assessing the performance of the groundwater model. Then, the salinity and groundwater level distributions under current conditions are described. Finally, the results of the risk analyses based on the defined indices are presented. In this study, the MATLAB platform is employed to execute all MCSs on a computer with a 3.50 GHz Intel (R) Xeon 6144 CPU. The computational time of each simulation model takes 25–30 min, which is needed to repeat the computation around 150 times to cover the number of required runs.

Model calibration and validation

The calibration procedure is based on head measurements in 16 observation wells from 2000 to 2018. Chloride concentration was measured in 20 observation wells (SWI-monitoring wells) from 2000 to 2003. In these observation wells, head and salinity are measured at different depths. For head, five wells are in the Upper Glacial aquifer; there are also six and five wells in the Magothy and Lloyd aquifers, respectively. For the measured chloride concentrations, there are observation-well screens in four wells that sample in Jameco aquifer, and 12 and 4 wells that sample Magothy and Lloyd aquifers, respectively (see Fig. 2 for the locations of all the multi-level observation wells). In the calibration procedure, hydraulic conductivity and recharge rates are considered. Calibration of chloride concentration is conducted in the steady-state mode based on the measured data (2000–2013). Calibration of chloride in the transient simulation mode is done by adjusting the chloride concentration at pressure boundaries and the concentration of water extracted from the wells (similar to Ehtiat et al. 2018; Mostafaei-Avandari and Ketabchi 2020).

For the steady-state calibration (Fig. 9.), the mean absolute error (MAE) between the observed and simulated heads is 0.19 m, and between the observed and simulated TDS concentrations is 0.30 g/L TDS. After the steady-state calibration, these results are used for the transient simulation as initial estimations. Monthly groundwater-level data at 16 observation wells for years 2000–2013 and 2014–2018 are used as the observed data for transient calibration and validation, respectively.

Fig. 9
figure 9

Comparison of observed and simulated data for the steady-state models of a head and b concentration of total dissolved solids (TDS)

Full size image

The transient model performance based on the error indicators, is summarized in Table 5. As shown in this table, the errors obtained from the steady-state and transient simulations indicate a good agreement between the observed and the simulated values.

Table 5 The values of errors for steady-state and transient modes
Full size table

Status of groundwater system in the study area

The groundwater system is simulated for 10,000 years to reach a steady-state equilibrium condition. For the duration of the steady-state equilibrium condition, it is assumed that the groundwater system is not affected by human intervention and climate-change factors. The results of the salinity and head simulations in the steady-state condition are used as the initial condition for a transient model, for which monitoring data are limited (see Michael et al. 2013; Mahmoodzadeh et al. 2014). In Fig. 10, the salinity and groundwater level distributions are shown for the year 2018.

Fig. 10
figure 10

3D modeling results of the study area: a salinity distribution in 3D, b salinity distribution in N1-S1 and N2-S2 cross-sections, and c groundwater level distributions (In Fig. 10b, the depths of the upper and lower slices are 100 and 500 m, respectively. Also in Fig. 10c, they are 100 and 400 m, respectively)

Full size image

As seen in Fig. 10a,b, SWI could be detected in the southern and southwestern part of Nassau County, in the Upper Glacial, Jameco, and Magothy aquifers. Based on the results obtained, SWI in this area could be a concern because the Magothy aquifer is used as a significant water-supply source near the coastline. However, in the Lloyd aquifer, it is not a major concern because the saltwater wedge is along the south shore and lies in the direction of slope of the ocean floor.

Groundwater level distributions are shown in Fig. 10c. The freshwater volume considering the 0.2% salinity concentration in saltwater, is estimated to be 101.44 million m3. As seen in this figure, the groundwater-level elevation in the north of the study area is about 9 m and it decreases gradually towards the south.

Risk analysis

The results of the risk analyses under uncertainty for both the hydraulic conductivity and recharge rate parameters, based on the four defined indices in section ‘Description of indices’, are given in the following. Note that the risk values for the all indices are presented as normalized values.

Decreasing groundwater level

The risk values of decreasing groundwater level under α = 5% are shown in Fig. 11. The results are presented for the Magothy aquifer, which is an unconfined aquifer and has the highest groundwater level. Water district No. 5 and a portion of water district No. 1 have a higher risk of decreasing groundwater level than water districts located on Long Beach in the southern part of Nassau County.

Fig. 11
figure 11

Risk of decreasing groundwater level in the Magothy aquifer. A red area(risk = ~1) means the probability of groundwater level decrease is higher compared to other areas (the depth of the slice is 250 m)

Full size image

In the water district Nos. 1 and 5, the groundwater consumption is about 80% from the Magothy aquifer. On Long Beach, groundwater is withdrawn only from the Lloyd aquifer. The results can be evaluated by water district managers in order to track trends in water usage throughout the study area and to monitor groundwater-level behavior. The average risk values under decreasing groundwater level for different confidence levels are shown in Table 6. The high confidence level (i.e. 100%) means that, if repeated, the simulations give the same results. Also, the low value of confidence (i.e. 0%) means there is no confidence that, if repeated, the simulations yield the same results.

Table 6 The average risk value of depletion of groundwater level for different confidence levels, for the Magothy aquifer
Full size table

The results obtained for various confidence levels are clearly consistent. A decrease in the average risk value is seen with an increase in confidence level. An increasing confidence level shows that the probability of exceedance (or probability of failure) is low and the risk of decreasing groundwater level has reduced. The average risk values are 0.53 and 0.47 for α = 5 and 60%, respectively.

Salinity concentration

The risks of high salinity concentration due to the SWI threat for the Upper Glacial, Jameco, Magothy and Lloyd aquifers are shown in Fig. 12a–d. The results are presented for 95% confidence level and 5% of salinity concentration. As shown in this figure, several areas along the coastline are currently vulnerable to SWI. A notable area of high risk is north of Long Beach, where a large amount of groundwater withdrawal (55.11 million m3/year) is occurring from the Magothy aquifer (Fig. 12c).

Fig. 12
figure 12

The risk of SWI in the Nassau County aquifers: a Upper Glacial, b Jameco, c Magothy, and d Lloyd aquifers (In Fig. 12a–d, the depths of the slices are 100, 150, 250 and 450 m, respectively)

Full size image

It is also observed that the risk of SWI has a no-significance value in the Lloyd aquifer since the aquifer is very deep and is protected by the low-permeability Raritan clay. Moreover, groundwater withdrawal from this aquifer is only 10% (5.9 million m3/year) of the total extracted. The resulting risk value highlights the areas near municipal extraction wells and other major pumping wells, showing a large part of the area potentially exposed to SWI. The resulting risk maps can be used for risk management concerning SWI in the study area.

In Table 7, the detailed analysis is summarized for the average risk of SWI based on the salinity concentration at different thresholds, i.e. 0.2, 5, 50, and 95% of salinity concentration in saltwater (Csw), with a certain confidence level (α = 5%). The higher value of risk for the aquifer is seen in the threshold of potable water. The average risk values of SWI are estimated to be 0.39 and 0.20 for the Magothy and Jameco aquifers, respectively. In Table 7, the values of 0.39 and 0.0005 show a higher and lower risk, respectively.

Table 7 The average risk value of SWI based on the salinity concentration for different thresholds of salinity concentration in saltwater (Csw); confidence level = 95%
Full size table

The average risk values of SWI (0.50 Csw) for different confidence levels are summarized in Table 8. Increasing average risk values mean decreasing confidence levels. The results show that an increasing probability of failure equates to larger increases in salinity with respect to the zero-extraction scenario. The zero-extraction scenario shows that groundwater withdrawal does not happen throughout the simulation period. For instance, the obtained values of average risk are 0.23 and 0.33 for the confidence levels of 95 and 40%, respectively, in the Magothy aquifer. These findings support the numerical results compared to the risk values of the first index that showed smaller risks while confidence levels increased.

Table 8 The average risk value of SWI for different confidence levels
Full size table

Filling ratio

The results of the risk of SWI based on the filling ratio are summarized in Table 9 for the Upper Glacial, Jameco, Magothy and Lloyd aquifers. The results are presented for α = 5% (a 95% confidence level), and at different thresholds of salinity concentration. The volumes of SWI based on the filling ratio, considering the 0.2, 5, 50, and 95% of salinity concentration of saltwater, are estimated as 14,118.8, 7983.7, 6003.3, and 1838.8 million m3, respectively. As seen in Table 9, the average risk of SWI is estimated to be 0.93 and 0.88 for the Magothy and Jameco aquifers, respectively. This finding shows that the risk value of SWI seen in the threshold for potable water is higher for these aquifers in comparison with Glacial and Lloyd aquifers.

Table 9 The average risk value of SWI based on the filling ratio at different thresholds of salinity concentration in saltwater, for the 95% confidence level
Full size table

Also, the average risk values of SWI (0.50 Csw) for different confidence levels are summarized in Table 10. As for the previous indices on the risk of salinity concentration and decreasing groundwater level, increasing the probability of failure permits larger increases in salinities with respect to the zero-extraction scenario. For instance, the obtained values of average risk in the Magothy aquifer are 0.018 and 0.98 for the confidence levels of 95 and 40%, respectively.

Table 10 The average risk value of SWI based on the filling ratio for different confidence levels
Full size table

Submarine groundwater discharge (SGD)

Figure 13 shows groundwater flow paths and discharge towards the coastal ecosystem in the north of Long Beach and towards the Atlantic Ocean. In this area, the average SGD is estimated to be 81.4 million m3/year; nitrate fluxes are associated with SGD and can damage the coastal ecosystems.

Fig. 13
figure 13

Groundwater flow paths and the locations of flow discharging in the study area (the depths of the upper and lower slices are 250 and 450 m, respectively)

Full size image

The average nitrate concentration, based on the water samples from wells, is classified as high (2.3 mg/L \( {\mathrm{NO}}_3^{-} \)), medium (0.86 mg/L \( {\mathrm{NO}}_3^{-} \)), and low (0.60 mg/L\( {\mathrm{NO}}_3^{-} \)). Most wells in the study area have been rated as highly sensitive to contamination by nitrate (NYSDOH 2003). The average risk values of nitrate-contamination load discharging through SGD were estimated (see Table 11). The results show that the average risk value increases with a decrease in confidence level. For instance, the values of the obtained average risk are 0.05 and 0.91 for the confidence level of 95 and 40%, respectively. Also, with a decrease in confidence level, the probability of failure permits larger increases in nitrate contamination load with respect to the zero-extraction scenario.

Table 11 The average risk to the aquifer of contamination load discharge through SGD
Full size table

Conclusions

To achieve reliable solutions in the real world and in practical situations, it would be beneficial to consider uncertainty analysis in groundwater models. Moreover, the risk analysis and assessment of potential threats in the groundwater system are important issues. In this study, a 3D numerical model of variable-density groundwater flow and coupled salinity transport is conducted to assess the current status of groundwater levels, SWI status, and nitrate contamination load through SGD. The computer code SEAWAT is used to develop a numerical model and calibration was undertaken using PEST code as an automated parameter estimation procedure. A risk-based groundwater modeling framework is provided to classify the risk of potential threats in a real coastal aquifer system, located in Nassau County, New York. Monte Carlo simulation and Latin Hypercube Sampling are used to consider the uncertainty in both the hydraulic conductivity and the recharge rate. In the proposed framework, four indices are defined for the coastal aquifer in order to quantify the risk of (1) decreasing groundwater levels, (2) SWI based on the salinity concentration, (3) SWI (volume) based on the filling ratio and (4) nitrate contamination discharging through SGD.

The results show that SWI could be detected in the southern and southwestern parts of the Nassau County groundwater system, especially in the Magothy aquifer. The volume of SWI based on the filling ratio, considering a 50% saltwater interface (the salinity concentration greater than 50% of the maximum salinity concentration), is estimated to be 6,003.3 million m3. This could be of concern because the Magothy aquifer is used as a significant water-supply source near the coastline. However, in the Lloyd aquifer it is not a major concern. In this study, the resulting indices are presented in spatial maps that classify areas of high risk to potential threats. The results show that water district No. 5 and a portion of water district No. 1 have a higher risk of decreasing groundwater level. Also, for SWI, a considerable area of high risk is seen in the northern part of Long Beach, where a high amount of groundwater withdrawal occurs from the Magothy aquifer. The SGDs associated with fluxes of nutrients are considerable and can damage the coastal ecosystems. The results of this study show that the proposed methodology is a valuable tool for water district managers to identify high-risk areas for short-term and long-term planning and it can be applied to other geographical settings.