1 Introduction

Since 2000, the three major oil companies in China, namely PetroChina, Sinopec, and CNOOC, have conducted four successive evaluations of oil and gas resources, including the third oil and gas resource evaluation, the new round of national oil and gas resource evaluation, the fourth oil and gas resource evaluation of CNPC, and the national oil and gas resource evaluation of the “13th Five-Year Plan”. Through the evaluation of oil and gas resources, the status and overall scale of oil and gas resources in China have been made clear (Li et al. 2019; Guo et al. 2015, 2016). However, in-depth studies on the spatial distribution of oil and gas resources have not been conducted in specific prospect zones or research blocks. In this study, using the technology for predicting the spatial distribution of oil and gas resources, the abundance of oil and gas resources was simulated, and the visualization of resource distribution was realized, which provides an important reference for the optimization of exploration targets and the deployment of drilling wells.

There are two types of technologies for predicting the spatial distribution of oil and gas resources. One is the quantitative assessment technology for geological risk, namely, the technology for predicting the probability of oil and gas discovery in space. The other is the technology for simulating oil and gas resource abundance, namely, the technology for predicting the spatial variation in the abundance of oil and gas resources.

Quantitative technologies for the evaluation of geological risks include early stochastic methods and multivariate statistical methods, such as the point process model (Kaufman and Lee 1992), conditional simulation (Pan 1997), and Mahalanobis’ distance method (Harff et al. 1992). With these types of methods, statistical models are used to predict the spatial distribution of oil and gas resources based on the spatial distribution of oil and gas wells and non-oil/gas well characteristics revealed by exploration wells. Since 2000, stochastic modeling methods have been used, such as object-oriented simulations (Gao et al. 2000; Chen et al. 2000) and those based on geological models (Chen and Osadetz 2006b). Guo et al. (2006) used the information integration method to integrate the geological, geophysical, and exploration engineering information in order to reflect the spatial distribution characteristics of oil and gas resources. In addition, the resource distribution is reflected in maps, which makes the prediction results more intuitive. Fu et al. (2006) proposed a method for predicting the spatial distribution of oil and gas resources based on grids and geographical information systems (GIS). Hu et al. (2007) proposed a method for predicting the spatial distribution of oil and gas resources by using multiple statistics and information-processing techniques, that is, integrating information by using the Mahalanobis distance discrimination method, calculating the hydrocarbon-bearing probability of the known samples by using the Bayesian formula, establishing a hydrocarbon-bearing probability template under different Mahalanobis distances, and then predicting the spatial distribution of oil and gas resources using the established template. Milkov (2015) summarized the relevant literature on decision-making psychology in petroleum exploration and risk assessment methods, and proposed a new risk probability algorithm that uses six geological risk factors (structure, reservoir facies, reservoir conductive capacity, capping layer, source rock, maturity, and migration) for estimation. This method shifts the focus of geological risk assessment from the calculation of probability values to the objective evaluation of geological data and models. Amiri et al. (2015) predicted the oil and gas potential of the study area using the evidence belief function approach, and evaluated the accuracy of prediction results through efficiency curves of success rate and prediction rate. Sheng et al. (2017) proposed the connotation and applicable conditions of geological models that can distinguish the marginal, conditional, and spatial probabilities, revealing the geological risks under the constraints of specific geological conditions, and improving the success rate of prospective targets or risk wells in areas with low exploration degree. Zhu et al. (2018) discussed the evaluation units, variables, and models related to geological risk and favorable evaluation, and proposed a data-driven model using logistic regression. The model can integrate the existing geoscience information and current exploration results to obtain a quantitative logistic regression relationship between the occurrence of oil and gas and key geological factors, and can be used to predict the probability of oil and gas occurrence. Jesus et al. (2020) considered that some uncertainties, such as geological complexity, lithostratigraphy, fluid content, and seismic resolution, are common risks in exploration, and proposed a method that uses spectral decomposition, pre-stack inversion, and seismic facies classification to reduce exploration risk. Chatterjee and Ghosh (2019) believes that comprehensive risk assessment methods can help to successfully drill horizontal wells in complex geological environments. Through identification, evaluation, and management of various risks, several horizontal wells in an offshore complex geological environment in Southeast Asia have been planned to reduce drilling and geological uncertainty. Sheng et al. (2020) proposed a gray correlation evaluation method based on the fuzzy analytic hierarchy process. This method can be used to predict the distribution of oil and gas resources based on the closeness between the evaluation index and the ideal index, multiple evaluation factors, and weights between the evaluation indexes. Ren et al. (2020) predicted the oil and gas distribution of the Dongying Formation in the Nanpu area in Bohai Bay Basin using a tree-augmented Bayesian network, and good results have been achieved.

Abundance simulation technology for oil and gas resources is a type of technology based on the prediction results of the exploration risk. Currently, abundance simulation technology is mainly implemented using stochastic simulations and conditional simulation technologies. Guo et al. (2009b) and Xie et al. (2011) proposed a two-dimensional fractal model based on stochastic simulation technology and a Fourier transform power spectrum method to describe the spatial distribution of oil and gas resources. The model can be used to modify the abundance of oil and gas resources, predict the resource amount in areas with different oil and gas probabilities, and to determine the spatial distribution of resources. Olea et al. (2010) established a new set of evaluation methods, including the use of a sequential Gaussian stochastic simulation method in areas where wells have been drilled and the use of a multi-point simulation method in areas with no drilled wells. Chen and Osadetz (2013) predicted the tight oil resources of the Cardium Formation in the Western Canada Basin by using the stochastic simulation method based on the geological model, and favorable areas have been optimized.

In summary, the simulation of resource abundance depends on the risk probability evaluation. The final predicted resource abundance and resource scale in favorable areas will provide a basis for decision-making in the exploration and optimization of exploration targets.

In this study, the focus is on the improvement of the fractal simulation method for predicting resource abundance. First, the overlapping maps and continued multiplication method, which is rapid and convenient, is used in the risk probability evaluation to provide key risk probability maps for resource abundance simulation. Then, to solve some problems, such as the fractal model of resource abundance presenting a negative resource abundance, which will lead to difficulty in convergence or non-convergence during conditional simulation, resulting in overestimation of the total resources, a method to improve the model has been proposed. That is, the traditional algebraic conservation model is improved to a square summation conservation model (Plancherel’s theorem), which ensures that all resource abundances are non-negative, that the total resources are conserved and not overestimated, and those conditional simulations can quickly converge. Finally, as a verification example, the application results of these technologies in the Sangonghe Formation in the central Junggar Basin are discussed. It is concluded that the coincidence rate between the predicted resources and the third-level reserves in the known area reached 99.98%, and the remaining resources in the unknown area are 0.7899\(\times \,10^8\) t, which are mainly distributed near the triangular area formed by Well Lunan1, Well Shimo1, and Well Shi008, around Well Mo11, east of Well Mo5, west of Well Pen7, southwest of Well Shidong1, and near as well as north of Well Fang2. The research methods and examples provide a reference for resource evaluation and target optimization.

2 Methods

2.1 Method for Making a Risk Probability Map

The evaluation of the risk probability of any evaluation unit (or pixel of the map) in a two-dimensional space is obtained by the product of the evaluation values of the main controlling factors for hydrocarbon accumulation. To satisfy the two-dimensional risk visualization, the method of “overlapping maps and continued multiplication” is used. The method of “overlapping maps and continued multiplication” includes two key steps.

  1. (i)

    Quantitative evaluation of the main controlling factors for hydrocarbon accumulation

The key to the quantitative evaluation of the main controlling factors for hydrocarbon accumulation is to determine the probability value of the main controlling factors based on geological knowledge. Different geological conditions correspond to different probability values. The probability value of each evaluation unit is between 0 and 1; 0 and 1 indicate that the occurrence probability of the main controlling factors for hydrocarbon accumulation are 0% and 100%, respectively. By evaluating any evaluation unit in the two-dimensional space one by one, a probability map of the occurrence of a single factor in the study area can be obtained.

  1. (ii)

    Quantitative calculation of risk probability

The evaluation results of the “five major” accumulation conditions, namely the probability map, are overlapped, obtaining the probability values for each pixel (a point representing an evaluation unit) under five accumulation conditions, and the accumulation risk probability at this pixel point can be obtained by multiplying the probability values continuously, namely,

$$\begin{aligned} p(i, j)=\prod _{k=1}^{5} q_{k}(i, j), \end{aligned}$$
(1)

where p is the probability value of accumulation risk, k is the number of main controlling factors of accumulation, q is the occurrence probability of a single factor, i is the serial number of the evaluation unit (calculation point) in the X direction, and j is the serial number of the evaluation unit in the Y direction. After calculating each evaluation unit individually, a risk probability map of the study area can be obtained.

2.2 Methods for Simulation of Resource Abundance

The theoretical basis for the simulation of resource abundance is that the distribution of oil and gas reservoir scales conforms to the fractal law (Chen and Osadetz 2013, 2006a; Song et al. 2006; Divi 2004; Laherrere 2000). Studies have found that the distribution of resource abundance also conforms to the fractal law (Guo et al. 2009a, b; Xie et al. 2011; Zou et al. 2012). Resource abundance simulation is used to predict the resource abundance of unknown areas based on the fractal characteristics of resource abundance. The key simulation data are as follows: (i) the abundance map \((M_0)\) of the discovered reserves, which is obtained by dividing reserves by the distribution area of the reserves (only one average reserve abundance is taken for a reserve area); and (ii) the probability map \((M_1)\) of oil and gas exploration risk or probability map of hydrocarbon accumulation, which is obtained by analyzing the accumulation conditions and by using the method of overlapping maps and continued multiplication.

2.2.1 Technical Procedure

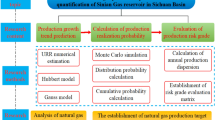
An important step in the fractal simulation of resource abundance is the fractal correction. That is to say, to predict the relatively low resource abundance that has not been discovered based on the high resource abundance that has been discovered. Fractal correction can only be performed within the frequency domain. Therefore, it is necessary to transform the reserve abundance in the space domain to the amplitude spectrum in the frequency domain through a fast Fourier transform (FFT), and then complete the fractal correction to predict the distribution of undiscovered resources. In addition, the inverse fast Fourier transform(IFFT) process of fractal simulation requires the amplitude spectrum of resource abundance in the frequency domain and the phase spectrum of risk probability. Therefore, it is also necessary to transform the risk probability in the space domain into amplitude and phase spectra in the frequency domain through FFT. In short, FFT and IFFT are used throughout the entire technical procedure. The technical workflow includes four key steps (as shown in Fig. 1), which are as follows:

  1. (i)

    Fast Fourier transform to obtain amplitude spectrum and phase spectrum

    By conducting the FFT on the reserve abundance map and the exploration risk probability map, which both belong to the spatial domain, we can obtain the original amplitude spectrum \((A_0)\) and phase spectrum \((P_0)\) of the reserve abundance map, as well as the original amplitude spectrum \((A_1)\) and phase spectrum \((P_1)\) of the risk probability map, where the reserve abundance map and the risk probability map are both in the frequency domain.

  2. (ii)

    Correct the original amplitude spectrum to form a new amplitude spectrum

    The fractal method is used to correct the original amplitude spectrum of the reserve abundance map based on the fractal distribution characteristics of the oil and gas resource abundance. Taking the center point of the \(A_0\) map as the starting point, draw the amplitude and frequency in the X and Y directions, respectively, to form diagrams \(f_x\) and \(f_y\). In the \(f_x\) and \(f_y\) diagrams, the amplitudes of the low frequencies were high, and the amplitudes of the high frequencies were low. The fractal correction corrects the low amplitude in the high-frequency region. Take the trend line with a high-amplitude change in low-frequency area as the reference line, and correct the low-amplitude line in the high-frequency area to the trend line. After the amplitude correction in the two special directions of \(f_x\) and \(f_y\) is completed, the amplitude of all high-frequency regions in the \(A_0\) map will be corrected by the spatial interpolation method, forming the amplitude spectrum\((A_\mathrm{new})\) of the total resource abundance.

  3. (iii)

    Inverse fast Fourier transform to form a map of resource abundance

    The amplitude spectrum \(A_\mathrm{new}\) of resource abundance has implicit information on resource abundance, and the phase spectrum \(P_1\) of the exploration risk probability map contains implicit information on the occurrence probability of oil and gas in different locations. Therefore, \(A_\mathrm{new}\) and \(P_1\) that both belong to the frequency domain are inverted back to the spatial domain using the IFFT to obtain the distribution map \((M_\mathrm{new})\) of the total resource abundance.

  4. (iv)

    Conditional simulation to form the final map of resource abundance

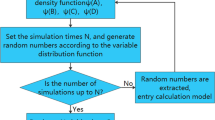
    The abundance in \(M_\mathrm{new}\) is substituted with the known abundance in all reserve areas, forming a temporary abundance map \((M_\mathrm{temp})\). The amplitude spectrum \((A_\mathrm{temp})\) and phase spectrum \((P_\mathrm{temp})\) are obtained using the FFT, and then the \(A_\mathrm{new}\) and \(P_\mathrm{temp}\) are inverted in the frequency domain back to the spatial domain with the IFFT, obtaining the distribution map \((M_\mathrm{new})\) of the total resource abundance. The known abundance of the reserve area is compared with the abundance of the corresponding position in \(M_\mathrm{new}\). If the difference in abundance is greater than the set error range, the above iteration is continued; otherwise, the simulation ends. The final \(M_\mathrm{new}\) obtained is the result map.

Fig. 1
figure 1

Technical flow chart

Full size image

2.2.2 Improved Mathematical Model

(I) Model improvement for predicting resource abundance

The mathematical formulas involved in the aforementioned fractal simulation methods include the FFT and IFFT.

In the two-dimensional Fourier transform, the equation for transforming the spatial domain (x, y) to the frequency domain \((\omega , v)\) is as follows

$$\begin{aligned} Z(\varvec{\omega }, v)={\mathscr {F}}[z(x, y)]=\iint _{(x, y)} z(x, y) {{e}}^{-i(\varvec{\omega } x+v y)} {\hbox {d}} x {\hbox {d}} y. \end{aligned}$$
(2)

In the two-dimensional inverse Fourier transform, the equation to transform the frequency domain \((\omega , v)\) back to the spatial domain (x, y) is as follows

$$\begin{aligned} z(x, y)={\mathscr {F}}^{-1}[Z(\varvec{\omega }, v)]=\frac{1}{4 \pi ^2} \iint _{(\varvec{\omega }, v)} Z(\varvec{\omega }, v) {{e}}^{i(\omega x+v y)} {\hbox {d}} \varvec{\omega } {\hbox {d}} v. \end{aligned}$$
(3)

According to the above technical process, the model for predicting resource abundance is initially determined; namely, the traditional algebraic summation conservation model.

$$\begin{aligned} f(x, y)={\mathscr {F}}^{-1}\left\{ \left\| {\mathscr {F}}\left[ f_{0}(x, y)\right] \right\| {{e}}^{i \measuredangle {\mathscr {F}}[p(x, y)]}\right\} . \end{aligned}$$
(4)

In Eqs. (2), (3), and (4), | | | | represents a module of a complex number, \(\Vert z\Vert \equiv {\bar{z}} \cdot z\); \(\measuredangle z \equiv {\text {Arg}}(z)\), \(e^{i\measuredangle z} \equiv \cos (\measuredangle z)+i \sin (\measuredangle z)\), \(e^{i\measuredangle z}\) is a complex exponential form; x, y are the positions or coordinates of the discrete points (simulated calculation points) in the map; f is the predicted resource abundance; \(f_0\) is the original resource abundance (reserve abundance); p is the probability value of accumulation risk; and \({\mathscr {F}}\) and \({\mathscr {F}}^{-1}\) are the FFT and IFFT, respectively.

During the FFT and IFFT, we should consider that resource abundance and reserve abundance have no non-negative values, and the actual map often has several zero-value regions. In the multiple processes of Fourier transform and inverse Fourier transform, the amplitude spectrum was corrected, and the phase spectrum was modified. Therefore, the calculated resource abundance is prone to produce many negative abundances around the zero-value regions if using the traditional algebraic summation conservation model, namely Eq. (4). The original method maintains the total resource conservation, which leads to a larger summation of the positive abundance. If all the calculation points of negative abundance are simply forced to be corrected to zero, then the total amount of resources obtained from all the calculation points will be exaggerated and overestimated, and the total amount of resources will not be conserved. Furthermore, it may cause difficulties in convergence or non-convergence during the iteration process. To solve this problem, it is necessary to ensure that all resource abundances are non-negative, and the total resources are conserved. Therefore, the algebraic summation conservation model is modified into a square summation conservation model. That is, Eq. (4) is transformed as follows

$$\begin{aligned} f(x, y)=\left\| {{\mathscr {F}}^{-1}}\left\{ \Vert {\mathscr {F}}\left[ \sqrt{f_{0}(x, y)}\right] || {{e}}^{i \measuredangle {\mathscr {F}}[p(x, y)]}\right\} \right\| ^{2}. \end{aligned}$$
(5)

Compared with the original model, the new model can ensure that the abundance of all resources is non-negative and that the total amount of resources is conserved.

(II) Objective function for conditional simulation

The conditional simulation equation of the original model is as follows

$$\begin{aligned} \left\{ \begin{array}{l} f_{1}(x, y)={\mathscr {F}}^{-1}\left\{ \left\| {\mathscr {F}}\left[ {f_{c}(x, y)}\right] \right\| \cdot e^{i \measuredangle {\mathscr {F}}[p(x, y)]}\right\} \cdots \cdots \cdots \cdots \cdots ( \text{ Initial } \text{ value } ), \\ \left. \begin{array}{l} {\hat{f}}_{k}(x, y)=\left\{ \begin{array}{ll} {f_{0}(x, y)} &{} \cdots \cdots \cdots ( \text{ known } \text{ area } ) \\ f_{k}(x, y) &{} \cdots \cdots \cdots ( \text{ area } \text{ to } \text{ be } \text{ evaluated } ) \end{array}\right. \\ f_{k+1}(x, y)={\mathscr {F}}^{-1}\left\{ \left\| {\mathscr {F}}\left[ {f_{c}(x, y)}\right] \right\| \cdot e^{i \measuredangle {\mathscr {F}}\left[ {\hat{f}}_{k}(x, y)\right] }\right\} \\ \end{array}\right\} ( \text{ iteration } ) \\ f(x, y)=\lim _{k \rightarrow \infty } f_{k}(x, y) \quad \quad \quad \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \text{(convergence) } \end{array}\right. .\nonumber \\ \end{aligned}$$
(6)

The conditional simulation equation of the improved model is as follows

$$\begin{aligned} \left\{ \begin{array}{l} f_{1}(x, y)={\mathscr {F}}^{-1}\left\{ \left\| {\mathscr {F}}\left[ \sqrt{f_{c}(x, y)}\right] \right\| \cdot e^{i \measuredangle {\mathscr {F}}[p(x, y)]}\right\} \cdots \cdots \cdots \cdots \cdots ( \text{ Initial } \text{ value } ), \\ \left. \begin{array}{l} {\hat{f}}_{k}(x, y)=\left\{ \begin{array}{ll} \sqrt{f_{0}(x, y)} &{} \cdots \cdots \cdots ( \text{ known } \text{ area } ) \\ f_{k}(x, y) &{} \cdots \cdots \cdots ( \text{ area } \text{ to } \text{ be } \text{ evaluated } ) \end{array}\right. \\ f_{k+1}(x, y)={\mathscr {F}}^{-1}\left\{ \left\| {\mathscr {F}}\left[ \sqrt{f_{c}(x, y)}\right] \right\| \cdot e^{i \measuredangle {\mathscr {F}}\left[ {\hat{f}}_{k}(x, y)\right] }\right\} \\ \end{array}\right\} ( \text{ iteration } ) \\ f(x, y)=\lim _{k \rightarrow \infty }\left\| f_{k}(x, y)\right\| ^{2} \quad \quad \quad \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \text{(convergence) } \end{array}\right. .\nonumber \\ \end{aligned}$$
(7)

In Eqs. (6) and (7), p(x, y) is the probability of the exploration risk; \(f_{0}(x, y)\) is the initial abundance; \(f_{c}(x, y)\) is the corrected abundance, which is derived from \(f_{0}(x, y)\) after fractal correction, then \(f_{c}(x, y) = f_{0}(x, y)\); \(f_{k}(x, y)\) is the intermediate result of the simulation process; and \({\hat{f}}_{k}(x, y)\) is the known correction result in the middle of the simulation process.

In the existing methods for simulating resource abundance, the errors in the objective functions for conditional simulation are all relative (Xie et al. 2011; Zou et al. 2012). The new model improved in this study can increase the iteration speed during the conditional simulation process and ensure iteration convergence. Therefore, the error in the objective function of resource abundance \(\mathrm{(10^4 t/km^2)}\) can be set to a very small absolute error value, such as \(\mathrm{10^{-9}(10^4~t/km^2)}\), thereby improving the overall simulation accuracy. The new objective function is as follows

$$\begin{aligned} E=\underset{(x, y) \in \varvec{\varOmega }}{{\text {Max}}} \mid f(x, y)-f_{0}(x, y)\mid . \end{aligned}$$
(8)

In Eq. (8), E is the maximum error value of the objective function of resource abundance, \(\mathrm{10^4 t/km^2}\); x, y are the positions or coordinates of discrete points (simulated calculation points) in the map; f is the predicted resource abundance; \(f_0\) is original resource abundance (reserve abundance); and \(\varvec{\varOmega }\) is the calculation points within the range of discovered reserve areas.

3 Application

3.1 Geological Setting of the Study Area

The study area is located in the hinterland of the Junggar Basin (as shown in Fig. 2), with a width of 160 km from east to west, a length of 170 km from north to south, and an area of approximately \(2.7 \times \) \(\mathrm{10^4~km^2}\), including the depression to the west of Well Pen1, the Mosuowan uplift, and the Luxi uplift. The target layer is the Jurassic Sangonghe Formation \((J_{1s})\), the source rock is the Permian Lower Wuerhe Formation \((P_{2w})\), and the cap layer is the Jurassic internal shale. The study area is low in the south and high in the north. The lithofacies are fine in the south and coarse in the north. Oil and gas migrated from bottom to top and from south to north, forming fault-nose, fault-block, and lithologic–stratigraphic oil and gas reservoirs.

Fig. 2
figure 2

Location of the first-level tectonic unit and the study area in the Junggar Basin

Full size image

3.2 Parameter Extraction and Evaluation

Based on the various data from the penetrated Sangonghe Formation, such as the drilling results of the exploration wells, reserve data, results of seismic interpretation, and basin simulation, evaluation has been conducted on the geological factors used for the prediction of the spatial distribution of oil and gas in the study area, and quantitative data were extracted from these factors.

3.2.1 Exploratory Wells and Reserve Data

Statistical analysis was conducted on 203 exploration and appraisal wells that encountered the Sangonghe Formation. Among the 203 wells, there were 109 wells with flowable hydrocarbons, and the other were non-oil/gas flow wells. The distribution characteristics of these wells have provided important information for geological understanding (as shown in Fig. 3). The discovered third-level petroleum geological reserves are \(1.2124 \times \) \(\mathrm{10^8 t}\), and the total hydrocarbon-bearing area is \(467.5\times \) km\(^2\), which are mainly distributed in the Mosuowan uplift, Mobei, Shixi, Shinan, and Xiayan areas (as shown in Fig. 3). Through statistical analysis of the evaluation data of the 38 oil reservoirs in the report about the proven reserve, the following data have been obtained: the average effective thickness of the reservoirs is 8.6 m, the average effective porosity is 13.87%, the average oil saturation is 58.7%, and the average crude oil density is 0.857 t/m\(^3\) (as shown in Table 1).

Fig. 3
figure 3

Reserve abundance distribution of the Sangonghe Formation in the Junggar Basin hinterland

Full size image
Table 1 Main parameters of the oil reservoirs in the Sangonghe Formation in the Junggar Basin hinterland
Full size table
Fig. 4
figure 4

Sedimentary microfacies of the Sangonghe Formation in the Junggar Basin hinterland

Full size image

3.2.2 Evaluation of Reservoir Conditions

According to the statistical results of the data from 38 oil reservoirs (Table 1) and the sedimentary microfacies map (Fig. 4), evaluation has been conducted on the reservoir development. In the Sangonghe Formation, delta and shore-shallow lake facies are mainly developed, including several microfacies, including underwater distributary channels, interdistributary bays, sandy detrital flow, sheet sand, beach bars, and shore-shallow lakes. From the underwater distributary channel, sheet sand, beach bar, sandy detrital flow, interdistributary bay, and shore-shallow lake, the reservoir quality gradually decreases. The corresponding evaluation values are listed in Table 2. Within the same sedimentary microfacies, the probability of each evaluation unit is a random sampling result between the minimum and maximum values of the facies zone. With the underwater distributary channel as an example, the random sampling range is from 0.7 to 0.9, and the sampling result is any real number between 0.7 and 0.9, including 0.7 and 0.9. According to the above method, the sedimentary microfacies map is transformed into a probability map to quantitatively evaluate the reservoir (Fig. 5).

Table 2 Evaluation value of the reservoirs in the Sangonghe Formation in the Junggar Basin hinterland
Full size table
Fig. 5
figure 5

Quantitative evaluation value of reservoir conditions in the Sangonghe Formation in the Junggar Basin hinterland

Full size image
Fig. 6
figure 6

Fracture distribution of the Sangonghe Formation in the Junggar Basin hinterland

Full size image

3.2.3 Evaluation of Hydrocarbon Source and Supply Conditions

The oil and gas in the Sangonghe Formation are mainly sourced from the source rocks of the Lower Wuerhe Formation of the underlying Permian strata. Vertically, hydrocarbons migrate through the fractures from the source rocks to reservoirs, and the lateral migration is mainly controlled by sand bodies and structural ridges (Guo et al. 2018). The southern region is close to the hydrocarbon source, where faults might play an important role in vertical communication. Therefore, the hydrocarbon source conditions are good in the southern region. The northern region is far away from the source rocks, and the faults play some role in lateral communication, but cannot directly connect the source rocks with the reservoirs. Oil and gas migrated laterally a long distance in “upstairs” type with a combination “sand body–fault–sand body” migration style. The overall evaluation of the northern region is that the hydrocarbon source is poor, and hydrocarbon accumulation occurs only near the migration channel. Considering the fault distribution (Fig. 6) and the simulation results of hydrocarbon migration and accumulation in this area (Guo et al. 2021), the values of hydrocarbon supply conditions (Table 3) have been evaluated and a probability map (Fig. 7) constructed.

Table 3 Evaluation value of hydrocarbon supply conditions in the Sangonghe Formation in the Junggar Basin hinterland
Full size table
Fig. 7
figure 7

Quantitative evaluation of hydrocarbon supply conditions of the Sangonghe Formation in the Junggar Basin hinterland

Full size image

3.2.4 Evaluation of Trap Conditions

Based on the structural map at the top and the trap interpretation results of the Sangonghe Formation, the structural traps are divided into confirmed and unconfirmed traps. According to the sedimentary microfacies map, the inferred lithological traps are also divided into two levels: lithological lenses (beach bar, etc.) and lithological barriers (bay, etc.). The evaluation level of the traps ranged from high to low as follows: confirmed structural traps, unconfirmed structural traps, lithological lenses, and lithological barriers. The higher the level, the lower the risk and the higher the evaluation value (Table 4). The trap risk probability map was drawn according to the evaluation level (Fig. 8).

Table 4 Evaluation value of the traps in the Sangonghe Formation in the Junggar Basin hinterland
Full size table
Fig. 8
figure 8

Quantitative evaluation of traps in the Sangonghe Formation in the Junggar Basin hinterland

Full size image

3.2.5 Evaluation of Cap Rocks and Preservation Conditions

By analyzing the distribution of oil/gas wells and non-oil/gas wells, it was found that the overlying local unconformity surface plays a very important role in sealing. Through analysis, in the same way, it was found that partial faults in the overlying strata play a destructive role on the cap rock. Therefore, it is believed that the overlying local unconformity-weathered clay has a good effect on sealing. Therefore, its evaluation value is high, ranging from 0.7 to 0.9, while the evaluation value of the areas with faults is low, ranging from 0.1 to 0.2. Finally, the valuation in other areas ranges from 0.4 to 0.6, where shale is relatively developed and can act as a local cap rock. On this basis, the quantitative evaluation values of the cap rocks and preservation conditions were obtained through random sampling (Fig. 9).

Fig. 9
figure 9

Quantitative evaluation of cap rocks and preservation conditions of the Sangonghe Formation in the Junggar Basin hinterland

Full size image
Fig. 10
figure 10

Risk probability distribution of the Sangonghe Formation in the Junggar Basin hinterland (the range within the black line is the reserve area)

Full size image

3.3 Simulation of Resource Abundance

3.3.1 Simulation Results of Risk Probability

After evaluating the hydrocarbon accumulation conditions, four risk probability maps of a single factor (Figs. 5, 7, 8, 9) were obtained. The risk probability for each evaluation unit in the study area was obtained using the method of overlapping maps and continued multiplication, and then the risk probability map was drawn (Fig. 10).

3.3.2 Fourier Transform of Abundance Map and Risk Probability Map

A FFT was conducted on the reserve abundance map (Fig. 3) to obtain the amplitude spectrum (Fig. 11) and phase spectrum for the original abundance. Similarly, we conducted a FFT on the risk probability map (Fig. 10) to obtain the amplitude spectrum and phase spectrum for the risk probability (Fig. 12). Figures 11 and 12 show the basic information about the spatial distribution of resources.

Fig. 11
figure 11

Amplitude spectrum of the original abundance

Full size image
Fig. 12
figure 12

Phase spectrum of the risk probability

Full size image

3.3.3 Fractal Correction to Resource Abundance

Taking the center point in the amplitude spectrum (Fig. 11) as the starting point, the correlation curve between amplitude and corresponding frequency was plotted in the X and Y directions (Fig. 13a and Fig. 14a). In Fig. 13a, the red line is the correlation curve between the amplitude and the corresponding frequency. Taking the change trend of the red line on the left side of Fig. 13a (area with high amplitude and low frequency) as a reference, the trend line for low amplitude (area with high frequency) can be drawn, namely the solid green line. After that, the software automatically extends the line to form a green dashed line, which is the calibration reference line. Then, another trend line (solid green line) is drawn for low amplitude (area with high frequency) in the same way. The scissors difference between the green solid line on the right and the green dashed line is the amplitude difference that needs to be corrected. The correction method is to pull the solid line up to make it coincide with the dashed line. During this process, the red line of low amplitude (area with high frequency) is also pulled up and corrected accordingly, forming Fig. 13b after completion. The correction in the Y direction is the same as that in the X direction, forming Fig. 14b after completion. After completing the amplitude correction in the two specific directions of X and Y, the other uncorrected amplitudes in Fig. 11 were corrected using spatial interpolation, forming the amplitude spectrum of the total resource abundance (Fig. 15).

Fig. 13
figure 13

Amplitude versus frequency in the X direction

Full size image
Fig. 14
figure 14

Amplitude versus frequency in Y direction

Full size image
Fig. 15
figure 15

Amplitude spectrum after correction

Full size image
Fig. 16
figure 16

Resource abundance of fractal simulation (the range within the black line is the reserve)

Full size image
Fig. 17
figure 17

Resource abundance of conditional simulation

Full size image
Fig. 18
figure 18

Remaining resource abundance (the range within the black line is the reserve)

Full size image
Fig. 19
figure 19

Resource abundance simulated by the original model

Full size image

3.3.4 Fractal Correction to Resource Abundance

Using the inverse Fourier transform, the corrected abundance amplitude spectrum (Fig. 15), and the risk probability phase spectrum (Fig. 12) back to the spatial domain, the source abundance map was obtained (Fig. 16). To obtain the simulated value within a known area in Fig. 16 that is equal to or close to the actual value, it is necessary to conduct a conditional simulation. With the reserve abundance in Fig. 3 as a constraint, an iterative simulation was conducted to obtain a map of resource abundance (Fig. 17). Excluding (empty) the abundance of the known area, the abundance map of the remaining resources was obtained (Fig. 18).

3.3.5 Comparison of the results from the improved model and the original model

To reveal the effectiveness and superiority of the improved model, with the same data and operation process, the prediction was conducted using the original model to obtain a map of resource abundance (Fig. 19) and corresponding result data (Table 5). It can be seen from Table 5 that the coincidence rate of the simulated quantities of the original model and the improved model with the actual reserves reached 99.98% after the conditional simulation, indicating that the conditional simulation is effective. In addition, with the improved model, the predicted remaining resources are 0.7899\(\times \,10^8\)t, which is 65% of the discovered reserves; the original model predicts that the remaining resources are 3.5033\(\,\times \,10^8\)t, which is 2.89 times the discovered reserves, and the prediction result is relatively higher. This is mainly because, in the original model, the traditional algebraic summation conservation calculation method was used. Therefore, the obtained resource abundance was prone to produce numerous negative abundances in the original zero-value area. In addition, because this method maintains the conservation of total resources, the sum of positive abundances is too large, resulting in an overestimation of the total resources. Compared with the original model, the resource amount predicted by the improved model is 1.65 times higher than the actual amount, and the prediction results are more objective and accurate. Comparing Fig. 19 with Fig. 17, it can be seen intuitively that due to the excessively high predicted resource amount, the resource amount is distributed throughout the region, resulting in great difficulty in the identification of the favorable areas. In summary, the improved model is significantly better than the original model in predicting the spatial change of the resource amount and in predicting the resource abundance.

3.3.6 Analysis of Simulation Results

As shown in Table 5, the predicted resource amount is \(2.0020 \times 10^8\)t. Among the resources, the resource amount within the known area is \(1.2122 \times 10^{8}\)t, and that outside the known area (the remaining resource amount) is \(0.7899 \times 10^8\)t.

The three-level reserves in the known area are \(1.2124 \times 10^8\)t, and the simulated predicted reserves are 1.2122\(\times 10^8\)t (the difference between them was very small), and the coincidence rate of the simulation was 99.98%, indicating that a good result was obtained by conditional simulation. In addition, the remaining resources are predicted to be 0.7899\(\times 10^8\)t, which is 65% of the discovered three-level reserves; that is, the remaining resources are close to 2/3 of the discovered reserves. This shows that the Sangonghe Formation still retains substantial resources to be explored and developed. This is consistent with the fact that the area is in the middle exploration stage. This shows that risk assessment, abundance correction, and fractal simulation can play a good role in predicting unknown areas.

Areas with higher and concentrated remaining resource abundance were considered favorable areas. Based on this, the following favorable areas were found from the remaining map of resource abundance (Fig. 18): (i) the triangular area formed by Well Lunan1, Well Shimo1, and Well Shi008 where the remaining resource abundance is the highest, and the distribution of resources is the densest; (ii) the neighborhood around Well Mo11, the east area of Well Mo5, and the west area of Well Pen7 where the remaining resource abundance is relatively high; and (iii) the southwest area of Well Shidong1, and the neighborhood as well as the north area of Well Fang2 where the remaining resource distribution is relatively dense.

By comparing the geological conditions and risk probability maps of the Sangonghe Formation (Fig. 10), it is concluded that the favorable areas and low-risk areas are consistent, indicating that the prediction results of the resource abundance are generally in line with geological understanding.

4 Conclusions

The conclusion of this study consists of six aspects:

  1. I.

    The technology for predicting spatial distribution of oil and gas resources based on fractal correction and conditional simulation, includes four key technical steps: (i) FFT to obtain the amplitude spectrum and phase spectrum; (ii) correct the original amplitude spectrum for the reserve abundance map to form new amplitude spectrum; (iii) IFFT to obtain a map of resource abundance; and (iv) conditional simulation, which can revise the map of resource abundance, and obtain the final map of resource abundance.

  2. II.

    The improved model for predicting resource abundance can realize square summation conservation for the resource amount and solve the exaggeration problem of the total resource amount. The new improved model can increase the iteration speed during the conditional simulation process and ensure iteration convergence. Therefore, the error of the objective function of resource abundance can be set to a very small absolute error value, thereby improving the overall simulation accuracy.

  3. III.

    Within the known area, the resource amount simulated by the improved model is \(1.2122 \times 10^8\)t, which is \(0.0002 \times 10^8\)t different from the actual value of \(1.2124 \times 10^8\)t, and the coincidence rate is 99.98%, indicating that a good result has been obtained by conditional simulation.

  4. IV.

    The predicted remaining resources are \(0.7899 \times 10^8\)t, which is approximately 39.45% of the total resources. This is consistent with the fact that the area was in the middle exploration stage. This shows that with the improved model, a good prediction result can be obtained for the unknown area.

  5. V.

    The remaining resources are mainly distributed in (i) the triangular area formed by Well Lunan1, Well Shimo1, and Well Shi008; (ii) the neighborhood around Well Mo11, the east area of Well Mo5, and the west area of Well Pen7; and (iii) the southwest area of Well Shidong1, and the neighborhood and the north area of Well Fang2.

  6. VI.

    The prediction technology for the spatial distribution of oil and gas resources, which is based on fractal correction and conditional simulation, is a new technology. It is necessary to continuously improve it in future applications.

Table 5 Comparison of results from the improved model and the original model
Full size table