Abstract
A SeaBat T50 calibration that combines measurements in a test tank with data from numerical models is presented. The calibration is assessed with data obtained from a series of tests conducted over a sandy seabed outside the harbor of Santa Barbara, California (April 2016). The tests include different tone-burst durations, sound pressure levels, and receive gains in order to verify that the estimated seabed backscattering strength \((S_b)\) is invariant to sonar settings. Finally, \(S_b\)-estimates obtained in the frequency range from 190 kHz in steps of 10 kHz up to 400 kHz, and for grazing angles from \(20^\circ\) up to 90\(^\circ\) in bins of width \(5^\circ ,\) are presented. The results are compared with results found in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In this paper, scattering strength \((S_b)\) refers to the backscattering strength from the seabed. During the last 2–3 decades, the number of multibeam echosounders (MBES) for bathymetric purposes has increased significantly. MBES systems are used in all ocean depths and operate at frequencies from about 10 kHz in the deepest oceans up to 400–500 kHz for shallow depths from 1 to 100 m.
For bathymetry the signal to noise ratio is one of the key parameters for successful bottom detection. For receivers in SeaBat systems older than the T-series, moderate clipping, low dynamics in the analog to digital converter (ADC), non-linear gain characteristics that lead to saturation, as well as temperature-dependent amplifiers do not have a crucial impact on bathymetry performance. Meanwhile, these properties are critical limitations, when the scattering strength of the seafloor is required, and compensation of the MBES’s influence on data is necessary. The successor, the SeaBat T50, has been designed for the acquisition of the seabed scattering strength, and it does to a far lesser extent suffer from the aforementioned limitations.
Between 2011 and 2016 efforts have been made to use the MBES for the estimation of the seafloor scattering strength (Wendelboe et al. 2012). This paper presents how the calibration has been made, and results from tests and verifications from subsequent field trials are presented.
The compensation of the MBES influence on the recorded data may be carried out in different ways. Hellequin et al. (2003) use the system specifications made available by the manufacturer and statistical analysis to remove artifacts from survey data. Measurements can be conducted in a large tank where the far-field beam pattern and sensitivity at different gains of the MBES system are measured by application of either a standard target (Foote et al. 1988; Lanzoni and Weber 2012), or a distributed target (Heaton et al. 2017). Lanzoni and Weber (2011) perform a field calibration of a MBES using a setup that includes a target sphere and a split-beam echosounder . Relative MBES calibration using reference areas on a seafloor with a high degree of temporal stability can be used to establish a common reference between different MBES systems (Weber et al. 2017; Roche et al. 2018); for a lone MBES system, a reference area can be applied repeatedly in order to compare changes in \(S_b\) due to changes in, e.g., sonar settings, temperature or ageing. Absolute in situ calibration of an MBES can be conducted by the use of a singlebeam echosounder (SBES) as reference (Ladroit et al. 2017; Eleftherakis et al. 2018). This method does not require a temporal stable seabed, and calibrations can be conducted frequently without large practical and time-consuming limitations. For the work presented here, absolute calibration was carried out in the RESON test tank. Separate tank measurements of the transmit sensitivity, the across-track directivity of the receiver elements, tone-burst durations, and the relations between the digitized machine unit value and the sound pressure value in front of the receiver array were conducted. A company proprietary model was applied to estimate the far-field beam pattern. In the sea trials, sonar setting tests served to validate that the scattering strength is independent of changes in tone-burst duration, source level and receive gain. Frequency dependence tests were also conducted, but they are complicated by the fact that the scattering strength may change with frequency depending on the sediment type. Therefore, the assessment included comparisons with \(S_b\)-values obtained by other measurements (Greenlaw et al. 2004; Weber and Ward 2015; Williams et al. 2009). Here, the tests were conducted over a sandy area 1 km outside the harbor of Santa Barbara, CA, USA.
MBES for backscatter
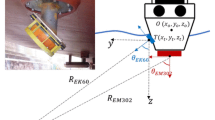
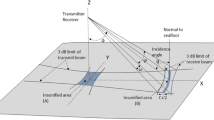
The SeaBat MBES is designed as a Mills Cross array (Urick 1983). It consists of two highly directive, approximately 1D, arrays placed perpendicular to each other. The transmit array emits sound onto an area which is wide in the across-track direction and narrow in the along-track direction. The receiver operates with narrow steered beams in the across-track direction and a much wider along-track opening angle. As a result one obtains an effective insonification which is limited to a small area around the receiver steering angle, see Fig. 1a. Figure 1b shows the bracket-mounted SeaBat T50 transmit and receive arrays applied for the tests presented here. For each receive beam a portion of the backscatter time series around the bottom detection point is applied for the estimation of the seabed backscattering cross section, \(\sigma\) [see, e.g., (Jackson and Richardson 2007) Eq. 2.15 for the definition and ideal case, and Eq. G.4 for a realistic application). Here, the scattering cross section for the MBES is
where \(\langle |p_s|^2\rangle\) is the mean square value of the backscattered sound pressure originating from a large number of small patches within an insonified area A, measured at the distance r. The transmit peak pressure at \(r_0=\) 1 m from the source is \(p_0,\) \(B_{Txz}\) is the normalized accros-track beam pattern of the transmitter, and \(k^{''}_w\) is the exponential coefficient for absorption in the water. The mean square value of the backscattered sound field is obtained from recorded data by
where the function F converts the magnitude of the digital IQ-valueFootnote 1, |a|, into the corresponding magnitude of the complex sound pressure, \(|p_s|,\) at the face of the receiver. Thus, \(|p_s|= p_{peak}\) is the peak pressure of the physical field which is also required for Eq. 1 since \(p_0\) is a peak pressure. The conversion in Eq. 2 depends on the receive gain G as well as the acoustic frequency f. The IQ-data are dimensionless, and \(|p_s|\) is in Pascal. The conversion function is based on measurements conducted in the RESON test tank at normal incidence; it is proprietary, but characteristic curves for \(f=\) 300 kHz are shown in Fig. 15 (see “Measurements of the \(|a|\rightarrow p_{peak}\) relation” section). The normalized across-track beam pattern of the receiver, \(B_{RCxz},\) in Eq. 2 ensures that \(\langle |p_s|^2 \rangle\) can be obtained for beams pointing away from normal incidence. Beam pattern normalization is made with respect to normal incidence.
The insonified area depends on the tone-burst duration \(\tau ,\) the along-track beam pattern of the transmitter, \(B_{Tyz}\) and the across-track beam pattern of the beamformed receiver beams, \(B_{Rxz}\). The equivalent beam widths (Lurton 2010) are derived from \(B_{Tyz}\) and \(B_{Rxz}\), and they are used in the calculation of the insonified area, A. For the current application the seabed is assumed flat in the along-track direction, whereas compensations for height variations are made for the across-track direction (Wendelboe et al. 2012). For the computation of the insonified area and the use of the zero-slope assumption see, e.g., the standard models (Lurton 2010; Amiri-Simkooei et al. 2009; Lurton and Lamarche 2015).
The number of samples applied for the calculation of \(\sigma\) increases gradually with the steering angle \(\vartheta\). From the nadir beam 2 samples are collected, about 7 samples around \(30^\circ ,\) and finally, approximately 13 samples at \(60^\circ\) are collected.
For most types of sea floor the \(\sigma\) depends on the grazing angle between the incoming field and the seafloor, \(\theta _g\). In addition it has been shown that \(\sigma\) depends on the frequency (Greenlaw et al. 2004; Weber and Ward 2015; Williams et al. 2009), hence:
Finally, results are evaluated in terms of the scattering strength
To summarize, estimation of the insonified area A includes \(\tau ,\) \(B_{Tyz}\) and \(B_{Rxz},\) the estimation of \(\langle |p_s|^2 \rangle\) includes \(B_{RCxz}\) and F, and finally, the sound pressure variations of the incoming field along the across-track direction is accounted for by using \(p_0\) and \(B_{Txz}\). In order to obtain the scattering strength, these parameters must be estimated, which is the purpose of the MBES calibration presented in the next section.
Calibration
The calibration was carried out in the RESON test tank, 4.5 m long, 2.5 m wide, and 3.0 m deep. The official uncertainty and accuracy in the test tank is \(\pm \,0.7\) dB for frequencies between 70 and 420 kHz (Teledyne-RESON 2018c). The dimensions of the test tank do not allow for far-field measurements of the transmit beam pattern. Therefore, the along-track beam pattern as well as the across-track beam pattern of the transmitter will be obtained from a company proprietary transducer model. The receive beam pattern generated by the beamformer is also obtained from a model (Murino and Trucco 2000). The tank calibrations include measurements of the transmitted tone-burst duration and measurements of the source level from which the peak sound pressure @ 1 m from the source is obtained. For the receiver, the tank calibrations include measurements of the IQ-magnitude and peak sound pressure relations, and the across-track beam pattern of the receiver elements, see Table 1. The calibrations in the tank have been conducted for center frequencies between 190 and 400 kHz in steps of 10 kHz.
Calibration transducers
The calibrations in the tank are based on the use of quasi-omnidirectional projectors (transmitting transducers) and quasi-omnidirectional hydrophones (receiving transducers). Two hydrophones are used: the RESON TC4034 (Teledyne-RESON 2018b) and the RESON TC4014-5 (Teledyne-RESON 2018a). The TC4034 can be used as either hydrophone or projector. The TC4014-5 is a TC4034 with a built-in preamplifier, which increases the receive sensitivity by about 40 dB. This is advantageous for the measurements of sound pressure levels close to the noise floor. The TC4014-5 can only be used as a hydrophone. Figure 2 is a sketch of the angle definitions used for describing the beam pattern of the hydrophones. The origin of the TC4034 or TC4014-5 is the point on the units where the serial number is engraved. The sensitivity of the hydrophone or projector is measured by a sound field which is, respectively, directed towards or away from the origin in the horizontal plane. This direction is defined as 0\(^\circ\) in the horizontal plane and − 90\(^\circ\) in the vertical plane. Figure 3a shows the transmit sensitivity of a TC4034 (SN-1611293) in the frequency range from 190 kHz up to 410 kHz. The transmit sensitivity is between 131 and 146 dB re 1 \(\mu\)Pa/V\(_{\text {rms}}\)@ 1 m with maximum at the resonance frequency at around 320 kHz. The receive sensitivity of a TC4014-5 (SN-3411076) is shown in Fig. 3b; it ranges from about − 183 to − 179 dB re 1 V\(_{\text {rms}}/\mu\)Pa. The receive resonance frequency is about 360 kHz.
The horizontal and vertical beam patterns of the TC4034 (SN-1611293) are shown in Fig. 4, but only for angles relevant for the measurements of the (\(|a|\rightarrow p_{peak}\)) relation of the receiver presented in “Measurements of the \(|a|\rightarrow p_{peak}\) relation” section). Although the beam patterns have been measured for all frequencies from 190 kHz in steps of 10 kHz up to 400 kHz, they are only shown for five selected frequencies, that is, 200, 250, 300, 350, and 400 kHz. The vertical dashed lines represent bearing angles to the TC4014-5 (SN-3411076) for the measurements of the (\(|a|\rightarrow p_{peak}\)) relation. In the angle range ± 11\(^\circ\) the horizontal beam patterns vary by ± 0.1 dB. In the angle range of − 90\(^\circ \pm\)7\(^\circ\) the vertical beam patterns vary by ± 0.4 dB. The horizontal and vertical beam patterns of the TC4014-5 (SN-3411076) are shown in Fig. 5. The vertical dashed lines represent bearings to the TC4034 (SN-1611293) for the (\(|a|\rightarrow p_{peak}\)) relation measurements. In the angle range ± 11\(^\circ\) the horizontal beam patterns vary by ± 0.5 dB. In the angle range of − 90\(^\circ \pm\)7\(^\circ\) the vertical beam patterns vary by ± 0.5 dB.
For the source level measurements described in “Source level” section and the across-track directivity of the receiver elements described in “Across-track beam pattern of the receiver element, \(B_{RCxz}\)” section, two other calibrated TC4034 hydrophones are used as a hydrophone and projector respectively.
Transmitter
Source level
Source levels are estimated from tank measurements where the TC4034 has been positioned in the center-line of the TC2181 at a distance of 3 m, see Fig. 6. LabView\(^\text {TM}\) is used to control the T50 source level, tone-burst duration, center frequency, and a trigger signal for transmission of the tone-burst. The signal received by the hydrophone is sampled and stored by an NI\(^\text {TM}\) PXI scope, and data is analyzed in Matlab\(^\text {TM}\). The source level is given in dB rms re 1 \(\mu\)Pa, i.e.,
where \(p_0\) is the acoustic peak pressure in Pascal at \(r_0 = 1\) meter away from an equivalent point source, and where \(p_{\text {ref}}=10^{-6}\) Pa is the reference pressure. Since the measurement point is within the near-field of the TC2181 transmitter, the field is not fully developed, and the pressure measured by the hydrophone, \(p_h,\) is lower than \(p_0\). The acoustic pressure measured by the hydrophone can be expressed as
where \(\xi\) \(([m^{-1}])\) has been estimated from a proprietary company model of the TC2181. Thus,
The sensitivity of the hydrophone, \(L_{s},\) is given in dB re 1 \(\text {V}_{\text {rms}}/\mu \text {Pa},\) i.e.,
where \(U_{p}\) is the peak voltage measured by the hydrophone. Thus, for a given \(U_{p}\)-value the pressure at the hydrophone is
Eq. 9 is inserted into Eq. 7 and rearranged so that
By combining Eqs. 10 and 5 the source level can be expressed as
Figure 7 shows a tone-burst with a center frequency of 300 kHz, a sonar commanded pulse duration of 100 \(\mu\)s, and a sonar commanded sound pressure level of 220 dB re 1 \(\mu\)Pa (denoted “Power” in the sonar User Interface (UI)). The signal has been sampled at 3 MHz. The red dashed vertical lines have been obtained from a company proprietary algorithm that detects the beginning and end of the signal. The part of the signal within the detected limits is used to estimate the source level using a DFT. Figure 8 shows the one-sided spectrum obtained by weighting the time-signal with a Flattop window (D’Antona and Ferrero 2006). A source level of 218.7 dB rms re 1 \(\mu\)Pa is estimated, and the difference of − 1.3 dB—with respect to the UI-Power value of 220 dB rms re 1 \(\mu\)Pa—is being compensated for when the scattering strength is estimated.
One-sided amplitude spectrum of the tone-burst in Fig. 7. There is a difference of 1.3 dB between the nominal value (220 dB re 1 \(\mu Pa\)), and the actual value, which is compensated for
Tone-burst duration
The transmitted signal uses a trapezoidal window as an approximation to the Tukey window (Bloomfield 2000). The tapering parameter
is the ratio of total taper-time, \(2 t_T,\) to the total duration, \(\tau\). The computation of the insonified area is based on the assumption that the envelope is rectangular. The transient part is taken into account by estimating the energy-equivalent rectangular-shaped tone-burst. In Fig. 9a the blue and solid curve represents the trapezoidal tapering function which increases in amplitude from \(\Lambda = 0\) at \(t = 0\) up to \(\Lambda = \Lambda _0\) at \(t = t_T\). Within the rising time the energy of the trapezoidal envelope is
and of the energy-equivalent it is
where \(t_R\) is time required for the rectangular envelope to have \(E_{R}=E_{T}\) (Fig. 9b). Thus, \(t_R = t_T/3\). Consequently, the duration of the energy-equivalent envelope is
which yields
The tone-burst applied here has \(\epsilon =0.2,\) which means that \(\tau _{e} \approx 0.87 \tau\). For small grazing angles where \(\tau\) is proportional to the insonified area (Lurton and Lamarche 2015), a lack of compensation will lead to an error estimate of \(S_b\) of approximately − 0.6 dB.
The tone-burst duration estimate based on the detected times of the beginning and end of the signal shown in Fig. 7 is 104 \(\mu\)s. It corresponds to a difference of 0.17 dB. Although the uncertainty of the edge detection method has not been quantified, an error of 4\(\%\) is believed to be within the uncertainty of the edge detection performance. Thus, the nominal \(\tau\)-value is maintained as the duration of the tone-burst.
Along-track beam pattern, \(B_{Tyz}\)
For the TC2181 transmitter the opening angle in the along-track direction depends on frequency. For example, in the far-field it is about \(2^\circ\) at 200 kHz and \(1^\circ\) at 400 kHz. The near-field of the TC2181 transmitter extends about 20 meters depending on frequency. Figure 10 shows how the along-track main beam increases with decreasing range. Thus, when computing the scattering cross section the influence from depth and frequency on the along-track beam pattern is taken into account. The transmit beam patterns predicted by the company proprietary model have regularly been compared with measured values in the near field (3 m) and on a single occasion in the far field (20 m) in a large tank at an external facility. Around the main lobes the predictions match well with the measurements, which supports the use of the model at other ranges.
Across-track beam pattern, \(B_{Txz}\)
The across-track beam pattern of the TC2181, \(B_{Txz},\) is based on results obtained from the transducer model. It is approximately range independent, and consequently, only depends on frequency. The − 3 dB opening angle is about \(\pm 75^\circ\) for all frequencies (Fig. 11) with a deviation of about ± 0.5 for angles above approximately 55\(^\circ\).
SeaBat T50 receiver (EM7218)
Measurements of the \(|a|\rightarrow p_{peak}\) relation
The setup used for measuring the relation between the magnitude of the digital IQ-signal, |a|, and the corresponding peak sound pressure at the face of the receive array, \(p_{peak},\) is sketched in Fig 12. The TC4034 (SN-1611293) transmitter is positioned 2.75 m from the center of the receiver along a line perpendicular to the receiver surface. The measurement includes a sequence of tone-bursts, where the input voltages to the TC4034 vary in order to generate different sound pressure levels in front of the receiver array. The sequence is controlled by LabView\(^\text {TM}\). An NI\(^\text {TM}\) PXI generates the requested tone-burst and transmits the signal to the TC4034. To obtain the highest possible source levels, a 50 dB amplifier is used. The maximum sound pressure level is governed by the maximum allowed input voltage of 100 V to the TC4034. For each sound pressure level the EM7218 records the in-phase and quadrature signals for all 256 channels and for all receive gains from 0 to 83 dB. Five pings are collected at each setting for averaging. The transmit sensitivity of TC4034 sound source is not being applied in the computations; the TC4034 transmitter is stretched to its upper voltage limit where the transmit sensitivity might change, and in addition, the 50 dB amplifier is not calibrated. Instead each acoustic tone-burst is measured by the TC4014-5 (SN-3411076) mounted next to the EM7218 and the signal is digitized by the NI\(^\text {TM}\) PXI and stored on the LabView\(^\text {TM}\) PC. Figure 13 shows the receiver in a bracket together with the TC4014-5 hydrophone with the housing for a preamplifier. Another TC4034, which is not the SN-1611293, is used as an extra reference hydrophone as a safety validation that the sound pressure levels measured by TC4014-5 levels are correct. The advantage of using a TC4034 as sound source is its nearly omnidirectional property, which should lead to a uniform sound pressure level across all receiver channels as well as on the receiving element on the TC4014-5. Meanwhile, as it was shown in “Calibration transducers” section, the beam patterns of the TC4034 (Fig. 4) and TC4014-5 (Fig. 5) are not perfectly omnidirectional. Figure 14a shows the vertical (left) and horizontal (right) offsets between the TC4034 and TC4014-5. The resulting deviations from the omnidirectional assumption are shown in Fig. 14b, and vary approximately \(\pm 0.4\) dB. Thus, the estimated calibration errors are within the tank uncertainty of ± 0.7 dB, and therefore, the experimental setup is considered acceptable.
Measurement of the EM7218 receiver sensitivity. The TC4034 works as a transducer with an approximately omnidirectional directivity and it insonifies the receiver array. A TC4014-5 hydrophone is mounted next to the EM7218, and it measures the sound pressure level, while the EM7218 acquires raw IQ data
Figure 15 shows, for a single receiver channel, |a| given in EM7218 machine units as a function of \(p_{peak}\) measured by the TC4014-5 and given in dB re 1 \(\mu\)Pa. The curves correspond to 6 different values of the receive gain G. The frequency of the incoming field is 300 kHz. The maximum value of |a| is \(2^{15}=32768\) indicated by the black, solid, horizontal line. The peak sound pressure level at the face of the receiver ranges between 115 dB re 1 \(\mu\)Pa to about 165 dB re 1 \(\mu\)Pa.
Across-track beam pattern of the receiver element, \(B_{RCxz}\)
The across-track beam pattern of the individual receiver elements must be compensated for. Figure 16 shows the measurement applied in the RESON test tank. The receiver array is mounted on a pole and can rotate around the vertical axis. A spherical sound source (TC4034) is positioned 3 m from the pole and it is used to insonify the array at angles from \(\vartheta =-90^\circ\) to \(\vartheta =90^\circ\) in steps of \(1^\circ\). For each angle raw IQ data is recorded, and the median value of the IQ-magnitude, \(\widetilde{|a|},\) across the 256 channels is found. This procedure results in a vector where each element is the \(\widetilde{|a|}\)-value associated with a discrete \(\vartheta\)-angle. Subsequently, this vector is normalized by its maximum value, and \(B_{RCxz}\) is obtained. This is repeated for each frequency. Figure 17 shows two examples of \(B_{RCxz}\) obtained at 220 and 360 kHz. The part of the tank calibration that involves the measurement of \(B_{RCxz}\) was conducted at 23\(^\circ\)C, whereas the sea tests were conducted at 15\(^\circ\)C. There is some degree of concern that the shape of \(B_{RCxz}\) will change with temperature. As water temperature decreases, the impedance contrast between the water and the receiver front layer increases, and thus, the beam pattern will pull back. A rough estimate provided by the array designer suggests that a temperature change from 23\(^\circ\)C down to 15\(^\circ\)C may result in a reduction of \(B_{RCxz}\) from 0 dB at 50\(^\circ\) steering angle down to − 1.5 dB at 70\(^\circ\). However, it is still uncertain by how much \(B_{RCxz}\) will decrease, and therefore, a temperature compensation cannot be included before further investigations have been carried out. Fortunately, the pull back of \(B_{RCxz}\) is not frequency dependent.
Beamformer
With 256 receiver channels the EM7218 has an aperture size of approximately 40 cm. At 400 kHz the center beam, i.e., the beam with the steering angle \(\vartheta =0,\) has a − 3 dB beam width of 0.5\(^\circ\). As the steering angle increases, the width of the main lobe increases as \(1/\cos (\vartheta )\) due to a reduced effective aperture size. The beamformer uses a -30 dB Chebyshev window (Harris 2004) to suppress side lobes. Auto-focusing ensures that the main-lobe width is approximately constant for all ranges. Figures 18a and b show the beam pattern for two steering angles at 400 kHz. Approximations are made when using fixed-point numbers on Field-Programmable Gate Array (FPGA); however, this is not expected to produce any significant errors. A tank measurement, equivalent to the one sketched in Fig. 16, has shown that at normal incidence, the magnitude level over all channels approximately follows a normal distribution, with 68% of the data within 0.36 dB of the median value, and a coefficient of variation of |a| of about 5\(\%\). The phase error has been estimated by acknowledging that the incoming field is spherical, and a standard deviation of the phase of about 5\(^\circ\) has been found. For an incoming field with an angle of \(\vartheta =70^\circ\) the magnitude level follows approximately a normal distribution with 68% of the data within 0.80 dB of the median, and a coefficient of variation of |a| of about 10\(\%\); the standard deviation of the estimated phase is about 5\(^\circ\). For both cases this will yield a beamformer error of less than 0.05 dB provided that beamforming is conducted using floating point numbers. For large amplitudes the beamformer may clip the signals which typically occurs in the center beam at normal incidence. The T50 user interface sets up a warning if the beamformer is clipping, so the operator can reduce either the source level or the receive gain. The time variant gain (TVG) delivers gain values with the same gain precision as the fixed gain. The TVG curve is an inherent part of the \(S_b\)-calculation.
Experimental site
The T50 field tests have been conducted 1 km offshore from the harbor of Santa Barbara, California, see Fig. 19. \(S_b\)-invariance tests with respect to changes in the receive gain and the tone-burst duration were conducted at 15 m depths. Due to a setting error no GPS data were recorded for the receive gain and the tone-burst duration tests, and consequently, their locations are not marked in Fig. 19. Fortunately, GPS data were recorded for the source level invariance test and the frequency dependence measurements. The source level invariance test was conducted at a depth of 10 m along a 195 m line, with a vessel speed of 2 knots. The frequency dependence measurements were conducted along four different lines within a sector of 356\(\times\)471 m. The average vessel speed was approximately 0.33 knots, so the boat was almost drifting. The lengths of the lines vary between 30 and 100 m, and the lengths are governed by the ping rate as well as the number of pings per frequency, which varies between 100 and 300 pings. The average depth within the sector is approximately 16 m. Figure 20a shows the bathymetric map obtained from Line 1 (\(L_1\)), and Fig. 20b the corresponding backscatter mosaic. The backscatter values in the mosaic are a result of a processing method, where the angle dependency on \(S_b\)-values, has been filtered out. The mosaic is based on data obtained from a sequence beginning at 190 kHz in steps of 10 kHz up to 400 kHz; preferably, it should have been made on a data set where the frequency is constant along the line, but such a data set was, unfortunately, never obtained. Meanwhile, the mosaic shows no dramatic changes in the backscattering level along the line, indicating that the seabed is homogeneous. No environmental characterization was made in connection with the test. However, back in 2009 the U.S. Geological Survey reported that the mean grain size over this area is 0.26 mm, i.e., medium-fine sand (Barnard et al. 2009). About 10 km west of Santa Barbara harbor, close to the university (UCSB), the inner continental shelf has a high density of naturally occurring gas and oil seeps (Fleischer et al. 2001). For the experimental site sonar images did not show any signs of bubbles. The water sound speed \(c_w\) is measured with a sound velocity probe (SVP) mounted next to the MBES. The water temperature T is measured with a thermometer inside the housing of the SVP. The temperature is not assumed very different from that of the ambient water. The MBES is mounted on a pole to the port side of vessel at a depth of about \(D=1.5\) m. Given D, \(c_w,\) and T, the salinity S can be estimated [(Medwin 1975), Eq. 1 ]. Subsequently, by assuming a pH value of 8, the acoustic absorption in the seawater is estimated (Jackson and Richardson 2007; Francois and Garrison 1982a, b), see Table 2. The sonar settings are changed by remote commands from a separate PC, which enables the use of numerous different settings over a short period of time. For each beam recorded \(S_b\)-values are stored as time series around the time of the bottom detection. The \(S_b\)-values are converted from the logarithmic domain into the absolute domain in order to obtain the corresponding \(\sigma\)-values. For each ping the mean \(\sigma\)-value is found within each beam, where it will be linked to the estimated grazing angle around the bottom detection point. All \((\sigma ,\theta )\) pairs obtained from a ping are sorted into bins of 1\(^\circ\) width ranging from 20\(^\circ\) up to 90\(^\circ\). Next, the mean and standard deviations of all the pings are found.
Survey lines 1 km outside Santa Barbara harbor, CA (Google Earth). \(\Box\): Frequency dependence test with the four lines \(L_1\)-\(L_4\) and \(\Diamond\): Source level test. No GPS-data were recorded during the receive gain and tone-burst tests, but they have been conducted within the area shown on the map
Results
The seafloor echo signals processed by the sonar have been beamformed in the equidistant mode, i.e., a beamforming mode with a constant ground range distance between the bottom detection points.
Sonar settings invariance test
The purpose of the Sonar Settings Invariance Tests is to validate that the estimated scattering strengths are invariant according to changes in source level, receive gain and the tone-burst duration. These tests have been conducted at 400 kHz. The source level settings is varied from 210 to 220 dB re 1 \(\mu\)Pa in 1 dB steps, while all the other sonar settings are kept constant. To each source level setting 300 pings have been recorded. Figure 21 shows the angular response (AR) curves obtained from the 11 measurements. For grazing angles below 50\(^\circ\) the variation is ± 1–2 dB, and above it is ± 0.5–1 dB. Figure 22 shows the AR-curves obtained at the receive gain test. The gain was varied in steps of 2 dB between 2 and 34 dB, while all other settings were constant. Data obtained at gain settings above 34 dB resulted in clipping and are not included here. Each curve represents an average of 100 pings. For each angle value the \(S_b\)-estimates vary by approximately ± 1–2 dB. Figure 23 shows the scattering strengths obtained when the tone-burst durations vary between 30 and 300 \(\mu\)s in 10 \(\mu\)s increments. Each sub-figure represents the average scattering strength taken from a 10\(^\circ\) angle interval, except at the lowest grazing angle, where it is 6\(^\circ\). About 100 pings were applied in the averages. The overall result is a random fluctuation around a mean value of about ± 1.5–2 dB. No trends as function of pulse duration are observed. The drop around 240 \(\mu s\) can probably be explained by a sudden change in the seafloor properties. The fluctuations are largest near normal incidence.
Frequency dependence test
The multifrequency measurements conducted along the lines \(L_1\)-\(L_4,\) shown in Fig. 19, range from 190 kHz in steps of 10 kHz up to 400 kHz. \(S_b\)-estimates are divided into 14 grazing angle bins of 5\(^\circ\) width from 20\(^\circ\) up to 90\(^\circ\). Figure 24 shows the \(S_b\)-estimates obtained from \(L_1\). The blue curves are the estimated mean \(S_b\)-values with the corresponding standard deviations on the error bars. The general picture shows a scattering strength that increases with increasing frequency. At 350 kHz a transition occurs, above which the scattering strength increases with frequency at a higher rate. For each grazing angle bin the scattering cross section as a function of frequency is fitted to a power function of the form
Result from Line 1 in Fig. 19. The blue curves are the estimated mean \(S_b\)-values with the corresponding standard deviations on the error bars. The green curves are the power law fits for \(f\le 350\) kHz, and the red curves for \(f> 350\) kHz
where f is the frequency [Hz], and where the parameter set, \((\alpha _1,\beta _1),\) is applied in the frequency range from 190 kHz up to a transition frequency \(f_t,\) which will be defined below, and where finally \((\alpha _2,\beta _2)\) is applied between \(f_t\) and 400 kHz. The power function estimations are carried out in the logarithmic domain by the use of the classical unweighted linear least square (LS) method. The chosen limit frequency between the low and high frequency LS-estimation is 350 kHz. The transition frequency \(f_t\) is the frequency, where the two power functions are equal. If they do not become equal between 190 and 400 kHz, \(f_t\) will be set equal to 350 kHz. The green and red curves in Fig. 24 represent the estimated power laws below and above 350 kHz respectively. The two sets of estimated power function parameters, (\(\alpha _1,\)\(\beta _1\)) and (\(\alpha _2\),\(\beta _2\)), are shown in Fig. 25 for all grazing angles, and for all four survey lines, \(L_1\)-\(L_4\). Considered from an average point of view, the \(\beta _1\)-values, the exponents for the low frequency regime, vary between 1 and 1.3 for angles below \(30^\circ\); as the grazing angle increases they decay approximately monotonically down to a common value of about − 0.1 at \(90^\circ\). For the high frequency regime the \(\beta _2\)-exponents increase from values of 1.3 to 2.3 at \(22.5^\circ\) up to a value of about 5 between \(60^\circ\) and \(90^\circ\). Plots of the scaling factors \(\alpha _1\) and \(\alpha _2\) are included for completeness.
Figure 26 shows the residuals between the \(S_b\)-values and the estimated power functions from the four lines. If one leaves out the 210 kHz component, the residuals do not exceed ± 1.5 dB for grazing angles below \(50^\circ ,\) and they all appear very coincident. It is unlikely that these coincident residuals can be explained by the same sudden local change in seafloor properties in all four measurements. It is unclear whether the constant residual levels can be explained by scattering mechanisms in the sediment or if they are caused by calibration errors. Above \(50^\circ ,\) the degree of correlation between the residuals drops slightly as the grazing angle approach \(90^\circ\). The 210 kHz component is deviating about 1.5–2 dB at all angles, and this is most likely caused by an error within the MBES-system.
Next, the \(S_b\)-estimates represented by the four power function fits will be compared with results obtained by other authors. Greenlaw et al. (2004) present data obtained from a sandy sediment with an average grain size of 0.41 mm (medium sand). The grazing angle was approximately \(\theta _g=20^\circ\). They obtained a spectral exponent of \(\beta =1.4\) between 265 and 400 kHz. Here, the estimated power-law parameters for \(\theta _g=22.5^\circ\) are listed in Table 3. The estimated transition frequencies range from 291 to 333 kHz. Parameters estimated for the entire frequency range from 190 to 400 kHz, (\(\alpha ,\beta\)), are also included in order to compare with the results from Greenlaw et al. (2004). Figure 27 shows the \(S_b\)-values as obtained from the estimated power functions for lines 1–4 for \(\theta _g = 22.5^\circ\). The results are presented in terms of the Lambert parameter (Williams et al. 2009) given as
The Lambert parameters for sand at \(\theta _g=22.5^\circ\). A straight-line fit to the five data points by Greenlaw et al. (2004) is also included (the thin dashed line). The Lambert-values from \(L_1\)–\(L_4\) are obtained from the power law model in Eq. 17, and by the use of the input parameters sets \((\alpha _1,\alpha _2,\beta _1,\beta _2,f_t)\) from Table 3
The mean value of the exponent of the four lines for the entire frequency range is \(\beta =1.31,\) which is close to the value found by Greenlaw et al. Finally, the \(S_b\)-estimates obtained here are about 1–2 dB higher than their values.
Weber and Ward (2015) measured the scattering strengths at a grazing angle of \(45^\circ\) at frequencies between 170 and 250 kHz; the sediment was sand with a mean grain size of 0.25–0.35 mm. They found spectral exponents of \(\beta =-0.09\) and \(\beta =0.32\) at two different sites. At SAX04 (Williams et al. 2009) scattering strengths were obtained for grazing angles between \(25^\circ\) and \(48^\circ\) in the frequency range from 200 to 500 kHz. The average grain size of the sand at SAX04 was 0.36 mm, but the sediment was a mixed composition of sand in mud. Table 4 shows the estimated power law parameters at \(\theta _g = 42.5^\circ\) obtained here. Figure 28 shows the estimated power law fit for \(\theta _g = 42.5^\circ\) for lines \(L_1\)–\(L_4,\) together with the \(S_b\)-values acquired by Weber and Ward (2015), Fig. 7), and finally, from SAX04 the mean values of \(S_b\) between \(\theta _g=39.4^\circ\) and \(44.7^\circ\) [(Williams et al. 2009), Fig. 8]. The spectral slopes found by Weber et al. 2017 are significantly weaker than the ones estimated here. The scattering strengths obtained at \(L_1\)-\(L_4\) are 2–3 dB lower than the values obtained at the site with \(\beta =-0.09\); they are about 1 dB higher than the \(S_b\)-values from the site with \(\beta =0.32\). The scattering strengths obtained at \(L_1\)–\(L_4\) are about 4 dB higher than the ones obtained at SAX04, but in terms of the spectral slope the SAX04 data do also show a change in the spectral slope between 300 and 350 kHz.
The scattering strength for sand at \(\theta _g=42.5^\circ\). Included are also \(S_b\)-data from two sandy sites obtained by Weber and Ward (2015), and data from SAX04 (Williams et al. 2009). The \(S_b\)-values from \(L_1\)–\(L_4\) are obtained from the power law model in Eq. 17, and by the use of the input parameters in Table 4
The author has not been able to find any results published on the scattering strength at normal incidence in the frequency range 190–400 kHz from a sandy seabed. However, Sessarego et al. (2008) have conducted normal incidence reflection measurements in a laboratory over flattened medium sand with a mean grain size of 0.25 mm. Unlike the laboratory measurement, the scattering strengths from \(L_1\)–\(L_4\) are obtained over a rough seabed, where the coherent reflection most likely is insignificant compared to the incoherent. Hence, the reflection loss based on the incoherent intensity is considered here, and data taken from [Sessarego et al. (2008), Fig. 6, top-left] are shown in Fig. 29. Table 5 shows the estimated power law parameters at \(\theta _g = 87.5^\circ\) obtained here. There is a drop in reflection loss of about 3 dB between 250 and 330 kHz, where a similar increase is not observed in the scattering strengths from \(L_1\)–\(L_4,\) see e.g., Fig. 24 for the case where \(85^\circ < \theta _g \le 85^\circ\). Above 330 kHz the reflection loss decreases to − 10.5 dB at 400 kHz with the same rate as the \(S_b\)-estimates from \(L_1\)–\(L_4\) increase.
The scattering strength for sand at \(\theta _g=87.5^\circ\). Included is also the incoherent reflection loss from flattened medium sand obtained in a laboratory (Sessarego et al. 2008)
Discussion
The angular response curves obtained at the different source levels gain settings all lie within a band \(\Delta S_b \approx \pm 1\) dB. The fluctuations are attributed to the random nature of the acoustic interaction with the seabed. The tone-burst duration test results in \(\Delta S_b\)-values fluctuating about 2–3 dB around the mean scattering strength at each grazing angle interval. Near normal incidence, however, the variations can be up to 4 dB for tone-burst durations above 100 \(\mu\)s. In general, no trends as a function of either source level, receive gain, or tone-burst duration are observed.
For the frequency dependence test, in general the power law estimations lead to residuals that are within ±1.5 dB (when the 210 kHz is not included). Provided the sediment is still medium sand as reported almost 10 years ago (Barnard et al. 2009) the scattering strengths obtained here are close to what researchers have found on medium sand for grazing angles of 22\(^\circ\) and 45\(^\circ\). The SAX04 data also seem to be described by two different regimes with a transition frequency very close to ones found here, i.e, at about 324–330 kHz. The resemblance is striking, and hence, the sediment here seems to have a scattering characteristics similar to the sediment at SAX04. One can only speculate about the causes: gas bubbles, shells in the sediment, bioturbations, and mud mixed with sand as at SAX04. Nevertheless, Hefner et al. (2010) conducted experiments in a large fresh water pool over a diver-smoothed sand bottom at frequencies between 200 and 500 kHz, and at grazing angles between 10\(^\circ\)–60\(^\circ\). Measurements with shell fragments distributed over the flat sand were also made. The results indicate that for sand, as well as for sand with shell fragments on top, a change in spectral slope occurs between 300 and 400 kHz ((Hefner et al. 2010), Fig. 4). Thus, it seems possible that for medium sand a transition between two different regimes occur around 320–340 kHz. At normal incidence the reflection loss decays and the scattering strength rises with the same rate above approximately 330 kHz. However, the reduced reflection loss between 250 and 330 kHz is not supported by similar increase in the scattering strength, and a reason for this disagreement is not possible to provide here.
Surveys over the test lines with fixed sonar settings, including the frequency, have unfortunately not been obtained; bathymetric maps and mosaics would have provided the investigation with essential information about the degree of homogeneity of the sediment. As already stated the residuals in Fig. 26 from \(L_1\)–\(L_4\) are almost the same (at least for \(\theta _g<50^\circ\)), and so are the estimated power laws. Therefore, a sudden significant change in seafloor properties at all four lines is considered unlikely.
Notes
\(a = a_I + i a_Q,\) where \(a_I\) is the in-phase component, \(a_Q\) is the quadrature component and i is imaginary number (Papoulis 1984).
References
Amiri-Simkooei A, Snellen M, Simons DG (2009) Riverbed sediment classification using multibeam echo-sounder backscatter data. J Acoust Soc Am 26(4):1724–1738. https://doi.org/10.1121/1.3205397
Barnard P, Revell D, Hoover D, Warrick J, Brocatus J, Draut A, Dartnell P, Elias E, Mustain N, Hart P, Ryan H (2009) Final report to the beach erosion authority for clean oceans and nourishment (BEACON), Coastal processes study of Santa Barbara and Ventura counties. https://pubs.usgs.gov/of/2009/1029. Accessed 5 Mar 2018
Bloomfield P (2000) Fourier analysis of time series: an introduction. Wiley, New York
D’Antona G, Ferrero A (2006) Digital signal processing for measurement systems. Theory and applications. Springer, Milano
Eleftherakis D, Berger L, Bouffant NL, Pacault A, Augustin JM, Lurton X (2018) Backscatter calibration of high-frequency multibeam echosounder using a reference single-beam system, on natural seafloor. In: G Lamarche , X Lurton (eds) Marine geophysical research, seafloor backscatter from swath mapping echosounders: from technological development to novel applications, Springer, New York
Fleischer P, Orsi TH, Richardson MD, Anderson AL (2001) Distribution of free gas in marine sediments: a global overview. Geo-Mar Lett 21:103–122. https://doi.org/10.1007/s003670100072
Foote KG, Zhu D, Hammar TR, Baldwin KC, Mayer LA, Hufnagle LC, Jech JM (1988) Protocols for calibrating multibeam sonar. J Acoust Soc Am 117(4):2013–2027. https://doi.org/10.1121/1.1869073
Francois RE, Garrison GR (1982a) Sound absorption based on ocean measurements: Part I: Pure water magnesium sulfate contributions. J Acoust Soc Am 72:896–907. https://doi.org/10.1121/1.388170
Francois RE, Garrison GR (1982b) Sound absorption based on ocean measurements: Part II: Boric acid contributions and equation for total absorption. J Acoust Soc Am 72:1879–1890. https://doi.org/10.1121/1.388673
Greenlaw CF, Holliday DV, McGehee DE (2004) High-frequency scattering from saturated sand sediments. J Acoust Soc Am 115(6):2818–2823. https://doi.org/10.1121/1.1707085
Harris FJ (2004) Multirate signal processing for communication systems, 1st edn. Prentice Hall PTR, London
Heaton JL, Rice G, Weber TC (2017) An extended surface target for high-frequency multibeam echo sounder calibration. J Acoust Soc Am 141(4):388–954. https://doi.org/10.1121/1.4980006
Hefner BT, Jackson DR, Ivakin AN, Tang D (2010) High frequency measurements of backscattering from heterogeneities and discrete scatteres in sand sediments. Proc Eur Conf Underwater Acoust 3:1386–1390
Hellequin L, Boucher J, Lurton X (2003) Processing of high-frequency multibeam echo sounder data for seafloor characterization. IEEE J Ocean Eng 28(10):1–12. https://doi.org/10.1109/JOE.2002.808205
Jackson DR, Richardson MD (2007) High-frequency seafloor acoustics. Springer, New York
Ladroit Y, Lamarche G, Pallentin A (2017) Seafloor multibeam backscatter calibration experiment: comparing 45\(^\circ\)-tilted 38-khz split-beam echosounder and 30-khz multibeam data. In: Lamarche G, Lurton X (eds) Marine geophysical research, seafloor backscatter from swath mapping echosounders: from technological development to novel applications. https://link.springer.com/article/10.1007/s11001-017-9340-5
Lanzoni JC, Weber TC (2011) A method for field calibration of a multibeam echo sounder. Proceedings of OCEAN’s 2011. https://doi.org/10.23919/OCEANS.2011.6107075
Lanzoni JC, Weber TC (2012) Calibration of multibeam echo sounders: a comparison between two methodologies. Proc Mtgs Acoust 17(070040):1–12 .https://doi.org/10.1121/1.4772734
Lurton X (2010) An introduction to underwater acoustics. Principles and applications. Springer, New York
Lurton X, Lamarche G (2015) Backscatter measurments by seafloor mapping sonars. Guidelines and recommendations. Geohab report. http://geohab.org/publications/.Last Accessed 8 Mar 2018
Medwin H (1975) Speed of sound in water: a simple equation for realistic parameters. J Acoust Soc Am 58(6):1318–1319. https://doi.org/10.1121/1.380790
Murino V, Trucco A (2000) Three-dimensional image generation and processing in underwater acoustic vision. Proc of IEEE 88(12):1903–1946. https://doi.org/10.1109/5.899059
Papoulis A (1984) Signal analysis. McGraw-Hill, New York
Roche M, Degrendele K, Vrignaud C, Loyer S, Le Bas T, Augustin JM, Lurton X (2018) Control of the repeatability of high frequency multibeam echosounder backscatter by using natural reference areas. In: Lamarche G, Lurton X (eds) Marine geophysical research, seafloor backscatter from swath mapping echosounders: from technological development to novel applications. https://link.springer.com/article/10.1007/s11001-018-9343-x
Sessarego JP, Guillermin R, Ivakin AN (2008) High-frequency sound reflection by water-saturated sediment interfaces. IEEE J Ocean Eng 33(4):375–385. https://doi.org/10.1109/JOE.2008.2002457
Teledyne-RESON (2018a) Hydrophone TC4014 broad band spherical hydrophone. http://www.teledynemarine.com/reson-tc-4014Last Accessed 7 Mar 2018
Teledyne-RESON (2018b) Hydrophone TC4034 broad band spherical hydrophone. http://www.teledynemarine.com/reson-tc-4034. Last Accessed 7 Mar 2018
Teledyne-RESON (2018c) Teledyne-RESON Acoustic tank accuracy and uncertainty. http://www.teledynemarine.com/Lists/Downloads/RESONtankTest.pdf.Last Accessed 7 Mar 2018
Urick RJ (1983) Principles of underwater sound, 3rd edn. Peninsula Publishing, Los Altos
Weber TC, Ward LG (2015) Observations on backscatter from sand and gravel seafloors between 170 khz and 250 khz. J Acoust Soc Am 138(4):2169–2180. https://doi.org/10.1121/1.4930185
Weber TC, Rice G, Smith M (2017) Toward a standard line for use in multibeam echo sounder calibration. In: Lamarche G, Lurton X (eds) Marine geophysical research, seafloor backscatter from swath mapping echosounders: from technological development to novel applications. https://link.springer.com/article/10.1007/s11001-017-9334-3
Wendelboe G, Barchard S, Maillard E, Bjorno L (2012) Towards a fully calibrated multibeam echosounder. Proc Mtgs Acoust 17(070025):1–9. https://doi.org/10.1121/1.4767979
Williams KL, Jackson DR, Tang D, Briggs KB, Thorsos EI (2009) Acoustic backscattering from a sand and a sand/mud environment: experiments and data/model comparisons. IEEE J Ocean Eng 34(4):388–398. https://doi.org/10.1109/JOE.2009.2018335
Acknowledgements
The Innovation Fund Denmark partly sponsored the development of the T50 system. The author would like to thank colleagues at Teledyne RESON: Henrik Dahl for building the calibration arrangement in the test tank, and Jesper T. Christoffersen for helpful discussions and input related to the T50 system. The author would also like to thank former colleagues James Coleman, the vessel operator, for providing expert support on the sea and for building the data acquisition software, and finally, Eric Maillard for contributing with algorithms, knowledge, and guidance during the work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wendelboe, G. Backscattering from a sandy seabed measured by a calibrated multibeam echosounder in the 190–400 kHz frequency range. Mar Geophys Res 39, 105–120 (2018). https://doi.org/10.1007/s11001-018-9350-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11001-018-9350-y