Introduction and motivation

Multibeam echo sounders (MBES) are frequently used for collecting both bathymetry and acoustic backscatter from the seafloor. Uses of MBES data include charting for navigation (Mayer 2006; Calder and Mayer 2003), benthic habitat mapping (e.g., Kostylev et al. 2001; Brown and Blondel 2009), marine geology (e.g., Gardner et al. 2001, 2003; Grevemeyer et al. 2002), and the identification of natural resources (e.g., Naudts et al. 2008). In each of these applications, the seafloor backscatter can be used to help infer characteristics of the substrate because of the backscatter’s dependence on the substrate grain size, surficial roughness, and volumetric inclusions. When using MBES systems, significant care is taken in removing artifacts and biases in seafloor bathymetry using, for example, the ubiquitous patch test (Herlihy et al. 1989). In contrast, seafloor backscatter often remains uncalibrated. A lack of calibration for MBES seafloor backscatter hinders interpretations of seafloor composition, the identification of substrates of a specific type when using multiple systems, and the ability to detect changes in substrate over time.

There are multiple types of acoustic backscatter calibrations that can be performed for a MBES system, and the most appropriate calibration will depend on the user’s overall objectives. At the most rigorous level, an absolute MBES backscatter calibration is useful in that it becomes easier to compare results with those of another: a reported angle-dependent seabed scattering strength is then independent of the system, apart from the frequency. Absolute backscatter estimates are also useful when comparing results to models (e.g., e.g., Williams et al. 2009), or when developing new models (e.g., Jackson et al. 1986). There are many components to consider when conducting an absolute MBES calibration, including the projector sensitivity and beam pattern, the receive element sensitivity and beam pattern, the analog signal conditioning electronics (e.g., gain and filtering), the analog-to-digital converters, the beamformer, and subsequent digital manipulation of the received signal (Brown et al. 2015). These components collectively lead to a requirement for a calibration that is a function of both beam-angle and frequency (e.g., a calibration for a MBES operating at 200 kHz is not valid for the same system when operating at 400 kHz). Absolute calibration procedures exist (e.g., Foote et al. 2005; Heaton et al. 2017), but often require specialized equipment such as acoustic test tanks. Given the complexity of MBES systems, and the lack of knowledge regarding their detailed construction (e.g., complete details of the signal conditioning electronics), some or all of the MBES components are typically treated as ‘black boxes’ during calibration. The methodology employed by Heaton et al., 2017, for example, combines the entire MBES system into a single calibration that is valid at one gain and power setting. Separate calibrations of gain and power settings (Greenaway and Weber 2010) then complete the calibration. Due in part to the requirements for specialized equipment, there are no broadly utilized techniques for MBES field calibration that are analogous to the commonly employed standard sphere calibrations exploited by users of split-beam echo sounders (Demer et al. 2015).

An alternative to the absolute calibration is a relative calibration (e.g., Clarke et al. 2008; Greenaway and Rice 2013; Rice et al. 2015). In the case of a relative calibration, the seabed backscatter observed with multiple systems, or with the same system at multiple times (e.g., spanning months or years), is referenced to a single system at a single time. Such a calibration would be related to an absolute reference only as much as the reference system is, but provides a value to users of MBES even if the reference system is itself uncalibrated. The many motivations for performing a relative calibration include using multiple systems (e.g., on multiple launches) at the same survey site and making an aggregate backscatter mosaic; revisiting an area to detect changes in substrate type; and comparing substrate types in the same general area but with different systems or different system settings, as might happen when working at different locations but out of the same port.

One way in which to generate a relative calibration, and the subject of this work, is to develop a ‘standard line’. A standard line is a common survey line for which seafloor backscatter is collected with multiple MBES (or the same MBES over time). Seafloor backscatter estimates of, presumably, the same substrate can then be compared and brought to a common reference level. Standard lines of this nature have been in use for some time for fisheries applications (e.g., Johannesson and Mitson 1983), but have not been developed for use with MBES. There are, of course, pitfalls in such a procedure. Scattering from the seabed—even if the substrate remains identical—is a random process and so care must be taken in generating a useful ensemble average for any specific calibration location. The standard line should also be located in an area that is convenient for MBES users—in the entrance to a port, for example. The substrate at these locations, which sometimes experience high currents, sedimentation, or significant bioturbation, can change over time and can lead to bias in the calibration results. Spatial heterogeneity in the substrate types can manifest as increased variability in seafloor backscatter and can, potentially, increase the variability of the calibration result.

In this work we describe our efforts toward establishing a standard line at the mouth of the Piscataqua River in New Castle, New Hampshire, USA. In developing this standard line, we conducted a detailed repeat-survey over many months using an absolutely calibrated split-beam echo sounder (SBES) to collect acoustic observations at 200 kHz from the seabed. We use the SBES observations to assess the temporal stability of the standard line. We subsequently choose a calibration location within the line to use as a relative calibration site, and select a reference MBES survey conducted with a Kongsberg EM 2040 to generate a relative calibration dataset. Our approach is to use the ‘raw’ angular-dependent seafloor backscatter as a reference, and we apply this reference to two other data sets: a Reson 7125 MBES survey and a survey conducted with a second EM 2040. The three 200 kHz MBES survey span 3 years, two MBES manufacturers, two different MBES from the same manufacturer, and two different operating modes for the same model MBES. Our objective in describing and assessing this calibration procedure is to (a) provide and promote a methodology for a relative calibration that can be used by MBES users in situ; and (b) provide an example, over several different substrate types as well as different MBES types, that helps demonstrate the level at which the proposed relative calibration procedure might be expected to succeed in removing bias between different MBES backscatter surveys.

The NEWBEX standard line

Several MBES surveys are conducted each year in the general vicinity of Portsmouth, NH, in support of the educational and research missions of the Center for Coastal and Ocean Mapping at the University of New Hampshire (UNH). These surveys are most often performed during day trips based out of the UNH marine facility in New Castle, NH. This marine facility also serves as home port for the NOAA hydrographic survey ship Ferdinand R. Hassler. As an aid for these MBES survey operations, a standard survey line was developed just south of the marine facility in order to facilitate the ease of collecting data over the line when departing or returning to the dock. This standard line was first established in 2012; the northern portion of the line was re-oriented in 2013 so that it better matched ship traffic conditions. The standard line has subsequently served as the location for several experiments related to seafloor backscatter (Weber and Ward 2015; Heaton et al. 2017) and is now commonly referred to as the NEWBEX (New Castle Backscatter Experiment) line.

The NEWBEX line (Fig. 1) is located at the mouth of the Piscataqua River, and the seafloor in this location is exposed to strong tidal currents and periodic storm waves. The line contains three segments. Starting from the northwest, the first line segment begins in the channel thalweg which is comprised of sandy pebble gravels or pebble gravels, cuts across a sand wave field comprised of medium sands with a high shell hash content, and returns to the channel thalweg at the southern edge of the sand wave field. The second leg begins in the channel thalweg, transitions to very fine, rippled sands, and then transitions to vegetated bedrock outcroppings. The third leg is largely characterized by heavily vegetated bedrock outcroppings. Water depths through this region are 10–20 m. A more complete description of this seafloor in the vicinity of the NEWBEX line, including grain sizes and images of the seafloor, can be found in Weber and Ward (2015).

Fig. 1
figure 1

The Newbex line in the mouth of the Piscataqua River on NOAA Charts 13283 and 13003 (inset) as described by the bathymetry from both the 2012 and 2013 configurations

Full size image

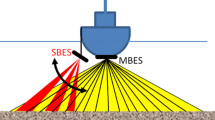
In order to examine potential changes in seafloor backscatter over time, the NEWBEX line was surveyed weekly between 26 April 2013 and 17 January 2014. The surveys were conducted with a 200-kHz EK60 SBES mounted on the UNH R/V Coastal Surveyor at a 45° mounting angle, oriented to the port side (Fig. 2). The one-way beamwidth of the SBES is 7°, and a \(\tau \hspace{0.17em}=\hspace{0.17em}128\) microsecond pulse with a 200-W transmit power setting was used for each survey. During survey work, the ship’s position was recorded using an Applanix POS MV motion and navigation system. The SBES data is used to characterize the gross characteristics of the NEWBEX line with a resolution of approximately 25 m (1–2 times the water depth), at a nominal incidence angle of 45° where the angular variation in seafloor backscatter is assumed to be negligible. Consequently, the vessel position was assumed to be adequate for positioning the SBES data and motion compensation was not applied to the data.

Fig. 2
figure 2

The 200-kHz Simrad EK80 transducer mounted at 45° in the retracted position

Full size image

The SBES transducer is split into four quadrants, enabling calibration using a standard target sphere (a 38.1 mm tungsten carbide ball bearing) following the methodology described by Demer et al. (2015). After an initial full calibration, where the standard target was swung throughout the entire main beam of the SBES, a weekly calibration was used mainly as a check on the initial result. The offset between the observed and modeled sphere response varied slightly from week to week, with a 0.5 dB difference between the 1st and 3rd quartiles of the 10’s of calibrations. Rather than apply the individual calibration result to the data for each survey, an average (across all weeks) calibration offset was applied to all of the data presented here. This approach was selected so that variations due to the implementation of the calibration procedure, which varied in terms of its duration and main beam coverage, did not couple un-necessarily into the observations.

Acoustic backscatter was recorded from the SBES in the Simrad native file format (.raw files). The data were extracted from the data files and converted to target strength (TS) using a MATLAB toolbox (Towler 2013). For each ping, a simple bottom detection was performed. This two-stage process began with a weighted-mean amplitude detection to identify the general vicinity of the bottom return. The weights used for this detection were calculated using data converted to a nominal seafloor scattering cross section, and limited to a contiguous cluster of backscatter values around the seafloor. The clusters were defined as contiguous data records where the nominal bottom scattering strength did not drop below a threshold value of − 50 dB for 20 pings or more. The cluster containing the most energy (i.e., the highest summed value) was considered to be the bottom return. The estimate of the range to the seafloor was then refined by using the split-beam capability of the SBES to find the zero-crossing of the phase-ramp associated with the seafloor return, similar to a phase-detection in a MBES (Lurton 2010). The TS value of the sample corresponding to the seafloor (i.e., at the phase-ramp zero-crossing) was then extracted from the full beam time-series.

SBES TS values were converted to seafloor scattering strength, \({S_b}\), by accounting for the insonified area, A, using a two-way equivalent along-track beamwidth of \({\theta }_{tw}=\)5°, similar to Weber and Ward (2015):

$${S_b}=TS - 10{\log _{10}}A=TS - 10{\log _{10}}\frac{{c\tau }}{{2\sin 45^\circ }}{\theta _{tw}}R$$
(1)

where c is the speed of sound, and R is the slant range to the seafloor. The two-way beamwidth is used for the SBES because the projector and receiver are the same physical transducer. The estimate of A assumes that the incidence angle is fixed at 45°. MBES bathymetry for the area shows that while the slopes vary by only a few degrees (< 5.0°), there are regions that exhibit slopes higher than 10°. These regions are specifically associated with crests in the sandwave field, which are approximately transverse to the direction of vessel travel and have along-track variations through the full range of slopes at scales that are similar to the along-track beamwidth. This geometry complicates the accurate estimate of the incidence angle. At a nominal incidence angle of 45°, however, the error in S b associated with assuming a flat seafloor for the entire NEWBEX line is generally well under 1 dB (for a 10° error, \(10{\log _{10}}{{\sin 45^\circ } \mathord{\left/ {\vphantom {1 {\sin 35^\circ }}} \right. \kern-0pt} {\sin 35^\circ }}=0.9\,{\text{dB}}\)). Vessel motion can induce similar errors in \({S_b}\), but was small enough (the root-mean-square roll for all surveys was 1.5°) to be neglected by the same argument. For the 10–20 m depths of the NEWBEX line, estimates of S b are also insensitive to errors associated with R in (1) and in adjustments for transmission loss (spreading and absorption): a 1% error in sound speed (15 m/s) results in an error in S b that is 0.2 dB.

For a given survey, individual observations (i.e., single ping results) of \({S}_{b}\) occurring within 12.5 m of 46 individual locations distributed along the standard line were averaged together. There is an underlying assumption in this approach that the seafloor properties affecting S b are stationary within the 12.5 m radius region. The choice of radius represents a balance between using a small region where the assumption that the seafloor properties are stationary is easier to meet, and a large region where the observation ensemble is large enough to generate statistically robust estimates of S b . It is difficult to precisely define how many samples are ‘large enough’, but a general guideline can be established from consideration of simple models for seafloor scattering. For example, if the scattered pressure from the seafloor is assumed to be drawn from a circularly-symmetric, complex Gaussian distribution, then the envelope of the scattered wave will be Rayleigh distributed (Jackson and Richardson 2007). The backscatter intensity (i.e., the squared envelope), I s , from which the SBES \({S}_{b}\) estimates are derived, will then be exponentially distributed. The variance of an exponential distribution is equal to its squared mean and so the expected range of S b estimates, defined here to be +/-2 standard deviations from the mean, is

$$10{\log _{10}}\left( {\overline {{{I_s}}} +2\frac{{\overline {{{I_s}}} }}{{\sqrt N }}} \right) - 10{\log _{10}}\left( {\overline {{{I_s}}} - 2\frac{{\overline {{{I_s}}} }}{{\sqrt N }}} \right)=10{\log _{10}}\left( {\frac{{\sqrt N +2}}{{\sqrt N - 2}}} \right)$$
(2)

The overbar on I s indicates an average over N observations. This result is strictly valid only when N is large enough for the distribution of I s averages to be normally distributed, which is often the case when N > 10 (Bendat and Piersol 2000). Equation (2) suggests a large advantage in increasing N from 10 to 50 (a range of 2.5 dB rather than 6.5 dB), but a much smaller advantage (1.8 dB rather than 2.5 dB) when increasing N from 50 to 100. This offers some motivation for the size of the region: it should contain enough observations (large enough N) that the result of (2) is, at least, slightly larger than the other sources of uncertainty, such as uncertainties associated with the estimate of (1), while not allowing the region to grow so large as to clearly violate any assumption of stationarity. Note that in the present case, the choice of a 12.5 m region resulted in slightly more than 50 observations for each estimate of S b , resulting in an expected range of 2.5 dB.

Each SBES survey provided one set of 46 \({S}_{b}\) estimates, and the survey was repeated a total of 32 times. The distribution of \({S}_{b}\) estimates for each of the 46 locations is shown in Fig. 3. Location numbers 1–17 correspond to the north–south portion of the line; location numbers 17–28 correspond to the northwest–southeast portion of the line; and location numbers 28–46 correspond to the east–west portion of the line (see Fig. 1). Examination of the time series for the individual sites (not shown here) shows no obvious trends with respect to, for example, season. Potential azimuthal variability in S b due to the orientation of small-scale ripples in the medium and fine sands (see Lurton et al. 2017) was not investigated as part of this work, and likely has little impact on the observations shown in Fig. 3 given the fixed orientation of the survey line.

Fig. 3
figure 3

A box plot of the 33 S b observations collected with the SBES over the 46 locations, corresponding to an incidence angle of 45°. The boxes represent the extent of S b estimates between the 25th and 75th percentiles, and the line within each box represents the median value. The ‘whiskers’ on the boxes represent the full range of the data, not including outliers (defined here as observations which are more than 1.5 times the interquartile length away from the top or bottom of the box) which are shown as crosses

Full size image

\({S}_{b}\) estimates within the sand wave field (location numbers 4–9) are amongst the least variable. For these locations, the full range of the estimates vary between 2 and 3 dB, in accordance with (2), and the extent of the 25th to 75th percentile of the \({S}_{b}\) estimates varies from 0.5 to 1.0 dB. S b estimates from the gravel seabed in the channel thalweg (location numbers 11–20) are slightly more variable than in the sand wave field, exhibiting a full range of up to 4 dB, and the extent of the 25th to 75th percentiles for this region is as large as 1.5 dB. The greatest variability in S b occurs near the eastern side of the northwest-southeast portion of the line (location numbers 25–31), where the seabed transitions from rippled sands to a vegetated rocky inner shelf (see Weber and Ward 2015).

Overall, the SBES results suggest that there are regions of the NEWBEX line that exhibit very stable (with time) seafloor backscatter. In particular, the sand wave field and the gravel in the channel thalweg appear to be useful candidate regions for a calibration site.

Multibeam data collected on the NEWBEX line, and a relative calibration

Several MBES surveys have been conducted in the vicinity of the NEWBEX line, and on some occasions the MBES operators have collected data over the standard line. Here we examine three of these occasions: an EM 2040 survey conducted in 2012, an EM 2040 survey conducted in 2014, and a Reson 7125 survey conducted in 2013. The EM 2040 surveys were conducted with different systems operating in different modes. The details of the settings for each system are provided in Table 1.

Table 1 MBES parameters and settings. Note that the mode description uses manufacturer-defined terms: ‘sectors’ are wide (10’s of degrees) transmit beams that are steered in different athwart-ships directions using the frequencies specified above (i.e., the full swath is divided into either 1 or more transmit sectors), and equidistant beams describes the manner in which the receive beam pointing angles are defined (in this case, so that they would provide observations that are uniformly spaced across a flat seafloor)
Full size table

Each survey was conducted at a frequency of 200 kHz, with pulse lengths varying from 100 to 288 µs and beamwidths varying between 1° and 2° (Table 1). Ordinarily we might choose to make seafloor backscatter mosaics with each system independently of one another. Our approach here is to perform a relative calibration for these data by choosing a single location along the line where we can extract the ‘raw’ (uncalibrated) angular response from each of the three systems. We then force two of these systems to match the third, which makes the third system the reference. If we desired to add more systems at a later date, we would maintain the same reference system. In the present case, we have chosen the EM 2040 data from 2012 as the reference survey.

EM 2040 data preparation

The data collected during both EM 2040 surveys were processed identically. Seafloor backscatter was extracted from the Kongsberg ‘Seabed Image’ datagram (identifier 89), stored in the raw data, although only data associated with the bottom detection range in each beam (i.e., the center sample) was subsequently used. This provided up to 400 values for the EM 2040, depending on the validity of the bottom detection. The raw EM 2040 seafloor backscatter data have had several adjustments made to them prior to being stored in the raw data (Hammerstad 2000). These adjustments essentially convert an estimate of the seafloor TS, made internally to the EM 2040 using parameters that are unavailable to the end-user, to the seafloor scattering strength using an estimate for the ensonified area. Additional adjustments are then made to the data including a Lambertian correction (Lurton 2010) at oblique incidence and an approximately linear angle-dependent correction near normal incidence. The goal of these adjustments is to remove the inherent angular dependence of the seafloor backscatter, thereby providing the user with a more easily interpretable image that can be used to detect changes in substrate types, anomalous regions, etc. These adjusted data, \({\hat {S}_{b,obl}}\), are stored in the Seabed Image datagram.

In preparing the data for calibration, we have removed all of the manufacturer-applied adjustments described above and applied a new, more accurate estimate for the insonified area. In employing this tactic, we are making the assumption that applying the calibration to the best estimate of S b available to us will provide the most accurate result by helping to avoid, for example, range-dependent errors in manufacturer-applied adjustments. Accordingly, we convert \({\hat {S}_{b,obl}}\) to S b using the following two equations:

$${S_b}={\hat {S}_{b,obl}} - 10{\log _{10}}A+10{\log _{10}}{A_k}+20{\log _{10}}\frac{{{r_n}}}{r} - \left( {1 - \sqrt {\frac{{r - {r_n}}}{{{r_{co}} - {r_n}}}} ~} \right){\Delta _{BS}}~$$
(3)
$${S_b}={\hat {S}_{b,obl}} - 10{\log _{10}}A+10{\log _{10}}{A_k}+20{\log _{10}}\frac{{{r_n}}}{r}$$
(4)

Equation (3) is used near normal incidence, at ranges less than a ‘crossover’ range,\({r}_{co}\), a value computed by the manufacturer and stored on a ping-by-ping basis in the raw data, and Eq. (4) is used at greater ranges. The Lambertian correction is approximated as \(20{\log _{10}}{{{r_n}} \mathord{\left/ {\vphantom {{{r_n}} r}} \right. \kern-0pt} r}\) and the final term in Eq. (3) provides a near-normal-incidence correction that adds an increasing offset with decreasing incidence angle, reaching a maximum backscatter value of \(B{S}_{n}\). \(B{S}_{o}\) and \(B{S}_{n}\)are both recorded with each ping in the Seabed Image datagram, and \(~{\Delta _{BS}}=B{S_o} - B{S_n}\) (Hammerstad 2000). In both equations (3) and (4), the manufacturer estimate for the insonified area, \({A}_{k}\), is also replaced by our estimate:

$${A_k}=\left\{ {\begin{array}{*{20}{c}} {{\Omega _{rx}}{\Omega _{tx}}{r^2}}&{r<\sqrt {r_{n}^{2}+{{\left( {\frac{{c{\tau _p}}}{{2{\Omega _{rx}}}}} \right)}^2}} } \\ {\frac{{c{\tau _p}}}{{2\sqrt {1 - {{\left( {\frac{{{r_n}}}{r}} \right)}^2}} }}{\Omega _{tx}}r}&{elsewhere} \end{array}} \right.~$$
(5)
$$A=\hbox{min} \left[ {\frac{{{\Omega _{rx}}}}{{\cos {\theta _i}}}{\Omega _{tx}}{r^2}~,\frac{{c{\tau _p}}}{{2\sin {\theta _i}}}{\Omega _{tx}}r~} \right]$$
(6)

In equations (5) and (6), \({{\Omega }}_{rx}\) and \({{\Omega }}_{tx}\) are the transmit and receive beamwidths in radians; r is the range from the transducer to the seafloor, r n is the range to normal incidence, \({\theta }_{i}\) is the incidence angle on the seafloor (note that the seafloor is assumed to be flat for the purposes of this work), c is the sound speed, and \({\tau }_{p}\) is the pulse length.

Equations (3) and (4) represent our best estimate of the seafloor scattering strength, but is not a calibrated result and the accuracy relies largely on the manufacturer’s ability to internally estimate the seabed target strength, accounting for the variety of gains and conversion factors inherent in MBES systems. In an absolute calibration we would seek to refine these internal estimates; here we are content to leave them unchanged for our relative calibration.

Reson 7125 data preparation

The Reson 7125 data used for this work is extracted from Reson’s bathymetry datagram (record ID 7006), which stores one so-called intensity value per beam. This value, s, is provided as a 16-bit integer, unreferenced to a voltage or pressure but proportional to the sound pressure amplitude at the bottom detect sample. The exact relationship between the raw data and the sound pressure amplitude is unknown but assumed to be linear. During the survey used in this work, the 7125 power setting (200) and fixed gain setting (35) remained constant and were set to avoid potential non-linearities in the system response (see Greenaway and Weber 2010a), and are assumed to provide a constant offset to the data but are otherwise ignored. The data are assumed to have been modified by user-selected time-varying gain settings according to \(X{\log _{10}}r+Yr\), where X is unitless and Y is in dB/m (both X and Y are selected by the user, and were 30 and 0.090, respectively, for the presented work). These gains are removed, a transmission loss estimate is reapplied, and the insonified area given by Eq. (6) is removed, resulting in data of the form

$$BS=20{\log _{10}}s - \left( {X{{\log }_{10}}r+Yr} \right)+2\left( {20{{\log }_{10}}r+\alpha r} \right) - 10{\log _{10}}A$$
(7)

The absorption coefficient, \(\alpha\), is estimated using CTD cast data and the model by Francois and Garrison (1982). The calculated values range from 59 dB/km (14.0 °C and 32 PSU) to 54.9 dB/km (12.6 °C and 31.1 PSU), and an average value represents an error of up to 0.3 dB at the furthest ranges. In Eq. (7), we use BS as an abbreviation for backscatter strength, which is given in decibels but with an arbitrary reference. It is assumed, however, that the range-dependence of the raw data has been removed.

Relative calibration

A single point along the NEWBEX line was chosen as a relative calibration location. The calibration location used here is near location number 18 (Fig. 3). At this location, 50% of the SBES observations were found to be within 1 dB of each other, and the full range of the S b observations extends from − 11.5 to − 15 dB. Given that the seabed type is gravel (Weber and Ward 2015) and the location of this point within the channel thalweg, it is assumed that this calibration site represents an area on the NEWBEX line (both versions) that is stable over time. The inherent assumption we are using for this site is that the seabed scattering strength will remain the same from 2012 to 2014.

At the calibration location, the 2012 EM 2040 data is used as a reference. Twenty-five sequential pings that are closest to this site are extracted from the raw data, modified according to equations (3) and (4), and averaged to provide a reference angle-dependent calibration, \({S_{b,ref}}\left( n \right)\). Similar to the SBES data, the choice of 25 pings is a balance between the size of the region assumed to be statistically stationary and the uncertainty in the resulting average. Because the goal is to translate the observations of one MBES to another MBES, we have chosen to be conservative with the assumption of stationarity and have computed our MBES averages with approximately half the number of observations used for the SBES averages. The predicted cost in uncertainty (i.e. increased range in the estimates) associated with this choice is approximately 1 dB, according to (2). It is important to note that \({S}_{b,ref}\left(n\right)\) is not derived from an absolutely calibrated system and is likely inaccurate; the calibrated SBES provides a backscatter value of − 15 dB at \({\theta }_{i}=45{^\circ}\) that is approximately 3 dB higher than the estimate from the 2012 EM 2040 (Fig. 4). It should also be noted that because the 2012 EM 2040 data was limited in angular range, a fixed value of − 19 dB was used for reference S b values outside of the observation range shown in Fig. 4.

Fig. 4
figure 4

Top: A 25-ping average of the 2012 EM 2040 seafloor backscatter data, as a function of incident angle, at the calibration site (near location number 18 in Fig. 3; box plot for location 18 is shown). Bottom: Relative calibration offsets for the 2014 EM 2040 (solid line) and Reson 7125 (dashed line), where the latter utilized a power setting of 200 and fixed gain setting of 35

Full size image

Twenty-five pings of data at the calibration location are subsequently extracted from the 2014 EM 2040 data and the 2013 Reson data, and used to generate an average ‘raw’ estimate of the angular response curves (\({S}_{b,2014}\) and \(BS\) for the EM 2040 and Reson 7125, respectively). The difference between these curves and the 2012 EM 2040 data is then calculated, and retained as relative calibration offsets:

$${C_{\text{EM\;2040}}}={S_{b,ref}} - {S_{b,2014}}$$
(8)
$${C_{7125}}={S_{b,ref}} - B{S_{{\text{calpoint}}}}$$
(9)

where \({S}_{b,2014}\) and \({BS}_{calpoint}\) are 25 ping averages for the 2014 EM 2040 and Reson 7125, respectively. These angle-dependent calibration factors, shown in Fig. 4, are subsequently applied to the data collected over the entire NEWBEX line.

The relative calibration results show that the 2012 and 2014 EM 2040 data, which were operated in different modes, have an angular response that varies by as much as 5 dB and a median offset of − 2.5 dB. The difference between the 2012 EM 2040 data and the Reson 7125 data is much greater, which is the expected result given that the Reson 7125 raw data are provided in arbitrary units, having an angular response that varies by as much as 10 dB over the full MBES swath and a median offset of − 94.0 dB. The large offset for the Reson 7125, which in this case is specific to the fixed gain and power settings used during acquisition, is similar to previous calibrations for Reson systems (Greenaway and Weber 2010; Heaton et al. 2017). Assuming that the calibration location has been well chosen, application of these angle-dependent calibration factors (i.e., equations (7) and (8)) to the full data collected with each system should result in identical data sets over regions of the seafloor that are not changing.

Mosaic generation

To assess the results of the relative calibration process, we have chosen to examine the simplest and most commonly employed seafloor backscatter product: the backscatter mosaic. To generate a mosaic for each data set, we remove the angular dependence in the data, normalizing the result to a specified range of angles, and then average the normalized backscatter in grid cells. The angular dependence in the calibrated data, given directly from equations (3) and (4) for the 2012 EM 2040 data and by \({{S}_{b,ref}+C}_{\text{EM\;2040}}\) and \({BS+C}_{7125}\) for the 2014 EM 2040 and Reson 7125 data, respectively, is removed using a 101-ping sliding window. For each ping, the average calibrated backscatter curve in the sliding window is estimated. This average is then subtracted from the data, and the value corresponding to an incidence angle of 45° is added. The flattened seafloor backscatter data are then averaged in 1 m × 1 m grid cells with the result shown in Fig. 5. The number of points within each grid cells ranges between 20 and 100 for the 2012 EM 2040 data, which was operated with a relatively narrow swath width, and between 5 and 25 for the 2014 EM 2040 and Reson 7125 data.

Fig. 5
figure 5

Seafloor backscatter mosaics on the NEWBEX line for the 2012 EM 2040 (left), 2014 EM 2040 (center), and Reson 7125 (right). All data share the same grayscale range. The inset areas identify the regions of comparison shown in Fig. 6. The size of the inset area is approximately 125 m × 125 m for region A and 50 m × 50 m for regions B and C

Full size image
Fig. 6
figure 6

Empirically estimated probability density functions describing the mosaic results at three locations (a, b, c; see Fig. 5). At each location, the data from the 2012 EM 2040, 2014 EM 2040, and Reson 7125 are compared

Full size image

Intercomparison of standard line survey results

The mosaics from the three MBES systems, collected over three subsequent years, appear qualitatively similar after the relative calibration (Fig. 5). Upon closer examination, the backscatter from a 15,900 m2 region within the sandwave field, region A in Fig. 5, show nearly identical distributions of mosaic backscatter values (Fig. 6). At this location, median values for the 2012 EM 2040, 2014 EM 2040, and Reson 7125 data fall within 1 dB of each other, and are − 28.1, − 27.9, and − 27.4 dB, respectively. To provide some sense of the overall range of mosaic backscatter values, the width of the distributions between the 12.5th and 87.5th quantiles (75% of the data) have been calculated. For region A, 75% of the mosaic values fall within approximately 5 dB (4.9, 5.6, and 4.7 dB for the 2012 EM 2040, 2014 EM 2040, and Reson 7125 data respectively). Two contributors to this relatively wide distribution of mosaic values, in comparison to regions B and C, are the local slopes of the sand waves (which have not been accounted for when removing the angular dependence of the data), and the sorting of shellhash which is thought to cause a difference in backscatter between the sandwave crests and troughs.

Region B is in close proximity to the calibration location, and unsurprisingly the mosaics from the three MBES systems exhibit the closest match in this region. At this gravely location, which comprises 2200 m2, the median values for the mosaic fall within 0.5 dB of one another (− 17.9, − 17.8, and − 18.2 dB for the 2012 EM 2040, 2014 EM 2040, and Reson 7125, respectively; Fig. 6). The overall range of the data is approximately half of that exhibited in the sand wave field at region A, with 75% of the mosaic values falling between 2.3, 3.1, and 2.4 dB for the 2012 EM 2040, 2014 EM 2040, and Reson 7125 data, respectively.

Region C is a 2860 m2 region in the lower portion of the NEWBEX line and contains fine rippled sands. The mosaic values here have median values that are slightly lower than those at region A but with a similar range of values, and are − 30.1, − 29.3, and − 29.3, respectively. The distribution of mosaic values is narrower than region A, and is approximately 3 dB for all systems (Fig. 6).

Given the similar swath widths, the spatial overlap between the 2014 EM 2040 and the Reson 7125 mosaics is near 100% for the northern two legs of the NEWBEX line. The difference between these two mosaics, which were processed for identical grid locations, is shown in Fig. 7. Mosaic differences within the sand wave field are variable, as was the case for region A which is at this same location, but shows a general similarity in terms of the calibrated (relatively) response for the two systems. This is particularly true between location numbers 4–6 and near location number 8, although the EM 2040 mosaic values are approximately 2 dB lower than that of the Reson 7125 in the general vicinity of location number 9. At the boundary between the sandwave field and the gravel seabed associated with the channel thalweg, the EM 2040 mosaic values are approximately 9 dB lower than that of the Reson 7125 over a distance (north to south) of approximately 50 m. This large change is suggestive of a change in the location of this boundary during the 8 months between these surveys, as can be seen in the original mosaics in Fig. 7. It is worth noting that the SBES survey at this same location exhibited a range of data that was less than 5 dB over a similar length of time (Fig. 3).

Fig. 7
figure 7

The difference, in decibels, between the NEWBEX line backscatter mosaics created with the 2014 EM 2040 and the Reson 7125. The panels on the right show the 2014 EM 2040 and Reson 7125 backscatter mosaics for the two areas where the mosaic difference is the largest. The grayscale range on these panels is identical to that shown in Fig. 5

Full size image

Further south along the NEWBEX line, at the gravel seabed near location number 11–16, the EM 2040 mosaic values are 1–2 dB lower than that of the Reson 7125 (Fig. 6). Regions near location numbers 17 and 19 show EM 2040 mosaic values that are 1–2 dB higher, and (not surprisingly), the EM 2040 and Reson 7125 show a nearly identical response at location number 18 which is the calibration location. This range of mosaic backscatter values is consistent with the range of values observed at these same locations with the SBES.

Portions of the rippled fine sands (e.g., location numbers 21 and 23) show nearly identical mosaic values as well, with a difference between EM 2040 and Reson 7125 mosaic values within ± 0.5 dB. However, this portion of the standard line also shows substantial variation between the two mosaics in other areas. These differences reach a maximum of 10 dB (the EM 2040 is lower) at location number 26, which is among the most variable locations along the line exhibited by the SBES data (with a range of approximately 7 dB). Approximately 100 m further to the southwest, at station location 27, the Reson 7125 mosaic backscatter values are approximately 5 dB higher than those of the EM 2040, suggesting that this general region of the NEWBEX line is quite variable over time (confirmed by the SBES data shown in Fig. 3).

Discussion

The general goal of this work is to provide a seafloor backscatter reference which can be efficiently used to provide a relative calibration between MBES systems. One of the main challenges in reaching this goal is identifying a region of the seabed that is stable over time. This challenge is mainly brought about by a desire to use a standard line for backscatter calibration over time scales of years. By contrast, if our goal were to perform a relative calibration for multiple MBES systems on, for example, multiple launches at a particular survey site that would be visited only once, a relative calibration could be performed on time scales of hours and potential problems associated with assuming the seafloor is stationary would be greatly mitigated.

Because we wish to use our standard line for relative backscatter calibrations over long time scales, we have put some effort into looking at the variability of the backscatter on a weekly effort over a duration of approximately 9 months. We were fortunate to have a readily accessible gravel seabed in a high current area (the channel thalweg) to use as part of the line, but one of the other features of the NEWBEX line is that it includes a variety of different seabed types ranging from fine sands to gravel and bedrock. There is an equally large range of seafloor scattering strengths and variabilities. Surprisingly, the SBES backscatter collected in the sandwave field (location number 4–9 in Fig. 3) are the least variable, even in comparison to the gravel seabed in the channel thalweg. This low variability is likely due at least in part to the relatively large size of the region over which the SBES backscatter were averaged, which may serve to smooth out some of the finer scale variability evidenced in the MBES mosaic for this same area (Fig. 4, region A). The relative constant backscatter in the sand wave field also suggests that although it is dynamic, with changes occurring on very short time scales (seconds) in response to the tidally influenced currents (Bajor 2015), there is not a net change in the stochastic properties of the seafloor in this region. That is, the sand and shellhash on the seafloor may be moved or resorted by the local currents, but the distribution of grain size and the average roughness of the seafloor interface does not appear to change.

Despite the stability of the SBES data from the sand wave field, we have chosen to use a relative calibration site associated with the gravel seabed in the channel thalweg. In doing so, we were partially motivated by our assumption that a gravel seabed in a high current area is likely to be stable over very long periods of time. But we were also motivated by the practical requirement for finding a location where all three MBES systems overlapped in terms of their coverage (an artifact of changing the northern section of the line between 2012 and 2014). That the overlapping coverage is incomplete emphasizes the importance of choosing a convenient standard line at the outset, so that the motivation for subsequent changes to the line is minimized. The results of the weekly SBES survey results (Fig. 3) suggest that we can expect to perform a relative calibration with a general accuracy of 1–2 dB over long time scales. Although not shown here, this range of variation was exhibited on a weekly basis. The source of this variation is not known, but is possibly attributed to some combination of errors associated with assuming a perfectly flat seafloor, heterogeneity in the seafloor composition itself, and inaccuracies in positioning the backscatter observations.

By using the calibration location within the standard line to perform a relative calibration, we were able to remove a significant amount of bias between the two EM 2040 systems. That this bias existed is not surprising—the systems were the same model but not otherwise identical, and were operated in different modes with small but potentially important (in terms of transducer sensitivity) changes in operating frequency (Table 1). The relative calibration offset (Fig. 4), \({C}_{\text{EM\;2040}}\), was not large, with a median value of 2.5 dB, but this offset is considered significant given that this is the same magnitude as the difference between regions A and C in Fig. 5, which are thought to contain medium and fine sands, respectively. This work focused on performing a relative calibration with the goal of constructing a mosaic, but if the full angular response of the seabed were the objective then the relative calibration offset would have an even larger impact, with greater than 5 dB differences between the uncalibrated and calibrated results.

The comparison between the two EM 2040 systems is really a best case scenario, where the same model MBES is used for multiple surveys. Assuming that the manufacturer has not made significant hardware changes between the two systems that are reflected in the ‘raw’ seafloor backscatter estimate—which is, of course, always a possibility—the relative calibration is likely most important for accommodating small changes associated differences between system modes (e.g., single sector versus multiple sector) and variations associated with the MBES manufacturing process. The greater challenge lies with using MBES systems from different manufacturers, where the manufacturer’s goal of providing ‘true’ seafloor scattering estimates (i.e., \({S}_{b}\) versus an arbitrarily referenced value) may be quite different. In the work described here, we were able to match the Reson 7125 backscatter to the reference data as well as we were able to do so for a system that was the same model as that which collected the reference data. This is a particularly important capability for the future, as MBES users upgrade to new models or change manufacturers, but wish to collect seafloor backscatter data with a common reference. That the Reson 7125 backscatter value has a 100 dB offset (ten orders of magnitude change in seafloor scattering cross section) from that of the EM 2040 is irrelevant if a relative calibration can be performed between the two.

The calibration reference data used in this work were derived from a 25-ping average, and show random variation across the swath of approximately 2 dB (Fig. 4). Because this average is applied in each ping of the 2014 EM 2040 and Reson 7125 data sets, this random variation essentially becomes a static angular-dependent offset in the data being calibrated. When generating a seafloor backscatter mosaic that is referenced to some oblique incidence angle, as was done in this case, this ‘static’ random variation is removed along with any other angular dependence in the underlying raw data, and is presumed to have no adverse effects on the final result (none is apparent in this work, at any rate). However, if the angular response of the seafloor is desired, the random variation in the reference data would be directly reflected in the final result unless the angular response were smoothed across incidence angle. If the angular response is the objective, a larger average and a subsequently reduced variation in the calibration reference would be advisable. This requires, however, that the seafloor be homogenous over a large enough region to generate such a reference.

One of the main limitations of the calibration procedure used here is that it requires the MBES systems being calibrated to be at the same location at some point in time prior to comparing their seafloor backscatter estimates. Although a relative calibration will work locally—for survey launches that utilize the same home port, for example—it will not help users compare seafloor responses in very different locations where the logistics of bringing multiple MBES systems to a single calibration location are so inconvenient as to be insurmountable. A potential way of resolving this is to augment the relative calibration described here with an absolute calibration. In the present work, this could be done by recognizing the offset between the absolutely calibrated SBES and the MBES being used to provide the reference, and adjusting the MBES upward or downward to match the best estimate for \({S}_{b}\). In this case, such a procedure would cause the MBES results to be adjusted upward by about 4 dB. Such a procedure would have the advantage of allowing useful comparisons of seafloor backscatter of medium and fine sands, gravel, and bedrock outcroppings in Portsmouth, NH and, for example, Wellington, NZ.

In summary, we have demonstrated a simple, in situ relative calibration procedure by which multiple MBES systems can be used to generate seafloor backscatter with a common reference. It is our hope that this procedure becomes a standard best-practices approach, in the nature of the best-practices guide of Lurton and Lamarche (2015).