Data driven discovery of systems of ordinary differential equations using nonconvex multitask learning

Abstract

In physical sciences, dynamic systems are modeled using their parameters within governing equations that often form a system of ordinary differential equations (SODE). This system consists of multiple equations, each of which relates the time derivative of a single parameter to several parameters. A parameter can appear in multiple equations, and this parameter potentially links the equations to each other. Although in certain cases the SODE can be written by domain experts, it is often unknown. With advances in sensor technology, large quantities of data can be sampled from dynamic systems, thus enabling the data-driven discovery of closed-form SODEs. State-of-the-art approaches are based on sparse single-task learning, which means that each equation from the SODE is learned independently. Omitting the coupling features of equations leads to SODEs that weakly identify the dynamic system. Furthermore, the convexity of the sparse penalty included in the learning criterion gives an SODE that is biased with respect to the true SODE. To reduce such a bias, we propose a multitask learning (MTL) based penalty which can learn the closed-form SODE with unbiasedness. The purpose of each task is to discover a single equation. But discovering an SODE is nontrivial, as dynamic systems are often nonlinear and the available data are noisy. Our proposal improves SODE identification by harnessing a nonconvex sparse matrix-structured penalty which takes into account the coupling feature as well as addresses the bias issue. Experimental results, based on noisy data simulated from known SODEs, confirm that, compared to single-task learning, MTL is more effective for recovering the closed-form SODE, and the proposed nonconvexity ensures that it can be estimated with unbiasedness. We also show the benefits of our approach on a real-world public dataset sampled from a laboratory-based ecological experiment.

1 Introduction

Governing equations are mathematical models, such as partial differential equations (e.g. Navier–Stokes equation for fluid dynamic modeling) or systems of ordinary differential equations (SODEs), which are widely used in science and engineering to model dynamic systems (Brunton et al., 2020; Li et al., 2019). A governing equation models the dependency relationships between several parameters like velocity or chemical concentration, known as state variables, in a dynamic system. The solution to a governing equation is a function depicting the temporal and/or spatial evolution of the state variables that correspond to physical quantities (e.g. current–voltage, motion). Traditionally, governing equations are derived from principles that have been formalized from general empirical observations consistent with certain hypotheses, for instance Newton’s laws are based on the constant-mass hypothesis (Greiner, 2006). However, in practice it is hard to derive governing equations from the existing rules, because either the practitioners do not have sufficient knowledge or they do not have sufficient time.

In line with the development of sensor technology, data can be sampled from dynamic systems. This provides new opportunities to extract knowledge about the physical behavior underlying a dynamic system. Consequently, there has been a growing interest over recent years in developing data-driven methods for the discovery of governing equations (Brunton et al., 2016; Long et al., 2018; Schaeffer, 2017; Schaeffer & McCalla, 2017; Zhang & Schaeffer, 2019).

Indeed, gaining access to the model that governs an unknown dynamic from data samples can improve our understanding of a physical system and is a challenging task of scientific interest. There is also the practical challenge of obtaining a surrogate model to simulate the system of interest in various conditions e.g. for prototype design in engineering (Li et al., 2019).

In this paper, we focus on the case where state variables are sampled from a dynamic system throughout a scalar variable $t \in {\mathbb {R}}$, that without loss of generality refers to time. Thus, the sampled state variable forms a multivariate time series. If we are to discover the dynamic relationship between the state variables, we have to assume that the resulting data represent the solution of an unknown SODE as proposed by Brunton et al. (2016). In an SODE, each equation models the dependency relationship between several scalar-dependent state variables and their first-order time derivatives. Famous SODEs include the Lorenz attractor in turbulence atmospheric modeling and the Lotka-Voltera in population dynamics, see (Ramsay & Hooker, 2017) for other examples.

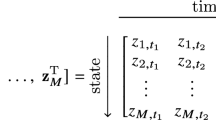
Let us recall how an SODE is formalized. Let $f = \big [ f_1, \ldots , f_p \big ]^T: {\mathbb {R}}^p \rightarrow {\mathbb {R}}^p$ be a continuous map which defines the evolution of a state variable $~{ {\textbf{x}}(t) \in {\mathbb {R}}^p }$ assumed first-order differentiable, then the SODE is expressed as $\frac{\textrm{d}{\textbf{x}}(t)}{\textrm{d}t}:= \dot{{\textbf{x}}}(t) = f({\textbf{x}} \big (t) \big )$, or equivalently:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1(t) = f_1\big ( x_1(t), \ldots , x_p(t) \big ) \\ \cdots \\ \dot{x}_p(t) = f_p\big ( x_1(t), \ldots , x_p(t) \big ) \end{array}\right. } \end{aligned}$$

(1)

Learning an SODE from data samples can be seen as predicting the time derivative of the state variables from a combination (often nonlinear) of the state variables. Hence, discovering an SODE signifies learning f in closed form from samples of $\dot{{\textbf{x}}}$ and ${\textbf{x}}$. An SODE comprises multiple equations (as many as state variables) that relate the variables equations to others. In other words, the equations are coupled (See Fig. 1, where the occurrence of $x_1^3$ and $x_2^3$ within both equations makes the SODE coupled). Our idea is that using multitask learning (MTL) to harness this coupling can improve the data-driven discovery of an SODE. That is why we hypothesize that in this context, MTL can be better than single-task learning.

In Fig. 1 we illustrate the core of the discovery of nonlinear dynamics framework with ${\textbf{x}}(t) \in {\mathbb {R}}^2$ and f polynomial in ${\textbf{x}}(t)$: (top) based on data (${\dot{X}}_n$ and ${\varvec{\Theta }}_{X_{n}}$) sampled from a dynamic system. We solve the minimization problem involving a data fidelity term $\ell ({\dot{X}}_n, {\varvec{\Theta }}_{X_{n}}{\varvec{\beta }})$ and a sparse penalty term $R({\varvec{\beta }})$ (bottom center) leading to the identification of an SODE (bottom left). This optimization instantiates the problem with $R:=\Vert \cdot \Vert _{1,1}$, which is convex. Then, the learned SODE is identified through the minimizer $\hat{{\varvec{\beta }}}$ whose entries and sparsity heavily rely on the chosen penalty. Thus, when the penalty is convex (e.g. LASSO) the nonzero values are statistically biased w.r.t the true unknown values. This means that the SODE is not estimated accurately. There exist nonconvex sparse penalties (e.g. smoothly clipped sbsolute deviation (Fan & Li, 2001)) to remedy the bias issue but they cannot consider the MTL feature. Existing MTL penalties (group-LASSO (Yuan & Lin, 2006), sparse-group-lasso (Simon et al., 2013)) are convex and thus result in a biased SODE. We propose a specific nonconvex sparse penalty as a mean for learning the matrix coefficient that both reduces its bias and takes into account the multitask feature of the SODE. As a result, when there is a coupling within the true SODE, its closed-form SODE can be better recovered using our penalty.

Fig. 1

(From top to center to bottom left) Generic workflow of the data-driven discovery of an SODE (here two-dimensional) with linear regression. Top: based on samples of estimated state variable time derivatives (${\dot{X}}_n$’s columns), and resulting from nonlinear transformations of the state variable samples (columns of the dictionary ${\varvec{\Theta }}_{X_{n}}$), a linear model is assumed for the two sets of samples. Center: the SODE is discovered by minimizing a learning criterion inducing sparsity in the minimizer. Bottom left: the SODE is identified using the learned coefficient matrix $\hat{{\varvec{\beta }}}$

Our contributions in this paper are as follows:

• We recast the discovery of a closed-form SODE as a multitask problem. We also formalize the learning as an optimization problem involving a matrix-structured, sparse and nonconvex regularizer to account for task relatedness, sparsity and unbiasedness.

• We highlight the bias of the learned coefficients, induced by the convexity of state-of-the-art regularizers, on the resulting SODE.

• Using experiments on reference SODEs, we show that learning via our multitask penalty rather than a convex single-task penalty leads to a better recovery of the equations. We also demonstrate the benefit of our recasting on a real dataset involving two adversarial biological quantities, and provide an interpretation of the SODE that was discovered.

The paper is organized as follows: We start by defining our notation in Table 1. in Sect. 2 we introduce the data-driven discovery of an SODE as a sparse regression problem (single-task and multitask) and then highlight the drawbacks of the state-of-the-art regularizers. In Sect. 3, we introduce our contribution, a regularizer that is multitask-based and involves unbiasedness. Then, we present a generic algorithm from the literature which solves the regression problem and can be used for all the regularizers introduced in the paper. Through numerical experiments on synthetic and real datasets, in Sect. 4 we show the benefit of learning an SODE with such a regularizer. We conclude and propose some perspectives in Sect. 5.

Table 1 Notations

2 Related work

Extracting information from noisy data resulting from physical experiments with standard machine learning algorithms can lead to irrelevant, or at worst, incorrect conclusions. This is because the scientist does not consider the physical feature of the solution in the learning objective. Recently thare has been increasing research on physics-informed methods to incorporate a physical prior into the learning process (Raissi et al., 2017; Raissi & Karniadakis, 2018; Brunton et al., 2016; Bhat & Rawat, 2019; Champion et al., 2019). Generally, these methods formulate a learning objective by leveraging a model from the physical sciences. In Raissi et al. (2017) the authors proposed a method to predict a state variable with Gaussian processes in which the covariance function derives from a known partial differential equation (PDE). Another line of research is about dynamic mode decomposition in which the goal is to learn both a linear operator and the associated eigenspace from time series and/or spatial data (Rowley et al., 2009). Several dynamic mode decomposition variants have been proposed, but the most popular and recent variants rely on the Koopman operator, which provides information on the growth rates and the frequencies of the long-term dynamics (Williams et al., 2015; Yeung et al., 2019; Kawahara, 2016). In Li et al. (2020), the authors assumed that a closed-form PDE can be recovered as a sparse plus low-rank combination of nonlinear terms of precomputed dictionary. Their approach relies on the robust principal component analysis of Candès et al. (2011). Our work is similar to the one of Li et al. (2020) in the sense that we attempt to discover a closed-form model, but here an SODE is based on a dictionary computed from noisy data.

Learning an SODE from data samples can be traced back to the seminal work of Schmidt and Lipson (2009). Schmidt and Lipson proposed a combinatorial approach based on genetic programming to select the parsimonious model that best recovers the data from among a large set of candidate models. As mentioned in Brunton et al. (2016), genetic programming methods do not scale to large datasets and tend to overfit. To remedy this, in Brunton et al. (2016) Brunton et al. recast learning an SODE as a sparse regression problem, referred to as the sparse identification of nonlinear dynamics in the literature. Our proposal is formalized according to this framework, which we introduce in the next section.

2.1 Sparse single-task learning of an SODE

State-of-the-art methods for discovering an SODE, Brunton et al. (2016); Rudy et al. (2019), implicitly assume that each of $\dot{x}_1, \ldots , \dot{x}_p$ in Equation (1) are uncorrelated targets which can be predicted by a sparse combination of elements included in a given dictionary of candidate functions. An example of a dictionary ${\varvec{\Theta }}_{X_{n}}$ and a two-dimensional SODE is given in Fig. 1. The dictionary is built by the user with linear and nonlinear candidate functions from the samples $X_n$ of ${\textbf{x}}$. This dictionary reflects the prior knowledge of the observed phenomenon and is possibly overcomplete. In Brunton et al. (2016); Schaeffer and McCalla (2017); Rudy et al. (2019), f is assumed to be linear with respect to the dictionary elements. The linear assumption on f with respect to the dictionary elements makes it easy to learn and interpret. Next $f_1,\ldots ,f_p$ are learned separately with a sparsity-promoting algorithm e.g. LASSO (Tishbirani, 1996) or elastic-net (Zou & Hastie, 2005).

2.1.1 Discovering an SODE using sparse linear regression

Starting from n noisy samples of a p-dimensional state variable stored as $X_n$ and the associated time derivative samples $\dot{X}_n$ (often estimated from $X_n$, e.g. with finite-difference, spline-based methods), we first build a dictionary of m arbitrary candidate functions, for instance one chooses to include linear and quadratic monomials, and one cosine term, then, ${\varvec{\Theta }}_{X_{n}}\overset{e.g. }{=}\ \big [ {\textbf{x}}_{\bullet 1}, {\textbf{x}}_{\bullet 2}, \ldots ,{\textbf{x}}_{\bullet 1}^2, {\textbf{x}}_{\bullet 2}^2,\dots ,\cos {{\textbf{x}}_{\bullet 1}}, \dots \big ] \in {\mathbb {R}}^{n \times m}$. Then from the linear assumption on f, i.e. $\dot{X}_n~=~f \big ( X_n \big ) = {\varvec{\Theta }}_{X_{n}}{\varvec{\beta }}$ with ${\varvec{\beta }} \in {\mathbb {R}}^{m \times p}$ wherein the q-th row refers to the coefficient vector associated with the candidate functions of the q-th SODE component, we can find a sparse estimate $\hat{{\varvec{\beta }}}$ by minimizing a data fidelity plus a sparsity term:

$$\begin{aligned} \hat{{\varvec{\beta }}}:= \arg \min _{{\varvec{\beta }} \in {\mathbb {R}}^{m \times p}} \big \{ \ell ({\dot{X}}_n, {\varvec{\Theta }}_{X_{n}}{\varvec{\beta }}) + \lambda R({\varvec{\beta }}) \big \} \end{aligned}$$

(2)

where $\lambda > 0$ is the sparsity amount. We learning of ${\varvec{\beta }}$ in Fig. 1 with a two-dimensional SODE. We present Algorithm.1 to solve Equation (2) when the loss is quadratic and when R is convex or nonconvex with a specific property in Sect. 3.

In Brunton et al. (2016); Rudy et al. (2019); Schaeffer (2017) Equation (2) is instantiated with $R:= R_{\ell _{1,1}} = \Vert \cdot \Vert _{1,1}$ i.e. $\hat{{\varvec{\beta }}}$ is a sparse estimate of the following problem:

$$\begin{aligned} \hat{{\varvec{\beta }}} = \arg \min _{{\varvec{\beta }} \in {\mathbb {R}}^{m \times p}} \big \{ \frac{1}{2} \Vert \dot{X}_n - {\varvec{\Theta }}_{X_{n}}{\varvec{\beta }} \Vert _{2,2}^2 + \lambda \Vert {\varvec{\beta }} \Vert _{1,1} \big \} \end{aligned}$$

(3)

which is a special case of Equation (2) with $\ell (\cdot , \cdot )$ being the quadratic loss. Since ${\varvec{\beta }} = \big [ \varvec{{\beta }}_{\bullet 1}, \cdots , \varvec{{\beta }}_{\bullet p} \big ]$, and $R_{\ell _{1,1}}$ acts independently on each entry of ${\varvec{\beta }}$, solving Equation (3) reduces to p independent LASSO (Tishbirani, 1996) subproblems where each estimates $\varvec{{\beta }}_{\bullet k}$ from $\big ( \dot{{\textbf{x}}}_{\bullet k}, {\textbf{x}}_{\bullet k} \big )$, for $k=1 \dots p$, with the $\ell _1$ penalty. Hence, the SODE is discovered using a single-task learning approach.

2.2 Background and limitations of sparse convex single-task regularizers

In Schaeffer (2017), the authors formalized the discovery of nonlinear dynamics using partial differential equations, thus their dictionary is built differently from our ${\varvec{\Theta }}_{X_{n}}$. The learning criterion used by the author is formalized similarly as in Equation (3) for an SODE. Since Equation (3) is convex in ${\varvec{\beta }}$, it can be solved by the Douglas-Rachford algorithm (Combettes & Pesquet, 2011) which is a proximal-type algorithm (Parikh & Boyd, 2013). Proximal operators are at the core of sparse learning, hence our proposal. In our context, we use these operators to solve Equation (2) (see Algorithm.1 in Sect. 3). We recall the general definition.

Definition 2.1

(proximal operator (Parikh & Boyd, 2013)) The proximal operator associated with a closed, proper and convex function in a Hilbert space, $h: {\mathcal {H}} \rightarrow {\mathbb {R}}$, is defined for any ${\textbf{y}} \in {\mathcal {H}}$, with $\lambda > 0$ as:

$$\begin{aligned} \text {prox}_{\lambda h}({\textbf{y}}):= \arg \min _{{\textbf{u}} \in {\mathcal {H}}} \big \{ \frac{1}{2} \Vert {\textbf{y}} - {\textbf{u}} \Vert _{{\mathcal {H}}}^2 + \lambda h({\textbf{u}}) \big \} \end{aligned}$$

Remark 2.2.1

Here ${\mathcal {H}}$ reduces either to ${\mathbb {R}}^p$ or ${\mathbb {R}}^{n \times p}$. If h is strongly convex, the minimizer in ${\mathcal {H}}$ is unique and $\text {prox}_{\lambda h}({\textbf{u}})$ is single-valued (Parikh & Boyd, 2013). If h is not convex (but remains closed and proper), the proximal operator is still defined well. In this case, since the minimizer set may not reduce to a singleton, the proximal operator can be multivalued.

When h is also separable, that is for any vector or matrix ${\varvec{W}}$, $h({\varvec{W}}) = \sum _{i,j} h_{ij}(w_{ij})$ with $h_{ij}: {\mathbb {R}} \rightarrow {\mathbb {R}}$, computing $\text {prox}_{\lambda h}({\varvec{W}})$ reduces to compute the proximal operator of $h_{ij}$ for every i, j and then to concatenate $\big \{ \text {prox}_{\lambda h_{ij}}(w_{ij}) \big \}_{i \le n, j \le p}$ according to the dimensions of ${\varvec{W}}$. In the case of a separable (i.e. single-task) vector or matrix regularize, evaluating the proximal operator for a given element is equivalent to evaluating the proximal operator for each of the separable parts. As the $\ell _{1,1}$ norm is separable, with $h_{ij}(w_{ij}) = | w_{ij} |$, we have $\text {prox}_{\lambda | \cdot |}(w_{ij}) = {{\,\textrm{sign}\,}}(w_{ij}) \max {(0, | w_{ij} | - \lambda )}$, which is known as the soft-thresholding operator (Tishbirani, 1996).

2.2.1 Single-task limitation of a separable regularizer

The proximal operator of $R_{\ell _{1,1}}$ serves as a shrinkage operator, assigning zero to coefficients in ${\varvec{\beta }}$ that do not sufficiently decrease the data fidelity. However, $R_{\ell _{1,1}}$ is separable and hence does not account for any matrix structure. Indeed, we can permute any element within the coefficient matrix ${\varvec{\beta }}$ for the purposes of learning, and the resulting $R_{\ell _{1,1}}$ remains unchanged. Therefore, for MTL, separability across tasks is not desirable. Consequently, the regularizer acts as if ${\varvec{\beta }}$ were a vector in ${\mathbb {R}}^{m p}$. More generally, if a vector structure is considered for ${\varvec{\beta }}$ using a fully separable norm regularizer rather than a matrix-structured regularizer, then the task relatedness i.e. correlations between columns $\big [ \varvec{{\beta }}_{\bullet 1}, \cdots , \varvec{{\beta }}_{\bullet p} \big ]$ is omitted.

2.2.2 The bias induced by a convex regularizer

Definition 2.2

Let $\hat{\beta }$ be an estimate of the ground-truth coefficient $\beta$, the bias is the expectation over the distribution of $\hat{\beta }$ of the estimation error thus defined as $\text {bias}(\hat{\beta }) = {\mathbb {E}}(|\hat{\beta } - \beta |)$.¹

Using triangle inequality, one can show that a regularizer inducing a norm in ${\mathbb {R}}^{m \times p}$ is convex and thus induces a bias toward zero in the learned coefficients [(Boyd & Vandenberghe, 2004), p. 73], which in our context degrades the SODE identification.

Example 2.2.1

Let us consider the proximal operator of the $\ell _{1,1}$ norm. An estimate of a true coefficient $\beta _{ik}$ is $\hat{\beta }_{ik}^{n} = \text {prox}_{\lambda | \cdot |}(\hat{w}_{ik}^{n}) = {{\,\textrm{sign}\,}}(\hat{w}_{ik}^{n}) \max (0, |\hat{w}_{ik}^{n} | - \lambda )$, where $\hat{w}_{ik}^{n}$ is an unregularized estimate of $\beta _{ik}$ (i.e. preceding the proximal step, see Algorithm.1) from n samples. Hence as $n \rightarrow \infty$:

• for $|\beta _{ik} | \in [0; \lambda ]$, $\text {bias}(\hat{\beta }_{ik}^{n}) \rightarrow \beta _{ik}$,

• for $|\beta _{ik} | \in ]\lambda ; \infty ]$, $\text {bias}(\hat{\beta }_{ik}^{n}) \rightarrow \lambda$.

Consequently, if the i-th candidate function is relevant to the k-th equation of the SODE, the estimate $\hat{\beta }_{ik}^{n}$ is necessarily biased. In Fig. 2 (right), it is clear that the soft-thresholding operator never reaches the identity function and, therefore, always returns a bias estimate of $\beta _{ik}$. Correcting the bias with $\lambda$ is equivalent to applying the hard-thresholding operator (Donoho & Johnstone, 1994), which is the proximal operator of the $\ell _0$ penalty (the nonzero indicator), and thus is unbiased, but makes the objective function of Equation (2) NP-hard since instantiating $R({\varvec{\beta }}_{ik}):= {\mathcal {I}}(\beta _{ik} \ne 0)$ makes the objective function discontinuous.

2.3 A nonconvex separable regularizer

Here we introduce the single-task version of a nonconvex regularizer: the smoothly clipped sbsolute deviation (SCAD) (Fan & Li, 2001) which induces unbiasedness for large coefficients and serves as a building block for our proposed regularizer that we introduce in Sect. 3.

Fig. 2

Left: The (convex) LASSO ($R_{\ell _{1,1}}$, blue) and (nonconvex) SCAD ($R^{SCAD}_{\lambda , \theta }$, red) regularizers, with $\lambda = 1, \theta = 2.01$. Right: Their associated proximal operator as a function of a coefficient $\beta _{ij}$. In the right plot, we can see hat the soft-thresholding operator $\text {prox}_{\lambda R_{\ell _{1,1}}}(\beta _{ij})$ (blue) induces a bias since it thresholds $\beta _{ij}$ toward zero and away from the identity (gray dotted lines), which represents the best unbiasedness for a true nonzero coefficient. In contrast, $\text {prox}_{r^{SCAD}_{\lambda , \theta }}(\beta _{ij})$ (red), continuously reaches the identity as $|\beta _{ij} |$ increases, meaning that SCAD induces less bias than the LASSO, as a true coefficient is high (Color figure online)

Definition 2.3

Let $\lambda > 0$ and $\theta > 2$ be hyperparameters that operate as the level of sparsity and unbiasedness, respectively; the SCAD is defined for $w \in {\mathbb {R}}$ as:

$$\begin{aligned} r^{SCAD}_{\lambda , \theta } (w) = \left\{ \begin{array}{ll} \lambda | w | &{} \text { if } | w | \le \lambda \\ - \frac{\lambda ^2 - 2 \theta \lambda | w | + w^2}{2(\theta -1)} &{} \text { if } \lambda < | w | \le \theta \lambda \\ \frac{(\theta + 1)\lambda ^2}{2} &{} \text { if } | w | > \theta \lambda \end{array} \right. \end{aligned}$$

(4)

Remark 2.3.1

$r^{SCAD}_{\lambda , \theta }$ is semiconcave (i.e. concave with respect to $| w |$).

• For $| w | \le \lambda$, the SCAD penalty behaves as $\ell _{1}$.

• For $\lambda < | w | \le \theta \lambda$, the SCAD interpolates quadratically between $\ell _1$ and $\ell _0$ and the transition between them is controlled by $\theta$.

• For $| w | > \theta \lambda$, the penalty level is constant, thus the SCAD behaves as $\ell _0$.

SCAD is illustrated in Fig. 2 (left).

Remark 2.3.2

$\lim _{\theta \rightarrow \infty } r^{SCAD}_{\lambda , \theta }(w) = \lambda | w |$, thus the SCAD induces $\ell _1$ sparsity as the upper limit with respect to $\theta$.

Remark 2.3.3

$\lim _{\theta \rightarrow 2, | w | \le 2 \lambda } r^{SCAD}_{\lambda , \theta }(w) = \lambda | w |$ and $\lim _{\theta \rightarrow 2, | w | > 2 \lambda } r^{SCAD}_{\lambda , \theta }(w) = \lambda {\mathcal {I}}(w \ne 0)$, thus the SCAD induces $\ell _1$ sparsity for small $|w |$ and $\ell _0$ sparsity (unbiased but discontinuous) for large $|w |$, as the lower limit with respect to $\theta$.

For any $w \in {\mathbb {R}}$, $\text {prox}_{ r^{SCAD}_{\lambda , \theta } }(w)$ is known analytically (Fan & Li, 2001) (see the Appendix 2) and, as plotted in Fig. 2 (right), since it reaches the identity line, induces less bias than $\text {prox}_{ {\lambda }{| \cdot |} }(w)$ for large coefficients, i.e. as $|w | > 2 \lambda$.

The matrix-extended version of the SCAD (4) is $R^{SCAD}_{\lambda , \theta } ({\varvec{W}}) = \sum _i \sum _j r^{SCAD}_{\lambda , \theta } (w_{ij})$, which is also separable. Hence, $\text {prox}_{R^{SCAD}_{\lambda , \theta }}({\varvec{W}})$ is the concatenation of $\big \{ \text {prox}_{ r^{SCAD}_{\lambda , \theta } }(w_{ij}) \big \}_{i \le n, j \le p}$ along the dimensions of ${\varvec{W}}$. However, as a separable regularizer cannot account for task relatedness, the only benefit of learning with $R^{SCAD}_{\lambda , \theta }$ over $R_{\ell _{1,1}}$ is unbiasedness. Indeed, the two summands in $R^{SCAD}_{\lambda , \theta }$ act similarly at the row and column levels of ${\varvec{\beta }}$, and therefore, do not resolve the shortcomings mentioned in Sect. 2.1.

2.4 Building block for MTL in linear regressions

MTL consists of learning p functions $\big [ f_1, \cdots , f_p \big ]$ jointly by assuming that they share a common set of features (Argyriou et al., 2008). For the k-th task, a dataset $\{ {\textbf{y}}_{ik}; z_{ik} \}_{i \le n_k}$ of $n_k$ samples with m features is given. Therefore, the p regression coefficient vectors can be represented in a matrix ${\varvec{\beta }} \in {\mathbb {R}}^{m \times p}$. The task similarity is reflected in the learning criterion by a regularizer R applied to this matrix. For p linear regressions, MTL is formulated as:

$$\begin{aligned} \hat{{\varvec{\beta }}} = \arg \min _{{\varvec{\beta }}:= [ \varvec{{\beta }}_{\bullet 1}, \cdots , \varvec{{\beta }}_{\bullet p} ]} \big \{ \sum _{k=1}^p \sum _{i=1}^{n_k} \frac{1}{2 n_k} (z_{ik} - {\textbf{y}}_{ik}^T \varvec{{\beta }}_{\bullet k})^2 + \lambda R({\varvec{\beta }}) \big \} \end{aligned}$$

(5)

where R may account for task relatedness. Equation (5) is a special case of Equation (2) and can be solved with Algorithm.1. Note that when $n_k = n$ and $R = R_{\ell _{1,1}}$, Equation (5) reduces to Equation (3). Thus, by choosing a regularizer that is more appropriate than the $\ell _{1,1}$ norm for considering task relatedness, discovering an SODE can be formulated as MTL.

2.4.1 Considering task relatedness

To account for task relatedness, the regularizer has to be matrix-structured, for instance, solving Equation (5) with $R_{\ell _{2,1}}({\varvec{\beta }}):= \Vert {\varvec{\beta }} \Vert _{{2,1}} = \sum _i^m \Vert \varvec{{\beta }}_{i \bullet } \Vert _{2}$ (i.e. group-lasso (Yuan & Lin, 2006)), makes ${\varvec{\beta }}$ row-sparse i.e. some rows are identically nonzero and all the others are null (Obozinski et al., 2010), due to the nonseparability with respect to $\varvec{{\beta }}_{i \bullet }$ and sparsity with respect to $\varvec{{\beta }}_{\bullet j}$. To discover an SODE, $R_{\ell _{2,1}}$ forces all the equations to share the same candidate functions of ${\varvec{\Theta }}_{X_{n}}$. The proximal operator associated with $R_{\ell _{2,1}}$ is given in the Appendix 2.

2.4.2 Considering task-specific elements

Although an SODE shares some candidate functions across its equations, it is sufficiently flexible to allow specific candidate functions for each equation. This can be achieved by taking a convex combination of two norms i.e. $R_{\ell _{2,1} + \ell _{1,1}, \alpha }({\varvec{\beta }}):= \alpha \Vert {\varvec{\beta }} \Vert _{2,1} + (1-\alpha ) \Vert {\varvec{\beta }} \Vert _{1,1}$ with $\alpha \in [0, 1]$ (Simon et al., 2013). For $\alpha > 0.5$, a greater level of importance is given to commonality in candidate functions across equations compared to specificity, and conversely, for $\alpha < 0.5$. In practice, $\alpha$ is chosen by cross validation. The proximal operator associated with $R_{\ell _{2,1} + \ell _{1,1}, \alpha }$ is given in Appendix 2. For the sake of clarity, we omit the index $\alpha$ in the notation and write $R_{\ell _{2,1} + \ell _{1,1}}$.

2.4.3 Limitations of sparse convex MTL regularizers

Despite being able to select relevant candidate functions, the convexity of $R_{\ell _{2,1}}$ and $R_{\ell _{2,1} + \ell _{1,1}}$ induces a bias, similarly to $R_{\ell _{1,1}}$, in $\hat{{\varvec{\beta }}}$ through their associated proximal operator (Simon et al., 2013).

In Sects. 2.1 and  2.4, task relatedness and nonconvexity are shown as being two important weaknesses that cannot be addressed by the $\ell _{1,1}$ regularizer. Our contribution harnesses both the nonconvexity and the task relatedness within a single regularizer to improve the discovery of an SODE.

3 A nonconvex matrix-structured regularizer

In this section, we introduce our proposal, a regularizer, which jointly accounts for task relatedness, sparsity and unbiasedness. Then we introduce a generative, iterative, thresholding learning algorithm (Gong et al., 2013) that can be instantiated with all the regularizers presented in this paper.

3.1 A nonconvex nonseparable regularizer

We propose to “un-separate” $R^{SCAD}_{\lambda , \theta }$ to unharness both from the nonseparability and the nonconvexity of the SCAD. The key technique is to replace the second summation in $R^{SCAD}_{\lambda , \theta }$ by $r^{SCAD}_{\lambda , \theta }(\Vert {\textbf{w}}_{i \bullet } \Vert _{1})$:

$$\begin{aligned} R_{\lambda , \theta }^{SCAD-\ell _1} ({\varvec{W}}):= \sum _{i=1}^{m} r^{SCAD}_{\lambda , \theta } \big ( \Vert {\textbf{w}}_{i \bullet } \Vert _{1} \big ) \end{aligned}$$

(6)

In this way, as the regularizer acts on the coefficient vector of the i-th candidate function using the SCAD of the $\ell _1$ norm, $R_{\lambda , \theta }^{SCAD-\ell _1}$ forces ${\textbf{w}}_{i \bullet }$ to be sparse, unbiased and correlated across the p tasks. Another way of understanding the rationale behind our proposal is to see the hierarchical sparsity. The first level (the “highest”) is the task-level: we enforce the set of nonzero coefficients to be the same across each task. Such a sparsity level is somehow a group sparsity and enforces the learning to be multitask. The second level (the “lowest”) is the component level: for a given task, we allow some (small) coefficients to be both nonzero and specific to each task. It is important to note the analytical similarity with $R_{\ell _{2,1}} = \sum _{i=1}^m \Vert {\textbf{w}}_{i \bullet } \Vert _{2}$ (Sect. 2.4), which does not allow each equation of the SODE to have a specific candidate function. Contrary to $R_{\ell _{2,1}}$, our proposal jointly enforces unbiasedness and sparsity in each ${\textbf{w}}_{i \bullet }$, and thereby enables the equations of the SODE to have specific candidate functions.

Despite $R^{SCAD-\ell 1}$ being nonconvex, it is closed and proper by construction. Thus the image of the proximal operator of our regularizer is nonempty and we can compute it analytically as follows: for any ${\varvec{W}} \in {\mathbb {R}}^{m \times p}$, $\lambda > 0$, $\theta > 2$ and $(i, q) \in \big \{ 1, \dots , m \big \} \times \big \{ 1, \dots , p \big \}$, let ${\tilde{w}}_{iq}$ be the element of the i-th row and q-th column of the matrix ${\widetilde{W}}$ returned by the proximal operator,

$$\begin{aligned}{} & {} {\tilde{w}}_{iq} \nonumber \\{} & {} \quad := {\left\{ \begin{array}{ll} \begin{aligned} {{\,\textrm{sign}\,}}(w_{iq}) \max (0, |w_{iq} | - \lambda ) &{}&{} \text { if } |w_{iq} | \le B^1_i, \end{aligned} \\ \begin{aligned} \frac{\theta -1}{\theta -2} {{\,\textrm{sign}\,}}(w_{iq}) \max (0, |w_{iq} | - \frac{\theta \lambda }{\theta -1} ) &{}&{} \text { if } B^1_i < |w_{iq} | \le B^2_i, \end{aligned} \\ \begin{aligned} w_{iq} &{}&{} \text { if } |w_{iq} | > B^2_i \end{aligned} \end{array}\right. } \end{aligned}$$

(7)

with $B^1_i:= 2 \lambda - \Vert {\textbf{w}}_{i \bullet , -q} \Vert _{1}$, $B^2_i:= \theta \lambda - \Vert {\textbf{w}}_{i \bullet , -q} \Vert _{1}$ and ${\textbf{w}}_{i \bullet , -q}$ denotes all the elements except the q-th of the vector ${\textbf{w}}_{i \bullet }$. Knowing this proximal operator is a computational benefit in solving Equation (2). We give a proof detailing the computational steps to obtain the above closed form in the Appendix 1.

Remark 3.1.1

In the first part, ($\le B_i^1$), $\text {prox}_{R_{\lambda , \theta }^{SCAD-\ell _1}}(\cdot )$ equals $\text {prox}_{R_{\ell _{1,1}}}(\cdot )$ (soft-thresholding operator). In the second part, $\text {prox}_{R_{\lambda , \theta }^{SCAD-\ell _1}}(\cdot )$ acts as a (group) soft-thresholding operator but with a rate $\frac{\theta -1}{\theta -2}$ which is greater than 1, thus outputs unbiased coefficient vectors. In the third part, $\text {prox}_{R_{\lambda , \theta }^{SCAD-\ell _1}}(\cdot )$ acts as a (group) hard-thresholding operator, returning $\tilde{{\textbf{w}}}_{i \bullet }$ identically.

Remark 3.1.2

Since $B^1_i$ and $B^2_i$ are only row dependent, each row of $\text {prox}_{R_{\lambda , \theta }^{SCAD-\ell _1}}({\varvec{W}})$ can be computed in parallel.

3.2 MTL with a nonconvex regularizer

We instantiate the general iterative shrinkage thresholding algorithm (GISTA) (Gong et al., 2013) in Algorithm 1 to perform learning. The GISTA can be instantiated with regularizers either convex, or nonconvex and expressed as a difference of two convex (DC) functions, see (Gasso et al., 2009; Rakotomamonjy et al., 2016; Le Thi et al., 2021) for examples of such regularizers. It generalizes FISTA (Beck & Teboulle, 2009) whose convergence is guaranteed when minimizing quadratic plus convex regularizers functions. Despite the nonconvexity of DC functions, convergence guarantees to a stationary point in finite time of the GISTA are established in Gong et al. (2013). $R^{SCAD-\ell _1}$ and $R^{SCAD}$ enjoy the DC property, thus we can use the GISTA to learn with any regularizers presented in this paper. Convergence is not ensured for other nonconvex penalties, such as the group bridge penalty $R_{\ell _{q,r}} (0< q,r < 1)$, since their associated proximal operator does not give rise to a closed-form expression. Hence, to compute the proximal operator the bridge penalty in Algorithm 1, an inner nonconvex optimization procedure is necessary and is likely to affect the convergence of GISTA.

GISTA consists of two nested loops. The outer loop (lines 4–12) consists of a loss gradient descent step (line 9) followed by a proximal step (line 10) that set to zero the coefficients that insignificantly decrease the loss term. The inner loop (lines 5–8) consists of the backtracking line search to compute the gradient step size $\gamma$, that given the current descent direction, ensures a sufficient decrease (Boyd & Vandenberghe, 2004). The value 0.8 (line 7) is typical and corresponds to the ’slow-rate’ parameter (Boyd & Vandenberghe, 2004). To limit the cost of one iteration, we precomputed ${\varvec{\Theta }}_{X_{n}}^T {\varvec{\Theta }}_{X_{n}}$ and ${\varvec{\Theta }}_{X_{n}}^T \dot{X}_n$ (line 2). A detailed complexity analysis of proximal gradient algorithms, such as GISTA, is given in Beck (2017).

4 Numerical experiments

4.1 Experimental setting

4.1.1 Synthetic datasets generated from known SODEs

We evaluated our approach on three SODEs (i.e. ground-truth) known from the literature (Schaeffer & McCalla, 2017; Brunton et al., 2016; Mangan et al., 2017): the damped oscillator with cubic dynamic (DOC) used to model the nonlinear pendulum in mechanics, the Lotka-Volterra (LV) system used as prey-predator interaction model and the Lorenz attractor (LAT) used to model atmospheric turbulence. Each one of these SODEs has common functions as well as specific other functions across their equations.

Fig. 3

Left: the ground-truth SODEs used in our experiments. Center: the numerical solution (black), i.e. the state variables $x_1, \dots , x_p$ plotted w.r.t time. The training data (blue) corresponds to a noisy version (in these plots the noise is Gaussian) of the numerical solution. Right: same data as in the center plotted as one state variable w.r.t the other(s) to visualize their correlation (Color figure online)

We base our experiments on those in Schaeffer and McCalla (2017).

Simulation of the state variables

We generated the state variables, $x_1, \dots , x_p$, along time (i.e. multivariate time series) by numerically solving the true SODEs with an implicit backward differentiation formula method of order five, implemented in the Scipy library (Oliphant et al., 2001). For each SODE, the resulting time series has $n = 5\times 10^3$ time steps.

In a real life scenario the data are noisy so we added white noise to the clean time series. We experimented with Gaussian noise, by varying the variance level in terms of logarithmic signal-to-noise ratio (log-SNR). The log-SNR is defined as:

$$\begin{aligned} \text {log-SNR}:= 10 \log _{10} \big ( \frac{\sum _{j=1}^{p} \sigma _{ground-truth, k}^2}{\sigma _{noise}^2} \big ) \end{aligned}$$

(8)

where $\sigma _{ground-truth, k}^2$ is the variance in the k-th state variable (without noise) and $\sigma _{noise}^2$ is the variance in the noise. This enables a comparison of the results across synthetic datasets with an equal amount of noise w.r.t the variance in the ground-truth. The lower the log-SNR, the higher the noise variance. In our experiments, for each SODE we fixed the log-SNR to $\{20, 30, 40, 50\}$ and then deducted $\sigma _{noise}^2$. Samples of the clean and noisy time series (for a log-SNR equal to 30) are plotted in Fig. 3 for each SODE. Since the noise may contain outliers in real life, we also experimented with a Student-t noise with five degrees of freedom (maximum kurtosis) i.e. the tail distribution is the heaviest.

Building the dictionary

The dictionary of candidate functions was built sufficiently large, involving both monomial and interaction terms ($x_1 x_2, x_1^2 x_2$) that can span polynomials up to degree three. It was computed from the noisy time series, hence the regression covariates were also corrupted.

Estimation of the derivative

We experimented with three methods to estimate the time derivative of the state variables from the noisy time series: the finite-difference (FD) method, the spectral (SP) method and the B-spline (BSP) method.

The FD method is the most basic derivative estimation method as it consists approximating the derivative pointwisely as follows ${\dot{y}}(t_j) = \frac{y(t_{j+1}) - y(t_{j-1})}{2}$. It is computationally inexpensive but sensitive to noise [(Ramsay & Hooker, 2017), ch. 5].

The SP method relies on the following property: let ${\mathcal {F}}_y(f)$ be the Fourier transform (FT) of the differentiable function y at frequency $f \in {\mathbb {R}}$, then ${\mathcal {F}}_{\frac{\textrm{d}y}{\textrm{d}t}}(f) = 2 \pi i f {\mathcal {F}}_y(f)$. In other words, the derivative can be estimated by taking the inverse FT of the original time series multiplied by a linear factor. Thus, by using this property, it benefits from the low computational cost of the inverse Fast FT algorithm (Cooley & Tukey, 1965) for estimating the derivative from the raw data. Since noise measurement resides in high frequencies, the FT spectrum is low-pass filtered before computing its inverse transform. We experimented three filter sizes.

The BSP method, widely used in functional data analysis (Ramsay & Silverman, 2006), consists of two steps. First, approximate the time series with a weighted linear combination of BSPs i.e. piecewise polynomial functions, usually of degree three or four. The weights are computed by minimizing standard least-square criteria as the data fidelity term. To balance between smoothness and data fitting error, the minimization is stopped when the error reaches a fixed amount s (the higher, the smoother the approximation). We experimented with six values of $s \in \{5, 10, 50, 100, 500, 1000, 5000 \}$. Second, knowing the analytical form of each BSP, the derivative is computed from the approximated function as a linear combination of the BSPs’ derivative. See [(Ramsay & Silverman, 2006), ch. 4,5] and Lejeune et al. (2020) for a detailed explanation of penalized curve smoothing and an application to outlier detection in functional data analysis, respectively.

4.1.2 Real data

As an example of a real-world application, we applied our approach to discover the dynamics of a laboratory-based ecological phenomenon whose SODE is unknown (Becks et al., 2010). In this system, algae of genus Chlorella is grown in a large glass test tube (chemostat) to which a nutrient-rich medium is continuously added, and from which the contents are removed (including the algae) at a constant rate. The growth of the algae population is limited by nutrition in the ecology and by predation by the rotifer, Brachionus, a genus of microscopic animals. The rotifers reproduce according to how much algae they consume, and die either from natural causes or when they are removed from the tank. Hence, there might be a predator–prey dynamic between these two quantities (Ramsay & Hooker, 2017). The goal is to discover the SODE that governs the dynamics underlying the growth rate of the algae and the rotifers.

The dataset (abbreviated Chemostat data) consists of a bivariate time series with 108 daily time steps. The first state variable, $x_1$, is the Chlorella concentration, and the second state variable, $x_2$, is the Brachionus concentration. As recommended in the analysis of Ramsay and Hooker (2017), we preprocessed the time series by approximating them with 103 cubic BSP (using the R packages FDA (Ramsay et al., 2020)). Then we reconstructed the time series by evaluating the approximation function on a regular grid of $5\times 10^3$ time steps in the interval [7; 114]. The resulting reconstruction can be considered nonnoisy, so we estimate the derivative with the FD method. We built the dictionary with monomial functions up to degree five, with first, second and third order interactions $x_1 x_2, x_1^2 x_2, x_1^3 x_2$.

4.2 Setting for the GISTA

We followed the settings of the original GISTA paper (Gong et al., 2013). We initialized the algorithm with ${\varvec{\beta }}_0 = {\varvec{0}}$ and set the step size $\gamma = 2$. We stopped the outer loop (lines 4-11 Algorithm.1) when the iteration number exceeded $10^3$. We stopped the inner loop when the objective function of Equation (2) was below its quadratic approximation or the number of inner iterations exceeds 10. The hyperparameters $\lambda$, $\theta$ (for $R_{\lambda , \theta }^{SCAD-\ell _1}$ and $R_{\lambda , \theta }^{SCAD}$) and $\alpha$ (for $R_{\ell _{2,1} + \ell _1}$) were selected with a time based five fold cross validation: each training/testing fold consists in successive samples of the state-variables (for a given fold, the last training sample “immediatly preceeds” the first testing sample). The training folds are of increasing size (25%, 40%, 55%, 70% and 85% of the whole dataset) and, the testing folds do not overlap and have a fixed size (15% of the whole dataset). Moreover, this strategy enables to asses the effect of the number of training time steps on the SODE recovery.

4.3 Comparison with baselines

We compare our proposal $R_{\lambda , \theta }^{SCAD-\ell _1}$ to four baselines $R_{\ell _{1,1}}$, $R_{\ell _{2,1}}$, $R_{\ell _{2,1} + \ell _{1,1}}$ and $R^{SCAD}_{\lambda , \theta }$. To fairly compare the effects of the baseline regularizers on the learned SODEs, all were instantiated them within GISTA.

We compared the learned SODEs with three metrics: $\epsilon _\beta = \frac{\Vert \hat{{\varvec{\beta }}} - {\varvec{\beta }}^* \Vert _{2,2}^2}{\Vert {\varvec{\beta }}^* \Vert _{2,2}^2}$, $\epsilon _T = \frac{\sum _{i=1}^{n} \Vert \hat{{\textbf{x}}}(t_i) - {\textbf{x}}^*(t_i) \Vert _{2}^2}{\sum _{i=1}^{n} \Vert {\textbf{x}}^*(t_i) \Vert _{2}^2}$² and $\epsilon _{MIS} = \frac{\sum _{i,j} {\mathcal {I}}( {\hat{\beta }}_{ij} \ne \beta _{ij}^{*} ) }{ \sum _{i,j} {\mathcal {I}}( \beta _{ij}^{*} \ne 0 ) }$.

$\epsilon _\beta$ measures the relative bias w.r.t the ground-truth coefficient matrix ${\varvec{\beta }}^*$. $\epsilon _T$ measures the relative squared error, along t, of the numerical solution for the learned SODE w.r.t to the numerical solution of the ground-truth SODE. $\epsilon _{MIS}$ measures the rate of misidentified candidate functions. The lower $\epsilon _{\beta }$, $\epsilon _T$ and $\epsilon _{MIS}$ are, the better the recovery of the SODE. Since the SODE is unknown for the Chemostat, note that only $\epsilon _T$, wherein ${\textbf{x}}^*$ refers to the learning data (preprocessed), can be computed.

4.4 Implementation

The GISTA was implemented in the Python library Lightning (Blondel & Pedregosa, 2016) which is a Scikit-learn compatible interface for linear regression and classification. The experiments were run in parallel on a cluster equiped with 24 Intel Xeon-Gold-6136 3GHz processors, each one holding 192Go RAM. The whole process, i.e. building the dictionary, derivative estimation, hyperparametrs selection and earned SODE simulation, is implemented within the Python API Pysindy (Kaptanoglu et al., 2022).³

4.5 Results

4.5.1 Synthetic datasets

Fig. 4

Results (average over five trials in percentage, standard deviation was computed and lower than $10^{-4}$ hence invisible in the plots) of the learning errors of the DOC SODE with four baseline regularizers and our proposal $R^{SCAD-\ell _1}$. Each subfigure title (’FD’, ’spectral’ or ’spline’) indicates the name of the derivative estimation method used. a Training data are contaminated by a Gaussian noise whose variance level is varied according to the log-SNR between 20 (high noise level) and 50 (low noise level), or by b a Student-t noise that results in a log-SNR $\approx 40$. $\epsilon _{\beta }$ measures unbiasedness of the SODE coefficients. $\epsilon _{MIS}$ measures the misidentification error of the learned SODE. $\epsilon _T$ measures the error of the numerical solution of the learned SODE w.r.t the clean ground-truth (Color figure online)

Fig. 5

Results of the learning errors of the LV SODE. Detailed comments in Fig. 4 (Color figure online)

Fig. 6

Results of the learning errors of the LAT SODE with five baseline regularizers. Detailed comments in Fig. 4 (Color figure online)

For each of these SODEs, we repeated the experiment five times. In Figs. 4, 5 and 6 we report the average and standard deviations of $\epsilon _{\beta }$, $\epsilon _T$ and $\epsilon _{MIS}$. We see that for all the experiments the bias is reduced with $R^{SCAD}$ and our proposal $R^{SCAD-\ell _1}$ (see purple curves and vertical bars for $\epsilon _{\beta }$). (given in the supplementary material as it results in many figures)

Effect of the derivative estimation methods

As can be seen in Figs. 4, 5 and 6, the variations in the three error metrics are high when the derivative is estimated with the FD method. That (unsurprisingly) tells us that this method is highly sensitive to noise. The SP method gives the worst results, which we explain with the non-stationarity of the time series resulting from the SODE. Indeed, only a part of the signal is seen during the time based cross validation, thus the Fourier spectrum of the training part might be a poor estimate of the whole ground-truth. The filter size selection is noise sensitive, and consequently, in the Fourier sepctrum, some ground-truth frequencies which are close to the noise frequencies might be abnormally removed, resulting in a poor derivative estimate. Therefore, the SP method is unreliable for derivative estimation used with (nonstationary) time based cross validation. When using BSP instead, the errors are quite stable against noise. This makes it a good candidate for inferring the derivative when the practitioner does not have prior knowledge about the noise measurement level.

Effect of the noise level and type

We observe that for low log-SNR values, learning with $R^{SCAD-\ell _1}$ in conjunction with the FD method is similar to learning with the baseline regularizers. The same observation holds when using the BSP method. However, as the log-SNR increases (i.e. the noise level decreases), the error decays are the highest with $R^{SCAD-\ell _1}$ whereas the decay is lower (or remains constant) with the convex regularizers. Also, note that with the BSP method, learning with convex regularizers increases $\epsilon _{MIS}$ w.r.t the log-SNR whereas with the nonconvex $R^{SCAD}$ and $R^{SCAD-\ell _1}$, it remains constant. Overall the Gaussian noise experiments suggest that with both the FD and BSP methods, and for moderate log-SNR levels $\ge 30$, (that means when dealing with high-quality samples of the state variables), the SODEs are best recovered with our proposal. The experiments with the Student-t noise partially confirm our observations made about the effect of the derivative estimation method. Since for the convex regularizers and $R^{SCAD}$, the errors are quite variable across the three SODEs, the FD method is not robust against noise (here heavy-tailed). Indeed, the errors are low with the LV SODE (see the first row of Fig. 5 ) and high with the DOC and LAT SODEs. Note however that, $R^{SCAD-\ell _1}$ is more robust than the baselines against the Student-t noise. The three errors are almost the highest with the SP method for the three SODEs, hence we confirmed that it is not suited to derivative estimation for SODE discovery. When the SODE is learned with the nonconvex regularizers, the BSP method gives much better results than both the FD and SP methods. Overall, the Student-t noise experiments suggest that the SODEs are better recovered with nonconvex regularizers.

Effect of the multitask consideration

We now compare the results of the multitask based regularizers ($R_{\ell _{2,1}}$, $R_{\ell _{2,1}+\ell _{1,1}}$, $R^{SCAD-\ell _1}$) w.r.t the single-task-based ones ($R_{\ell _{1,1}}$, $R^{SCAD}$). First, we analyze the results of DOC experiments, in which the SODE has the same terms across across its equations (see (a) Fig. 3). Hence, among the baselines, since $R_{\ell _{2,1}}$ enforces the equations to share the same terms, it should better recover the ground-truth SODE than the single-task-based ones. This is confirmed by our results since the single-task-based regularizers (blue and red in Fig. 4) are outperformed by $R_{\ell _{2,1}}$ and $R^{SCAD-\ell _1}$ (orange and purples curves). We note however that the decay of $\epsilon _T$ with $R_{\ell _{2,1}}$ is similar to $R^{SCAD-\ell _1}$, and the latter gives lower errors. Similarly, we analyze the results of the LV experiments, in which the SODE (see (b) Fig. 3) has one common and one specific term across its two equations. In this context, we expect $R_{\ell _{2,1}+\ell _{1,1}}$ to recover the ground-truth SODE well. This is partly confirmed by our results, we see that $R_{\ell _{2,1}+\ell _{1,1}}$ performs similarly to $R_{\ell _{1,1}}$, but both are outperformed by $R^{SCAD-\ell _1}$ (blue and green in Fig. 5). The decays of $\epsilon _T$ are also similar and $R^{SCAD-\ell _1}$ is slightly better. Finally and equivalently, we analyze the results of the LAT experiments in which the SODE has approximately the same number of shared and specific terms (see (c) Fig. 3). For this kind of SODE, we again expect $R_{\ell _{2,1}+\ell _{1,1}}$ to perform best. This is clearly not the case as both $R^{SCAD}$ and $R^{SCAD-\ell _1}$ behave similarly (red and purple in Fig. 6), the former being slightly better. As for the LV SODE, $R_{\ell _{2,1}+\ell _{1,1}}$ and $R^{SCAD-\ell _1}$ show similar results and $R_{\ell _{2,1}}$ gives the worst results. Overall, we see that task relatedness is an important feature in SODE discovery and that our proposal improves it. Although $R_{\ell _{2,1}+\ell _{1,1}}$ was designed to trade off between task relatedness and task specificity, the balance is driven by a hyperparameter whose selection is sensitive. Contrarily, by construction, our proposal is shown by our experiments to be adaptive to the balance between task relatedness and task specificity.

Effect of the number of training time steps

We remind that in time based cross validation, each training/testing fold consists in successive samples of the observed time series, the training folds are of increasing size and the size of the testing folds is fixed. Hence, the number of training time steps increases w.r.t the fold index. The testing folds do not overlap but the training ones do. Consequently, as mentioned in Sect. 4.2, time based cross validation enables to assess the relationship between the recovery errors and the number of training time steps. We assess this effect on the three synthetics SODEs with a log-SNR value of 30. For that, we train the models (one for each regularizer) on each (training) fold and then we compute the three errors metrics on the associated testing folds. We report the results on Figs. 7, 8, 9. From these figures, we confirm that as the fold number index increases, the errors decrease or remain stationary, with an exception for the spectral derivative estimator. We note that the highest error decays occur with $R^{SCAD-\ell _1}$ and $R^{SCAD}$. The convex baselines are similar.

Fig. 7

Test errors of the five cross validation folds for the three synthetic SODEs. Remind that the size of the training set increases along the folds but the size of the test set is fixed. Same legend as in Fig. 4

Fig. 8

Test errors of the five cross validation folds for the LV SODEs

Fig. 9

Test errors of the five cross validation folds for the LAT SODEs

Statistical assesment of the experimental results

Table 2 Mean rank of each regularizer w.r.t the three error metrics

We assess the relevance of our conclusion with a two step statistical hypothesis test. We apply the method of Demsar (2006). The first step aims to confirm that not all the regularizers are similar, i.e. at least one is different w.r.t the other ones. This step is accomplished with the non-parametric Friedman test. If the latter concludes that at leat one regularizer is different from the others, then in the second step all the regularizers are compared pairwisely through their mean rank: if the difference between two average ranks is greater than what is called a “critical distance” statistic, the two regularizers are said to be different. The second step is done with the Nemenyi post-hoc test. See (Demsar, 2006) for more details. For any hypothesis tests, we set the p-value to 5%. We repeat the whole procedure for each one of the three error metrics on all the results (derivative estimator, log-SNR value, etc). The null hypothesis of the Friedman test is rejected with probability of error $10^{-40}$ for $\epsilon _{\beta }$, $10^{-86}$ for $\epsilon _{MIS}$ and $10^{-14}$ for $\epsilon _{T}$, thus there is a difference between the regularizers. We report the mean ranks in Table 2. It confirms our empirical comparisons made in the previous paragraphs.

Fig. 10

a Training/test data and numerical solution the SODEs learned with the four baseline regularizers and our proposal from the Chemostat dataset. b Analytic form of the learned SODEs

4.5.2 Chemostat dataset

We show the numerical solution, as well as the analytic form, of the SODEs learned for each regularizer in Fig. 10a, b respectively. As for the synthetic datasets, the results show that learning with $R^{SCAD-\ell _1}$ improves the recovery performance (smallest $\epsilon _T$ in Table 3) compared to $R^{SCAD}$ and the convex baselines.

Table 3 $\epsilon _T$ for the Chemostat SODE learned with the four baseline regularizers and our proposal $R^{SCAD-\ell _1}$

We interpret the dynamics of the underlying biological phenomenon by examining the closed-form SODE discovered with $R^{SCAD-\ell _1}$ (Fig. 10b last column). Based on the analysis carried out in Ramsay and Hooker (2017) and noting the strong similarity with the LV model (i.e. only linear and same first-order interaction terms in the two equations), we can interpret the discovered SODE as a predator–prey model as follows: within both equations, we observe the presence of a first-order interaction term $x_1 x_2$ that models the rate (decreasing or increasing depending on the coefficient sign) at which the Chlorella, $x_1$, and the Brachionus, $x_2$, meet in the chemostat. Note that among the five SODEs displayed, only $R^{SCAD-\ell _1}$ enabled the discovery of this interaction term in both equations, which emphasizes the importance of considering the SODE coupling using MTL. The linear terms in the two equations can be interpreted as the exponential reproduction of each ”species”. This exponential dynamic reproduction is limited by the species interaction and is only true for the experimental time frame.

5 Conclusion and future work

We recast the discovery of a closed-form SODE as an MTL problem. We proposed a penalty that (i) accommodates the coupling within an SODE and (ii) provides unbiased coefficients. The learning was conducted by instantiating GISTA (Gong et al., 2013). Numerical experiments on synthetic and real datasets confirmed that harnessing both MTL and nonconvexity outperforms learning with state-of-the-art MTL-based convex regularizers.

Scientific data analysts also face the case where an experiment has been repeated under various experimental designs and they have to deal with multiple datasets. In future work, we will address the joint discovery of SODEs from multiple multivariate time series. We also plan to extend our work to partial differential equations to discover dynamics from spatiotemporal data, and thereby understand both time and spatial dynamics.

Appendices

Appendix 1

Proof of the results in Eq. 7

We detail the steps to obtain the closed form of the proximal operator of $R_{SCAD-\ell _1}$, defined for any ${\varvec{W}} \in {\mathbb {R}}^{m \times p}$ as:

$$\begin{aligned} R_{\lambda , \theta }^{SCAD-\ell _1} ({\varvec{W}}) = \sum _{i=1}^{m} r^{SCAD}_{\lambda , \theta } \big ( \Vert {\textbf{w}}_{i \bullet } \Vert _{1} \big ) = \left\{ \begin{array}{ll} \lambda \Vert {\textbf{w}}_{i \bullet } \Vert _{1} &{} \text { if } \Vert {\textbf{w}}_{i \bullet } \Vert _{1} \le \lambda \\ - \frac{\lambda ^2 - 2 \theta \lambda \Vert {\textbf{w}}_{i \bullet } \Vert _{1} + \Vert {\textbf{w}}_{i \bullet } \Vert _{1}^2}{2(\theta -1)} &{} \text { if } \lambda < \Vert {\textbf{w}}_{i \bullet } \Vert _{1} \le \theta \lambda \\ \frac{(\theta + 1)\lambda ^2}{2} &{} \text { if } \Vert {\textbf{w}}_{i \bullet } \Vert _{1} > \theta \lambda \end{array} \right. \end{aligned}$$

(9)

We first note that $R^{SCAD-\ell _1}$ is row-separable. We compute $\text {prox}_{R^{SCAD}_{\lambda , \theta }}(\cdot )$ according to the bounds $\lambda$ and $\theta \lambda$. We denote the subdifferential of a function g at ${\textbf{u}} \in {\mathbb {R}}^p$ as $\partial g ( {\textbf{u}} ) = \{ {\textbf{y}}, g({\textbf{z}}) \ge g({\textbf{u}}) + {\textbf{y}}^{\top } ( {\textbf{z}} - {\mathbf {x )}}, \text {where } {\textbf{z}} \text { is in the domain of } g \}$. By abuse of notation, the ${{\,\textrm{sign}\,}}$ function is used equivalently for vectors and scalars.

For the first bound, the optimization problem is:

$$\begin{aligned} {\textbf{z}}^* \arg \min _{{\textbf{z}} \in {\mathbb {R}}^p} \frac{1}{2} \Vert {\textbf{x}} - {\textbf{z}} \Vert _{2}^2 + \lambda \Vert {\textbf{z}} \Vert _{1} \end{aligned}$$

From the first-order optimality condition, we have the necessary conidition:

$$\begin{aligned} {\textbf{0}} \in \nabla \Vert {\textbf{x}} - {\textbf{z}} \Vert _{2}^2 + \lambda \partial \Vert {\textbf{z}} \Vert _{1} \end{aligned}$$

Which is separable in p scalar problems. For $z_j \ne 0$, we have $\partial \Vert {\textbf{z}} \Vert _{1} = {{\,\textrm{sign}\,}}{{\textbf{z}}}$, thus we have:

$$\begin{aligned} \begin{aligned} 0&= z_j - x_j + \lambda {{\,\textrm{sign}\,}}{z_j} \\ \iff z_j&= x_j - \lambda {{\,\textrm{sign}\,}}{z_j} \end{aligned} \end{aligned}$$

Thus, on the first hand we have $|x_j | > \lambda$ and ${{\,\textrm{sign}\,}}{z_j} = {{\,\textrm{sign}\,}}{x_j}$ and we also have:

$$\begin{aligned} \begin{aligned} \Vert {\textbf{z}} \Vert _{1} \le \lambda&\iff \Vert {\textbf{x}} - \lambda {{\,\textrm{sign}\,}}{{\textbf{x}}} \Vert _{1} \le \lambda \\ {}&\iff \sum _j | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} | = | x_q - \lambda {{\,\textrm{sign}\,}}{x_q} | + \sum _{j \ne q} + | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} | \le \lambda \\ {}&\iff |x_q | - \lambda \le | x_q - \lambda {{\,\textrm{sign}\,}}{x_q} | \le \lambda - \sum _{j \ne q} | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} | \\ {}&\iff |x_q | \le 2\lambda - \sum _{j \ne q} | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} | \end{aligned} \end{aligned}$$

Thus for $z_j \ne 0$, the q-th component of the minimizer is $z_q^* = x_q - \lambda {{\,\textrm{sign}\,}}{x_q}$ if $\lambda < |x_q | \le 2\lambda - \sum _{j \ne q} | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} |$. For $z_j = 0$ we have:

$$\begin{aligned} \begin{aligned} 0 \in -x_j + [-\lambda , \lambda ] \iff |x_j | \le \lambda \end{aligned} \end{aligned}$$

And then, putting it all together, for the first bound, the q-th component of the minimizer is:

$$\begin{aligned} z_q^* = {{\,\textrm{sign}\,}}{x_q} \max (|x_q | - \lambda , 0) \text { if } |x_q | \le 2\lambda - \sum _{j \ne q} | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} | \end{aligned}$$

(10)

For the second bound, we follow a very similar path and so we write it shorter. The optimization problem is:

$$\begin{aligned} {\textbf{z}}^* = \arg \min _{{\textbf{z}} \in {\mathbb {R}}^p} \frac{1}{2} \Vert {\textbf{x}} - {\textbf{z}} \Vert _{2}^2 - \frac{ \lambda ^2 - 2 \theta \lambda \Vert {\textbf{z}} \Vert _{1} + \Vert {\textbf{z}} \Vert _{1}^2}{2(\theta -1)} \end{aligned}$$

Then, writting the optimality condition, we obtain for $z_j \ne 0$:

$$\begin{aligned} z_j = \frac{\theta - 1}{\theta - 2} x_j - \frac{\lambda \theta }{\theta - 2} {{\,\textrm{sign}\,}}{z_j} \end{aligned}$$

And so we have $|z_j | > \frac{\lambda \theta }{\theta -1}$ and ${{\,\textrm{sign}\,}}{z_j} = {{\,\textrm{sign}\,}}{x_j}$, which, by again using the boundedness of ${\textbf{z}}$, $\lambda < \Vert {\textbf{z}} \Vert _{1} \le \lambda \theta$ and separating the sum, lead to:

$$\begin{aligned} z_q^* = \frac{\theta -1}{\theta -2} {{\,\textrm{sign}\,}}{x_q} \max (|x_q | - \frac{\lambda \theta }{\theta - 2}, 0) \text { if } 2\lambda - A_q < |x_q | \le \lambda \theta - A_q \end{aligned}$$

(11)

with $A_q = \sum _{j \ne q} | x_j - \lambda {{\,\textrm{sign}\,}}{x_j} |$. Finally, for the third bound, the result is trivial since the second term in the optimization problem is a constant, thus the minimizer is necessarily $z_q^* = x_q$. Now by gathering (10)(11) and the last term, we obtain the q-th component $w_q$ of the output of the proximal operator evaluated on, ${\textbf{w}}_{i \bullet }$, the i-th row of ${\varvec{W}}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} {{\,\textrm{sign}\,}}(w_{q}) \max (0, |w_{q} | - \lambda ) &{}&{} \text { if } |w_{q} | \le 2 \lambda - \Vert {\textbf{w}}_{i \bullet , -q} \Vert _{1}, \end{aligned} \\ \begin{aligned} \frac{\theta -1}{\theta -2} {{\,\textrm{sign}\,}}(w_{q}) \max (0, |w_{q} | - \frac{\theta }{\theta -1} \lambda ) \\ \text { if } 2 \lambda - \Vert {\textbf{w}}_{i \bullet , -q} \Vert _{1} < |w_q | \le \theta \lambda - \Vert {\textbf{w}}_{i \bullet , -q} \Vert _{1}, \end{aligned} \\ \begin{aligned} w_{q} &{}&{} \text { if } |w_q | > \theta \lambda - \Vert {\textbf{w}}_{i \bullet , -q} \Vert _{1}, \end{aligned} \end{array}\right. } \end{aligned}$$

$\square$

Appendix 2

For reproducibility, we give the formulaes of the proximal operators associated with the four baseline regularizers used in our experiments. ${\varvec{W}} \in {\mathbb {R}}^{n \times p}$, ${\textbf{w}}_{i \bullet }$ denotes the i-th row (vector) of ${\varvec{W}}$, $\lambda > 0$ and $\theta > 2$.

1.1 2.1 LASSO

$R_{\ell _{1,1}} ({\varvec{W}}) = \sum _{i} \sum _{j} |w_{ij} |$

$$\begin{aligned} \text {prox}_{\lambda R_{\ell _{1,1}}}( {\varvec{W}} )_{ij} = {{\,\textrm{sign}\,}}({w_{ij}}) \max {(0, |w_{ij} | - \lambda )} \end{aligned}$$

for any entry $w_{ij}$ of ${\varvec{W}}$ (Tishbirani, 1996).

1.2 2.2 Group-LASSO

$R_{\ell _{2,1}} ({\varvec{W}}) = \sum _i \Vert {\textbf{w}}_{i \bullet } \Vert _{2}$

$$\begin{aligned} \text {prox}_{ \lambda R_{\ell _{2,1}} }( {\varvec{W}})_{i \bullet } = {\textbf{w}}_{i \bullet } \Big ( 1 - \frac{\lambda }{ \max (\lambda , \Vert {\textbf{w}}_{i \bullet } \Vert _{2}) } \Big ) \end{aligned}$$

for any row-vector ${\textbf{w}}_{i \bullet }$ of ${\varvec{W}}$ (Yuan & Lin, 2006).

1.3 2.3 Sparse-Group-LASSO

$R_{\ell _{2,1} + \ell _{1,1}} ({\varvec{W}}) = \alpha \sum _i \Vert {\textbf{w}}_{i \bullet } \Vert _{2} + (1-\alpha ) \sum _{i} \sum _{j} |w_{ij} |$

$$\begin{aligned} \text {prox}_{ \lambda R_{\ell _{2,1} + \ell _{1,1}}}( {\varvec{W}})_{i \bullet } = \text {prox}_{(1 - \alpha ) \lambda R_{\ell _{1,1}}}( \text {prox}_{\alpha \lambda R_{\ell _{2,1}} }( {\varvec{W}})_{i \bullet } )_{i \bullet } \end{aligned}$$

for $\alpha \in [0,1]$ and a row-vector ${\textbf{w}}_{i \bullet }$ of ${\varvec{W}}$. It corresponds to applying the “outer” proximal operator of $R_{\ell _{1,1}}$ entrywisely on the vector output by the “inner” proximal operator of $R_{\ell _{2,1}}$ (Simon et al., 2013).

1.4 2.4 SCAD

$R_{\lambda , \theta }^{SCAD}$

$$\begin{aligned} \text {prox}_{ R_{\lambda , \theta }^{SCAD} }({w_{ij}}) = {\left\{ \begin{array}{ll} {{\,\textrm{sign}\,}}({w_{ij}}) \max (0, |w_{ij} | - \lambda ) &{} \text { if } |w_{ij} | \le 2 \lambda \\ {{\,\textrm{sign}\,}}({w_{ij}}) \frac{\theta -1}{\theta -2} \max (0, |w_{ij} | - \frac{\lambda \theta }{\theta -1}) &{} \text { if } 2 \lambda < |w_{ij} | \le \lambda \theta \\ w_{ij} &{} \text { if } |w_{ij} | > \lambda \theta \end{array}\right. } \end{aligned}$$

for any entry $w_{ij}$ of ${\varvec{W}}$ (Fan & Li, 2001).