IA-NGM: A bidirectional learning method for neural graph matching with feature fusion

Abstract

Most existing deep learning methods for graph matching tasks tend to focus on affinity learning in a feedforward fashion to assist the neural network solver. However, the potential benefits of a direct feedback from the neural network solver to the affinity learning are usually underestimated and overlooked. In this paper, we propose a bidirectional learning method to tackle the above issues. Our method leverages the output of a neural network solver to perform feature fusion on the input of affinity learning. Such direct feedback helps augment the input feature maps of the raw images according to the current solution. A feature fusion procedure is proposed to enhance the raw features with pseudo features that contain deviation information of the current solution from the ground-truth one. As a result, the bidrectional alternation enables the learning component to benefit from the feedback, while keeping the strengths of learning affinity models. According to the results of experiments conducted on five benchmark datasets, our methods outperform the corresponding state-of-the-art feedforward methods.

1 Introduction

Graph matching (GM) refers to finding node correspondences between two graphs such that the similarity between the matched graphs is maximized. To find node correspondences between two graphs, GM usually leverages node-wise and edge-wise information. When considering node-wise and edge-wise information, GM can be represented in the following Lawler’s quadratic assignment programming (QAP) form Lawler (1963):

$$\begin{aligned} \begin{aligned} J({\mathbf {X}})={\text {vec}}({\mathbf {X}})^{\mathbf {T}}{\mathbf {K}}{\text {vec}}({\mathbf {X}}),\\ {\mathbf {X}} \in \{0,1\}^{n \times n}, {{\mathbf {X}}}{{\mathbf {1}}}={\mathbf {1}},\mathbf {X^{T}1}={\mathbf {1}} \end{aligned} \end{aligned}$$

(1)

where ${\mathbf {K}}$ is the so-called affinity matrix (Leordeanu & Hebert, 2005). Solving the general QAP is known to be NP-hard, and it is difficult to find the global optimal solution for large graphs. GM has been applied in many fields, such as visual tracking, action recognition, robotics, weak-perspective 3-D reconstruction, and so on. For a more comprehensive survey on GM applications, please refer to Vento and Foggia (2013).

Traditional GM methods are mostly developed on predefined, hand-crafted affinity matrix, which is limited to represent real-world data’s structure. To tackle this issue, Caetano et al. (2009) introduced free parameters and turned the affinity matrix into a learnable function. Recently, it was developed in Zanfir and Sminchisescu (2018) to learn the affinity in an end-to-end deep learning model, and later deep learning frameworks became popular to build learning models for GM. Typically, a deep graph neural network is constructed to encode the node-wise and edge-wise structural information into the affinity matrix, and the affinity is subsequently used in a GM solver, e.g., Hungarian algorithm. For example, Wang et al. (2019) relaxed GM as a linear assignment problem by employing deep graph embedding models to learn intra-graph and cross-graph affinity functions, while Wang et al. (2021) regarded the affinity matrix as an association graph and transformed GM to a vertex classification problem, solving GM in the Lawler’s QAP form directly. However, these methods mainly focus on the design of the feedforward pipeline, and do not notice the potential benefits of a possible feedback from the GM solver to the affinity learning.

In this paper, we take into account not only the assistance from affinity learning to GM solving, but also the feedback benefits from GM solving. Recently, a general bidirectional learning scheme, called IA-DSM, was suggested in Xu (2019), to solve double stochastic matrix (DSM) featured combinatorial tasks like GM. The IA-DSM framework consists of a learning component and an optimization component, and the intermediate discrete solution from the optimization component is fed back into the learning component through a feature enrichment and fusion process. Taking this framework into GM problem solving, Zhao et al. (2021) proposed a bidirectional learning method, IA-GM, to impose the output of the feedforward model into the graph embedding to enhance the affinity learning. Although IA-GM (Zhao et al., 2021) has been demonstrated with promising improvement over the existing GM methods, it still has several limitations. First, IA-GM was implemented by relaxing GM as a linear assignment problem, and whether the bidirectional learning paradigm works for GM in the general Lawler’s QAP form is unknown. Second, the performance of IA-GM was mainly evaluated on PASCAL VOC keypoint (Bourdev & Malik, 2009), and the generalization ability to other benchmarks requires further investigations. Third, it deserves more explorations on the effective ways of circulating the information from the optimization component back to the affinity learning.

To address the above issues, we propose a deep bidirectional learning method for solving GM in the Lawler’s QAP form, under the IA-DSM framework (Xu, 2019). A new feature fusion technique is employed to enhance the structural patterns using the images which are constructed via the output of the learning component (i.e. current estimation of the solution). In this way, each input sample would bring one similar sample in each bidirectional alternation, helping the model to learn better features. Our main contributions are summarized as follows:

• We propose a deep bidirectional learning method that works for solving GM in the general Lawler’s QAP form. Our method employs the DSM given by Sinkhorn algorithm rather than the hard assignment solution after the computation by Hungarian algorithm, and construct image-like input in the feature space for the subsequent feature fusion. In this manner, the constructed features of a node contain information of all possible matching nodes, and enable the learning component to adjust its matching result in the next bidirectional alternation.

• We present a gated feature fusion technique to combine the features of the raw samples in the actual world and their constructed image-like input in the bidirectional alternation. The fused features enforce the learning component to focus more on certain nodes according to the guiding information from the intermediate matching output by Sinkhorn algorithm. In comparisons with Zhao et al. (2021), our bidirectional learning employs a longer feedback path on the features directly.

• We evaluate the proposed method and the existing state-of-the-art ones on four image benchmark datasets and one QAPLIB (Burkard et al., 1997) dataset. Experiments demonstrate that our method is able to improve the matching accuracies consistently and robustly. We also extend IA-GM’s bidirectional learning paradigm directly to the QAP form, and empirical analysis indicate that the IA-DSM framework can be flexibly implemented and still has room to improve for solving GM.

2 Related work

2.1 Progresses in learning GM

Traditionally, researchers viewed building the affinity model and finding the solution as two separate steps. They focused on the latter, seeking approximate solution while leaving the affinity model hand-crafted, for example, the elements of the affinity matrix ${\mathbf {K}}$ are calculated according to the fixed Gaussian kernel with Eucildean distance:

$$\begin{aligned} {\mathbf {K}}_{ia,jb}=\exp \left( \frac{||\text {f}_{ij}-\text {f}_{ab}||^{2}}{\sigma ^{2}}\right) , \end{aligned}$$

(2)

where $\text {f}_{ij},\text {f}_{ab}$ are edges’ feature vectors of two graphs respectively. Caetano et al. (2009) first proposed a method to learn the affinity model. Later in 2013, Cho et al. (2013) defined a joint feature map by aligning node-wise and edge-wise similarities into a vectorial form, and introduced weights to all elements of the feature map. However, these predefined methods tend to have limitations in representing real-world data’s affinity.

Recently, with the development of deep learning, great progresses have been made in GM. Zhou and De la Torre (2015) proposed a novel closed-form factorization of the pairwise affinity matrix, making it easier to incorporate global geometric transformation in GM. Meanwhile, there is no need to calculate the affinity matrix explicitly as its structure is decoupled. Then, the end-to-end model proposed by Zanfir and Sminchisescu (2018), which learns an $n^{2}\times n^{2}$ quadratic affinity matrix to guide the GM optimization, presented an efficient way to back-propagate gradients from the loss function to the feature layers. Wang et al. (2019) employed deep graph embedding networks to encode structure affinity into a node-wise affinity matrix so that GM is relaxed as a linear assignment problem, and its devised permutation loss is more powerful than the offset loss used in Zanfir and Sminchisescu (2018). Later, Rolínek et al. (2020) replaced Graph Neural Network (GNN) with SplineCNN (Fey et al., 2018) to process features, pushing the accuracy on PASCAL VOC keypoint up to around 80%. However, these works can not directly deal with the general Lawler’s QAP form when individual graph information is unprovided as QAPLIB (Burkard et al., 1997). Therefore, following these work, Wang et al. (2021) proposed Neural Graph Matching (NGM) network by translating the GM task to a vertex classification task to directly solve it in the QAP form, as well as NGM-v2 by using SplineCNN for feature refinement.

2.2 Bidirectional learning

Bidirectional intelligence was recently reviewed in Xu (2018). In the bidirectional intelligence system, there are two domains defined: A-domain and I-domain. A-domain denotes the Actual-world and I-domain denotes the Inner-space. Between the two domains, there are two mappings: A-mapping (from A-domain to I-domain along the inward direction) and I-mapping (from I-domain to A-domain along the outward direction). A general bidirectional learning scheme, called IA-DSM, was first sketched in Xu (2019), under the framework of the system. Featured by an IA-alternation of A-mapping and I-mapping, the IA-DSM is to solve DSM featured combinatorial tasks. For instance, Xu (2019) suggested that traveling salesman problem can be solved in a bidirectional way by employing CNN as A-mapping to obtain a policy and its goodness from the current state, thus guiding the I-mapping for iterative learning. Zhao et al. (2021) provided a GM implementation of the IA-DSM scheme called IA-GM, which follows Wang et al. (2019), relaxing GM as a linear assignment problem. The A-mapping is implemented by an SR-GGNN, and the I-mapping consists of Sinkhorn algorithm and Hungarian algorithm.

Our work falls in the framework of IA-DSM, but has several differences. Most rencent deep learning GM methods (1) learn affinity matrix from features and (2) find a solution based on the affinity matrix. Zhao et al. (2021) implements the IA-DSM framework by (3) imposing the feedback to graph embedding to enhance the affinity learning, and our method implements the IA-DSM framework by (4) employing the feedback to perform feature fusion. Therefore, the key difference between our work and Zhao et al. (2021) is the bidirectional learning fashion. Unlike Zhao et al. (2021), we lengthen the feedback path to assist the learning component by affecting features directly. Meanwhile, we employ neural network solver of state-of-the-art models and Sinkhorn algorithm as the A-mapping, and we regard pseudo feature generation and feature fusion as the I-mapping. Moreover, we implement IA-DSM to solve GM in the Lawler’s QAP form directly while (Zhao et al., 2021) solves GM by relaxing it as a linear assignment problem.

3 Methods

3.1 Overview of our method

Fig. 1

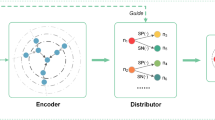
An overview of IA-NGM. a The pipeline of IA-NGM for graph matching problem, where Solver represents a neural network solver, Fusion is implemented by Eq. (10); b The Fusion process of the pipeline; c The gating network for adjusting the fusion weights

We propose a bidirectional learning method for solving GM in the general form of Lawler’s QAP. Our method is developed under the IA-DSM framework (Xu, 2019) by adopting NGM (Wang et al., 2021) as the network backbone, and thus we call it as IA-NGM. An overview of our method is given in Fig. 1a. IA-NGM consists of a learning component (black arrows) and an optimization component (red arrows) that produces feedback into the learning part. The learning component takes two types of feature maps as input. One type is the primal feature map which is extracted from a real-world image by a CNN-based extractor (e.g., VGG-16 (Simonyan & Zisserman, 2014)). The learning component learns the unary and quadratic affinity across graphs through a neural network solver, and outputs a score matrix ${\mathbf {B}}$ whose entries represent the confidences of node correspondences between two graphs. Then Sinkhorn algorithm is performed to get a soft assignment matrix ${\mathbf {P}}$, where its entries indicate how likely the corresponding two nodes are matched to each other. The soft matching solution ${\mathbf {P}}$ is used to construct pseudo feature maps for the two input real images, and the pseudo feature maps are circulated back into the learning component via a linear feature fusion module. The fused features are fed into the neural network solver for further learning, and the affinity learning is augmented on the pseudo feature maps which contain the deviation information of the current matching solution to the ground-truth correspondences. The feedback from the current matching status completes an IA-alternation under the bidirectional intelligence framework (Xu, 2018). The key difference between our IA-alternation and the one in Zhao et al. (2021) is that the affinity learning is more involved in the alternating path, enhancing the representation learning in a more through way.

3.2 Feature extraction and neural network solver

For two input images, we construct two graphs ${\mathcal {G}}_1, {\mathcal {G}}_2$ using the annotated key points as graph nodes. We adopt VGG-16 architecture to extract their node features $U_1, U_2$ from layer relu4_2, edge features $F_1, F_2$ from layer relu5_1 when using NGM’s neural network solver. We use layer relu4_2 and relu5_1 to extract init node features and use relu5_3 to extract global features g when using NGM-v2’s solver.

The neural network solver can be viewed as a function as follows:

$$\begin{aligned} {\mathbf {B}}=Solver({\mathbf {F}}_{1}^{*},{\mathbf {F}}_{2}^{*}), \end{aligned}$$

(3)

where ${\mathbf {B}}$ is the score matrix for node-wise correspondence between ${\mathcal {G}}_1$ and ${\mathcal {G}}_2$, and ${\mathbf {F}}_{1}^{*}$, ${\mathbf {F}}_{2}^{*}$ represent the features of two graphs, respectively, including node features $U_1, U_2$, edge features $F_1, F_2$, and global features g if available. In this paper, we adopt NGM and NGM-v2 (Wang et al., 2021) to learn the score matrix.

3.3 Pseudo feature generation

Following (Adams & Zemel, 2011), Sinkhorn algorithm is computed as follows:

$$\begin{aligned} {{\textbf {S}}}_{k+1}={\left\{ \begin{array}{ll} {{\textbf {S}}}_{k}[{\mathbf {1}}_{n}^{{\textbf {T}}}{{\textbf {S}}}_{k}]^{-1},&{}k\,\text {mod}\,2 = 0\\ {[}{{\textbf {S}}}_{k}{\mathbf {1}}_{n}^{{\textbf {T}}}]^{-1}{{\textbf {S}}}_{k},&{}k\,\text {mod}\,2 = 1 \end{array}\right. } \end{aligned}$$

(4)

where $k=0,1,2,\ldots$ denotes the iteration serial number. Then, the soft assignment matrix ${\mathbf {P}}$ is obtained by Sinkhorn procedure taking the score matrix ${\mathbf {B}}$ as input,

$$\begin{aligned} {\mathbf {P}}=Sinkhorn({\mathbf {B}}), \quad \text {i.e., } {\mathbf {S}}_{0}={\mathbf {B}}. \end{aligned}$$

(5)

Then, the hard assignment matrix ${\mathbf {X}}\in \{0,1\}^{n\times n}$ is calculated by the Hungarian algorithm:

$$\begin{aligned} {\mathbf {X}}=\textit{Hungarian}({\mathbf {P}}). \end{aligned}$$

(6)

If the matching solution ${\mathbf {X}}$ is close to optimum, the permuted features of one graph will be similar to those of the other graph. Specifically, define the pseudo node features as:

$$\begin{aligned} {\widetilde{U}}_{1}={\mathbf {X}}U_{2}, \quad {\widetilde{U}}_{2}={\mathbf {X}}^{\mathbf {T}}U_{1}, \end{aligned}$$

(7)

where $U_{1},U_{2}\in {\mathbb {R}}^{n\times d}$ are primal node features extracted directly from the input images. Generally, we calculate the pseudo overall features as follows:

$$\begin{aligned} \widetilde{{\mathbf {F}}}_{1} = {\mathbf {X}}{\mathbf {F}}_{2}, \quad \widetilde{{\mathbf {F}}}_{2} = {\mathbf {X}}^{\mathbf {T}}{\mathbf {F}}_{1}, \end{aligned}$$

(8)

where ${\mathbf {F}}_1, {\mathbf {F}}_2$ are primal overall features extracted from the input images. It is noted that the pseudo features depend on the accuracy of the matching solution ${\mathbf {X}}$. If ${\mathbf {X}}$ is optimal, the discrepancy between $\widetilde{{\mathbf {F}}}_i$ and ${\mathbf {F}}_i$ is minimized. However, at the beginning of the training process, the intermediate solution ${\mathbf {X}}$ is not the optimal one, including the correctly matched part and the error part. The matched part does not affect the affinity learning, but the error part would change the affinity.

Since ${\mathbf {X}}$ by Eq. (6) is a binary permutation matrix, the pseudo feature generation by Eq. (8) is not flexible enough to continuously capture the learning status of the model. Moreover, it does not take into account the uncertainty of the learning process which is large at the beginning. Therefore, we further replace ${\mathbf {X}}$ in Eq. (8) with the soft assignment matrix ${\mathbf {P}}$, and get

$$\begin{aligned} \widetilde{{\mathbf {F}}}_{1}={\mathbf {P}}{\mathbf {F}}_{2}; \quad \widetilde{{\mathbf {F}}}_{2}={\mathbf {P}}^{\mathbf {T}}{\mathbf {F}}_{1}. \end{aligned}$$

(9)

In this way, the constructed pseudo features are more sensitive to deviation of the learning output from the optimal solution, and they are helpful and more effective in guiding the learning process towards the optimal solution.

3.4 Gated feature fusion

We present a linear fusion scheme to integrate the pseudo features back into the learning component, as illustrated in Fig. 1b:

$$\begin{aligned} {\mathbf {F}}_{1}^{*}=\alpha {\mathbf {F}}_{1} +(1-\alpha )\widetilde{{\mathbf {F}}}_{1}, \quad {\mathbf {F}}_{2}^{*}=\alpha {\mathbf {F}}_{2} +(1-\alpha )\widetilde{{\mathbf {F}}}_{2}, \end{aligned}$$

(10)

where we have constrained the sum of the combining coefficients $\alpha$ and $1-\alpha$ to be one. The obtained ${\mathbf {F}}_1^*, {\mathbf {F}}_2^*$ are the features augmented with deviation information of the current GM solution from the optimum, and they are fed into Eq. (3) to improve the affinity learning.

In practice, the coefficients can be predefined according to the empirical experience. However, prefixed coefficients may not adapt to the learning dynamics well because feature extractors like SplineCNN may change the distribution of the primal features as learning proceeds. We propose a two fully-connected (FC) layer network with feature channels $l_{1}=1024, l_{2}=32$, which is shown in Fig. 1c, to learn the weight $\alpha$ according to the current state of the input. It is worth noticing that the Feature Extraction in Fig. 1a and c is same, but we use all features extracted in Fig. 1a and only use global features in Fig. 1c. The global features $g_1, g_2$ are computed as the relu5_3 layer of VGG-16 for the two input graphs ${\mathcal {G}}_1, {\mathcal {G}}_2$, as described in Sect. 3.2. Mathematically, the gating network is computed as follows:

$$\begin{aligned} \alpha =\tanh (\text {FC}(\tanh (\text {FC}(concat(g_{1},g_{2}))))), \end{aligned}$$

(11)

where concat denotes the concatenation operator.

3.5 IA-alternation

With the gated fusion between the primal features and the pseudo ones by Eq. (10), it completes the circle of IA-alternation, i.e.,

$$\begin{aligned} {\mathbf {P}}^{(k)}=Sinkhorn(Solver({\mathbf {F}}_{1}^{*(k)},{\mathbf {F}}_{2}^{*(k)})), \end{aligned}$$

(12)

$$\begin{aligned} {\mathbf {F}}_{i}^{*(k+1)}=Fusion(Construct({\mathbf {P}}^{(k)},{\mathbf {F}}_{i}^{*(k)})), ~~~~i\in \{1,2\} \end{aligned}$$

(13)

where $k=1,2,\cdots ,K$ represents the serial number of the IA-alternations and Construct is implemented by Eq. (9). At the beginning, there is no pseudo features, and we set ${\mathbf {F}}_{1}^{*(1)}={\mathbf {F}}_{1}, {\mathbf {F}}_{2}^{*(1)}={\mathbf {F}}_{2}$ or equivalently setting $\alpha =1$ in Eq. (10). The soft assignment matrix ${\mathbf {P}}^{(k)}$ encodes the cross-graph affinity via the neural network solver, and the gated feature fusion guides the learning in the next alternation to pay more attention to the matching pairs that have large deviation from the optimum in the previous alternation. As a consequence, the IA-alternation benefits the GM solving model from both directions. After the last IA-alternation, the predicted assignment matrix is calculated by Eq. (6) as:

$$\begin{aligned} {\mathbf {X}}^{*}=\textit{Hungarian}({\mathbf {P}}^{(K)}). \end{aligned}$$

(14)

3.6 Loss function

Fig. 2

Unfolded structure of the proposed network during training

We leverage the ground-truth correspondences to supervise the learning process. We adopt the permutation loss (Wang et al., 2019), which has been proved effective for graph matching tasks, as the loss function:

$$\begin{aligned} {\mathcal {L}}= -\frac{1}{n}\sum \limits _{i,j}\left[ x^{gt}_{ij}\ln {p^{(K)}_{ij}}+(x^{gt}_{ij})\ln {(1-p^{(K)}_{ij})} \right] \end{aligned}$$

(15)

where ${\mathbf {X}}^{gt}=[x^{gt}_{ij}],x^{gt}_{ij}\in \{0,1\}$ represents the ground-truth assignment matrix, and ${\mathbf {P}}^{(K)}=[p_{ij}^{(K)}]$ is the soft assignment matrix of the last IA-alternation by Eqs. (12) and (13). We illustrate the computational procedure in Fig. 2. It is noted that, in the end-to-end training, the Hungarian algorithm is only used in the end to get the output matrix, while Sinkhorn is used in each feedback loop to generate the intermediate solution matrix. The loss function by Eq. (15) is applied on the soft assignment matrix output by the K-th Sinkhorn block, before the Hungarian algorithm is activated in the end. In testing, the model follows the blue arrow in Fig. 2 to get ${\mathbf {X}}^{*}$, and there is no back propagation involved.

4 Experiments

We evaluate our models on five benchmark datasets. Specifically, in line with Wang et al. (2021), we use PASCAL VOC keypoint and Willow ObjectClass (Cho et al., 2013) as benchmark datasets, to compare with previous closely-related GM methods: (1) GMN (Zanfir & Sminchisescu, 2018) learns affinity functions, (2) PIA-GM (Wang et al., 2019) learns intra-graph affinity, (3) PCA-GM (Wang et al., 2019) learns cross-graph affinity, (4) IA-GM (Zhao et al., 2021) implements the IA-DSM framework by relaxing GM to linear, (5) BBGM employs SplineCNN (Fey et al., 2018) in GM and (6) NGM & NGM-v2 (Wang et al., 2021)) solve GM in QAP form directly.

For further exploration on the benefits of different bidirectional learning fashion, we also include IMC-PT-SparseGM¹ and CUB2011 (Wah et al., 2011) as benchmark datasets, to compare with NGM and NGM-v2 (Wang et al., 2021), and IA-GM (Zhao et al., 2021). Our models are named as IA-NGM and IA-NGM-v2, which correspond to the versions of employing the neural network solvers of NGM and NGM-v2 respectively. We set the value of $\alpha$ in feature fusion by Eq. (10) to be 0.6 for IA-NGM according to our empirical experience, and leave it to be learned by the gating learning network in IA-NGM-v2. We set the number of IA-alternation to be 3 for IA-NGM and 2 for IA-NGM-v2, because a big number of IA-alternations would possibly lead to over-smoothing. For fair comparisons with IA-GM, we extend it to be IA-GM-v1 and IA-GM-v2 by modifying the network backbone from the weights-shared residual gated graph neural network (SR-GGNN) to be NGM and NGM-v2 respectively.

In line with Wang et al. (2021), the neural network solvers of IA-NGM and IA-NGM-v2 both use a three-layer GNN with feature channels $l_{1}=l_{2}=l_{3}=16$ to perform association graph embedding. The maximum iteration number is set to 20 for Sinkhorn algorithm. The initial learning rate of the neural network solver in IA-NGM/IA-NGM-v2 and the gating network for $\alpha$ in Eq. (10) starts at $10^{-3}$ and decays by 10 every 10,000 steps. The learning rate of the feature extractor is set to $2\times 10^{-6}$ in IA-NGM-v2. All experiments are conducted on a Linux workstation with Titan XP GPU.

4.1 Results on PASCAL VOC keypoint

Fig. 3

Keypoint number distribution of PASCAL VOC dataset. Each of 20 subfigures corresponds to a semantic class. The name of each class is marked at top-right of the subfigure. The x-axis denotes the number of keypoints in a graph, and the y-axis denotes the number of samples containing corresponding number of keypoints

The PASCAL VOC keypoint dataset, containing 20 semantic classes with annotated examples, is challenging as the images differ in size and the number of keypoints varies from 6 to 23. We count the keypoints of samples for each class in Fig. 3. It is observed that some classes contain samples of more than 10 keypoints while others may have only a few.

Table 1 Matching accuracy (%) on Pascal VOC keypoint

The matching accuracies on PASCAL VOC keypoint are reported in Table 1. Our bidirectional methods all outperform the corresponding feedforward baselines, indicating that the feedback of the pseudo features is beneficial to the affinity learning. Specifically, IA-NGM improves the mean accuracy by $2.5\%$ with respect to NGM, while IA-NGM-v2 improves the performance by $0.8\%$ with respect to NGM-v2. Meanwhile, IA-NGM and IA-NGM-v2 outperforms IA-GM-v1 and IA-GM-v2, respectively, indicating that the affinity fusion by Zhao et al. (2021) is not so effective as the proposed feature fusion by Eq. (10). The NGM-v2 based methods are superior to the NGM-based ones, with about $15\%$ increment contributed mainly by using SplineCNN as the feature extractor. The increment $2.5\%$ by IA-NGM is more than $0.8\%$ by IA-NGM-v2, probably because it becomes more difficult to improve the performance from a very high level. Looking into the detailed accuracies for each class in Table 1, we observe that our bidirectional methods can make the neural network solver learn better on its weak classes while keeping its comparable results on other classes. For example, on the class “chair", IA-NGM-v2 exceeds NGM-v2 by 11.7%; on the class “table", IA-NGM achieves a 29.9% improvement over NGM.

To evaluate the performance on each class, we train and test NGM, IA-NGM, NGM-v2 and IA-NGM-v2 on individual classes, and the results are shown in Table 2. The results are consistent with Table 1. IA-NGM-v2 exceeds NGM-v2 on the class “chair" and “sofa" by over 10%, while NGM-v2’s in-class accuracy is lower than its cross-class accuracy. Some classes can have similar features with other classes so that NGM-v2’s learning is enhanced when trained on all classes, while IA-NGM-v2 already fused the similarity into features so that it has similar in-class and cross-class performances.

Table 2 In-class performances on certain classes of PASCAL VOC keypoint

Moreover, IA-GM/IA-GM-v2 are comparable to IA-NGM/IA-NGM-v2, respectively, which confirms the effectiveness of the feedback and fusion scheme in Zhao et al. (2021). For the performance on 20 classes, the accuracy gaps between the two methods are mostly small except for the class “table" where IA-NGM-v2 exceeds IA-GM-v2 by $20.3\%$. We also notice that the accuracies on the class “aero" and “person" remain relatively low, because the images of the two classes have a wide range of keypoints, making it very difficult to learn.

4.2 Results on willow ObjectClass

Table 3 Matching accuracy (%) on Willow ObjectClass

Willow ObjectClass, containing 5 categories and all instances in same class share 10 distinct image keypoints, is easier than PASCAL VOC keypoint for the GM task. The results are given in Table 3. We see that our bidirectional methods outperform their corresponding feedforward baselines, which is consistent with the results in Table 1. In particular, the mean accuracy of IA-NGM is $10\%$ higher than NGM. Although the mean accuracy of NGM-v2 is already very high at $97.5\%$, IA-NGM-v2 still improves by a $1\%$ increment to $98.5\%$. IA-NGM and IA-NGM-v2 are again separately better than IA-GM-v1 and IA-GM-v2, consistently indicating that our gated feature fusion scheme is more effective than the fusion scheme in Zhao et al. (2021).

4.3 Results on IMC-PT-SparseGM

IMC-PT-SparseGM is developed based on Image Matching Challenge dataset (Jin et al., 2021), which contains 16 classes of images of popular landmarks. We use 3 classes for testing and the others for training. Due to the limit of memory, we set the batch size to 2. The results in Table 4 again confirm the advantages of our bidirectional learning methods over the feedforward baselines. Both IA-NGM-v2 and IA-GM-v2 outperform NGM-v2, while IA-NGM-v2 achieves the highest mean matching accuracy.

Table 4 Matching accuracy (%) on IMC-PT-SparseGM

4.4 Results on CUB2011

The CUB2011 dataset by Wah et al. (2011) contains 11788 images of 200 subcategories belonging to birds, 5994 for training and 5794 for testing. Detailed annotations are provided for each image, including its subcategory label, 15 part locations, 312 binary attributes and 1 bounding box. Unlike other datasets we used, all images of CUB2011 are regarded as one class only. The matching accuracies are reported in Table 5. We can find that the bidirectional method IA-NGM-v2 improves the accuracy by about $1.1\%$ over NGM-v2, while IA-NGM is slightly better than NGM.

Table 5 Matching accuracy (%) on CUB2011

To summarize the results on the four image datasets, i.e., PASCAL VOC keypoint, Willow ObjectClass, IMC-PT-SparseGM, and CUB2011, our bidirectional learning methods IA-NGM and IA-NGM-v2 are both able to improve the matching performance with respect to their baselines NGM or NGM-v2. Generally, the NGM/NGM-v2 based formulations of GM in the form of Lawler’s QAP is relatively more powerful than the relaxed linear assignment version and IA-NGM-v2 is the best for all four datasets.

4.5 Results on QAPLIB

We also evaluate our bidirectional learning method for pure QAP tasks on QAPLIB benchmark,² in comparisions with RRWM (Cho et al., 2010), SM (Leordeanu & Hebert, 2005), SK-JA (Kushinsky et al., 2019) and NGM/NGM-G5k (Wang et al., 2021). As the affinity matrix of pure QAP instances are constructed using Kronecker product rather than features of images, our feature fusion method is not applicable. Therefore, we just try one sharping method like Eq. (9), regarding the input matrix as feature map. The final solution is obtained using the original input after three IA-alternations during training. Due to the limit of memory, we can only run experiments on 100 instances, and the settings are different from NGM-G5k’s suggested settings. We train one model for each category, and use the normalized objective score (lower is better) as the evaluation metric, i.e.,

$$\begin{aligned} norm\_score=\frac{solved\_score-upper\_bnd}{SM\_score-upper\_bnd}, \end{aligned}$$

(16)

where the upper bound (primal bound) is provided by the up-to-date online benchmark, and the baseline solver is given by SM (Leordeanu & Hebert, 2005).

In spite of these difficulties, our method still gets lower objective scores on 45 instances than NGM-G5k according to Table 10 in the Appendix 1. Examples of the results are visualized in Fig. 4. It is noted that the result on kra32 is abnormal. We have checked the data, and find that the data might be problematic, because the ground truth objective score cannot be obtained by the ground truth solution and two input matrices. Meanwhile, although the data of ste36a has the same problem, its result is normal. We also found the orders of two input matrice of the kronecker product of several instances are reversed which seems have little influence on the result.

Fig. 4

Normalized objective score (lower is better) of different methods on selected QAP instances due to the space limit. The instances are sorted by alphabet order

4.6 Study on variants of our method

In this section, we investigate the performances of different variants of our bidirectional method, to explain why we choose the linear mixture as our feature fusion technique for NGM’s neural network solver and why we choose the soft assignment matrix ${\mathbf {P}}$ for feature fusion rather than the hard assignment matrix ${\mathbf {X}}$.

Table 6 Matching accuracy (%) on PASCAL VOC keypoint when choosing different numbers of IA-alternation

Table 6 provides the results of experiments on the choice of the number of IA-alternations of IA-NGM. To avoid the over-smoothing problem, we only vary the number of IA-alternations from 2 to 4. We observe that the model of 3 IA-alternations achieves the highest performances.

4.6.1 Exploration on IA-alternation and feature fusion technique

We have tried several ways of feature fusion, including the linear mixture, concatenation, and the combination of these two approaches. The mean matching accuracies are reported in Table 7, which also includes the results when the number of IA-alternation varies. We observe that most feature fusion models improve the performance except for the case of 7 IA-alternations and linear mixture, which leads to the over-smoothing problem. The input feature is fused in every IA-alternation, and after too many times of IA-alternation, the features of nodes and edges tend to be close to each other due to the GNN used in the neural network solver, where all the nodes share the same transition function and the same output function (Uwents et al., 2011). From the second and the third row, we can see that the linear mixture outperforms the concatenation by 1.33%, and from the third and the last row, we can find that the linear mixture also outperforms the combination method. Therefore, we choose the linear mixture for feature fusion in IA-NGM, and also in IA-NGM-v2 for consistency.

Table 7 Matching accuracy (%) on PASCAL VOC keypoint

Meanwhile, the choice of $\alpha$ in Eq. (10) is important, as it affects the influence of pseudo features on affinity learning. Inappropriate value may cause the fused features to deviate from the original correct one. As the learning proceeds, the uncertainty conveyed in pseudo features gradually changes. Therefore, a fixed $\alpha$ may limit the performance of the model. As in Table 8, the case of determining $\alpha$ via a learnable gating network can adapt the learning dynamics well and outperforms the case of fixing $\alpha$ at a certain constant.

Table 8 Matching accuracy (%) on four image datasets when choosing different fusion weights while the number of IA-alternations is $K=2$

4.6.2 Choice of feedback matrix

Table 9 shows the average testing accuracies of the first ten epochs on PASCAL VOC keypoint of IA-NGM using the soft assignment matrix ${\mathbf {P}}$ or the hard assignment matrix ${\mathbf {X}}$ for feature fusion. It is found that IA-NGM using ${\mathbf {P}}$ learns faster and better than IA-NGM using ${\mathbf {X}}$. As a result, we choose ${\mathbf {P}}$ for feature fusion in IA-NGM and also in IA-NGM-v2.

Table 9 Average accuracy on PASCAL VOC of IA-NGM using ${\mathbf {P}}$ or ${\mathbf {X}}$ for feature fusion

5 Conclusion

We have proposed a deep bidirectional learning method named IA-NGM for graph matching problem. Our method is featured by an IA-alternation of a learning component for affinity learning and an optimization component that produces feedback via feature fusion into the affinity learning. The feedback is leveraged to construct the feature maps by a gated feature fusion of not only raw features directly extracted from images, but also pseudo features that convey the deviation information of the current optimization output from the ground-truth optimum. We devise a gating network to instruct the feature fusion based on the global features of two graphs, and the gating network adapts to the learning dynamics well for improved performance. Experimental results on benchmark datasets indicate that our method can fit two different neural network solvers appropriately, and demonstrate that the bidirectional learning scheme is effective to further improve the matching accuracies. Last but not least, we also find that our bidirectional learning fashion can be applied effectively on pure QAP tasks of QAPLIB benchmark, and there is still room for further improvement.

Appendix 1

1.1 Detailed results on QAPLIB

See Table 10.

Table 10 Per-instance results by objective score (lower is better) on QAPLIB